Depletion Interactions at Interfaces Induced by Ferromagnetic Colloidal Polymers
Abstract
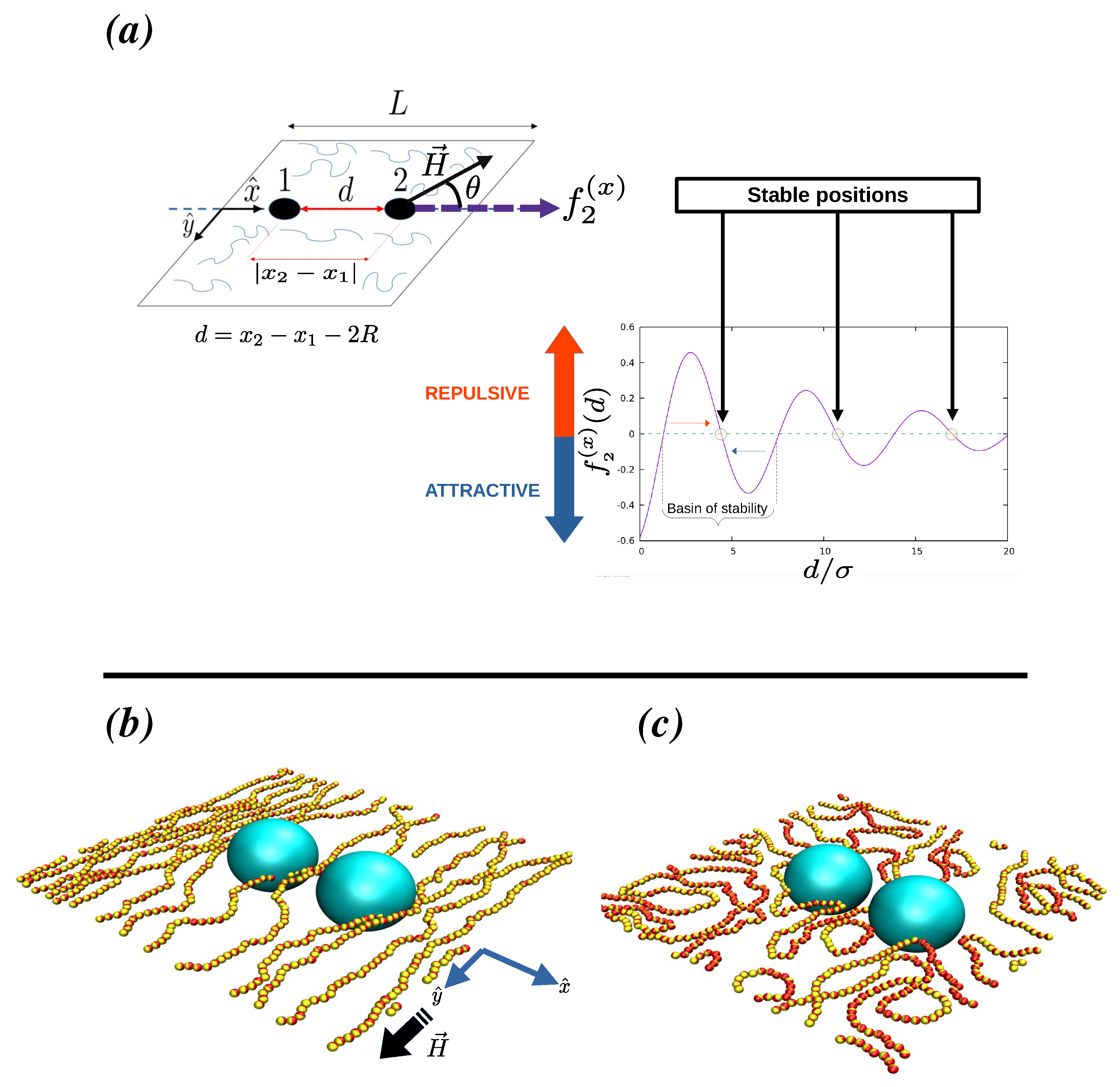
1. Introduction
2. Numerical Method
3. Results and Discussion
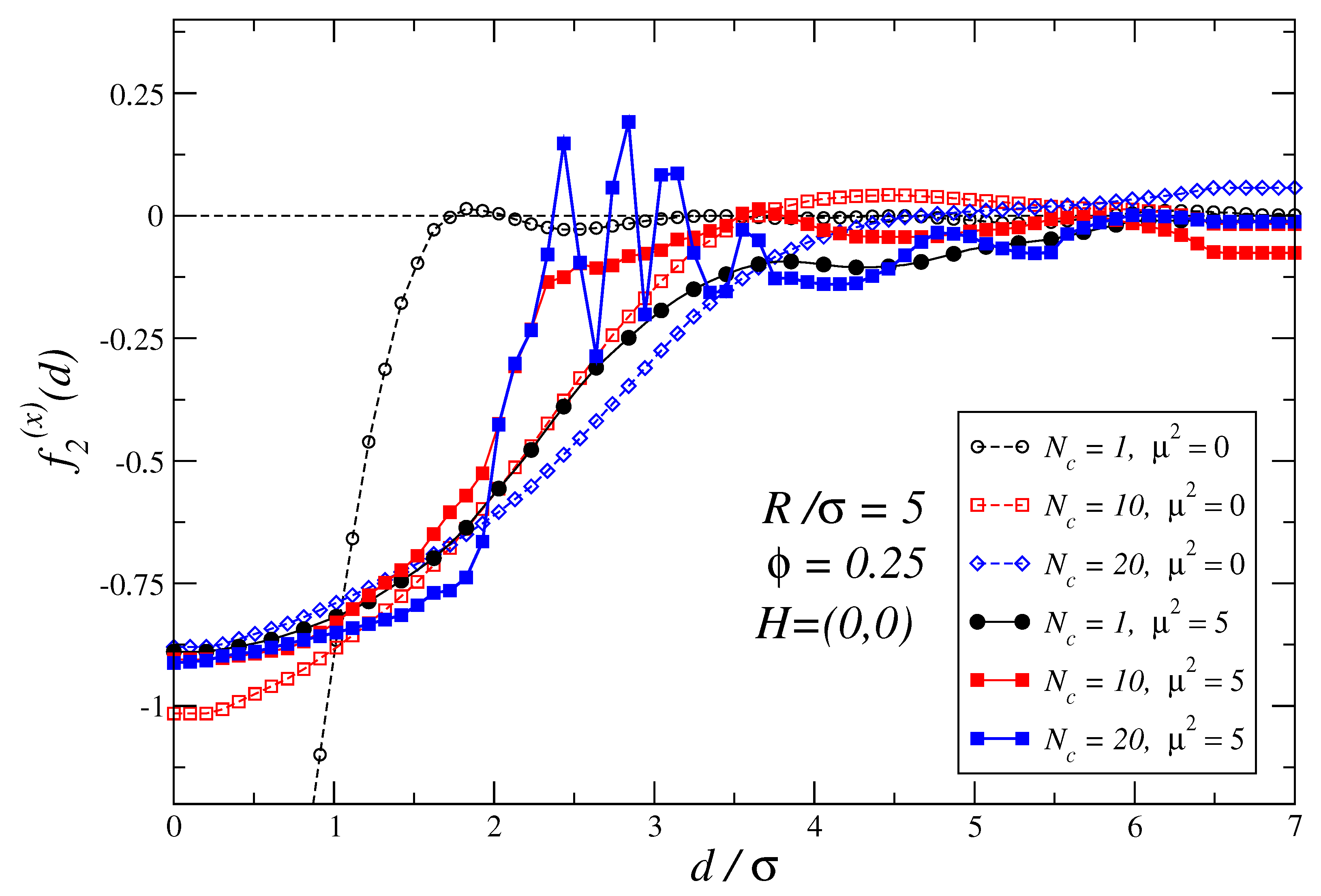
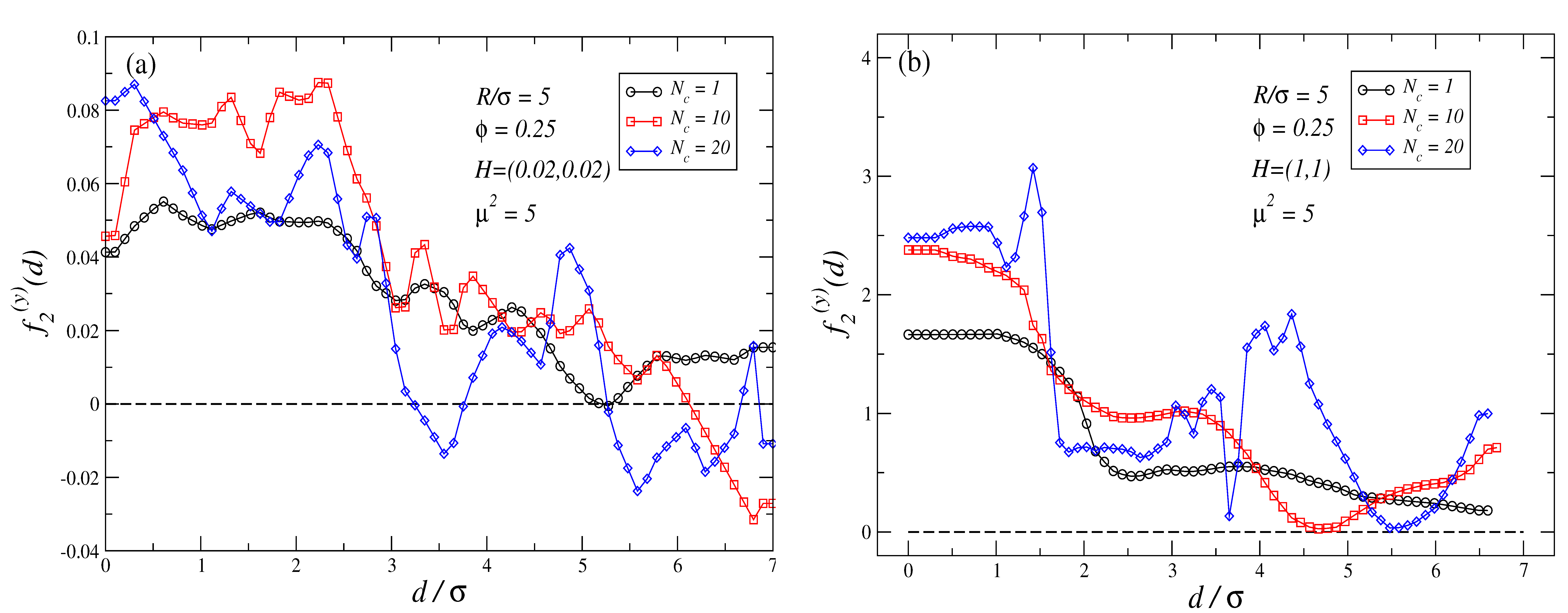
3.1. Force Profiles for
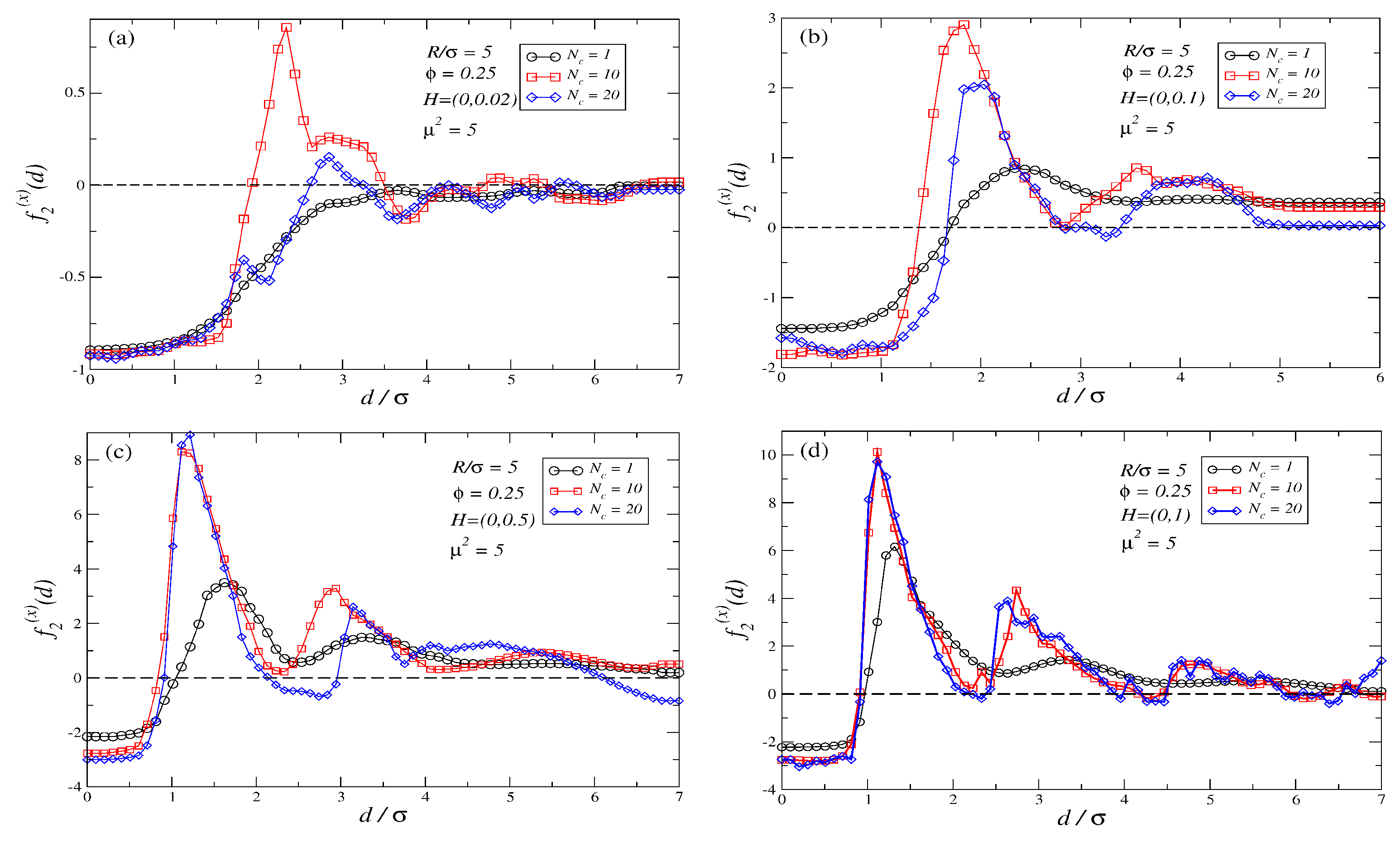
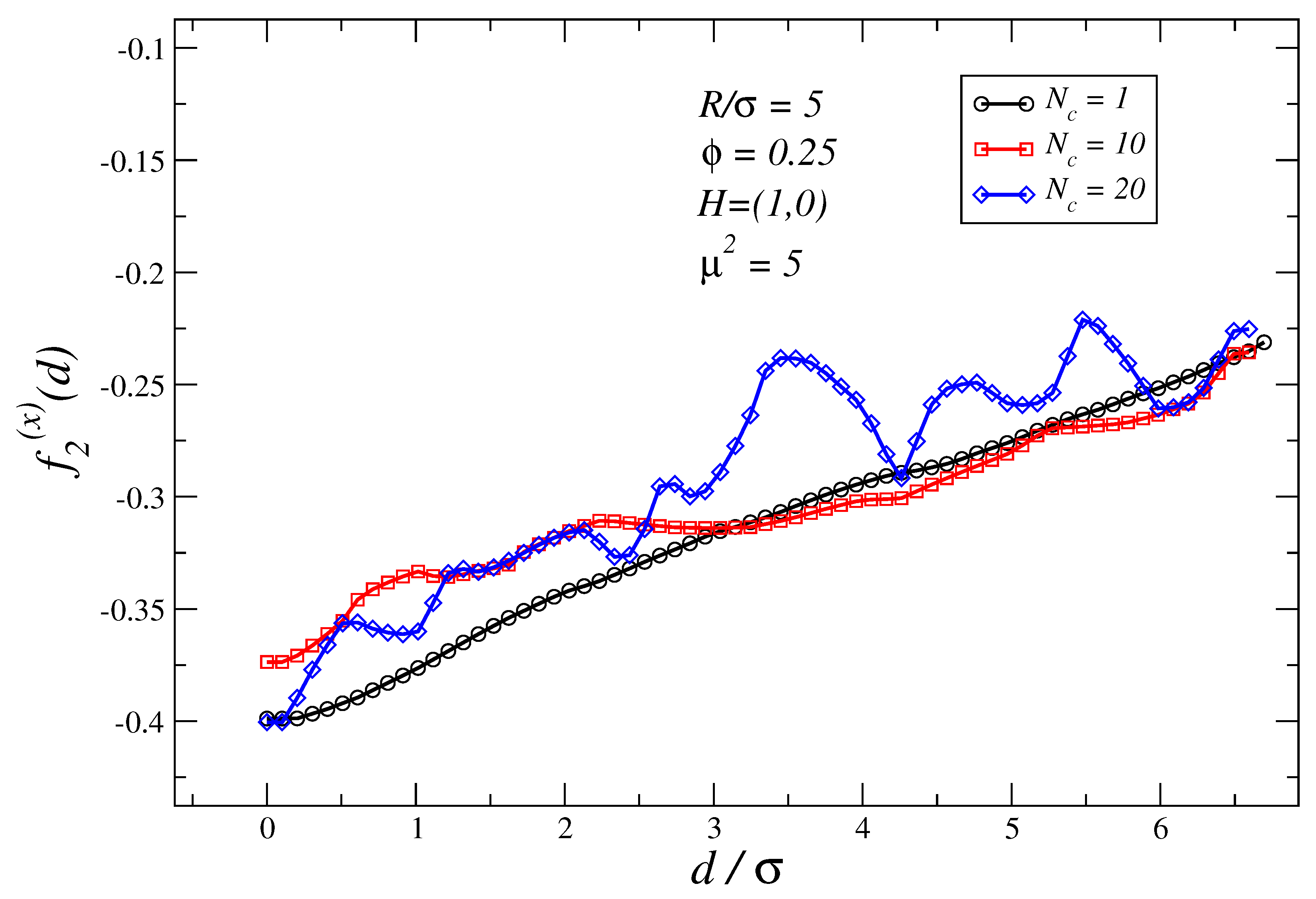
3.2. Force Profiles for
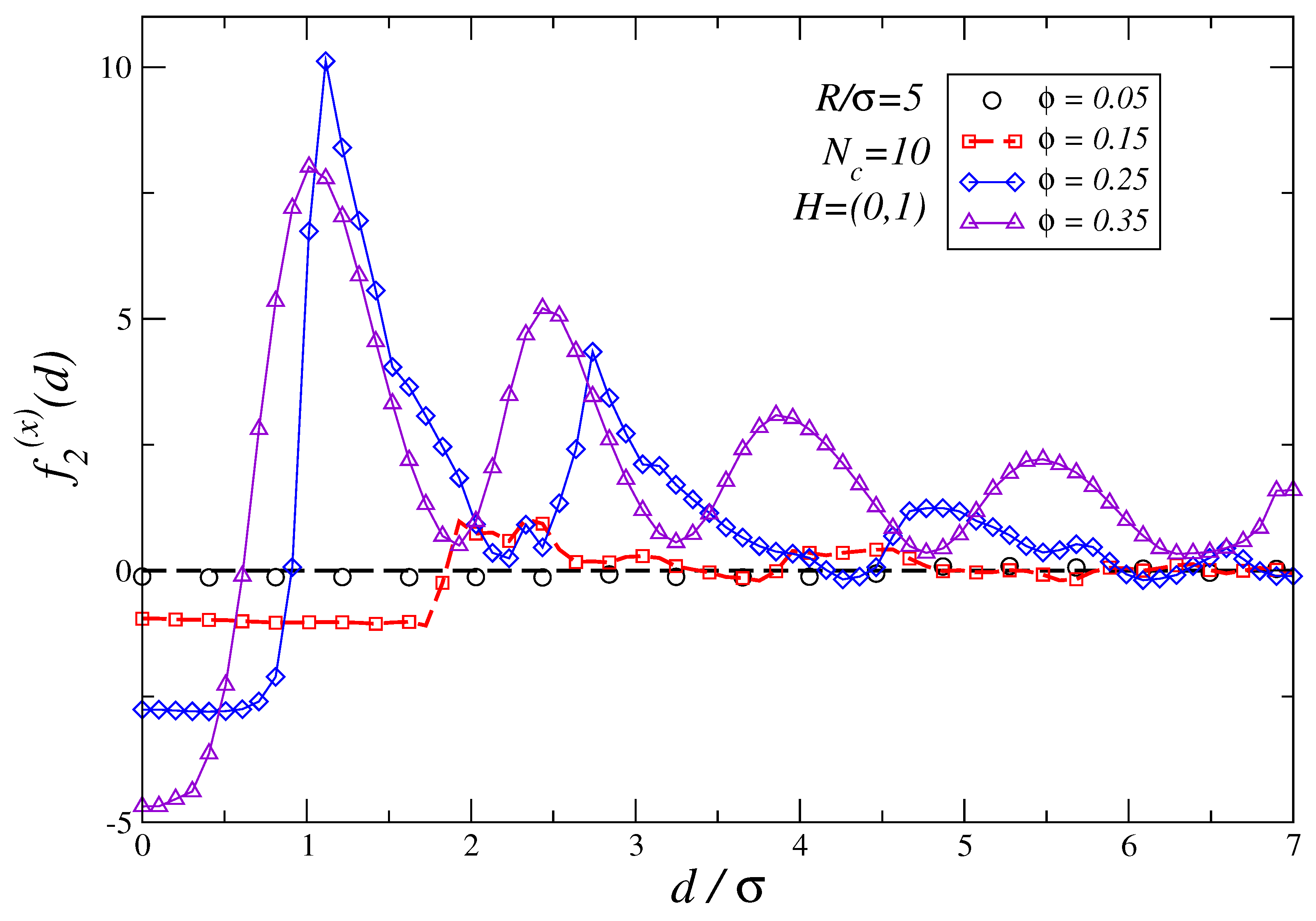
3.3. Dependence of the Force Profiles on and
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hunter, R. Introduction to Modern Colloid Science; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Russel, W.; Russel, W.; Saville, D.; Schowalter, W. Colloidal Dispersions; Cambridge Monographs on Mechanics; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Lekkerkerker, H.; Tuinier, R. Colloids and the Depletion Interaction; Lecture notes in physics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Fahraeus, R. The suspension stability of blood. Physiol. Rev. 1929, 9, 241. [Google Scholar] [CrossRef]
- Traube, J. Konzentrierung von kautschukmilchsften. Gummi Zeitung 1925, 39, 434. [Google Scholar]
- Sharma, A.; Walz, J.Y. Direct measurement of the depletion interaction in a charged colloidal dispersion. J. Chem. Soc.—Faraday Trans. 1996, 92, 4997–5004. [Google Scholar] [CrossRef]
- Helden, L.; Roth, R.; Koenderink, G.H.; Leiderer, P.; Bechinger, C. Direct Measurement of Entropic Forces Induced by Rigid Rods. Phys. Rev. Lett. 2003, 90, 048301. [Google Scholar] [CrossRef]
- Kleshchanok, D.; Tuinier, R.; Lang, P.R. Depletion Interaction Mediated by a Polydisperse Polymer Studied with Total Internal Reflection Microscopy. Langmuir 2006, 22, 9121–9128. [Google Scholar] [CrossRef][Green Version]
- Xing, X.; Hua, L.; Ngai, T. Depletion versus stabilization induced by polymers and nanoparticles: The state of the art. Curr. Opin. Colloid Interface Sci. 2015, 20, 54–59. [Google Scholar] [CrossRef]
- Ohshima, Y.; Sakagami, H.; Okumoto, K.; Tokoyoda, A.; Igarashi, T.; Shintaku, B.; Toride, S.; Sekino, H.; Kabuto, K.; Nishio, I. Direct measurement of infinitesimal depletion force in a colloid-polymer mixture by laser radiation pressure. Phys. Rev. Lett. 1997, 78, 3963–3966. [Google Scholar] [CrossRef]
- Milling, A.; Biggs, S. Direct Measurement of the Depletion Force Using an Atomic Force Microscope. J. Colloid Interface Sci. 1995, 170, 604–606. [Google Scholar] [CrossRef]
- Richetti, P.; Kékicheff, P. Direct measurement of depletion and structural forces in a micellar system. Phys. Rev. Lett. 1992, 68, 1951–1954. [Google Scholar] [CrossRef]
- Dimitrova, T.D.; Leal-Calderon, F. Forces between emulsion droplets stabilized with Tween 20 and proteins. Langmuir 1999, 15, 8813–8821. [Google Scholar] [CrossRef]
- Kleshchanok, D.; Tuinier, R.; Lang, P.R. Direct measurements of polymer-induced forces. J. Phys. Condens. Matter 2008, 20, 073101. [Google Scholar] [CrossRef]
- Tuinier, R.; Rieger, J.; de Kruif, C. Depletion-induced phase separation in colloid–polymer mixtures. Adv. Colloid Interface Sci. 2003, 103, 1–31. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. On Interaction between Two Bodies Immersed in a Solution of Macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Joanny, J.F.; Leibler, L.; De Gennes, P.G. Effects of polymer solutions on colloid stability. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1073–1084. [Google Scholar] [CrossRef]
- Feigin, R.I.; Napper, D.H. Depletion stabilization and depletion flocculation. J. Colloid Interface Sci. 1980, 75, 525–541. [Google Scholar] [CrossRef]
- Scheutjens, J.M.H.M.; Fleer, G.J. Statistical theory of the adsorption of interacting chain molecules. 1. Partition function, segment density distribution, and adsorption isotherms. J. Phys. Chem. 1979, 83, 1619–1635. [Google Scholar] [CrossRef]
- De Hek, H.; Vrij, A. Interactions in mixtures of colloidal silica spheres and polystyrene molecules in cyclohexane: I. Phase separations. J. Colloid Interface Sci. 1981, 84, 409–422. [Google Scholar] [CrossRef]
- Gast, A.; Hall, C.; Russel, W. Polymer-induced phase separations in nonaqueous colloidal suspensions. J. Colloid Interface Sci. 1983, 96, 251–267. [Google Scholar] [CrossRef]
- Taniguchi, T.; Kawakatsu, T.; Kawasaki, K. Concentration profile of polymers near a spherical surface. AIP Conf. Proc. 1992, 256, 503–504. [Google Scholar]
- E. Eisenriegler, A.; Hanke, S.D. Polymers interacting with spherical and rodlike particles. Phys. Rev. E 1996, 54, 1134. [Google Scholar] [CrossRef] [PubMed]
- Lekkerkerker, H. Osmotic equilibrium treatment of the phase separation in colloidal dispersions containing non-adsorbing polymer molecules. Colloids Surfaces 1990, 51, 419. [Google Scholar] [CrossRef]
- Roth, R.; Evans, R.; Dietrich, S. Depletion potential in hard-sphere mixtures: Theory and applications. Phys. Rev. E 2000, 62, 5360–5377. [Google Scholar] [CrossRef] [PubMed]
- Brader, J.; Evans, R. The fluid-fluid interface of a model colloid-polymer mixture. Europhys. Lett. 2000, 49, 678. [Google Scholar] [CrossRef]
- Schmidt, M.; Luffdwen, H.; Brader, J.M.; Evans, R. Condens. J. Phys. Condes. Matter 2002, 14, 9353. [Google Scholar] [CrossRef]
- Dzubiella, J.; Likos, C.N.; Luffdwen, H. Phase behavior and structure of star-polymer-colloid mixture. J. Chem. Phys. 2002, 116, 9518. [Google Scholar] [CrossRef][Green Version]
- Likos, C. Effective interactions in soft condensed matter physics. Phys. Rep. 2001, 348, 267–439. [Google Scholar] [CrossRef]
- Louis, A.; Bolhuis, P.; Hansen, J.; Meijer, E. Can Polymer Coils be modeled as Soft Colloids? Phys. Rev. Lett. 2000, 85, 2522. [Google Scholar] [CrossRef] [PubMed]
- Bolhuis, P.; Louis, A. How to derive and parametrize effective potentials in colloid-polymr mixtures. Macromolecules 2002, 35, 1860. [Google Scholar] [CrossRef]
- Louis, A.; Bolhuis, P.; Meijer, E.; Hansen, J.P. Polymer induced depletion potentials in polymer-colloid mixtures. J. Chem. Phys. 2002, 117, 1893. [Google Scholar] [CrossRef]
- Hu, S.W.; Sheng, Y.J.; Tsao, H.K. Depletion-induced size fractionation of nanorod dispersions. Soft Matter 2013, 9, 7261–7266. [Google Scholar] [CrossRef]
- Mao, Y.; Cates, M.E.; Lekkerkerker, H.N.W. Depletion Stabilization by Semidilute Rods. Phys. Rev. Lett. 1995, 75, 4548–4551. [Google Scholar] [CrossRef]
- Lang, P.R. Depletion interaction mediated by polydisperse rods. J. Chem. Phys. 2007, 127, 124906. [Google Scholar] [CrossRef]
- De Sio, S.; July, C.; Dhont, J.K.G.; Lang, P.R. Near wall dynamics of a spherical particle in crowded suspensions of colloidal rods—Dynamic information from TIRM revisited. Soft Matter 2018, 14, 9232–9242. [Google Scholar] [CrossRef]
- Buitenhuis, J.; Donselaar, L.N.; Buining, P.A.; Stroobants, A.; Lekkerkerker, H.N.W. Phase Separation of Mixtures of Colloidal Boehmite Rods and Flexible Polymer. J. Colloid Interface Sci. 1995, 175, 46. [Google Scholar] [CrossRef]
- Dogic, Z.; Purdy, K.R.; Grelet, E.; Adams, M.; Fraden, S. Isotropic-Nematic Phase transition in suspensions of filamentous virus and the neutral polymer Dextran. Phys. Rev. E 2004, 69, 051702. [Google Scholar] [CrossRef] [PubMed]
- July, C.; Kleshchanok, D.; Lang, P.R. Depletion interactions caused by polydisperse, hard platelets. Soft Matter 2011, 7, 6444–6450. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. Interaction between particles suspended in solutions of macromolecules. J. Polym. Sci. 1958, 33, 183–192. [Google Scholar] [CrossRef]
- Bohmer, M.R.; Evers, O.A.; Scheutjens, J.M.H.M. Weak polyelectrolytes between two surfaces: Adsorption and stabilization. Macromolecules 1990, 23, 2288–2301. [Google Scholar] [CrossRef]
- Ferreira, P.G.; Dymitrowska, M.; Belloni, L. Mixtures of charged colloids and nonadsorbing flexible polyelectrolytes: An integral equation study. J. Chem. Phys. 2000, 113, 9849–9862. [Google Scholar] [CrossRef]
- Ojeda-Mendoza, G.J.; Moncho-Jordá, A.; González-Mozuelos, P.; Haro-Pérez, C.; Rojas-Ochoa, L.F. Evidence of electrostatic-enhanced depletion attraction in the structural properties and phase behavior of binary charged colloidal suspensions. Soft Matter 2018, 14, 1355–1364. [Google Scholar] [CrossRef]
- Peláez-Fernández, M.; Moncho-Jordá, A.; García-Jimeno, S.; Estelrich, J.; Callejas-Fernández, J. Role of the electrostatic depletion attraction on the structure of charged liposome-polymer mixtures. Phys. Rev. E 2012, 85, 051405. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Walz, J.Y. Interaction potentials between two colloidal particles surrounded by an extremely bidisperse particle suspension. J. Colloid Interface Sci. 2013, 394, 611–618. [Google Scholar] [CrossRef]
- Denton, A.R.; Schmidt, M. Mixtures of charged colloid and neutral polymer: Influence of electrostatic interactions on demixing and interfacial tension. J. Chem. Phys. 2005, 122, 244911. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Girard, M.; Shen, M.; Millan, J.A.; Olvera de la Cruz, M. Strong attractions and repulsions mediated by monovalent salts. Proc. Natl. Acad. Sci. USA 2017, 114, 11838–11843. [Google Scholar] [CrossRef]
- Wensink, H.H.; Lekkerkerker, H.N.W. Sedimentation and multi-phase equilibria in mixtures of platelets and ideal polymer. Europhys. Lett. 2004, 66, 125. [Google Scholar] [CrossRef]
- Harnau, L.; Dietrich, S. Bulk and wetting phenomena in a colloidal mixture of hard spheres and platelets. Phys. Rev. E 2005, 71, 011504. [Google Scholar] [CrossRef] [PubMed]
- Oversteegen, S.M.; Vonk, C.; Wijnhoven, J.E.G.J.; Lekkerkerker, H.N.W. Crystallization in settling mixtures of colloidal spheres and plates. Phys. Rev. E 2005, 71, 041406. [Google Scholar] [CrossRef]
- Wijmans, C.M.; Zhulina, E.B.; Fleer, G.J. Effect of Free Polymer on the Structure of a Polymer Brush and Interaction between Two Polymer Brushes. Macromolecules 1994, 27, 3238–3248. [Google Scholar] [CrossRef]
- Aarts, D.G.A.L.; Tuinier, R.; Lekkerkerker, H.N.W. Phase behavior or mixtures of colloidal spheres and excluded-volume polymer chains. J. Phys. Condens. Matter 2002, 14, 7551. [Google Scholar] [CrossRef]
- Tuinier, R.; Smith, P.A.; Poon, W.C.K.; Egelhaaf, S.U.; Aarts, D.G.A.L.; Lekkerkerker, H.N.W.; Fleer, G.J. Phase diagram for a mixture of colloids and polymers with equal size. Europhys. Lett. 2008, 82, 68002. [Google Scholar] [CrossRef]
- Fleer, G.J.; Tuinier, R. Analytical phase diagrams for colloids and non-adsorbing polymer. Adv. Colloid Interface Sci. 2008, 143, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Lajovic, A.; Tomšič, M.; Jamnik, A. Depletion effects in a mixture of hard and attractive colloids. J. Chem. Phys. 2009, 130, 104101. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Walz, J.Y. Depletion forces and flocculation with surfactants, polymers and particles—Synergistic effects. Curr. Opin. Colloid Interface Sci. 2015, 20, 39–45. [Google Scholar] [CrossRef]
- Liu, S.; Hu, Y.; Xia, J.; Fang, S.; Duan, M. In Situ Measurement of Depletion Caused by SDBS Micelles on the Surface of Silica Particles Using Optical Tweezers. Langmuir 2019, 35, 13536–13542. [Google Scholar] [CrossRef] [PubMed]
- Ilg, P. Importance of depletion interactions for structure and dynamics of ferrofluids. Eur. Phys. J. E 2008, 26, 169–176. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chen, K.; Ma, Y.Q. Interactions between Colloidal Particles Induced by Polymer Brushes Grafted onto the Substrate. J. Phys. Chem. B 2005, 109, 17617–17622. [Google Scholar] [CrossRef][Green Version]
- Santos, A.; López de Haro, M.; Fiumara, G.; Saija, F. The effective colloid interaction in the Asakura–Oosawa model. Assessment of non-pairwise terms from the virial expansion. J. Chem. Phys. 2015, 142, 224903. [Google Scholar] [CrossRef]
- Woodward, C.E.; Forsman, J. A Many-Body Hamiltonian for Nanoparticles Immersed in a Polymer Solution. Langmuir 2015, 31, 22–26. [Google Scholar] [CrossRef]
- Glaser, J.; Karas, A.S.; Glotzer, S.C. A parallel algorithm for implicit depletant simulations. J. Chem. Phys. 2015, 143, 184110. [Google Scholar] [CrossRef]
- Chervanyov, A.I.; Heinrich, G. Potential theory of the depletion interaction in the colloid-polymer mixtures. J. Chem. Phys. 2009, 131, 234907. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Wan, H.; Xu, D.; Dai, X.; Li, G.; Yan, L.T. Hydrodynamic Anisotropy of Depletion in Nonequilibrium. Phys. Rev. Lett. 2023, 131, 134002. [Google Scholar] [CrossRef]
- Gong, X.J.; Xing, X.C.; Wei, X.L.; Ngai, T. Direct measurement of weak depletion force between two surfaces. Chin. J. Polym. Sci. 2011, 29, 1–11. [Google Scholar] [CrossRef]
- Ghosh, S.; Pradhan, N.R.; Mashayekhi, H.; Dickert, S.; Thantirige, R.; Tuominen, M.T.; Tao, S.; Xing, B. Binary Short-Range Colloidal Assembly of Magnetic Iron Oxides Nanoparticles and Fullerene (nC60) in Environmental Media. Environ. Sci. Technol. 2014, 48, 12285–12291. [Google Scholar] [CrossRef]
- Ji, S.; Walz, J.Y. Depletion Flocculation Induced by Synergistic Effects of Nanoparticles and Polymers. J. Phys. Chem. B 2013, 117, 16602–16609. [Google Scholar] [CrossRef] [PubMed]
- Ji, S.; Walz, J.Y. Synergistic Effects of Nanoparticles and Polymers on Depletion and Structural Interactions. Langmuir 2013, 29, 15159–15167. [Google Scholar] [CrossRef] [PubMed]
- Meng, D.; Kumar, S.K.; Grest, G.S.; Mahynski, N.A.; Panagiotopoulos, A.Z. Reentrant equilibrium disordering in nanoparticle–polymer mixtures. Npj Comput. Mater. 2017, 3, 3. [Google Scholar] [CrossRef][Green Version]
- Briscoe, W.H. Depletion forces between particles immersed in nanofluids. Curr. Opin. Colloid Interface Sci. 2015, 20, 46–53. [Google Scholar] [CrossRef]
- Xing, X.; Li, Z.; Ngai, T. pH-Controllable Depletion Attraction Induced by Microgel Particles. Macromolecules 2009, 42, 7271–7274. [Google Scholar] [CrossRef]
- Zhang, H.; Kong, D.; Zhang, W.; Liu, H. Depletion attraction in colloidal and bacterial systems. Front. Mater. 2023, 10, 1206819. [Google Scholar] [CrossRef]
- Trokhymchuk, A.; Henderson, D. Depletion forces in bulk and in confined domains: From Asakura–Oosawa to recent statistical physics advances. Curr. Opin. Colloid Interface Sci. 2015, 20, 32–38. [Google Scholar] [CrossRef]
- Moncho-Jordá, A.; Odriozola, G. Wall–particle interactions and depletion forces in narrow slits. Curr. Opin. Colloid Interface Sci. 2015, 20, 24–31. [Google Scholar] [CrossRef]
- Curtis, R.A.; Lue, L. Depletion forces due to image charges near dielectric discontinuities. Curr. Opin. Colloid Interface Sci. 2015, 20, 19–23. [Google Scholar] [CrossRef]
- July, C.; Kleshchanok, D.; Lang, P.R. Shear-affected depletion interaction. Eur. Phys. J. E 2012, 35, 60. [Google Scholar] [CrossRef]
- Moncho-Jorda, A.; Louis, A.; Bolhuis, P.; Roth, R. The Asakura-Oosawa model in the protein limit: The role of many-body interactions. J. Phys. Condens. Matter 2003, 15, S3429. [Google Scholar] [CrossRef][Green Version]
- Bolhuis, P.; Meijer, E.; Louis, A. Colloid-Polymer Mixtures in the Protein Limit. Phys. Rev. Lett. 2003, 90, 068304. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; van Roij, R.; Roth, R.; Fortini, A. Effect of many-body interactions on the bulk and interfacial phase behavior of a model colloid-polymer mixture. Phys. Rev. E 2006, 73, 041404. [Google Scholar] [CrossRef]
- Fortini, A.; Bolhuis, P.; Dijkstra, M. Effect of excluded volume interactions on the interfacial properties of colloid-polymer mixtures. J. Chem. Phys. 2008, 128, 024904. [Google Scholar] [CrossRef] [PubMed]
- der Schoot, P.V. Protein-induced collapse of polymer chains. Macromolecules 1998, 31, 4635. [Google Scholar] [CrossRef]
- Fuchs, M.; Schweizer, K. Structure of colloid-polymer suspensions. J. Phys. Condens. Matter 2002, 14, R239. [Google Scholar] [CrossRef]
- Kim, S.C.; Seong, B.S.; Suh, S.H. Depletion interactions in two-dimensional colloid-polymer mixtures: Molecular dynamics simulations. J. Phys. Condens. Matter 2008, 21, 035101. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.S.; Szleifer, I. Depletion Effect on Polymers Induced by Small Depleting Spheres. J. Phys. Chem. C 2010, 114, 20864–20869. [Google Scholar] [CrossRef]
- Castañeda-Priego, R.; Rodríguez-López, A.; Méndez-Alcaraz, J.M. Depletion forces in two-dimensional colloidal mixtures. J. Phys. Condens. Matter 2003, 15, S3393. [Google Scholar] [CrossRef]
- Biben, T.; Bladon, P.; Frenkel, D. Depletion effects in binary hard-sphere fluids. J. Phys. Condens. Matter 1996, 8, 10799. [Google Scholar] [CrossRef]
- Fantoni, R.; Santos, A. Depletion force in the infinite-dilution limit in a solvent of nonadditive hard spheres. J. Chem. Phys. 2014, 140, 244513. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Ramírez, A.; Figueroa-Gerstenmaier, S.; Odriozola, G. Colloid-polymer mixtures under slit confinement. J. Chem. Phys. 2017, 146, 104903. [Google Scholar] [CrossRef] [PubMed]
- Rupprecht, N.; Vural, D.C. Depletion force between disordered linear macromolecules. Phys. Rev. E 2020, 101, 022607. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Zhang, D.; He, L.; Zhang, L. Entropic Interactions in Semiflexible Polymer Nanocomposite Melts. J. Phys. Chem. B 2016, 120, 572–582. [Google Scholar] [CrossRef]
- Handle, P.H.; Zaccarelli, E.; Gnan, N. Effective potentials induced by mixtures of patchy and hard co-solutes. J. Chem. Phys. 2021, 155, 064901. [Google Scholar] [CrossRef]
- Miao, H.; Li, Y.; Ma, H. Depletion interaction between two ellipsoids. J. Chem. Phys. 2014, 140, 154904. [Google Scholar] [CrossRef]
- Shendruk, T.N.; Bertrand, M.; Harden, J.L.; Slater, G.W.; de Haan, H.W. Coarse-grained molecular dynamics simulations of depletion-induced interactions for soft matter systems. J. Chem. Phys. 2014, 141, 244910. [Google Scholar] [CrossRef]
- Feng, F.; Lei, T.; Zhao, N. Tunable depletion force in active and crowded environments. Phys. Rev. E 2021, 103, 022604. [Google Scholar] [CrossRef]
- Fazelabdolabadi, B.; Walz, J.Y.; Van Tassel, P.R. Influence of Charged Nanoparticles on Colloidal Forces: A Molecular Simulation Study. J. Phys. Chem. B 2009, 113, 13860–13865. [Google Scholar] [CrossRef] [PubMed]
- Reščič, J. Effect of excluded volume and chain flexibility on depletion interaction between proteins. J. Mol. Liq. 2016, 219, 728–736. [Google Scholar] [CrossRef]
- Guo, J.-Y.; Xiao, C.-M. Grand Canonical Ensemble Monte Carlo Simulation of Depletion Interactions in Colloidal Suspensions. Chin. Phys. Lett. 2008, 25, 314. [Google Scholar] [CrossRef]
- Camargo, M.; Likos, C.N. Unusual Features of Depletion Interactions in Soft Polymer-Based Colloids Mixed with Linear Homopolymers. Phys. Rev. Lett. 2010, 104, 078301. [Google Scholar] [CrossRef] [PubMed]
- Rovigatti, L.; Gnan, N.; Parola, A.; Zaccarelli, E. How soft repulsion enhances the depletion mechanism. Soft Matter 2015, 11, 692–700. [Google Scholar] [CrossRef] [PubMed]
- Bertolini, D.; Cinacchi, G.; Tani, A. On the Distribution Functions of Depletion Interactions. J. Phys. Chem. B 2011, 115, 6608–6615. [Google Scholar] [CrossRef] [PubMed]
- De los Santos-López, N.M.; Pérez-Ángel, G.; Castañeda-Priego, R.; Méndez-Alcaraz, J.M. Determining depletion interactions by contracting forces. J. Chem. Phys. 2022, 157, 074903. [Google Scholar] [CrossRef]
- Zarif, M.; Naji, A. Confinement-induced alternating interactions between inclusions in an active fluid. Phys. Rev. E 2020, 102, 032613. [Google Scholar] [CrossRef]
- Zaeifi Yamchi, M.; Naji, A. Effective interactions between inclusions in an active bath. J. Chem. Phys. 2017, 147, 194901. [Google Scholar] [CrossRef]
- Leite, L.R.; Lucena, D.; Potiguar, F.Q.; Ferreira, W.P. Depletion forces on circular and elliptical obstacles induced by active matter. Phys. Rev. E 2016, 94, 062602. [Google Scholar] [CrossRef] [PubMed]
- Harder, J.; Mallory, S.A.; Tung, C.; Valeriani, C.; Cacciuto, A. The role of particle shape in active depletion. J. Chem. Phys. 2014, 141, 194901. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Liu, P.; Chen, K.; Zheng, N.; Yang, M. Active depletion torque between two passive rods. Soft Matter 2022, 18, 4265–4272. [Google Scholar] [CrossRef] [PubMed]
- Shendruk, T.; Bertrand, M.; de Haan, H.; Harden, J.; Slater, G. Simulating the Entropic Collapse of Coarse-Grained Chromosomes. Biophys. J. 2015, 108, 810–820. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; van Roij, R.; Evans, R. Direct Simulation of the Phase Behavior of Binary Hard-Sphere Mixtures: Test of the Depletion Potential Description. Phys. Rev. Lett. 1999, 82, 117–120. [Google Scholar] [CrossRef]
- Jungblut, S.; Tuinier, R.; Binder, K.; Schilling, T. Depletion induced isotropic-isotropic phase separation in suspensions of rod-like colloids. J. Chem. Phys. 2007, 127, 244909. [Google Scholar] [CrossRef]
- Wood, J.A.; Liu, Y.; Widmer-Cooper, A. Crystal nucleation in colloidal rod suspensions: The effect of depletant size. J. Chem. Phys. 2021, 154, 244505. [Google Scholar] [CrossRef]
- Cinacchi, G.; Martínez-Ratón, Y.; Mederos, L.; Navascués, G.; Tani, A.; Velasco, E. Large attractive depletion interactions in soft repulsive–sphere binary mixtures. J. Chem. Phys. 2007, 127, 214501. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, X.; Gao, L.; Xu, D.; Wan, H.; Wang, Y.; Yan, L.T. The entropy-controlled strategy in self-assembling systems. Chem. Soc. Rev. 2023, 52, 6806–6837. [Google Scholar] [CrossRef]
- Calero, C.; Pagonabarraga, I. Self-Assembly of Microscopic Rods Due to Depletion Interaction. Entropy 2020, 22, 1114. [Google Scholar] [CrossRef]
- Deng, Z.; Jiang, Y.; He, L.; Zhang, L. Aggregation–Dispersion Transition for Nanoparticles in Semiflexible Ring Polymer Nanocomposite Melts. J. Phys. Chem. B 2016, 120, 11574–11581. [Google Scholar] [CrossRef]
- Nehring, A.; Shendruk, T.N.; de Haan, H.W. Morphology of depletant-induced erythrocyte aggregates. Soft Matter 2018, 14, 8160–8171. [Google Scholar] [CrossRef] [PubMed]
- Cerdà, J.J.; Bona-Casas, C.; Cerrato, A.; Sintes, T.; Massó, J. Colloidal magnetic brushes: Influence of the magnetic content and presence of short-range attractive forces in the micro-structure and field response. Soft Matter 2021, 17, 5780–5791. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Warner, H.R., Jr. Kinetic Theory and Rheology of Dilute Suspensions of Finitely Extendible Dumbbells. Ind. Eng. Chem. Fundam. 1972, 11, 379–387. [Google Scholar] [CrossRef]
- Cerdà, J.J.; Ballenegger, V.; Lenz, O.; Holm, C. P3M algorithm for dipolar interactions. J. Chem. Phys. 2008, 129, 234104. [Google Scholar] [CrossRef]
- Arnold, A.; de Joannis, J.; Holm, C.J. Electrostatics in periodic slab geometries. J. Chem. 2002, 117, 2496. [Google Scholar] [CrossRef]
- Wang, Z.; Holm, C. Estimate of the cutoff errors in the Ewald summation for dipolar systems. J. Chem. 2001, 115, 6351. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 1st ed.; Oxford Science Publications; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Limbach, H.J.; Arnold, A.; Mann, B.A.; Holm, C. ESPResSo—An Extensible Simulation Package for Research on Soft Matter Systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Blügel, S.; Müller-Krumbhaar, H.; Winkler, R. Computational Condensed Matter Physics. Lecture Manuscripts of the 37th Spring School of the Institute of Solid State Reseach; Lecture notes; Forschungszentrum Jülich: Darmstadt, Germany, 2006. [Google Scholar]
- Cerdà, J.J.; Kantorovich, S.; Holm, C. Aggregate formation in ferrofluid monolayers: Simulations and theory. J. Phys. Condens. Matter 2008, 20, 204125. [Google Scholar] [CrossRef]
- Suwa, M.; Tsukahara, S.; Watarai, H. Applications of magnetic and electromagnetic forces in micro-analytical systems. Lab Chip 2023, 23, 1097–1127. [Google Scholar] [CrossRef]
- Skjeltorp, A.T. One- and Two-Dimensional Crystallization of Magnetic Holes. Phys. Rev. Lett. 1983, 51, 2306–2309. [Google Scholar] [CrossRef]
- Ramos, J.; Klingenberg, D.J.; Hidalgo-Alvarez, R.; de Vicente, J. Steady shear magnetorheology of inverse ferrofluids. J. Rheol. 2011, 55, 127–152. [Google Scholar] [CrossRef]
- Egorov, S.A. Depletion Interactions between Nanoparticles: The Effect of the Polymeric Depletant Stiffness. Polymers 2022, 14, 5398. [Google Scholar] [CrossRef] [PubMed]
- Martens, C.M.; Tuinier, R.; Vis, M. Depletion interaction mediated by semiflexible polymers. J. Chem. Phys. 2022, 157, 154102. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Pedrero, F. Static and dynamic behavior of magnetic particles at fluid interfaces. Adv. Colloid Interface Sci. 2020, 284, 102233. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Pedrero, F.; González-Banciella, A.; Camino, A.; Mateos-Maroto, A.; Ortega, F.; Rubio, R.G.; Pagonabarraga, I.; Calero, C. Static and Dynamic Self-Assembly of Pearl-Like-Chains of Magnetic Colloids Confined at Fluid Interfaces. Small 2021, 17, 2101188. [Google Scholar] [CrossRef]
- Vandewalle, N.; Obara, N.; Lumay, G. Mesoscale structures from magnetocapillary self-assembly. Eur. Phys. J. E 2013, 36, 127. [Google Scholar] [CrossRef]
- Gunatilake, U.B.; Morales, R.; Basabe-Desmonts, L.; Benito-Lopez, F. Magneto Twister: Magneto Deformation of the Water–Air Interface by a Superhydrophobic Magnetic Nanoparticle Layer. Langmuir 2022, 38, 3360–3369. [Google Scholar] [CrossRef]
- Yang, Y.; Fu, L.; Marcoux, C.; Socolar, J.E.S.; Charbonneau, P.; Yellen, B.B. Phase transformations in binary colloidal monolayers. Soft Matter 2015, 11, 2404–2415. [Google Scholar] [CrossRef] [PubMed]
- Lefebure, S.; Ménager, C.; Cabuil, V.; Assenheimer, M.; Gallet, F.; Flament, C. Langmuir Monolayers of Monodispersed Magnetic Nanoparticles Coated with a Surfactant. J. Phys. Chem. B 1998, 102, 2733–2738. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerdà, J.J.; Batle, J.; Bona-Casas, C.; Massó, J.; Sintes, T. Depletion Interactions at Interfaces Induced by Ferromagnetic Colloidal Polymers. Polymers 2024, 16, 820. https://doi.org/10.3390/polym16060820
Cerdà JJ, Batle J, Bona-Casas C, Massó J, Sintes T. Depletion Interactions at Interfaces Induced by Ferromagnetic Colloidal Polymers. Polymers. 2024; 16(6):820. https://doi.org/10.3390/polym16060820
Chicago/Turabian StyleCerdà, Joan Josep, Josep Batle, Carles Bona-Casas, Joan Massó, and Tomàs Sintes. 2024. "Depletion Interactions at Interfaces Induced by Ferromagnetic Colloidal Polymers" Polymers 16, no. 6: 820. https://doi.org/10.3390/polym16060820
APA StyleCerdà, J. J., Batle, J., Bona-Casas, C., Massó, J., & Sintes, T. (2024). Depletion Interactions at Interfaces Induced by Ferromagnetic Colloidal Polymers. Polymers, 16(6), 820. https://doi.org/10.3390/polym16060820






