Kinetics Study of PVA Polymer by Model-Free and Model-Fitting Methods Using TGA
Abstract
1. Introduction
2. Experimental Methods
2.1. PVA Material with TGA
2.2. Kinetic Equations Derivation
2.3. Thermodynamic Parameters of PET Pyrolysis
3. Results and Discussion
3.1. The TG Analysis
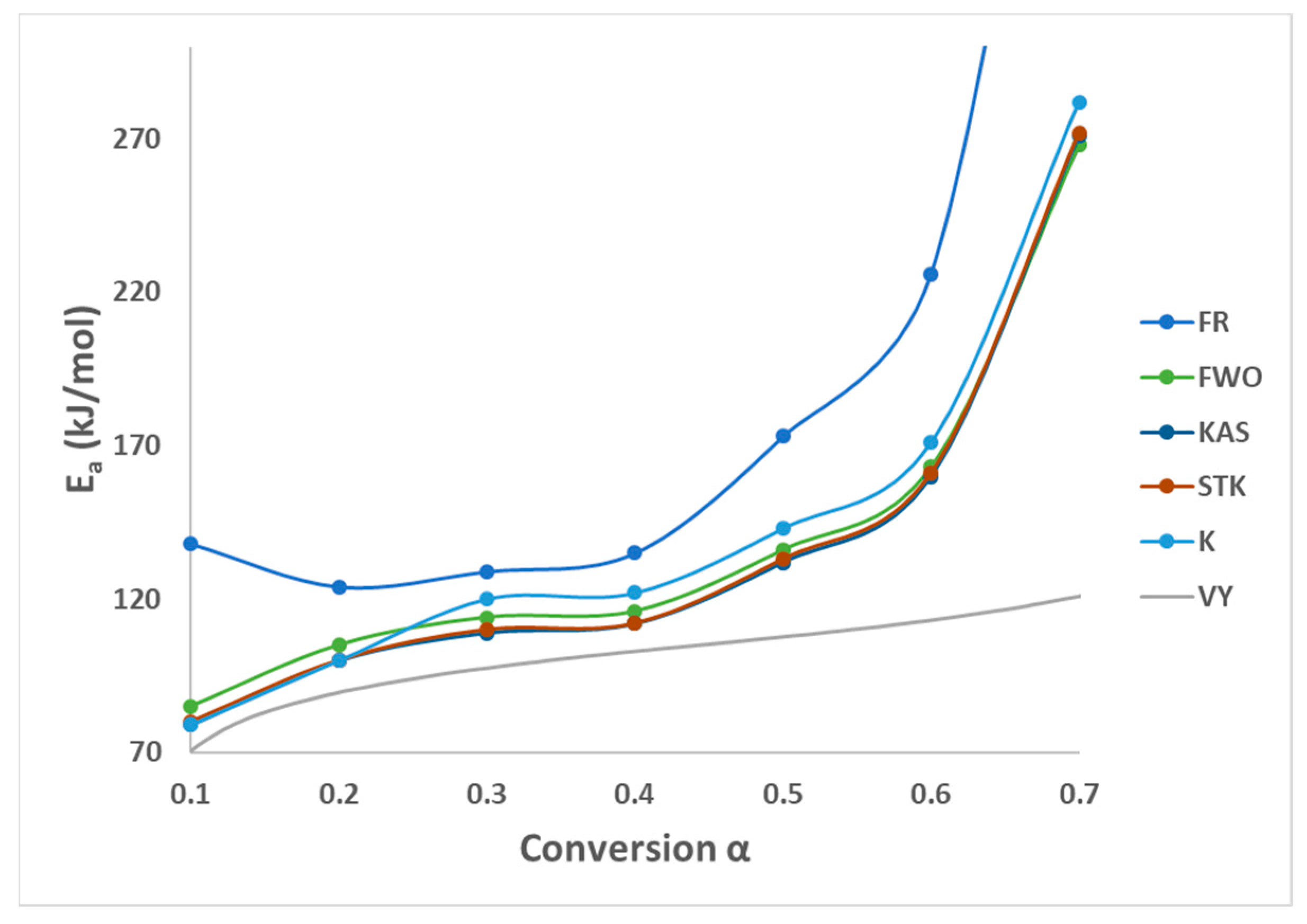
3.2. Model-Free Methods
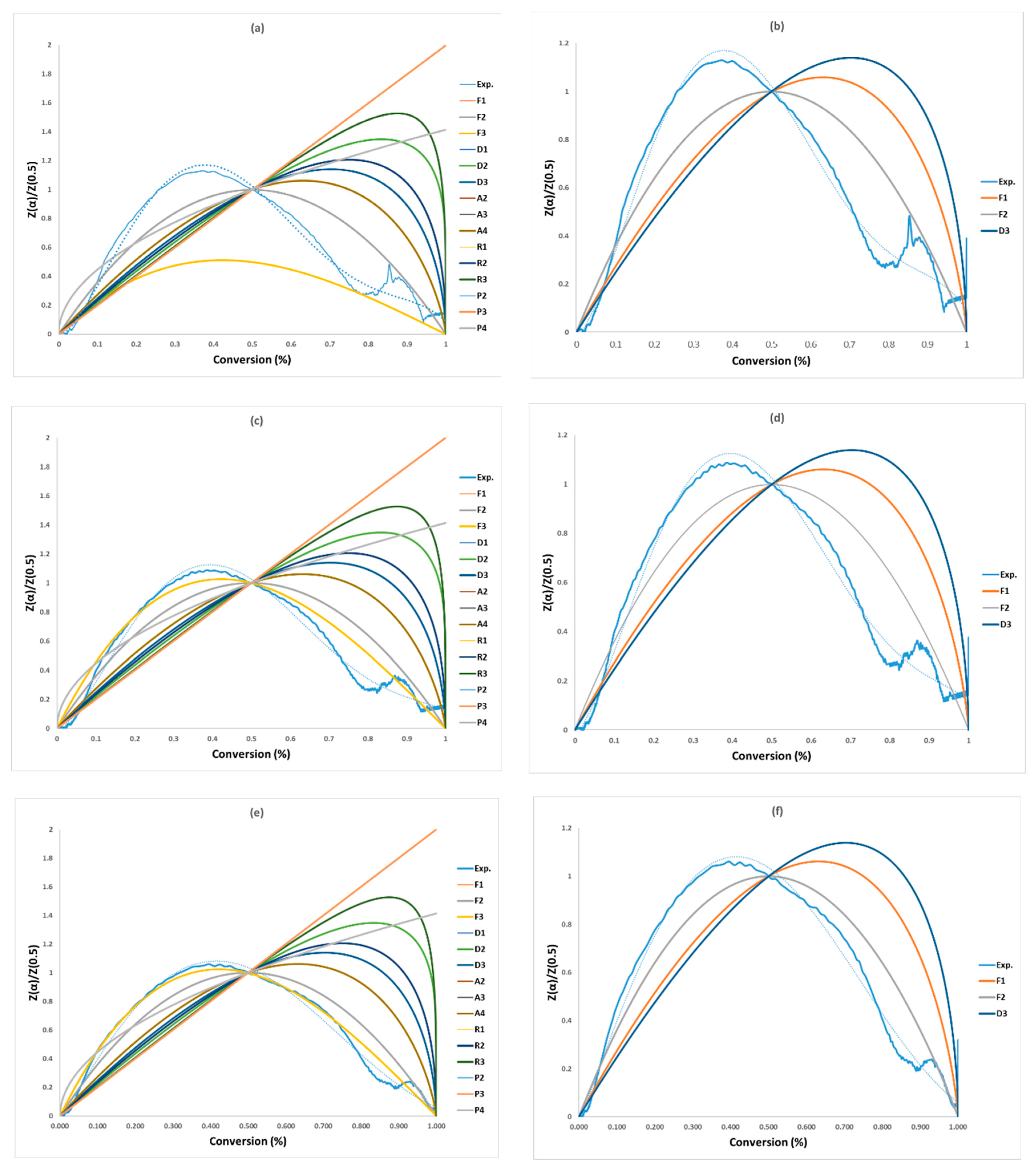
3.3. Model-Fitting Methods
3.4. Thermodynamic Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Abraham, A.; Soloman, P.A.; Rejini, V.O. Preparation of chitosan-polyvinyl alcohol blends and studies on thermal and mechanical properties. Procedia Technol. 2016, 24, 741–748. [Google Scholar] [CrossRef]
- George, J.; Sabapathi, S.N.; Siddaramaiah. Water soluble polymer-based nanocomposites containing cellulose nanocrystals. In Eco-Friendly Polymer Nanocomposites: Processing and Properties; Springer: Berlin/Heidelberg, Germany, 2015; pp. 259–293. [Google Scholar]
- Sarkodie, B.; Feng, Q.; Xu, C.; Xu, Z. Desizability and Biodegradability of Textile Warp Sizing Materials and Their Mechanism: A Review. J. Polym. Environ. 2023, 31, 3317–3337. [Google Scholar] [CrossRef]
- Patel, B.M.; Bhrambhatt, D. Nonwoven Technology; Textile Technology; M. S. University: Vadodara, India, 2008; pp. 1–54. [Google Scholar]
- Sheik, S.; Sheik, S.; Nairy, R.; Nagaraja, G.K.; Prabhu, A.; Rekha, P.D.; Prashantha, K. Study on the morphological and biocompatible properties of chitosan grafted silk fibre reinforced PVA films for tissue engineering applications. Int. J. Biol. Macromol. 2018, 116, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, P.; Niazi, M.B.K.; Jahan, Z.; Rafiq, S.; Ahmad, T.; Sikander, U.; Javaid, F. Improving functional properties of PVA/starch-based films as active and intelligent food packaging by incorporating propolis and anthocyanin. Polym. Polym. Compos. 2021, 29, 1472–1484. [Google Scholar] [CrossRef]
- Channa, I.A.; Ashfaq, J.; Gilani, S.J.; Chandio, A.D.; Yousuf, S.; Makhdoom, M.A.; Jumah, M.N.B. Sustainable and Eco-Friendly Packaging Films Based on Poly (Vinyl Alcohol) and Glass Flakes. Membranes 2022, 12, 701. [Google Scholar] [CrossRef]
- Cascone, S.; Lamberti, G. Hydrogel-based commercial products for biomedical applications: A review. Int. J. Pharm. 2020, 573, 118803. [Google Scholar] [CrossRef] [PubMed]
- Kamoun, E.A.; Kenawy, E.R.S.; Chen, X. A review on polymeric hydrogel membranes for wound dressing applications: PVA-based hydrogel dressings. J. Adv. Res. 2017, 8, 217–233. [Google Scholar] [CrossRef]
- Thong, C.C.; Teo, D.C.L.; Ng, C.K. Application of polyvinyl alcohol (PVA) in cement-based composite materials: A review of its engineering properties and microstructure behavior. Constr. Build. Mater. 2016, 107, 172–180. [Google Scholar] [CrossRef]
- Kazaryan, R.; Khvan, V. Environmentally friendly building materials for residential high-rise construction. In E3S Web of Conferences; EDP Sciences: Les Ulis Cedex A, France, 2019; Volume 91, p. 02008. [Google Scholar]
- Asthana, N.; Pal, K.; Aljabali, A.A.; Tambuwala, M.M.; de Souza, F.G.; Pandey, K. Polyvinyl alcohol (PVA) mixed green–clay and aloe vera based polymeric membrane optimization: Peel-off mask formulation for skin care cosmeceuticals in green nanotechnology. J. Mol. Struct. 2021, 1229, 129592. [Google Scholar] [CrossRef]
- Islam, M.S. Polyvinyl Alcohol and Polyvinyl Acetate. In Industrial Applications of Biopolymers and Their Environmental Impact; CRC: Boca Raton, FL, USA, 2020; pp. 135–152. [Google Scholar]
- de Oliveira, M.J.S.; Bezerra, M.V.F.; Loiola, R.A.; de Lima, G.S.; da Rocha, G.H.O.; de Oliveira, R.T.D.; Barioni, É.D. Effects of slime toy poisoning in children and teenagers. Rev. Paul. De Pediatria. 2022, 41, e2021357. [Google Scholar] [CrossRef]
- Yan, X.; Fang, J.; Gu, J.; Zhu, C.; Qi, D. Flame Retardancy, Thermal and Mechanical Properties of Novel Intumescent Flame Retardant/MXene/Poly (Vinyl Alcohol) Nanocomposites. Nanomaterials 2022, 12, 477. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Chen, Z.; Bian, H. A combined kinetic analysis for thermal characteristics and reaction mechanism based on non-isothermal experiments: The case of poly(vinyl alcohol) pyrolysis. Therm. Sci. Eng. Prog. 2023, 39, 101692. [Google Scholar] [CrossRef]
- Mittal, A.; Garg, S.; Bajpai, S. Thermal decomposition kinetics and properties of grafted barley husk reinforced PVA/starch composite films for packaging applications. Carbohydr. Polym. 2020, 240, 116225. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Liu, Y.; Li, T.; Ma, P.; Bai, H.; Xie, Y.; Chen, M.; Dong, W. Structure and thermal behaviors of poly(vinyl alcohol)/surfactant composites: Investigation of molecular interaction and mechanism. Polym. Adv. Technol. 2018, 29, 2224–2229. [Google Scholar] [CrossRef]
- Radoor, S.; Kandel, D.R.; Park, K.; Jayakumar, A.; Karayil, J.; Lee, J. Low-cost and eco-friendly PVA/carrageenan membrane to efficiently remove cationic dyes from water: Isotherms, kinetics, thermodynamics, and regeneration study. Chemosphere 2024, 350, 140990. [Google Scholar] [CrossRef]
- Khalid, F.; Roy, A.S.; Parveen, A.; Roberto Castro-Muñoz, R. Fabrication of the cross-linked PVA/TiO2/C nanocomposite membrane for alkaline direct methanol fuel cells. Mater. Sci. Eng. B 2024, 299, 116929. [Google Scholar] [CrossRef]
- Reguieg, F.; Ricci, L.; Bouyacoub, N.; Belbachir, M.; Bertoldo, M. Thermal characterization by DSC and TGA analyses of PVA hydrogels with organic and sodium MMT. Polym. Bull. 2020, 77, 929–948. [Google Scholar] [CrossRef]
- Chowdhury, T.; Wang, Q. Study on Thermal Degradation Processes of Polyethylene Terephthalate Microplastics Using the Kinetics and Artificial Neural Networks Models. Processes 2023, 11, 496. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; El Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I Pyrolysis kinetics and mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of Low Density Polyethylene: Kinetic Study Using TGA Data and ANN Prediction. Polymers 2020, 12, 891. [Google Scholar] [CrossRef]
- Yousef, S.; Eimontas, J.; Striūgas, N.; Mohamed, A.; Abdelnaby, M.A. Pyrolysis Kinetic Behavior and Thermodynamic Analysis of PET Nonwoven Fabric. Materials 2023, 16, 6079. [Google Scholar] [CrossRef] [PubMed]
- Al-Salem, S.M.; Antelava, A.; Constantinou, A.; Manos, G.; Dutta, A. A review on thermal and catalytic pyrolysis of plastic solid waste (PSW). J. Environ. Manag. 2017, 197, 177–198. [Google Scholar] [CrossRef]
- Drozin, D.; Sozykin, S.; Ivanova, N.; Olenchikova, T.; Krupnova, T.; Krupina, N.; Avdin, V. Kinetic calculation: Software tool for determining the kinetic parameters of the thermal decomposition process using the Vyazovkin Method. SoftwareX 2020, 11, 100359. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]


| Method | Formula | Draw | |
|---|---|---|---|
| FR | (3) | ||
| FWO | (4) | ||
| KAS | (5) | ||
| STK | (6) | ||
| K | (7) | ||
| VY | (8) | minimizing the function | |
| Method | Formula | |
|---|---|---|
| CR | (9) | |
| Criado | (10) | |
| Model Series | Reaction Mechanism | Code | ||
|---|---|---|---|---|
| F | Reaction order models–1st order | F1 | 1 − α | |
| 2nd order | F2 | |||
| 3rd order | F3 | |||
| D | Diffusion model–1 dimension | D1 | ||
| 2 dimension | D2 | |||
| 3 dimension | D3 | |||
| A | Nucleation models–2 dimension | A2 | ||
| 3 dimension | A3 | |||
| 4 dimension | A4 | |||
| R | Geometrical contraction models–One dimension | R1 | 1 | |
| - sphere | R2 | |||
| - cylinder | R3 | |||
| P | Nucleation models–2-Power law | P2 | ||
| 3-Power law | P3 | |||
| 4-Power law | P4 |
| Test No. | Heating Rate (K min−1) | Symbol | Step 1 Reaction | Step 2 Reaction | ||||
|---|---|---|---|---|---|---|---|---|
| On-Set Temp. (K) | Peak Temp. (K) | Final Temp. (K) | On-Set Temp. (K) | Peak Temp. (K) | FinalTemp. (K) | |||
| 1 | 20 | PVA20 | 550 | 620 | 700 | 700 | 740 | 790 |
| 2 | 30 | PVA30 | 560 | 630 | 720 | 720 | 750 | 800 |
| 3 | 40 | PVA40 | 570 | 640 | 730 | 730 | 760 | 810 |
| Conversion | FR | FWO | KAS | STK | K | VY | Average | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | |
| 0.1 | 138 | 0.9623 | 85 | 0.9022 | 79 | 0.8791 | 80 | 0.8801 | 79 | 0.8791 | 71 | NA * | 89 | 0.90056 |
| 0.2 | 124 | 0.9856 | 105 | 0.9387 | 100 | 0.9264 | 100 | 0.9269 | 100 | 0.9264 | 90 | NA * | 103 | 0.9408 |
| 0.3 | 129 | 0.9945 | 114 | 0.9623 | 109 | 0.9551 | 110 | 0.9554 | 120 | 0.9623 | 97 | NA * | 113 | 0.96592 |
| 0.4 | 135 | 1 | 116 | 0.9863 | 112 | 0.9835 | 112 | 0.9836 | 122 | 0.9863 | 130 | NA * | 121 | 0.98794 |
| 0.5 | 173 | 0.9998 | 136 | 0.9886 | 132 | 0.9866 | 133 | 0.9867 | 143 | 0.9886 | 108 | NA * | 138 | 0.99006 |
| 0.6 | 226 | 0.9949 | 163 | 0.9978 | 160 | 0.9975 | 161 | 0.9975 | 171 | 0.9978 | 113 | NA * | 166 | 0.9971 |
| 0.7 | 468 | 0.9278 | 268 | 0.9867 | 271 | 0.9856 | 272 | 0.9856 | 282 | 0.9867 | 121 | NA * | 280 | 0.97448 |
| Average | 199 | 0.9807 | 148 | 0.9961 | 138 | 0.9591 | 138 | 0.9594 | 145 | 0.9610 | 104 | NA * | 145 | 0.97126 |
| 1st Stage | 2nd Stage | |||
|---|---|---|---|---|
| References | E (kJ mol−1) | Method | E (kJ mol−1) | Method |
| Zhao et al. (2023) [16] | 135.97 | FWO | 269.34 | FWO |
| 133.78 | KAS | 271.16 | KAS | |
| 142.20 | FR | 234.33 | FR | |
| 134.05 | AIC | 270.38 | AIC | |
| Mittal et al. (2020) [17] | 298.73 | FWO | ||
| 304.55 | KAS | |||
| 309.67 | FR | |||
| 304.64 | Modified CR | |||
| Wang et al. (2018) [18] | 122.5 | FWO | ||
| Reaction Mechanism 1 Step Reaction | Code | Test 1 PVA20 | Test 2 PVA30 | Test 3 PVA40 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ea (kJ/mol) | Ln (A0) | R2 | Ea (kJ/mol) | Ln (A0) | R2 | Ea (kJ/mol) | Ln (A0) | R2 | ||
| Reaction order models–First order | F1 | 91 | 16.28 | 0.9912 | 92 | 16.67 | 0.9878 | 107 | 19.66 | 0.9868 |
| Reaction order models–Second order | F2 | 119 | 22.3 | 0.9969 | 119 | 22.28 | 0.9971 | 139 | 26.14 | 0.9974 |
| Reaction order models–Third order | F3 | 152 | 29.21 | 0.9993 | 150 | 28.71 | 0.9998 | 176 | 33.63 | 1 |
| Diffusion models–One dimension | D1 | 145 | 25.96 | 0.9829 | 151 | 27.07 | 0.9729 | 174 | 31.31 | 0.9682 |
| Diffusion models–Two dimension | D2 | 159 | 28.27 | 0.9864 | 164 | 29.16 | 0.979 | 189 | 33.78 | 0.9757 |
| Diffusion models–Three dimension | D3 | 175 | 30.17 | 0.9897 | 179 | 30.81 | 0.9848 | 207 | 35.89 | 0.9828 |
| Nucleation models–Two dimension | A2 | 40 | 16.92 | 0.9886 | 41 | 17.37 | 0.9842 | 195 | 33.48 | 0.9783 |
| Nucleation models–Three-dimension | A3 | 23 | 19.51 | 0.9848 | 24 | 19.98 | 0.9788 | 48 | 16.56 | 0.9835 |
| Nucleation models–Fourth dimension | A4 | 15 | 20.65 | 0.9789 | 15 | 21.08 | 0.9704 | 29 | 19.63 | 0.9788 |
| Geometrical contraction models–One dimension phase boundary | R1 | 67 | 12.83 | 0.98 | 70 | 12.95 | 0.9685 | 19 | 20.99 | 0.972 |
| Geometrical contraction models–Contracting sphere | R2 | 78 | 12.9 | 0.9865 | 81 | 13.5 | 0.9796 | 82 | 14.26 | 0.9638 |
| Geometrical contraction models–Contracting cylinder | R3 | 82 | 13.37 | 0.9882 | 84 | 13.89 | 0.9827 | 94 | 16.14 | 0.9771 |
| Nucleation models–Power law | P2 | 9 | 21.34 | 0.931 | 30 | 19.29 | 0.9561 | 98 | 16.64 | 0.9807 |
| Nucleation models–Power law | P3 | 15 | 20.69 | 0.9578 | 16 | 21.06 | 0.9355 | 35 | 18.81 | 0.952 |
| Nucleation models–Power law | P4 | 28 | 18.97 | 0.9719 | 10 | 21.79 | 0.8981 | 28 | 19.66 | 0.9994 |
| Reaction mechanism 2 step reaction | Code | Test 1 PVA20 | Test 2 PVA30 | Test 3 PVA40 | ||||||
| Ea (kJ/mol) | Ln (A0) | R2 | Ea (kJ/mol) | Ln (A0) | R2 | Ea (kJ/mol) | Ln (A0) | R2 | ||
| Reaction order models–First order | F1 | 29 | 18.85 | 0.9993 | 27 | 19.62 | 1 | 25 | 19.98 | 0.9933 |
| Reaction order models–Second order | F2 | 92 | 16.01 | 0.9994 | 85 | 15.1 | 0.9996 | 90 | 16.52 | 0.9932 |
| Reaction order models–Third order | F3 | 176 | 31.83 | 0.9991 | 163 | 29.86 | 0.9994 | 176 | 32.92 | 0.9932 |
| Diffusion models–One dimension | D1 | 10 | 21.9 | 0.9795 | 9 | 22.39 | 0.9936 | 5 | 22.77 | 0.9961 |
| Diffusion models–Two dimension | D2 | 22 | 21 | 0.994 | 20 | 21.6 | 0.9986 | 15 | 23.14 | 0.9961 |
| Diffusion models–Three dimension | D3 | 44 | 19 | 0.9986 | 41 | 19.88 | 0.9998 | 36 | 20.68 | 0.9963 |
| Nucleation models–Two dimension | A2 | 8 | 22.58 | 0.9977 | 7 | 21.82 | 0.9998 | 6 | 22.03 | 0.9754 |
| Nucleation models–Three-dimension | A3 | 1 | 20.5 | 0.9654 | 1 | 21.06 | 0.991 | NA | NA | NA |
| Nucleation models–Fourth dimension | A4 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Geometrical contraction models–One dimension phase boundary | R1 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Geometrical contraction models–Contracting sphere | R2 | 10 | 21.94 | 0.9931 | 9 | 22.56 | 0.9986 | 7 | 22.96 | 0.9883 |
| Geometrical contraction models–Contracting cylinder | R3 | 16 | 21.89 | 0.9971 | 14 | 22.44 | 0.9996 | 12 | 22.89 | 0.9918 |
| Nucleation models–Power law | P2 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Nucleation models–Power law | P3 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| Nucleation models–Power law | P4 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
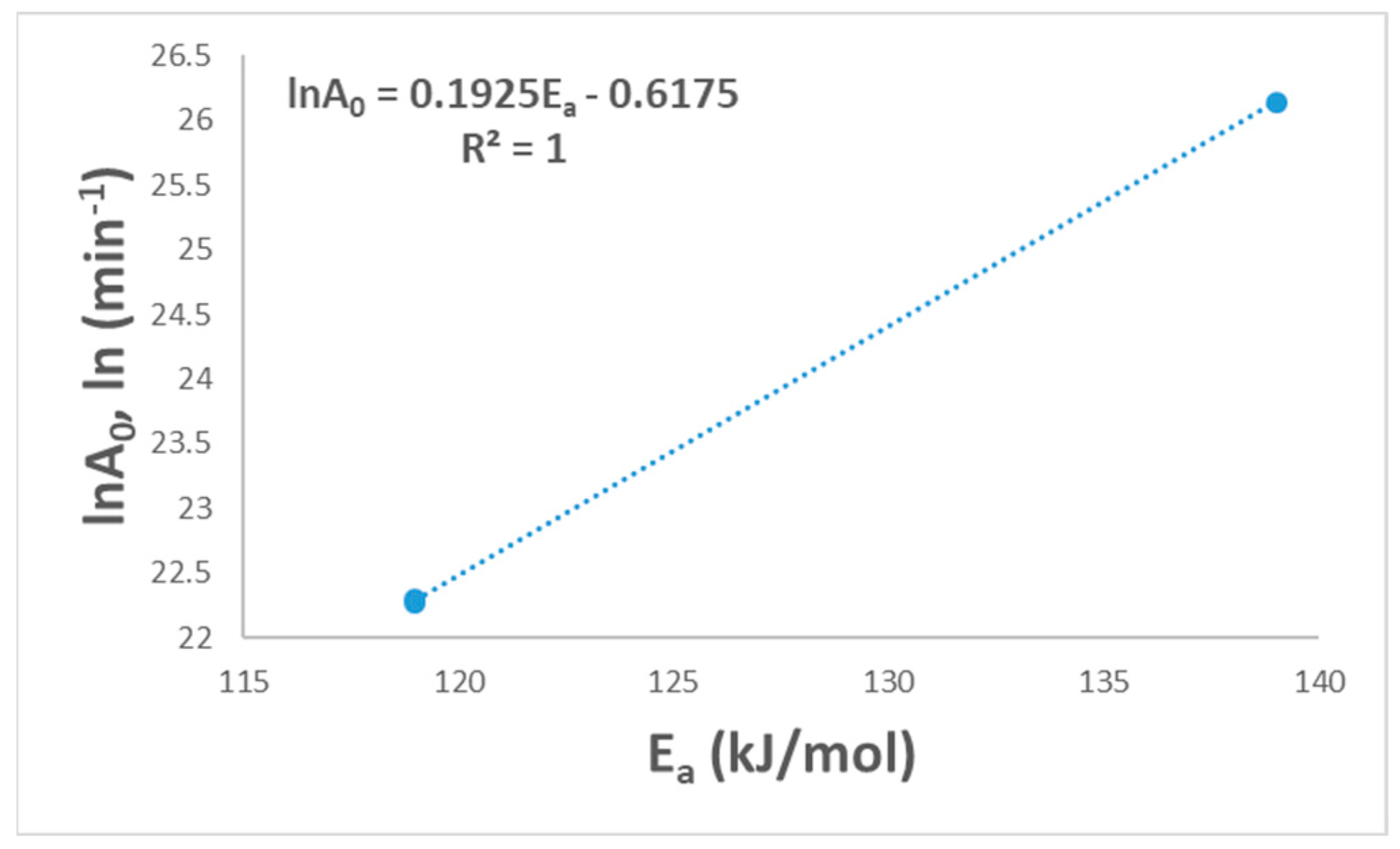
| Test No. | Ea (kJ/mol) | Ln (A0) | R2 | Reaction Mechanism |
|---|---|---|---|---|
| 1 | 119 | 22.3 | 0.9969 | Reaction order models-Second order (F2) |
| 2 | 119 | 22.28 | 0.9971 | Reaction order models-Second order (F2) |
| 3 | 139 | 26.14 | 0.9974 | Reaction order models-Second order (F2) |
| Conversion | ln [A0 (min−1)] | |||||
|---|---|---|---|---|---|---|
| FR | FWO | KAS | STK | K | Average | |
| 0.1 | 26.06 | 15.37 | 13.66 | 14.26 | 15.85 | 36.88 |
| 0.2 | 23.32 | 19.52 | 18.19 | 18.79 | 19.58 | 26.40 |
| 0.3 | 24.43 | 21.48 | 20.29 | 20.89 | 23.18 | 25.48 |
| 0.4 | 25.52 | 22.07 | 20.90 | 21.49 | 23.36 | 26.08 |
| 0.5 | 32.43 | 25.78 | 24.89 | 25.50 | 26.98 | 27.40 |
| 0.6 | 41.86 | 30.70 | 30.16 | 30.76 | 31.57 | 36.88 |
| 0.7 | 84.54 | 49.87 | 50.30 | 50.90 | 51.29 | 26.40 |
| Average | 17.04 | 19.88 | 22.05 | 22.67 | 27.12 | 28.45 |
| Heating Rates (K/min) | 20 | 30 | 40 |
|---|---|---|---|
| Kinetic Parameters | |||
| Ea (kJ/mol) | 199 | ||
| A (min−1) | 2.30 × 1015 | ||
| Tp (K) | 620 | 630 | 640 |
| Thermodynamic Parameters | |||
| ∆H (kJ/mol) | 193.85 | 193.76 | 193.68 |
| ∆G (kJ/mol) | 172.30 | 171.94 | 171.60 |
| ∆S (kJ/mol.K) | 0.034767 | 0.034634 | 0.034503 |
| Potential Energy Barrier | |||
| Ea − ∆H (kJ/mol) * | 5.15 | 5.32 | 5.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhulaybi, Z.A.; Dubdub, I. Kinetics Study of PVA Polymer by Model-Free and Model-Fitting Methods Using TGA. Polymers 2024, 16, 629. https://doi.org/10.3390/polym16050629
Alhulaybi ZA, Dubdub I. Kinetics Study of PVA Polymer by Model-Free and Model-Fitting Methods Using TGA. Polymers. 2024; 16(5):629. https://doi.org/10.3390/polym16050629
Chicago/Turabian StyleAlhulaybi, Zaid Abdulhamid, and Ibrahim Dubdub. 2024. "Kinetics Study of PVA Polymer by Model-Free and Model-Fitting Methods Using TGA" Polymers 16, no. 5: 629. https://doi.org/10.3390/polym16050629
APA StyleAlhulaybi, Z. A., & Dubdub, I. (2024). Kinetics Study of PVA Polymer by Model-Free and Model-Fitting Methods Using TGA. Polymers, 16(5), 629. https://doi.org/10.3390/polym16050629







