The Effect of Powder Re-Use on the Coalescence Behaviour and Isothermal Crystallisation Kinetics of Polyamide 12 within Powder Bed Fusion
Abstract
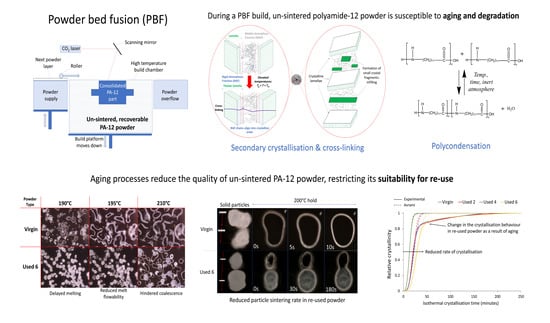
1. Introduction
2. Experimental Method
2.1. Powder Characterisation
2.1.1. Hot-Stage Microscopy (HSM)
2.1.2. Differential Scanning Calorimetry (DSC)—Isothermal Crystallisation
3. Results and Discussion
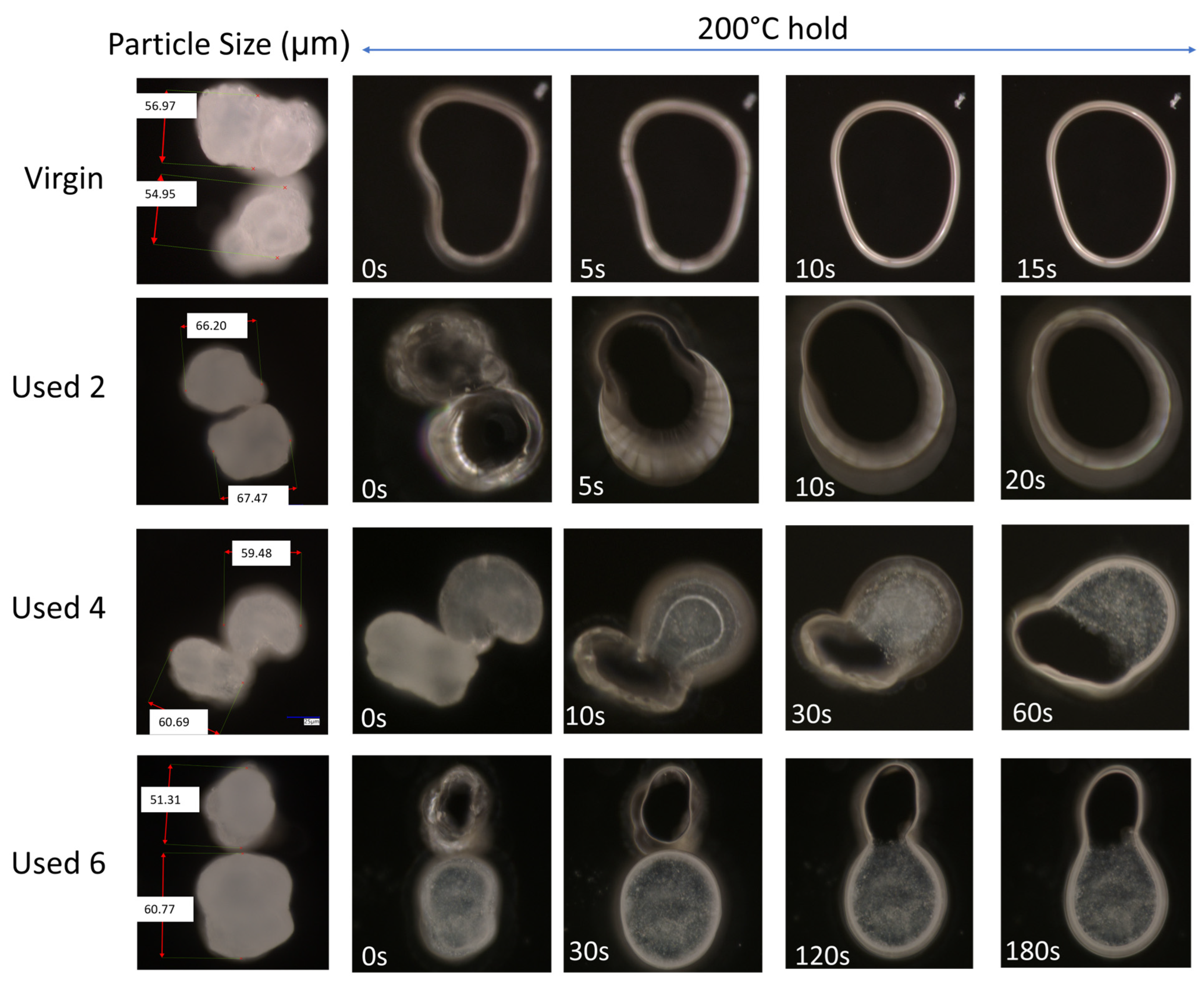
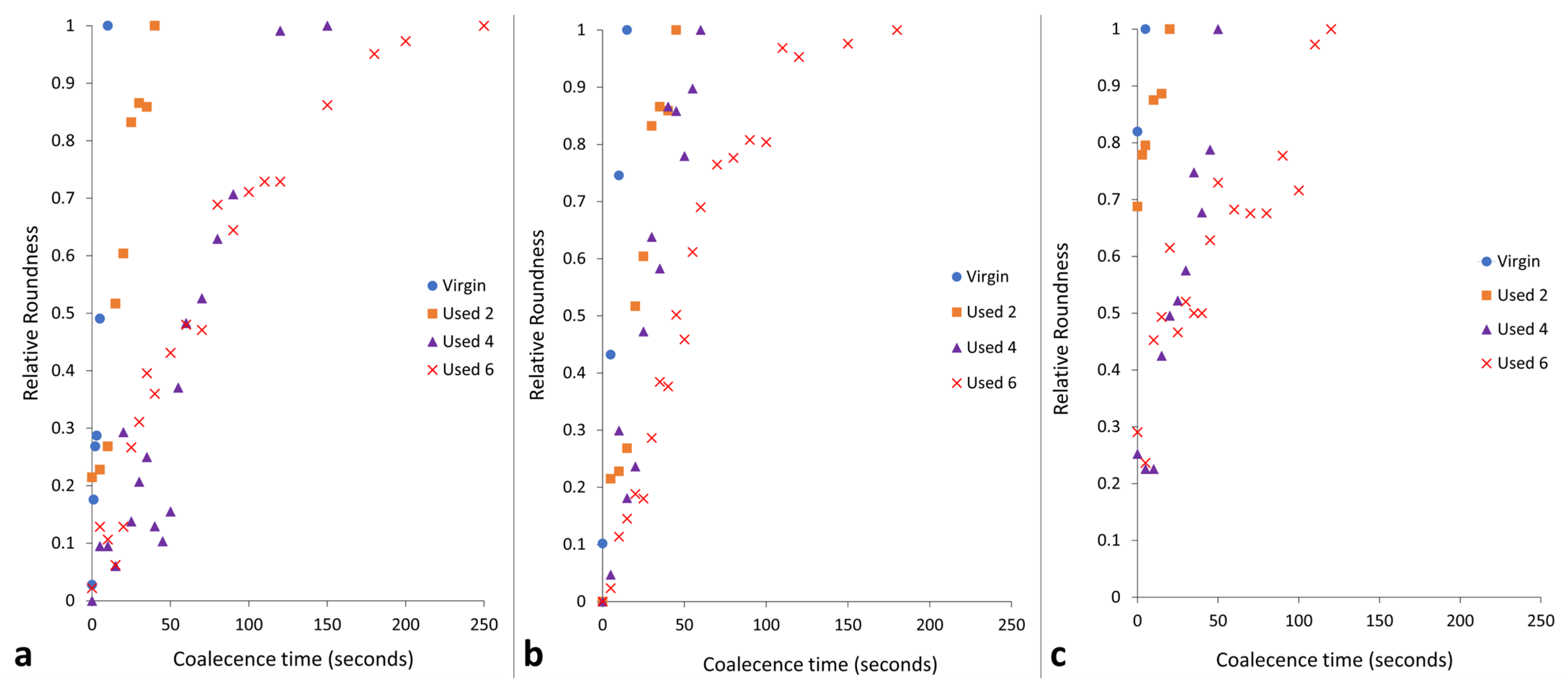
3.1. The Effect of Powder Re-Use on Sintering and Coalescence Behaviour of PA-12
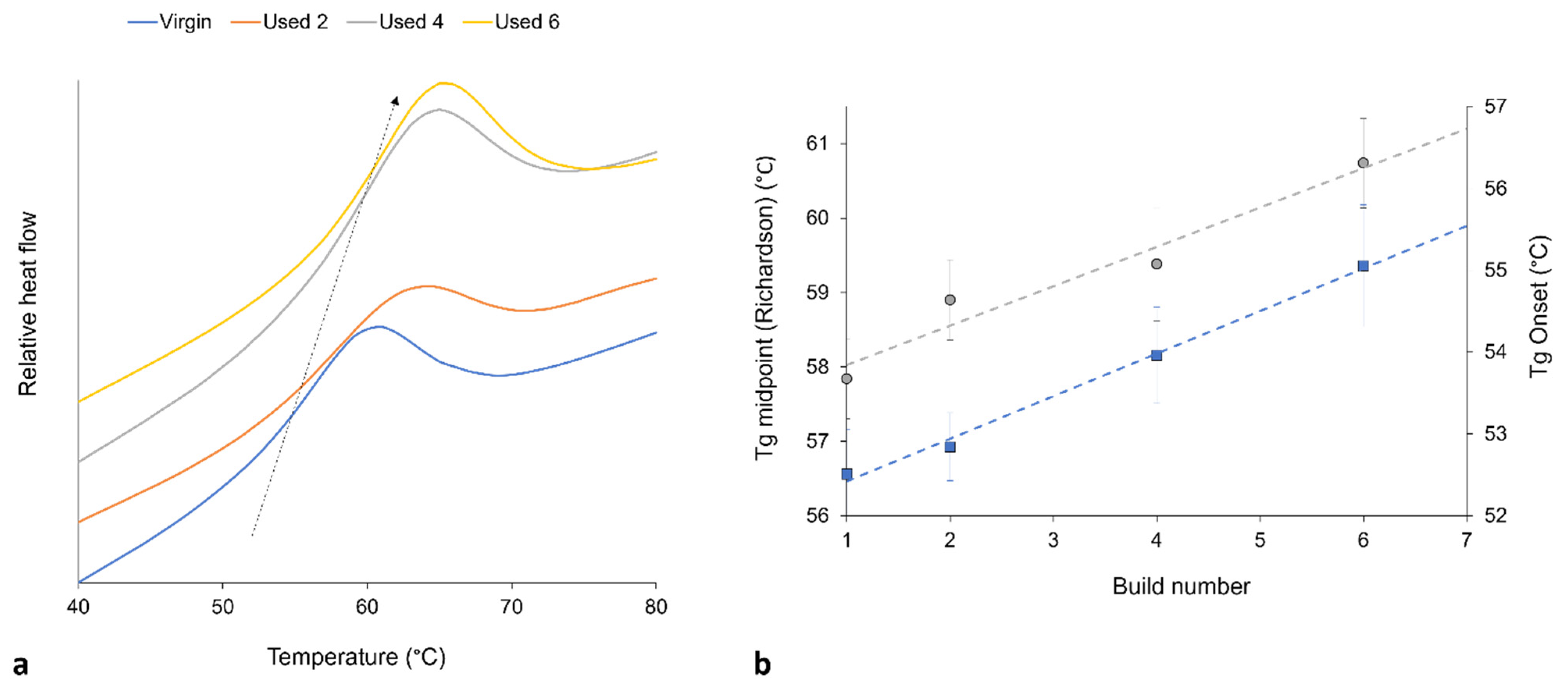
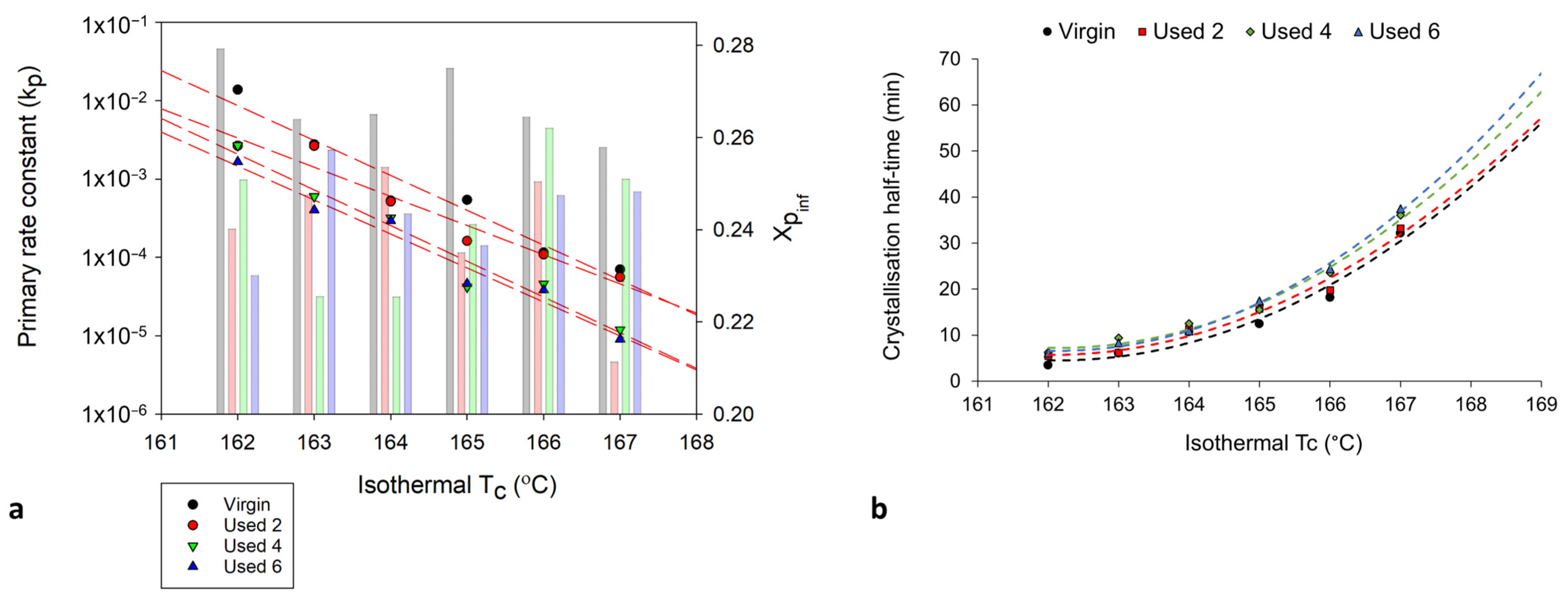
3.2. The Effect of Powder Re-Use on Crystallisation Behaviour of PA-12
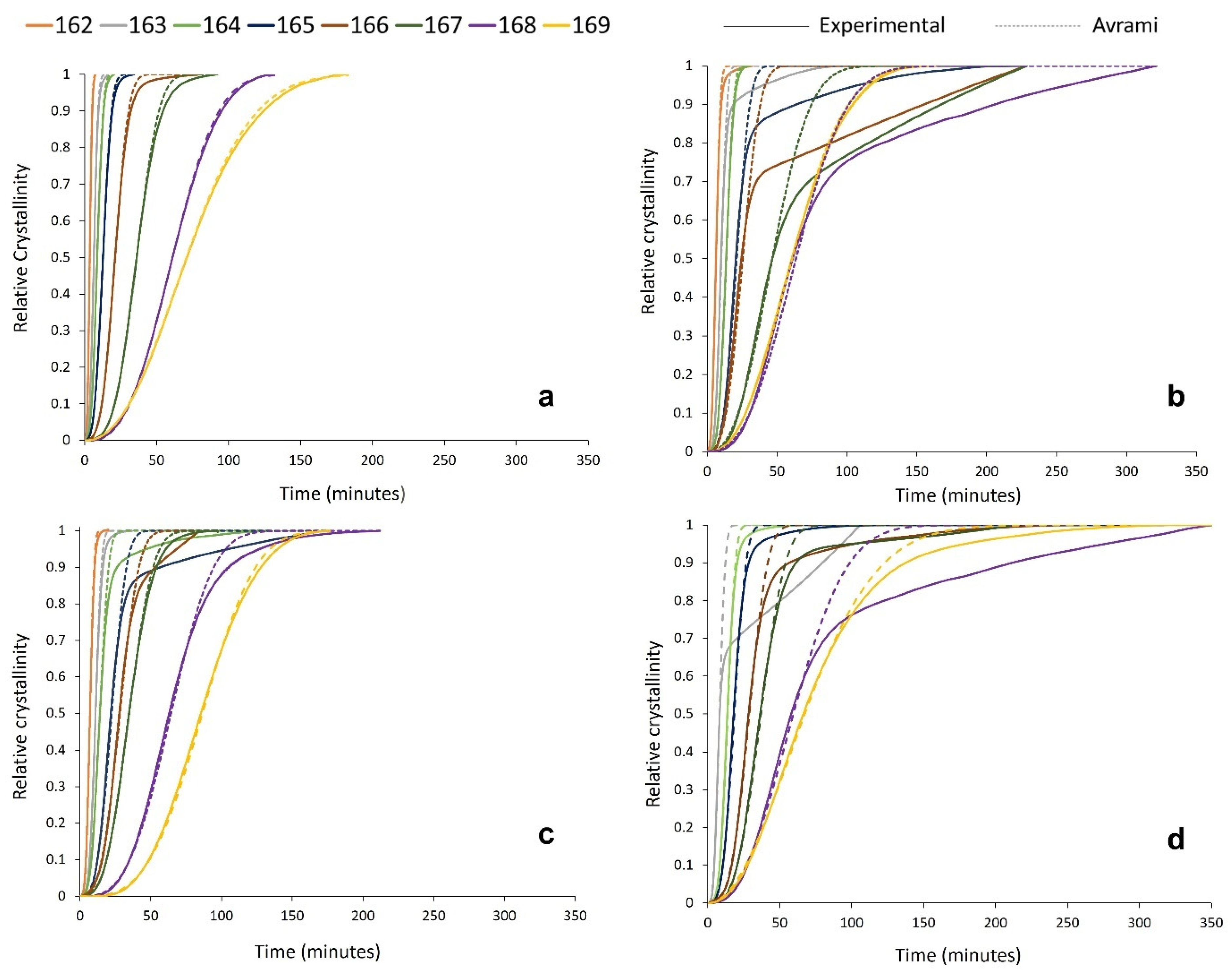
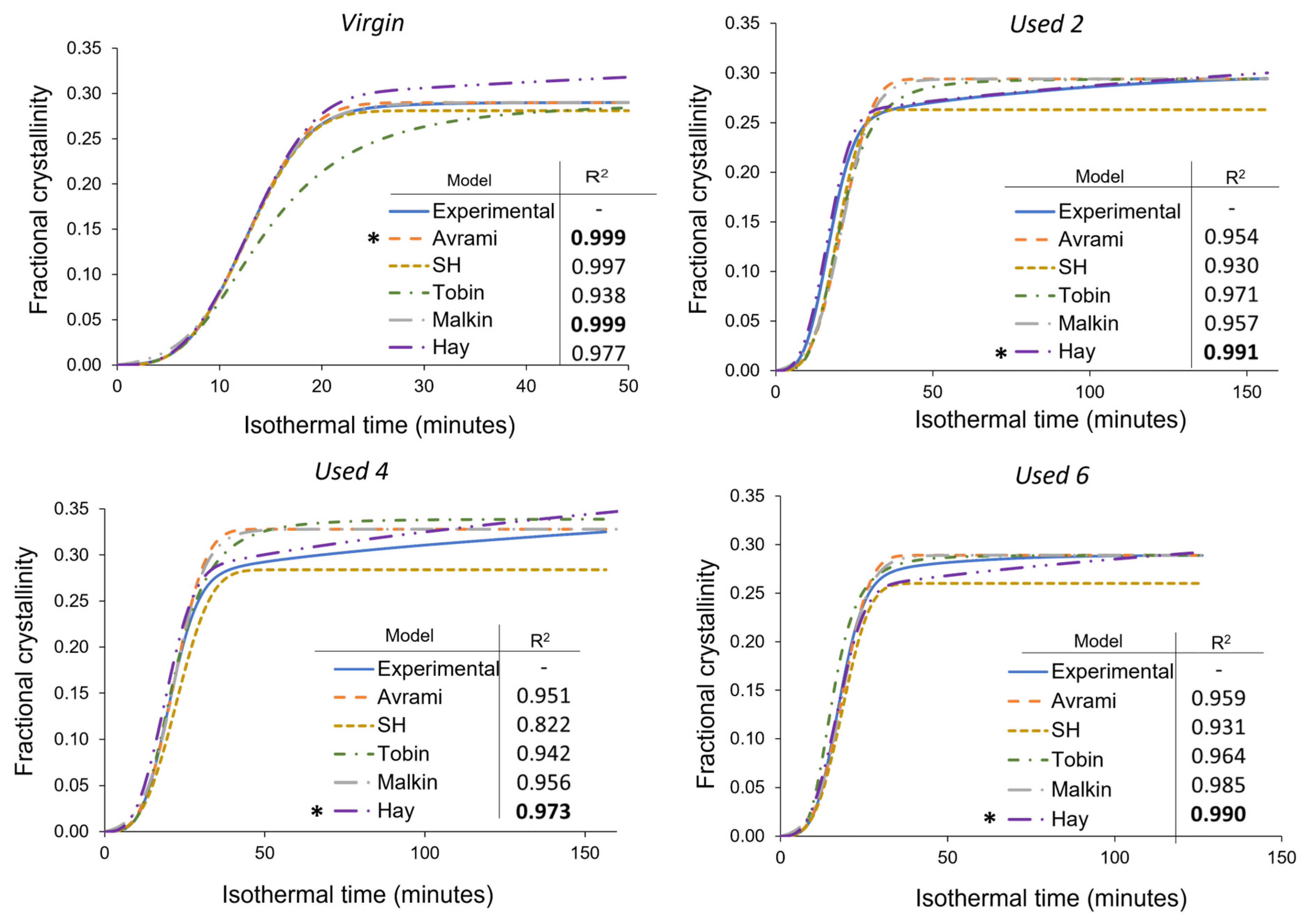
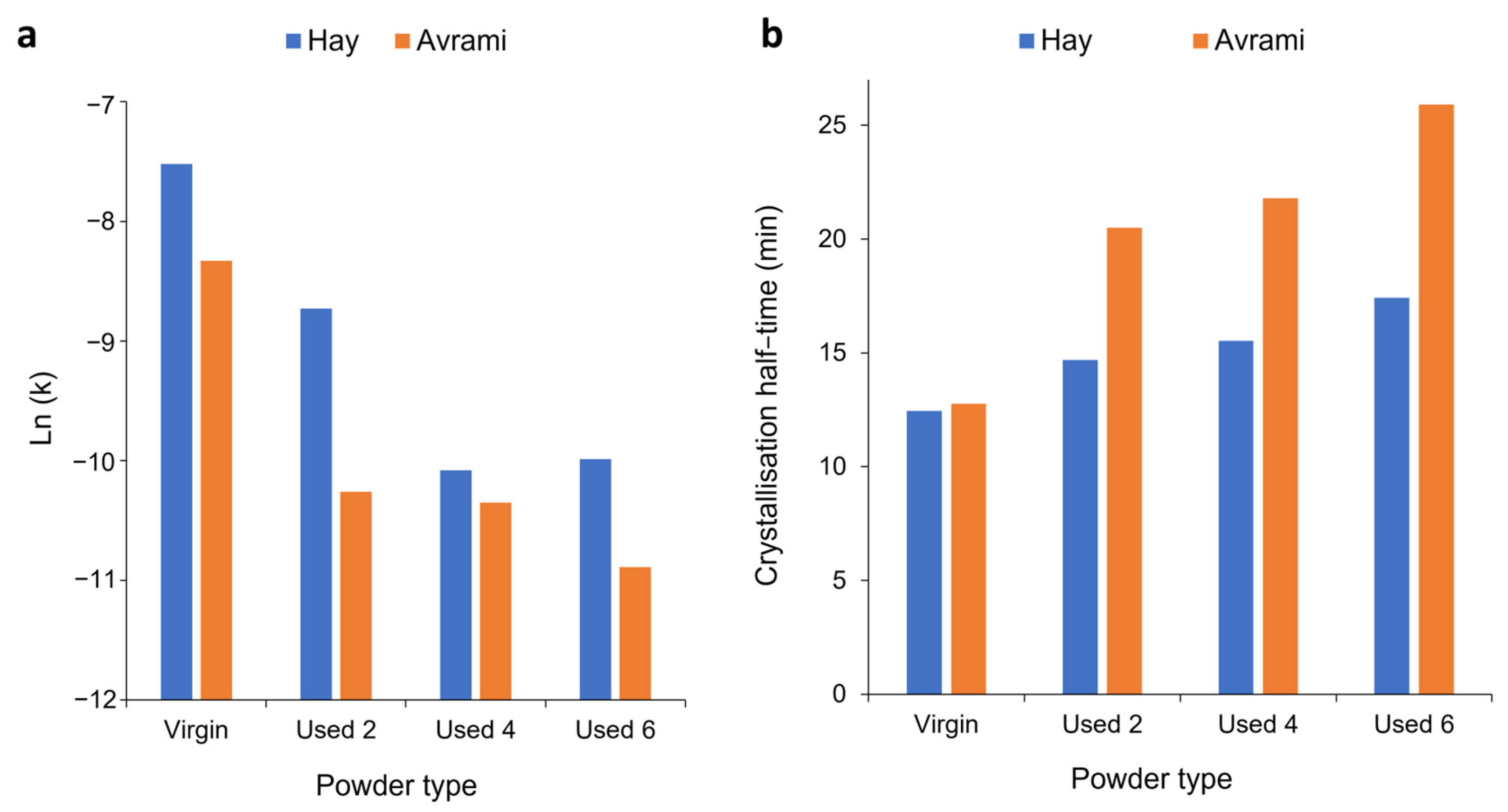
3.3. Avrami Analysis of Isothermal Crystallisation
3.4. Modelling the Crystallisation Kinetics of Re-Used PA-12 Powder
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodridge, R.D.; Tuck, C.J.; Hague, R.J.M. Laser sintering of polyamides and other polymers. Prog. Mater. Sci. 2012, 57, 229–267. [Google Scholar] [CrossRef]
- Sillani, F.; Kleijnen, R.G.; Vetterli, M.; Schmid, M.; Wegener, K. Selective laser sintering and multi jet fusion: Process-induced modification of the raw materials and analyses of parts performance. Addit. Manuf. 2019, 27, 32–41. [Google Scholar] [CrossRef]
- Goodridge, R.D.; Ziegelmeier, S. 7—Powder bed fusion of polymers. In Laser Additive Manufacturing; Woodhead Publishing: Sawston, UK, 2017; pp. 181–204. [Google Scholar] [CrossRef]
- Dadbakhsh, S.; Verbelen, L.; Verkinderen, O.; Strobbe, D.; Van Puyvelde, P.; Kruth, J.-P. Effect of PA12 powder reuse on coalescence behaviour and microstructure of SLS parts. Eur. Polym. J. 2017, 92, 250–262. [Google Scholar] [CrossRef]
- Zarringhalam, H.; Hopkinson, N.; Kamperman, N.F.; de Vlieger, J.J. Effects of processing on microstructure and properties of SLS Nylon 12. Mater. Sci. Eng. A 2006, 435–436, 172–180. [Google Scholar] [CrossRef]
- Josupeit, S.; Schmid, H.-J. Experimental analysis and modeling of local ageing effects during laser sintering of polyamide 12 in regard to individual thermal histories. J. Appl. Polym. Sci. 2017, 134, 45435. [Google Scholar] [CrossRef]
- Paolucci, F.; van Mook, M.J.H.; Govaert, L.E.; Peters, G.W.M. Influence of post-condensation on the crystallization kinetics of PA12: From virgin to reused powder. Polymer 2019, 175, 161–170. [Google Scholar] [CrossRef]
- Wudy, K.; Drummer, D. Aging behavior of polyamide 12: Interrelation between bulk characteristics and part properties. In Proceedings of the 26th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 10–12 August 2016; pp. 17–19. [Google Scholar]
- Kuehnlein, F.; Drummer, D.; Rietzel, D.; Seefried, A. Degradation Behavior and Material Properties of PA12-Plastic Powders Processed by Powder Based Additive Manufacturing Technologies. In Proceedings of the 21st International DAAAM Symposium, Vienna, Austria, 20–23 October 2010; Volume 21. [Google Scholar]
- Dotchev, K.; Yusoff, W. Recycling of polyamide 12 based powders in the laser sintering process. Rapid Prototyp. J. 2009, 15, 192–203. [Google Scholar] [CrossRef]
- Pham, D.T.; Dotchev, K.D.; Yusoff, W.A.Y. Deterioration of polyamide powder properties in the laser sintering process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 2163–2176. [Google Scholar] [CrossRef]
- Weinmann, S.; Bonten, C. Recycling of PA12 powder for selective laser sintering. AIP Conf. Proc. 2020, 2289, 020056. [Google Scholar] [CrossRef]
- De Santis, F.; Pantani, R.; Titomanlio, G. Nucleation and crystallization kinetics of poly(lactic acid). Thermochim. Acta 2011, 522, 128–134. [Google Scholar] [CrossRef]
- Neugebauer, F.; Ploshikhin, V.; Ambrosy, J.; Witt, G. Isothermal and non-isothermal crystallization kinetics of polyamide 12 used in laser sintering. J. Therm. Anal. Calorim. 2016, 124, 925–933. [Google Scholar] [CrossRef]
- Kelly, C.A.; Jenkins, M.J. Modeling the crystallization kinetics of polymers displaying high levels of secondary crystallization. Polym. J. 2022, 54, 249–257. [Google Scholar] [CrossRef]
- Wunderlich, B. Macromolecular Physics: Crystal Nucleation, Growth, Annealing; Academic Press: New York, NY, USA, 1976; Volume 2. [Google Scholar]
- Hoffman, J.D. Role of reptation in the rate of crystallization of polyethylene fractions from the melt. Polymer 1982, 23, 656–670. [Google Scholar] [CrossRef]
- Chen, Z.; Jenkins, M.; Hay, J. Annealing of poly (ethylene terephthalate). Eur. Polym. J. 2014, 50, 235–242. [Google Scholar] [CrossRef]
- Fischer, E.W. Effect of annealing and temperature on the morphological structure of polymers. Pure Appl. Chem. 1972, 31, 113–132. [Google Scholar] [CrossRef]
- Chen, Z.; Hay, J.N.; Jenkins, M. The kinetics of crystallization of poly (ethylene terephthalate) measured by FTIR spectroscopy. Eur. Polym. J. 2013, 49, 1722–1730. [Google Scholar] [CrossRef]
- Chen, Z.; Hay, J.; Jenkins, M. The effect of secondary crystallization on melting. Eur. Polym. J. 2013, 49, 2697–2703. [Google Scholar] [CrossRef]
- Phillipson, K.; Jenkins, M.J.; Hay, J.N. The effect of a secondary process on crystallization kinetics–Poly (є-caprolactone) revisited. Eur. Polym. J. 2016, 84, 708–714. [Google Scholar] [CrossRef]
- Biddlestone, F.; Harris, A.; Hay, J.; Hammond, T. The physical ageing of amorphous poly (hydroxybutyrate). Polym. Int. 1996, 39, 221–229. [Google Scholar] [CrossRef]
- Wang, Z.G.; Hsiao, B.S.; Sauer, B.B.; Kampert, W.G. The nature of secondary crystallization in poly(ethylene terephthalate). Polymer 1999, 40, 4615–4627. [Google Scholar] [CrossRef]
- Verma, R.; Marand, H.; Hsiao, B. Morphological changes during secondary crystallization and subsequent melting in poly (ether ether ketone) as studied by real time small angle X-ray scattering. Macromolecules 1996, 29, 7767–7775. [Google Scholar] [CrossRef]
- Hay, J.N. Secondary crystallization kinetics. Polym. Cryst. 2018, 1, e10007. [Google Scholar] [CrossRef]
- Abo el Maaty, M.I.; Bassett, D.C. Evidence for isothermal lamellar thickening at and behind the growth front as polyethylene crystallizes from the melt. Polymer 2005, 46, 8682–8688. [Google Scholar] [CrossRef]
- Wudy, K.; Drummer, D. Aging effects of polyamide 12 in selective laser sintering: Molecular weight distribution and thermal properties. Addit. Manuf. 2019, 25, 1–9. [Google Scholar] [CrossRef]
- Sanders, B.; Cant, E.; Amel, H.; Jenkins, M. The Effect of Physical Aging and Degradation on the Re-Use of Polyamide 12 in Powder Bed Fusion. Polymers 2022, 14, 2682. [Google Scholar] [CrossRef] [PubMed]
- Riedelbauch, J.; Rietzel, D.; Witt, G. Analysis of material aging and the influence on the mechanical properties of polyamide 12 in the Multi Jet Fusion process. Addit. Manuf. 2019, 27, 259–266. [Google Scholar] [CrossRef]
- Paolucci, F.; Baeten, D.; Roozemond, P.C.; Goderis, B.; Peters, G.W.M. Quantification of isothermal crystallization of polyamide 12: Modelling of crystallization kinetics and phase composition. Polymer 2018, 155, 187–198. [Google Scholar] [CrossRef]
- Wudy, K.; Drummer, D.; Kühnlein, F.; Drexler, M. Influence of degradation behavior of polyamide 12 powders in laser sintering process on produced parts. AIP Conf. Proc. 2014, 1593, 691–695. [Google Scholar] [CrossRef]
- Yang, F.; Jiang, T.; Lalier, G.; Bartolone, J.; Chen, X. A process control and interlayer heating approach to reuse polyamide 12 powders and create parts with improved mechanical properties in selective laser sintering. J. Manuf. Process. 2020, 57, 828–846. [Google Scholar] [CrossRef]
- Cholewa, S.; Jaksch, A.; Drummer, D. Coalescence Behavior of Polyamide 12 as Function of Zero-Shear Viscosity and Influence on Mechanical Performance. In Proceedings of the 2022 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 25–27 July 2022. [Google Scholar]
- Alo, O.A.; Otunniyi, I.O.; Mauchline, D. Correlation of reuse extent with degradation degree of PA 12 powder during laser powder bed fusion and mechanical behavior of sintered parts. Polym. Eng. Sci. 2023, 63, 126–138. [Google Scholar] [CrossRef]
- Abbott, C.S.; Sperry, M.; Crane, N.B. Relationships between porosity and mechanical properties of polyamide 12 parts produced using the laser sintering and multi-jet fusion powder bed fusion processes. J. Manuf. Process. 2021, 70, 55–66. [Google Scholar] [CrossRef]
- Li, X.; He, Y.; Dong, X.; Ren, X.; Gao, H.; Hu, W. Effects of hydrogen-bonding density on polyamide crystallization kinetics. Polymer 2020, 189, 122165. [Google Scholar] [CrossRef]
- Liu, S.; Yu, Y.; Cui, Y.; Zhang, H.; Mo, Z. Isothermal and nonisothermal crystallization kinetics of nylon-11. J. Appl. Polym. Sci. 1998, 70, 2371–2380. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, L.; Xiong, Y.; Liu, G.; Xu, W. Isothermal crystallization kinetics of high-flow nylon 6 by differential scanning calorimetry. J. Appl. Polym. Sci. 2009, 111, 2930–2937. [Google Scholar] [CrossRef]
- Zhao, M.; Wudy, K.; Drummer, D. Crystallization Kinetics of Polyamide 12 during Selective Laser Sintering. Polymers 2018, 10, 168. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, A.T.; Arnal, M.L.; Albuerne, J.; Müller, A.J. DSC isothermal polymer crystallization kinetics measurements and the use of the Avrami equation to fit the data: Guidelines to avoid common problems. Polym. Test. 2007, 26, 222–231. [Google Scholar] [CrossRef]
- Supaphol, P.; SPRUIELL, J.E. Application of the Avrami, Tobin, Malkin, and simultaneous Avrami macrokinetic models to isothermal crystallization of syndiotactic polypropylenes. J. Macromol. Sci. Part B 2000, 39, 257–277. [Google Scholar] [CrossRef]
- Hillier, I. Modified avrami equation for the bulk crystallization kinetics of spherulitic polymers. J. Polym. Sci. Part A Gen. Pap. 1965, 3, 3067–3078. [Google Scholar] [CrossRef]
- Tobin, M.C. Theory of phase transition kinetics with growth site impingement. I. Homogeneous nucleation. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 399–406. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Beghishev, V.; Keapin, I.A.; Bolgov, S. General treatment of polymer crystallization kinetics—Part 1. A new macrokinetic equation and its experimental verification. Polym. Eng. Sci. 1984, 24, 1396–1401. [Google Scholar] [CrossRef]
- Hay, J.N. Application of the modified avrami equations to polymer crystallisation kinetics. Br. Polym. J. 1971, 3, 74–82. [Google Scholar] [CrossRef]
- Kelly, C.A.; Hay, J.N.; Turner, R.P.; Jenkins, M.J. The effect of a secondary process on the analysis of isothermal crystallisation kinetics by differential scanning calorimetry. Polymers 2019, 12, 19. [Google Scholar] [CrossRef] [PubMed]
- McFerran, N.L.; Armstrong, C.G.; McNally, T. Nonisothermal and isothermal crystallization kinetics of nylon-12. J. Appl. Polym. Sci. 2008, 110, 1043–1058. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. I General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Ravindranath, K.; Jog, J.P. Polymer crystallization kinetics: Poly(ethylene terephthalate) and poly(phenylene sulfide). J. Appl. Polym. Sci. 1993, 49, 1395–1403. [Google Scholar] [CrossRef]
- Chen, Z.; Hay, J.N.; Jenkins, M.J. The effect of secondary crystallization on crystallization kinetics–Polyethylene terephthalate revisited. Eur. Polym. J. 2016, 81, 216–223. [Google Scholar] [CrossRef]
- Drummer, D.; Wudy, K.; Drexler, M. Influence of Energy Input on Degradation Behavior of Plastic Components Manufactured by Selective Laser Melting. Phys. Procedia 2014, 56, 176–183. [Google Scholar] [CrossRef]
- Cai, C.; Tey, W.S.; Chen, J.; Zhu, W.; Liu, X.; Liu, T.; Zhao, L.; Zhou, K. Comparative study on 3D printing of polyamide 12 by selective laser sintering and multi jet fusion. J. Mater. Process. Technol. 2021, 288, 116882. [Google Scholar] [CrossRef]
- Samulski, E.; Wignall, G.; Koenig, J.; Mark, J.; Ngai, K.; Mandelkern, L.; Graessley, W. (Eds.) The crystalline state. In Physical Properties of Polymers, 3rd ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 209–315. [Google Scholar]
- Bourell, D.L.; Watt, T.J.; Leigh, D.K.; Fulcher, B. Performance Limitations in Polymer Laser Sintering. Phys. Procedia 2014, 56, 147–156. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Weeks, J.J. Melting process and the equilibrium melting temperature of polychlorotrifluoroethylene. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1962, 66, 13–28. [Google Scholar] [CrossRef]
- Sanders, B.; Cant, E.; Jenkins, M. Re-use of polyamide-12 in powder bed fusion and its effect on process-relevant powder characteristics and final part properties. Addit. Manuf. 2024, 80, 103961. [Google Scholar] [CrossRef]
- Gogolewski, S.; Czerntawska, K.; Gastorek, M. Effect of annealing on thermal properties and crystalline structure of polyamides. Nylon 12 (polylaurolactam). Colloid Polym. Sci. 1980, 258, 1130–1136. [Google Scholar] [CrossRef]
- Gornet, T.J.; Davis, K.R.; Starr, T.L.; Mulloy, K.M. Characterization of Selective Laser Sintering™ Materials to Determine Process Stability. In Proceedings of the 2002 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 5–7 August 2002. [Google Scholar]
- Agapov, A.L.; Sokolov, A.P. Does the Molecular Weight Dependence of Tg Correlate to Me? Macromolecules 2009, 42, 2877–2878. [Google Scholar] [CrossRef]
- Roland, C.; Casalini, R. Temperature dependence of local segmental motion in polystyrene and its variation with molecular weight. J. Chem. Phys. 2003, 119, 1838–1842. [Google Scholar] [CrossRef]
- Izuka, A.; Winter, H.H.; Hashimoto, T. Molecular weight dependence of viscoelasticity of polycaprolactone critical gels. Macromolecules 1992, 25, 2422–2428. [Google Scholar] [CrossRef]
- Burfield, D.R.; Doi, Y. Differential scanning calorimetry characterization of polypropylene. Dependence of Tg on polymer tacticity and molecular weight. Macromolecules 1983, 16, 702–704. [Google Scholar] [CrossRef]
- Ergoz, E.; Fatou, J.; Mandelkern, L. Molecular weight dependence of the crystallization kinetics of linear polyethylene. I. Experimental results. Macromolecules 1972, 5, 147–157. [Google Scholar] [CrossRef]




| Powder Type | Region | Xt Range | Avrami | Simplified Hillier | Tobin | Malkin | Hay | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DLP | CF | DLP | CF | DLP | CF | DLP | CF | DLP | CF | |||
| Virgin | Initial | 0.0–0.1 | 0.0003 | 0.0011 | 0.0003 | 0.0003 | 0.0004 | 0.0052 | 0.0044 | 0.0034 | 0.0009 | 0.0058 |
| Primary | 0.1–0.8 | 0.0010 | 0.0020 | 0.0016 | 0.0004 | 0.0286 | 0.0064 | 0.0018 | 0.0017 | 0.0020 | 0.0109 | |
| Transition | 0.8–0.95 | 0.0053 | 0.0020 | 0.0013 | 0.0008 | 0.0527 | 0.0049 | 0.0007 | 0.0012 | 0.0101 | 0.0173 | |
| Secondary | 0.95–1.0 | 0.0024 | 0.0019 | 0.0077 | 0.0077 | 0.0232 | 0.0032 | 0.0006 | 0.0005 | 0.0212 | 0.0135 | |
| Used 2 | Initial | 0.0–0.1 | 0.002 | 0.010 | 0.003 | 0.002 | 0.003 | 0.005 | 0.002 | 0.008 | 0.002 | 0.006 |
| Primary | 0.1–0.7 | 0.037 | 0.012 | 0.029 | 0.002 | 0.032 | 0.010 | 0.037 | 0.007 | 0.011 | 0.011 | |
| Transition | 0.7–0.9 | 0.026 | 0.013 | 0.009 | 0.002 | 0.020 | 0.010 | 0.023 | 0.009 | 0.009 | 0.007 | |
| Secondary | 0.9–1.0 | 0.013 | 0.013 | 0.022 | 0.022 | 0.010 | 0.008 | 0.013 | 0.008 | 0.002 | 0.003 | |
| Used 4 | Initial | 0.0–0.1 | 0.0012 | 0.0149 | 0.0008 | 0.0016 | 0.0004 | 0.0201 | 0.0058 | 0.0123 | 0.0076 | 0.0019 |
| Primary | 0.1–0.7 | 0.0121 | 0.0186 | 0.0257 | 0.0018 | 0.0041 | 0.0240 | 0.0045 | 0.0113 | 0.0225 | 0.0023 | |
| Transition | 0.7–0.9 | 0.0293 | 0.0226 | 0.0140 | 0.0058 | 0.0254 | 0.0213 | 0.0317 | 0.0173 | 0.0108 | 0.0014 | |
| Secondary | 0.9–1.0 | 0.0172 | 0.0169 | 0.0309 | 0.0309 | 0.0253 | 0.0136 | 0.0172 | 0.0107 | 0.0163 | 0.0006 | |
| Used 6 | Initial | 0.0–0.1 | 0.0008 | 0.0035 | 0.0005 | 0.0004 | 0.0048 | 0.0054 | 0.0055 | 0.0010 | 0.0018 | 0.0015 |
| Primary | 0.1–0.8 | 0.0061 | 0.0051 | 0.0193 | 0.0012 | 0.0062 | 0.0038 | 0.0324 | 0.0035 | 0.0023 | 0.0012 | |
| Transition | 0.8–0.95 | 0.0125 | 0.0073 | 0.0157 | 0.0081 | 0.0075 | 0.0055 | 0.0083 | 0.0047 | 0.0012 | 0.0004 | |
| Secondary | 0.95–1.0 | 0.0050 | 0.0036 | 0.0258 | 0.0258 | 0.0046 | 0.0033 | 0.0031 | 0.0021 | 0.0014 | 0.0005 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanders, B.; Cant, E.; Kelly, C.A.; Jenkins, M. The Effect of Powder Re-Use on the Coalescence Behaviour and Isothermal Crystallisation Kinetics of Polyamide 12 within Powder Bed Fusion. Polymers 2024, 16, 612. https://doi.org/10.3390/polym16050612
Sanders B, Cant E, Kelly CA, Jenkins M. The Effect of Powder Re-Use on the Coalescence Behaviour and Isothermal Crystallisation Kinetics of Polyamide 12 within Powder Bed Fusion. Polymers. 2024; 16(5):612. https://doi.org/10.3390/polym16050612
Chicago/Turabian StyleSanders, Benjamin, Edward Cant, Catherine A. Kelly, and Michael Jenkins. 2024. "The Effect of Powder Re-Use on the Coalescence Behaviour and Isothermal Crystallisation Kinetics of Polyamide 12 within Powder Bed Fusion" Polymers 16, no. 5: 612. https://doi.org/10.3390/polym16050612
APA StyleSanders, B., Cant, E., Kelly, C. A., & Jenkins, M. (2024). The Effect of Powder Re-Use on the Coalescence Behaviour and Isothermal Crystallisation Kinetics of Polyamide 12 within Powder Bed Fusion. Polymers, 16(5), 612. https://doi.org/10.3390/polym16050612