Numerical Modelling of the Thermoforming Behaviour of Thermoplastic Honeycomb Composite Sandwich Laminates
Abstract
1. Introduction
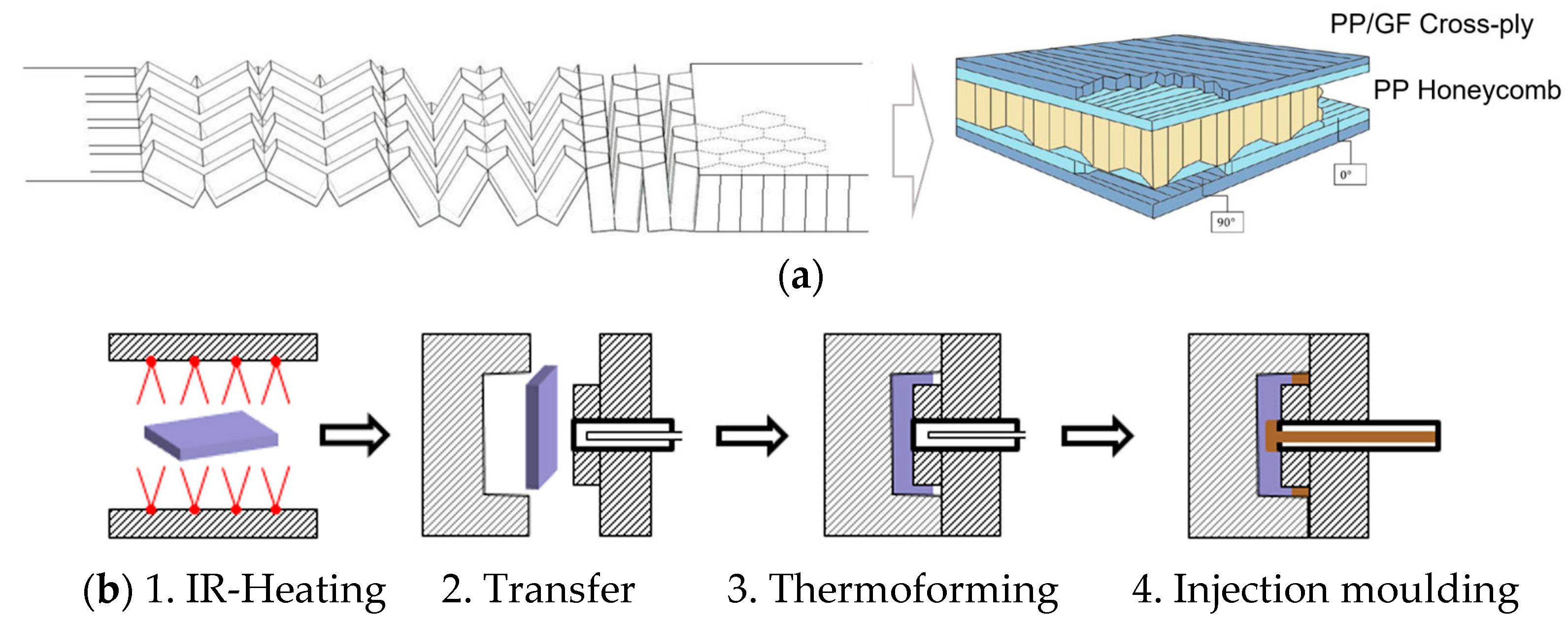
2. Thermoplastic Sandwich Forming
3. Materials and Finite Element Modelling
3.1. Sandwich Material Description
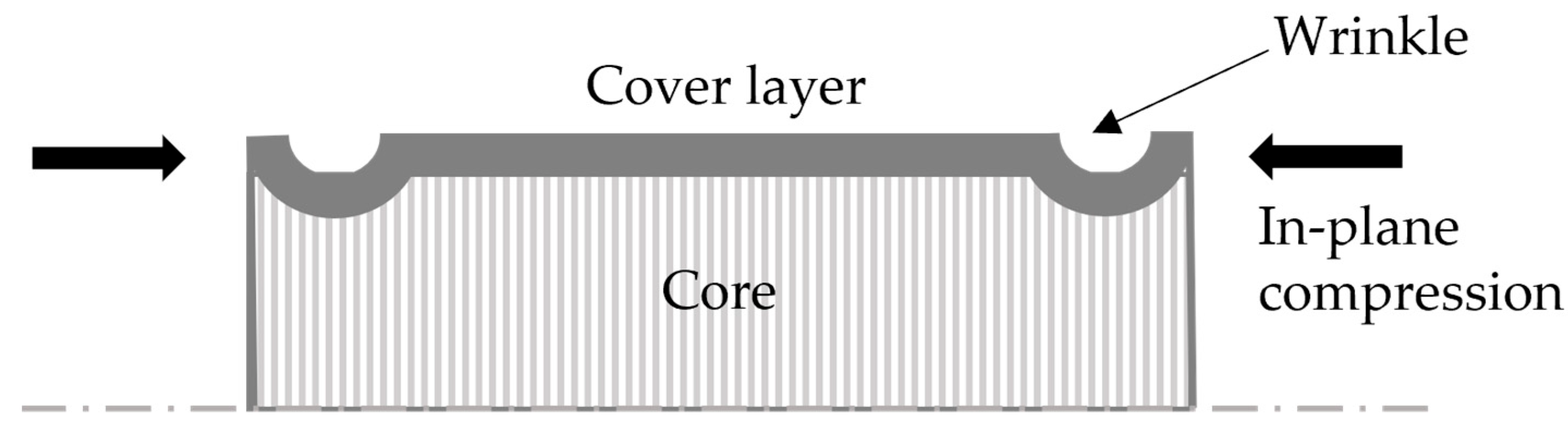
3.2. Cover Layers Wrinkle Analysis
3.3. Spatial Discretisation of Organosandwich
3.4. Thermo-Mechanical Modelling
- is the temperature at point and for time ;
- is the internal strength of heat source;
- is the density;
- is the specific heat;
- are thermal conductivities in the directions, respectively, at initial conditions , temperature is [14].
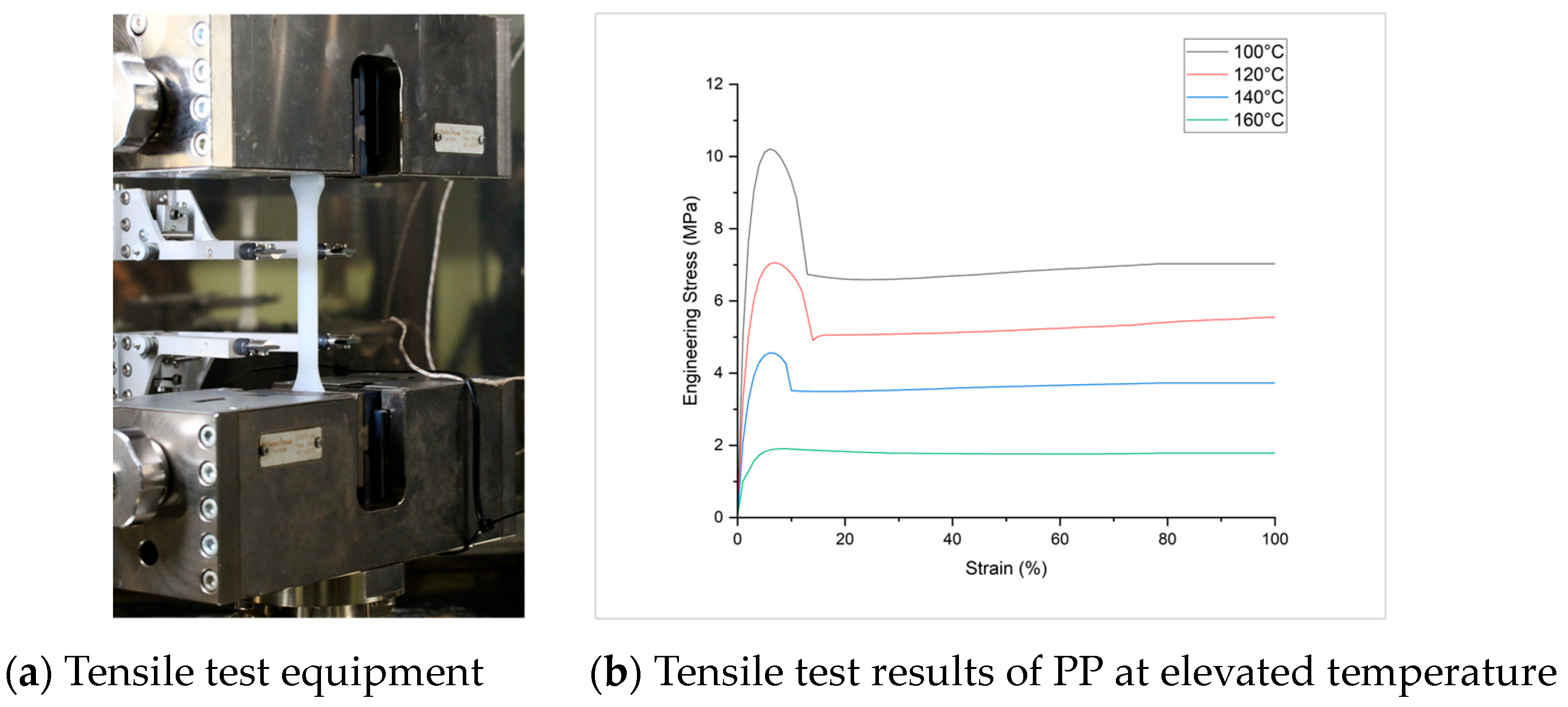
3.5. Materials and Methods
3.6. Boundary Conditions
4. Results and Discussion
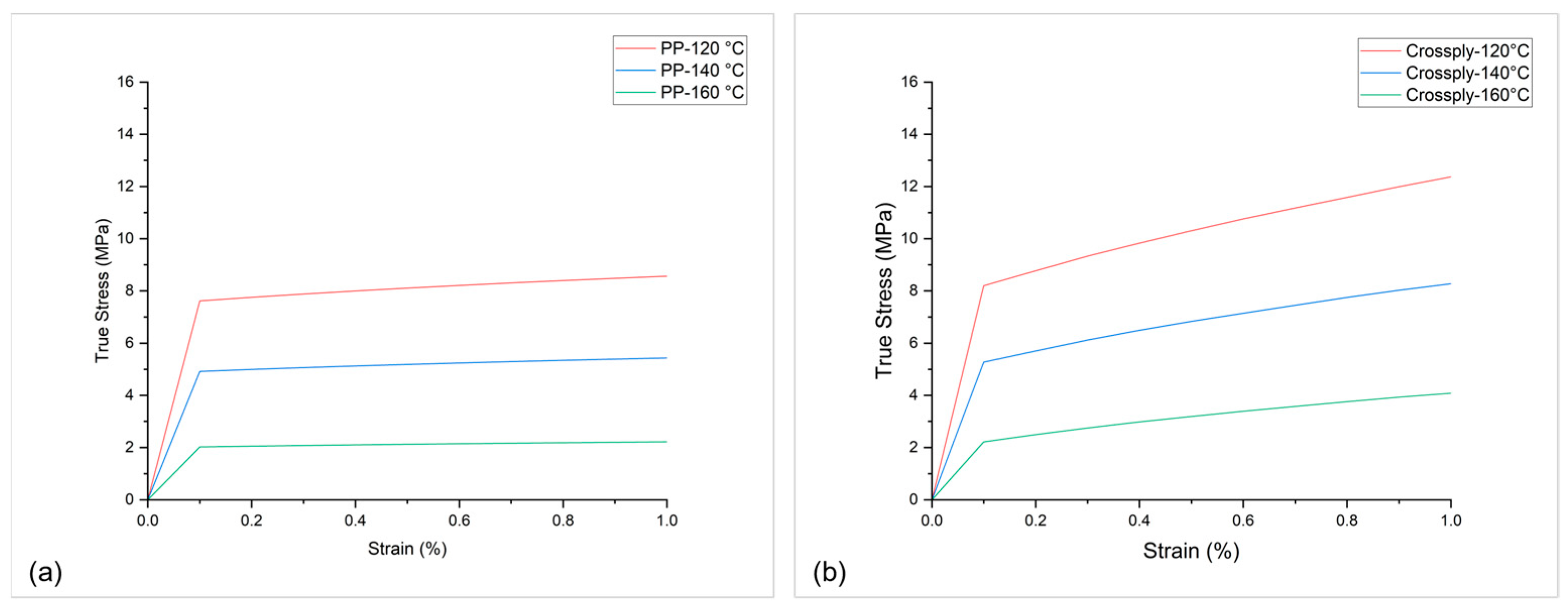
4.1. Thermoforming
4.2. Critical Stress Analysis
4.3. Considerations and Product Optimisation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, X. Investigation on Processing and Mechanical Properties of the Continuously Produced Thermoplastic Honeycomb. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2006. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 0-521-49911-9. [Google Scholar]
- Pflug, J.; Vangrimde, B.; Verpoest, I.; Bratfisch, P.; Vandepitte, D. Honeycomb Core Materials: New Concepts for Continuous Production. Sampe J. 2003, 39, 22–30. [Google Scholar]
- Minupala, V.K.; Glaesser, T.; Zscheyge, M. Simulation of thermoforming process of thermoplastic based sandwich laminates made of cross-ply and honeycomb core. In Proceedings of the 5th International Conference & Exhibition on Thermoplastic Composites, Bremen, Germany, 13–15 October 2020. [Google Scholar]
- Pflug, J.; Zerling, F.; Schlimper, R.; Minupala, V.K.; Glaesser, T. (Eds.) Continuous Production of Thermoplastic Honeycomb Sandwich Panels for Thermoformed and Functionalized Automotive Parts. In Proceedings of the International Conference on Sandwich Structures (ICSS-13), Knoxville, TN, USA, 23–26 October 2022. [Google Scholar]
- Gläßer, T. Beitrag zur Großserientauglichen Fertigung von Thermoplastischen Endlosfaserverstärkten Sandwichbauteilen. Ph.D. Thesis, Otto-von-Guericke-University, Magdeburg, Germany, 2022. [Google Scholar]
- ThermHex GmbH. ThermHex Wabenkerne—Das Leistungsstarke Kernmaterial für Leichtbauanwendungen. Available online: https://thermhex.com/de (accessed on 23 November 2018).
- Bhattacharyya, D. (Ed.) Composite Sheet Forming; Elsevier: Amsterdam, The Netherlands; Oxford, UK, 1997; ISBN 0-444-82641-6. [Google Scholar]
- Robert, P.L.; Weichuan, L.; Uy, M. Facesheet Wrinkling in Sandwich Structures; NASA/CR-1999-208994; NASA: Washington, DC, USA, 1999. [Google Scholar]
- William, D. Sandwich Contruction: A Practical Approach for the Use of Designers; HM Stationery Office: Richmond, UK, 1947. [Google Scholar]
- Belytschko, T.; Organ, D.; Krongauz, Y. A coupled finite element-element-free Galerkin method. Comput. Mech. 1995, 17, 186–195. [Google Scholar] [CrossRef]
- Fourier, J. Theorie Analytique de la Chaleur (1822); Chez Firmin Didot, père et fils; Elsevier Science: Amsterdam, The Netherlands, 2005. [Google Scholar] [CrossRef]
- Li, G.; Cinefra, M.; Carrera, E. Coupled thermo-mechanical finite element models with node-dependent kinematics for multi-layered shell structures. Int. J. Mech. Sci. 2020, 171, 105379. [Google Scholar] [CrossRef]
- Zhang, S.; Cai, Y.; Wang, H.; Li, E.; Li, G.; Wu, Y. A fast reanalysis solver for 3D transient thermo-mechanical problems with temperature-dependent materials. Comput. Struct. 2020, 238, 106298. [Google Scholar] [CrossRef]
- Liu, G.R. A generalized gradient smoothing technique and the smoothed bilinear form for Galerkin formulation of a wide class of computational methods. Int. J. Comput. Methods 2008, 5, 199–236. [Google Scholar] [CrossRef]
- Liu, Y.; Long, H.; Zhang, S.; Song, J.; Zhou, Q.; Wei, Y. Coupling effect of strain gradient strengthening and thermal softening on the microscale plastic behavior of metallic materials. Eur. J. Mech. A Solids 2023, 102, 105117. [Google Scholar] [CrossRef]
- ISO 527-2:2012; Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics. Beuth: Berlin, Germany, 2012.
- Heimbs, S. Sandwichstrukturen mit Wabenkern: Experimentelle und Numerische Analyse des Schädigungsverhaltens unter Statischer und Kurzzeitdynamischer Belastung. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2008. [Google Scholar]
- Advani, S.G.; Hsiao, K.-T. Manufacturing Techniques for POLYMER Matrix Composites (PMCs); Woodhead: Cambridge, UK, 2012; ISBN 978-0-85709-625-8. [Google Scholar]
- Minupala, V.K. Numerical Analysis of Thermoforming Behavior of Sandwich Components with Continuous Fiber Reinforced Thermoplastic Face Sheets and Honeycomb Core. Master’s Thesis, University Duisburg-Essen, Essen, Germany, 17 December 2018. [Google Scholar]
- Haanappel, S. Forming of UD Fibre Reinforced Thermoplastics: A Critical Evaluation of Intra-Ply Shear: A Critical Evaluation of Intra-Ply Shear; University of Twente: Enschede, The Netherlands, 2013. [Google Scholar]
- Minupala, V.K.; Vynhal, M.; John, M.; Zscheyge, M. Simulation of process techniques involved in advanced manufacturing of CFRTP composite parts. In Proceedings of the 6th International Conference & Exhibition on Thermoplastic Composites, Bremen, Germany, 12–13 October 2022. [Google Scholar]
- HyWaSand Effiziente Sandwich-Leichtbaustrukturen mit Hoher Oberflächengute. Hybride Materialien | HyWaSand. Available online: https://www.werkstoffplattform-hymat.de/Group/HyWaSand/Pages (accessed on 15 December 2023).
- Glaesser, T.; Stache, P.; Zscheyge, M.; Koelzig, K. International Patent on Method for Producing a Sandwichcomposite Component with Pressed Two- or Three-Dimensional Shape and Such a Sandwich Component. WO Patent 2020/200796 A2, 2020. Fraunhofer-Gesellschaft zur Förderung der Angewandten Forschung E. V.. [Google Scholar]
- Glaesser, T.; Stache, P.; Zscheyge, M. TS-Moulding Fertigungstechnologie zur Großserientauglichen Herstellung Endlosfaserverstärkter Thermoplastsandwichstrukturen: Fachaufsatz Werkstoffe, Konstruktion; VDI-Fachmedien: Dusseldorf, Germany, 2022. [Google Scholar]
- Nartey, M.; Zhang, T.; Gong, B.; Wang, J.; Peng, S.; Wang, H.; Peng, H.-X. Understanding the impact of fibre wrinkle architectures on composite laminates through tailored gaps and overlaps. Compos. Part B Eng. 2020, 196, 108097. [Google Scholar] [CrossRef]


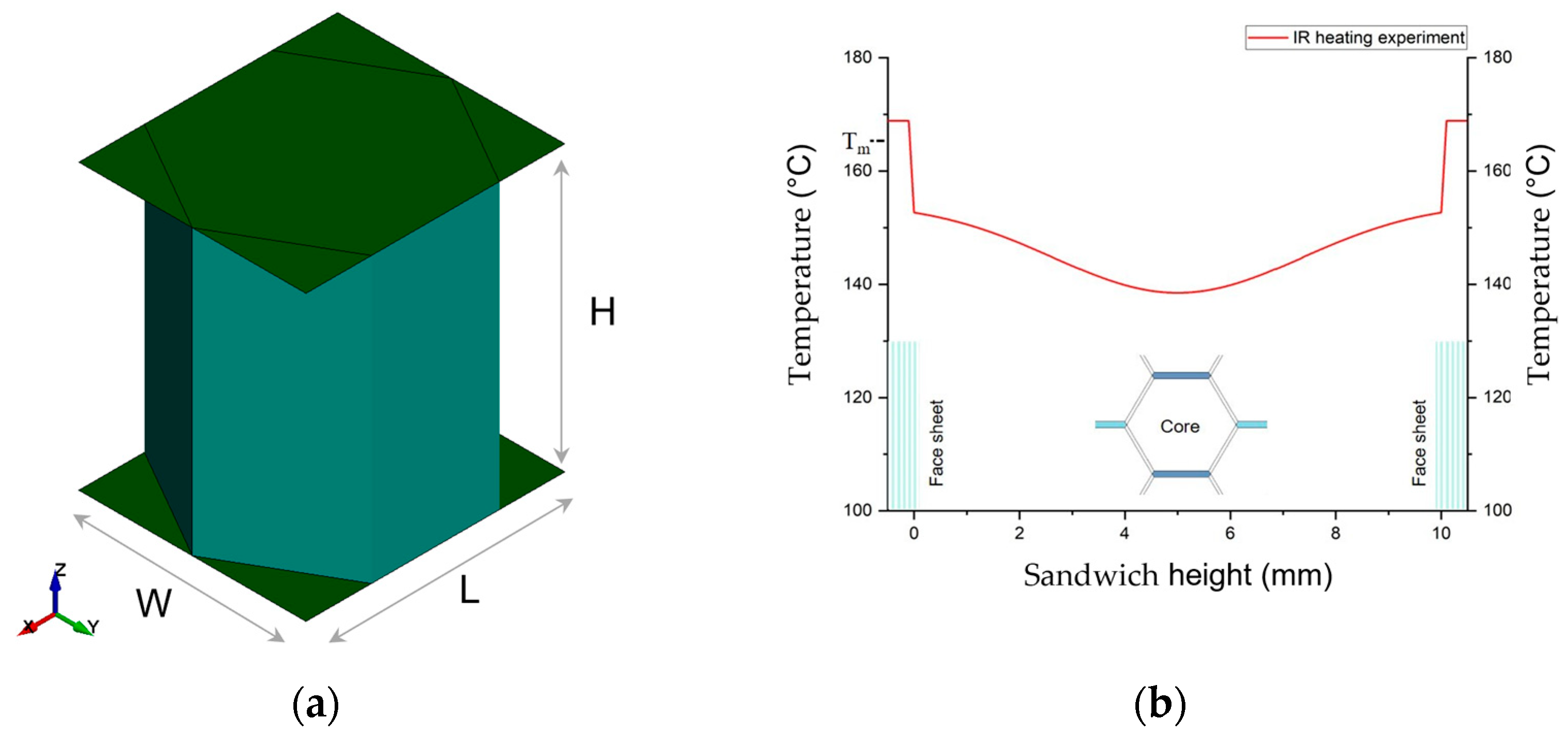




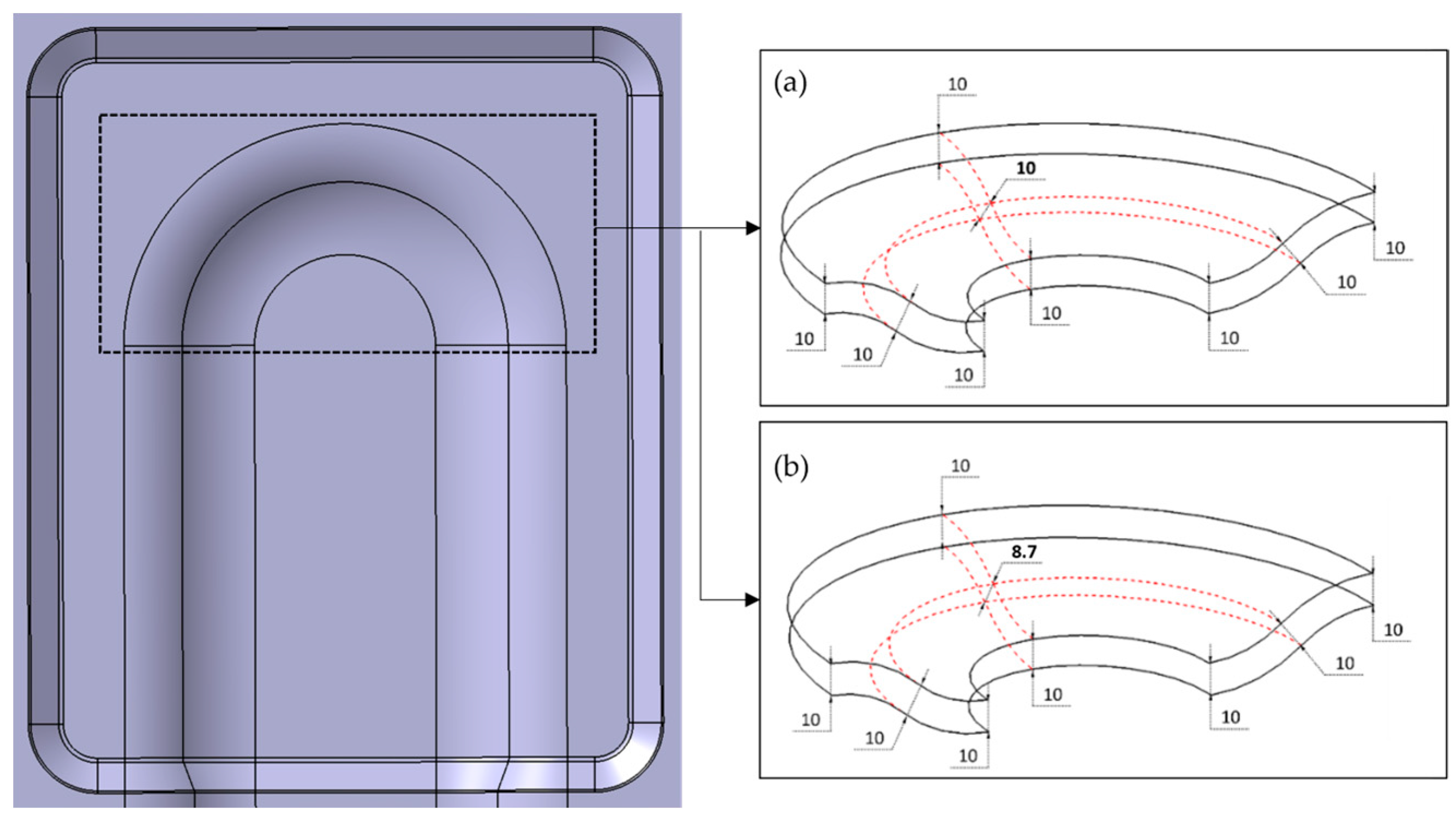
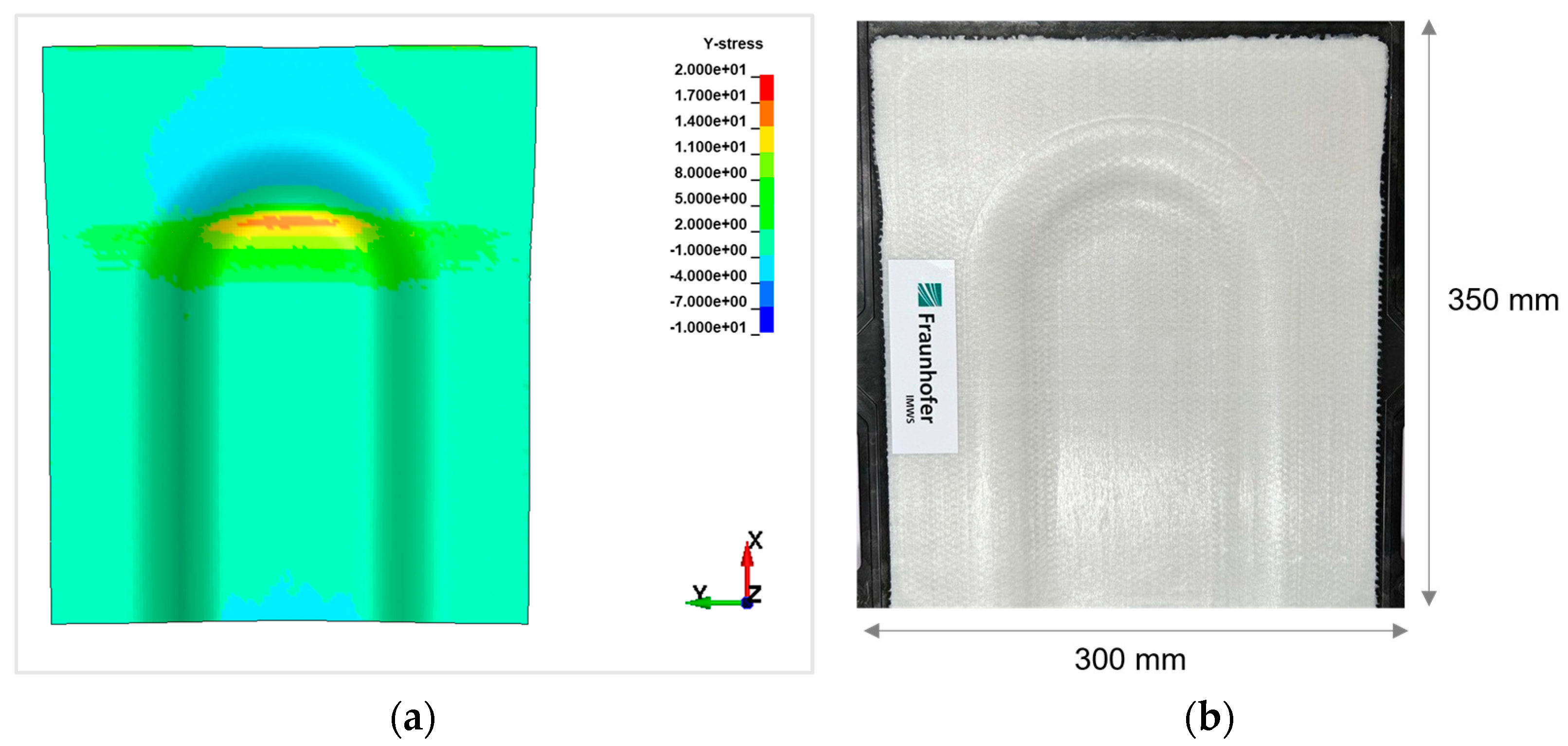
| Sandwich Entity | Dimension |
|---|---|
| Sandwich thickness | 12 mm |
| Cover layer thickness | 0.5 mm |
| Honeycomb core thickness | 11 mm |
| Cell size | 5 mm |
| Standard panel dimension | 1200 mm × 2500 mm (L × W) |
| Weight per unit density | 3120–3240 g/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minupala, V.K.; Zscheyge, M.; Glaesser, T.; Feldmann, M.; Altenbach, H. Numerical Modelling of the Thermoforming Behaviour of Thermoplastic Honeycomb Composite Sandwich Laminates. Polymers 2024, 16, 594. https://doi.org/10.3390/polym16050594
Minupala VK, Zscheyge M, Glaesser T, Feldmann M, Altenbach H. Numerical Modelling of the Thermoforming Behaviour of Thermoplastic Honeycomb Composite Sandwich Laminates. Polymers. 2024; 16(5):594. https://doi.org/10.3390/polym16050594
Chicago/Turabian StyleMinupala, Varun Kumar, Matthias Zscheyge, Thomas Glaesser, Maik Feldmann, and Holm Altenbach. 2024. "Numerical Modelling of the Thermoforming Behaviour of Thermoplastic Honeycomb Composite Sandwich Laminates" Polymers 16, no. 5: 594. https://doi.org/10.3390/polym16050594
APA StyleMinupala, V. K., Zscheyge, M., Glaesser, T., Feldmann, M., & Altenbach, H. (2024). Numerical Modelling of the Thermoforming Behaviour of Thermoplastic Honeycomb Composite Sandwich Laminates. Polymers, 16(5), 594. https://doi.org/10.3390/polym16050594








