Optimization of Charpy Impact Strength of Tough PLA Samples Produced by 3D Printing Using the Taguchi Method
Abstract
1. Introduction
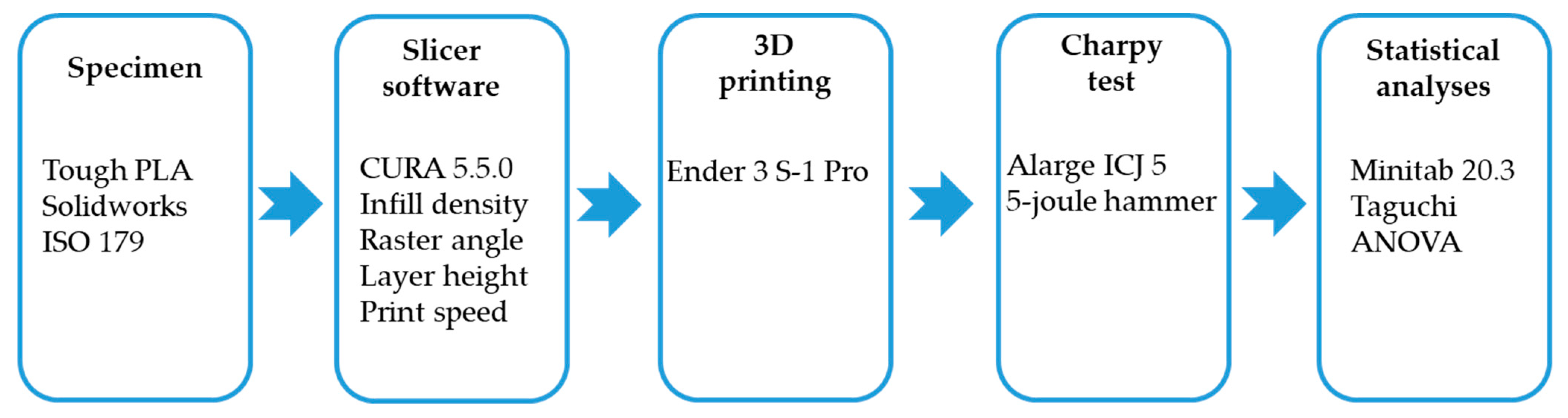
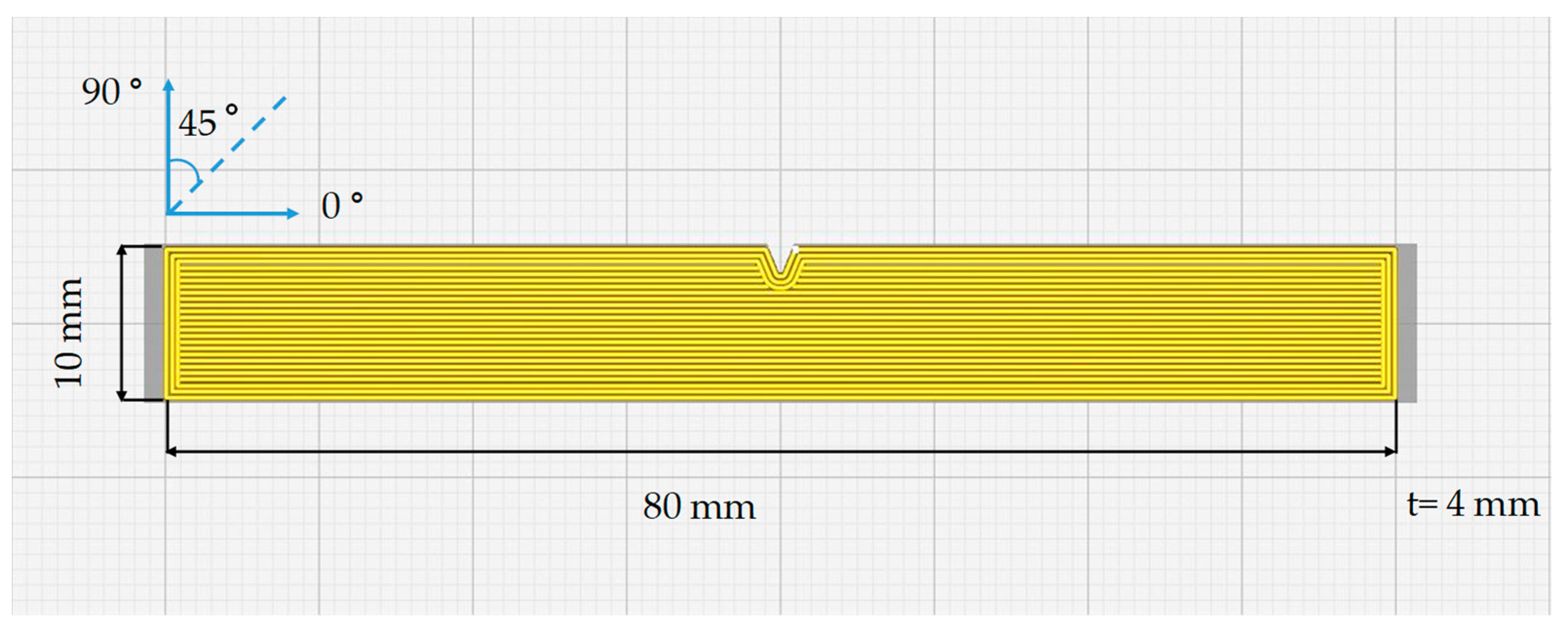
2. Materials and Methods
3. Results and Discussion
4. Conclusions
- Charpy impact strength results varied within a range of 9.7% (34.66 kJ/m2 to 38.01 kJ/m2).
- In Taguchi optimization, the S/N response table revealed that printing speed had the most significant effect, followed by infill density, layer height, and raster angle.
- The impact strength value of 38.54 kJ/m2 obtained with the optimized parameter set (A4B4C4D3) and the Taguchi method is 1.39% higher than the value of 38.01 kJ/m2 obtained in the experimental design. The results show that the optimum 3D printing parameters are infill density (100%), raster angle (45/−45°), layer height (0.25 mm), and print speed (75 mm/s).
- ANOVA highlighted infill density (38.93%) and print speed (36.51%) as influential factors.
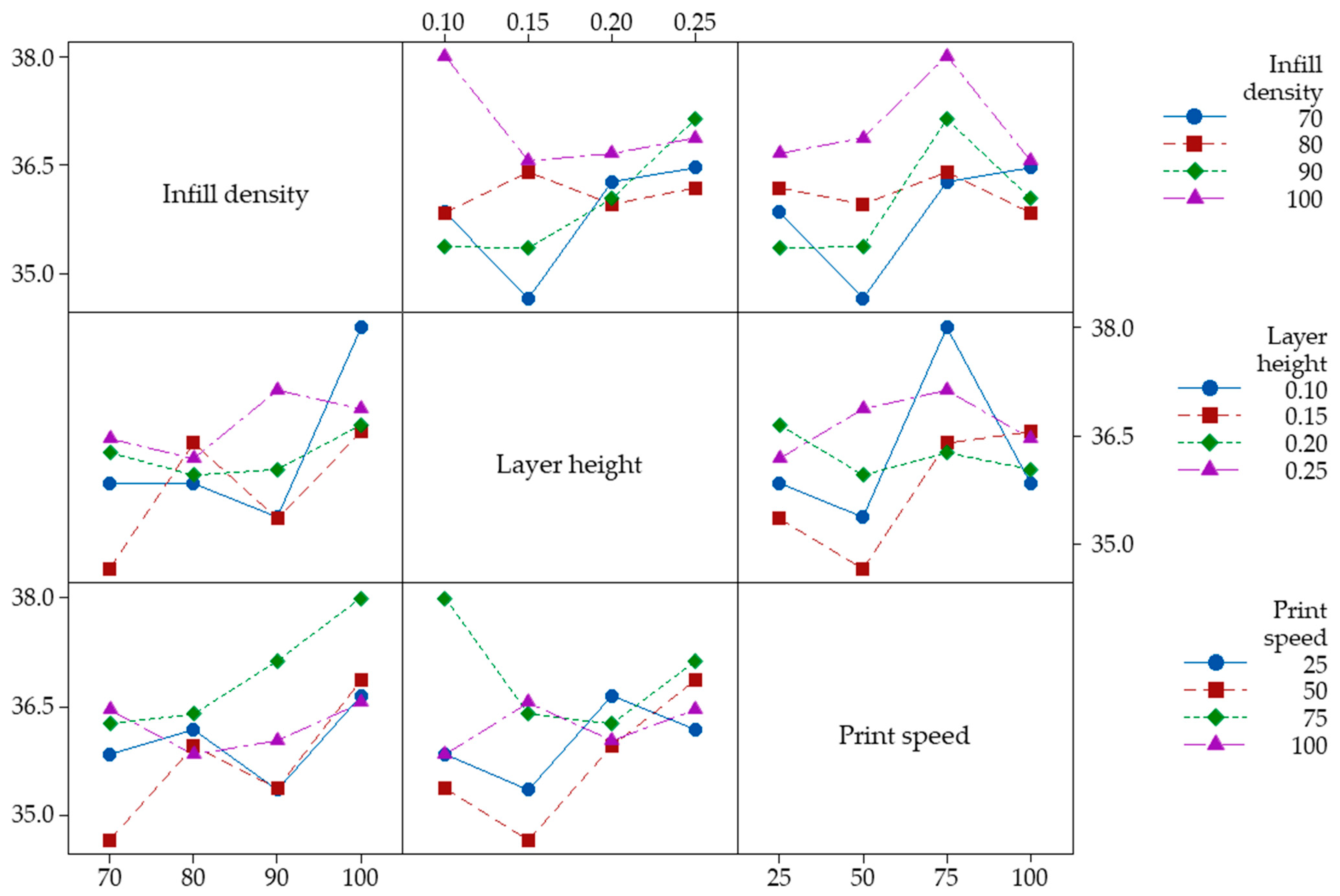
- Interaction plots demonstrated strong interactions between parameters, especially emphasizing the positive impact of 100% infill density and 75 mm/s print speed on impact strength.
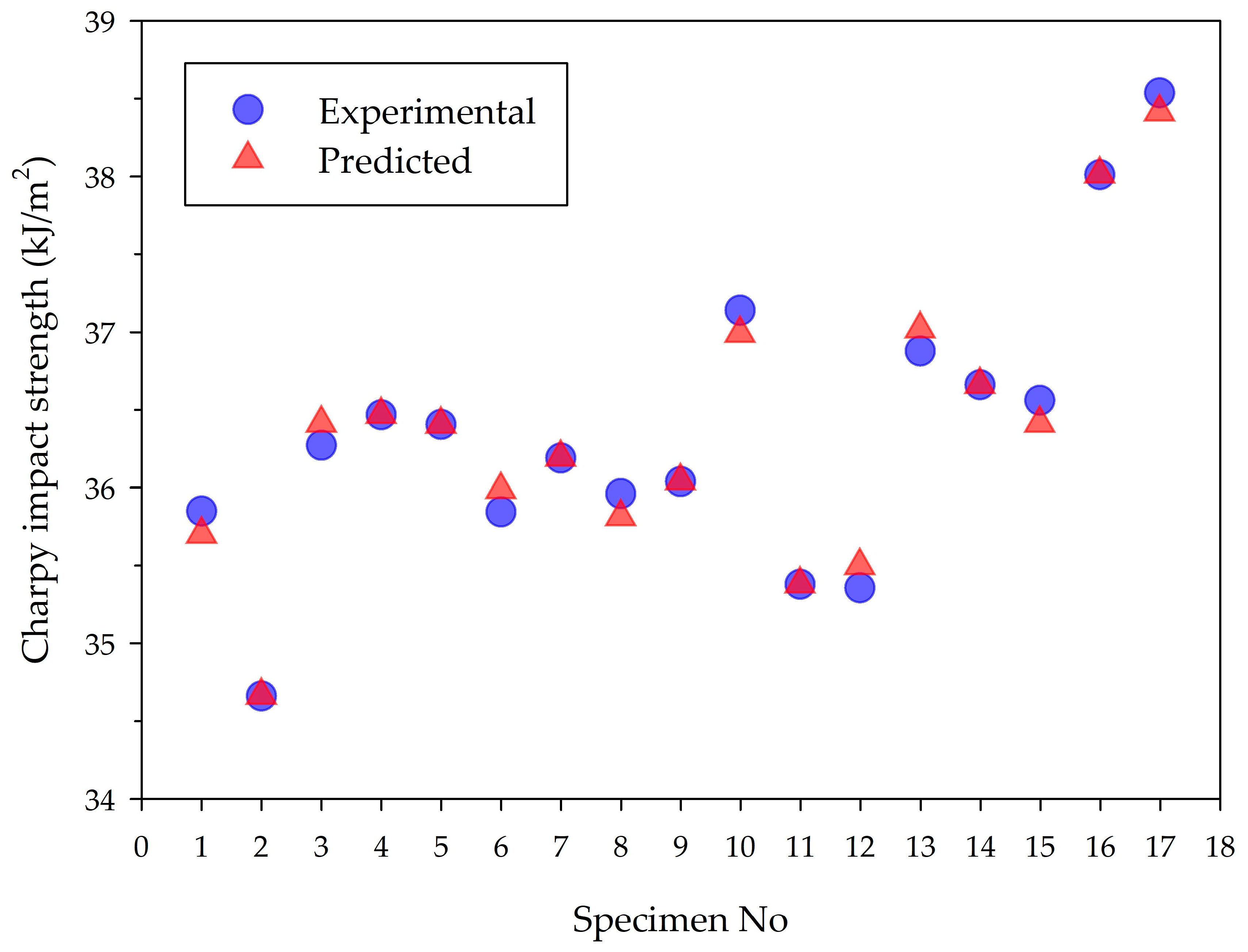
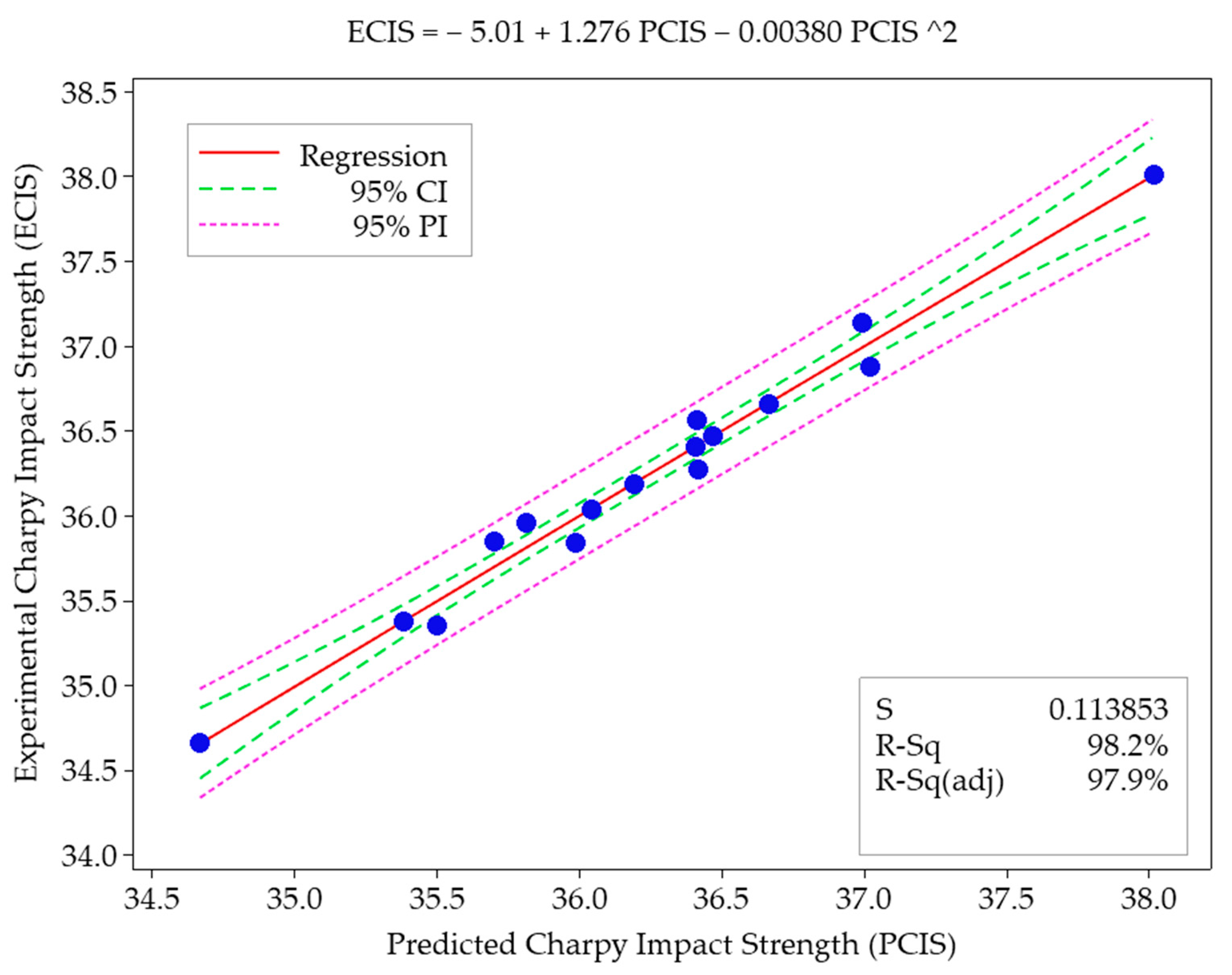
- The regression model successfully predicted impact strength (R2 = 98.16%), validated with a low prediction error (0.34%).
- The Taguchi method effectively optimized FDM parameters for enhanced tough PLA impact strength.
- Fracture surface analysis revealed that optimized specimens with higher infill density and specific raster angles exhibited more ductile fractures than lower performing specimens.
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, S.; Singh, M.; Prakash, C.; Gupta, M.K.; Mia, M.; Singh, R. Optimization and Reliability Analysis to Improve Surface Quality and Mechanical Characteristics of Heat-Treated Fused Filament Fabricated Parts. Int. J. Adv. Manuf. Technol. 2019, 102, 1521–1536. [Google Scholar] [CrossRef]
- Tüfekci, K.; Çakan, B.G.; Küçükakarsu, V.M. Stress Relaxation of 3D Printed PLA of Various Infill Orientations under Tensile and Bending Loadings. J. Appl. Polym. Sci. 2023, 140, e54463. [Google Scholar] [CrossRef]
- Prajapati, A.R.; Dave, H.K.; Raval, H.K. Effect of Fiber Volume Fraction on the Impact Strength of Fiber Reinforced Polymer Composites Made by FDM Process. Mater. Today Proc. 2021, 44, 2102–2106. [Google Scholar] [CrossRef]
- Tutar, M. A Comparative Evaluation of the Effects of Manufacturing Parameters on Mechanical Properties of Additively Manufactured PA and CF-Reinforced PA Materials. Polymers 2023, 15, 38. [Google Scholar] [CrossRef]
- Başcı, Ü.G.; Yamanoğlu, R. New Generation Production Technology: Additive Manufacturing via FDM. Int. J. 3D Print Technol. Digit. Ind. 2021, 5, 339–352. [Google Scholar]
- Doǧan, O.; Kamer, M.S. Experimental Investigation of the Creep Behavior of Test Specimens Manufactured with Fused Filament Fabrication Using Different Manufacturing Parameters. J. Fac. Eng. Archit. Gazi Univ. 2023, 38, 1839–1848. [Google Scholar]
- İriç, S. Experimental Investigation on Effect to the Specific Strength of FDM Fabrication Parameters Using Taguchi Method. Sak. Univ. J. Sci. 2020, 24, 984–990. [Google Scholar] [CrossRef]
- Wang, X.; Shujaat, S.; Shaheen, E.; Jacobs, R. Accuracy of Desktop versus Professional 3D Printers for Maxillofacial Model Production. A Systematic Review and Meta-Analysis. J. Dent. 2021, 112, 103741. [Google Scholar] [CrossRef]
- Mazzanti, V.; Malagutti, L.; Mollica, F. FDM 3D Printing of Polymers Containing Natural Fillers: A Review of Their Mechanical Properties. Polymers 2019, 11, 1094. [Google Scholar] [CrossRef]
- Tunçel, O. Optimizing Printing Parameters for Enhanced Mechanical Properties of 3D Printed PLA Octet Lattice Structures. Eur. Mech. Sci. 2023, 7, 278–284. [Google Scholar] [CrossRef]
- Bolat, Ç.; Ergene, B. An Experimental Effort on Impact Properties of Polylactic Acid Samples Manufactured by Additive Manufacturing. Düzce Univ. J. Sci. Technol. 2023, 11, 998–1013. [Google Scholar] [CrossRef]
- Chokshi, H.; Shah, D.B.; Patel, K.M.; Joshi, S.J. Experimental Investigations of Process Parameters on Mechanical Properties for PLA during Processing in FDM. Adv. Mater. Process. Technol. 2022, 8, 696–709. [Google Scholar] [CrossRef]
- Cuiffo, M.A.; Snyder, J.; Elliott, A.M.; Romero, N.; Kannan, S.; Halada, G.P. Impact of the Fused Deposition (FDM) Printing Process on Polylactic Acid (PLA) Chemistry and Structure. Appl. Sci. 2017, 7, 579. [Google Scholar] [CrossRef]
- Tan, E. Experimentally Assessing the Wear Characteristics of 3D-Printed PLA and Tough PLA Materials Based on Fused Deposition Modeling. Gazi J. Eng. Sci. 2023, 9, 213–226. [Google Scholar] [CrossRef]
- Eda, H.T.; Husnu, Y.E. Extrusion-Based 3D Printing Applications of PLA Composites: A Review. Coatings 2021, 11, 390. [Google Scholar]
- Naveed, N. Investigating the Material Properties and Microstructural Changes of Fused Filament Fabricated PLA and Tough-PLA Parts. Polymers 2021, 13, 1487. [Google Scholar] [CrossRef]
- Al-Tamimi, A.A.; Pandžić, A.; Kadrić, E. Investigation and Prediction of Tensile, Flexural, and Compressive Properties of Tough PLA Material Using Definitive Screening Design. Polymers 2023, 15, 4169. [Google Scholar] [CrossRef]
- Beylergil, B.; Al-Nadhari, A.; Yildiz, M. Optimization of Charpy-Impact Strength of 3D-Printed Carbon Fiber/Polyamide Composites by Taguchi Method. Polym. Compos. 2023, 44, 2846–2859. [Google Scholar] [CrossRef]
- Ansari, A.A.; Kamil, M. Izod Impact and Hardness Properties of 3D Printed Lightweight CF-Reinforced PLA Composites Using Design of Experiment. Int. J. Light. Mater. Manuf. 2022, 5, 369–383. [Google Scholar] [CrossRef]
- Atakok, G.; Kam, M.; Koc, H.B. Tensile, Three-Point Bending and Impact Strength of 3D Printed Parts Using PLA and Recycled PLA Filaments: A Statistical Investigation. J. Mater. Res. Technol. 2022, 18, 1542–1554. [Google Scholar] [CrossRef]
- Erkendirci, Ö.F. Charpy Impact Behavior of Plain Weave S-2 Glass/HDPE Thermoplastic Composites. J. Compos. Mater. 2012, 46, 2835–2841. [Google Scholar] [CrossRef]
- Kam, M.; İpekçi, A.; Şengül, Ö. Investigation of the Effect of FDM Process Parameters on Mechanical Properties of 3D Printed PA12 Samples Using Taguchi Method. J. Thermoplast. Compos. Mater. 2023, 36, 307–325. [Google Scholar] [CrossRef]
- Lee, D.; Wu, G.Y. Parameters Affecting the Mechanical Properties of Three-Dimensional (3D) Printed Carbon Fiber-Reinforced Polylactide Composites. Polymers 2020, 12, 2456. [Google Scholar] [CrossRef] [PubMed]
- Lambiase, F.; Stamopoulos, A.G.; Pace, F.; Paoletti, A. Influence of the Deposition Pattern on the Interlayer Fracture Toughness of FDM components. Int. J. Adv. Manuf. Technol. 2023, 128, 4269–4281. [Google Scholar] [CrossRef]
- Sharif, A.; Khan, H.; Bashir, N.; Alam, W. Parametric Optimization and Evaluating Mechanical Properties of Poly Lactic Acid Proceed by FDM Additive Manufacturing. J. Mater. Manuf. 2023, 2, 11–20. [Google Scholar]
- Zisopol, D.G.; Portoaca, A.I.; Tanase, M. Improving the Impact Resistance through Annealing in PLA 3D Printed Parts. Eng. Technol. Appl. Sci. Res. 2023, 13, 11768–11772. [Google Scholar] [CrossRef]
- Tanveer, M.Q.; Haleem, A.; Suhaib, M. Effect of Variable Infill Density on Mechanical Behaviour of 3-D Printed PLA Specimen: An Experimental Investigation. SN Appl. Sci. 2019, 1, 1701. [Google Scholar] [CrossRef]
- Nagendra, J.; Prasad, M.S.G. FDM Process Parameter Optimization by Taguchi Technique for Augmenting the Mechanical Properties of Nylon–Aramid Composite Used as Filament Material. J. Inst. Eng. Ser. C 2020, 101, 313–322. [Google Scholar] [CrossRef]
- Solouki, A.; Aliha, M.; Makui, A. A Methodology for Optimizing Impact Strength, Dimensional Accuracy and Costs of Manufacturing with Three-Dimensional Printing of Polylactic Acid. Arab. J. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Rubies, E.; Palacín, J. Design and FDM/FFF Implementation of a Compact Omnidirectional Wheel for a Mobile Robot and Assessment of ABS and PLA Printing Materials. Robotics 2020, 9, 43. [Google Scholar] [CrossRef]
- Anaç, N. Assessment of Adhesively Bonded Joints of Similar and Dissimilar Materials: Industrial Case Study. Processes 2023, 11, 1312. [Google Scholar] [CrossRef]
- Lluch-Cerezo, J.; Benavente, R.; Meseguer, M.D.; García-Manrique, J.A. Effect of a Powder Mould in the Post-Process Thermal Treatment of ABS Parts Manufactured with FDM Technology. Polymers 2021, 13, 2422. [Google Scholar] [CrossRef] [PubMed]
- López Taborda, L.L.; Pérez, E.; Quintero, D.; Noguera Polania, J.F.; Zambrano Rodriguez, H.; Maury, H.; Esparragoza, I.E. Experimental Study of Resin Coating to Improve the Impact Strength of Fused Filament Fabrication Process Pieces. Rapid Prototyp. J. 2021, 27, 475–486. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Li, S.; Si, L.; Peng, J.; Hu, Y. Mechanical Property Parametric Appraisal of Fused Deposition Modeling Parts Based on the Gray Taguchi Method. Int. J. Adv. Manuf. Technol. 2017, 89, 2387–2397. [Google Scholar] [CrossRef]
- Ahmed, H.; Hussain, G.; Gohar, S.; Ali, A.; Alkahtani, M. Impact Toughness of Hybrid Carbon Fiber-PLA/ABS Laminar Composite Produced through Fused Filament Fabrication. Polymers 2021, 13, 3057. [Google Scholar] [CrossRef] [PubMed]
- Başar, G.; Kahraman, F.; Kuş, H. Optimization of Transverse Rupture Strength Using the Taguchi Method for Fly Ash Reinforced Bronze-Based Composite Friction Materials. El-Cezerî J. Sci. Eng. 2018, 5, 626–634. [Google Scholar]
- Tutar, M.; Aydin, H.; Yuce, C.; Yavuz, N.; Bayram, A. The Optimisation of Process Parameters for Friction Stir Spot-Welded AA3003-H12 Aluminium Alloy Using a Taguchi Orthogonal Array. Mater. Des. 2014, 63, 789–797. [Google Scholar] [CrossRef]
- Canbolat, A.S.; Bademlioglu, A.H.; Kaynakli, O. Thermohydraulic Performance Optimization of Automobile Radiators Using Statistical Approaches. J. Therm. Sci. Eng. Appl. 2022, 14, 051014. [Google Scholar] [CrossRef]
- Öktem, H.; Kır, D.; Simooğlu Sarı, E.; Çöl, M. Determination of Optimum Injection Process Parameters Affecting Mechanical Properties of Plastic Products by Taguchi Method. Mach. Des. Manuf. J. 2016, 14, 8–16. [Google Scholar]
- Yuce, B.E.; Nielsen, P.V.; Wargocki, P. The Use of Taguchi, ANOVA, and GRA Methods to Optimize CFD Analyses of Ventilation Performance in Buildings. Build. Environ. 2022, 225, 109587. [Google Scholar] [CrossRef]
- Akkuş, H.; Yaka, H. Experimental and Statistical Investigation of the Effect of Cutting Parameters on Surface Roughness, Vibration and Energy Consumption in Machining of Titanium 6Al-4V ELI (Grade 5) Alloy. Meas. J. Int. Meas. Confed. 2021, 167, 108465. [Google Scholar] [CrossRef]
- Kumar Mishra, P.; Ponnusamy, S.; Reddy Nallamilli, M.S. The Influence of Process Parameters on the Impact Resistance of 3D Printed PLA Specimens under Water-Absorption and Heat-Treated Conditions. Rapid Prototyp. J. 2021, 27, 1108–1123. [Google Scholar] [CrossRef]
- Kumar, K.R.; Mohanavel, V.; Kiran, K. Mechanical Properties and Characterization of Polylactic Acid/Carbon Fiber Composite Fabricated by Fused Deposition Modeling. J. Mater. Eng. Perform. 2022, 31, 4877–4887. [Google Scholar] [CrossRef]
- Kekik, M.; Aslanlar, S.; Apay, S. Optimization of Welding Parameters of AHSS Sheet Metals in Electric Resistance Spot Welding by Taguchi Method. Düzce Univ. J. Sci. Technol. 2021, 9, 702–711. [Google Scholar]
- Mohamed, O.A.; Masood, S.H.; Bhowmik, J.L.; Nikzad, M.; Azadmanjiri, J. Effect of Process Parameters on Dynamic Mechanical Performance of FDM PC/ABS Printed Parts Through Design of Experiment. J. Mater. Eng. Perform. 2016, 25, 2922–2935. [Google Scholar] [CrossRef]
- Gao, G.; Xu, F.; Xu, J. Parametric Optimization of FDM Process for Improving Mechanical Strengths Using Taguchi Method and Response Surface Method: A Comparative Investigation. Machines 2022, 10, 750. [Google Scholar] [CrossRef]
- Equbal, A.; Sood, A.K.; Equbal, M.I.; Badruddin, I.A.; Khan, Z.A. RSM Based Investigation of Compressive Properties of FDM Fabricated Part. CIRP J. Manuf. Sci. Technol. 2021, 35, 701–714. [Google Scholar] [CrossRef]
- Kaya, A.; Aslan, M.; Yilmaz, N.F.; Kurt, H.İ. Taguchi Analysis of Apparent Densities of Al-Mg-Sic Composites. El-Cezeri J. Sci. Eng. 2020, 7, 773–780. [Google Scholar]
- Raju, R.; Varma, M.M.; Baghel, P.K. Optimization of Process Parameters for 3D Printing Process Using Taguchi Based Grey Approach. Mater. Today Proc. 2022, 68, 1515–1520. [Google Scholar] [CrossRef]
- Yaka, H.; Atılkan, R. Optimization of Machining Parameters in Drilling of Nickel Based Superalloys with Gray Relational Analysis and Taguchi. Kahramanmaras Sutcu Imam Univ. J. Eng. Sci. 2023, 26, 363–378. [Google Scholar]
- Hasdiansah, H.; Yaqin, R.I.; Pristiansyah, P.; Umar, M.L.; Priyambodo, B.H. FDM-3D Printing Parameter Optimization Using Taguchi Approach on Surface Roughness of Thermoplastic Polyurethane Parts. Int. J. Interact. Des. Manuf. 2023, 17, 3011–3024. [Google Scholar] [CrossRef]





| Properties | PLA | Tough PLA |
|---|---|---|
| Manufacturer | Porima (Türkiye) | Porima (Türkiye) |
| Density (g/cm3) | 1.23 | 1.22 |
| Melt flow index (g/10min) | 17.3 | 17.3 |
| Heat bending temperature (°C) | 55 | 58 |
| Glass transition temperature (°C) | 55–65 | 55–65 |
| Tensile strength (MPa) | 56 | 50 |
| Elastic modulus (MPa) | 2850 | 2400 |
| Strain at break (%) | 7 | 50 |
| Notch impact energy (kJ/m2) | 14.2 | 36 |
| Properties | Values |
|---|---|
| Model | Creality Ender-3 S1 Pro |
| Printing size (mm) | 220 × 220 × 270 |
| Printing accuracy (mm) | ±0.1 |
| Filament diameter (mm) | 1.75 |
| Nozzle diameter (mm) | 0.4 |
| Print temperature (°C) | 220 |
| Table temperature (°C) | 70 |
| Top and bottom line | 3 |
| Wall line | 3 |
| Fan speed (%) | 100 |
| CAD program | Solidworks 2020 |
| Slicer program | Ultimaker Cura 5.5.0 |
| Parameters | Levels | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| A | Infill density (%) | 70 | 80 | 90 | 100 |
| B | Raster angle (°) | 0 | 90 | 0/90 | 45/−45 |
| C | Layer height (mm) | 0.10 | 0.15 | 0.20 | 0.25 |
| D | Print speed (mm/s) | 25 | 50 | 75 | 100 |
| No | Levels | Charpy Impact Strength (kJ/m2) | Standard Deviation (%) | S/N (dB) | |||
|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||
| 1 | 1 | 1 | 1 | 1 | 35.85 ± 0.53 | 1.48 | 31.09 |
| 2 | 1 | 2 | 2 | 2 | 34.66 ± 0.51 | 1.46 | 30.80 |
| 3 | 1 | 3 | 3 | 3 | 36.27 ± 0.44 | 1.21 | 31.19 |
| 4 | 1 | 4 | 4 | 4 | 36.47 ± 0.49 | 1.34 | 31.24 |
| 5 | 2 | 1 | 2 | 3 | 36.41 ± 0.59 | 1.63 | 31.22 |
| 6 | 2 | 2 | 1 | 4 | 35.84 ± 0.43 | 1.21 | 31.09 |
| 7 | 2 | 3 | 4 | 1 | 36.19 ± 0.34 | 0.93 | 31.17 |
| 8 | 2 | 4 | 3 | 2 | 35.96 ± 0.61 | 1.68 | 31.12 |
| 9 | 3 | 1 | 3 | 4 | 36.04 ± 0.31 | 0.85 | 31.14 |
| 10 | 3 | 2 | 4 | 3 | 37.14 ± 0.44 | 1.17 | 31.40 |
| 11 | 3 | 3 | 1 | 2 | 35.38 ± 0.50 | 1.41 | 30.98 |
| 12 | 3 | 4 | 2 | 1 | 35.36 ± 0.43 | 1.23 | 30.97 |
| 13 | 4 | 1 | 4 | 2 | 36.88 ± 0.55 | 1.49 | 31.34 |
| 14 | 4 | 2 | 3 | 1 | 36.66 ± 0.45 | 1.24 | 31.28 |
| 15 | 4 | 3 | 2 | 4 | 36.56 ± 0.47 | 1.28 | 31.26 |
| 16 | 4 | 4 | 1 | 3 | 38.01 ± 0.51 | 1.33 | 31.60 |
| Level | A—Infill Density (%) | B—Raster Angle (°) | C—Layer Height (mm) | D—Print Speed (mm/s) |
|---|---|---|---|---|
| 1 | 31.08 | 31.20 | 31.19 | 31.13 |
| 2 | 31.15 | 31.14 | 31.06 | 31.06 |
| 3 | 31.12 | 31.15 | 31.18 | 31.35 |
| 4 | 31.37 | 31.23 | 31.29 | 31.18 |
| Delta | 0.29 | 0.09 | 0.22 | 0.30 |
| Rank | 2 | 4 | 3 | 1 |
| Source | DF | Seq SS | Adj SS | Adj MS | F-Value | p-Value | Contribution |
|---|---|---|---|---|---|---|---|
| Infill density (%) | 3 | 3.5651 | 3.5651 | 1.18836 | 21.13 | 0.016 | 38.93% |
| Raster angle (°) | 3 | 0.3690 | 0.3690 | 0.12302 | 2.19 | 0.268 | 4.03% |
| Layer height (mm) | 3 | 1.7120 | 1.7120 | 0.57065 | 10.15 | 0.044 | 18.69% |
| Print speed (mm/s) | 3 | 3.3433 | 3.3433 | 1.11443 | 19.82 | 0.018 | 36.51% |
| Error | 3 | 0.1687 | 0.1687 | 0.05623 | 1.84% | ||
| Total | 15 | 9.1581 | 100.00% | ||||
| S | R-sq | R-sg (adj) | PRESS | R-sq (pred) | |||
| 0.237132 | 98.16% | 90.79% | 4.79841 | 47.60% |
| Optimum Level: A4B4C4D3 | Predicted Value (kJ/m2) | Experimental Result (kJ/m2) |
|---|---|---|
| 38.41 | 38.54 | |
| Prediction Error (%) | 0.34 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tunçel, O. Optimization of Charpy Impact Strength of Tough PLA Samples Produced by 3D Printing Using the Taguchi Method. Polymers 2024, 16, 459. https://doi.org/10.3390/polym16040459
Tunçel O. Optimization of Charpy Impact Strength of Tough PLA Samples Produced by 3D Printing Using the Taguchi Method. Polymers. 2024; 16(4):459. https://doi.org/10.3390/polym16040459
Chicago/Turabian StyleTunçel, Oğuz. 2024. "Optimization of Charpy Impact Strength of Tough PLA Samples Produced by 3D Printing Using the Taguchi Method" Polymers 16, no. 4: 459. https://doi.org/10.3390/polym16040459
APA StyleTunçel, O. (2024). Optimization of Charpy Impact Strength of Tough PLA Samples Produced by 3D Printing Using the Taguchi Method. Polymers, 16(4), 459. https://doi.org/10.3390/polym16040459






