Efficient Prediction of Fatigue Damage Analysis of Carbon Fiber Composites Using Multi-Timescale Analysis and Machine Learning
Abstract
1. Introduction
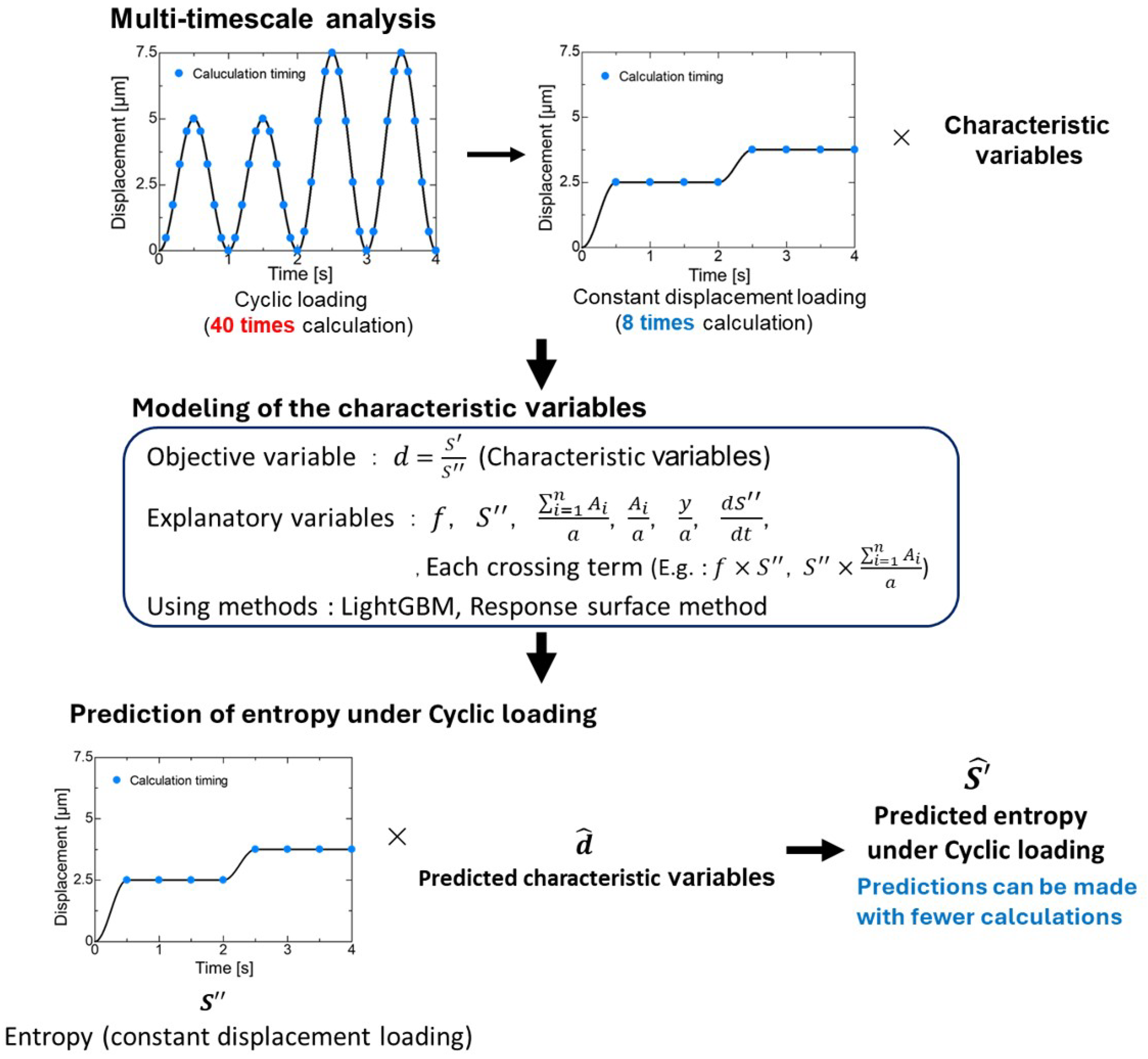
2. Multi-Timescale Analysis and Prediction Modeling Methods
2.1. Multi-Timescale Analysis
2.2. LightGBM and Response Surface Method
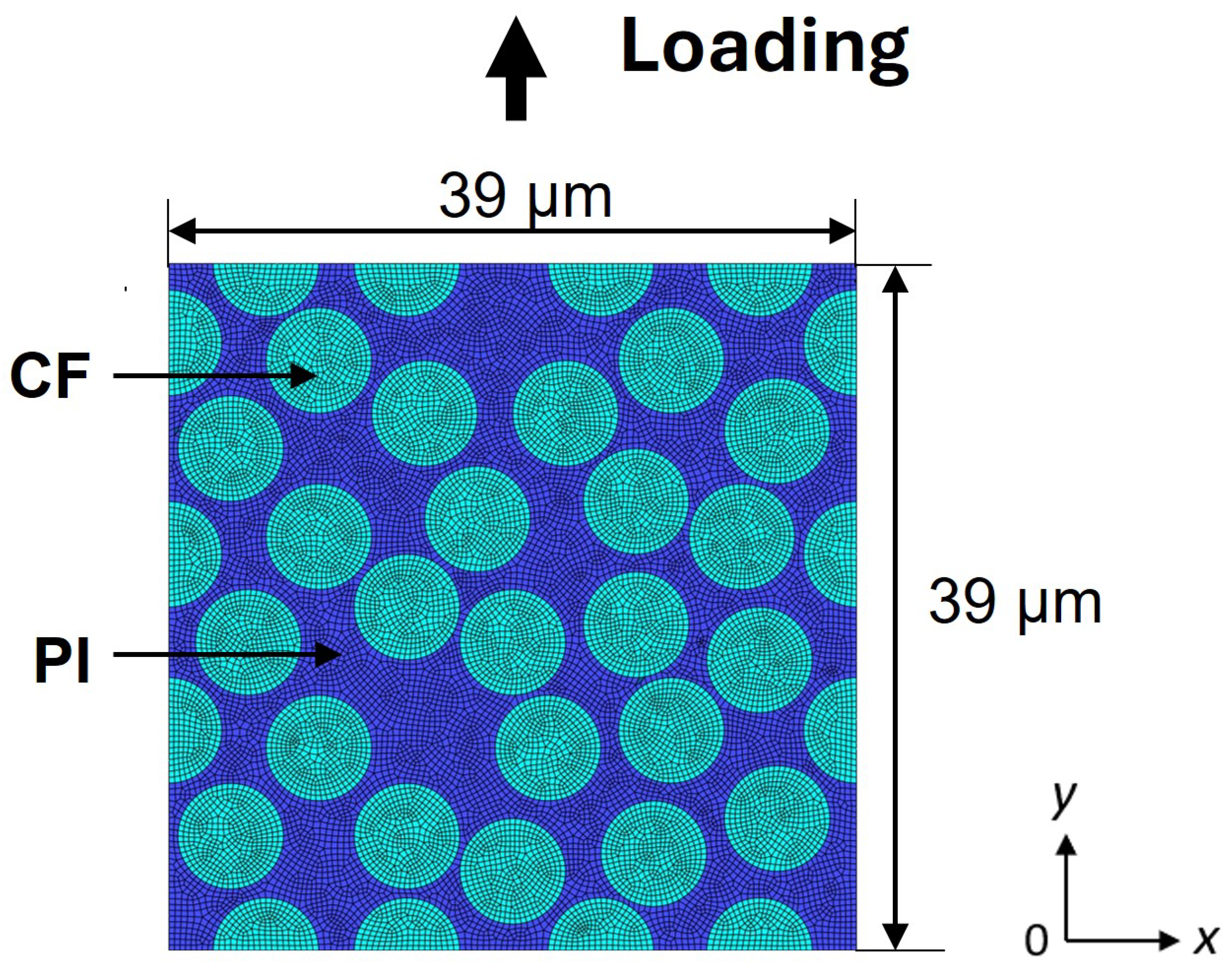
3. Analysis Conditions
3.1. Finite Element Model of CFRP
3.2. Prediction Modeling
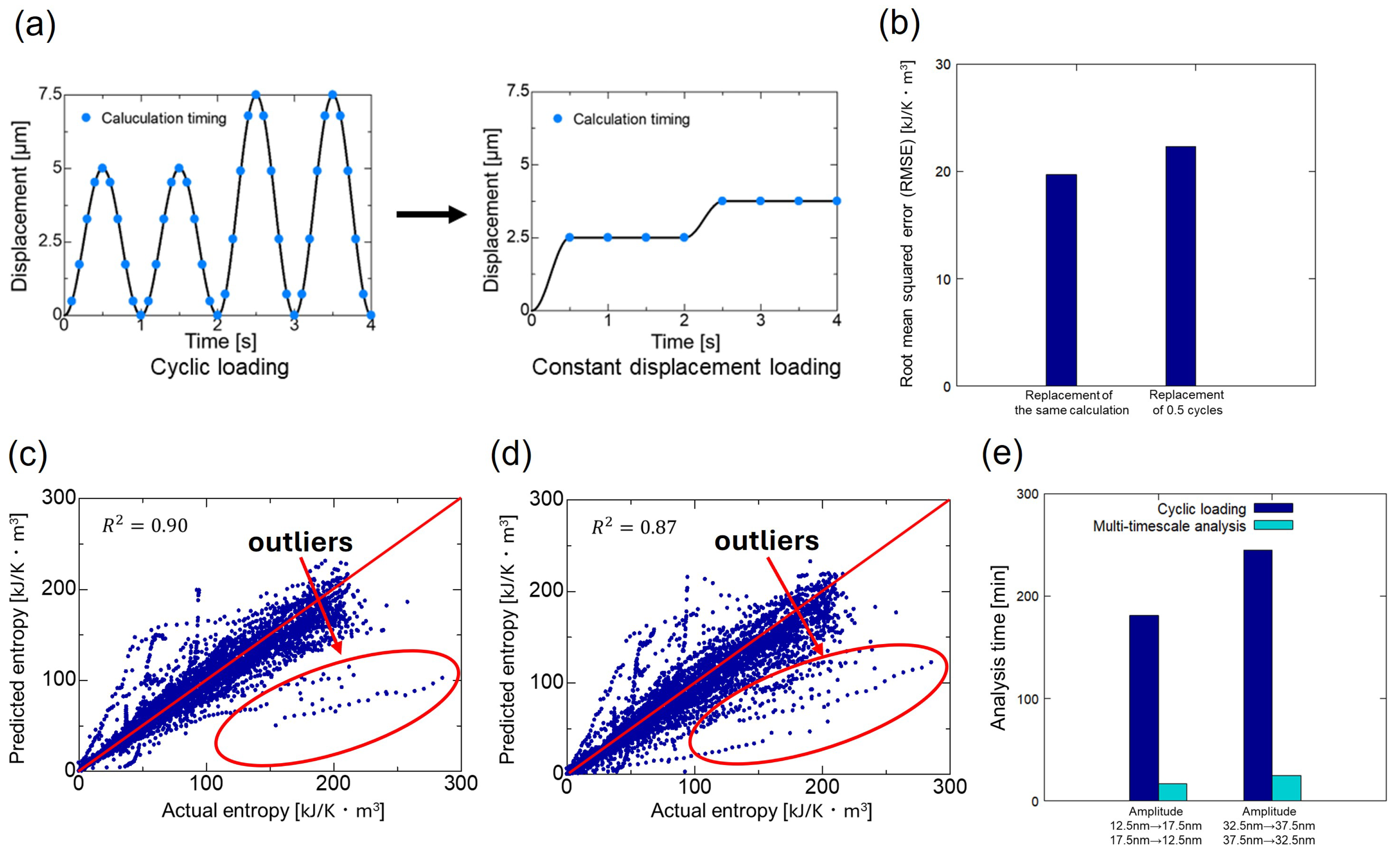
4. Analysis Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Timmis, A.; Hodžić, A.; Koh, L.; Bonner, M.; Schäfer, A.; Dray, L. Lifecycle assessment of cfrp aircraft fuselage. In Proceedings of the ECCM16—16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Séguin-Charbonneau, L. Automated defect detection for ultrasonic inspection of CFRP aircraft components. NDT E Int. 2021, 122, 102478. [Google Scholar] [CrossRef]
- Ozkan, D.; Gok, M.S.; Karaoglanli, A.C. Carbon fiber reinforced polymer (CFRP) composite materials, their characteristic properties, industrial application areas and their machinability. In Advanced Structured Materials; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 235–253. [Google Scholar]
- Saringer, W.; Nöbauer-Huhmann, I.; Knosp, E. Cranioplasty with individual carbon fibre reinforced polymere (CFRP) medical grade implants based on CAD/CAM technique. Acta Neurochir. 2002, 144, 1193–1203. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Kim, Y.M.; Song, S.; Kim, E.; Kim, D.G.; Jung, Y.C.; Yu, W.R.; Na, W.; Choi, Y.S. Manufacture of antibacterial carbon fiber-reinforced plastics (CFRP) using imine-based epoxy vitrimer for medical application. Heliyon 2023, 9, e16945. [Google Scholar] [CrossRef] [PubMed]
- Hosoi, A.; Sakuma, S.; Fujita, Y.; Kawada, H. Prediction of initiation of transverse cracks in cross-ply CFRP laminates under fatigue loading by fatigue properties of unidirectional CFRP in 90° direction. Compos. Part A Appl. Sci. Manuf. 2015, 68, 398–405. [Google Scholar] [CrossRef]
- Reuter, C.; Tröster, T. Crashworthiness and numerical simulation of hybrid aluminium-CFRP tubes under axial impact. Thin-Walled Struct. 2017, 117, 1–9. [Google Scholar] [CrossRef]
- Kelkel, B.; Popow, V.; Gurka, M. Inline quantification and localization of transverse matrix cracking in cross-ply CFRP during quasi-static tensile testing by a joint event-based evaluation of acoustic emission and passive IR thermography. Compos. Sci. Technol. 2020, 190, 108013. [Google Scholar] [CrossRef]
- Ogihara, S.; Takeda, N.; Kobayashi, S.; Kobayashi, A. Effects of stacking sequence on microscopic fatigue damage development in quasi-isotropic CFRP laminates with interlaminar-toughened layers. Compos. Sci. Technol. 1999, 59, 1387–1398. [Google Scholar] [CrossRef]
- Yu, F.; Saito, O.; Okabe, Y. Detection of a single transverse crack in a CFRP cross-ply laminate by visualizing mode conversion of Lamb waves. Compos. Struct. 2022, 283, 115118. [Google Scholar] [CrossRef]
- Kolanu, N.R.; Raju, G.; Ramji, M. A unified numerical approach for the simulation of intra and inter laminar damage evolution in stiffened CFRP panels under compression. Compos. B Eng. 2020, 190, 107931. [Google Scholar] [CrossRef]
- Fu, Q.; Wu, S.; Li, C.; Xu, J.; Wang, D. Delamination and chip breaking mechanism of orthogonal cutting CFRP/Ti6Al4V composite. J. Manuf. Process. 2022, 73, 183–196. [Google Scholar] [CrossRef]
- Berthelot, J.M. Transverse cracking and delamination in cross-ply glass-fiber and carbon-fiber reinforced plastic laminates: Static and fatigue loading. Appl. Mech. Rev. 2003, 56, 111–147. [Google Scholar] [CrossRef]
- Ke, L.; Li, Y.; Li, C.; Cheng, Z.; Ma, K.; Zeng, J. Bond behavior of CFRP-strengthened steel structures and its environmental influence factors: A critical review. Sustain. Struct. 2024, 4, 000038. [Google Scholar] [CrossRef]
- Guo, R.; Xian, G.; Li, C.; Hong, B. Effect of fiber hybrid mode on the tension–tension fatigue performance for the pultruded carbon/glass fiber reinforced polymer composite rod. Eng. Fract. Mech. 2022, 260, 108208. [Google Scholar] [CrossRef]
- Guo, R.; Li, C.; Niu, Y.; Xian, G. The fatigue performances of carbon fiber reinforced polymer composites—A review. J. Mater. Res. Technol. 2022, 21, 4773–4789. [Google Scholar] [CrossRef]
- Schapery, R.A. Nonlinear viscoelastic and viscoplastic constitutive equations based on thermodynamics. Mech. Time Depend. Mater. 1997, 1, 209–240. [Google Scholar] [CrossRef]
- Machado, J.J.M.; Marques, E.A.S.; Campilho, R.; da Silva, L.F.M. Mode I fracture toughness of CFRP as a function of temperature and strain rate. J. Compos. Mater. 2017, 51, 3315–3326. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Mohammadi, B. On the evaluation of damage-entropy model in cross-ply laminated composites. Eng. Fract. Mech. 2019, 219, 106626. [Google Scholar] [CrossRef]
- Naderi, M.; Khonsari, M.M. Thermodynamic analysis of fatigue failure in a composite laminate. Mech. Mater. 2012, 46, 113–122. [Google Scholar] [CrossRef]
- Takase, N.; Koyanagi, J.; Mori, K.; Sakai, T. Molecular Dynamics Simulation for Evaluating Fracture Entropy of a Polymer Material under Various Combined Stress States. Materials 2021, 14, 1884. [Google Scholar] [CrossRef]
- Sato, M.; Hasegawa, K.; Koyanagi, J.; Higuchi, R.; Ishida, Y. Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage. Compos. Part A Appl. Sci. Manuf. 2021, 141, 106178. [Google Scholar] [CrossRef]
- Akai, A.; Shiozawa, D.; Sakagami, T. Dissipated energy evaluation for austenitic stainless steel. J. Soc. Mater. Sci. Jpn. 2013, 62, 554–561. [Google Scholar] [CrossRef][Green Version]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Schick, C. Differential scanning calorimetry (DSC) of semicrystalline polymers. Anal. Bioanal. Chem. 2009, 395, 1589–1611. [Google Scholar] [CrossRef]
- Harvey, J.P.; Saadatkhah, N.; Dumont-Vandewinkel, G.; Ackermann, S.L.G.; Patience, G.S. Experimental methods in chemical engineering: Differential scanning calorimetry-DSC. Can. J. Chem. Eng. 2018, 96, 2518–2525. [Google Scholar] [CrossRef]
- Ishizaki, T.; Nagano, H. Measurement of three-dimensional anisotropic thermal diffusivities for carbon fiber-reinforced plastics using lock-in thermography. Int. J. Thermophys. 2015, 36, 2577–2589. [Google Scholar] [CrossRef]
- Alasli, A.; Fujita, R.; Nagano, H. Thermophysical properties mapping of composites by lock-in thermography: Applications on carbon fiber reinforced plastics. Int. J. Thermophys. 2022, 43, 176. [Google Scholar] [CrossRef]
- Akai, A.; Shiozawa, D.; Yamada, T.; Sakagami, T. Energy dissipation measurement in improved spatial resolution under fatigue loading. Exp. Mech. 2020, 60, 181–189. [Google Scholar] [CrossRef]
- Sakai, T.; Takase, N.; Oya, Y.; Koyanagi, J. A Possibility for Quantitative Detection of Mechanically-Induced Invisible Damage by Thermal Property Measurement via Entropy Generation for a Polymer Material. Materials 2022, 15, 737. [Google Scholar] [CrossRef] [PubMed]
- Kudo, N.; Fujita, R.; Oya, Y.; Sakai, T.; Nagano, H.; Koyanagi, J. Identification of invisible fatigue damage of thermosetting epoxy resin by non-destructive thermal measurement using entropy generation. Adv. Compos. Mater. 2024, 33, 233–249. [Google Scholar] [CrossRef]
- Koyanagi, J.; Mochizuki, A.; Higuchi, R.; Tan, V.B.C.; Tay, T.E. Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings. Int. J. Fatigue 2022, 165, 107204. [Google Scholar] [CrossRef]
- Deng, H.; Toda, K.; Sato, M.; Koyanagi, J. Micro-scale numerical simulation of fatigue failure for CFRP subjected to multiple-amplitude cyclic loadings based on entropy damage criterion. Materials 2023, 16, 6120. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fikry, M.J.M.; Koyanagi, J. Numerical simulation for durability of a viscoelastic polymer material subjected to variable loadings fatigue based on entropy damage criterion. Polymers 2024, 16, 2857. [Google Scholar] [CrossRef] [PubMed]
- Takamura, M.; Uehara, K.; Koyanagi, J.; Takeda, S. Multi-timescale simulations of temperature elevation for ultrasonic welding of CFRP with energy director. J. Multiscale Model. 2021, 12, 2143003. [Google Scholar] [CrossRef]
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology: Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Li, Z.; Wang, K.; Song, J.; Xu, Q.; Kobayashi, N. Preparation of activated carbons from polycarbonate with chemical activation using response surface methodology. J. Mater. Cycles Waste Manag. 2014, 16, 359–366. [Google Scholar] [CrossRef]
- Ye, W.; Wang, X.; Liu, Y.; Chen, J. Analysis and prediction of the performance of free- piston Stirling engine using response surface methodology and artificial neural network. Appl. Therm. Eng. 2021, 188, 116557. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A highly efficient Gradient Boosting Decision Tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.; Pang, W.; Ren, L.; Wang, Y. Novel monitoring method for material removal rate considering quantitative wear of abrasive belts based on LightGBM learning algorithm. Int. J. Adv. Manuf. Technol. 2021, 114, 3241–3253. [Google Scholar] [CrossRef]
- Abaqus/CAE. 2023. Available online: https://www.3ds.com/products/simulia/abaqus/cae (accessed on 13 November 2024).
- Kagawa, H.; Umezu, Y.; Sakaue, K.; Koyanagi, J. Numerical simulation for the tensile failure of randomly oriented short fiber reinforced plastics based on a viscoelastic entropy damage criterion. Compos. Part C Open Access 2023, 10, 100342. [Google Scholar] [CrossRef]
- The Power of JMP Pro. 2024. Available online: https://www.jmp.com/en_us/software/predictive-analytics-software.html (accessed on 13 November 2024).
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Amin, M.N.; Salami, B.A.; Zahid, M.; Iqbal, M.; Khan, K.; Abu-Arab, A.M.; Alabdullah, A.A.; Jalal, F.E. Investigating the bond strength of FRP laminates with concrete using LIGHT GBM and SHAPASH analysis. Polymers 2022, 14, 4717. [Google Scholar] [CrossRef] [PubMed]

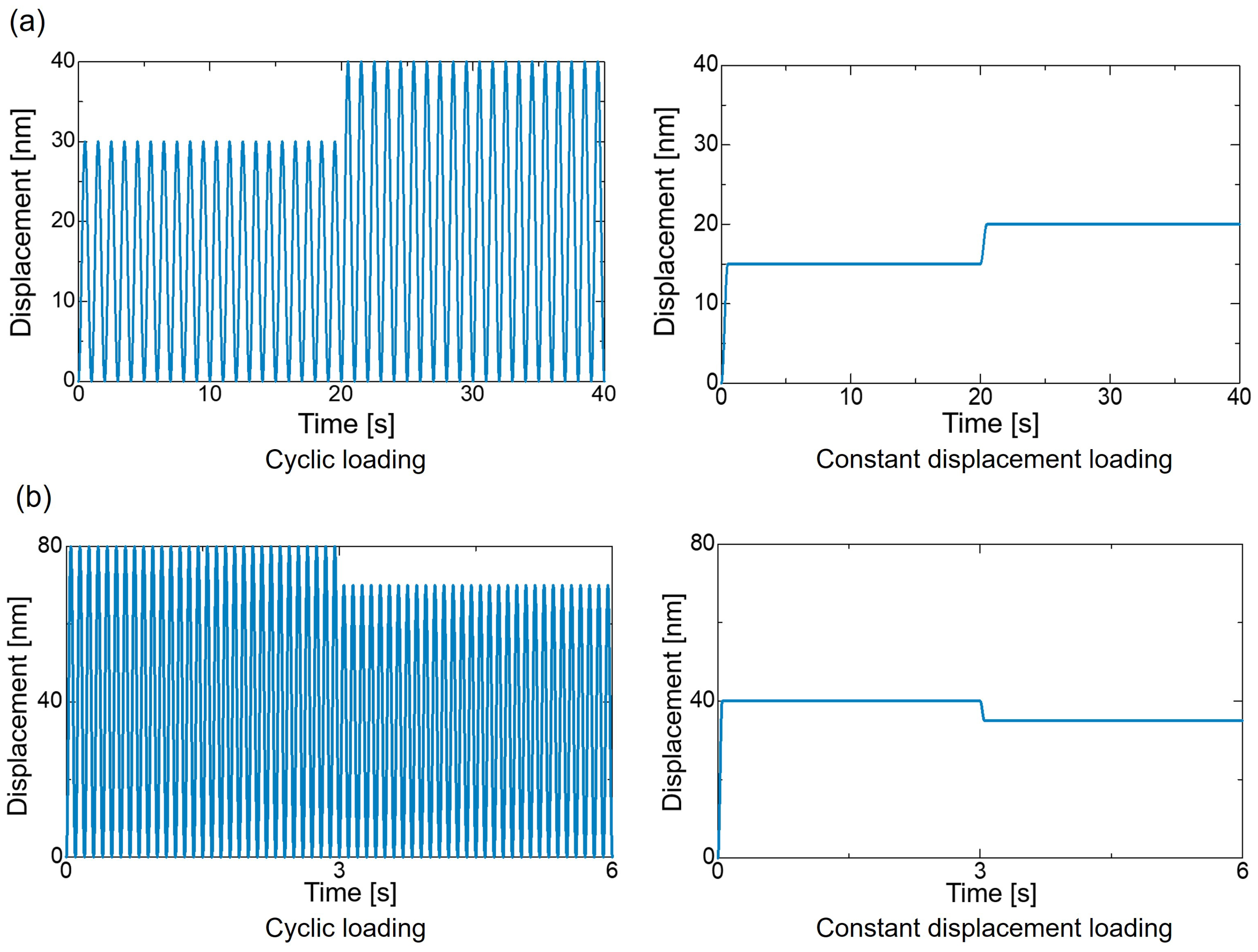


| Learning Data | |
| Frequency [Hz] | Amplitude Change [nm] |
| 1 | 10 (30 cycles) → 15 (30 cycles) |
| 1 | 15 (30 cycles) → 10 (30 cycles) |
| 1 | 15 (20 cycles) → 20 (20 cycles) |
| 1 | 20 (20 cycles) → 15 (20 cycles) |
| 10 | 30 (40 cycles) → 35 (40 cycles) |
| 10 | 35 (40 cycles) → 30 (40 cycles) |
| 10 | 35 (30 cycles) → 40 (30 cycles) |
| 10 | 40 (30 cycles)→ 35 (30 cycles) |
| Test Data | |
| Frequency [Hz] | Amplitude Change [nm] |
| 1 | 12.5 (25 cycles) → 17.5 (25 cycles) |
| 1 | 17.5 (25 cycles) → 12.5 (25 cycles) |
| 10 | 32.5 (35 cycles) → 37.5 (35 cycles) |
| 10 | 37.5 (35 cycles) → 32.5 (35 cycles) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoshimori, S.; Koyanagi, J.; Matsuzaki, R. Efficient Prediction of Fatigue Damage Analysis of Carbon Fiber Composites Using Multi-Timescale Analysis and Machine Learning. Polymers 2024, 16, 3448. https://doi.org/10.3390/polym16233448
Yoshimori S, Koyanagi J, Matsuzaki R. Efficient Prediction of Fatigue Damage Analysis of Carbon Fiber Composites Using Multi-Timescale Analysis and Machine Learning. Polymers. 2024; 16(23):3448. https://doi.org/10.3390/polym16233448
Chicago/Turabian StyleYoshimori, Satoru, Jun Koyanagi, and Ryosuke Matsuzaki. 2024. "Efficient Prediction of Fatigue Damage Analysis of Carbon Fiber Composites Using Multi-Timescale Analysis and Machine Learning" Polymers 16, no. 23: 3448. https://doi.org/10.3390/polym16233448
APA StyleYoshimori, S., Koyanagi, J., & Matsuzaki, R. (2024). Efficient Prediction of Fatigue Damage Analysis of Carbon Fiber Composites Using Multi-Timescale Analysis and Machine Learning. Polymers, 16(23), 3448. https://doi.org/10.3390/polym16233448






