Prediction of the Specific Energy of Supercapacitors with Polymeric Materials Using Advanced Molecular Dynamics Simulations
Abstract
1. Introduction
- -
- Charge–discharge processes (galvanostatic charging): in improved variants [12], when the charging and discharging processes of supercapacitors are simulated using advanced modeling approaches, the electric (galvanostatic) current can be regulated and a constant potential across each atom can be maintained within the electrode. This represents a complex technique but does not adequately describe the hysteretic phenomenon when charging and discharging occur in different conditions.
- -
- Cyclic voltammetry (CV) [13] represents an electrochemical technique that records the response in a current while a potential scan is applied to the working electrode at a constant scan rate in the forward and reverse directions, once or several times. It is a very successful technique in practice, based on the measurements’ results, but does not offer a fair description of phenomena at an atomistic level.
- -
- Electrochemical impedance spectroscopy (EIS) [14]: when the impedance spectroscopy analysis of the system aids in examining the physical origin of the different electrical components involved in the device. In improved variants, by transforming the impedance data into frequency-dependent capacitance, the Impedance Spectroscopy Genetic Programming (ISGP) can be used in order to find the distribution function of relaxation times (DFRT) of the processes taking place in the supercapacitor. The method does not adequately describe the conduction phenomena at the electrode interface.
- -
- ANSYS (e.g., Ansys 2024 R2 version) is a powerful finite element analysis (FEA) software used for structural 3D simulations. With the help of ANSYS, we can describe not only the electrochemical aspects but also the structural aspects of the flexible supercapacitor.
- -
- Comsol Multiphysics (e.g., COMSOL 6.3 Version 6.3.0.290, 19 November 2024) is a versatile multiphysics simulation software used for a wide range of applications. In the case of supercapacitors, it helps us to simulate not only the electrochemical behavior but also consider other physical phenomena, such as thermal effects or structural deformation.
- -
- Simulink (e.g., R2024b MATLAB and Simulink version) is used for dynamic system modeling and simulation. Dynamic system analysis and control can be performed in the case of the supercapacitors. For electrochemical modeling, it is necessary to integrate additional toolboxes or custom components.
- -
- GROMACS (e.g., GROMACS 2024.4 version) is a software package for molecular dynamics simulations of biomolecules that can be used for simulating the electrochemical properties of batteries and supercapacitors.
2. Materials and Methods
2.1. Materials
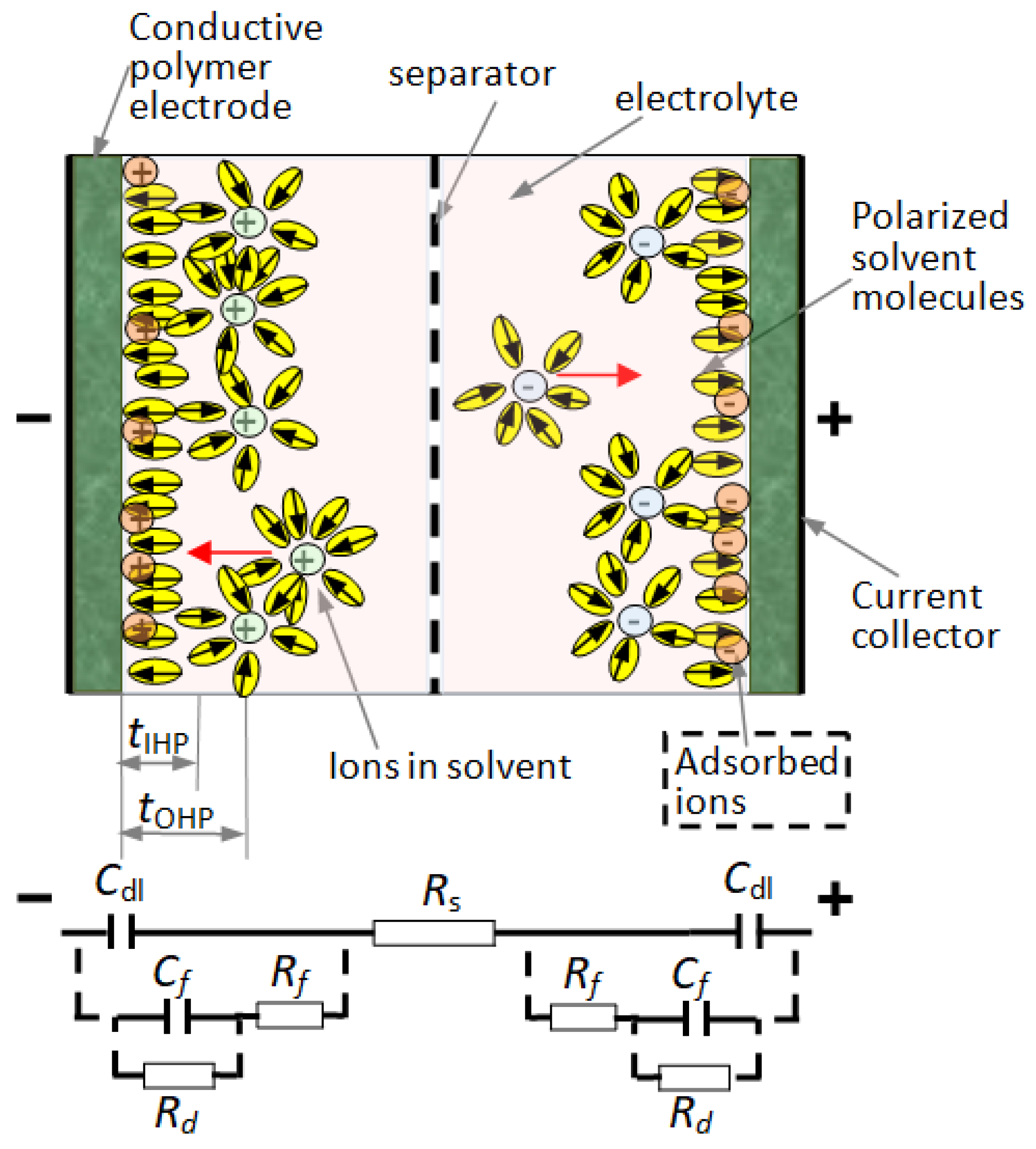
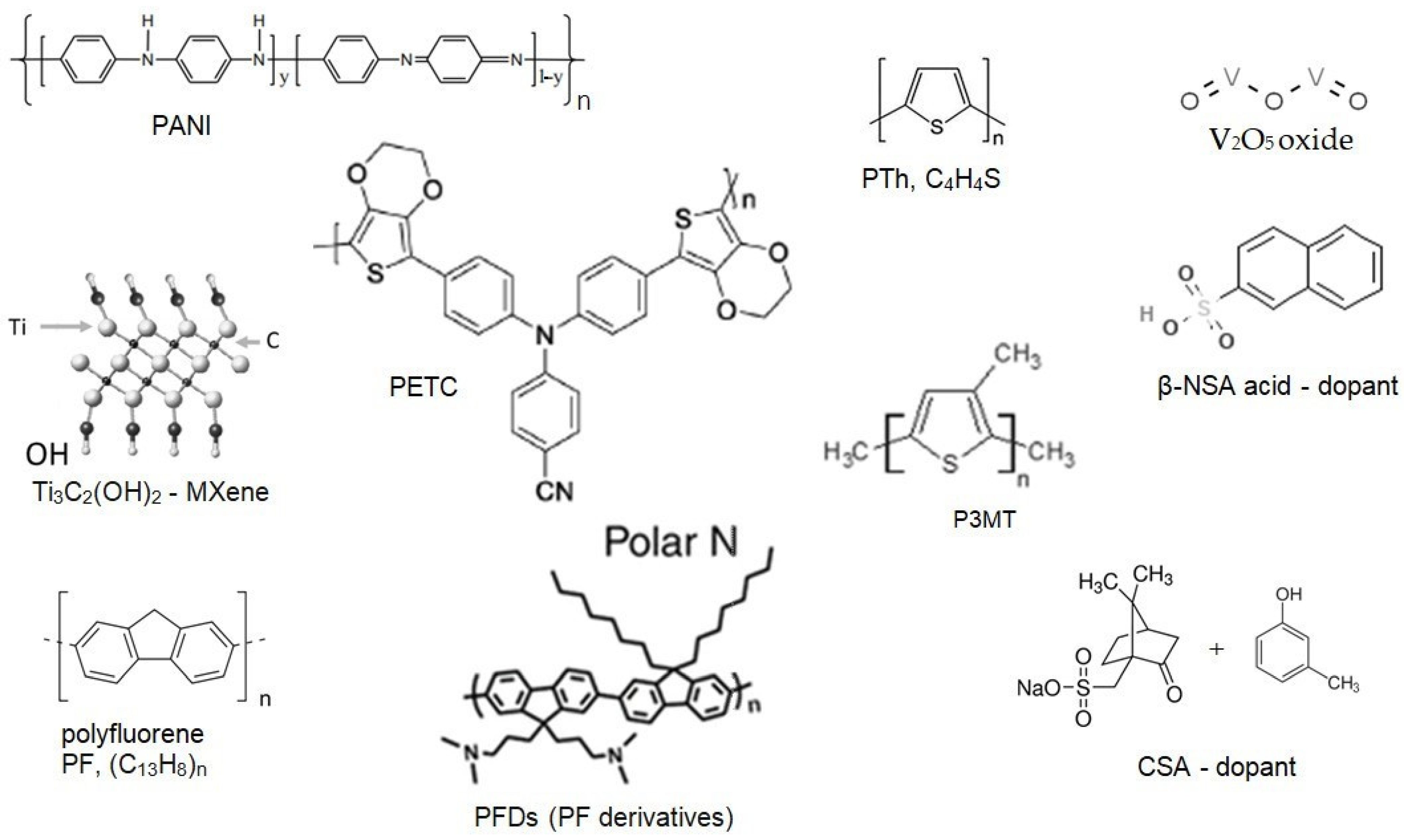

2.2. Workflow for Analyzing the Supercapacitors with Polymeric Materials
2.2.1. Choosing the Model for the Double Layer
- The Helmholtz model, usually used, is appropriate for modeling the spatial charge distribution at double-layer interfaces. The charge of the electrodes is neutralized by opposite sign ions from the electrolyte at a specific distance from the solid, in the so-called inner Helmholtz layer (this distance is defined from the surface to the center of the opposite-sign ions). Is the simplest model for the double layer.
- The Gouy–Chapman model is a model in which the structure of the electrical double layer takes the form of a charged plane (IHL) close to the interface, where ions of opposite sign are dense, and an outer Helmholtz plane (OHP), where the ions are rarefying when the distance to the electrode is increasing. The model also considers the charge carrier distribution when the distance from interface increases.
- The Gouy–Chapman–Stern model assumes that the equilibrium ion concentration decays exponentially with the distance from the interface, following a Boltzmann distribution function with respect to the mean electrostatic potential energy in the electrical double layer (Figure 2). The model was improved by assuming some small perturbations superposed on top of its Boltzmann distribution of ion concentrations using the Tsallis non-extensive statistics framework [34]. This extended model (Figure 4) was used in our work for describing the physical phenomena in the double layer.
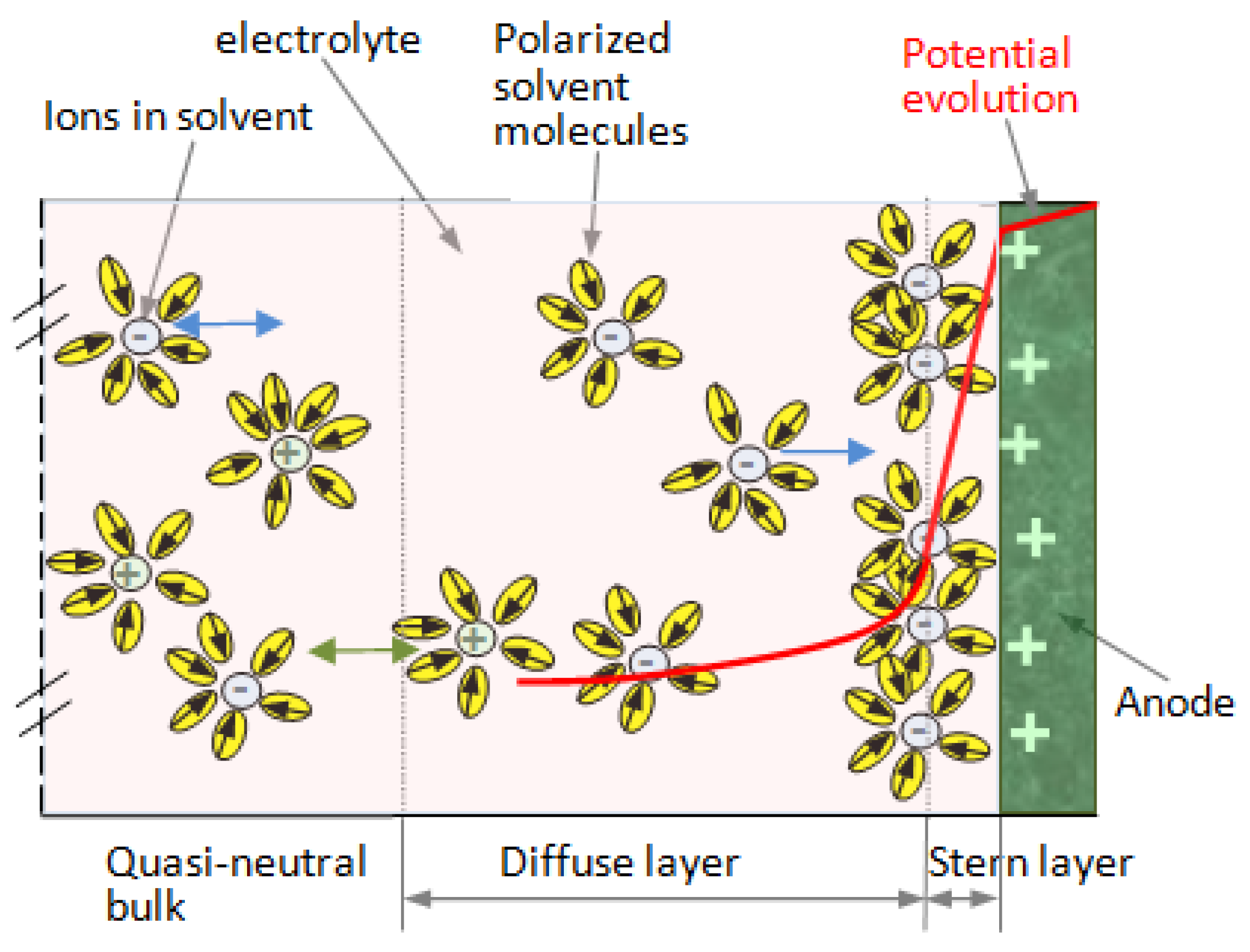
2.2.2. Choosing the Simulation Method for Analysis
- The three-electrode system is developed by defining a working electrode (WE, where the potential is controlled and the current is measured), reference electrode (RE), and counter electrode (CE). The experimental method provides accurate analytical results for electrochemical parameters such as specific capacitance, stability, and impedance. When it is implemented with the help of the simulation programs, due to the macroscopic description of the materials, the precision is low.
- The cluster analysis method is when an algorithm is used to explore the naturally occurring groups within a data set (clusters of ionic groups in the electrolyte) [35]. The method uses particular algorithms, applied for each physical system, and is difficult to generalize for categories of supercapacitors.
- Molecular dynamics (MD) simulation represents a technique for sampling the meta-stable and transitional conformations of molecules for different substances in contact in a medium (polymers, metallic oxides, ionic liquids, etc.) [36,37,38]. Materials have to be described at molecular level, and their equations of motion have to be considered, including defining the interaction forces in the system. MD is a complex method; the accuracy of the results competes with measurement results and can predict materials’ behavior in working conditions that haven not been explored in practice.
- Density functional theory (DFT) represents a method for determining the properties of a many-electron system by using functionals, i.e., functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density in the electrolyte. In the supercapacitors’ case, the method is difficult to extend to a realistic representation of the porous electrodes or complex ion structures. A spatially dependent electron density cannot be fairly represented in an inhomogeneous media; the geometrical parameter values have to be averaged, but the average values are relative, e.g., the degree of porosity can be defined, but porosities are random and never the same if different material samples are considered. The situation is the same with the solvated ions in the electrolyte. Only a description of interaction forces at the molecular level can solve the problem.
- The finite element method (FEM) involves a large system being subdivided into finite elements and differential equations being solved for describing the physical behavior [39]. The method is generally implemented using a continuum model (e.g., Nernst–Plank equations) and commonly fails to capture the capacitive behaviors of nanoporous electrodes with densely packed electrolytes (e.g., ionic liquids).
2.2.3. Charge Carrier Transport and Control Parameters
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2.4. Selecting the Atomic Groups and Bead Groups in the Polymer Structures
2.2.5. Calculating All the Interaction Forces
2.2.6. Establishing the Conduction Mechanism and Calculating the Effective Conductivity
- -
- Defining the atomic groups/polymeric beads: the chemical functional groups of the complex molecules and polymer chains play a vital role in determining the properties exhibited by these complex molecules and polymers.
- -
- Establishing the equilibrium and initial configuration: Establishing the number of interacting particles N (energy minimization is performed to obtain the starting geometry where there is no overlap of particles). The equations of motion for every particle were solved for describing the time evolution of the system. The force field is established (each force is a gradient of the potential; the force fields provide the total potential energy of the system as a function of the atomic coordinates. Force field expressions for polymeric systems are indicated in the literature). The bounded potential and non-bounded potential were defined. By solving the equation of motion, positions of the particles can be found, and consequently, their trajectory can be established.
- -
- The simulation was performed using the NPT ensemble, Nose-Hoover thermostat, and Parrinello-Rahman barostat. The Coulomb cutoff scheme with a cutoff distance of about 1 nm was applied during the equilibration in all systems, in order to reduce the simulation time. The simulation time was set to tens of ns (≈100 ns), with a time step 1 fs to 4 fs. The absolute displacements of the atomic groups in the simulation box were determined and averaged in each given region, where different atomic groups/beads were present.
- -
- The atomic group/bead dynamics are influenced by the adsorption at the electrode surface, which restrains movement in the interface vicinity; the electrostatic affinity between groups, which determines the increase of the charge accumulation and decrease of the free movement of the atomic groups near the interface of electrode/electrolyte; and the interlocking of the functional groups with the polymer chain.
2.2.7. Calculating the Current Density
- The parameters that characterize the electrode and the electrolyte;
- The parameters corresponding to structural elements’ nature and characterizing the atomic groups or polymeric beads, including pair distance between neighbor atomic groups or beads, chemical bond length, bond angles, and dihedral angles. These parameters are very important in deciding the simulation mesh for each analyzed system;
- External parameters, including the electric field applied for charging and testing and the temperature.
3. Results
- -
- Electrolyte parameters: concentration, ion size, number of charge carriers, ionic mobility and valency of the ions, and viscosity;
- -
- Electrode parameters: conductivity, charge mobility, surface area, ion diffusion efficiency, pore size, crystalline structure or polymer structure of the basis material, doping level, and structural morphology;
- -
- Molecular structure parameters: atomic group/bead distance, chemical bond length, bond angles, and dihedral angles;
- -
- External parameters: electric field for charging and testing as well as temperature.
- Level 1: electrolyte concentration, ionic mobility;
- Level 2: surface area, charge transfer coefficient (depending on pore size, etc.);
- Level 3: electrode conductivity, external electrical field.

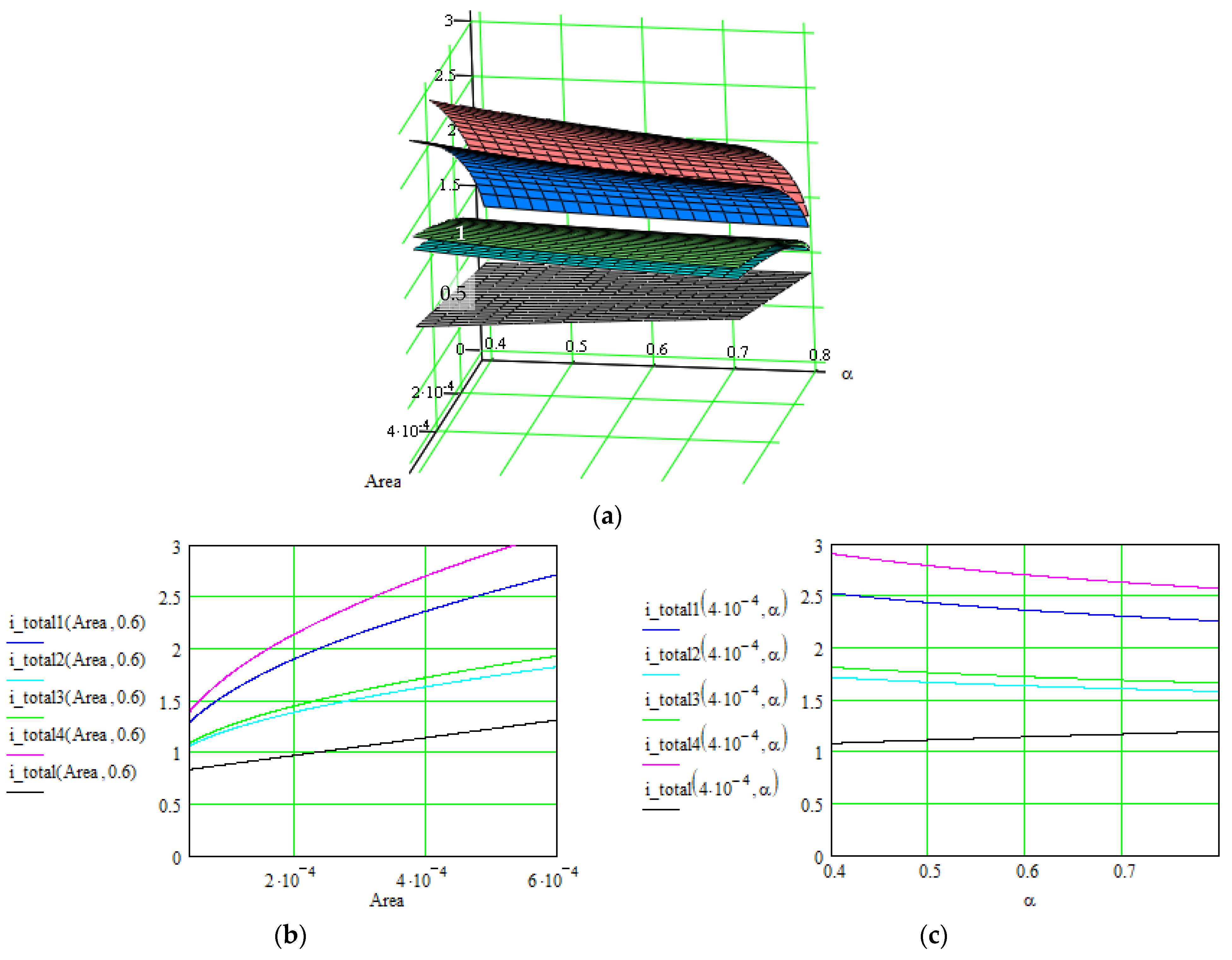

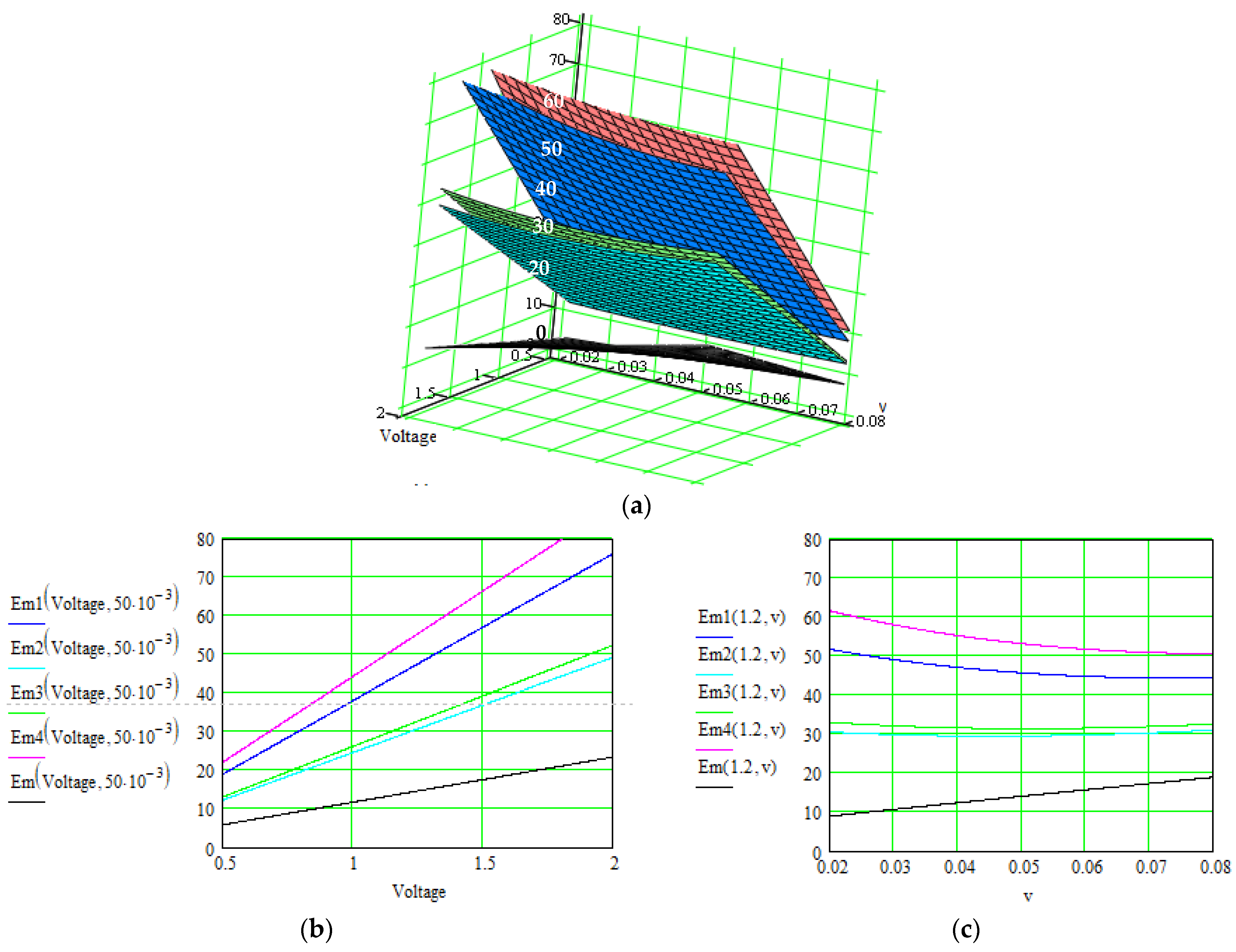
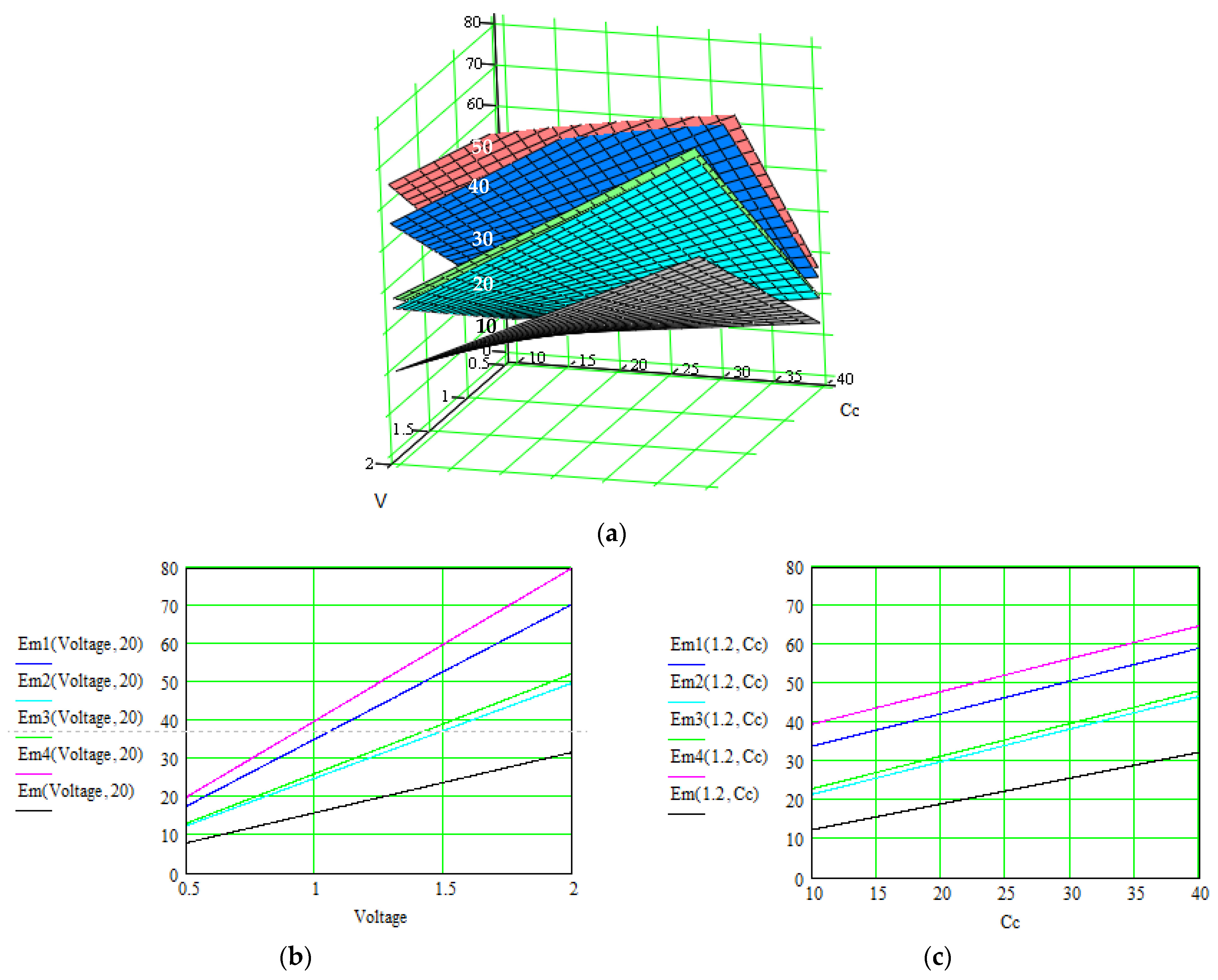
| No. | Material: Electrode + Electrolyte | Specific Capacitance/Current Density/Total Current/ Specific Energy | Control Parameters | Applications/ Characteristics | Method of Determination/Source |
|---|---|---|---|---|---|
| 1. | MXene-polymer compounds: (a) PANi/Ti3C2 electrodes + Na2SO4 electrolyte (b) PFDs/Ti3C2Tx (Tx = O, OH, F) electrodes + H2SO4 electrolyte | Reported in the literature: | |||
| solvent nature and concentration ion nature charge density of CP temperature ((−20)–115 °C) | Wearable devices, electric vehicles, and grid energy storage | Experimental:
| ||
| Electrode film layer: 18–105 μm | Abdah, 2023 [21] | ||||
| Our method—results after each level of correlation: | |||||
|
| similar |
| ||
| |||||
| |||||
| Electrode thickness: 20–200 μm | |||||
| No. | Material: Electrode + Electrolyte | Specific Capacitance/Current Density/Total Current | Control Parameters | Applications/ Characteristics | Method of Determination/Source |
| 2. | PETC electrode + PVA or gel electrolyte | Reported in the literature: | |||
| Up to 82.2 F g−1 at 0.1 mA cm−2 | electrode area and mass; redox activity, conductivity, doping level, charge mobility; crystal structure, morphology, surface area, pore size, and ion diffusion efficiency | renewable energy systems, electric vehicles | Cyclic voltammetry; Galvanostatic charge–discharge (GCD); Electrochemical impedance spectroscopy; SEM scanning | ||
| Genene [6] | |||||
| Our method—results after each level of correlation: | |||||
|
| similar |
| ||
| |||||
| |||||
| Electrode thickness: 20–200 μm | |||||
| No. | Material: Electrode + Electrolyte | Specific Capacitance/Current Density/Total Current/ Specific Energy | Control Parameters | Applications/ Characteristics | Method of Determination/Source |
| 3. | PTh and P3MT electrodes + PVA/H2SO4 gel electrolyte | Reported in the literature: | |||
| Applied voltage Charging time Electrolyte concentration Electrode area Mechanical pressure Current collector Temperature | Flexible sensors and wearable electronics; portable microelectronics systems, |
| ||
| Collector: length = 6 cm, adjacent spacing = 0.2 cm, maximum height = 5 cm | |||||
| Wang, 2023 [5] | |||||
| Our method—results after each level of correlation: | |||||
|
| similar |
| ||
| Electrode thickness: 20–200 μm | |||||
| No. | Material: Electrode + Electrolyte | Specific Capacitance/Current Density/Total Current/ Specific Energy | Control Parameters | Applications/ Characteristics | Method of Determination/Source |
| 4. | Doped PANI/V2O5 (3:1) composite electrodes + H2SO4 electrolyte | Reported in the literature: | |||
| Molar report of the electrode components Dopant concentration Current density | high power applications; flexible, lightweight, wearable electronic |
| ||
| Rohith 2023 [13] | |||||
| Our method—results after each level of correlation: | |||||
|
| similar |
| ||
| Electrode thickness: 20–200 μm | |||||
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Zhu, M.; Pei, Z.; Xue, Q.; Li, H.; Huang, Y.; Zhi, C. Polymers for supercapacitors: Boosting the development of the flexible and wearable energy storage. Mater. Sci. Eng. R Rep. 2020, 139, 100520. [Google Scholar]
- Loganathan, N.N.; Perumal, V.; Pandian, B.R.; Atchudan, R.; Edison, T.N.J.I.; Ovinis, M. Recent studies on polymeric materials for supercapacitor development. J. Energy Storage 2022, 49, 104149. [Google Scholar]
- Butnicu, D.; Lazar, A. Workbench Study Concerning the Highest Reliability Outcome for PoL Converters with Different Output Capacitor Technologies. Energies 2023, 16, 2768. [Google Scholar] [CrossRef]
- Fu, Z.; Hannula, M.; Jauho, A.; Väisänen, K.-L.; Välimäki, M.; Keskinen, J.; Mäntysalo, M. Cyclic Bending Reliability and Failure Mechanism of Printed Biodegradable Flexible Supercapacitor on Polymer Substrate. ACS Appl. Mater. Interfaces 2022, 14, 40145–40157. [Google Scholar] [CrossRef]
- Butnicu, D. A Derating-Sensitive Tantalum Polymer Capacitor’s Failure Rate within a DC-DC eGaN-FET-Based PoL Converter Workbench Study. Micromachines 2023, 14, 221. [Google Scholar] [CrossRef]
- Ates, M.; Chebil, A.; Yoruk, O.; Dridi, C.; Turkyilmaz, M. Reliability of electrode materials for supercapacitors and batteries in energy storage applications: A review. Ionics 2022, 28, 27–52. [Google Scholar]
- Shaikh, N.S.; Ubale, S.B.; Mane, V.J.; Shaikh, J.S.; Lokhande, V.C.; Praserthdam, S.; Lokhande, C.D.; Kanjanaboos, P. Novel electrodes for supercapacitor: Conducting polymers, metal oxides, chalcogenides, carbides, nitrides, MXenes, and their composites with grapheme. J. Alloys Compd. 2022, 893, 161998. [Google Scholar]
- Tadesse, M.G.; Ahmmed, A.S.; Lübben, J.F. Review on Conductive Polymer Composites for Supercapacitor Applications. J. Compos. Sci. 2024, 8, 53. [Google Scholar] [CrossRef]
- Gao, Y.; Qu, F.; Wang, W.; Li, F.; Zhao, X.; Zhang, L. Increasing the electrical conductivity of polymer nanocomposites under the external field by tuning nanofiller shape. Compos. Sci. Technol. 2019, 176, 37–45. [Google Scholar] [CrossRef]
- Appiah, E.S.; Dzikunu, P.; Mahadeen, N.; Ampong, D.N.; Mensah-Darkwa, K.; Kumar, A.; Gupta, R.K.; Adom-Asamoah, M. Biopolymers-Derived Materials for Supercapacitors: Recent Trends, Challenges, and Future Prospects. Molecules 2022, 27, 6556. [Google Scholar] [CrossRef]
- Helseth, L.E. Comparison of methods for finding the capacitance of a supercapacitor. J. Energy Storage 2021, 35, 102304. [Google Scholar]
- Zeng, L.; Wu, T.; Ye, T.; Mo, T.; Qiao, R.; Feng, G. Modeling galvanostatic charge–discharge of nanoporous supercapacitors. Nat. Comput. Sci. 2021, 1, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Bograchev, D.A.; Volfkovich, Y.M.; Martemianov, S. Diagnostics of supercapacitors using cyclic voltammetry: Modeling and experimental applications. J. Electroanal. Chem. 2023, 935, 117322. [Google Scholar] [CrossRef]
- Sunil, V.; Pal, B.; Misnon, I.I.; Jose, R. Characterization of supercapacitive charge storage device using electrochemical impedance spectroscopy. Mater. Today Proc. 2021, 46 Pt 4, 1588–1594. [Google Scholar] [CrossRef]
- Nandi, A.K.; Chatterjee, D.P. Hybrid polymer gels for energy applications. J. Mater. Chem. A 2023, 11, 12593–12642. [Google Scholar] [CrossRef]
- Kumar, N.; Kim, S.-B.; Lee, S.-Y.; Park, S.-J. Recent Advanced Supercapacitor: A Review of Storage Mechanisms, Electrode Materials, Modification, and Perspectives. Nanomaterials 2022, 12, 3708. [Google Scholar] [CrossRef]
- Sharma, S.; Chand, P. Supercapacitor and electrochemical techniques: A brief review. Results Chem. 2023, 5, 100885. [Google Scholar]
- Genene, Z.; Xia, Z.; Yang, G.; Mammo, W.; Wang, E. Recent Advances in the Synthesis of Conjugated Polymersfor Supercapacitors. Adv. Mater. Technol. 2024, 9, 2300167. [Google Scholar] [CrossRef]
- Narayanan, S.; Pankajakshan, A.E.; Padmanabhan, V.T.; Joseph, A. Conducting Polymer Nanocomposites for Supercapacitors. In Polymer Nanocomposites in Supercapacitors, 1st ed.; George, S.C., John, S., Rajeevan, S., Eds.; CRC Press: Boca Raton, FL, USA, 2022; p. 25. [Google Scholar]
- Rajeevan, S.; John, S.; George, S.C. Polymers for Supercapacitors. An Overview. In Polymer Nanocomposites in Supercapacitors, 1st ed.; George, S.C., John, S., Rajeevan, S., Eds.; CRC Press: Boca Raton, FL, USA, 2022; p. 15. [Google Scholar]
- Li, W.; Wang, X.; Hu, Y.; Sun, L.; Gao, C.; Zhang, C.; Liu, H.; Duan, M. Hydrothermal Synthesized of CoMoO4 Microspheres as Excellent Electrode Material for Supercapacitor. Nanoscale Res. Lett. 2018, 13, 120. [Google Scholar] [CrossRef]
- Li, Z.; Fu, J.; Zhou, X.; Gui, S.; Wei, L.; Yang, H.; Li, H.; Guo, X. Ionic Conduction in Polymer-Based Solid Electrolytes. Adv. Sci. 2023, 10, 2201718. [Google Scholar] [CrossRef]
- Wang, W.; Cao, J.; Yu, J.; Tian, F.; Luo, X.; Hao, Y.; Huang, J.; Wang, F.; Zhou, W.; Xu, J.; et al. Flexible Supercapacitors Based on Stretchable Conducting Polymer Electrodes. Polymers 2023, 15, 1856. [Google Scholar] [CrossRef] [PubMed]
- Wustoni, S.; Ohayon, D.; Hermawan, A.; Nuruddin, A.; Inal, S.; Indartono, Y.S.; Yuliarto, B. Material Design and Characterization of Conducting Polymer-Based Supercapacitors. Polym. Rev. 2024, 64, 192–250. [Google Scholar]
- Eom, H.; Kang, J.; Jang, S.; Kwon, O.; Choi, S.; Shin, J.; Nam, I. Evaluating the Electrochemical Properties of Supercapacitors using the Three-Electrode System. J. Vis. Exp. 2022, 179, e63319. [Google Scholar] [CrossRef]
- Adedoja, O.S.; Sadiku, E.R.; Hamam, Y. An Overview of the Emerging Technologies and Composite Materials for Supercapacitors in Energy Storage Applications. Polymers 2023, 15, 2272. [Google Scholar] [CrossRef]
- Rohith, R.; Prasannakumar, A.T.; Manju, V.; Mohan, R.R.; Varma, S.J. Flexible, symmetric supercapacitor using self-stabilized dispersion-polymerised polyaniline/V2O5 hybrid electrodes. J. Chem. Eng. 2023, 467, 143499. [Google Scholar] [CrossRef]
- Ghriga, M.A.; Grassi, B.; Gareche, M.; Khodja, M. Review of recent advances in polyethylenimine crosslinked polymer gels used for conformance control applications. Polym. Bull. 2019, 76, 6001–6029. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, G.; Rawach, D.; Fu, C.; Wang, C.; Liu, X.; Dubois, M.; Lai, C.; Sun, S. Polymer gel electrolytes for flexible supercapacitors: Recent progress, challenges, and perspectives. Energy Storage Mater. 2021, 34, 320–355. [Google Scholar]
- Tombolesi, S.; Zanieri, N.; Bargnesi, L.; Mernini, M.; Lacarbonara, G.; Arbizzani, C. A Sustainable Gel Polymer Electrolyte for Solid-State Electrochemical Devices. Polymers 2023, 15, 3087. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, Z.; Yin, H.; Hou, S.; Lin, H.; Zhou, J.; Zhuo, S. Investigation on the role of different conductive polymers in supercapacitors based on a zinc sulfide/reduced graphene oxide/conductive polymer ternary composite electrode. RSC Adv. 2020, 10, 3122–3129. [Google Scholar] [CrossRef]
- Abdah, M.A.A.M.; Awan, H.T.A.; Mehar, M.; Mustafa, M.N.; Walvekar, R.; Alam, M.W.; Khalid, M.; Umapathi, R.; Chaudhary, V. Advancements in MXene-polymer composites for high-performance supercapacitor applications. J. Energy Storage 2023, 63, 106942. [Google Scholar] [CrossRef]
- Fleischmann, S.; Mitchell, J.B.; Wang, R.; Zhan, C.; Jiang, D.; Presser, V.; Augustyn, V. Pseudocapacitance: From Fundamental Understanding to High Power Energy Storage Materials. Chem. Rev. 2020, 120, 6738. [Google Scholar] [PubMed]
- Allagui, A.; Hachemi Benaoum, H.; Olendski, O. On the Gouy–Chapman–Stern model of the electricaldouble-layer structure with a generalized Boltzmann factor. Phys. A 2021, 582, 126252. [Google Scholar] [CrossRef]
- Dębska, B.; Wianowska, E. Application of cluster analysis method in prediction of polymer properties. Polym. Test. 2002, 21, 43–47. [Google Scholar] [CrossRef]
- Phillips, J.L.; Colvin, M.E.; Newsam, S. Validating clustering of molecular dynamics simulations using polymer models. BMC Bioinform. 2011, 12, 445. [Google Scholar] [CrossRef] [PubMed]
- Bo, Z.; Li, C.; Yang, H.; Ostrikov, K.; Yan, J.; Cen, K. Design of Supercapacitor Electrodes Using Molecular Dynamics Simulations. Nano-Micro Lett. 2018, 10, 33. [Google Scholar] [CrossRef]
- Zeng, L.; Peng, J.; Zhang, J.; Tan, X.; Ji, X.; Li, S.; Feng, G. Molecular dynamics simulations of electrochemical interfaces. J. Chem. Phys. 2023, 159, 091001. [Google Scholar]
- Wei, T.; Ren, C. Cap. 6—Theoretical simulation approaches to polymer research. In Polymer Science and Innovative Applications; AlMaadeed, M.A.A., Ponnamma, D., Carignano, M.A., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 207–228. [Google Scholar]
- Suriyakumar, S.; Bhardwaj, P.; Grace, A.N.; Stephan, A.M. Role of Polymers in Enhancing the Performance of Electrochemical Supercapacitors: A Review. Batter. Supercaps 2021, 4, 571–584. [Google Scholar]
- Guo, F.; Gupta, N.; Teng, X. Enhancing Pseudocapacitive Process for Energy Storage Devices: Analyzing the Charge Transport Using Electro-kinetic Study and Numerical Modeling. In Supercapacitors—Theoretical and Practical Solutions; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Nguyen, D.; Tao, L.; Li, Y. Integration of Machine Learning and Coarse-Grained Molecular Simulations for Polymer Materials: Physical Understandings and Molecular Design. Front. Chem. 2022, 9, 820417. [Google Scholar]
- Wang, J.; Han, Y.; Xu, Z.; Yang, X.; Ramakrishna, S.; Liu, Y. Dissipative Particle Dynamics Simulation: A Review on Investigating Mesoscale Properties of Polymer Systems. Macromol. Mater. Eng. 2021, 306, 2000724. [Google Scholar]
- Santo, K.P.; Neimark, A.V. Dissipative particle dynamics simulations in colloid and Interface science: A review. Adv. Colloid Interface Sci. 2021, 298, 102545. [Google Scholar] [CrossRef]
- Zhang, B.; Guan, B.; Liu, W.; Peng, B.; Cong, S. Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding. Processes 2023, 11, 1411. [Google Scholar] [CrossRef]
- Ye, H.; Xian, W.; Li, Y. Machine Learning of Coarse-Grained Models for Organic Molecules and Polymers: Progress, Opportunities, and Challenges. ACS Omega 2021, 6, 1758–1772. [Google Scholar] [PubMed]
- Wang, Y.; Xie, T.; France-Lanord, A.; Berkley, A.; Johnson, J.A.; Shao-Horn, Y.; Grossman, J.C. Toward Designing Highly Conductive Polymer Electrolytes by Machine Learning Assisted Coarse-Grained Molecular Dynamics. Chem. Mater. 2020, 32, 4144–4151. [Google Scholar] [CrossRef]
- Yellam, K.; Katiyar, R.S.; Jha, P.K. Current Perspective on Atomistic Force Fields of Polymers. In Force Fields for Atomistic-Scale Simulations: Materials and Applications; Verma, A., Mavinkere Rangappa, S., Ogata, S., Siengchin, S., Eds.; Lecture Notes in Applied and Computational Mechanics; Springer: Singapore, 2022; Volume 99. [Google Scholar]
- Bačová, P.; Rissanou, A.N.; Harmandaris, V. Modelling of novel polymer materials through atomistic molecular dynamics simulations. Procedia Comput. Sci. 2018, 136, 341–350. [Google Scholar] [CrossRef]
- Ishraaq, R.; Das, S. All-atom molecular dynamics simulations of polymer and polyelectrolyte brushes. Chem. Commun. 2024, 60, 6093–6129. [Google Scholar] [CrossRef]
- Stone, J. Chapter 18—Electrostatic potential map. In Programming Massively Parallel Processors, A Hands-On Approach, 4th ed.; Hwu, W.W., Kirk, D.B., El Hajj, I., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2022; pp. 415–431. [Google Scholar]
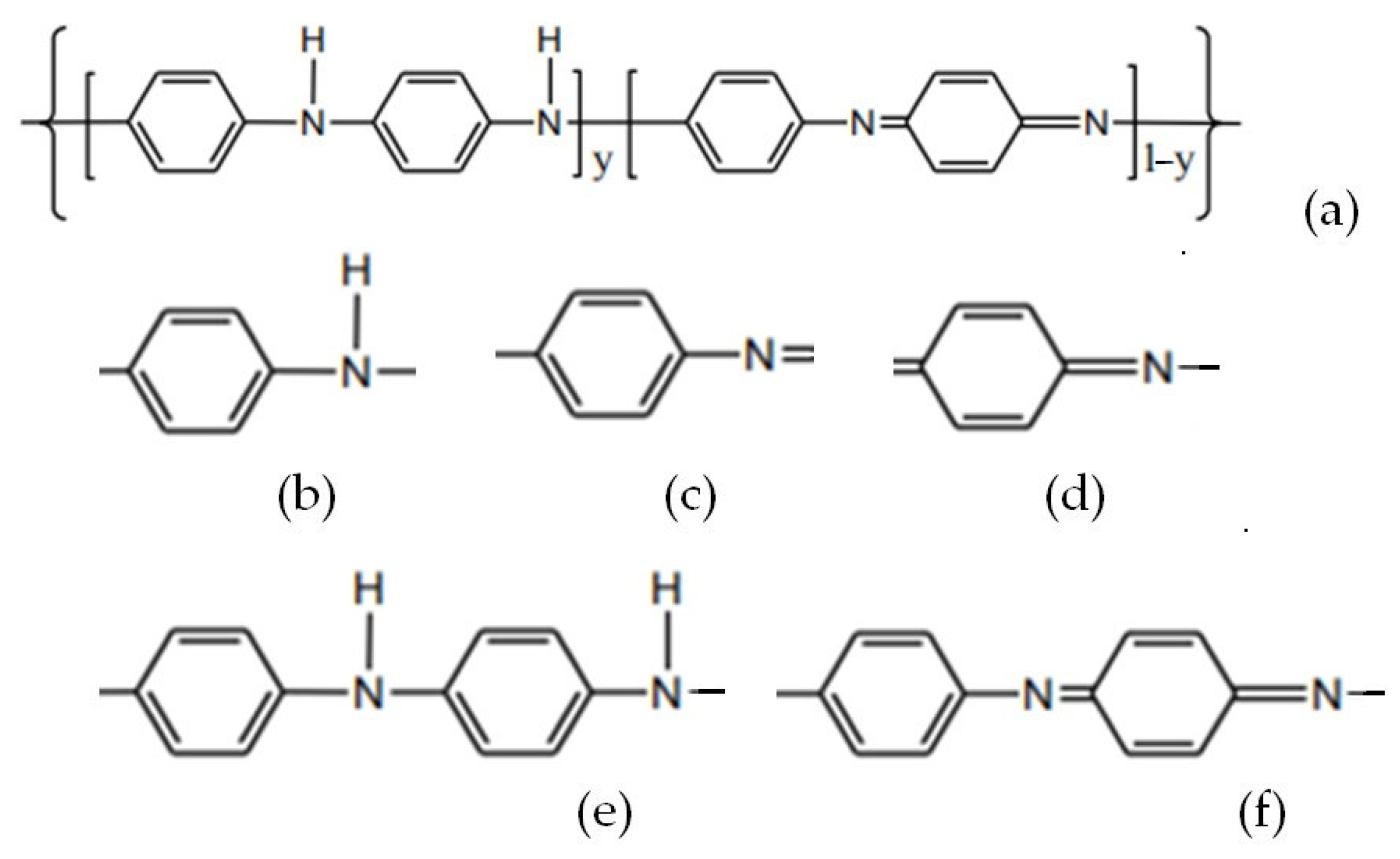
| No. | Electrode | Reference | Electrolyte | Gel Polymer Electrolyte | Characteristics | No. |
|---|---|---|---|---|---|---|
| 1. | Polymer-MXene * (a) Polyaniline (PANI)/Ti3C2 (b) polyfluorene derivatives PFDs/Ti3C2Tx (Tx = O, OH, F) | Abdah 2023 [32] | (a) Na2SO4 (b) H2SO4
|
| (2D) transition metal carbides high electrical conductivity, excellent mechanical strength, low-cost processing, molecular tunability, environmental benignity, and high mechanical flexibility | 1. |
| 2. | PETC (EDOT and triphenylamine with electron-withdrawing cyano group) (P6) | Genene [18] |
| Conjugated polymers ⇔ large-area, portable, stretchable, flexible SC fabrication | 2. | |
| 3. | Polythiophene (PTh, C4H4S) and Poly(3-methylthiophene) (P3MT) | Wang [23] |
| Electrode—stretchable conducting polymer | 3. | |
| 4. | Doped PANI/V2O5 (3:1) composite | Rohith 2023 [27] |
|
| 4. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ionescu, D.; Kovaci, M. Prediction of the Specific Energy of Supercapacitors with Polymeric Materials Using Advanced Molecular Dynamics Simulations. Polymers 2024, 16, 3404. https://doi.org/10.3390/polym16233404
Ionescu D, Kovaci M. Prediction of the Specific Energy of Supercapacitors with Polymeric Materials Using Advanced Molecular Dynamics Simulations. Polymers. 2024; 16(23):3404. https://doi.org/10.3390/polym16233404
Chicago/Turabian StyleIonescu, Daniela, and Maria Kovaci. 2024. "Prediction of the Specific Energy of Supercapacitors with Polymeric Materials Using Advanced Molecular Dynamics Simulations" Polymers 16, no. 23: 3404. https://doi.org/10.3390/polym16233404
APA StyleIonescu, D., & Kovaci, M. (2024). Prediction of the Specific Energy of Supercapacitors with Polymeric Materials Using Advanced Molecular Dynamics Simulations. Polymers, 16(23), 3404. https://doi.org/10.3390/polym16233404







