Modelling Across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 2-Multiscale Approach
Abstract
1. Introduction
2. Materials and Methods
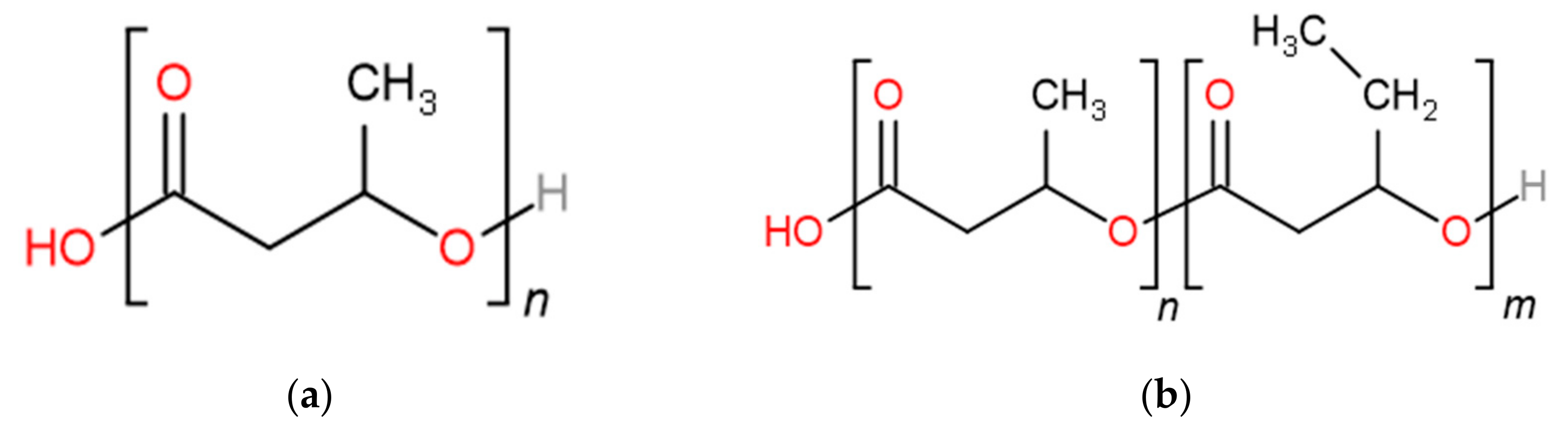
2.1. Materials
2.2. Theoretical Background
2.2.1. Gas Transport in Polymeric Membranes
2.2.2. Molecular Simulations of Gas Solubility
2.2.3. Multiscale Procedure for the Parametrisation of the SL EoS and Solubility Calculation
2.3. Simulation and Modelling
2.3.1. MD Simulations—Generation of Initial Configurations
2.3.2. Multiscale Model—Parameterisation of the SL EoS
2.3.3. Multiscale Model—Gas Solubility Prediction with SL EoS
3. Results and Discussion
3.1. MD Simulations
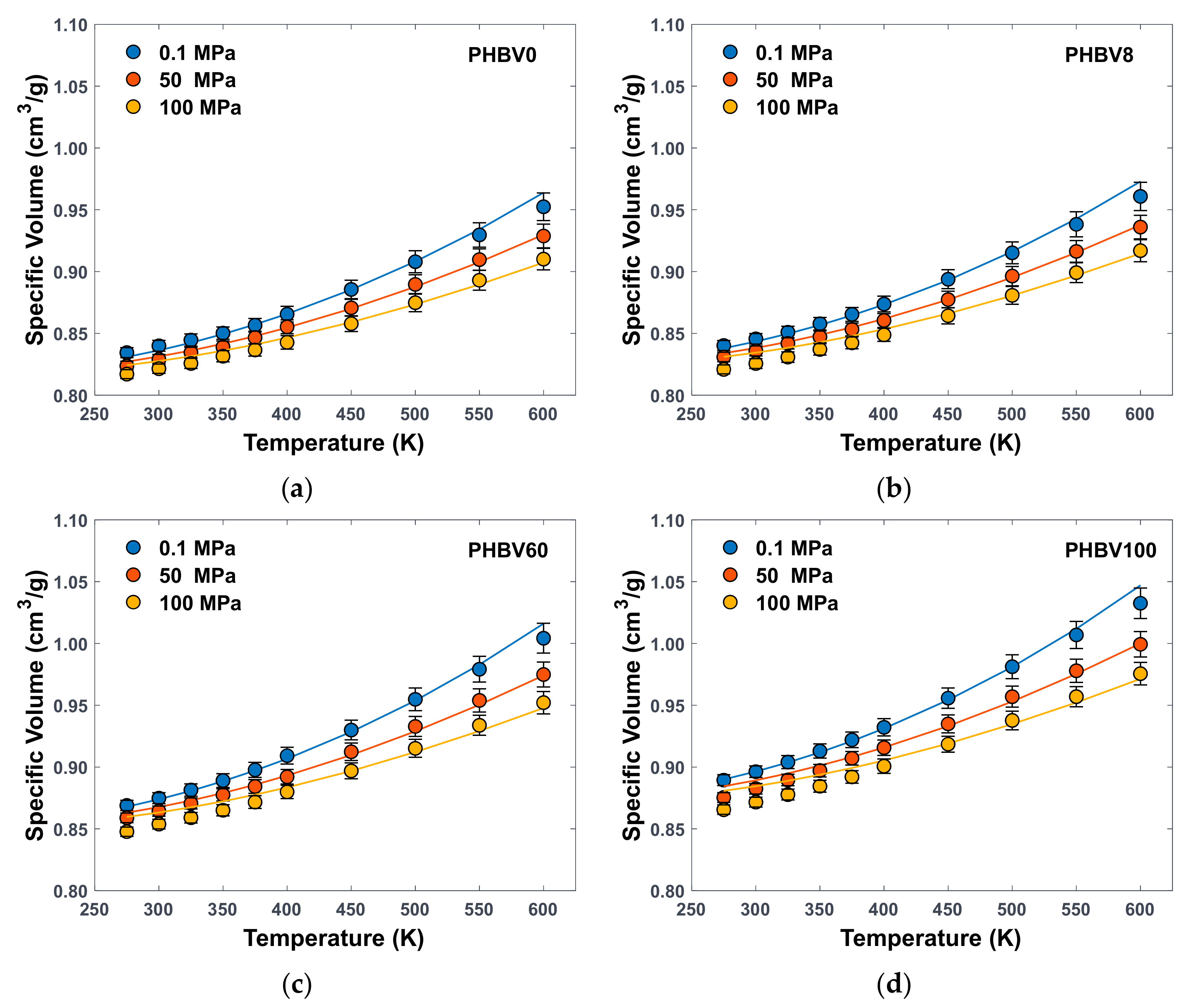
3.1.1. PVT Data
3.1.2. Retrieval of SL Characteristic Parameters
3.2. Gas Sorption
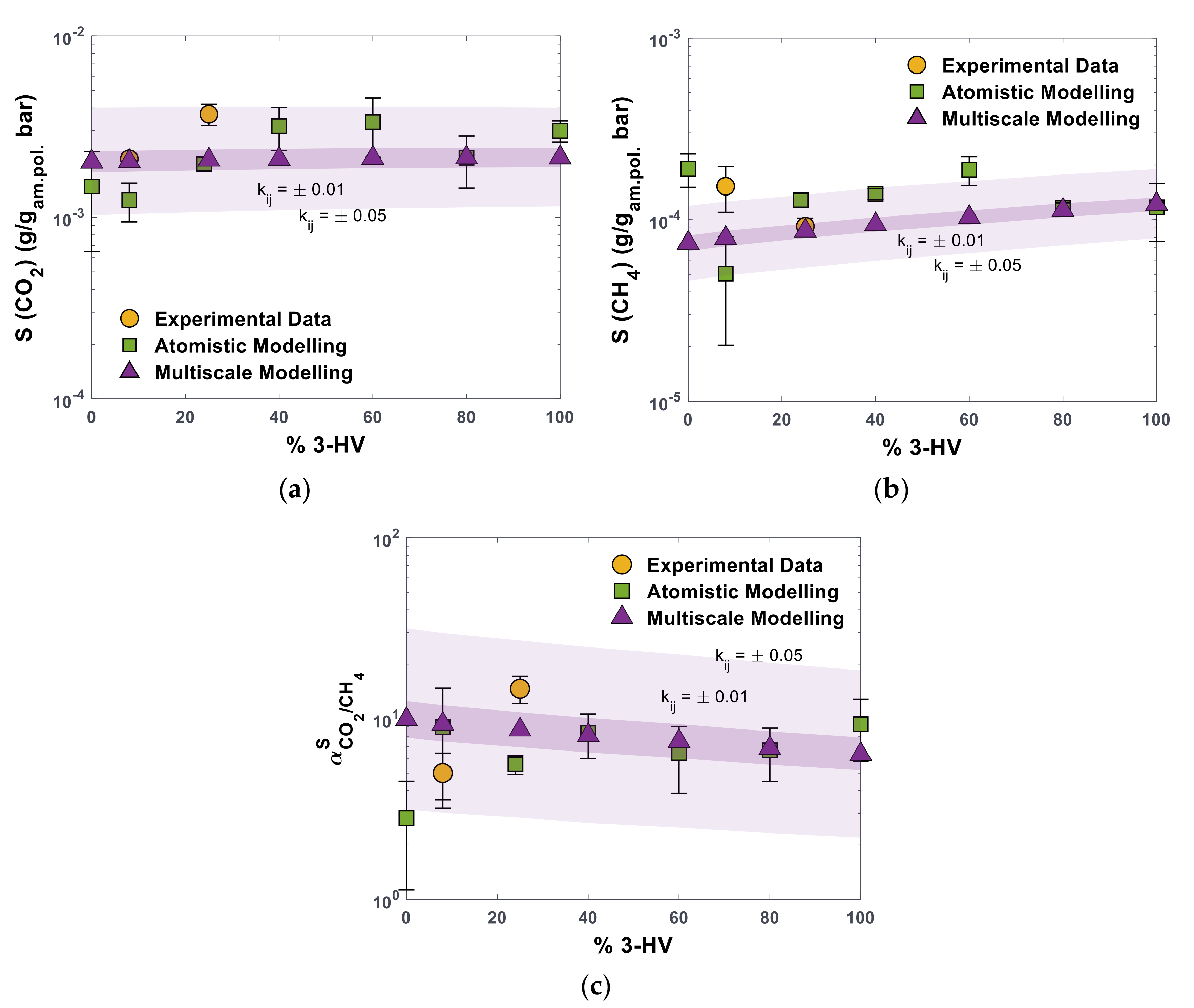
3.2.1. Prediction of Pure CO2 and CH4 Solubility
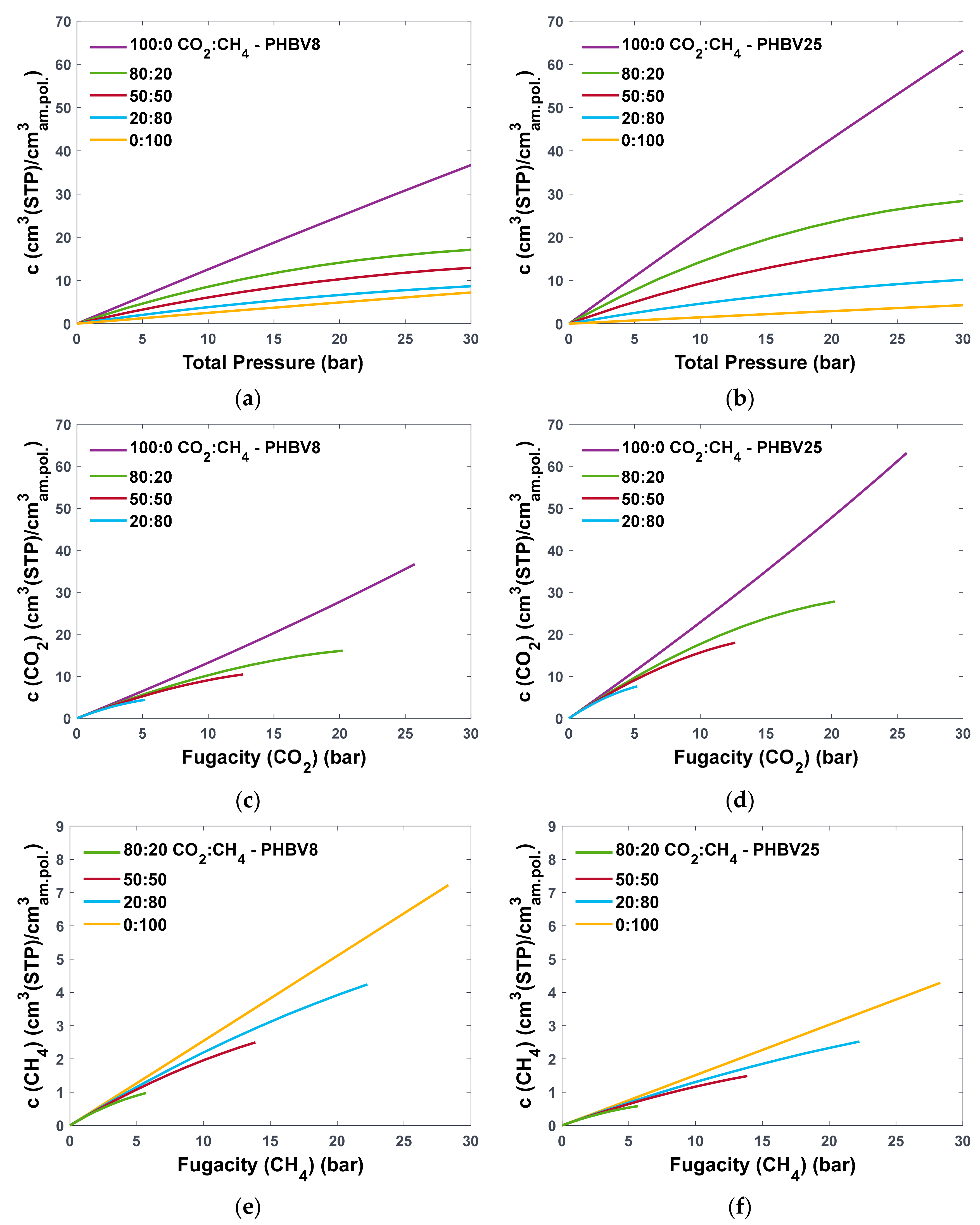
3.2.2. Prediction of Solubility of CO2 and CH4 under Mixed-Gas Conditions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Naeem, A.; Saeed, B.; AlMohamadi, H.; Lee, M.; Gilani, M.A.; Nawaz, R.; Khan, A.L.; Yasin, M. Sustainable and Green Membranes for Chemical Separations: A Review. Sep. Purif. Technol. 2024, 336, 126271. [Google Scholar] [CrossRef]
- Vieira, M.G.A.; Da Silva, M.A.; Dos Santos, L.O.; Beppu, M.M. Natural-Based Plasticizers and Biopolymer Films: A Review. Eur. Polym. J. 2011, 47, 254–263. [Google Scholar] [CrossRef]
- Iulianelli, A.; Russo, F.; Galiano, F.; Manisco, M.; Figoli, A. Novel Bio-Polymer Based Membranes for CO2/CH4 Separation. Int. J. Greenh. Gas Control. 2022, 117, 103657. [Google Scholar] [CrossRef]
- Bandehali, S.; Sanaeepur, H.; Ebadi Amooghin, A.; Shirazian, S.; Ramakrishna, S. Biodegradable Polymers for Membrane Separation. Sep. Purif. Technol. 2021, 269, 118731. [Google Scholar] [CrossRef]
- Drioli, E.; Macedonio, F.; Tocci, E. Membrane Science and Membrane Engineering for a Sustainable Industrial Development. Sep. Purif. Technol. 2021, 275, 119196. [Google Scholar] [CrossRef]
- Nunes, S.P.; Culfaz-Emecen, P.Z.; Ramon, G.Z.; Visser, T.; Koops, G.H.; Jin, W.; Ulbricht, M. Thinking the Future of Membranes: Perspectives for Advanced and New Membrane Materials and Manufacturing Processes. J. Membr. Sci. 2020, 598, 117761. [Google Scholar] [CrossRef]
- Russo, F.; Galiano, F.; Iulianelli, A.; Basile, A.; Figoli, A. Biopolymers for Sustainable Membranes in CO2 Separation: A Review. Fuel Process. Technol. 2021, 213, 106643. [Google Scholar] [CrossRef]
- Doi, Y.; Kitamura, S.; Abe, H. Microbial Synthesis and Characterization of Poly(3-Hydroxybutyrate-Co-3-Hydroxyhexanoate). Macromolecules 1995, 28, 4822–4828. [Google Scholar] [CrossRef]
- Boey, J.Y.; Mohamad, L.; Khok, Y.S.; Tay, G.S.; Baidurah, S. A Review of the Applications and Biodegradation of Polyhydroxyalkanoates and Poly(Lactic Acid) and Its Composites. Polymers 2021, 13, 1544. [Google Scholar] [CrossRef]
- Vert, M. Aliphatic Polyesters: Great Degradable Polymers That Cannot Do Everything. Biomacromolecules 2005, 6, 538–546. [Google Scholar] [CrossRef]
- Degli Esposti, M.; Chiellini, F.; Bondioli, F.; Morselli, D.; Fabbri, P. Highly Porous PHB-Based Bioactive Scaffolds for Bone Tissue Engineering by in Situ Synthesis of Hydroxyapatite. Mater. Sci. Eng. C 2019, 100, 286–296. [Google Scholar] [CrossRef] [PubMed]
- Papchenko, K.; Degli Esposti, M.; Minelli, M.; Fabbri, P.; Morselli, D.; De Angelis, M.G. New Sustainable Routes for Gas Separation Membranes: The Properties of Poly(Hydroxybutyrate-Co-Hydroxyvalerate) Cast from Green Solvents. J. Membr. Sci. 2022, 660, 120847. [Google Scholar] [CrossRef]
- Ricci, E.; Minelli, M.; De Angelis, M.G. Modelling Sorption and Transport of Gases in Polymeric Membranes across Different Scales: A Review. Membranes 2022, 12, 857. [Google Scholar] [CrossRef] [PubMed]
- Atiq, O.; Ricci, E.; Baschetti, M.G.; De Angelis, M.G. Modelling Solubility in Semi-Crystalline Polymers: A Critical Comparative Review. Fluid Phase Equilibria 2022, 556, 113412. [Google Scholar] [CrossRef]
- Theodorou, D.N. Principles of Molecular Simulation of Gas Transport in Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; Wiley: New York, NY, USA, 2006; pp. 49–94. ISBN 978-0-470-85345-0. [Google Scholar]
- Theodorou, D.N.; Suter, U.W. Detailed Molecular Structure of a Vinyl Polymer Glass. Macromolecules 1985, 18, 1467–1478. [Google Scholar] [CrossRef]
- Antoniadis, S.J.; Samara, C.T.; Theodorou, D.N. Molecular Dynamics of Atactic Polypropylene Melts. Macromolecules 1998, 31, 7944–7952. [Google Scholar] [CrossRef]
- Ricci, E.; Vergadou, N.; Vogiatzis, G.G.; De Angelis, M.G.; Theodorou, D.N. Molecular Simulations and Mechanistic Analysis of the Effect of CO2 Sorption on Thermodynamics, Structure, and Local Dynamics of Molten Atactic Polystyrene. Macromolecules 2020, 53, 3669–3689. [Google Scholar] [CrossRef]
- Lacombe, R.H.; Sanchez, I.C. Statistical Thermodynamics of Fluid Mixtures. J. Phys. Chem. 1976, 80, 2568–2580. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. An Elementary Molecular Theory of Classical Fluids. Pure Fluids. J. Phys. Chem. 1976, 80, 2352–2362. [Google Scholar] [CrossRef]
- Chapman, W.G.; Gubbins, K.E.; Jackson, G.; Radosz, M. SAFT: Equation-of-State Solution Model for Associating Fluids. Fluid Phase Equilibria 1989, 52, 31–38. [Google Scholar] [CrossRef]
- De Angelis, M.G.; Sarti, G.C.; Doghieri, F. NELF Model Prediction of the Infinite Dilution Gas Solubility in Glassy Polymers. J. Membr. Sci. 2007, 289, 106–122. [Google Scholar] [CrossRef]
- Minelli, M.; De Angelis, M.G.; Hofmann, D. A Novel Multiscale Method for the Prediction of the Volumetric and Gas Solubility Behavior of High-Tg Polyimides. Fluid Phase Equilibria 2012, 333, 87–96. [Google Scholar] [CrossRef]
- Ricci, E.; Minelli, M.; De Angelis, M.G. A Multiscale Approach to Predict the Mixed Gas Separation Performance of Glassy Polymeric Membranes for CO2 Capture: The Case of CO2/CH4 Mixture in Matrimid®. J. Membr. Sci. 2017, 539, 88–100. [Google Scholar] [CrossRef]
- Papchenko, K.; Ricci, E.; De Angelis, M.G. Modelling across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 1—Atomistic Approach. Polymers 2023, 15, 1805. [Google Scholar] [CrossRef]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Mitomo, H.; Morishita, N. Structural Changes of Poly(3-Hydroxybutyrate-Co-3-HydroxyvaIerate) Fractionated with Acetone-Water Solution. Polymer 1995, 36, 2573–2578. [Google Scholar] [CrossRef]
- Terada, M.; Marchessault, R.H. Determination of Solubility Parameters for Poly(3-Hydroxyalkanoates). Int. J. Biol. Macromol. 1999, 25, 207–215. [Google Scholar] [CrossRef]
- Jacquel, N.; Lo, C.-W.; Wu, H.-S.; Wei, Y.-H.; Wang, S.S. Solubility of Polyhydroxyalkanoates by Experiment and Thermodynamic Correlations. AIChE J. 2007, 53, 2704–2714. [Google Scholar] [CrossRef]
- Capitán, M.J.; Rueda, D.R.; Ezquerra, T.A. Inhibition of the Crystallization in Nanofilms of Poly(3-Hydroxybutyrate). Macromolecules 2004, 37, 5653–5659. [Google Scholar] [CrossRef]
- Hurrell, B.L.; Hurrell, B.L. A Wide-Angle X-Ray Scattering Study of the Ageing of Poly(Hydroxybutyrate). J. Mater. Sci. 1998, 33, 1709–1713. [Google Scholar] [CrossRef]
- Righetti, M.C.; Aliotta, L.; Mallegni, N.; Gazzano, M.; Passaglia, E.; Cinelli, P.; Lazzeri, A. Constrained Amorphous Interphase and Mechanical Properties of Poly(3-Hydroxybutyrate-Co-3-Hydroxyvalerate). Front. Chem. 2019, 7, 790. [Google Scholar] [CrossRef]
- Sudesh, K.; Abe, H.; Doi, Y. Synthesis, Structure and Properties of Polyhydroxyalkanoates: Biological Polyesters. Prog. Polym. Sci. 2000, 25, 1503–1555. [Google Scholar] [CrossRef]
- Koller, M.; Mukherjee, A. A New Wave of Industrialization of PHA Biopolyesters. Bioengineering 2022, 9, 74. [Google Scholar] [CrossRef]
- Alkandari, S.H.; Ching, M.; Lightfoot, J.C.; Berri, N.; Leese, H.S.; Castro-Dominguez, B. Recycling and 3D-Printing Biodegradable Membranes for Gas Separation─toward a Membrane Circular Economy. ACS Appl. Eng. Mater. 2024, 2, 1515–1525. [Google Scholar] [CrossRef] [PubMed]
- Corre, Y.-M.; Bruzaud, S.; Audic, J.-L.; Grohens, Y. Morphology and Functional Properties of Commercial Polyhydroxyalkanoates: A Comprehensive and Comparative Study. Polym. Test. 2012, 31, 226–235. [Google Scholar] [CrossRef]
- Carrasco, F.; Dionisi, D.; Martinelli, A.; Majone, M. Thermal Stability of Polyhydroxyalkanoates. J. Appl. Polym. Sci. 2006, 100, 2111–2121. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fund. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Ricci, E.; Benedetti, F.M.; Dose, M.E.; De Angelis, M.G.; Freeman, B.D.; Paul, D.R. Competitive Sorption in CO2/CH4 Separations: The Case of HAB-6FDA Polyimide and Its TR Derivative and a General Analysis of Its Impact on the Selectivity of Glassy Polymers at Multicomponent Conditions. J. Membr. Sci. 2020, 612, 118374. [Google Scholar] [CrossRef]
- Shing, K.S.; Chung, S.T. Computer Simulation Methods for the Calculation of Solubility in Supercritical Extraction Systems. J. Phys. Chem. 1987, 91, 1674–1681. [Google Scholar] [CrossRef]
- Sanchez, I.C.; Lacombe, R.H. Statistical Thermodynamics of Polymer Solutions. Macromolecules 1978, 11, 12. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, C.; Lv, J.; Lv, P.; Zhang, Y. Density Characteristics of the CO2–CH4 Binary System: Experimental Data at 313–353 K and 3–18 MPa and Modeling from the PC-SAFT EoS. J. Chem. Eng. Data 2018, 63, 4368–4380. [Google Scholar] [CrossRef]
- Barker, P.A.; Mason, F.; Barham, P.J. Density and Crystallinity of Poly (3-Hydroxybutyrate/3-Hydroxyvalerate) Copolymers. J. Mater. Sci. 1990, 25, 1952–1956. [Google Scholar] [CrossRef]
- Cravo, C.; Duarte, A.R.C.; Duarte, C.M.M. Solubility of Carbon Dioxide in a Natural Biodegradable Polymer: Determination of Diffusion Coefficients. J. Supercrit. Fluids 2007, 40, 194–199. [Google Scholar] [CrossRef]
- Genduso, G.; Litwiller, E.; Ma, X.; Zampini, S.; Pinnau, I. Mixed-Gas Sorption in Polymers via a New Barometric Test System: Sorption and Diffusion of CO2-CH4 Mixtures in Polydimethylsiloxane (PDMS). J. Membr. Sci. 2019, 577, 195–204. [Google Scholar] [CrossRef]
- Ricci, E.; Benedetti, F.M.; Noto, A.; Merkel, T.C.; Jin, J.; De Angelis, M.G. Enabling Experimental Characterization and Prediction of Ternary Mixed-Gas Sorption in Polymers: C2H6/CO2/CH4 in PIM-1. Chem. Eng. J. 2021, 426, 130715. [Google Scholar] [CrossRef]




| PHBV0 | PHBV8 | PHBV16 * | PHBV25 * | PHBV40 * | PHBV60 | PHBV80 * | PHBV100 | |
|---|---|---|---|---|---|---|---|---|
| [K] | 859.4 | 857.1 | 852.5 | 848.9 | 843.3 | 836.4 | 830.3 | 824.7 |
| [MPa] | 607.4 | 595.8 | 588.4 | 578.5 | 562.9 | 546.4 | 527.0 | 511.5 |
| [g/cm3] | 1.226 | 1.216 | 1.211 | 1.203 | 1.191 | 1.176 | 1.161 | 1.148 |
| 0.991 | 0.989 | – | – | – | 0.988 | – | 0.985 | |
| 0.330 | 0.349 | – | – | – | 0.399 | – | 0.487 | |
| 0.236 | 0.183 | 0.626 | 0.198 | 0.416 | 0.126 | 0.147 | 0.102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papchenko, K.; Ricci, E.; De Angelis, M.G. Modelling Across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 2-Multiscale Approach. Polymers 2024, 16, 2776. https://doi.org/10.3390/polym16192776
Papchenko K, Ricci E, De Angelis MG. Modelling Across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 2-Multiscale Approach. Polymers. 2024; 16(19):2776. https://doi.org/10.3390/polym16192776
Chicago/Turabian StylePapchenko, Kseniya, Eleonora Ricci, and Maria Grazia De Angelis. 2024. "Modelling Across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 2-Multiscale Approach" Polymers 16, no. 19: 2776. https://doi.org/10.3390/polym16192776
APA StylePapchenko, K., Ricci, E., & De Angelis, M. G. (2024). Modelling Across Multiple Scales to Design Biopolymer Membranes for Sustainable Gas Separations: 2-Multiscale Approach. Polymers, 16(19), 2776. https://doi.org/10.3390/polym16192776









