Tensile Properties of Cattail Fibres at Various Phenological Development Stages
Abstract
1. Introduction
2. Materials and Methods
2.1. Cattail Plant Collection and Fibre Extraction
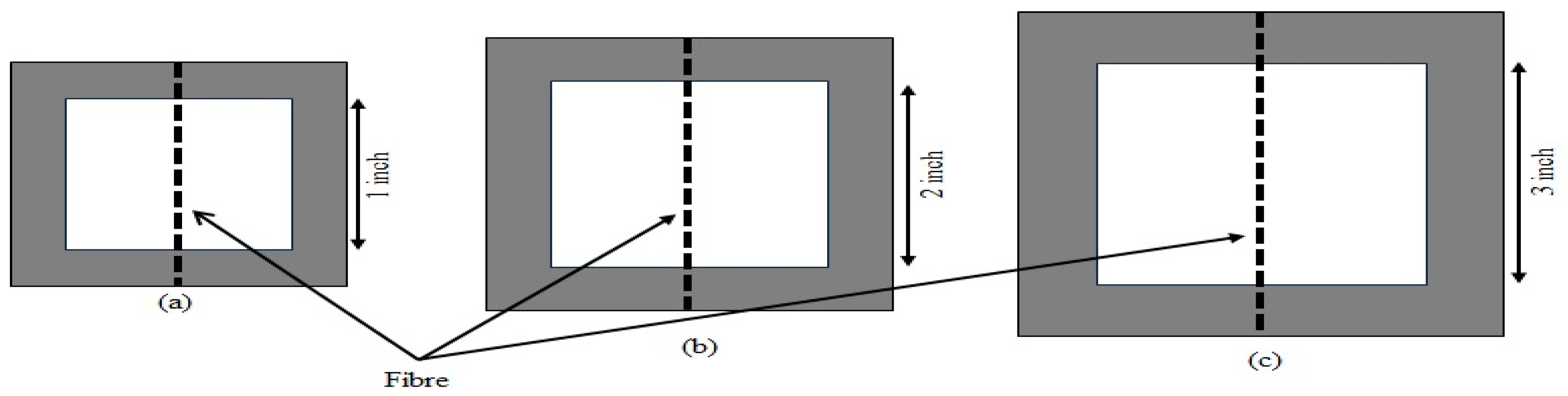
2.2. Mechanical Properties Measurement
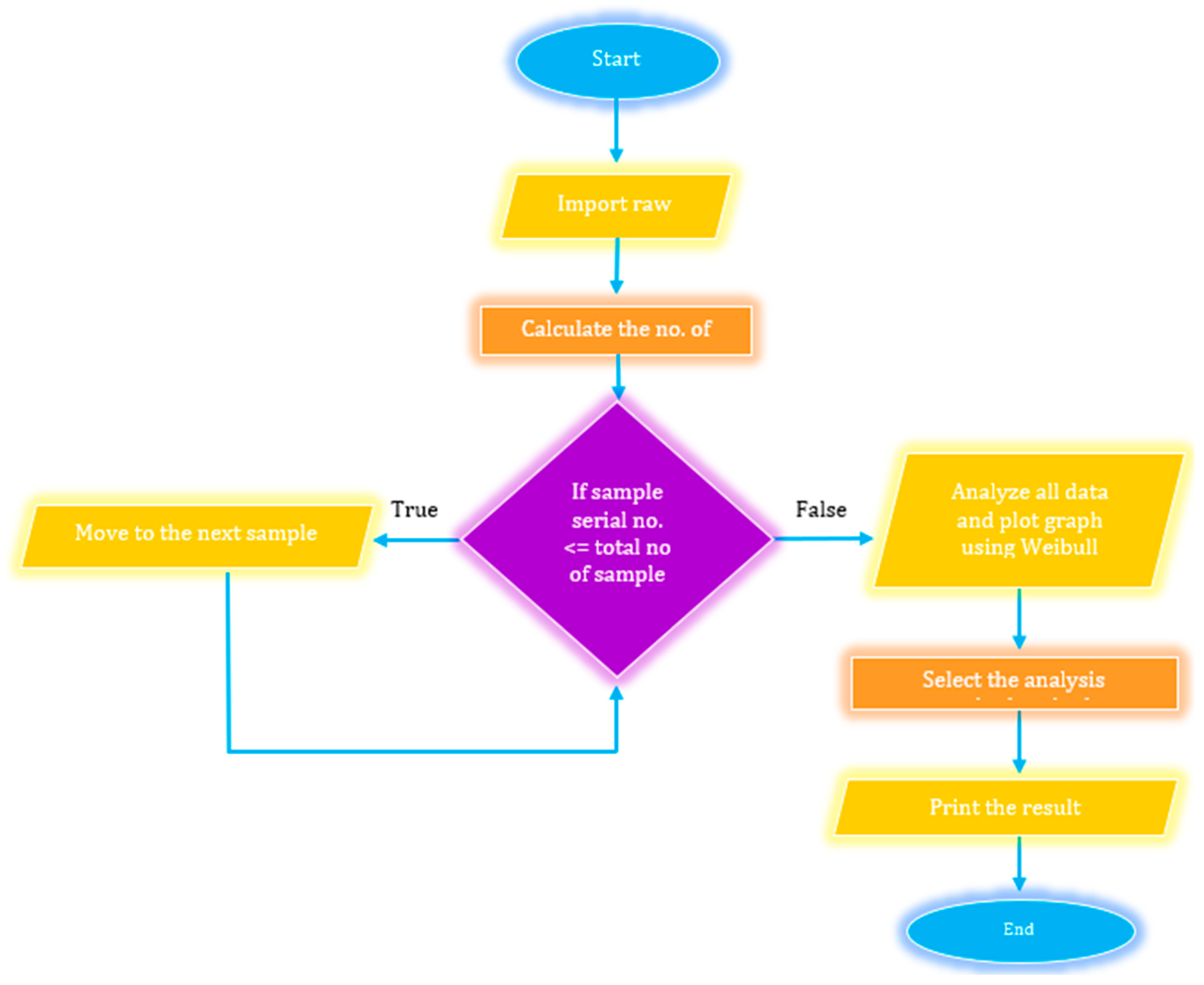
2.3. Weibull Analysis
2.3.1. Manual Calculation with Least Square Regression (LSR) Method Using Microsoft Excel
2.3.2. Weibull Analysis Using Computational Method
2.4. Chemical Development Analysis
2.4.1. Energy-Dispersive X-ray Spectroscopy (EDS)
2.4.2. Fourier Transform Infrared
3. Results and Discussion
3.1. Weibull Analysis of Mechanical Properties of Cattail Fibre
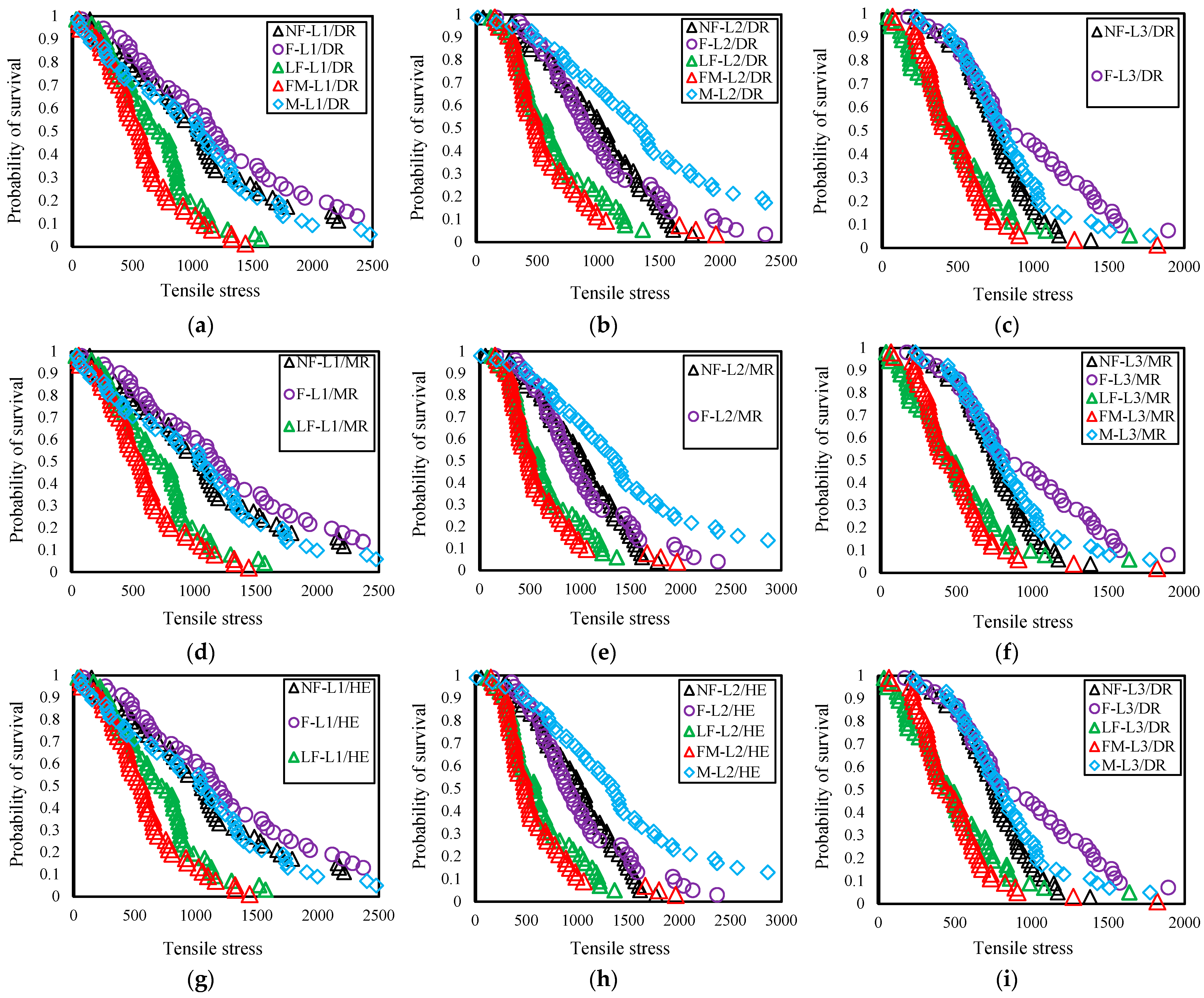
3.1.1. Weibull Analysis of Tensile Stress
3.1.2. Weibull Analysis of Modulus
3.2. Fibre Development at Various Growth Stages
Morphological Development
3.3. Chemical Development
3.3.1. Energy Dispersive X-ray Spectroscopy
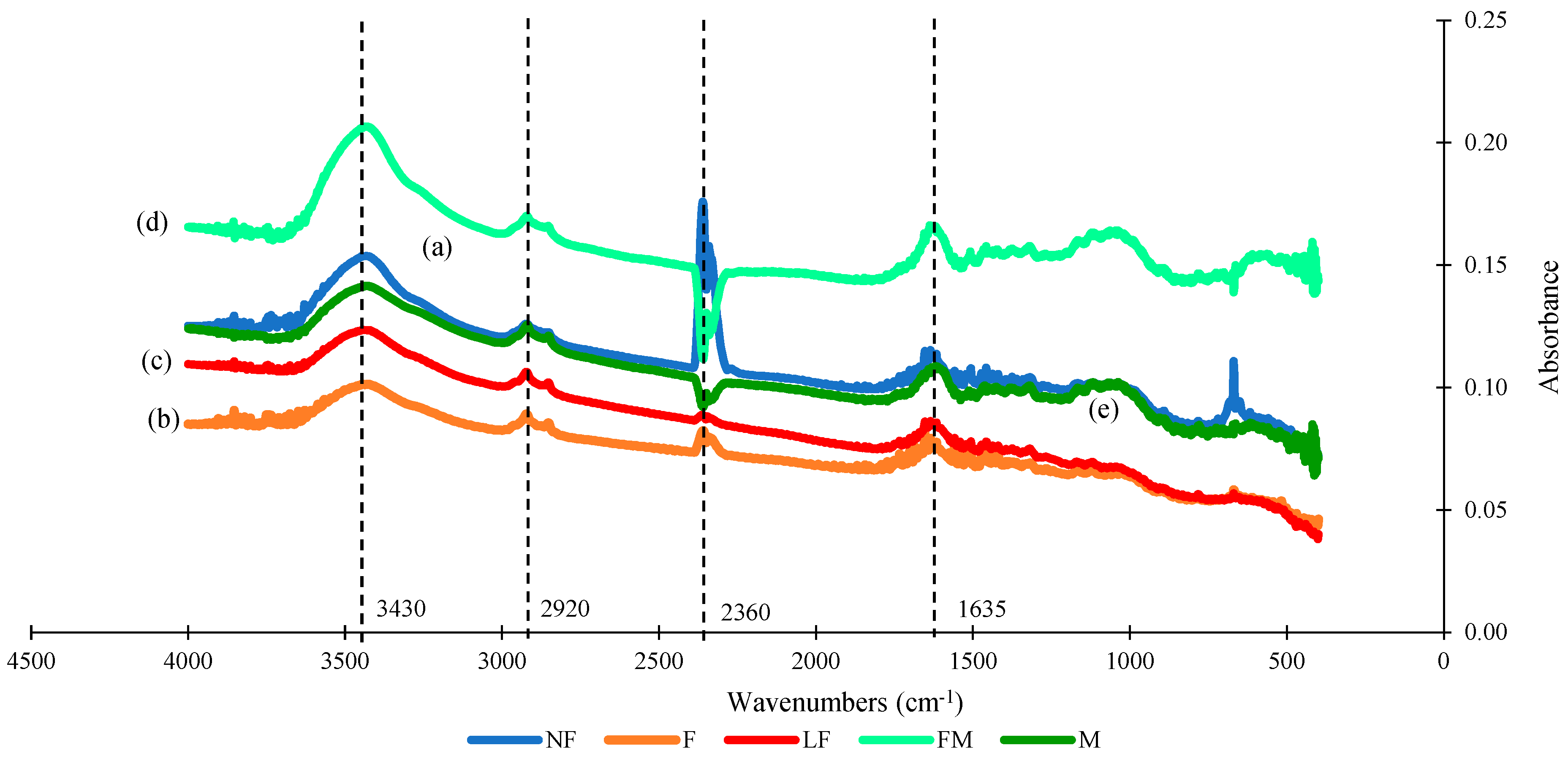
3.3.2. FTIR Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozturk, E.; Koseoglu, H.; Karaboyacı, M.; Yigit, N.; Yetis, U.; Kitis, M. Sustainable textile production: Cleaner production assessment/eco-efficiency analysis study in a textile mill. J. Clean. Prod. 2016, 138, 248–263. [Google Scholar] [CrossRef]
- Hoekstra, A.Y. Chapter 7—The water footprint of industry. In Assessing and Measuring Environmental Impact and Sustainability; Klemeš, J.J., Ed.; Butterworth-Heinemann: Oxford, UK, 2015; pp. 221–254. [Google Scholar] [CrossRef]
- Väisänen, T.; Das, O.; Tomppo, L. A review on new bio-based constituents for natural fibre-polymer composites. J. Clean. Prod. 2017, 149, 582–596. [Google Scholar] [CrossRef]
- Sathishkumar, G.K.; Ibrahim, M.; Mohamed Akheel, M.; Rajkumar, G.; Gopinath, B.; Karpagam, R.; Karthik, P.; Martin Charles, M.; Gautham, G.; Gowri Shankar, G. Synthesis and Mechanical Properties of Natural Fibre Reinforced Epoxy/Polyester/Polypropylene Composites: A Review. J. Nat. Fibres 2022, 19, 3718–3741. [Google Scholar] [CrossRef]
- Barth, M.; Carus, M. Carbon Footprint and Sustainability of Different Natural Fibres for Biocomposites and Insulation Material Study Providing Data for the Automotive and Insulation Industry MultiHemp. 2015. Available online: www.nova-institut.eu (accessed on 22 August 2022).
- Dellaert, S.N.C. Sustainability Assessment of the Production of Sisal Fibre in Brazil. 2014. Available online: https://studenttheses.uu.nl/handle/20.500.12932/17383 (accessed on 15 December 2022).
- Eichhorn, S.J.; Baillie, C.A.; Zafeiropoulos, N.; Mwaikambo, L.Y.; Ansell, M.P.; Dufresne, A.; Entwistle, K.M.; Herrera-Franco, P.J.; Escamilla, G.C.; Groom, L.; et al. Review: Current international research into cellulosic fibres and composites. J. Mater. Sci. 2001, 36, 2107–2131. [Google Scholar] [CrossRef]
- Gschwandtner, C. Outlook on Global Fibre Demand and Supply 2030. Growth 2022, 65, 113. [Google Scholar]
- Hasan, M.; Rahman, M.; Chen, Y.; Cicek, N. Optimization of Typha Fibre Extraction and Properties for Bio-Composite Applications Using Desirability Function Analysis. Polymers 2022, 14, 1685. [Google Scholar] [CrossRef]
- Mortazavi, S.M.; Moghadam, M.K. Introduction of a new vegetable fibre for textile application. J. Appl. Polym. Sci. 2009, 113, 3307–3312. [Google Scholar] [CrossRef]
- Rahman, M.; Cicek, N.; Chakma, K. The optimum parameters for fibre yield (%) and characterization of Typha latifolia L. fibres for textile applications. Fibres Polym. 2021, 22, 1543–1555. [Google Scholar] [CrossRef]
- Shadhin, M.; Rahman, M.; Jayaraman, R.; Mann, D. Novel cattail fibre composites: Converting waste biomass into reinforcement for composites. Bioresour. Bioprocess. 2021, 8, 101. [Google Scholar] [CrossRef]
- Shadhin, M. Comparative Evaluation of Flax, Cattail, and Hemp Fibre Composites. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2021. [Google Scholar]
- Grace, J.; Harrison, J. The biology of Canadian weeds. 73. Typha latifolia L.; Typha angustifolia L. and Typha xglauca Godr. Can. J. Plant Sci. 1986, 66, 361–379. [Google Scholar] [CrossRef]
- Euliss, N.H.; Gleason, R.A.; Olness, A.; McDougal, R.L.; Murkin, H.R.; Robarts, R.D.; Bourbonniere, R.A.; Warner, B.G. North American prairie wetlands are important nonforested land-based carbon storage sites. Sci. Total Environ. 2006, 361, 179–188. [Google Scholar] [CrossRef] [PubMed]
- The Canadian Encyclopedia. Wetlands. Available online: https://www.thecanadianencyclopedia.ca/en/article/wetlands (accessed on 19 April 2023).
- Tyler, H.L.; Moore, M.T.; Locke, M.A. Influence of Three Aquatic Macrophytes on Mitigation of Nitrogen Species from Agricultural Runoff. Water Air Soil Pollut. 2012, 223, 3227–3236. [Google Scholar] [CrossRef]
- Iowa State University. Alternative Grain Crops. Available online: https://www.extension.iastate.edu/alternativeag/alternative-grain-crops (accessed on 20 April 2023).
- Ulrich, A.; Challenges to Producing Flax in Canada. Biolin Research/Crop Fibres Canada. 2013. Available online: https://www.saskflax.com/news/challenges-to-producing-flax-in-canada (accessed on 10 March 2022).
- Hernandez, A.; Westerhuis, W.; Dam, J. Microscopic Study on Hemp Bast Fibre Formation. J. Nat. Fibres 2007, 3, 1–12. [Google Scholar] [CrossRef]
- Mokshina, N.; Chernova, T.; Galinousky, D.; Gorshkov, O.; Gorshkova, T. Key stages of fibre development as determinants of bast fibre yield and quality. Fibres 2018, 6, 20. [Google Scholar] [CrossRef]
- Grégoire, M.; Bar, M.; De Luycker, E.; Musio, S.; Amaducci, S.; Gabrion, X.; Placet, V.; Ouagne, P. Comparing flax and hemp fibres yield and mechanical properties after scutching/hackling processing. Ind. Crops Prod. 2021, 172, 114045. [Google Scholar] [CrossRef]
- Brook, H.; Slaski, J.; James, B. Industrial Hemp Harvest and Storage Best Management Practices. Available online: https://www1.agric.gov.ab.ca/$department/deptdocs.nsf/all/crop15539/$file/HempHarvestStorage.pdf?OpenElement (accessed on 6 April 2023).
- Daily Canola Prices. Alberta Canola. 2023. Available online: https://albertacanola.com/daily-canola-prices/ (accessed on 20 December 2023).
- Dubbe, D.R.; Garver, E.G.; Pratt, D.C. Production of cattail (Typha spp.) biomass in Minnesota, USA. Biomass 1988, 17, 79–104. [Google Scholar] [CrossRef]
- Sobrero, M.T.; Sabbatini, M.R.; Fernandez, O.A. Phenology and biomass dynamics of cattail (Typha subulata) in southern Argentina. Weed Sci. 1997, 45, 419–422. [Google Scholar] [CrossRef]
- Fink, S. The micromorphological distribution of bound calcium in needles of Norway spruce [Picea abies (L.) Karst.]. New Phytol. 1991, 119, 33–40. [Google Scholar] [CrossRef]
- Franceschi, V.; Horner, H. Calcium oxalate crystals in plants. Bot. Rev. 1980, 46, 361–427. [Google Scholar] [CrossRef]
- Shadhin, M.; Mann, D.; Rahman, M. Probabilistic model for cattail and canola fibers: Effect of environmental conditions, structural parameters, fiber length, and estimators. Text. Res. J. 2022, 92, 2513–2528. [Google Scholar] [CrossRef]
- Shadhin, M.; Rahman, M.; Jayaraman, R.; Chen, Y.; Mann, D.; Zhong, W. Natural biomass & waste biomass fibers–structures, environmental footprints, sustainability, degumming methods; surface modifications. Ind. Crops Prod. 2023, 204, 117252. [Google Scholar]
- Rahmadiawan, D.; Abral, H.; Shi, S.C.; Huang, T.T.; Zainul, R.; Ambiyar; Nurdin, H. Tribological Properties of Polyvinyl Alcohol/Uncaria Gambir Extract Composite as Potential Green Protective Film. Tribol. Ind. 2023, 45, 367–374. [Google Scholar] [CrossRef]
- Pardini, L.; Borzani, M. Influence of the Testing Gage Length on the Strength, Young’s Modulus and Weibull Modulus of Carbon Fibres and Glass Fibres. Mater. Res. 2002, 5, 411–420. [Google Scholar] [CrossRef]
- Wang, F.; Shao, J. Modified Weibull Distribution for Analyzing the Tensile Strength of Bamboo Fibres. Polymers 2014, 6, 3005–3018. [Google Scholar] [CrossRef]
- Zureick, A.-H.; Bennett, R.; Ellingwood, B. Statistical Characterization of Fibre-Reinforced Polymer Composite Material Properties for Structural Design. J. Struct. Eng.-ASCE 2006, 132, 1320–1327. [Google Scholar] [CrossRef]
- Hossain, S.M. Suitability of Typha Fibre in Composite Applications at Different Stages of Plant Development. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2022. Available online: https://mspace.lib.umanitoba.ca/server/api/core/bitstreams/bec579a8-0c95-4ba9-be4c-1e5e4d50e02e/content (accessed on 12 March 2023).
- Quinn, J.B.; Quinn, G.D. A practical and systematic review of Weibull statistics for reporting strengths of dental materials. Dent. Mater. 2010, 26, 135–147. [Google Scholar] [CrossRef]
- Alzeer, M.; Mackenzie, K. Synthesis and mechanical properties of novel composites of inorganic polymers (geopolymers) with unidirectional natural flax fibres (phormium tenax). Appl. Clay Sci. 2013, 75–76, 148–152. [Google Scholar] [CrossRef]
- Duval, A.; Bourmaud, A.; Augier, L.; Baley, C. Influence of the sampling area of the stem on the mechanical properties of hemp fibres. Mater. Lett. 2011, 65, 797–800. [Google Scholar] [CrossRef]
- Shuvo, I.I.; Rahman, M.; Vahora, T.; Morrison, J.; DuCharme, S.; Choo-Smith, L.-P. Producing light-weight bast fibres from canola biomass for technical textiles. Text. Res. J. 2019, 90, 1311–1325. [Google Scholar] [CrossRef]
- Liu, M.; Fernando, D.; Daniel, G.; Madsen, B.; Meyer, A.S.; Ale, M.T.; Thygesen, A. Effect of harvest time and field retting duration on the chemical composition, morphology and mechanical properties of hemp fibres. Ind. Crops Prod. 2015, 69, 29–39. [Google Scholar] [CrossRef]
- Lefeuvre, A.; Bourmaud, A.; Lebrun, L.; Morvan, C.; Baley, C. A study of the yearly reproducibility of flax fibre tensile properties. Ind. Crops Prod. 2013, 50, 400–407. [Google Scholar] [CrossRef]
- Martin, N.; Mouret, N.; Davies, P.; Baley, C. Influence of the degree of retting of flax fibres on the tensile properties of single fibres and short fibre/polypropylene composites. Ind. Crops Prod. 2013, 49, 755–767. [Google Scholar] [CrossRef]
- Charlet, K.; Jernot, J.P.; Gomina, M.; Bréard, J.; Morvan, C.; Baley, C. Influence of an Agatha flax fibre location in a stem on its mechanical, chemical and morphological properties. Compos. Sci. Technol. 2009, 69, 1399–1403. [Google Scholar] [CrossRef]
- Kanade, P. Role of Instrumental Parameters on Yarn Properties. Int. J. Innov. Res. Sci. Eng. Technol. 2007, 5, 3202–3207. [Google Scholar] [CrossRef]
- Shamsuyeva, M.; Chang, B.P.; Vellguth, N.; Misra, M.; Mohanty, A.; Endres, H.-J. Surface Modification of Flax Fibres for Manufacture of Engineering Thermoplastic Biocomposites. J. Compos. Sci. 2020, 4, 64. [Google Scholar] [CrossRef]
- Zafeiropoulos, N.E.; Baillie, C.A. A study of the effect of surface treatments on the tensile strength of flax fibres: Part II. Application of Weibull statistics. Compos. Part A: Appl. Sci. Manuf. 2007, 38, 629–638. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Srikanta, R. Effect of ageing of sisal fibres on properties of sisal—Polypropylene composites. Polym. Degrad. Stab. 2008, 93, 2048–2051. [Google Scholar] [CrossRef]
- Placet, V.; Cisse, O.; Lamine, M. Influence of environmental relative humidity on the tensile and rotational behaviour of hemp fibres. J. Mater. Sci. 2012, 47, 3435–3446. [Google Scholar] [CrossRef]
- Stamboulis, A.; Baillie, C.A.; Peijs, T. Effects of environmental conditions on mechanical and physical properties of flax fibres. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1105–1115. [Google Scholar] [CrossRef]
- Lamy, B.; Baley, C. Stiffness prediction of flax fibres-epoxy composite materials. J. Mater. Sci. Lett. 2000, 19, 979–980. [Google Scholar] [CrossRef]
- Baley, C. Analysis of the flax fibres tensile behaviour and analysis of the tensile stiffness increase. Compos. ParHast A Appl. Sci. Manuf. 2002, 33, 939–948. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Jayaraman, K. Flax fibre and its composites–A review. Compos. Part B Eng. 2014, 56, 296–317. [Google Scholar] [CrossRef]
- Gassan, J.; Chate, A.; Bledzki, A. Calculation of elastic properties of natural fibres. J. Mater. Sci. 2001, 36, 3715–3720. [Google Scholar] [CrossRef]
- Xia, Z.P.; Yu, J.Y.; Cheng, L.D.; Liu, L.F.; Wang, W.M. Study on the breaking strength of jute fibres using modified Weibull distribution. Compos. Part A Appl. Sci. Manuf. 2009, 40, 54–59. [Google Scholar] [CrossRef]
- Koronis, G.; Silva, A.; Fontul, M. Green composites: A review of adequate materials for automotive applications. Compos. Part B Eng. 2013, 44, 120–127. [Google Scholar] [CrossRef]
- Gourier, C.; Le Duigou, A.; Bourmaud, A.; Baley, C. Mechanical analysis of elementary flax fibre tensile properties after different thermal cycles. Compos. Part A Appl. Sci. Manuf. 2014, 64, 159–166. [Google Scholar] [CrossRef]
- Stacey, A.G. Robust parameterisation of ages of references in published research. J. Informetr. 2020, 14, 101048. [Google Scholar] [CrossRef]
- Reddit. What is the Difference between Linear Regression Computed Simply in an Application like Excel, and Linear Regression Created in a Programming Environment Such as Python with Machine Learning? 28 February 2018. Available online: https://www.reddit.com/r/datascience/comments/80yw17/what_is_the_difference_between_linear_regression/ (accessed on 7 November 2022).
- Ghosh, S.; Dever, M.; Thomas, H.; Tewksbury, C. Effects of selected fibre properties and needlepunch density on thennally-treated nonwoven fabrics. Iridian J. Fibre Text. Res. 1994, 19, 203–208. [Google Scholar]
- Hearle, J.W.S.; Sultan, M.A.I.; Choudhari, T.N. 9—A Study of Needled Fabrics. Part II: Effects of the Needling Process. J. Text. Inst. 1968, 59, 103–116. [Google Scholar] [CrossRef]
- Ishikawa, T.; Ishii, Y.; Nakasone, K.; Ohkoshi, Y.; Kyoung Hou, K. Structure analysis of needle-punched nonwoven fabrics by X-ray computed tomography. Text. Res. J. 2017, 89, 20–31. [Google Scholar] [CrossRef]
- Akampumuza, O.; Wambua, P.M.; Ahmed, A.; Li, W.; Qin, X.-H. Review of the applications of biocomposites in the automotive industry. Polym. Compos. 2017, 38, 2553–2569. [Google Scholar] [CrossRef]
- Monteiro, S.; Perissé Duarte Lopes, F.; Ferreira, A.S. Weibull analysis for the diameter dependence of the elastic modulus of curaua fibres. Matéria 2012, 18, 46–54. [Google Scholar] [CrossRef][Green Version]
- Evans, J.; Kretschmann, D.; Green, D. Procedures for Estimation of Weibull Parameters; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2019. [Google Scholar] [CrossRef]
- Papargyris, A.D. Estimator type and population size for estimating the Weibull modulus in ceramics. J. Eur. Ceram. Soc. 1998, 18, 451–455. Available online: https://api.semanticscholar.org/CorpusID:136957335 (accessed on 6 September 2022). [CrossRef]
- Grace, J.B.; Wetzel, R.G. Niche differentiation between two rhizomatous plant species: Typha latifolia and Typha angustifolia. Can. J. Bot. 1982, 60, 46–57. [Google Scholar] [CrossRef]
- Nakata, P.A. Advances in our understanding of calcium oxalate crystal formation and function in plants. Plant Sci. 2003, 164, 901–909. [Google Scholar] [CrossRef]
- National Geographic. The Carbon Cycle. Available online: https://education.nationalgeographic.org/resource/carbon-cycle/ (accessed on 1 April 2023).
- Chen, J.; Li, F.; Wang, R.; Fan, Y.; Raza, M.A.; Liu, Q.; Wang, Z.; Cheng, Y.; Wu, X.; Yang, F.; et al. Estimation of nitrogen and carbon content from soybean leaf reflectance spectra using wavelet analysis under shade stress. Comput. Electron. Agric. 2019, 156, 482–489. [Google Scholar] [CrossRef]
- Mosaic Crop Nutrition. Oxygen—Crop Nutrients. Available online: https://www.cropnutrition.com/nutrient-knowledge/oxygen (accessed on 3 April 2023).
- Marschner, H.; George, E.; Römheld, V. Preface to Second Edition. In Mineral Nutrition of Higher Plants, 2nd ed.; Marschner, H., Ed.; Academic Press: Cambridge, MA, USA, 1995; pp. vii–viii. [Google Scholar] [CrossRef]
- Sana, R.; Mounir, J.; Slah, M. Study of Structure and Properties of Tunisian Typha Leaf Fibers. Int. J. Eng. Res. Technol. 2014, 3, 539–546. [Google Scholar]
- César, N.R.; Pereira-da-Silva, M.A.; Botaro, V.R.; de Menezes, A.J. Cellulose nanocrystals from natural fiber of the macrophyte Typha domingensis: Extraction and characterization. Cellulose 2015, 22, 449–460. [Google Scholar] [CrossRef]
- Vahora, T. Characterization of Controlled Aerobically Retted Linseed Flax (Linum usitatisimum L.) and Canola (Brassica napus L.) Stems. Ph.D. Thesis, University of Manitoba, Winnipeg, MB, Canada, 2023. [Google Scholar]
- Gurunathan, T.; Mohanty, S.; Nayak, S.K. A review of the recent developments in biocomposites based on natural fibres and their application perspectives. Compos. Part A Appl. Sci. Manuf. 2015, 77, 1–25. [Google Scholar] [CrossRef]
- Shahzad, A. A Study in Physical and Mechanical Properties of Hemp Fibres. Adv. Mater. Sci. Eng. 2013, 2013, 325085. [Google Scholar] [CrossRef]





| Fibre | Tensile Stress (MPa) | Modulus (GPa) |
|---|---|---|
| Cattail | 30–1106 | 3.0–74.7 |
| Canola | 40–502 | 14–54 |
| Banana | 355 | 33.8 |
| Flax | 45–1500 | 3–27 |
| Hemp | 550–900 | 6–50 |
| Jute | 320–800 | 13–26.5 |
| Sisal | 468–700 | 9.4–22 |
| Bamboo | 140–800 | 9.9–32 |
| M-L1 | FM-L1 | LF-L1 | F-L1 | NF-L1 |
| M-L2 | FM-L2 | LF-L2 | F-L2 | NF-L2 |
| M-L3 | FM-L3 | LF-L3 | F-L3 | NF-L3 |
| ID | stress | Manual Calculation (LR Method) | Computational Method | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | σavg (MPa) | α | β (MPa) | R2σ | LR Method (DR Estimator) | MLE Method | |||||||||||||
| DR | HE | MR | DR | HE | MR | DR | HE | MR | DR | HE | MR | α | β (MPa) | R2σ | α | β (MPa) | σavg (MPa) | ||
| NF-L1 | 1215 ± 903 | 1053 | 1056 | 1049 | 1.52 | 1.57 | 1.46 | 1340 | 1333 | 1348 | 0.97 | 0.97 | 0.98 | 1.56 | 1326 | 0.97 | 1.45 | 1347 | 1046 |
| NF-L2 | 1047 ± 614 | 986.0 | 987.8 | 984.2 | 1.81 | 1.88 | 1.73 | 1207 | 1200 | 1217 | 0.93 | 0.94 | 0.92 | 1.95 | 1182 | 0.93 | 1.81 | 1177 | 961.3 |
| NF-L3 | 747 ± 252 | 744.1 | 745.0 | 742.8 | 3.01 | 3.12 | 2.89 | 840.3 | 837.9 | 843.4 | 0.98 | 0.98 | 0.98 | 3.07 | 837.1 | 0.98 | 3.31 | 832 | 744.8 |
| F-L1 | 1288 ± 824 | 1138 | 1142 | 1135 | 1.47 | 1.52 | 1.41 | 1460 | 1452 | 1473 | 0.98 | 0.98 | 0.98 | 1.49 | 1451 | 0.98 | 1.61 | 1436 | 1144 |
| F-L2 | 1035 ± 534 | 989.4 | 990.7 | 987.1 | 2.23 | 2.30 | 2.14 | 1166 | 1162 | 1172 | 0.97 | 0.97 | 0.97 | 2.29 | 1157 | 0.97 | 2.09 | 1173 | 984.3 |
| F-L3 | 958 ± 483 | 912.9 | 914.8 | 911.0 | 2.18 | 2.25 | 2.09 | 1080 | 1076 | 1085 | 0.98 | 0.98 | 0.99 | 2.22 | 1076 | 0.98 | 2.13 | 1084 | 912.6 |
| LF-L1 | 738 ± 440 | 681.7 | 683.0 | 680.2 | 1.66 | 1.73 | 1.59 | 849.8 | 844.2 | 857.0 | 0.95 | 0.96 | 0.94 | 1.75 | 835.9 | 0.95 | 1.76 | 828.7 | 672.9 |
| LF-L2 | 684 ± 472 | 626.7 | 628.4 | 625.2 | 1.92 | 1.98 | 1.85 | 758.3 | 756.0 | 762.3 | 0.94 | 0.94 | 0.95 | 2.03 | 746.4 | 0.94 | 1.62 | 769.6 | 613.8 |
| LF-L3 | 542 ± 429 | 458.5 | 459.6 | 456.9 | 1.41 | 1.46 | 1.35 | 594.5 | 591.0 | 598.9 | 0.98 | 0.98 | 0.98 | 1.44 | 590.2 | 0.98 | 1.37 | 594.6 | 455.0 |
| FM-L1 | 584 ± 334 | 535.4 | 536.5 | 533.9 | 1.64 | 1.70 | 1.57 | 669.5 | 665.8 | 674.2 | 0.97 | 0.97 | 0.97 | 1.69 | 662.3 | 0.97 | 1.82 | 655.9 | 536.3 |
| FM-L2 | 645 ± 531 | 580.8 | 582.2 | 579.1 | 1.86 | 1.91 | 1.79 | 707.7 | 705.3 | 710.9 | 0.87 | 0.86 | 0.87 | 2.14 | 679.6 | 0.87 | 1.45 | 720.7 | 559.7 |
| FM-L3 | 500 ± 298 | 471.1 | 471.8 | 470.2 | 2.04 | 2.12 | 1.95 | 563.7 | 561.0 | 567.1 | 0.95 | 0.95 | 0.94 | 2.15 | 556.0 | 0.95 | 1.82 | 564.6 | 461.6 |
| M-L1 | 1058 ± 881 | 843.5 | 846.8 | 839.7 | 1.14 | 1.18 | 1.09 | 1164 | 1156 | 1176 | 0.97 | 0.97 | 0.97 | 1.17 | 1148 | 0.97 | 1.24 | 1135 | 844.6 |
| M-L2 | 1500 ± 973 | 1369 | 1372 | 1366 | 1.81 | 1.88 | 1.74 | 1676 | 1668 | 1687 | 0.98 | 0.98 | 0.98 | 1.85 | 1666 | 0.97 | 1.67 | 1688 | 1355 |
| M-L3 | 834 ± 367 | 817.1 | 818.4 | 815.7 | 2.67 | 2.76 | 2.56 | 937.3 | 934.7 | 941.3 | 0.97 | 0.96 | 0.96 | 2.77 | 930.5 | 0.97 | 2.40 | 941.2 | 807.9 |
| ID | modulus | Manual Calculation (LR Method) | Computational Method | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (GPa) | Eavg (GPa) | α | β (GPa) | R2E | LR Method (DR Estimator) | MLE Method | |||||||||||||
| DR | HE | MR | DR | HE | MR | DR | HE | MR | DR | HE | MR | α | β (GPa) | R2E | α | β (GPa) | Eavg (GPa) | ||
| NF-L1 | 45.19 ± 28.78 | 41.65 | 41.76 | 41.51 | 1.91 | 1.97 | 1.83 | 50.47 | 50.31 | 50.69 | 0.94 | 0.93 | 0.95 | 2.03 | 49.60 | 0.94 | 1.72 | 51.00 | 41.21 |
| NF-L2 | 55.29 ± 26.38 | 53.42 | 53.52 | 53.30 | 2.40 | 2.48 | 2.30 | 62.23 | 62.04 | 62.49 | 0.98 | 0.98 | 0.98 | 2.45 | 61.90 | 0.98 | 2.25 | 62.60 | 53.19 |
| NF-L3 | 47.32 ± 19.77 | 46.23 | 46.30 | 46.14 | 2.45 | 2.53 | 2.35 | 53.68 | 53.51 | 53.92 | 0.98 | 0.98 | 0.98 | 2.50 | 53.40 | 0.98 | 2.59 | 53.30 | 46.27 |
| F-L1 | 65.44 ± 41.72 | 59.01 | 59.17 | 58.82 | 1.73 | 1.78 | 1.66 | 72.94 | 72.66 | 73.33 | 0.97 | 0.96 | 0.97 | 1.79 | 72.10 | 0.97 | 1.67 | 73.60 | 59.10 |
| F-L2 | 29.51 ± 14.76 | 28.34 | 28.41 | 28.27 | 2.32 | 2.38 | 2.24 | 33.20 | 33.13 | 33.30 | 0.94 | 0.93 | 0.95 | 2.47 | 32.72 | 0.94 | 2.17 | 33.50 | 28.29 |
| F-L3 | 65.59 ± 27.96 | 64.68 | 64.80 | 64.56 | 2.90 | 2.99 | 2.78 | 73.41 | 73.25 | 73.65 | 0.91 | 0.90 | 0.92 | 3.19 | 72.14 | 0.91 | 2.51 | 74.11 | 64.04 |
| LF-L1 | 37.22 ± 22.53 | 34.67 | 34.75 | 34.57 | 1.99 | 2.05 | 1.92 | 41.67 | 41.54 | 41.85 | 0.95 | 0.94 | 0.96 | 2.10 | 41.09 | 0.95 | 1.79 | 42.09 | 34.30 |
| LF-L2 | 43.37 ± 29.97 | 39.80 | 39.89 | 39.68 | 1.93 | 1.99 | 1.86 | 48.11 | 47.95 | 48.31 | 0.91 | 0.90 | 0.91 | 2.13 | 46.82 | 0.91 | 1.62 | 48.89 | 38.99 |
| LF-L3 | 44.06 ± 31.03 | 39.96 | 40.06 | 39.84 | 1.83 | 1.89 | 1.76 | 48.81 | 48.65 | 49.03 | 0.93 | 0.92 | 0.93 | 1.98 | 47.73 | 0.93 | 1.58 | 49.52 | 39.27 |
| FM-L1 | 32.79 ± 15.29 | 31.83 | 31.90 | 31.75 | 2.49 | 2.56 | 2.39 | 36.88 | 36.80 | 37.00 | 0.94 | 0.93 | 0.95 | 2.63 | 36.42 | 0.94 | 2.32 | 37.14 | 31.71 |
| FM-L2 | 40.77 ± 23.29 | 39.07 | 39.14 | 38.99 | 2.37 | 2.45 | 2.28 | 45.60 | 45.46 | 45.78 | 0.92 | 0.91 | 0.92 | 2.59 | 44.71 | 0.92 | 1.91 | 46.20 | 38.13 |
| FM-L3 | 33.35 ± 21.19 | 31.72 | 31.77 | 31.65 | 2.31 | 2.39 | 2.23 | 37.16 | 37.05 | 37.31 | 0.88 | 0.87 | 0.88 | 2.79 | 34.68 | 0.91 | 1.91 | 35.93 | 29.66 |
| M-L1 | 55.71 ± 30.22 | 53.39 | 53.53 | 53.24 | 2.31 | 2.39 | 2.22 | 62.56 | 62.39 | 62.82 | 0.91 | 0.90 | 0.92 | 2.54 | 61.24 | 0.91 | 2.00 | 63.21 | 52.63 |
| M-L2 | 47.87 ± 26.92 | 45.22 | 45.32 | 45.10 | 2.14 | 2.21 | 2.06 | 53.66 | 53.51 | 53.88 | 0.95 | 0.94 | 0.96 | 2.25 | 53.00 | 0.95 | 1.93 | 54.28 | 44.89 |
| M-L3 | 60.72 ± 28.10 | 59.48 | 59.56 | 59.36 | 2.77 | 2.86 | 2.66 | 67.89 | 67.72 | 68.12 | 0.93 | 0.93 | 0.94 | 2.97 | 66.97 | 0.93 | 2.29 | 68.68 | 58.52 |
| Growth Stage | Elements | EDS Spots # | ||||||
|---|---|---|---|---|---|---|---|---|
| Carbon (C) | Oxygen (O) | Calcium (Ca) | ||||||
| Plate Area | Non-Plate Area | Plate Area | Non-Plate Area | Plate Area | Non-Plate Area | Plate Area | Non-Plate Area | |
| NF | 59.5 [2.3] | 75.1 [0.7] | 31.1 [1.4] | 21.8 [0.6] | 8.48 [0.9] | b 1.44 [0.3] | 1,2 (Figure 9a) | 3,4 (Figure 9a) |
| F | 62.2 [1.6] | 77.5 [0.9] | 27.7 [2.2] | 19.9 [2.0] | 8.78 [0.6] | 1.17 [0.7] | 1,2 (Figure 9b) | 3,4 (Figure 9b) |
| LF | 67.0 [4.9] | 76.7 [0.6] | 27.5 [2.7] | 22.8 [0.7] | 5.29 [2.2] | b 0.36 [0.1] | 1,2 (Figure 9c) | 3,4 (Figure 9c) |
| FM | a 61.0 [0.1] | 76.7 [0.3] | 29.9 [0.1] | 21.8 [0.9] | 8.93 [0.1] | 1.30 [0.5] | 1,2 (Figure 9d) | 3,4 (Figure 9d) |
| M | a 62.3 [0.1] | 76.4 [0.1] | 29.3 [0.7] | 22.1 [0.4] | 7.63 [0.9] | 0.70 [0.4] | 1,2 (Figure 9e) | 3,4 (Figure 9e) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.S.; Rahman, M.; Cicek, N. Tensile Properties of Cattail Fibres at Various Phenological Development Stages. Polymers 2024, 16, 2692. https://doi.org/10.3390/polym16192692
Hossain MS, Rahman M, Cicek N. Tensile Properties of Cattail Fibres at Various Phenological Development Stages. Polymers. 2024; 16(19):2692. https://doi.org/10.3390/polym16192692
Chicago/Turabian StyleHossain, Mohammed Shahadat, Mashiur Rahman, and Nazim Cicek. 2024. "Tensile Properties of Cattail Fibres at Various Phenological Development Stages" Polymers 16, no. 19: 2692. https://doi.org/10.3390/polym16192692
APA StyleHossain, M. S., Rahman, M., & Cicek, N. (2024). Tensile Properties of Cattail Fibres at Various Phenological Development Stages. Polymers, 16(19), 2692. https://doi.org/10.3390/polym16192692







