The Influence of the Heat Flux of the Infrared Heater on the Charring Rate of Spruce Wood
Abstract
1. Introduction
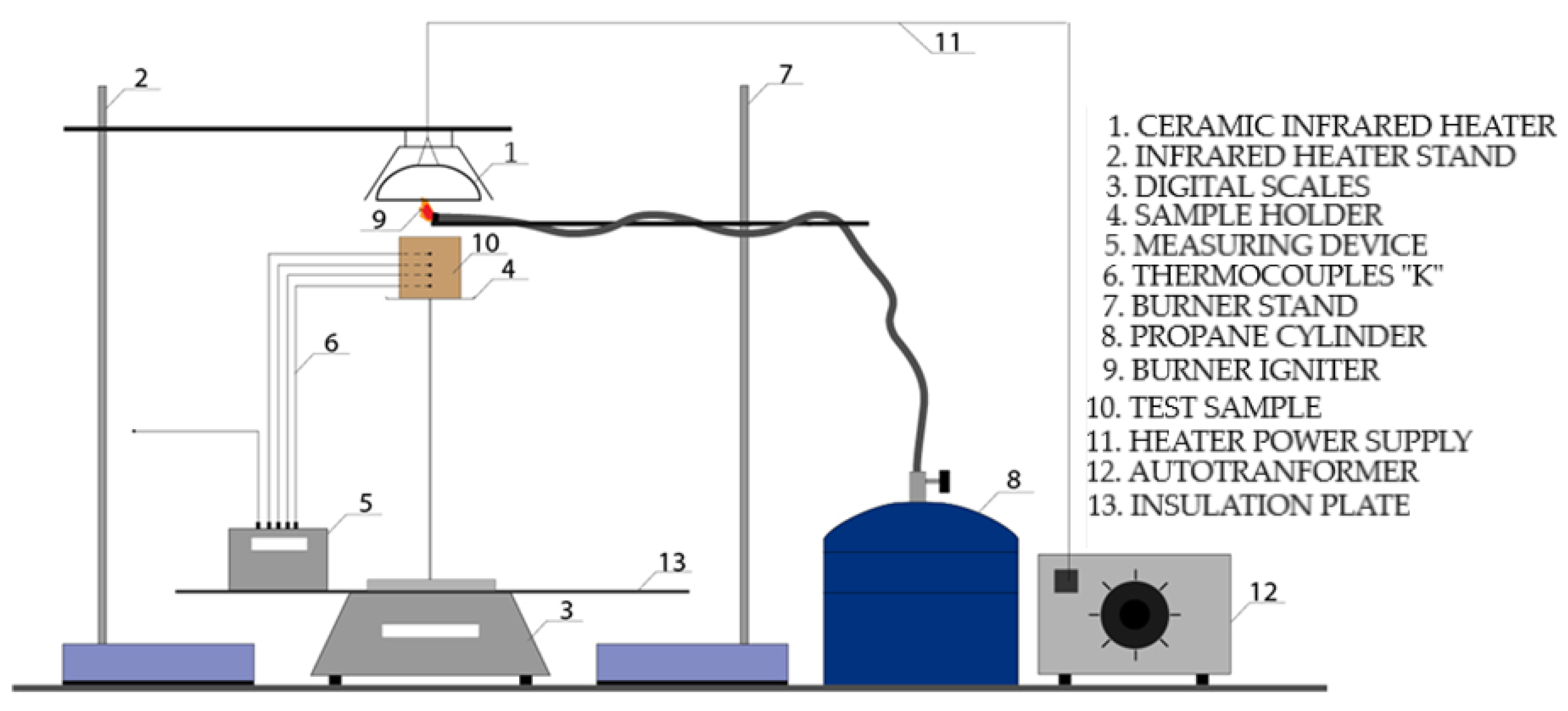
2. Materials and Methods
- —absolute moisture content of the wood (%);
- —weight of wood at a given moisture content (kg);
- —weight of wood at the constant weight (kg).
- —density (kg·m−3);
- —weight (kg);
- —volume (m−3).
- β—charring rate (mm∙min−1);
- Lchar—thickness of the charred layer (mm);
- t—time of heat loading (min).
- Lchar—thickness of the charred layer (mm);
- —average thickness of the sample before testing (mm);
- —average thickness of the sample after testing (mm).
- Babrauskas, 2005 [14] calculated the charring rate based on Equation (5):
- β—charring rate (mm∙min−1);
- q—heat flux (kW∙m−2);
- t—time of heat loading (min).
- 2.
- According Lizhong et al., 2008 [21], the charring rate can be calculated based on Equation (6):
- β—charring rate (mm∙min−1);
- q—heat flux (kW∙m−2);
- t—time of heat loading (min);
- —wood density (kg∙m−3).
- 3.
- In his study, Butler, 1971 [22] analyzed his own data and some additional results, concluding that the data correspond to Equation (7):
- β—charring rate (mm∙min−1);
- q—heat flux (kW∙m−2).
3. Results
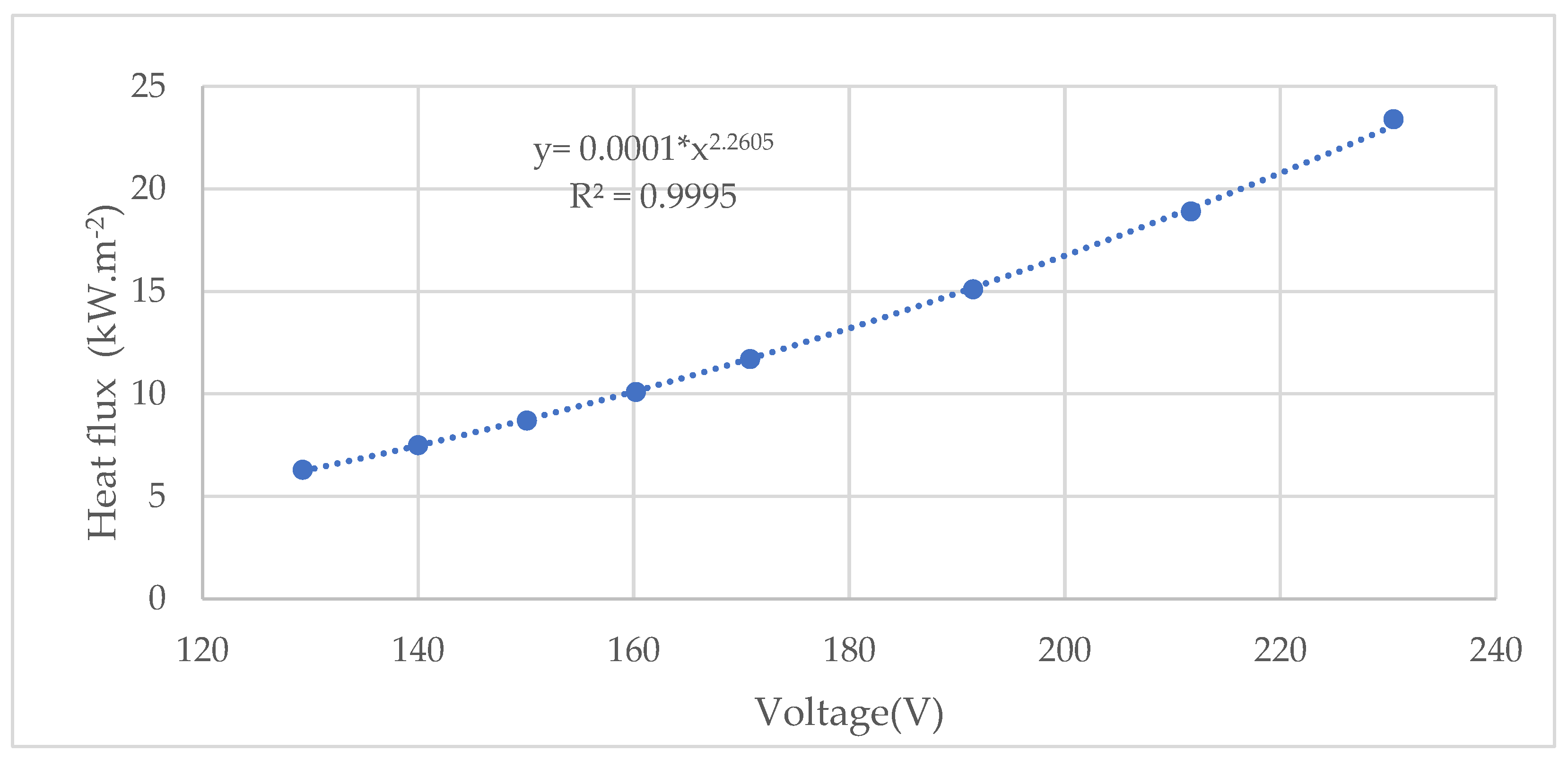
3.1. Determining the Heat Flux of the Heater Based on Voltage
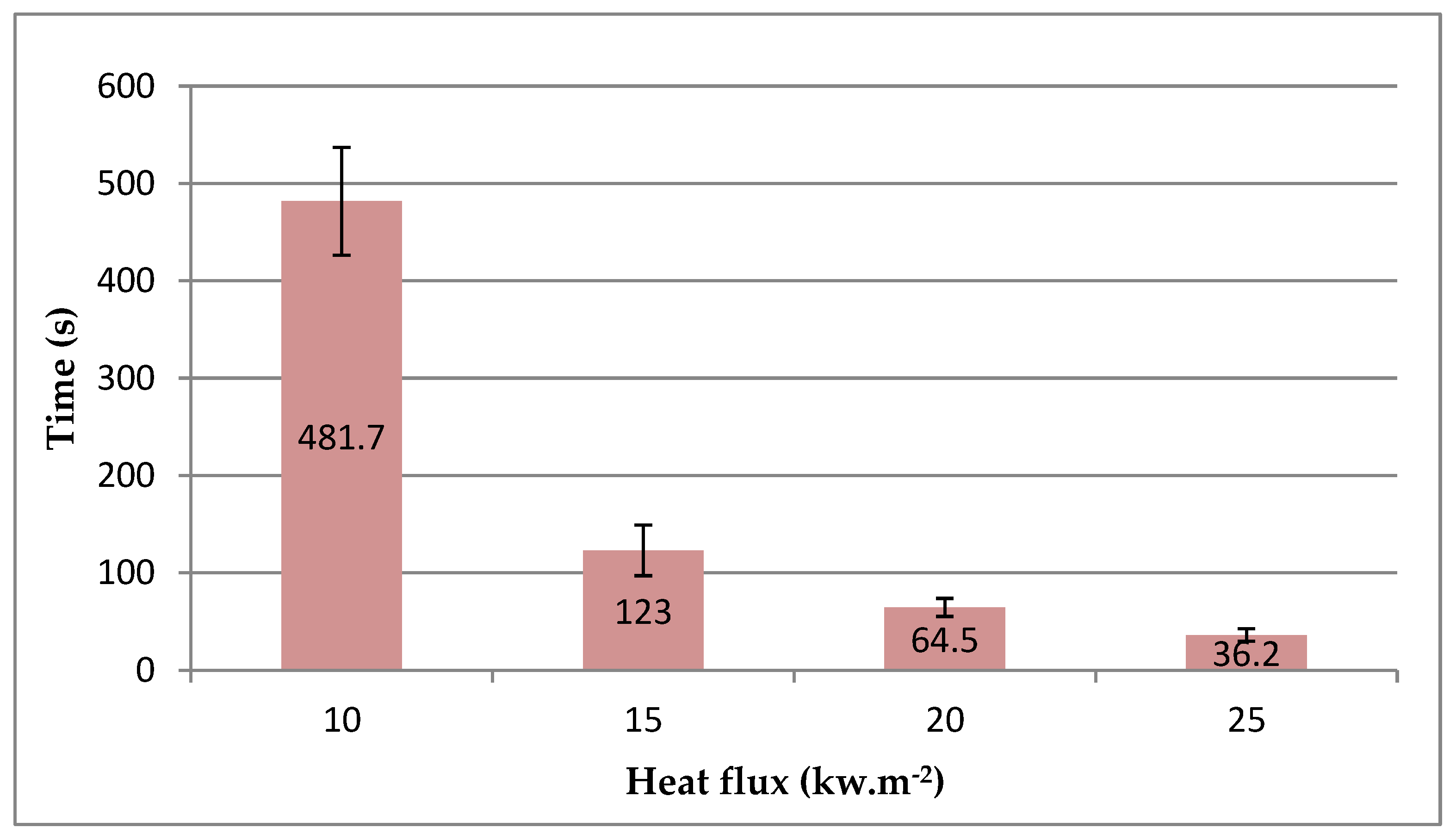
3.2. Determining the Ignition Time
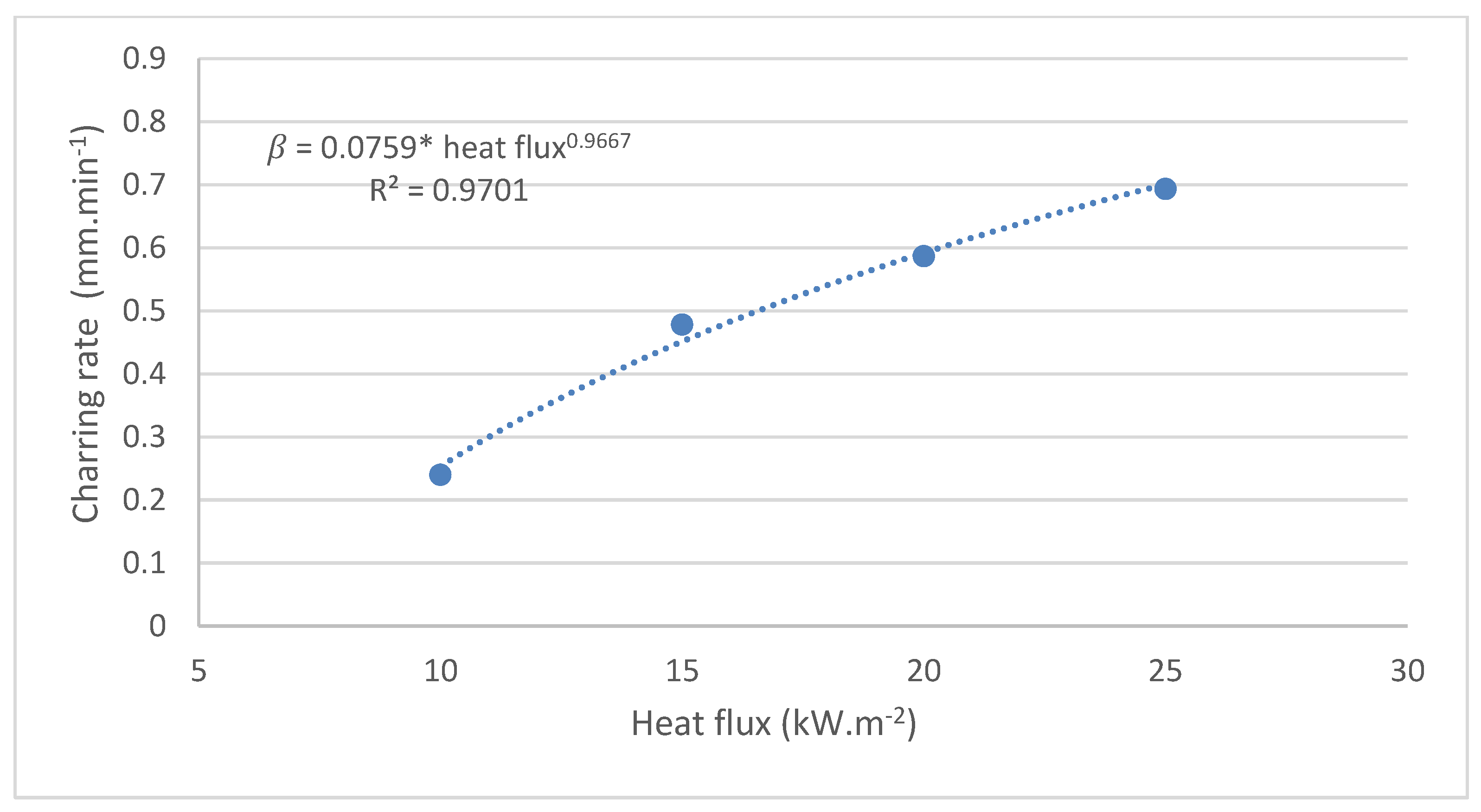
3.3. Method 1—The Charring Rate of Spruce Samples Calculated Based on the Value of the Char Layer Thickness
3.4. Method 2—Charring Rate Determined Based on the Charring Thickness Achieved at a Temperature of 300 °C
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Hrovatin, J. Contemporary systems of prefabricated wooden house construction. Wood in the Construction Industry: Durability and Quality of Wooden Construction Products. In Proceedings of the 7th International Conference, Zagreb, Croatia, 22 April 2005; pp. 21–26, ISBN 953-6307-80-4. [Google Scholar]
- Zachar, M.; Čabalová, I.; Kačíková, D.; Zacharová, L. The Effect of Heat Flux to the Fire-Technical and Chemical Properties of Spruce Wood (Picea abies L.) Advances in Fire Retardant Materials. Materials 2021, 14, 4989. [Google Scholar] [CrossRef] [PubMed]
- Kačíková, D.; Balog, K.; Tureková, I.; Mitterová, I. Materials in Fire Protection; Technical University of Zvolen: Zvolen, Slovakia, 2011; 367 s.; ISBN 978-80-228-2317-3. [Google Scholar]
- Marková, I.; Ladomerský, J.; Hroncová, E.; Mračková, E. Thermal parameters of beech wood dust. BioResources 2018, 13, 3098–3109. [Google Scholar] [CrossRef]
- Martinka, J.; Rantuch, P.; Liner, M. Calculation of charring rate and char depth of spruce and pine wood from mass loss. J. Therm. Anal. Calorim. 2018, 132, 1105–1113. [Google Scholar] [CrossRef]
- Salmen, L.; Olsson, A.M.; Stevanic, J.S.; Simonovic, J.; Radotic, K. Structural organisation of the wood polymers in the wood fibre structure. BioResources 2011, 7, 7–12, WOS:000394407800002. [Google Scholar] [CrossRef]
- Rinta-Paavola, A.; Sukhomlinov, D.; Hostikka, S. Modelling Charring and Burning of Spruce and Pine Woods During Pyrolysis, Smoldering Flaming. Fire Technol. 2023, 59, 2751–2786. [Google Scholar] [CrossRef]
- Bartlett, A.I.; Hadden, R.M.; Bisby, L.A. A Review of Factors Affecting the Burning Behaviour of Wood for Application to Tall Timber Construction. Fire Technol. 2019, 55, 1–49. [Google Scholar] [CrossRef]
- Kačíková, D.; Makovická-Osvaldová, L. Woodburning rate of various tree parts from selected soft woods. Acta Fac. Xylologiae 2009, 51, 27–32. [Google Scholar]
- Xu, M.; Tu, L.; Cui, Z.; Chen, Z. Charring properties and temperature profiles of laminated bamboo under single side of ISO 834 fire exposure. Bio. Resour. 2020, 15, 1445–1462. [Google Scholar] [CrossRef]
- Špilák, D.; Tereňová, L.; Dúbravská, K.; Majlingová, A. Analysis of Carbonized Layer of Wood Beams with Different Geometric Cross-Section Shape. Delta 2018, 12, 65–81. [Google Scholar] [CrossRef]
- STN EN 1995-1-1 + A1; Eurocode 5: Design of Timber Structures—Part 1-1: General Rules—Common Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2010.
- Richter, F.; Atreya, A.; Kotsovinos, P.; Rein, G. The effect of chemical composition on the charring of wood across scales. Proc. Combust. Inst. 2019, 37, 4053–4061. [Google Scholar] [CrossRef]
- Babrauskas, V. Charring rate of wood as a tool for fire investigations. Fire Saf. J. 2005, 40, 528–554. [Google Scholar] [CrossRef]
- Cachim, P.B.; Franssen, J.M. Comparison between the charring rate model and the conductive model of Eurocode 5. Fire Mater. 2009, 33, 129–143. [Google Scholar] [CrossRef]
- Špilák, D.; Majlingová, A. Progressive Methods in Studying the Charred Layer Parameters Change in Relation to Wood Moisture Content. Polymers 2022, 14, 4997. [Google Scholar] [CrossRef] [PubMed]
- Kačík, F.; Giertlová, Z.; Marková, I.; Osvald, A.; Čunderlík, I. The Effect of Burning on the Chemical and Microscopic Changes of Spruce Wood; Technical University of Zvolen: Zvolen, Slovakia, 2001; 85 s; ISBN 80-228-1034-7. [Google Scholar]
- NFPA 921: Guide for Fire and Explosion Investigations; National Fire Protection Association: Quincy, MA, USA, 2021.
- Friquin, K.L. Material properties and external factors influencing the charring rate of solid wood and glue-laminated timber. Wiley Online Libr. 2011, 5, 303–327. [Google Scholar] [CrossRef]
- PUV 50121-2020 Method of Measuring the Rate of Burning and Charring of Polymers with Flame Initiation and a System for Its Implementation. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/50121-2020 (accessed on 12 March 2024).
- Lizhong, Y.; Yupeng, Z.; Yafei, W.; Zaifu, G. Predicting charring rate of woods exposed to time increasing and constant heat fluxes. J. Anal. Appl. Pyrolysis 2008, 81, 1–6. [Google Scholar] [CrossRef]
- Butler, C.P.; Notes on charring rates of wood (FR Note 896). Borehamwood: Fire Research Station; 1971. Available online: https://publications.iafss.org/publications/frn/896/-1/view/frn_896.pdf (accessed on 30 June 2024).
- Bilbao, R.; Mastral, J.; Aldea, M.; Ceamanos, J.; Betrán, M.; Lana, J.A. Experimental and theoretical study of the ignition and smoldering of wood including convective effects. Combust. Flame 2001, 126, 1363–1372. [Google Scholar] [CrossRef]
- Jaskólovski, W.; Ogrodnik, P.; Lukaszek-Chmielewska, A. The study of time to ignition of woods under external heat flux by piloted ignition and autoignition. Annals of Warsaw University of Life Sciences—SGGW. For. Wood Technol. 2014, 86, 133–137. [Google Scholar]
- Kamenická, Z.; Sandanus, J.; Klas, T.; Rantuch, P.; Martinka, J.; Balog, K. Experimental and numerical analysis of the influence of cracks on the charring of wooden elements. Czech J. Civ. Eng. 2008, 4, 58–64. [Google Scholar] [CrossRef]
- Pang, S.-J.; Ahn, K.-S.; Kim, M.-J.; Hwang, S.-W.; Kang, S.G.; Kwak, H.W.; Yeo, H.; Oh, J.-K. Effect of intumescent coating on the charring rate of nail-laminated timber. Bio. Resour. 2022, 17, 5999–6018. [Google Scholar] [CrossRef]
- Hakkarainen, T. Post-flashover fires in light and heavy timber construction compartments. J. Fire Sci. 2002, 20, 133–175. [Google Scholar] [CrossRef]
- Lawson, D.I.; Webster, C.T.; Ashton, L.A. The fire endurance of timber beams and floors. Struct. Eng. 1952, 30, 27–34. [Google Scholar]
- ISO 834; Fire-Resistance Tests—Elements of Building Construction. International Organization for Standardization (ISO): Geneva, Switzerland, 1999.
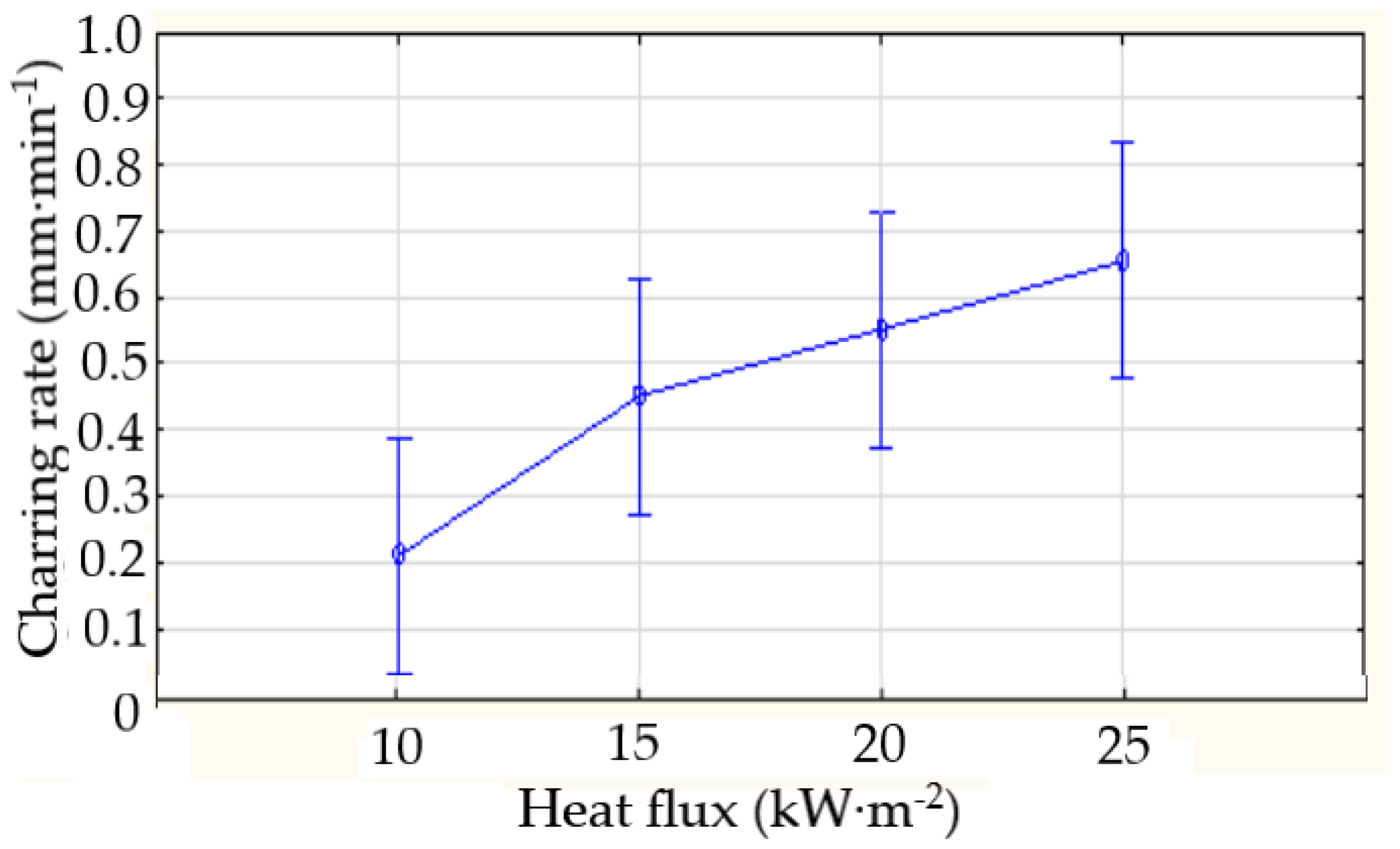
| Heat Flux (kW·m−2) | Thickness of the Sample before Testing (1) (mm) | Thickness of the Sample after Testing (2) (mm) | Thickness of the Charred Layer (Lchar) (mm) | Charring Rate (mm·min−1) |
|---|---|---|---|---|
| 10 | 50.87 ± 0.13 | 43.68 ± 0.38 | 7.19 ± 0.21 | 0.2397 |
| 15 | 51.28 ± 0.20 | 36.94 ± 0.18 | 14.34 ± 0.51 | 0.4780 |
| 20 | 51.01 ± 0.97 | 33.41 ± 0.29 | 17.60 ± 0.59 | 0.5867 |
| 25 | 51.17 ± 0.13 | 30.37 ± 0.71 | 20.80 ± 0.27 | 0.6933 |
| Heat Flux (kW·m−2) | The Temperature within the Sample at a Depth of 10 mm (°C) | Time of Heat Loading (s) | The Charring Rate in the Time Interval of 0 to 850 s (mm·min−1) |
|---|---|---|---|
| 10 | - | - | - |
| 15 | 300 | 850 | 0.7059 |
| 20 | 300 | 700 | 0.8571 |
| 25 | 300 | 580 | 1.0344 |
| Heat Flux (kW·m−2) | β Based on Reaching 300 °C | β Measured Using Caliper | Calculation of β According to Equation (5) | Calculation of β According to Equation (6) | Calculation of β According to Equation (7) |
|---|---|---|---|---|---|
| 10 | - | 0.2397 | 0.2622 | 0.2716 | 0.2800 |
| 15 | 0.7059 | 0.4780 | 0.3211 | 0.3326 | 0.4200 |
| 20 | 0.8571 | 0.5867 | 0.3708 | 0.3841 | 0.5600 |
| 25 | 1.0344 | 0.6933 | 0.4145 | 0.4294 | 0.7000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Párničanová, A.; Zachar, M.; Kačíková, D. The Influence of the Heat Flux of the Infrared Heater on the Charring Rate of Spruce Wood. Polymers 2024, 16, 2657. https://doi.org/10.3390/polym16182657
Párničanová A, Zachar M, Kačíková D. The Influence of the Heat Flux of the Infrared Heater on the Charring Rate of Spruce Wood. Polymers. 2024; 16(18):2657. https://doi.org/10.3390/polym16182657
Chicago/Turabian StylePárničanová, Alena, Martin Zachar, and Danica Kačíková. 2024. "The Influence of the Heat Flux of the Infrared Heater on the Charring Rate of Spruce Wood" Polymers 16, no. 18: 2657. https://doi.org/10.3390/polym16182657
APA StylePárničanová, A., Zachar, M., & Kačíková, D. (2024). The Influence of the Heat Flux of the Infrared Heater on the Charring Rate of Spruce Wood. Polymers, 16(18), 2657. https://doi.org/10.3390/polym16182657








