Diffusion Wave Spectroscopy Microrheological Characterization of Gelling Agarose Solutions
Abstract
1. Introduction
Theoretical Background
2. Materials and Methods
2.1. Sample Characteristics and Preparation
2.2. Microrheological Measurements
2.3. Thermal History of the Samples
3. Results and Discussion
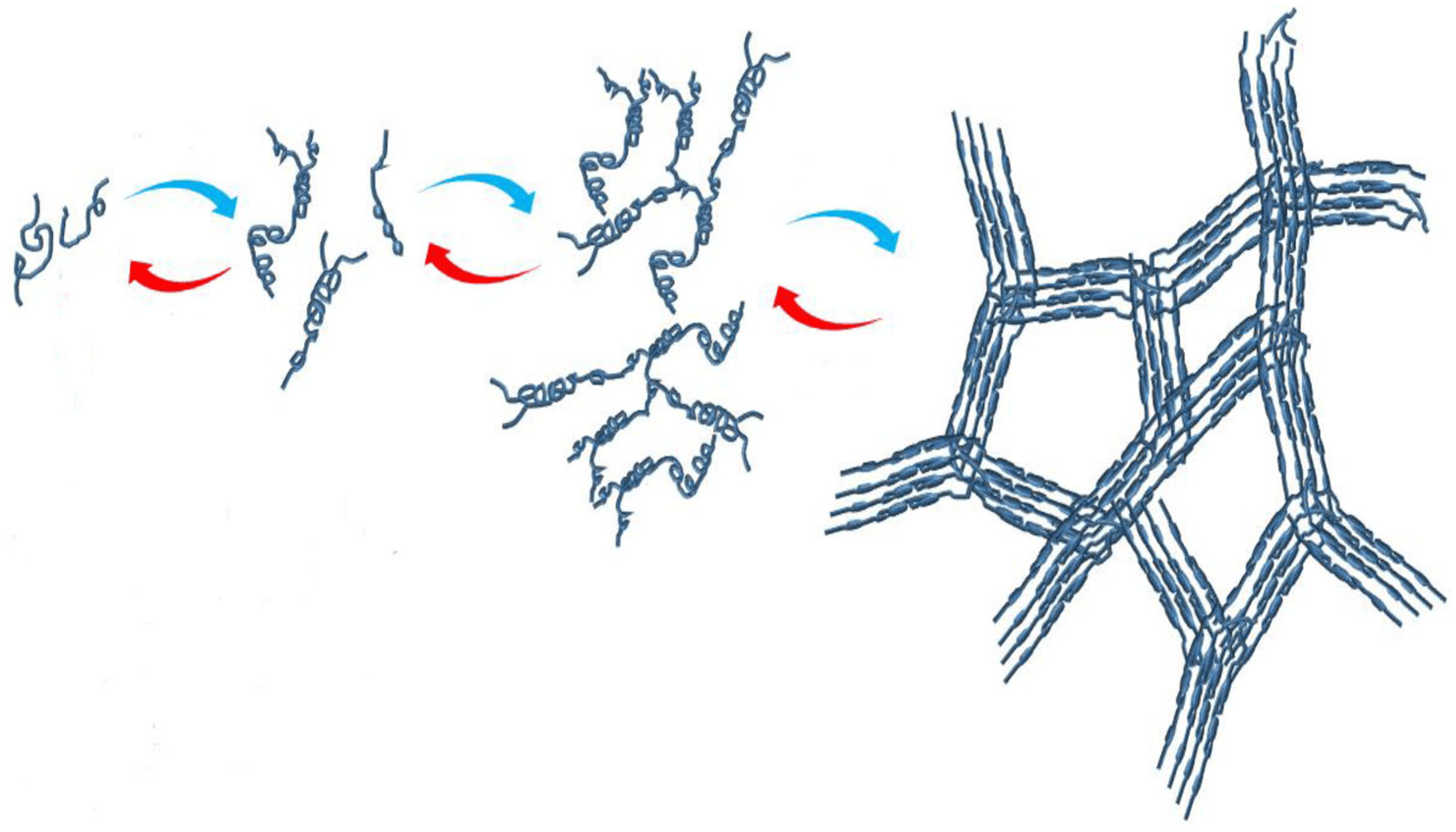
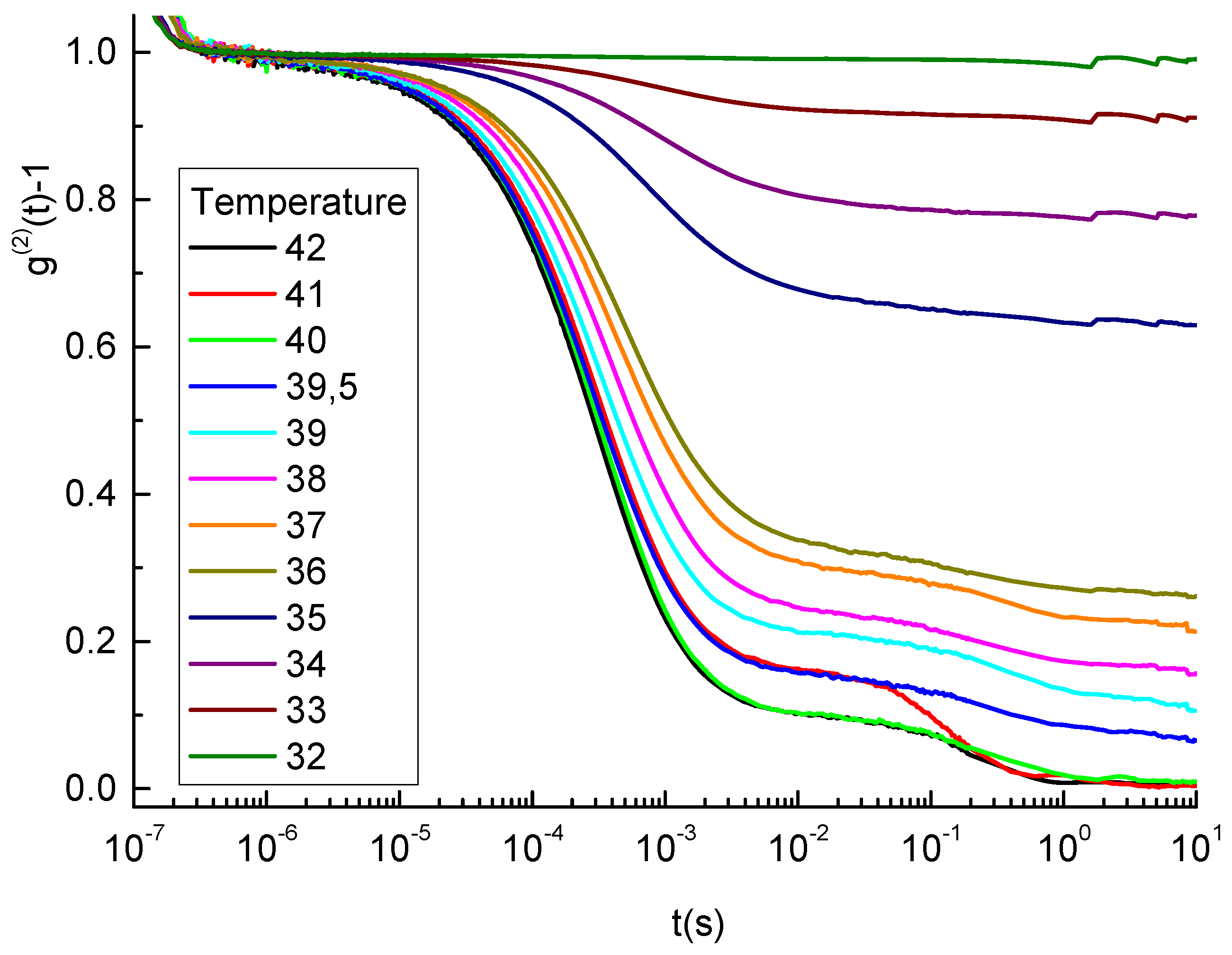
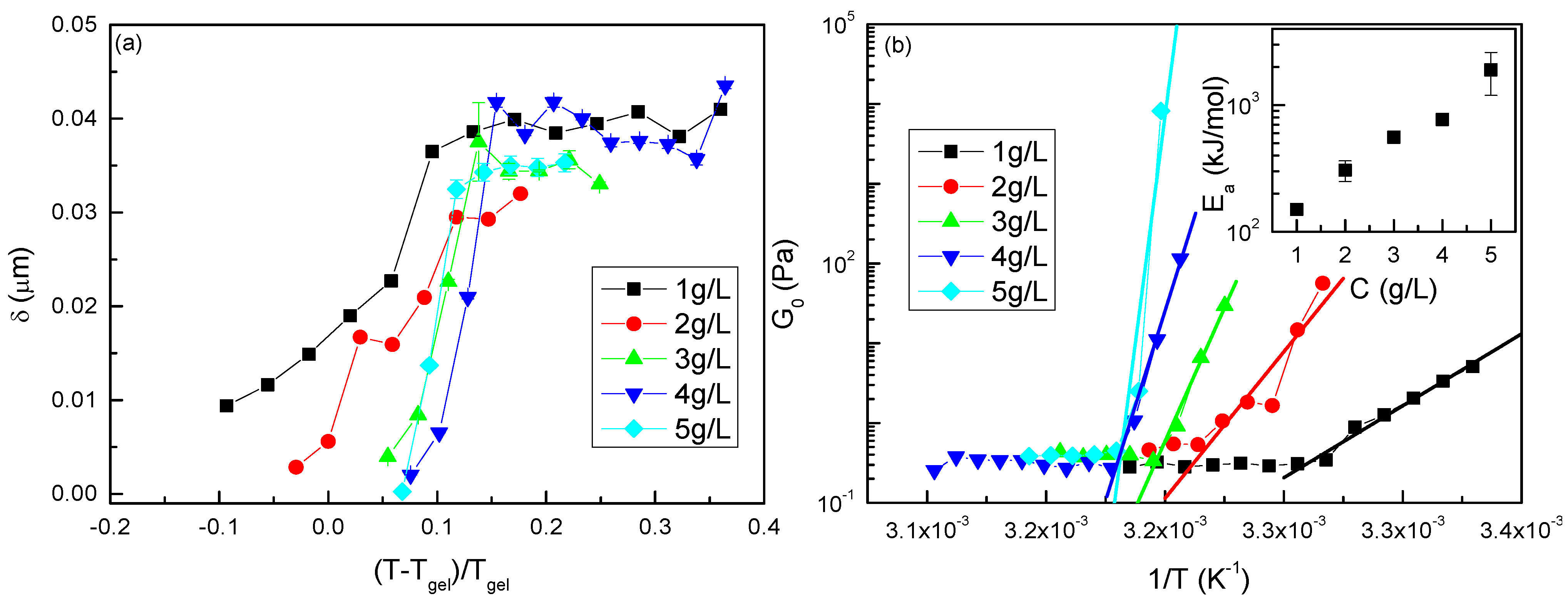
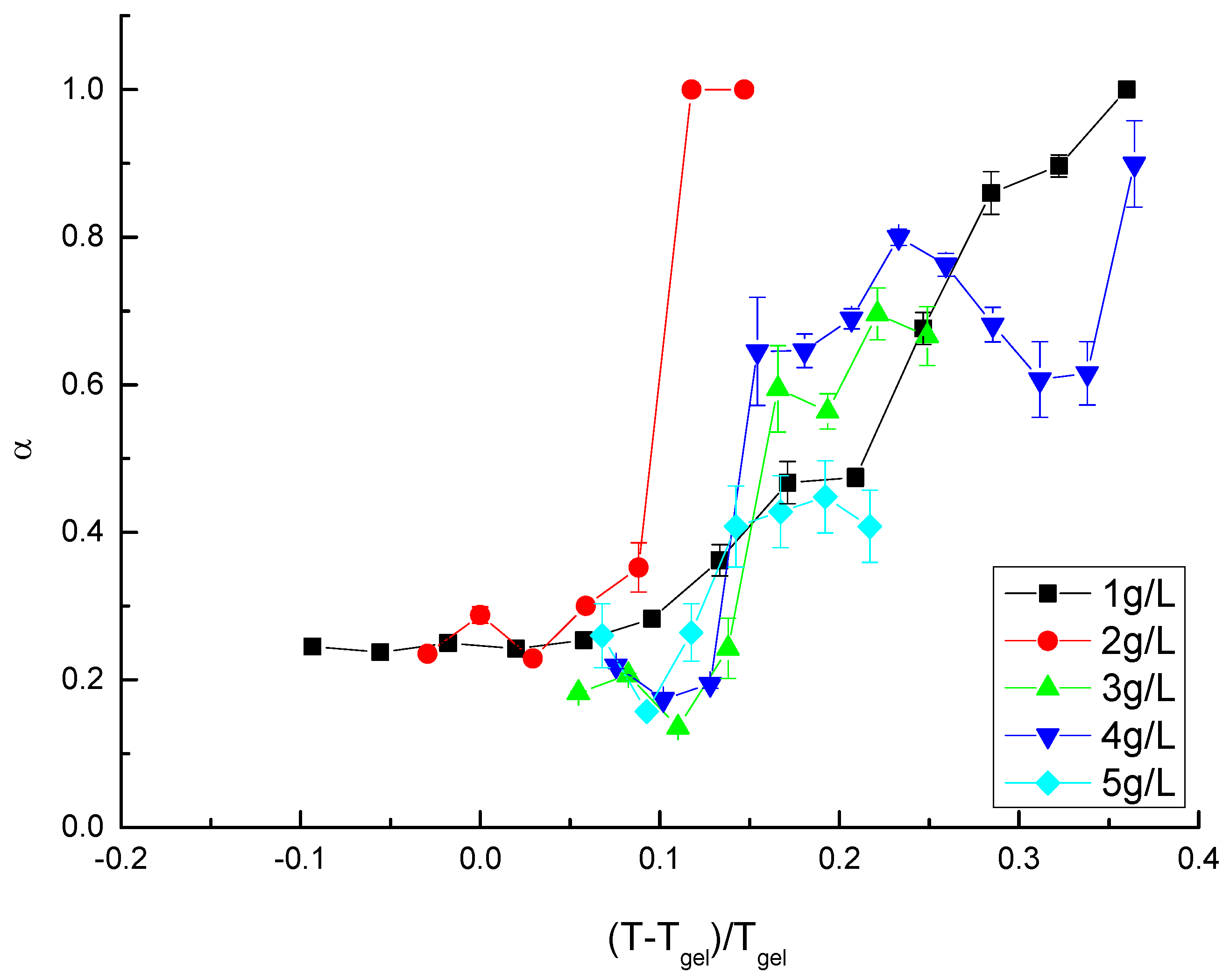
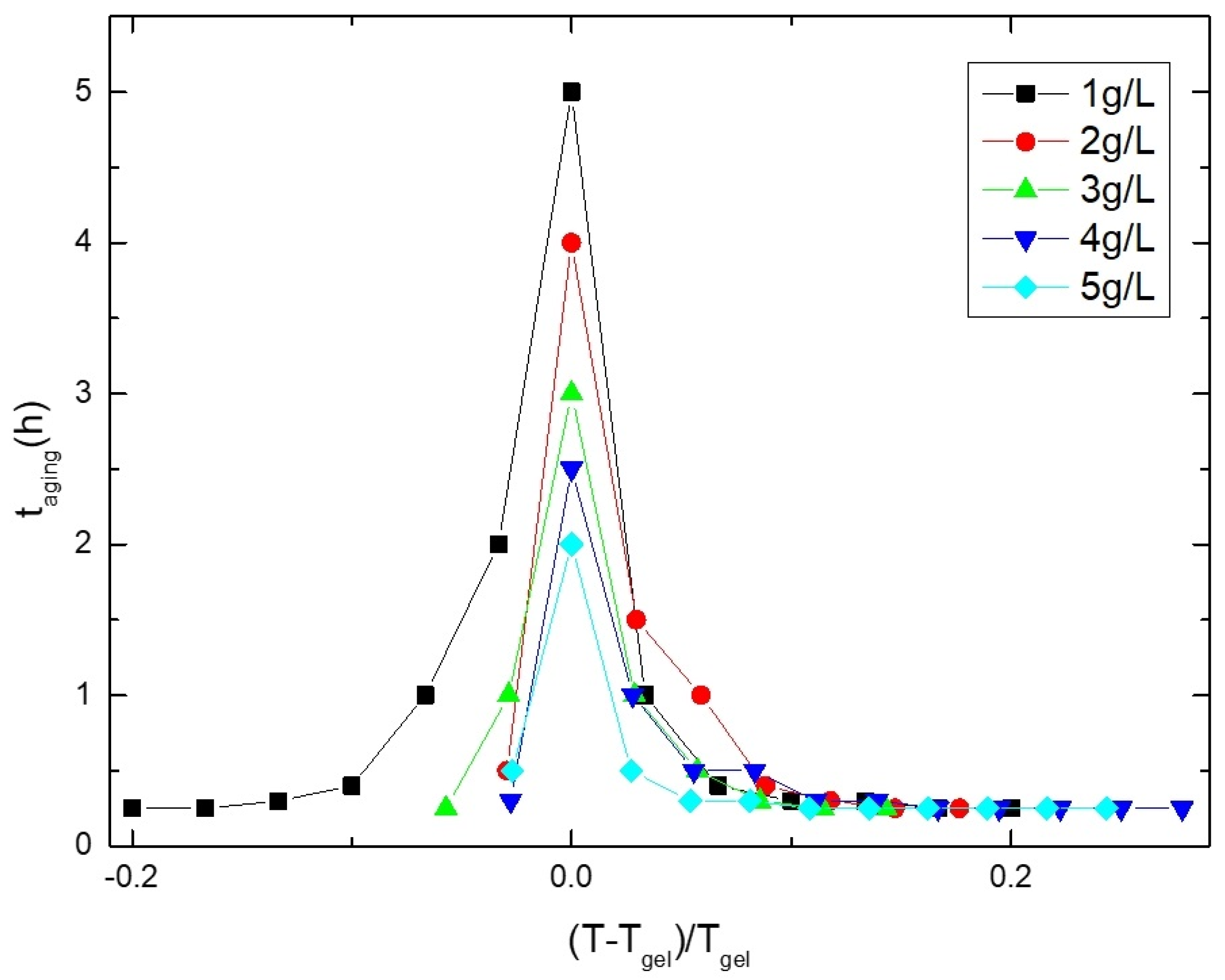
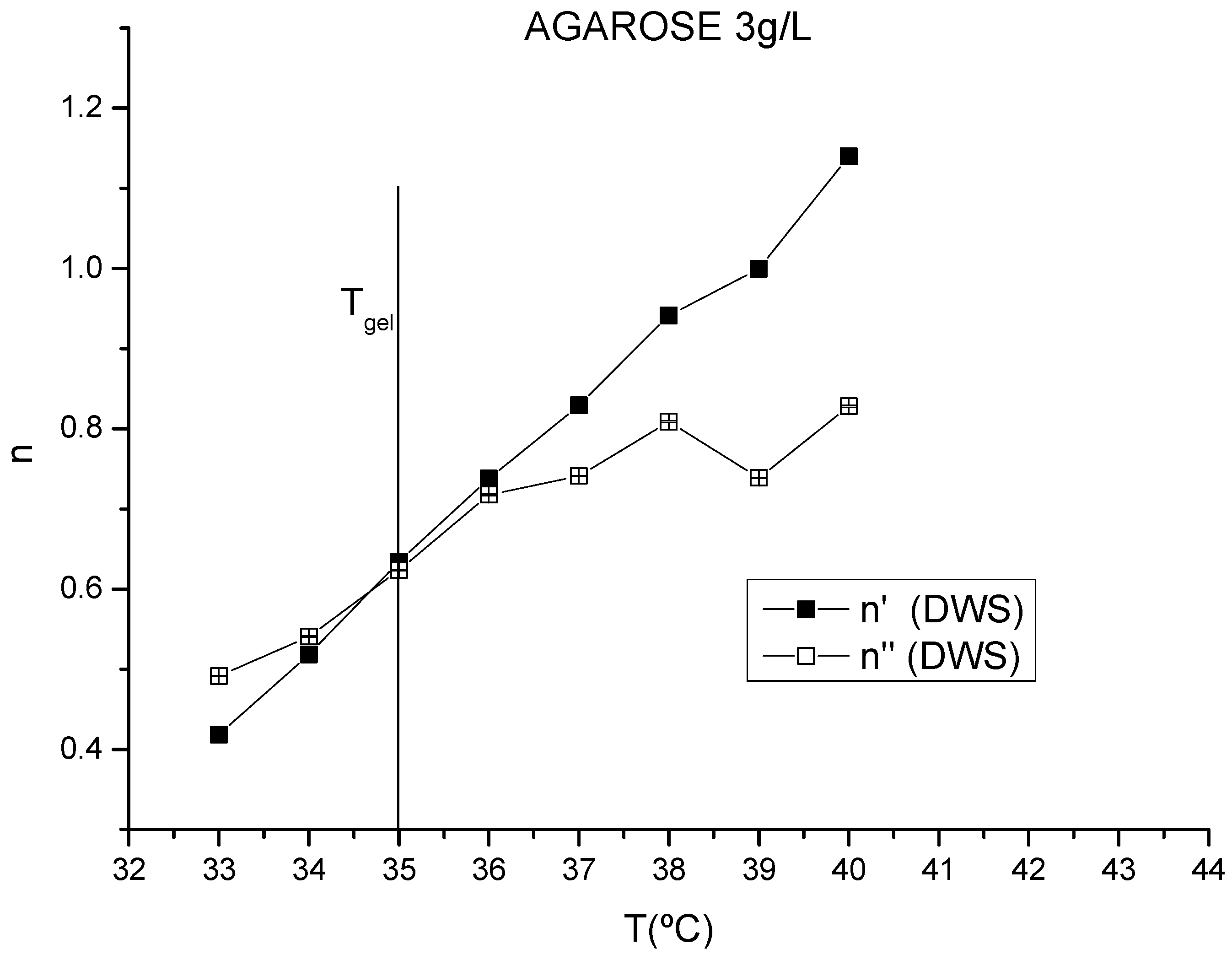
3.1. Gelling Kinetics Effects on the Mechanical Behavior
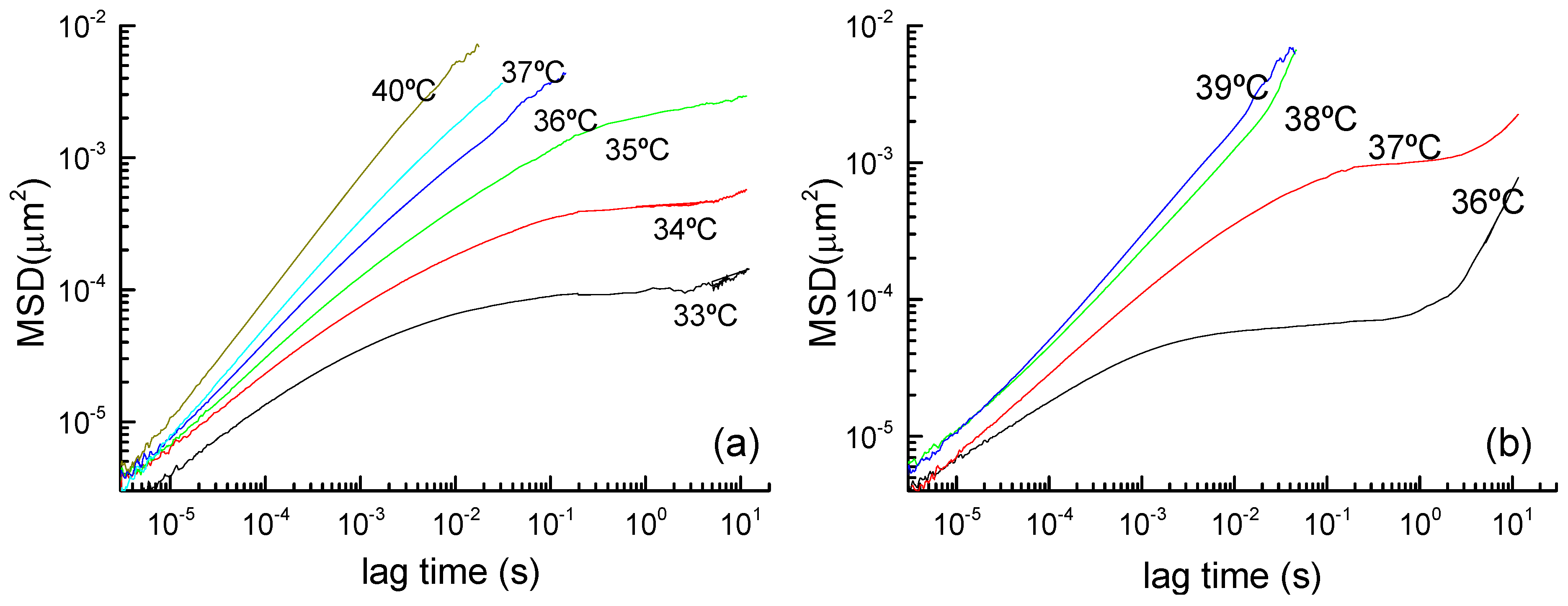
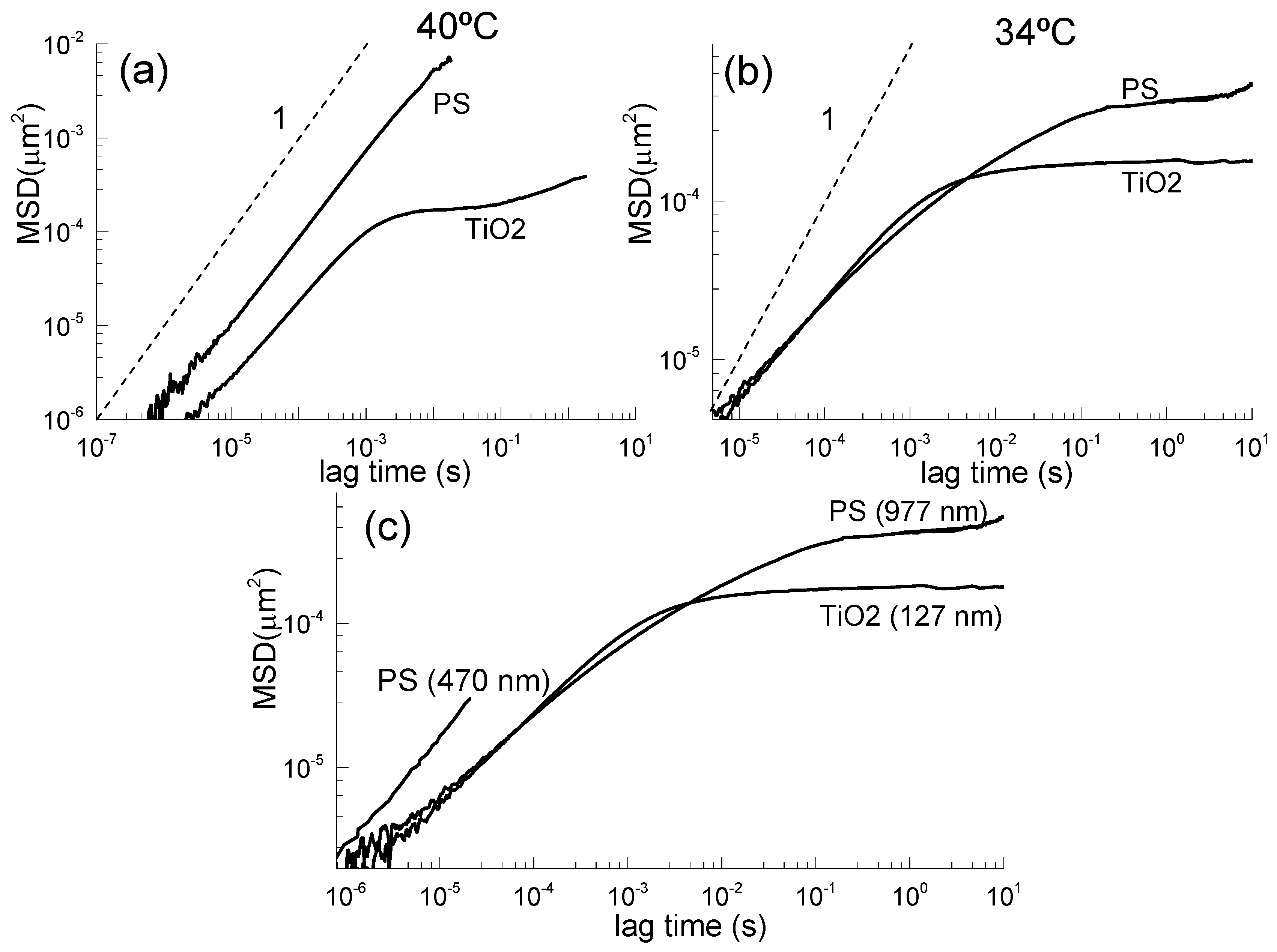
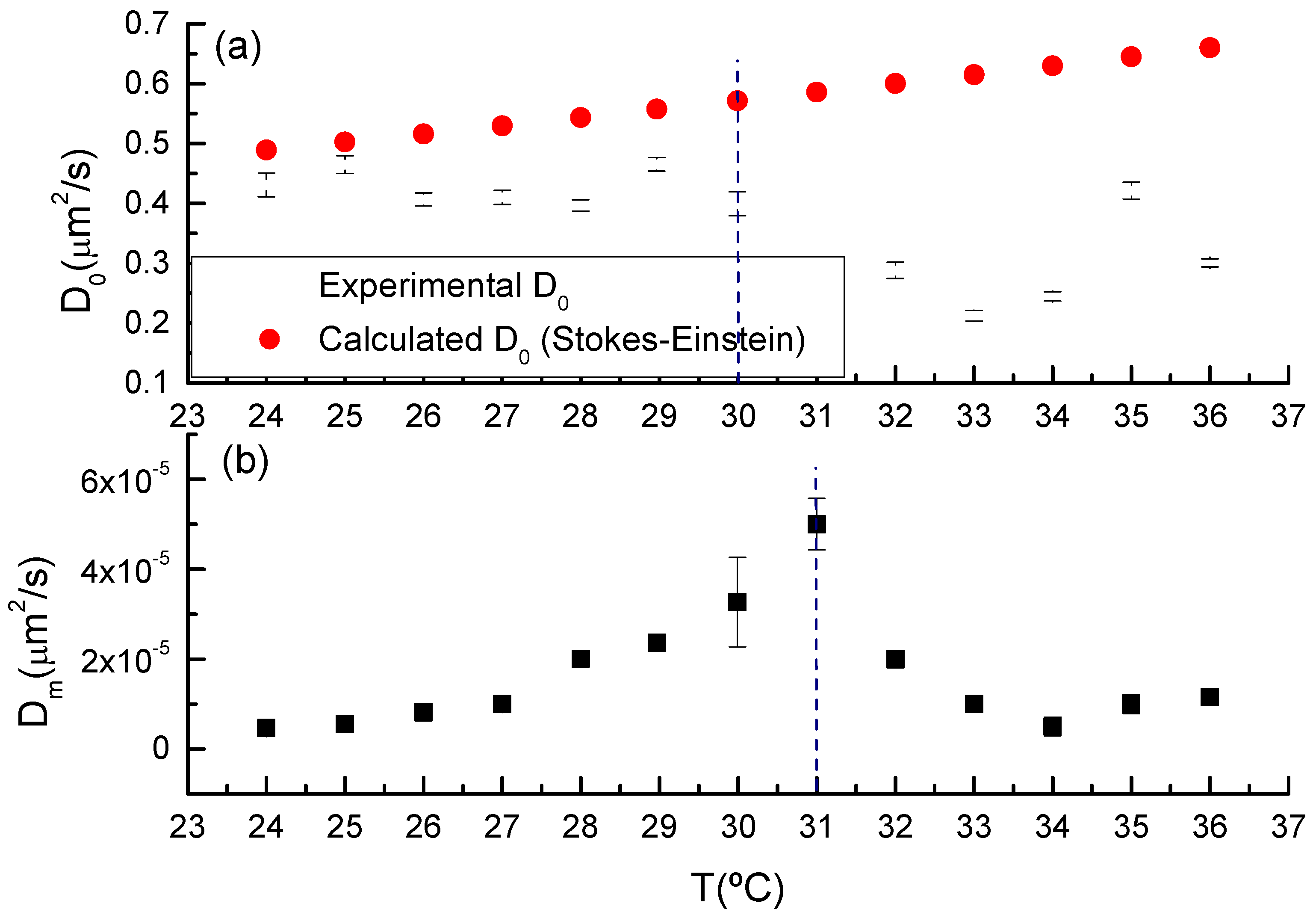
3.2. Viscoelastic Behavior
3.3. Viscoelastic Models
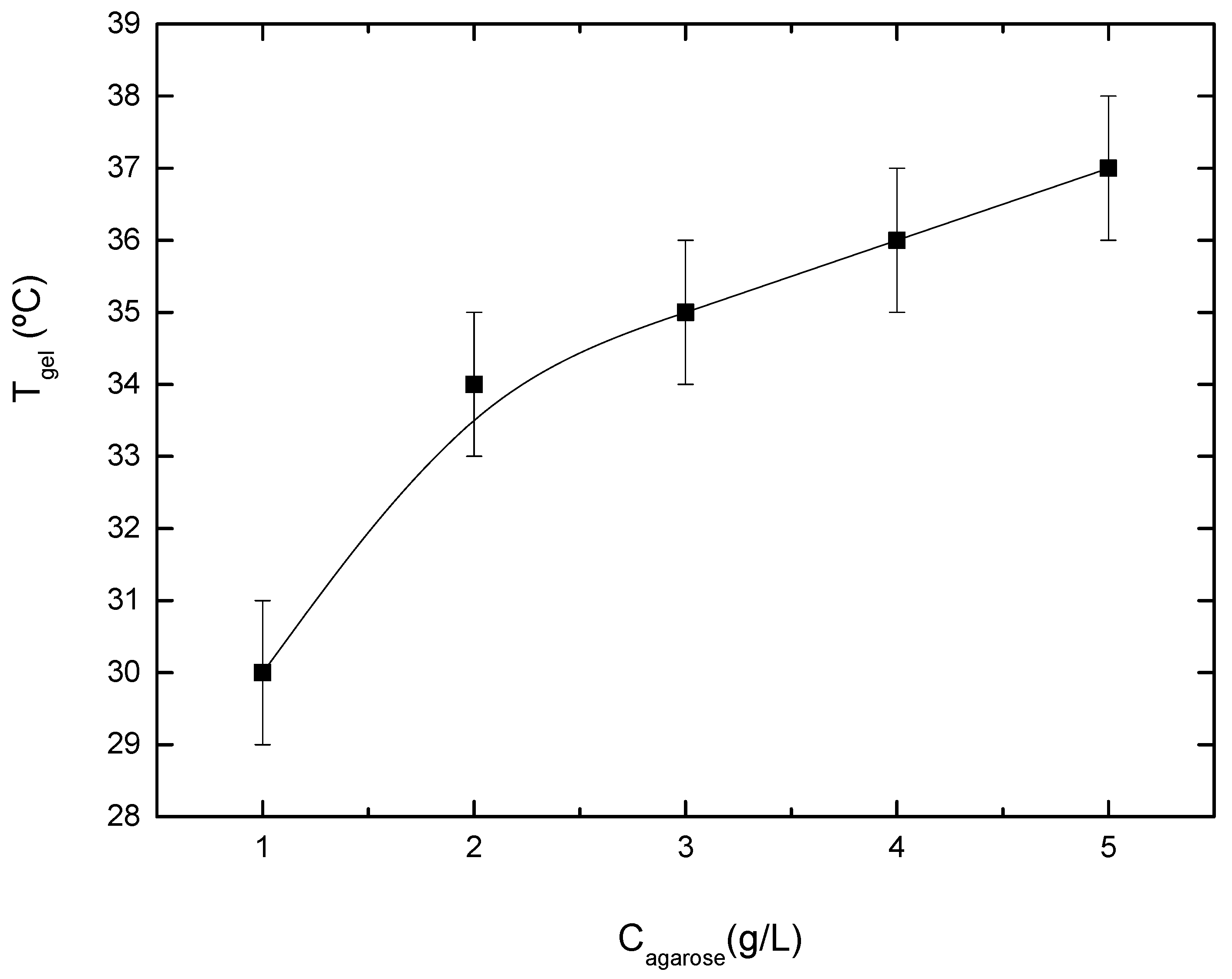
3.4. Gel Temperature
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Owens, G.J.; Singh, R.K.; Foroutan, F.; Alqaysi, M.; Han, C.-M.; Mahapatra, C.; Kim, H.-W.; Knowles, J.C. Sol–gel based materials for biomedical applications. Progr. Mat. Sci. 2016, 77, 1–79. [Google Scholar] [CrossRef]
- Lu, Z.-l.; Lindner, E.; Mayer, H.A. Applications of Sol−Gel-Processed Interphase Catalysts. Chem. Rev. 2002, 102, 3543–3578. [Google Scholar] [CrossRef] [PubMed]
- Dehghanghadikolaei, A.; Ansary, J.; Ghoreishi, R. Sol-gel process applications: A mini-review. Proc. Nature Res. Soc. 2018, 2, 02008. [Google Scholar] [CrossRef]
- Argudo, P.G.; Guzmán, E.; Lucia, A.; Rubio, R.G.; Ortega, F. Preparation and Application in Drug Storage and Delivery of Agarose Nanoparticles. Int. J. Polymer Sci. 2018, 2018, 7823587. [Google Scholar] [CrossRef]
- Orsi, D.; Rimoldi, T.; Guzmán, E.; Liggieri, L.; Ravera, F.; Ruta, B.; Cristofolini, L. Hydrophobic Silica Nanoparticles Induce Gel Phases in Phospholipid Monolayers. Langmuir 2016, 32, 4868–4876. [Google Scholar] [CrossRef]
- Salati, M.A.; Khazai, J.; Tahmuri, A.M.; Samadi, A.; Taghizadeh, A.; Taghizadeh, M.; Zarrintaj, P.; Ramsey, J.D.; Habibzadeh, S.; Seidi, F.; et al. Agarose-Based Biomaterials: Opportunities and Challenges in Cartilage Tissue Engineering. Polymers 2020, 12, 1150. [Google Scholar] [CrossRef]
- Jin, N.; Zhang, H.; Jin, S.; Dadmun, M.D.; Zhao, B. Tuning of thermally induced sol-to-gel transitions of moderately concentrated aqueous solutions of doubly thermosensitive hydrophilic diblock copolymers poly(methoxytri(ethylene glycol) acrylate)-b-poly(ethoxydi(ethylene glycol) acrylate-co-acrylic acid). J. Phys. Chem. B 2012, 116, 3125–3137. [Google Scholar] [CrossRef]
- Parmar, I.A.; Shedge, A.S.; Badiger, M.V.; Wadgaonkar, P.P.; Lele, A.K. Thermo-reversible sol–gel transition of aqueous solutions of patchy polymers. RSC Adv. 2017, 7, 5101–5110. [Google Scholar] [CrossRef]
- Park, H.; Gasek, N.; JadenHwang; Weiss, D.J.; Lee, C.P. Effect of temperature on gelation and cross-linking of gelatin methacryloyl for biomedical applications. Phys. Fluids 2020, 32, 033102. [Google Scholar] [CrossRef]
- Eskens, O.; Villani, G.; Amin, S. Rheological Investigation of Thermoresponsive Alginate-Methylcellulose Gels for Epidermal Growth Factor Formulation. Cosmetics 2021, 8, 3. [Google Scholar] [CrossRef]
- Riande, E.; Diaz-Calleja, R.; Prolongo, M.G.; Masegosa, R.; Salom, C. Polymer Viscoelasticity: Stress and Strain in Practice; Marcel Dekker Inc.: New York, NY, USA, 2000. [Google Scholar]
- Pal, K.; Banerjee, I. (Eds.) Polymeric Gels: Characterization, Properties and Biomedical Applications; Woodhead Publishing: Cambridge, UK, 2018. [Google Scholar]
- Guzmán, E.; Tajuelo, J.; Pastor, J.M.; Rubio, M.Á.; Ortega, F.; Rubio, R.G. Shear rheology of fluid interfaces: Closing the gap between macro- and micro-rheology. Curr. Opin. Colloid Interface Sci. 2018, 37, 33–48. [Google Scholar] [CrossRef]
- Mendoza, A.J.; Guzmán, E.; Martínez-Pedrero, F.; Ritacco, H.; Rubio, R.G.; Ortega, F.; Starov, V.M.; Miller, R. Particle laden fluid interfaces: Dynamics and interfacial rheology. Adv. Colloid Interface Sci. 2014, 206, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Ortega, F.; Ritacco, H.; Rubio, R.G. Interfacial microrheology: Particle tracking and related techniques. Curr. Opin. Colloid Interface Sci. 2010, 15, 237–245. [Google Scholar] [CrossRef]
- Squires, T.M.; Mason, T.G. Fluid Mechanics of Microrheology. Ann. Rev. Fluid Mechan. 2010, 42, 413–438. [Google Scholar] [CrossRef]
- Mason, T.G.; Ganesan, K.; van Zanten, J.H.; Wirtz, D.; Kuo, S.C. Particle Tracking Microrheology of Complex Fluids. Phys. Rev. Lett. 1997, 79, 3282–3285. [Google Scholar] [CrossRef]
- Lorusso, V.; Orsi, D.; Salerni, F.; Liggieri, L.; Ravera, F.; McMillin, R.; Ferri, J.; Cristofolini, L. Recent developments in emulsion characterization: Diffusing Wave Spectroscopy beyond average values. Adv. Colloid Interface Sci. 2021, 288, 102341. [Google Scholar] [CrossRef] [PubMed]
- Salerni, F.; Orsi, D.; Santini, E.; Liggieri, L.; Ravera, F.; Cristofolini, L. Diffusing wave spectroscopy for investigating emulsions: II. Characterization of a paradigmatic oil-in-water emulsion. Colloids Surf. A 2019, 580, 123724. [Google Scholar] [CrossRef]
- Orsi, D.; Salerni, F.; Macaluso, E.; Santini, E.; Ravera, F.; Liggieri, L.; Cristofolini, L. Diffusing wave spectroscopy for investigating emulsions: I. Instrumental aspects. Colloids and Surf. A 2019, 580, 123574. [Google Scholar] [CrossRef]
- Cristofolini, L.; Orsi, D.; Isa, L. Characterization of the dynamics of interfaces and of interface-dominated systems via spectroscopy and microscopy techniques. Curr. Opin. Colloid Interface Sci. 2018, 37, 13–32. [Google Scholar] [CrossRef]
- Weihs, D.; Mason, T.G.; Teitell, M.A. Bio-microrheology: A frontier in microrheology. Biophys. J. 2006, 91, 4296–4305. [Google Scholar] [CrossRef]
- Amin, S.; Rega, C.A.; Jankevics, H. Detection of viscoelasticity in aggregating dilute protein solutions through dynamic light scattering-based optical microrheology. Rheol. Acta 2012, 51, 329–342. [Google Scholar] [CrossRef]
- Xu, L.; Amin, S. Microrheological study of ternary surfactant-biosurfactant mixtures. Int. J. Cosmet. Sci. 2019, 41, 364–370. [Google Scholar] [CrossRef] [PubMed]
- Xia, Q.; Xiao, H.; Pan, Y.; Wang, L. Microrheology, advances in methods and insights. Adv. Colloid Interface Sci. 2018, 257, 71–85. [Google Scholar] [CrossRef] [PubMed]
- Pine, D.; Weitz, D.A.; Chaikin, P.M.; Herbolzheimer, E. Diffusing wave spectroscopy. Phys. Rev. Lett. 1988, 60, 1134. [Google Scholar] [CrossRef]
- Sheng, P. (Ed.) Scattering and Localization of Classical Waves in Random Media; World Scientific: London, UK, 1990. [Google Scholar]
- Hernandez, M.P.; Ortega, F.; Rubio, R.G. Crossover critical phenomena in an aqueous electrolyte solution: Light scattering, density and viscosity of the 3-methylpyridine plus water plus NaBr system. J. Chem. Phys. 2003, 119, 4428–4436. [Google Scholar] [CrossRef]
- Mason, T.G. Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation. Rheol. Acta 2000, 39, 371–378. [Google Scholar] [CrossRef]
- Cicuta, P.; Donald, A.M. Microrheology: A review of the method and applications. Soft Matter. 2007, 3, 1449–1455. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover Publishing: Mineola, NY, USA, 1972. [Google Scholar]
- Galvan-Miyoshi, J.; Delgado, J.; Castillo, R. Diffusing wave spectroscopy in Maxwellian fluids. Eur. Phys. J. E 2008, 26, 369–377. [Google Scholar] [CrossRef]
- Hurnaus, T.; Plank, J. Behavior of titania nanoparticles in cross-linking hydroxypropyl guar in hydraulic fracturing fluids for oil recovery. Energy Fuels 2015, 29, 3601–3608. [Google Scholar] [CrossRef]
- Atkins, P.W. Physical Chemistry; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Maxwell, J.C., IV. On the dynamical theory of gases. Philos. Trans. R. Soc. London 1867, 157, 49–88. [Google Scholar] [CrossRef]
- Raikher, Y.L.; Rusakov, V.V. Theory of Brownian motion in a Jeffreys fluid. J. Exp. Theor. Phys. 2010, 111, 883–889. [Google Scholar] [CrossRef]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Lopez-Diaz, D.; Castillo, R. Microrheology of solutions embedded with thread-like supramolecular structures. Soft Matter. 2011, 7, 5926–5937. [Google Scholar] [CrossRef]
- Encinar, M.; Guzmán, E.; Prolongo, M.G.; Rubio, R.G.; Sandoval, C.; González-Nilo, F.; Gargallo, L.; Radić, D. Dielectric and dynamic-mechanical study of the mobility of poly(t-butylacrylate) chains in diblock copolymers: Polystyrene-b-poly(t-butylacrylate). Polymer 2008, 49, 5650–5658. [Google Scholar] [CrossRef]
- Encinar, M.; Prolongo, M.G.; Rubio, R.G.; Ortega, F.; Ahmadi, A.; Freire, J.J. Dielectric and molecular dynamics study of the secondary relaxations of poly(styrene-co-methylmethacrylate) copolymers: Influence of the molecular architecture. Eur. Phys. J. E 2011, 34, 134. [Google Scholar] [CrossRef] [PubMed]
- Orsi, D.; Guzmán, E.; Liggieri, L.; Ravera, F.; Ruta, B.; Chushkin, Y.; Rimoldi, T.; Cristofolini, L. 2D dynamical arrest transition in a mixed nanoparticle-phospholipid layer studied in real and momentum spaces. Sci. Rep. 2015, 5, 17930. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-Z.; Zhang, X.-H.; Zhang, J.-X. New insight into the kinetic behavior of the structural formation process in agar gelation. Rheol. Acta 2013, 52, 39–48. [Google Scholar] [CrossRef]
- Mineo, W.; Kiyoshi, A. Rheological Properties of Hydrogels of Agar-agar. III. Stress Relaxation of Agarose Gels. Bull. Chem. Soc. Japan 1968, 41, 1830–1834. [Google Scholar] [CrossRef]
- Te Nijenhuis, K. Thermoreversible Networks: Viscoelastic Properties and Structure of Gels; Springer: Berlin, Germany, 1997. [Google Scholar]
- Götze, W. Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Hilles, H.M.; Ortega, F.; Rubio, R.G.; Monroy, F. Long-Time Relaxation Dynamics of Langmuir Films of a Glass-Forming Polymer: Evidence of Glasslike Dynamics in Two Dimensions. Phys. Rev. Lett. 2004, 92, 25503. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior: An Introduction; Springer: Berlin, Germany, 1989. [Google Scholar]
- Winter, H.H.; Mours, M. Rheology of Polymers Near Liquid-Solid Transitions. In Neutron Spin Echo Spectroscopy Viscoelasticity Rheology; Springer: Berlin/Heidelberg, Germany, 1997; pp. 165–234. [Google Scholar]
- Te Nijenhuis, K.; Winter, H.H. Mechanical properties at the gel point of a crystallizing poly(vinyl chloride) solution. Macromolecules 1989, 22, 411–414. [Google Scholar] [CrossRef]
- Boral, S.; Saxena, A.; Bohidar, H.B. Universal Growth of Microdomains and Gelation Transition in Agar Hydrogels. J. Phys. Chem. B 2008, 112, 3625–3632. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mancebo, N.; Rubio, R.G.; Ortega, F.; Carbone, C.; Guzmán, E.; Martínez-Pedrero, F.; Rubio, M.A. Diffusion Wave Spectroscopy Microrheological Characterization of Gelling Agarose Solutions. Polymers 2024, 16, 2618. https://doi.org/10.3390/polym16182618
Mancebo N, Rubio RG, Ortega F, Carbone C, Guzmán E, Martínez-Pedrero F, Rubio MA. Diffusion Wave Spectroscopy Microrheological Characterization of Gelling Agarose Solutions. Polymers. 2024; 16(18):2618. https://doi.org/10.3390/polym16182618
Chicago/Turabian StyleMancebo, Nuria, Ramon G. Rubio, Francisco Ortega, Carlo Carbone, Eduardo Guzmán, Fernando Martínez-Pedrero, and Miguel A. Rubio. 2024. "Diffusion Wave Spectroscopy Microrheological Characterization of Gelling Agarose Solutions" Polymers 16, no. 18: 2618. https://doi.org/10.3390/polym16182618
APA StyleMancebo, N., Rubio, R. G., Ortega, F., Carbone, C., Guzmán, E., Martínez-Pedrero, F., & Rubio, M. A. (2024). Diffusion Wave Spectroscopy Microrheological Characterization of Gelling Agarose Solutions. Polymers, 16(18), 2618. https://doi.org/10.3390/polym16182618









