Size Effects in Climatic Aging of Epoxy Basalt Fiber Reinforcement Bar
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Specimen Preparation
2.3. Climate Aging Test
2.4. Aging Parameter Determination Methods
2.4.1. Coefficient of Linear Thermal Expansion (CLTE)
2.4.2. The Glass Transition Temperature ()
2.4.3. Mechanical Parameters (, , )
2.4.4. Moisture Transfer Parameters (, , , )
2.4.5. Kinetics of Absorption–Desorption
3. Results and Discussion
3.1. Size Effect in the Deformability of Exposed BFRP Bars
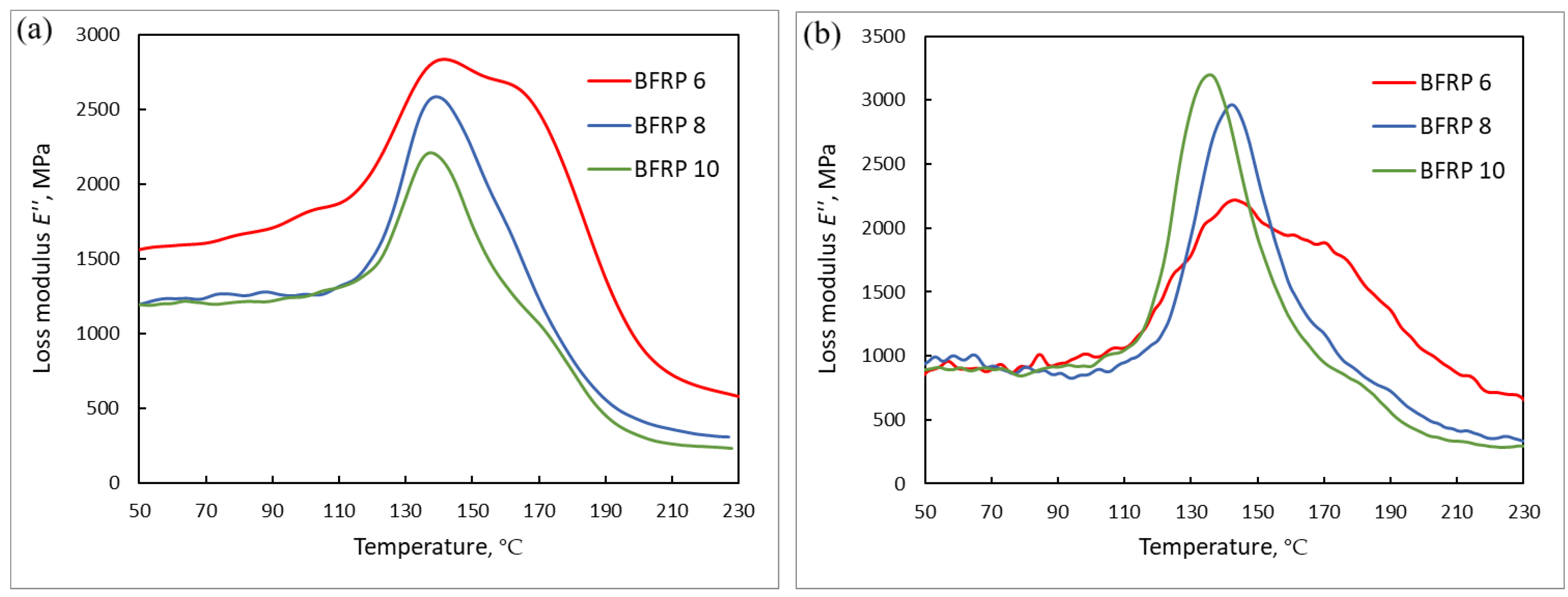
3.2. Size Effect in the Post-Curing of Exposed BFRP Bars
3.3. Size Effect in the Strength of Exposed BFRP Bars
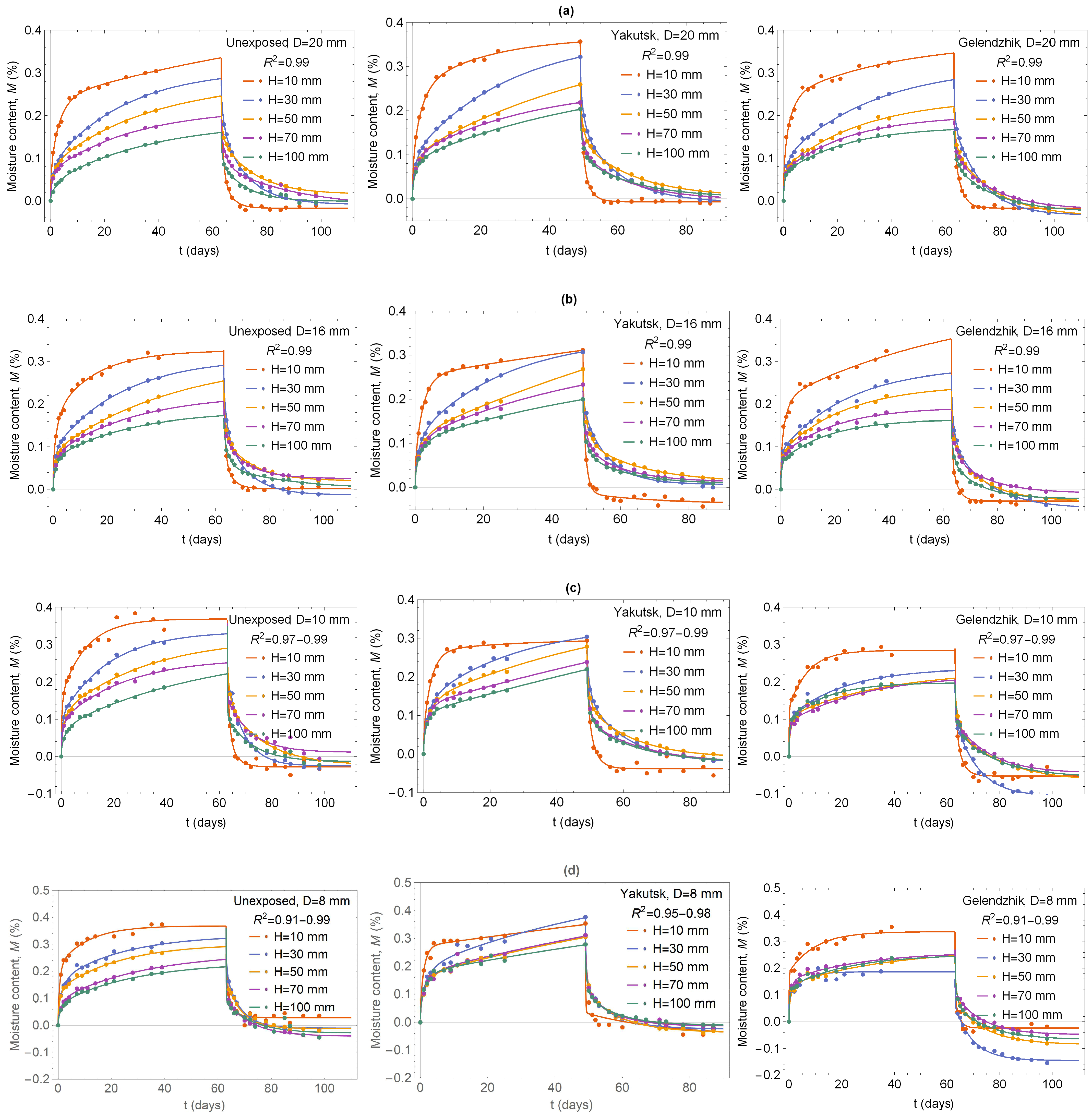
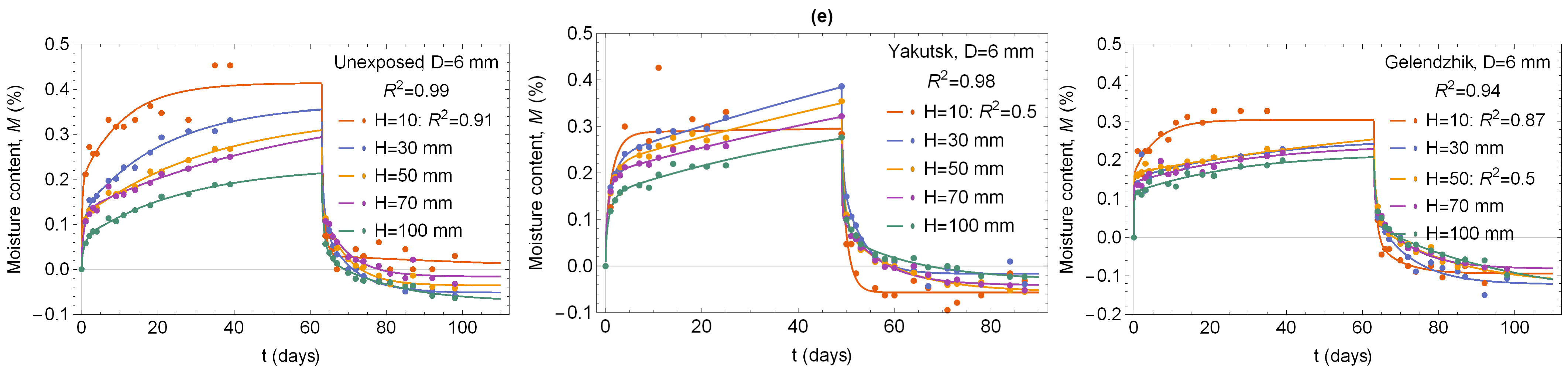
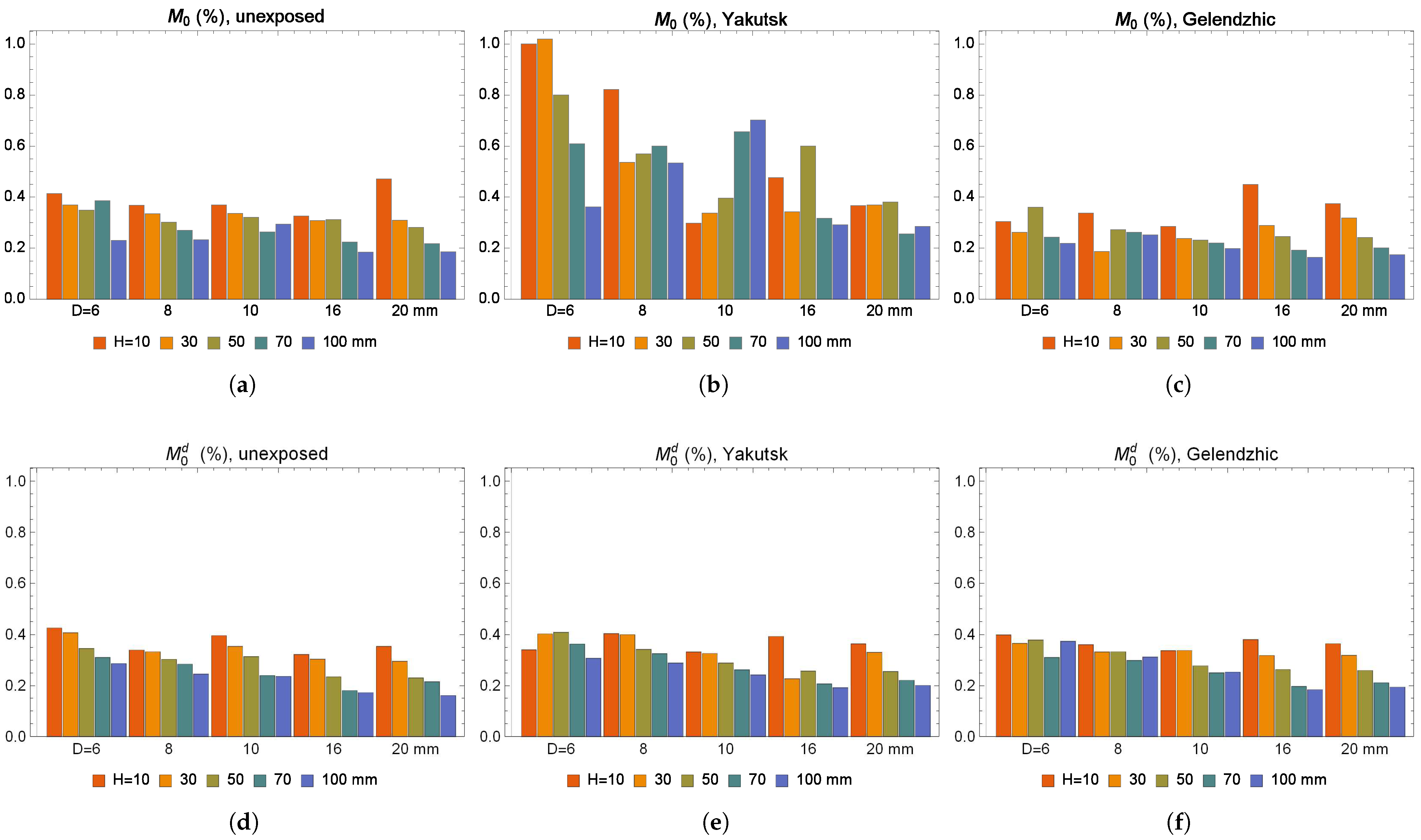
3.4. Size Effect in the Moisture Transfer Parameters of Exposed BFRP Bars
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FRPs | Fiber-reinforced Polymers |
| BFRP | basalt fiber reinforcement polymer |
| CLTE | coefficient of linear thermal expansion |
| glass transition temperature | |
| tensile strength | |
| compressive strength | |
| bending strength | |
| moisture equilibrium content | |
| radial component of the diffusion coefficient | |
| component of the diffusion coefficient along the reinforcement | |
| proportion of pseudo-equilibrium in the total equilibrium content of moisture | |
| BFRP 6 | basalt fiber reinforcement polymer bar with a nominal diameter 6 mm |
| BFRP 8 | basalt fiber reinforcement polymer bar with a nominal diameter 8 mm |
| BFRP 10 | basalt fiber reinforcement polymer bar with a nominal diameter 10 mm |
| BFRP 16 | basalt fiber reinforcement polymer bar with a nominal diameter 16 mm |
| BFRP 20 | basalt fiber reinforcement polymer bar with a nominal diameter 20 mm |
References
- Dh, V.; Mittal, G.; Rhee, K.Y.; Park, S.J.; Hui, D. A short review on basalt fiber reinforced polymer composites. Compos. Part B Eng. 2015, 73, 166–180. [Google Scholar]
- Parnas, R.; Shaw, M.; Liu, Q. Basalt Fiber Reinforced Polymer Composites; Technical Report NETCR63; Institute of Materials Science, University of Connecticut: Mansfield, CT, USA, 2007; p. 133. [Google Scholar]
- Dalinkevich, A.A.; Gumargalieva, K.Z.; Marakhovsky, S.S.; Soukhanov, A.V. Modern basalt fibrous materials and basalt fiber-based polymeric composites. J. Nat. Fibers 2009, 6, 248–271. [Google Scholar] [CrossRef]
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber—A review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Vikas, G.; Sudheer, M. A review on properties of basalt fiber reinforced polymer composites. Am. J. Mater. Sci. 2017, 7, 156–165. [Google Scholar]
- Koval, T.I. Investigation of the Reliability of Bridge Elements Reinforced with Basalt Plastic Fibers. Mech. Compos. Mater. 2017, 53, 479–486. [Google Scholar] [CrossRef]
- Monaldo, E.; Nerilli, F.; Vairo, G. Basalt-based fiber-reinforced materials and structural applications in civil engineering. Compos. Struct. 2019, 214, 246–263. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.S.; Al-Saadi, S.; Haque, A. Long-term durability of basalt- and glass-fibre reinforced polymer (BFRP/GFRP) bars in seawater and sea sand concrete environment. Constr. Build. Mater. 2017, 139, 467–489. [Google Scholar] [CrossRef]
- Sharma, S.; Zhang, D.; Zhao, Q. Degradation of basalt fiber-reinforced polymer bars in seawater and sea sand concrete environment. Adv. Mech. Eng. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Blaznov, A.N.; Krasnova, A.S.; Krasnov, A.A.; Zhurkovsky, M.E. Geometric and mechanical characterization of ribbed FRP rebars. Polym. Test. 2017, 63, 434–439. [Google Scholar] [CrossRef]
- Cao, S.; Wu, Z. Tensile properties of FRP composites at elevated and high temperatures. J. Appl. Mech. 2008, 11, 963–970. [Google Scholar] [CrossRef]
- Dorigato, A.; Pegoretti, A. Flexural and impact behaviour of carbon/basalt fibers hybrid laminates. J. Compos. Mater. 2014, 48, 1121–1130. [Google Scholar] [CrossRef]
- Golla, S.K.; Prasanthi, P. Prediction of Micromechanical Behavior of Fiber (Glass/Basalt) Reinforced Polymer Composites. Int. Res. J. Eng. Technol. 2016, 3, 1557–1563. [Google Scholar]
- Lapena, M.H.; Marinucci, G. Mechanical Characterization of Basalt and Glass Fiber Epoxy Composite Tube. Mater. Res. 2017, 21, 1–7. [Google Scholar] [CrossRef]
- Plappert, D.; Ganzenmüller, G.C.; May, M.; Beisel, S. Mechanical Properties of a Unidirectional Basalt-Fiber/Epoxy Composite. J. Compos. Sci. 2020, 4, 101. [Google Scholar] [CrossRef]
- Dorigato, A.; Pegoretti, A. Fatigue resistance of basalt fibers-reinforced laminates. J. Compos. Mater. 2012, 46, 1773–1785. [Google Scholar] [CrossRef]
- Startsev, O.V.; Blaznov, A.N.; Petrov, M.G.; Atyasova, E.V. Study of durability of polymer composite materials under static loads. Vse Mater. Entsiklopedicheskii Sprav. 2019, 6, 9–20. [Google Scholar]
- Startsev, O.V.; Lebedev, M.P.; Blaznov, A.N. Aging of polymer composite materials under load. Vse Mater. Entsiklopedicheskii Sprav. 2020, 11, 2–12. [Google Scholar]
- Startsev, O.V.; Lebedev, M.P.; Kychkin, A.K. Aging of polymer composite materials in extremely cold climates. Bull. Altai. State Univ. 2020, 1, 41–51. [Google Scholar]
- Vafaeva, K.M.; Dhyani, M.; Acharya, P.; Parik, K.; Ledalla, S. Glass-basalt-plastic materials for construction in temperate and Arctic climatic regions. BIO Web Conf. 2024, 86, 01111. [Google Scholar]
- Zhigun, I.G.; Polyakov, V.A.; Mikhailov, V.V. Compression testing of composites. Mech. Compos. Mater. 1980, 15, 775–781. [Google Scholar] [CrossRef]
- Bazli, M.; Ashrafi, H.; Jafari, A.; Zhao, X.-L.; Raman, R.K.S.; Bai, Y. Effect of fibers configuration and thickness on tensile behavior of GFRP laminates exposed to harsh environment. Polymers 2019, 11, 1401. [Google Scholar] [CrossRef]
- Ronagh, H.; Saeed, N. Changes in mechanical properties of GFRP composite after exposure to warm seawater. J. Compos. Mater. 2017, 51, 2733–2742. [Google Scholar] [CrossRef]
- Benmokrane, B.; Manal, A.; Bouhet, J.-C.; Mohame, K.; Robert, M. Effects of diameter on the durability of glass fiber-reinforced polymer bars conditioned in alkaline solution. J. Compos. Constr. 2017, 21, 04017040. [Google Scholar] [CrossRef]
- Ashrafi, H.; Bazli, M.; Jafari, A.; Ozbakkaloglu, T. Tensile properties of GFRP laminates after exposure to elevated temperatures: Effect of fiber configuration, sample thickness, and time of exposure. Compos. Struct. 2020, 238, 111971. [Google Scholar] [CrossRef]
- Kavai, M.; Watanabe, K.; Hoshi, H.; Hara, E.; Iwahoti, Y. Effect of specimen size on longitudinal strength of unidirectional carbon/epoxy composite laminates (part 1, unnotched strength). Adv. Compos. Mater. 2018, 28, 1–19. [Google Scholar]
- Startsev, O.V.; Krotov, A.S.; Startseva, L.T. Interlayer shear strength of polymer composite materials during long term climatic ageing. Polym. Degrad. Stab. 1999, 63, 183–186. [Google Scholar] [CrossRef]
- Startsev, O.V.; Lebedev, M.P.; Vapirov, Y.M.; Kychkin, A.K. Comparison of glass-transition temperatures for epoxy polymers obtained by methods of thermal analysis. Mech. Compos. Mater. 2020, 56, 227–240. [Google Scholar] [CrossRef]
- Startsev, O.V.; Nikolayev, Y.V. Stability of properties of VKU-49 black-reinforced plastic boards under conditions of long-term water storage. Vse Mater. Entsiklopedicheskii Sprav. 2018, 12, 13–20. [Google Scholar]
- Startsev, O.V.; Blaznov, A.N.; Krasnov, A.A.; Krasnova, A.S. Determination accuracy improvement of mechanical indexes of polymer composite materials. Part 1. Analysis of standardized methods of tensile test. Vse Mater. Entsiklopedicheskii Sprav. 2016, 1, 57–67. [Google Scholar]
- Startsev, O.V.; Blaznov, A.N.; Zimin, D.E.; Samoylenko, V.V. Determination accuracy improvement of mechanical indexes of polymer composite materials. Part 2. Analysis of standardized methods of tensile test. Vse Mater. Entsiklopedicheskii Sprav. 2016, 2, 57–68. [Google Scholar]
- Strartsev, O.V.; Blaznov, A.N.; Firsov, V.V.; Uglova, T.K. Determination accuracy improvement of mechanical indexes of polymer composite materials. Part 3. Analysis of standardized methods of bending test. Vse Mater. Entsiklopedicheskii Sprav. 2016, 3, 60–69. [Google Scholar]
- Mlyniec, A.; Korta, J.; Kudelski, R.; Uhl, T. The influence of the laminate thickness, stacking sequence and thermal aging on the static and dynamic behavior of carbon/epoxy composites. Compos. Struct. 2014, 118, 208–216. [Google Scholar] [CrossRef]
- Cinquin, J.; Medda, B. Influence of laminate thickness on composite durability for long term utilization at intermediate temperature (100–150 °C). Compos. Sci. Technol. 2009, 69, 1432–1436. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, W.; Zhang, X.; Cai, G.; Wan, B. Influence of thickness on water absorption and tensile strength of BFRP laminates in water or alkaline solution and a thickness-dependent accelerated ageing method for BFRP laminates. Appl. Sci. 2020, 10, 3618. [Google Scholar] [CrossRef]
- Strartsev, O.V.; Lebedev, M.P.; Kychkin, A.K. Influence of moderately warm and extremely cold climate on properties of basalt plastic armature. Heliyon 2018, 4, e01060. [Google Scholar] [CrossRef]
- Lebedev, M.P.; Startsev, O.V.; Kychkin, A.K.; Petrov, M.G.; Kopyrin, M.M. Contributing Factors of Uneven Climatic Aging for Polymeric Composite Materials: Methods and Modelling. Polymers 2023, 15, 1458. [Google Scholar] [CrossRef]
- Kychkin, A.K.; Gavrilieva, A.A.; Kychkin, A.A.; Lukachevskaya, I.G.; Lebedev, M.P. The Initial Stage of Climatic Aging of Basalt-Reinforced and Glass-Reinforced Plastics in Extremely Cold Climates: Regularities. Polymers 2024, 16, 866. [Google Scholar] [CrossRef]
- Kychkin, A.K.; Gavrilieva, A.A.; Vasilieva, A.A.; Kychkin, A.A.; Lebedev, M.P.; Sivtseva, A.V. Assessment of Extremely Cold Subarctic Climate Environment Destruction of the Basalt Fiber Reinforced Epoxy (BFRE) Rebar Using Its Moisture Uptake Kinetics. Polymers 2021, 13, 4325. [Google Scholar] [CrossRef]
- Bonniau, P.; Bunsell, A.R. A comparative study of water absorption theories applied to glass epoxy composites. J. Compos. Mater. 1981, 15, 272–293. [Google Scholar] [CrossRef]
- Korkees, F. Moisture absorption behavior and diffusion characteristics of continuous carbon fiber reinforced epoxy composites: A review. Polym.-Plast. Technol. Mater. 2023, 62, 1789–1822. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, C.; Jin, L.; Tu, Y.; Zhang, Y.; An, Z.; Zhao, Y. A modified Langmuir model for moisture diffusion in UGFRE of composite insulator considering the composite degradation. Polymers 2022, 14, 2922. [Google Scholar] [CrossRef]
- Weitsman, Y.J.; Elahi, M. Effects of Fluids on the Deformation, Strength and Durability of Polymeric Composites—An Overview. Mech. Time Depend. Mater. 2000, 3, 107–126. [Google Scholar] [CrossRef]
- RussianGost. Available online: https://www.russiangost.com/p-59266-gost-9708-83.aspx (accessed on 28 August 2024).
- RussianGost. Available online: https://www.russiangost.com/p-64695-gost-326182-2014.aspx (accessed on 28 August 2024).
- RussianGost. Available online: https://www.russiangost.com/p-288708-gost-r-57739-2017.aspx (accessed on 28 August 2024).
- RussianGost. Available online: https://www.russiangost.com/p-138607-gost-32492-2015.aspx (accessed on 28 August 2024).
- ASTM. Available online: https://www.astm.org/d0790-17.html (accessed on 28 August 2024).
- Aniskevich, A.; Glaskova-Kuzmina, T. Effect of moisture on elastic and viscoelastic properties of fiber reinforced plastics: Retrospective and current trends. In Creep and Fatigue in Polymer Matrix Composites; Elsevier Ltd.: Amsterdam, The Netherlands, 2019; pp. 83–120. [Google Scholar]
- Carter, H.G.; Kibler, K.G. Langmuir-type model for anomalous moisture diffusion in composite resins. J. Compos. Mater. 1978, 12, 118–131. [Google Scholar] [CrossRef]
- Lykov, A.V. Teoriya Teploprovodnosti; Higher School: Moscow, Russia, 1967. [Google Scholar]
- ASTM D5229/D5229M-20 (2020); Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM E1356-08 (2014); Standard Test Method for Assignment of the Glass Transition Temperatures by Differential Scanning Calorimetry. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM E1640-13 (2018); Standard Test Method for Assignment of the Glass Transition Temperature by Dynamic Mechanical Analysis. ASTM International: West Conshohocken, PA, USA, 2018.
- ISO 11357-2 (2020); Plastics—Differential Scanning Calorimetry (DSC)—Determination of Glass Transition Temperature and Glass Transition Step Height. ISO: Geneva, Switzerland, 2013.
- ISO 6721-11 (2019); Plastics—Determination of Dynamic Mechanical Properties—Part 11: Glass-Transition Temperature. ISO: Geneva, Switzerland, 2019.
- Bussu, G.; Lazzeri, A. On the use of dynamic mechanical thermal analysis (DMTA) for measuring glass transition temperature of polymer matrix fibre reinforced composites. J. Mater. Sci. 2006, 41, 6072–6076. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, W.; Wan, B.; Meng, Z.; Han, B. Hygrothermal ageing behavior and mechanism of carbon nanofibers modified flax fiber-reinforced epoxy laminates. Compos. Part A 2021, 140, 106142. [Google Scholar] [CrossRef]
- Zulueta, K.; Burgoa, A.; Martinez, I. Effects of hygrothermal aging on the thermomechanical properties of a carbon fiber reinforced epoxy sheet molding compound: An experimental research. J. Appl. Polym. Sci. 2020, 138, 50009. [Google Scholar] [CrossRef]
- Zuo, P.; Tcharkhtchi, A.; Shirinbayan, M.; Fitoussi, J.; Bakir, F. Effect of thermal aging on crystallization behaviors and dynamic mechanical properties of glass fiber reinforced polyphenylene sulfide (PPS/GF) composites. J. Polym. Res. 2020, 27, 77. [Google Scholar] [CrossRef]
- Glazkova, T.I.; Guedes, R.M.; Morais, J.J.; Aniskevich, A.N. A comparative analysys of moisture transport models as applied to an epoxy binder. Mech. Compos. Mater. 2007, 43, 377–388. [Google Scholar] [CrossRef]
- Popineau, S.; Rondeau-Mouro, C.; Sulpice-Gaillet, C.; Shanahan, M. Free/bound water absorption in an epoxy adhesive. Polymer 2005, 406, 10733–10740. [Google Scholar] [CrossRef]





| ED-22 | iso-MTHFA | UP-606/2 | RBN 13-2400-4S | ||||
|---|---|---|---|---|---|---|---|
| Epoxy group (wt. %) | 21.4 | Main substance (wt.%) | 99.2 | Main substance (wt.%) | 98.4 | Linear density (tex) | 2400 |
| Viscosity at 25 °C (Pa·sec) | 16 | Viscosity at 20 °C (sec) | 28 | Density at 25 °C (kg/m)3 | 10 | Breaking load (mN/tex) | 46 |
| Appearance | Transparent | Appearance | Transparent | Appearance | yellow | fiber diameter (m) | 13 |
| Nominal Bar Diameter 1 (mm) | Central Rod Diameter (mm) | Tension of Polyamide Winding Threads (kg) | Polymerizer Temperature (°C) | Tensile Strength (MPa) 2 | Tensile Modulus (GPa) 2 |
|---|---|---|---|---|---|
| 6 | 4 | 3 | 125 | 1260 | 53 |
| 8 | 6 | 4 | 125 | 1220 | 52 |
| 10 | 8 | 6 | 125 | 1210 | 52 |
| 16 | 13 | 6 | 130 | 1199 | 51 |
| 20 | 17 | 8 | 140 | 1190 | 50 |
| Impact Factor | Yakutsk | Gelendzhik |
|---|---|---|
| Relative humidity (%) | 68 | 73 |
| Wind speed (m/s) | 1.8 | 3.5 |
| Average maximum air temperature (°C) | −3.4 | 24.8 |
| Average minimum air temperature (°C) | −14.1 | 5 |
| Average air temperature (°C) | −8.8 | 14.8 |
| Precipitation rate (mm) | 237 | 665 |
| Climate Aging Test | Nominal Bar Diameter (mm) | |||
|---|---|---|---|---|
| unexposed | 6 | 104 ± 1 | 133 ± 1 | 190 ± 1 |
| 8 | 105 ± 1 | 133 ± 1 | 190 ± 1 | |
| 10 | 104 ± 1 | 134 ± 1 | 190 ± 1 | |
| exposed for 51 month in Yakutsk | 6 | 110 ± 2 | 139 ± 1 | 200 ± 2 |
| 8 | 107 ± 2 | 137 ± 1 | 200 ± 2 | |
| 10 | 105 ± 2 | 135 ± 1 | 200 ± 2 | |
| exposed for 54 month in Gelendzhik | 6 | 110 ± 2 | 143 ± 1 | 200 ± 2 |
| 8 | 110 ± 2 | 140 ± 1 | 200 ± 2 | |
| 10 | 106 ± 2 | 136 ± 1 | 200 ± 2 |
| Climate Aging Test | Nominal Bar Diameter (mm) | Tensile Strength (MPa) | Bending Strength (MPa) | Compressive Strength (MPa) |
|---|---|---|---|---|
| unexposed | 6 | 1120 (1.0) 1 | 1209 (1.0) | 410 (1.0) |
| 8 | 1003 (1.0) | 764 (1.0) | 466 (1.0) | |
| 10 | - | 624 (1.0) | 432 (1.0) | |
| exposed for 28 months in Yakutsk | 6 | 1206 (1.0) | 1087 (0.90) | 428 (1.04) |
| 8 | 1078 (1.07) | 733 (0.96) | 474 (1.02) | |
| 10 | - | 639 (1.02) | 452 (1.05) | |
| exposed for 51 months in Yakutsk | 6 | 1275 (1.14) | 976 (0.80) | - |
| 8 | 1080 (1.03) | 666 (0.87) | - | |
| 10 | - | 695 (1.11) | - | |
| exposed for 30 months in Gelendzhik | 6 | - | 1094 (0.90) | 427 (1.04) |
| 8 | - | 658 (0.86) | 420 (0.90) | |
| 10 | - | 612 (0.98) | 454 (1.05) | |
| exposed for 54 months in Gelendzhik | 6 | 1193 (1.07) | 920 (0.76) | - |
| 8 | 1029 (1.03) | 730 (0.96) | - | |
| 10 | - | 677 (1.08) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilieva, A.A.; Startsev, O.V.; Lebedev, M.P.; Krotov, A.S.; Kychkin, A.K.; Lukachevskaya, I.G. Size Effects in Climatic Aging of Epoxy Basalt Fiber Reinforcement Bar. Polymers 2024, 16, 2550. https://doi.org/10.3390/polym16182550
Gavrilieva AA, Startsev OV, Lebedev MP, Krotov AS, Kychkin AK, Lukachevskaya IG. Size Effects in Climatic Aging of Epoxy Basalt Fiber Reinforcement Bar. Polymers. 2024; 16(18):2550. https://doi.org/10.3390/polym16182550
Chicago/Turabian StyleGavrilieva, Anna A., Oleg V. Startsev, Mikhail P. Lebedev, Anatoly S. Krotov, Anatoly K. Kychkin, and Irina G. Lukachevskaya. 2024. "Size Effects in Climatic Aging of Epoxy Basalt Fiber Reinforcement Bar" Polymers 16, no. 18: 2550. https://doi.org/10.3390/polym16182550
APA StyleGavrilieva, A. A., Startsev, O. V., Lebedev, M. P., Krotov, A. S., Kychkin, A. K., & Lukachevskaya, I. G. (2024). Size Effects in Climatic Aging of Epoxy Basalt Fiber Reinforcement Bar. Polymers, 16(18), 2550. https://doi.org/10.3390/polym16182550






