Development of a Cure Model for Unsaturated Polyester Resin Systems Based on Processing Conditions
Abstract
1. Introduction
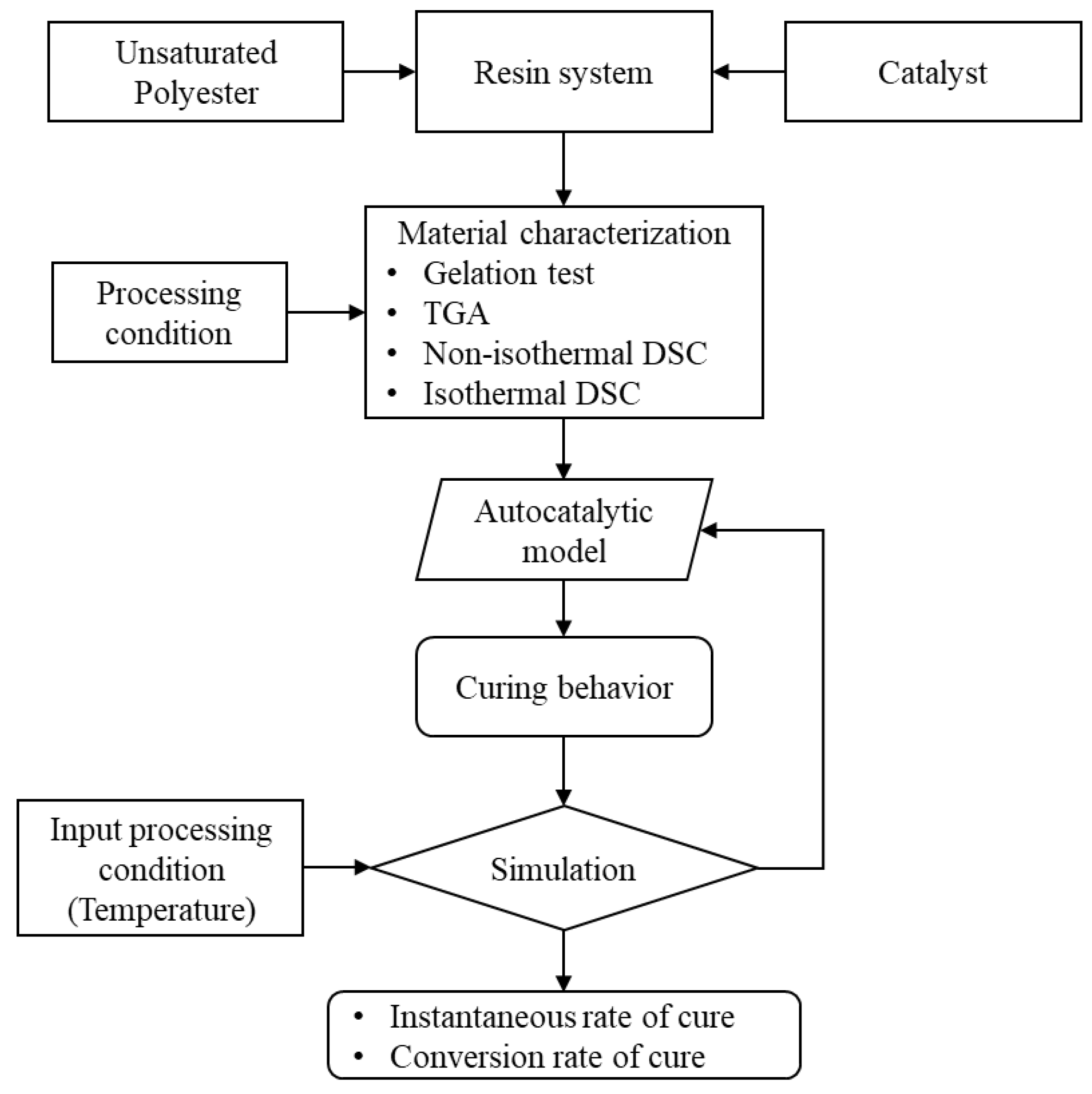
2. Experimental and Numerical Methodology
2.1. Polymer Characterization
2.2. Cure Simulation
3. Results and Discussion
3.1. Characterization Results
3.2. Cure Behavior
4. Summary and Conclusions
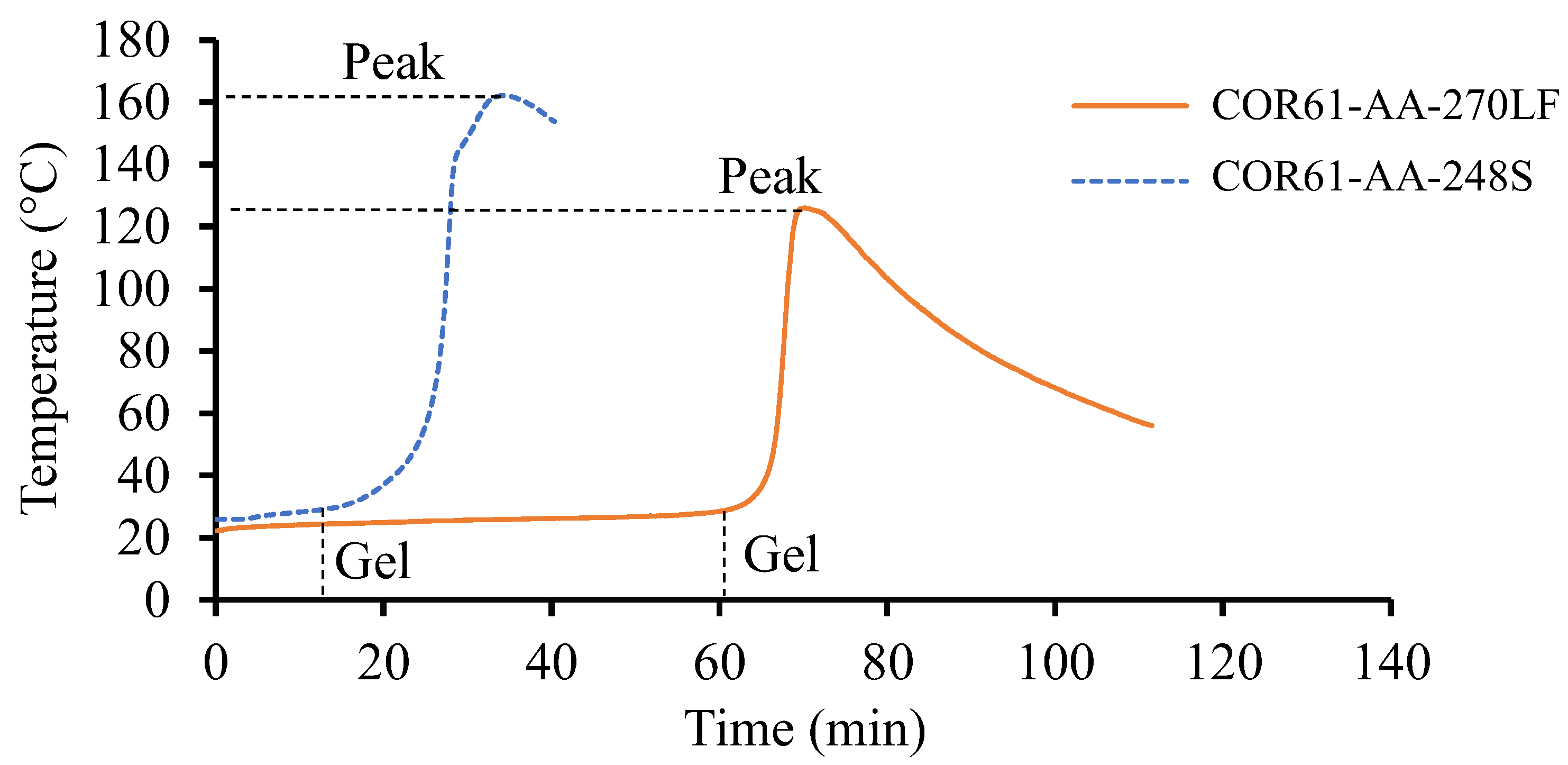
- For the gel time, COR61-AA-248S started transitioning from a liquid to gel state after 13 min, while the COR61-AA-270LF reaction started after 60 min, making it a 361.5% longer time. COR61-AA-248S reached its highest temperature of 162 °C after 34 min, while COR61-AA-270LF exhibited a 20% lower peak (126 °C) after 70 min, a 105.9% longer time. The difference in behaviors between the two polyester resins was caused by their distinct chemistries and crosslinking networks.
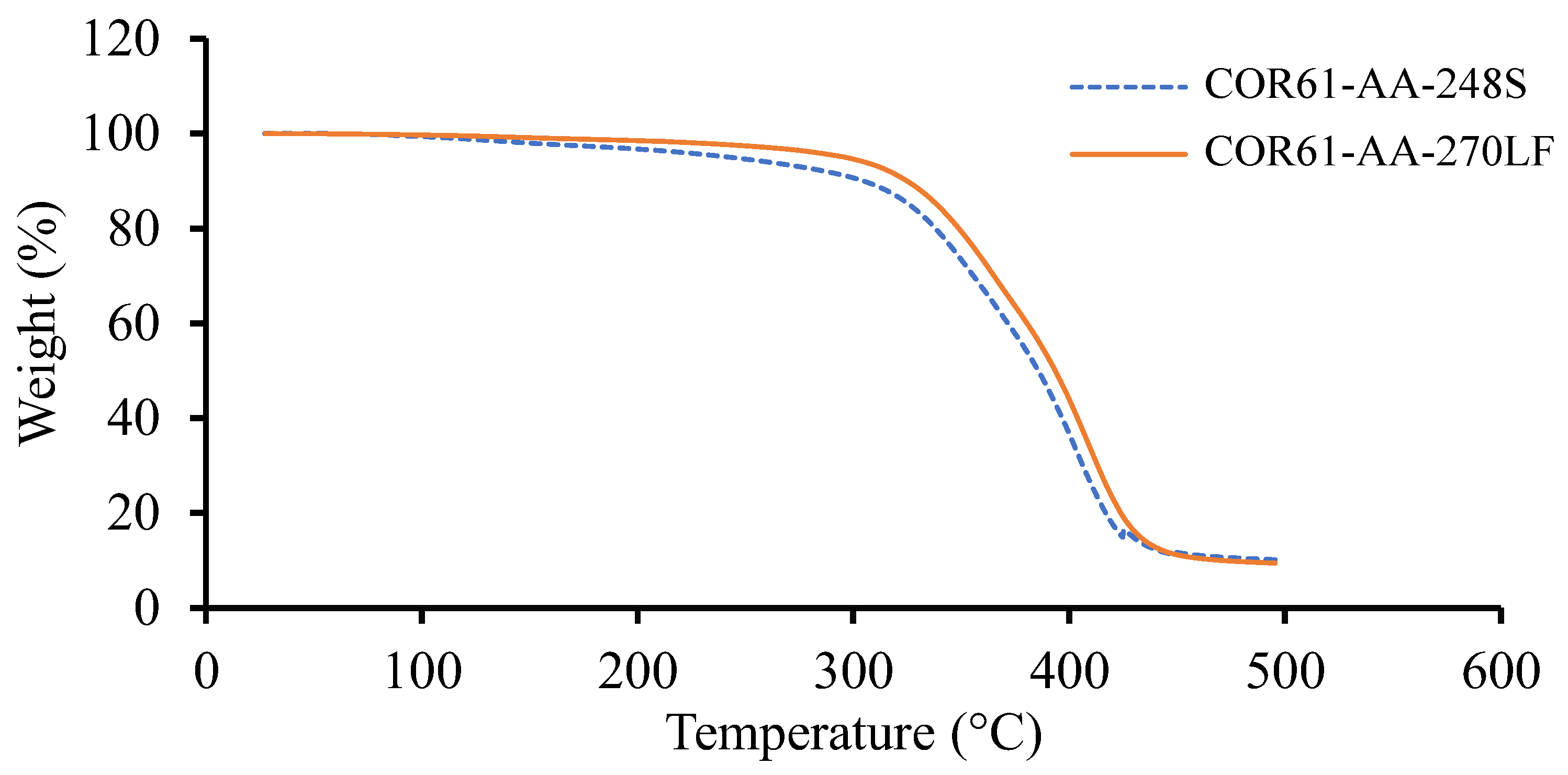
- The TGA showed that Resin 1 had a of 243.03 °C, of 304.64 °C, and a of 416.88 °C, while Resin 2 gave higher values of of 296.44 °C (22% higher), of 324.87 °C (6.6% higher), and a of 423.84 °C (1.7% higher).
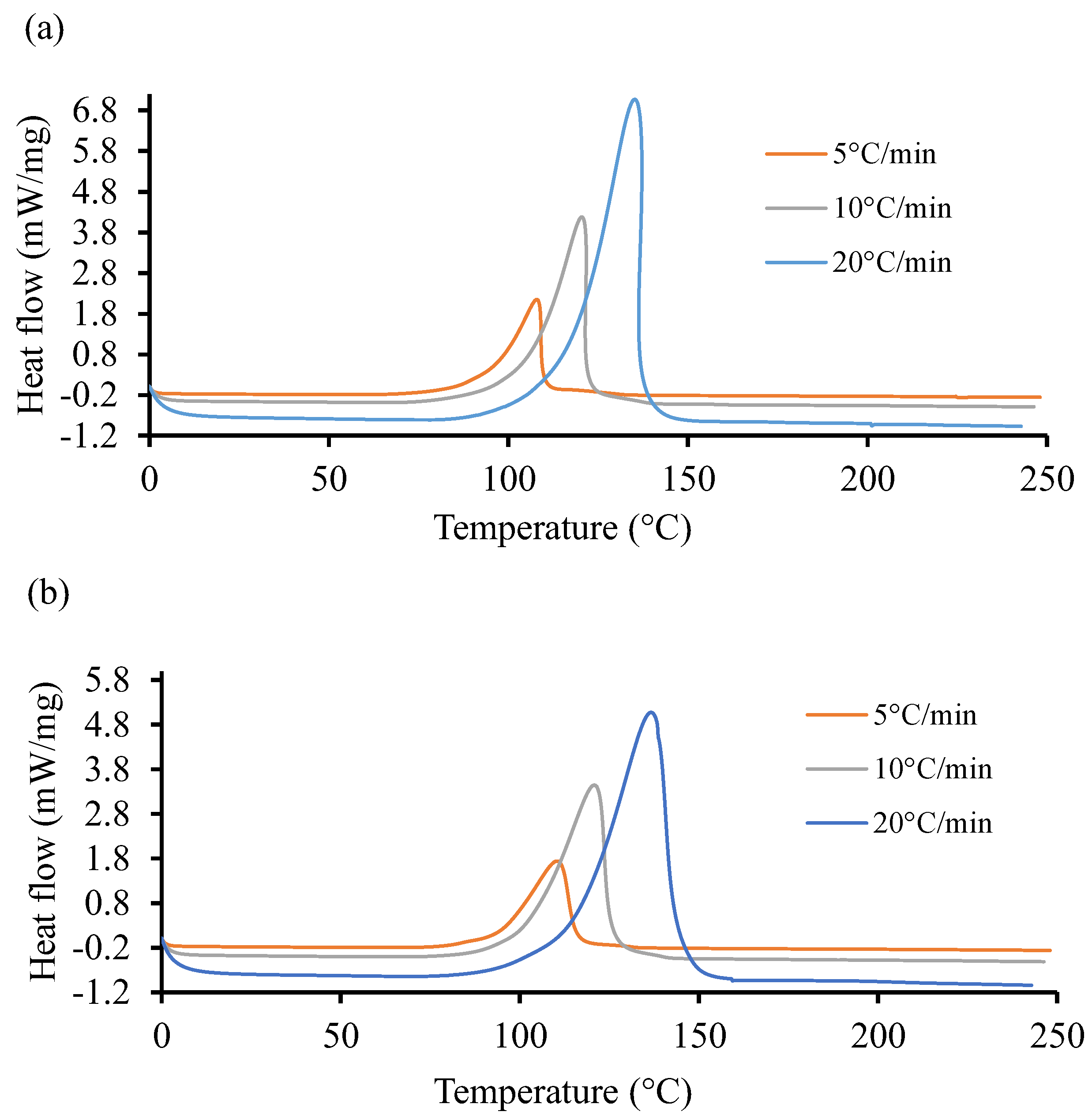
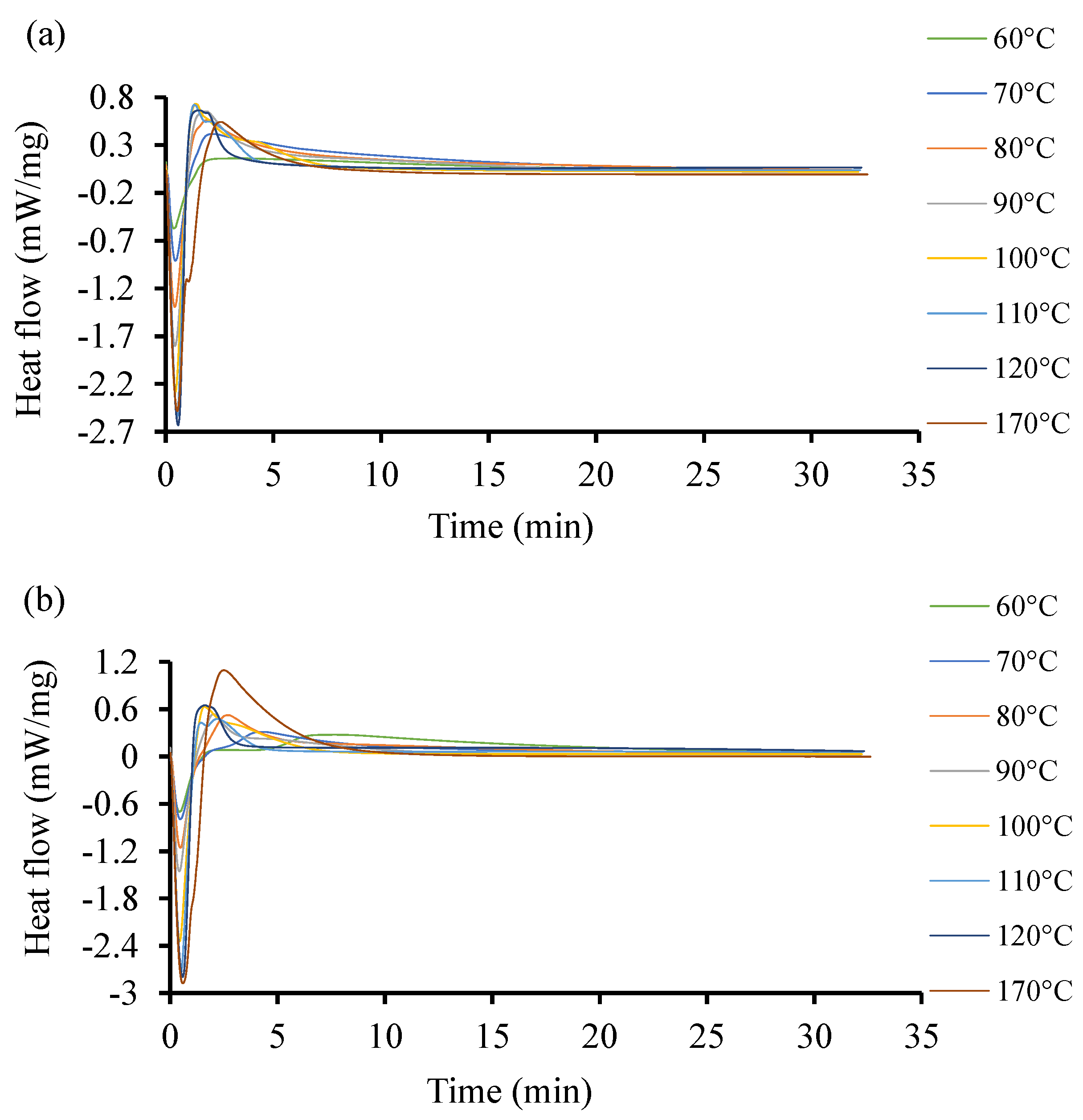
- At the lowest rate of 5 °C/min, Resin system 1 had a peak cure temperature () of 110 °C, and Resin 2 had a of 115.9 °C, resulting in a 5.3 °C difference. At the maximum rate of 20 °C/min, Resin 1 had a of 146.3 °C, while Resin 2 had a of 148.1 °C, resulting in a 2.0 °C difference. The Resin 2 additive has a strong effect on non-isothermal cure at low cooling rates but is more pronounced at higher rates.
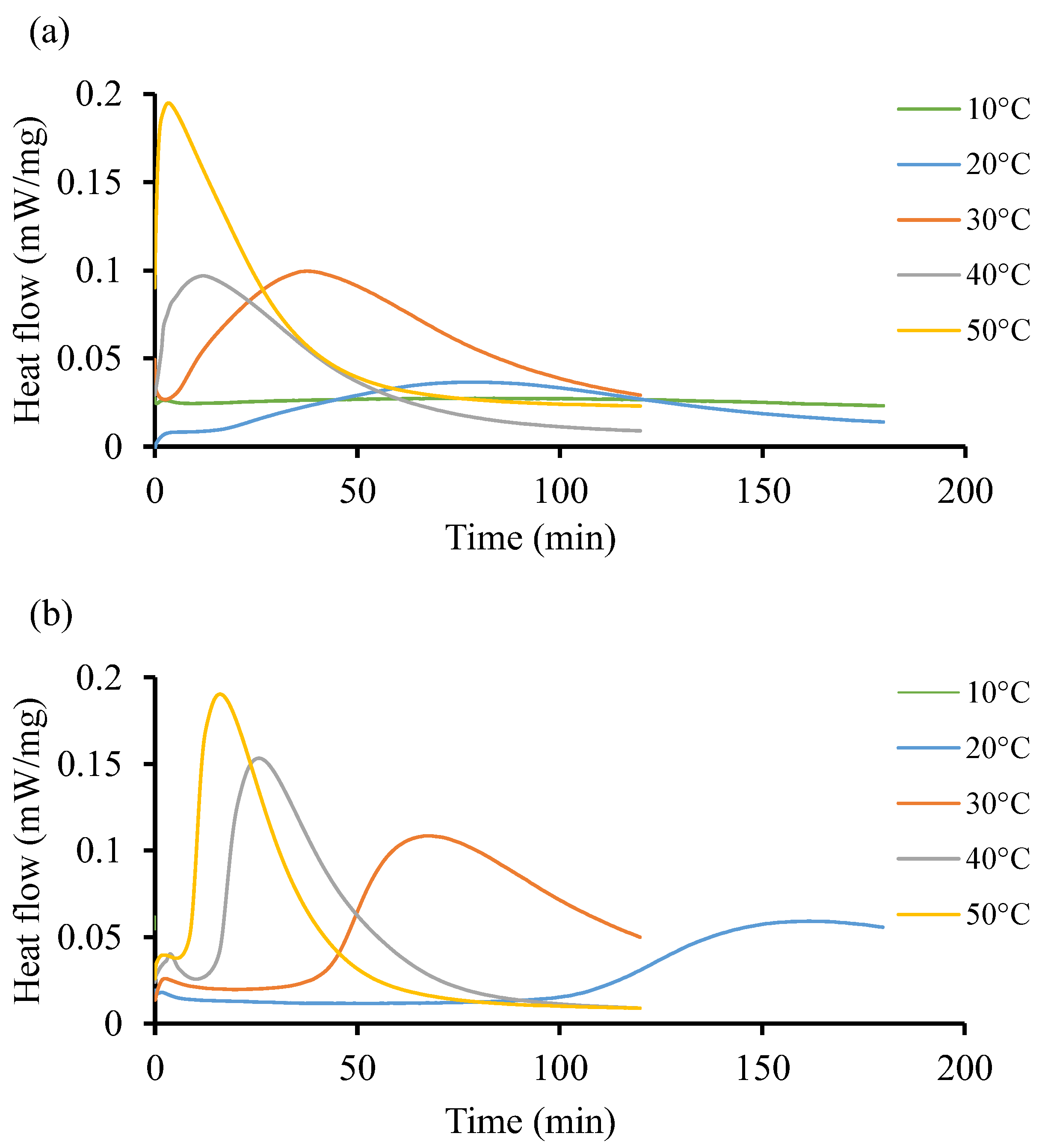
- The instantaneous rate of cure of the tested temperatures were measured. It was observed that as the temperature increased from 10 °C up to 170 °C, the rate of cure reduced, and the heat of reaction increased. The amount of heat released from the different samples were close to each other.
- For a constant applied temperature, the conversion rate behaved in a constant fashion and depended on the instantaneous rate of cure. The amount of added catalyst defined the total degree of cure and was based on the total activation energy. For the variable heating temperature, the curing cycle was controlled as desired and provided the desired amount of cure with a proper peak during the thermal cycle.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nitin, M.S.; Suresh Kumar, S. Ballistic performance of synergistically toughened Kevlar/epoxy composite targets reinforced with multiwalled carbon nanotubes/graphene nanofillers. Polym. Compos. 2022, 43, 782–797. [Google Scholar] [CrossRef]
- Gieparda, W.; Rojewski, S.; Wüstenhagen, S.; Kicinska-Jakubowska, A.; Krombholz, A. Chemical modification of natural fibres to epoxy laminate for lightweight constructions. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106171. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.; Chen, Y.; Wu, Q.; Wang, S. An Effective Method for Preparation of Liquid Phosphoric Anhydride and Its Application in Flame Retardant Epoxy Resin. Materials 2021, 14, 2205. [Google Scholar] [CrossRef]
- Zhang, M.; Singh, R.P. Mechanical reinforcement of unsaturated polyester by Al2O3 nanoparticles. Mater. Lett. 2004, 58, 408–412. [Google Scholar] [CrossRef]
- Boyard, N.; Vayer, M.; Sinturel, C.; Seifert, S.; Erre, R. Investigation of phase separation mechanisms of thermoset polymer blends by time-resolved SAXS. Eur. Polym. J. 2005, 41, 1333–1341. [Google Scholar] [CrossRef]
- Penczek, P.; Czub, P.; Pielichowski, J. Unsaturated polyester resins: Chemistry and technology. In Crosslinking in Materials ScienceI; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–95. [Google Scholar]
- Saleh, H.E.-D.M. Polyester; BoD–Books on Demand: Norderstedt, Germany, 2012. [Google Scholar]
- Leroy, E.; Dupuy, J.; Maazouz, A.; Seytre, G. Evolution of the coefficient of thermal expansion of a thermosetting polymer during cure reaction. Polymer 2005, 46, 9919–9927. [Google Scholar] [CrossRef]
- Chatham, C.A.; Washington, A.L. A framework for forming thermoset polymer networks during laser powder bed fusion additive manufacturing. Addit. Manuf. 2023, 72, 103620. [Google Scholar] [CrossRef]
- Liang, Q.; Feng, X.-P.; Zhang, K.; Hui, X.-M.; Hou, X.; Ye, J.-R. Effect of curing pressure on the curing behavior of an epoxy system: Curing kinetics and simulation verification. Polymer 2022, 256, 125162. [Google Scholar] [CrossRef]
- Hsu, C.P.; Kinkelaar, M.; Hu, P.; Lee, L.J. Effects of thermoplastic additives on the cure of unsaturated polyester resins. Polym. Eng. Sci. 1991, 31, 1450–1460. [Google Scholar] [CrossRef]
- Li, W.; Lee, L.J. Low temperature cure of unsaturated polyester resins with thermoplastic additives. II. Structure formation and shrinkage control mechanism. Polymer 2000, 41, 697–710. [Google Scholar] [CrossRef]
- de la Caba, K.; Guerrero, P.; Eceiza, A.; Mondragon, I. Kinetic and rheological studies of an unsaturated polyester cured with different catalyst amounts. Polymer 1996, 37, 275–280. [Google Scholar] [CrossRef]
- Sachin, W.; Babu, B.J.C.; Amit, R. Curing studies of unsaturated polyester resin used in FRP products. Indian J. Eng. Mater. Sci. 2011, 18, 31–39. [Google Scholar]
- Silva, M.P.; Santos, P.; Parente, J.M.; Valvez, S.; Reis, P.N.B.; Piedade, A.P. Effect of Post-Cure on the Static and Viscoelastic Properties of a Polyester Resin. Polymers 2020, 12, 1927. [Google Scholar] [CrossRef]
- Akbari, S.; Root, A.; Skrifvars, M.; Ramamoorthy, S.K.; Åkesson, D. Novel Bio-based Branched Unsaturated Polyester Resins for High-Temperature Applications. J. Polym. Environ. 2023, 32, 2031–2044. [Google Scholar] [CrossRef]
- Tarnacka, M.; Madejczyk, O.; Dulski, M.; Wikarek, M.; Pawlus, S.; Adrjanowicz, K.; Kaminski, K.; Paluch, M. Kinetics and Dynamics of the Curing System. High Pressure Studies. Macromolecules 2014, 47, 4288–4297. [Google Scholar] [CrossRef]
- Tarnacka, M.; Wikarek, M.; Pawlus, S.; Kaminski, K.; Paluch, M. Impact of high pressure on the progress of polymerization of DGEBA cured with different amine hardeners: Dielectric and DSC studies. RSC Adv. 2015, 5, 105934–105942. [Google Scholar] [CrossRef]
- Li, S.J.; Zhan, L.H.; Chen, R.; Peng, W.F.; Zhang, Y.A.; Zhou, Y.Q.; Zeng, L.R. The influence of cure pressure on microstructure, temperature field and mechanical properties of advanced polymer-matrix composite laminates. Fibers Polym. 2014, 15, 2404–2409. [Google Scholar] [CrossRef]
- Xie, F.; Wang, X.; Li, M.; Zhang, Z. Experimental research on pressure distribution and resin flow of T-stiffened skins in autoclave process. Fuhe Cailiao Xuebao/Acta Mater. Compos. Sin. 2009, 26, 66–71. [Google Scholar]
- Muric-Nesic, J.; Compston, P.; Stachurski, Z.H. On the void reduction mechanisms in vibration assisted consolidation of fibre reinforced polymer composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 320–327. [Google Scholar] [CrossRef]
- Hernández, S.; Sket, F.; Molina-Aldareguía, J.M.; González, C.; Llorca, J. Effect of curing cycle on void distribution and interlaminar shear strength in polymer-matrix composites. Compos. Sci. Technol. 2011, 71, 1331–1341. [Google Scholar] [CrossRef]
- Hernández, S.; Sket, F.; González, C.; Llorca, J. Optimization of curing cycle in carbon fiber-reinforced laminates: Void distribution and mechanical properties. Compos. Sci. Technol. 2013, 85, 73–82. [Google Scholar] [CrossRef]
- Yang, X.; Zhan, L.; Jiang, C.; Zhao, X.; Guan, C.; Chang, T. Evaluating random vibration assisted vacuum processing of carbon/epoxy composites in terms of interlaminar shear strength and porosity. J. Compos. Mater. 2019, 53, 2367–2376. [Google Scholar] [CrossRef]
- Struzziero, G.; Skordos, A.A. Multi-objective optimisation of the cure of thick components. Compos. Part A Appl. Sci. Manuf. 2017, 93, 126–136. [Google Scholar] [CrossRef]
- Pillai, V.; Beris, A.N.; Dhurjati, P. Heuristics guided optimization of a batch autoclave curing process. Comput. Chem. Eng. 1996, 20, 275–294. [Google Scholar] [CrossRef]
- Rai, N.; Pitchumani, R. Optimal cure cycles for the fabrication of thermosetting-matrix composites. Polym. Compos. 1997, 18, 566–581. [Google Scholar] [CrossRef]
- Skordos, A.A.; Partridge, I.K. Inverse heat transfer for optimization and on-line thermal properties estimation in composites curing. Inverse Probl. Sci. Eng. 2004, 12, 157–172. [Google Scholar] [CrossRef]
- Li, M.; Zhu, Q.; Geubelle, P.H.; Tucker Iii, C.L. Optimal curing for thermoset matrix composites: Thermochemical considerations. Polym. Compos. 2001, 22, 118–131. [Google Scholar] [CrossRef]
- Yang, Z.L.; Lee, S. Optimized curing of thick section composite laminates. Mater. Manuf. Process. 2001, 16, 541–560. [Google Scholar] [CrossRef]
- Carlone, P.; Palazzo, G.S. A Simulation Based Metaheuristic Optimization of the Thermal Cure Cycle of Carbon-Epoxy Composite Laminates. AIP Conf. Proc. 2011, 1353, 5–10. [Google Scholar] [CrossRef]
- White, S.R.; Hahn, H.T. Cure Cycle Optimization for the Reduction of Processing-Induced Residual Stresses in Composite Materials. J. Compos. Mater. 1993, 27, 1352–1378. [Google Scholar] [CrossRef]
- Olivier, P.; Cottu, J.P. Optimisation of the co-curing of two different composites with the aim of minimising residual curing stress levels. Compos. Sci. Technol. 1998, 58, 645–651. [Google Scholar] [CrossRef]
- Gopal, A.K.; Adali, S.; Verijenko, V.E. Optimal temperature profiles for minimum residual stress in the cure process of polymer composites. Compos. Struct. 2000, 48, 99–106. [Google Scholar] [CrossRef]
- Bailleul, J.L.; Sobotka, V.; Delaunay, D.; Jarny, Y. Inverse algorithm for optimal processing of composite materials. Compos. Part A Appl. Sci. Manuf. 2003, 34, 695–708. [Google Scholar] [CrossRef]
- Zhu, Q.; Geubelle, P.H. Dimensional accuracy of thermoset composites: Shape optimization. J. Compos. Mater. 2002, 36, 647–672. [Google Scholar] [CrossRef]
- Khorsand, A.; Raghavan, J.; Wang, G. Tool-shape optimization to minimize warpage in autoclave processed L-shaped composite part. In Proceedings of the International SAMPE Technical Conference, Memphis, TN, USA, 8–11 September 2008; pp. 8–11. [Google Scholar]
- Yuan, Z.; Tong, X.; Yang, G.; Yang, Z.; Song, D.; Li, S.; Li, Y. Curing Cycle Optimization for Thick Composite Laminates Using the Multi-Physics Coupling Model. Appl. Compos. Mater. 2020, 27, 839–860. [Google Scholar] [CrossRef]
- Tziamtzi, C.K.; Chrissafis, K. Optimization of a commercial epoxy curing cycle via DSC data kinetics modelling and TTT plot construction. Polymer 2021, 230, 124091. [Google Scholar] [CrossRef]
- Hu, J.; Xie, H.; Zhu, Z.; Yang, W.; Tan, W.; Zeng, K.; Yang, G. Reducing the melting point and curing temperature of aromatic cyano-based resins simultaneously through a Brønsted acid-base synergistic strategy. Polymer 2022, 246, 124745. [Google Scholar] [CrossRef]
- Ding, A.; Li, S.; Wang, J.; Ni, A.; Zu, L. A new path-dependent constitutive model predicting cure-induced distortions in composite structures. Compos. Part A Appl. Sci. Manuf. 2017, 95, 183–196. [Google Scholar] [CrossRef]
- Svanberg, J.M.; Holmberg, J.A. Prediction of shape distortions Part I. FE-implementation of a path dependent constitutive model. Compos. Part A Appl. Sci. Manuf. 2004, 35, 711–721. [Google Scholar] [CrossRef]
- Sorrentino, L.; Polini, W.; Bellini, C. To design the cure process of thick composite parts: Experimental and numerical results. Adv. Compos. Mater. 2014, 23, 225–238. [Google Scholar] [CrossRef]
- Sorrentino, L.; Tersigni, L. A Method for Cure Process Design of Thick Composite Components Manufactured by Closed Die Technology. Appl. Compos. Mater. 2012, 19, 31–45. [Google Scholar] [CrossRef]
- Bogetti, T.A.; Gillespie, J.W. Two-Dimensional Cure Simulation of Thick Thermosetting Composites. J. Compos. Mater. 1991, 25, 239–273. [Google Scholar] [CrossRef]
- Johnston, A.A. An Integrated Model of the Development of Process-Induced Deformation in Autoclave Processing of Composite Structures; University of British Columbia: Vancouver, BC, Canada, 1997. [Google Scholar]
- Malik, M.; Choudhary, V.; Varma, I.K. Current Status of Unsaturated Polyester Resins. J. Macromol. Sci. Part C 2000, 40, 139–165. [Google Scholar] [CrossRef]
- Özeroğlu, C. The Effect of Tertiary Amines on the Free Radical Copolymerization of Unsaturated Polyester and Styrene. Polym. Plast. Technol. Eng. 2004, 43, 661–670. [Google Scholar] [CrossRef]
- Matušková, E.; Vinklárek, J.; Honzíček, J. Effect of Accelerators on the Curing of Unsaturated Polyester Resins: Kinetic Model for Room Temperature Curing. Ind. Eng. Chem. Res. 2021, 60, 14143–14153. [Google Scholar] [CrossRef]
- Naderi, N.; Mazinani, S.; Beheshty, M.H.; Rajab, M.M. Cure kinetics of hot cured unsaturated polyester (UP)/nanoclay nanocomposite including dual initiators. Plast. Rubber Compos. 2015, 44, 19–25. [Google Scholar] [CrossRef]
- Li, L.; Liao, X.; Hao, Z.; Sheng, X.; Zhang, Y.; Liu, P. Investigation on cure kinetics of epoxy resin containing carbon nanotubes modified with hyper-branched polyester. RSC Adv. R. Soc. Chem. 2018, 8, 29830–29839. [Google Scholar] [CrossRef]
- Calabrese, E.; Raimondo, M.; Catauro, M.; Vertuccio, L.; Lamberti, P.; Raimo, R.; Tucci, V.; Guadagno, L. Thermal and Electrical Characterization of Polyester Resins Suitable for Electric Motor Insulation. Polymers 2023, 15, 1374. [Google Scholar] [CrossRef]
- Nacher, L.S.; Amoros, J.E.C.; Moya, M.D.S.; Martinez, J.L. Mechanical Properties of Polyester Resins in Saline Water Environments. Int. J. Polym. Anal. Charact. 2007, 12, 373–390. [Google Scholar] [CrossRef]
- Stuck, M.; Krenz, I.; Kökelsum, B.S.; Boye, S.; Voit, B.; Lorenz, R. Improving glass transition temperature of unsaturated polyester thermosets: Conventional unsaturated polyester resins. J. Appl. Polym. Sci. 2021, 138, 49825. [Google Scholar] [CrossRef]
- Delaite, C.; Bistac, S.; Dreyer, E.; Schuller, A.-S. Influence of glass transition temperature of crosslinked unsaturated polyester resin/styrene formulations on the final conversion after an isothermal curing at 100 °C. Polym. Adv. Technol. 2020, 31, 2031–2037. [Google Scholar] [CrossRef]
- Pączkowski, P.; Puszka, A.; Gawdzik, B. Investigation of Degradation of Composites Based on Unsaturated Polyester Resin and Vinyl Ester Resin. Materials 2022, 15, 1286. [Google Scholar] [CrossRef]
- Aktas, A.; Krishnan, L.; Kandola, B.; Boyd, S.; Shenoi, R. A Cure Modelling Study of an Unsaturated Polyester Resin System for the Simulation of Curing of Fibre-Reinforced Composites during the Vacuum Infusion Process. J. Compos. Mater. 2015, 49, 2529–2540. [Google Scholar] [CrossRef]
- Ton-That, M.-T.; Cole, K.C.; Jen, C.-K.; França, D.R. Polyester Cure Monitoring by Means of Different Techniques. Polym. Compos. 2000, 21, 605–618. [Google Scholar] [CrossRef]
- Salla, J.M.; Ramis, X. Comparative Study of the Cure Kinetics of an Unsaturated Polyester Resin Using Different Procedures. Polym. Eng. Sci. 1996, 36, 835–851. [Google Scholar] [CrossRef]
- Dusi, M.R.; Lee, W.I.; Ciriscioli, P.R.; Springer, G.S. Cure Kinetics and Viscosity of Fiberite 976 Resin. J. Compos. Mater. 1987, 21, 243–261. [Google Scholar] [CrossRef]
- Lang, M.; Hirner, S.; Wiesbrock, F.; Fuchs, P. A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization. Polymers 2022, 14, 2074. [Google Scholar] [CrossRef]
- Cure, T. Determination of autocatalytic kinetic model parameters describing thermoset cure. J. Appl. Polym. Sci. 1994, 51, 761–764. [Google Scholar]
- Voto, G.; Sequeira, L.; Skordos, A.A. Formulation based predictive cure kinetics modelling of epoxy resins. Polymer 2021, 236, 124304. [Google Scholar] [CrossRef]
- Toyota, K. Products and kinetics of the cationic ring-opening polymerization of 3-glycidoxypropylmethyldimethoxysilane by lithium perchlorate. Polymer 2021, 218, 123490. [Google Scholar] [CrossRef]
- Sourour, S.; Kamal, M.R. Differential scanning calorimetry of epoxy cure: Isothermal cure kinetics. Thermochim. Acta 1976, 14, 41–59. [Google Scholar] [CrossRef]
- Vilas, J.L.; Laza, J.M.; Garay, M.T.; Rodríguez, M.; León, L.M. Unsaturated polyester resins cure: Kinetic, rheologic, and mechanical-dynamical analysis. I. Cure kinetics by DSC and TSR. J. Appl. Polym. Sci. 2001, 79, 447–457. [Google Scholar] [CrossRef]
- Pattanaik, A.; Mukherjee, M.; Mishra, S.B. Influence of curing condition on thermo-mechanical properties of fly ash reinforced epoxy composite. Compos. Part B Eng. 2019, 176, 107301. [Google Scholar] [CrossRef]
- Putzien, S.; Louis, E.; Nuyken, O.; Crivello, J.V.; Kühn, F.E. UV curing of epoxy functional hybrid silicones. J. Appl. Polym. Sci. 2012, 126, 1188–1197. [Google Scholar] [CrossRef]
- Johnston, K.; Pavuluri, S.; Leonard, M.; Desmulliez, M.; Arrighi, V. Microwave and thermal curing of an epoxy resin for microelectronic applications. Thermochim. Acta 2015, 616, 100–109. [Google Scholar] [CrossRef]
- Kim, Y.C.; Min, H.; Yu, J.; Suhr, J.; Lee, Y.K.; Kim, K.J.; Kim, S.H.; Nam, J.-D. Nonlinear and complex cure kinetics of ultra-thin glass fiber epoxy prepreg with highly-loaded silica bead under isothermal and dynamic-heating conditions. Thermochim. Acta 2016, 644, 28–32. [Google Scholar] [CrossRef]
- Mphahlele, K.; Ray, S.S.; Kolesnikov, A. Cure kinetics, morphology development, and rheology of a high-performance carbon-fiber-reinforced epoxy composite. Compos. Part B Eng. 2019, 176, 107300. [Google Scholar] [CrossRef]
- Baghad, A.; El Mabrouk, K. The isothermal curing kinetics of a new carbon fiber/epoxy resin and the physical properties of its autoclaved composite laminates. Mater. Today Proc. 2022, 57, 922–929. [Google Scholar] [CrossRef]
- Cook, W.D.; Lau, M.; Mehrabi, M.; Dean, K.; Zipper, M. Control of gel time and exotherm behaviour during cure of unsaturated polyester resins. Polym. Int. 2001, 50, 129–134. [Google Scholar] [CrossRef]
- Pandiyan Kuppusamy, R.R.; Neogi, S. Influence of curing agents on gelation and exotherm behaviour of an unsaturated polyester resin. Bull. Mater. Sci. 2013, 36, 1217–1224. [Google Scholar] [CrossRef]
- Dai, K.; Song, L.; Jiang, S.; Yu, B.; Yang, W.; Yuen, R.K.; Hu, Y. Unsaturated polyester resins modified with phosphorus-containing groups: Effects on thermal properties and flammability. Polym. Degrad. Stab. 2013, 98, 2033–2040. [Google Scholar] [CrossRef]
- Tibiletti, L.; Longuet, C.; Ferry, L.; Coutelen, P.; Mas, A.; Robin, J.-J.; Lopez-Cuesta, J.-M. Thermal degradation and fire behaviour of unsaturated polyesters filled with metallic oxides. Polym. Degrad. Stab. 2011, 96, 67–75. [Google Scholar] [CrossRef]
- Bai, Z.; Song, L.; Hu, Y.; Yuen, R.K. Preparation, flame retardancy, and thermal degradation of unsaturated polyester resin modified with a novel phosphorus containing acrylate. Ind. Eng. Chem. Res. 2013, 52, 12855–12864. [Google Scholar] [CrossRef]
- Sultania, M.; Rai, J.S.P.; Srivastava, D. Modeling and simulation of curing kinetics for the cardanol-based vinyl ester resin by means of non-isothermal DSC measurements. Mater. Chem. Phys. 2012, 132, 180–186. [Google Scholar] [CrossRef]
- Hwang, S.S.; Park, S.Y.; Kwon, G.C.; Choi, W.J. Cure Kinetics and Viscosity Modeling for the Optimization of Cure Cycles in a Vacuum-Bag-Only Prepreg Process. Int. J. Adv. Manuf. Technol. 2018, 99, 2743–2753. [Google Scholar] [CrossRef]
- Gohn, A.M.; Seo, J.; Ferris, T.; Venkatraman, P.; Foster, E.J.; Rhoades, A.M. Quiescent and flow-induced crystallization in polyamide 12/cellulose nanocrystal composites. Thermochim. Acta 2019, 677, 99–108. [Google Scholar] [CrossRef]
- Halim, Z.A.A.; Yajid, M.A.M.; Idris, M.H.; Hamdan, H. Effects of Rice Husk Derived Amorphous Silica on the Thermal-Mechanical Properties of Unsaturated Polyester Composites. J. Macromol. Sci. Part B 2018, 57, 479–496. [Google Scholar] [CrossRef]
- Ramos, J.A.; Pagani, N.; Riccardi, C.C.; Borrajo, J.; Goyanes, S.N.; Mondragon, I. Cure kinetics and shrinkage model for epoxy-amine systems. Polymer 2005, 46, 3323–3328. [Google Scholar] [CrossRef]



| Temperature (°C) | DSC Run Time (min) |
|---|---|
| 10–20 | 180 |
| 30–50 | 120 |
| 60–120 | 30 |
| 170 | 30 |
| Resin Type | (°C) | (°C) | (°C) |
|---|---|---|---|
| Resin 1 | 243.05 | 304.64 | 416.88 |
| Resin 2 | 296.44 | 324.87 | 423.84 |
| Literature Study | (°C) | (°C) | (°C) |
|---|---|---|---|
| Dai et al. [75] | - | 348 | 419 |
| Pączkowski et al. [56] | - | 336 | 394 |
| Tibiletti et al. [76] | 287 | - | 427 |
| Bai et al. [77] | 307 | - | 433 |
| Average value | 297 | 342 | 418 |
| Temperature Profile | Ramp Up (°C/min) for 30 min | Dwell Time (min) | Ramp Down (°C/min) for 30 min | Maximum Calculated DOC (%) |
|---|---|---|---|---|
| 1 | 0.15 | 30 | 0.10 | 63.19 |
| 2 | 0.25 | 30 | 0.25 | 66.05 |
| 3 | 0.75 | 30 | 0.50 | 73.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barakat, A.; Al Ghazal, M.; Fono Tamo, R.S.; Phadatare, A.; Unser, J.; Hagan, J.; Vaidya, U. Development of a Cure Model for Unsaturated Polyester Resin Systems Based on Processing Conditions. Polymers 2024, 16, 2391. https://doi.org/10.3390/polym16172391
Barakat A, Al Ghazal M, Fono Tamo RS, Phadatare A, Unser J, Hagan J, Vaidya U. Development of a Cure Model for Unsaturated Polyester Resin Systems Based on Processing Conditions. Polymers. 2024; 16(17):2391. https://doi.org/10.3390/polym16172391
Chicago/Turabian StyleBarakat, Abdallah, Marc Al Ghazal, Romeo Sephyrin Fono Tamo, Akash Phadatare, John Unser, Joshua Hagan, and Uday Vaidya. 2024. "Development of a Cure Model for Unsaturated Polyester Resin Systems Based on Processing Conditions" Polymers 16, no. 17: 2391. https://doi.org/10.3390/polym16172391
APA StyleBarakat, A., Al Ghazal, M., Fono Tamo, R. S., Phadatare, A., Unser, J., Hagan, J., & Vaidya, U. (2024). Development of a Cure Model for Unsaturated Polyester Resin Systems Based on Processing Conditions. Polymers, 16(17), 2391. https://doi.org/10.3390/polym16172391






