Computational Methodologies in Synthesis, Preparation and Application of Antimicrobial Polymers, Biomolecules, and Nanocomposites
Abstract
1. Introduction
2. Overview of Antimicrobial Materials
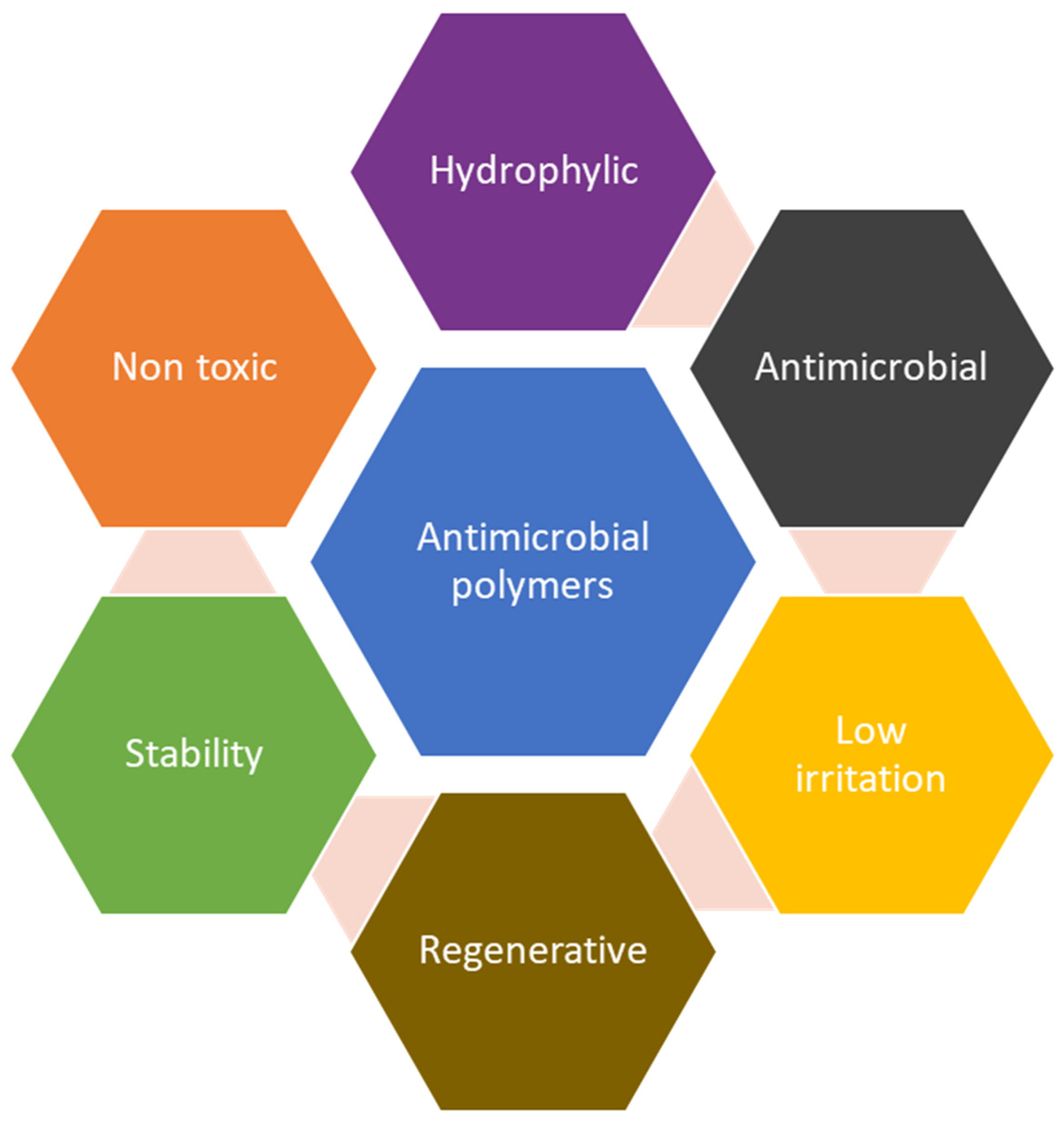
2.1. Antimicrobial Polymers
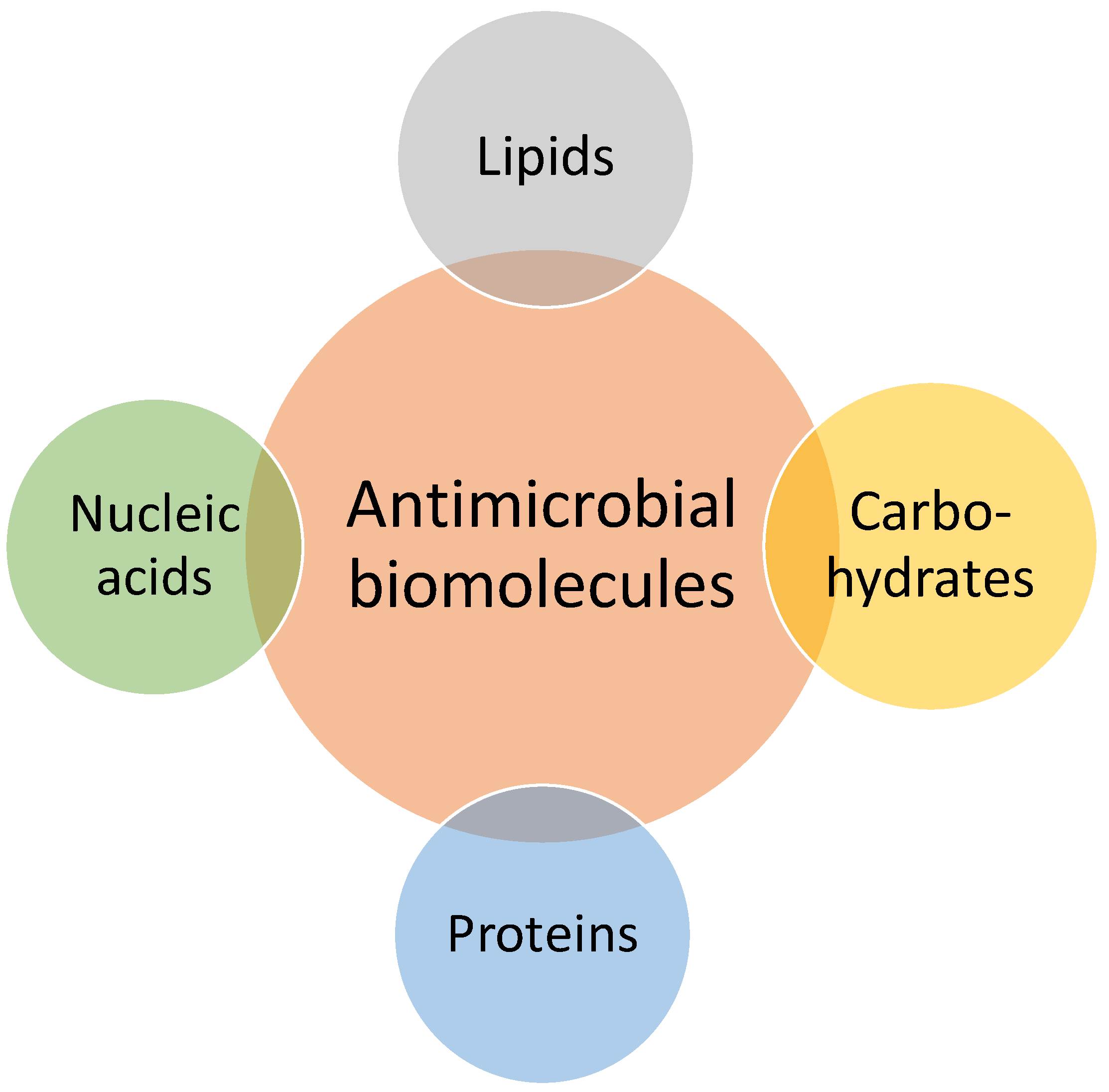
2.2. Antimicrobial Biomolecules
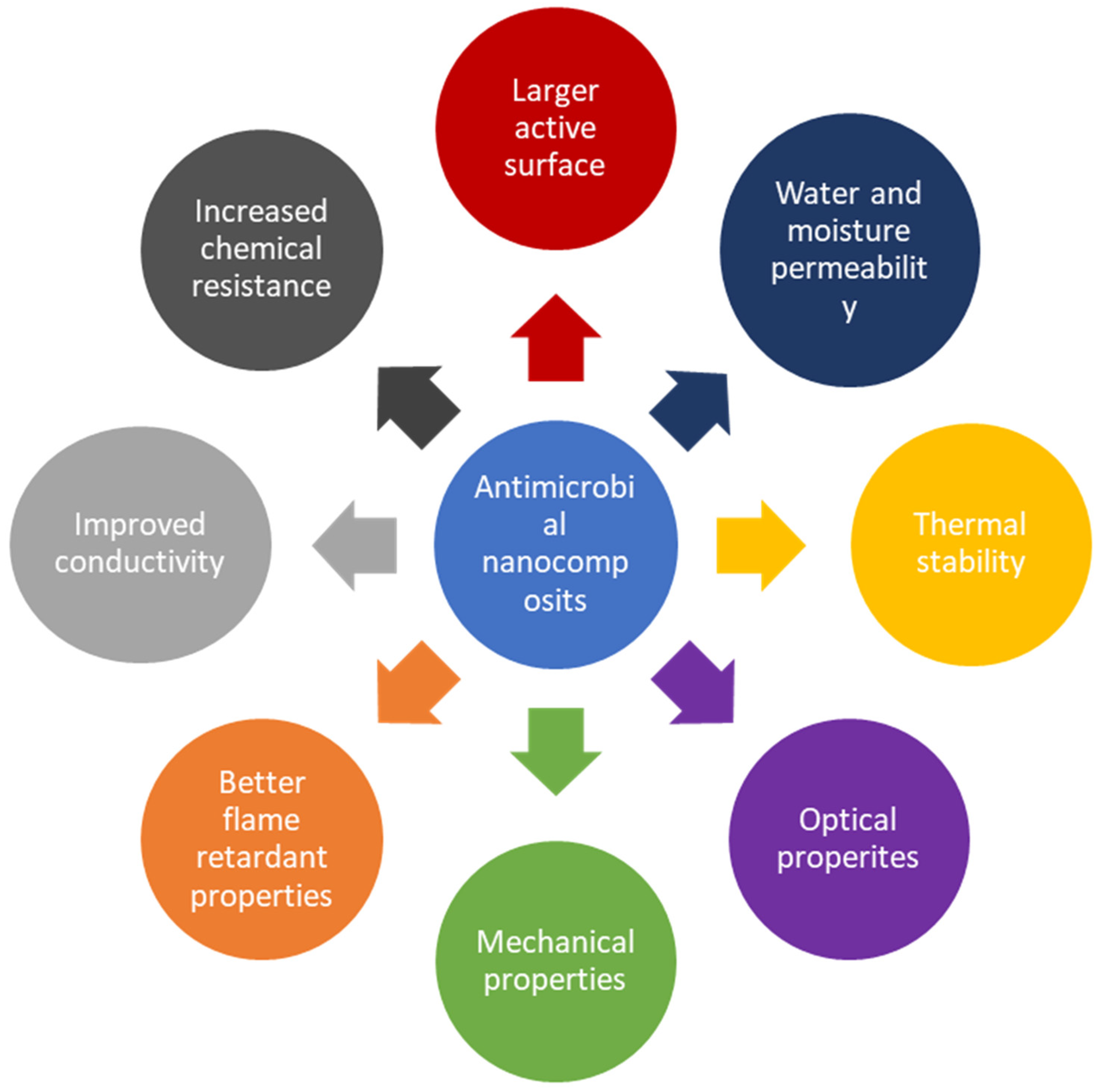
2.3. Antimicrobial Nanocomposites
3. Molecular Dynamics (MD) Simulations
3.1. Polymer–Nanoparticle Interactions
3.2. Biomolecular Dynamics
- (A)
- Protein Dynamics: Proteins are dynamic entities that undergo conformational changes essential for their function. MD simulations provide insights into these conformational changes, enabling the study of protein folding, ligand binding, enzyme catalysis, and allosteric regulation. By simulating the time evolution of protein structures, researchers can identify transient states and pathways that are not easily accessible through experimental techniques [26]. Nucleic Acid Dynamics: DNA and RNA molecules exhibit significant structural flexibility, which is crucial for processes such as replication, transcription, and translation. MD simulations help in understanding how nucleic acids interact with proteins, small molecules, and other nucleic acids. They also reveal the dynamics of secondary and tertiary structures, such as DNA helix melting, RNA folding, and ribosome function.
- (B)
- Membrane Dynamics: Biological membranes are complex assemblies of lipids, proteins, and carbohydrates. MD simulations allow for the study of membrane organization, lipid–lipid and lipid–protein interactions, and the dynamics of membrane-bound proteins. These simulations are vital for understanding membrane permeability, signaling, and transport mechanisms. Enzyme–Substrate Interactions: Enzymes facilitate biochemical reactions by stabilizing transition states and lowering activation energy. MD simulations provide detailed views of enzyme–substrate interactions, revealing the dynamic process of substrate binding, product formation, and enzyme conformational changes. This information is critical for drug design and enzyme engineering [27].
- (C)
- Molecular Recognition: Biomolecular interactions, such as protein–protein, protein–ligand, and protein–DNA interactions, are fundamental to cellular functions. MD simulations help elucidate the principles of molecular recognition, including binding affinity, specificity, and induced fit mechanisms. Understanding these interactions is essential for designing therapeutic agents and synthetic biomolecules [28]. Pathways and Mechanisms: MD simulations enable the exploration of dynamic pathways and mechanisms of biological processes. For example, they can simulate the entire catalytic cycle of an enzyme or the translocation of a substrate across a membrane. These simulations provide a comprehensive picture of the molecular events leading to biological outcomes.
4. Machine Learning (ML)
4.1. Property Prediction by Deep Learning
4.2. Optimization of Synthesis Parameters
4.3. Integration in Composite Materials
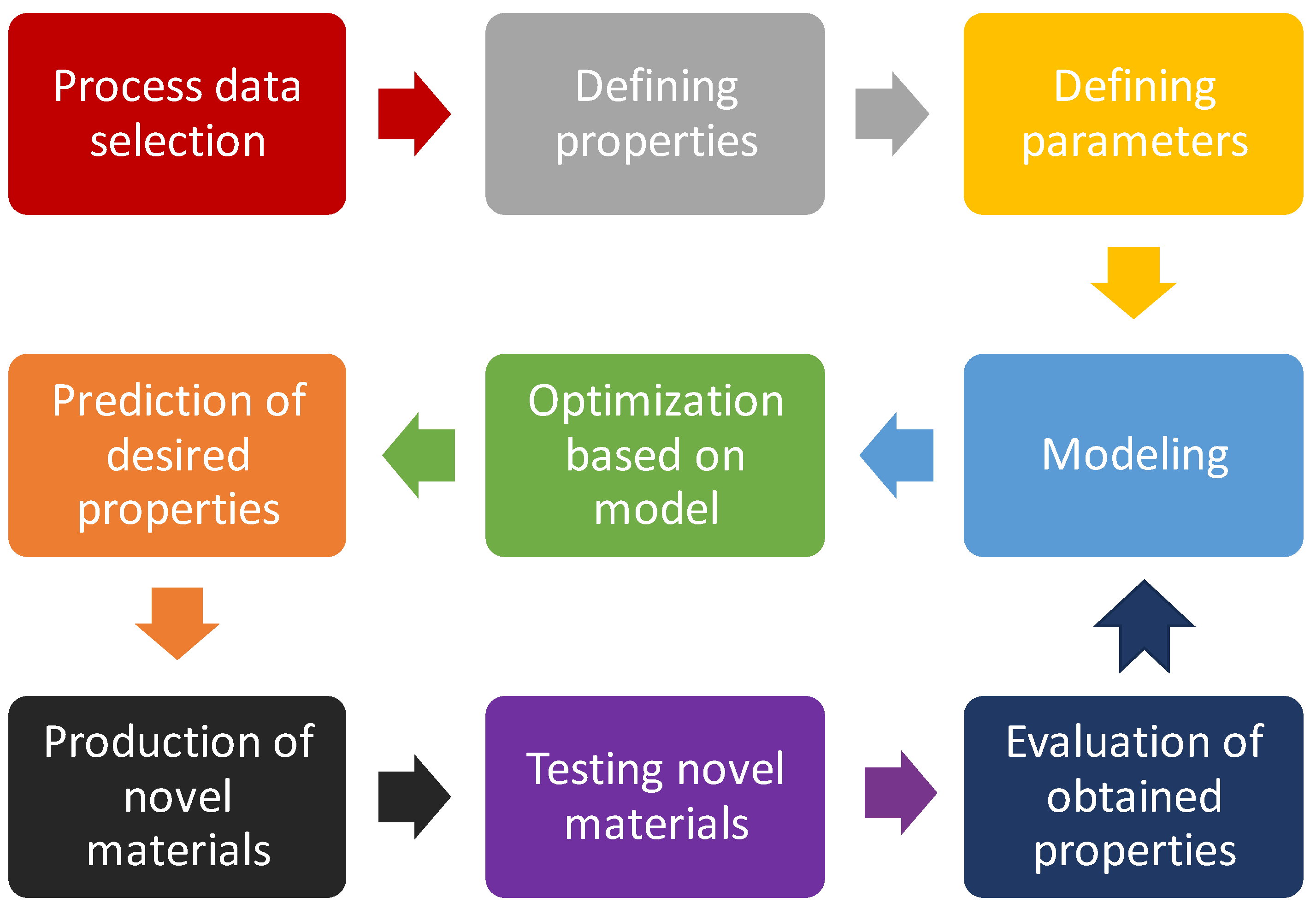
5. Design of Experiment
6. Case Study—Optimization of Preparation of Antimicrobial Polymer by Using Design of Experiments
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Levy, S.B.; Marshall, B. Antibacterial resistance worldwide: Causes, challenges and responses. Nat. Med. 2004, 10 (Suppl. S12), S122–S129. [Google Scholar] [CrossRef] [PubMed]
- Cetin-Karaca, H.; Newman, M.C. Antimicrobial efficacy of natural phenolic compounds against gram positive foodborne pathogens. J. Food Res. 2015, 4, 14. [Google Scholar] [CrossRef]
- Shlaes, D.M. Research and Development of Antibiotics: The Next Battleground. ACS Infect. Dis. 2015, 1, 232–233. [Google Scholar] [CrossRef] [PubMed]
- Darouiche, R.O. Treatment of infections associated with surgical implants. N. Engl. J. Med. 2004, 350, 1422–1429. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Bauman, L.; Nogueira, C.L.; Aucoin, M.G.; Anderson, W.A.; Zhao, B. Antimicrobial polymeric composites for high-touch surfaces in healthcare applications. Curr. Opin. Biomed. Eng. 2022, 22, 100395. [Google Scholar] [CrossRef]
- Muñoz-Bonilla, A.; Fernández-García, M. Polymeric materials with antimicrobial activity. Prog. Polym. Sci. 2012, 37, 281–339. [Google Scholar] [CrossRef]
- Wang, L.; Hu, C.; Shao, L. The antimicrobial activity of nanoparticles: Present situation and prospects for the future. Int. J. Nanomed. 2017, 12, 1227–1249. [Google Scholar] [CrossRef] [PubMed]
- Lam, S.J.; Wong, E.H.; Boyer, C.; Qiao, G.G. Antimicrobial polymeric nanoparticles. Prog. Polym. Sci. 2018, 76, 40–64. [Google Scholar] [CrossRef]
- Lam, S.J.; O’Brien-Simpson, N.M.; Pantarat, N.; Sulistio, A.; Wong, E.H.; Chen, Y.-Y.; Lenzo, J.C.; Holden, J.A.; Blencowe, A.; Reynolds, E.C.; et al. Combating multidrug-resistant Gram-negative bacteria with structurally nanoengineered antimicrobial peptide polymers. Nat. Microbiol. 2016, 1, 16162. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, Z. Nanomaterials for Medical Applications; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Sadybekov, A.V.; Katritch, V. Computational Approaches Streamlining Drug Discovery. Nature 2023, 616, 673–685. [Google Scholar] [CrossRef]
- Jiménez-Luna, J.; Grisoni, F.; Weskamp, N.; Schneider, G. Artificial intelligence in drug discovery: Recent advances and future perspectives. Expert Opin. Drug Discov. 2021, 16, 949–959. [Google Scholar] [CrossRef] [PubMed]
- Sabe, V.T.; Ntombela, T.; Jhamba, L.A.; Maguire, G.E.; Govender, T.; Naicker, T.; Kruger, H.G. Current trends in computer aided drug design and a highlight of drugs discovered via computational techniques: A review. Eur. J. Med. Chem. 2021, 224, 113705. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; MacKerell, A.D. Computer-aided drug design methods. In Antibiotics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–106. [Google Scholar]
- Gurung, A.B.; Ali, M.A.; Lee, J.; Farah, M.A.; Al-Anazi, K.M. An Updated Review of Computer-Aided Drug Design and Its Application to COVID-19. BioMed Res. Int. 2021, 2021, 8853056. [Google Scholar] [CrossRef] [PubMed]
- Song, C.M.; Lim, S.J.; Tong, J.C. Recent advances in computer-aided drug design. Brief. Bioinform. 2009, 10, 579–591. [Google Scholar] [CrossRef] [PubMed]
- Zhong, F.; Xing, J.; Li, X.; Liu, X.; Fu, Z.; Xiong, Z.; Lu, D.; Wu, X.; Zhao, J.; Tan, X. Artificial intelligence in drug design. Sci. China Life Sci. 2018, 61, 1191–1204. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Xu, X. Recent development and application of virtual screening in drug discovery: An overview. Curr. Pharm. Des. 2004, 10, 1011–1033. [Google Scholar] [CrossRef] [PubMed]
- Hill, R.G.; Richards, D. Drug Discovery and Development E-Book: Technology in Transition; Elsevier Health Sciences: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Durrant, J.D.; McCammon, J.A. Molecular dynamics simulations and drug discovery. BMC Biol. 2011, 9, 71. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Caflisch, A. Molecular dynamics in drug design. Eur. J. Med. Chem. 2015, 91, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Caflisch, A. The free energy landscape of small molecule unbinding. PLoS Comput. Biol. 2011, 7, e1002002. [Google Scholar] [CrossRef] [PubMed]
- Labanowski, J.K.; Andzelm, J.W. Density Functional Methods in Chemistry; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Banegas-Luna, A.-J.; Cerón-Carrasco, J.P.; Pérez-Sánchez, H. A review of ligand-based virtual screening web tools and screening algorithms in large molecular databases in the age of big data. Future Med. Chem. 2018, 10, 2641–2658. [Google Scholar] [CrossRef] [PubMed]
- Hasan, A.S.; Mohammed, F.Q.; Takz, M.M. Design and synthesis of graphene oxide-based glass substrate and its antimicrobial activity against MDR Bacterial Pathogens. J. Mech. Eng. Res. Dev. 2020, 43, 11–17. [Google Scholar]
- Honarparvar, B.; Govender, T.; Maguire, G.E.; Soliman, M.E.; Kruger, H.G. Integrated approach to structure-based enzymatic drug design: Molecular modeling, spectroscopy, and experimental bioactivity. Chem. Rev. 2014, 114, 493–537. [Google Scholar] [CrossRef] [PubMed]
- Surabhi, S.; Singh, B. Computer aided drug design: An overview. J. Drug Deliv. Ther. 2018, 8, 504–509. [Google Scholar] [CrossRef]
- Kore, P.P.; Mutha, M.M.; Antre, R.V.; Oswal, R.J.; Kshirsagar, S.S. Computer-aided drug design: An innovative tool for modeling. Open J. Med. Chem. 2012, 2, 139–148. [Google Scholar] [CrossRef]
- Baig, M.H.; Ahmad, K.; Roy, S.; Ashraf, J.M.; Adil, M.; Siddiqui, M.H.; Khan, S.; Kamal, M.A.; Provazník, I.; Choi, I. Computer aided drug design: Success and limitations. Curr. Pharm. Des. 2016, 22, 572–581. [Google Scholar] [CrossRef] [PubMed]
- Sohraby, F.; Bagheri, M.; Aryapour, H. Performing an in silico repurposing of existing drugs by combining virtual screening and molecular dynamics simulation. In Computational Methods for Drug Repurposing; Springer: Berlin/Heidelberg, Germany, 2019; pp. 23–43. [Google Scholar]
- Lima, A.N.; Philot, E.A.; Trossini, G.H.G.; Scott, L.P.B.; Maltarollo, V.G.; Honorio, K.M. Use of machine learning approaches for novel drug discovery. Expert Opin. Drug Discov. 2016, 11, 225–239. [Google Scholar] [CrossRef] [PubMed]
- Coley, C.W.; Green, W.H.; Jensen, K.F. Machine learning in computer-aided synthesis planning. Acc. Chem. Res. 2018, 51, 1281–1289. [Google Scholar] [CrossRef] [PubMed]
- Klambauer, G.; Hochreiter, S.; Rarey, M. Machine Learning in Drug Discovery. J. Chem. Inf. Model. 2019, 59, 945–946. [Google Scholar] [CrossRef]
- Carpenter, K.A.; Huang, X. Machine learning-based virtual screening and its applications to Alzheimer’s drug discovery: A review. Curr. Pharm. Des. 2018, 24, 3347–3358. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tan, J.; Han, D.; Zhu, H. From machine learning to deep learning: Progress in machine intelligence for rational drug discovery. Drug Discov. Today 2017, 22, 1680–1685. [Google Scholar] [CrossRef] [PubMed]
- Bohr, H. Drug discovery and molecular modeling using artificial intelligence. In Artificial Intelligence in Healthcare; Elsevier: Amsterdam, The Netherlands, 2020; pp. 61–83. [Google Scholar]
- Krishnan, S.R.; Bung, N.; Bulusu, G.; Roy, A. Accelerating de novo drug design against novel proteins using deep learning. J. Chem. Inf. Model. 2021, 61, 621–630. [Google Scholar] [CrossRef] [PubMed]
- Gawehn, E.; Hiss, J.A.; Schneider, G. Deep learning in drug discovery. Mol. Inform. 2016, 35, 3–14. [Google Scholar] [CrossRef]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar] [CrossRef] [PubMed]
- Mendolia, I.; Contino, S.; Perricone, U.; Ardizzone, E.; Pirrone, R. Convolutional architectures for virtual screening. BMC Bioinform. 2020, 21, 310. [Google Scholar] [CrossRef] [PubMed]
- Gimeno, A.; Ojeda-Montes, M.J.; Tomás-Hernández, S.; Cereto-Massagué, A.; Beltrán-Debón, R.; Mulero, M.; Pujadas, G.; Garcia-Vallvé, S. The light and dark sides of virtual screening: What is there to know? Int. J. Mol. Sci. 2019, 20, 1375. [Google Scholar] [CrossRef]
- Liu, X.; Shi, D.; Zhou, S.; Liu, H.; Liu, H.; Yao, X. Molecular dynamics simulations and novel drug discovery. Expert Opin. Drug Discov. 2018, 13, 23–37. [Google Scholar] [CrossRef] [PubMed]
- Yan, T.; Yu, L.; Zhang, N.; Peng, C.; Su, G.; Jing, Y.; Zhang, L.; Wu, T.; Cheng, J.; Guo, Q. The advanced development of molecular targeted therapy for hepatocellular carcinoma. Cancer Biol. Med. 2022, 19, 802–817. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Wang, Y.; Ma, N.; Tian, J.; Shao, Y.; Zhu, B.; Wong, Y.K.; Liang, Z.; Zou, C.; Wang, J. Target identification of natural medicine with chemical proteomics approach: Probe synthesis, target fishing and protein identification. Signal Transduct. Target. Ther. 2020, 5, 72. [Google Scholar] [CrossRef] [PubMed]
- Peters, M.B.; Raha, K.; Merz, K. Quantum mechanics in structure-based drug design. Curr. Opin. Drug Discov. Dev. 2006, 9, 370. [Google Scholar]
- Hassan, A.U.; Sumrra, S.H. Exploring the bioactive sites of new sulfonamide metal chelates for multi-drug resistance: An experimental versus theoretical design. J. Inorg. Organomet. Polym. Mater. 2022, 32, 513–535. [Google Scholar] [CrossRef]
- Amusengeri, A.; Tata, R.B.; Bishop, Ö.T. Understanding the pyrimethamine drug resistance mechanism via combined molecular dynamics and dynamic residue network analysis. Molecules 2020, 25, 904. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Guvench, O. Molecular mechanics. Curr. Pharm. Des. 2014, 20, 3281–3292. [Google Scholar] [CrossRef] [PubMed]
- Shoichet, B.K. Virtual screening of chemical libraries. Nature 2004, 432, 862–865. [Google Scholar] [CrossRef] [PubMed]
- Sliwoski, G.; Kothiwale, S.; Meiler, J.; Lowe, E.W. Computational methods in drug discovery. Pharmacol. Rev. 2014, 66, 334–395. [Google Scholar] [CrossRef] [PubMed]
- Hoque, I.; Chatterjee, A.; Bhattacharya, S.; Biswas, R. An approach of computer-aided drug design (CADD) tools for in silico pharmaceutical drug design and development. Int. J. Adv. Res. Biol. Sci. 2017, 4, 60–71. [Google Scholar] [CrossRef]
- Dos Santos Nascimento, I.J.; De Aquino, T.M.; Da Silva-Júnior, E.F. Drug repurposing: A strategy for discovering inhibitors against emerging viral infections. Curr. Med. Chem. 2021, 28, 2887–2942. [Google Scholar] [CrossRef] [PubMed]
- Yadava, U. Search algorithms and scoring methods in protein-ligand docking. Endocrinol. Metab. Int. J. 2018, 6, 359–367. [Google Scholar] [CrossRef]
- Melo-Filho, C.C.; Braga, R.C.; Andrade, C.H. 3D-QSAR approaches in drug design: Perspectives to generate reliable CoMFA models. Curr. Comput. Aided Drug Des. 2014, 10, 148–159. [Google Scholar] [CrossRef] [PubMed]
- Verma, J.; Khedkar, V.M.; Coutinho, E.C. 3D-QSAR in drug design—A review. Curr. Top. Med. Chem. 2010, 10, 95–115. [Google Scholar] [CrossRef] [PubMed]
- Cherkasov, A.; Muratov, E.N.; Fourches, D.; Varnek, A.; Baskin, I.; Cronin, M.; Dearden, J.; Gramatica, P.; Martin, Y.C.; Todeschini, R. QSAR modeling: Where have you been? Where are you going to? J. Med. Chem. 2014, 57, 4977–5010. [Google Scholar] [CrossRef] [PubMed]
- Patel, H.M.; Noolvi, M.N.; Sharma, P.; Jaiswal, V.; Bansal, S.; Lohan, S.; Kumar, S.S.; Abbot, V.; Dhiman, S.; Bhardwaj, V. Quantitative structure–activity relationship (QSAR) studies as strategic approach in drug discovery. Med. Chem. Res. 2014, 23, 4991–5007. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Sun, H.; Wang, J.; Shen, C.; Weng, G.; Chai, X.; Li, H.; Cao, D.; Hou, T. Deep learning approaches for de novo drug design: An overview. Curr. Opin. Struct. Biol. 2022, 72, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Chenthamarakshan, V.; Das, P.; Hoffman, S.; Strobelt, H.; Padhi, I.; Lim, K.W.; Hoover, B.; Manica, M.; Born, J.; Laino, T. CogMol: Target-specific and selective drug design for COVID-19 using deep generative models. Adv. Neural Inf. Process. Syst. 2020, 33, 4320–4332. [Google Scholar]
- Schneider, P.; Walters, W.P.; Plowright, A.T.; Sieroka, N.; Listgarten, J.; Goodnow, R.A.; Fisher, J.; Jansen, J.M.; Duca, J.S.; Rush, T.S. Rethinking drug design in the artificial intelligence era. Nat. Rev. Drug Discov. 2020, 19, 353–364. [Google Scholar] [CrossRef] [PubMed]
- Rifaioglu, A.S.; Atas, H.; Martin, M.J.; Cetin-Atalay, R.; Atalay, V.; Doğan, T. Recent applications of deep learning and machine intelligence on in silico drug discovery: Methods, tools and databases. Brief. Bioinform. 2019, 20, 1878–1912. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Liu, T.; Baitaluk, M.; Nicola, G.; Hwang, L.; Chong, J. BindingDB in 2015: A public database for medicinal chemistry, computational chemistry and systems pharmacology. Nucleic Acids Res. 2016, 44, D1045–D1053. [Google Scholar] [CrossRef] [PubMed]
- Mouchlis, V.D.; Afantitis, A.; Serra, A.; Fratello, M.; Papadiamantis, A.G.; Aidinis, V.; Lynch, I.; Greco, D.; Melagraki, G. Advances in de novo drug design: From Conventional to Machine Learning Methods. Int. J. Mol. Sci. 2021, 22, 1676. [Google Scholar] [CrossRef] [PubMed]
- Arús-Pous, J.; Patronov, A.; Bjerrum, E.J.; Tyrchan, C.; Reymond, J.-L.; Chen, H.; Engkvist, O. SMILES-based deep generative scaffold decorator for de-novo drug design. J. Cheminform. 2020, 12, 38. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; IJzerman, A.P.; van Westen, G.J. Computational approaches for de novo drug design: Past, present, and future. Artif. Neural Netw. 2021, 2190, 139–165. [Google Scholar]
- Gentile, F.; Agrawal, V.; Hsing, M.; Ton, A.-T.; Ban, F.; Norinder, U.; Gleave, M.E.; Cherkasov, A. Deep docking: A deep learning platform for augmentation of structure based drug discovery. ACS Cent. Sci. 2020, 6, 939–949. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Engkvist, O. Has drug design augmented by artificial intelligence become a reality? Trends Pharmacol. Sci. 2019, 40, 806–809. [Google Scholar] [CrossRef]
- Klebe, G. On the validity of popular assumptions in computational drug design. J. Cheminform. 2011, 3, O18. [Google Scholar] [CrossRef]
- Renz, P.; Van Rompaey, D.; Wegner, J.K.; Hochreiter, S.; Klambauer, G. On failure modes in molecule generation and optimization. Drug Discov. Today Technol. 2019, 32–33, 55–63. [Google Scholar] [CrossRef]
- Rezić, I.; Rezić, T.; Bokić, L.J. Optimization of the TLC separation of seven amino acids. J. Planar Chromatogr. Mod. TLC 2007, 20, 173–177. [Google Scholar] [CrossRef]
- Rezić, I. Prediction of the surface tension of surfactants mixtures for detergent formulation using Design Expert software. Chem. Month. 2011, 142, 1219–1225. [Google Scholar] [CrossRef]
- Rezić, I. Optimization of ultrasonic extraction of 23 elements from cotton. Ultrason. Sonochemistry 2009, 16, 63–69. [Google Scholar] [CrossRef]
- Martinaga Pintarić, L.; Somogi Škoc, M.; Ljoljić Bilić, V.; Pokrovac, I.; Kosalec, I.; Rezić, I. Synthesis, Modification and Characterization of Antimicrobial Textile Surface Containing ZnO Nanoparticles. Polymers 2020, 12, 1210. [Google Scholar] [CrossRef]
- Rezić, I.; Kiš, A. Design of Experiment Approach to Optimize Hydrophobic Fabric Treatments. Polymers 2020, 12, 2131. [Google Scholar] [CrossRef] [PubMed]
- Rezić, I.; Majdak, M.; Ljoljić Bilić, V.; Pokrovac, I.; Martinaga, L.; Somogyi Škoc, M.; Kosalec, I. Development of Antibacterial Protective Coatings Active Against MSSA and MRSA on Biodegradable Polymers. Polymers 2021, 13, 659. [Google Scholar] [CrossRef]
- Rezić, I.; Somogyi Škoc, M.; Majdak, M.; Jurić, S.; Sopko Stracenski, K.; Vinceković, M. Functionalization of Polymer Surface with Antimicrobial Microcapsules. Polymers 2022, 14, 1961. [Google Scholar] [CrossRef]
- Rezić, I.; Somogyi Škoc, M.; Majdak, M.; Jurić, S.; Sopko Stracenski, K.; Vlahoviček-Kahlina, K.; Vinceković, M. ICP-MS Determination of Antimicrobial Metals in Microcapsules. Molecules 2022, 27, 3219. [Google Scholar] [CrossRef]
- Vukoja, D.; Vlainić, J.; Ljoljić Bilić, V.; Martinaga, L.; Rezić, I.; Brlek Gorski, D.; Kosalec, I. Innovative Insights into In Vitro Activity of Colloidal Platinum Nanoparticles against ESBL-Producing Strains of Escherichia coli and Klebsiella pneumoniae. Pharmaceutics 2022, 14, 1714. [Google Scholar] [CrossRef] [PubMed]
- Rezić, I.; Kracher, D.; Oros, D.; Mujadžić, S.; Anđelini, M.; Kurtanjek, Ž.; Ludwig, R.; Rezić, T. Application of Causality Modelling for Prediction of Molecular Properties for Textile Dyes Degradation by LPMO. Molecules 2022, 27, 6390. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, M. Molecular Dynamics Simulation of Antimicrobial Peptides and Their Interactions with Polymer Nanocomposites. J. Phys. Chem. B 2019, 123, 3101–3111. [Google Scholar]
- Chen, X.; Cheng, Y.; Huang, J. Insights into the Dispersion and Interaction of Silver Nanoparticles in Polymer Matrices Using Molecular Dynamics Simulations. ACS Appl. Nano Mater. 2020, 3, 6534–6542. [Google Scholar]
- Su, C.H.; Chen, H.L.; Ju, S.P.; Chen, H.Y.; Shih, C.W.; Pan, C.T.; You, T.D. The Mechanical Behaviors of Polyethylene/Silver Nanoparticle Composites: An Insight from Molecular Dynamics study. Sci. Rep. 2020, 10, 7600. [Google Scholar] [CrossRef] [PubMed]
- Hussain, F.; Hojjati, M.; Okamoto, M.; Gorga, R.E. Polymer-matrix nanocomposites, processing, manufacturing, and application: An overview. J Comput. Mater. 2006, 40, 1511–1575. [Google Scholar] [CrossRef]
- Ray, S.S.; Okamoto, M. Polymer/layered silicate nanocomposites: A review from preparation to processing. Prog. Polym. Sci. 2003, 28, 1539–1641. [Google Scholar]
- Ajayan, P.M.; Schadler, L.S.; Braun, P.V. Nanocomposite Science and Technology; Wiley-VCH Verlag: Weinheim, Germany, 2003. [Google Scholar]
- Alexandre, M.; Dubois, P. Polymer-layered silicate nanocomposites: Preparation, properties and uses of a new class of materials. Mater. Sci. Eng. R 2000, 28, 1–63. [Google Scholar] [CrossRef]
- Tjong, S.C. Structural and mechanical properties of polymer nanocomposites. Mater. Sci. Eng. R 2006, 53, 73–197. [Google Scholar] [CrossRef]
- Singh, S.; Sharma, P. Computational Modeling of Nanocomposite Systems for Antimicrobial Applications: A Molecular Dynamics Approach. J. Mater.Sci. 2021, 56, 13418–13430. [Google Scholar]
- Zhang, W.; Wang, L.; Zhao, X. MD Simulation Study of the Interaction Mechanism between Antimicrobial Polymers and Bacterial Cell Membranes. Biomater. Sci. 2018, 6, 3283–3292. [Google Scholar]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Truhlar, D.G. QM/MM: What Have We Learned, Where Are We, and Where Do We Go from Here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Morokuma, K. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Karelina, M.; Kulik, H.J. Systematic Quantum Mechanical Region Determination in QM/MM Simulation. J. Chem. Theory Comput. 2017, 13, 563–576. [Google Scholar] [CrossRef] [PubMed]


| Concentration of Precursor mg/L | Nanoparticle Concentration % | Frequency of Homogenizator, Hz | Time, s | Obtained Flexibility, Angle ° | |
|---|---|---|---|---|---|
| 1 | 45.0 | 0.70 | 67.5 | 2700 | 132.6 |
| 2 | 45.0 | 0.70 | 67.5 | 2700 | 126.6 |
| 3 | 45.0 | 0.70 | 67.5 | 2700 | 117.7 |
| 4 | 50.0 | 0.40 | 55.0 | 3600 | 121.7 |
| 5 | 35.9 | 0.70 | 67.5 | 2700 | 112.8 |
| 6 | 40.0 | 1.00 | 55.0 | 3600 | 130.7 |
| 7 | 45.0 | 0.70 | 67.5 | 1062 | 128.8 |
| 8 | 40.0 | 0.40 | 80.0 | 3600 | 129.3 |
| 9 | 45.0 | 0.70 | 44.7 | 2700 | 136.2 |
| 10 | 45.0 | 0.15 | 67.5 | 2700 | 129.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezić, I.; Somogyi Škoc, M. Computational Methodologies in Synthesis, Preparation and Application of Antimicrobial Polymers, Biomolecules, and Nanocomposites. Polymers 2024, 16, 2320. https://doi.org/10.3390/polym16162320
Rezić I, Somogyi Škoc M. Computational Methodologies in Synthesis, Preparation and Application of Antimicrobial Polymers, Biomolecules, and Nanocomposites. Polymers. 2024; 16(16):2320. https://doi.org/10.3390/polym16162320
Chicago/Turabian StyleRezić, Iva, and Maja Somogyi Škoc. 2024. "Computational Methodologies in Synthesis, Preparation and Application of Antimicrobial Polymers, Biomolecules, and Nanocomposites" Polymers 16, no. 16: 2320. https://doi.org/10.3390/polym16162320
APA StyleRezić, I., & Somogyi Škoc, M. (2024). Computational Methodologies in Synthesis, Preparation and Application of Antimicrobial Polymers, Biomolecules, and Nanocomposites. Polymers, 16(16), 2320. https://doi.org/10.3390/polym16162320






