Multiscale Modeling of Vinyl-Addition Polynorbornenes: The Effect of Stereochemistry
Abstract
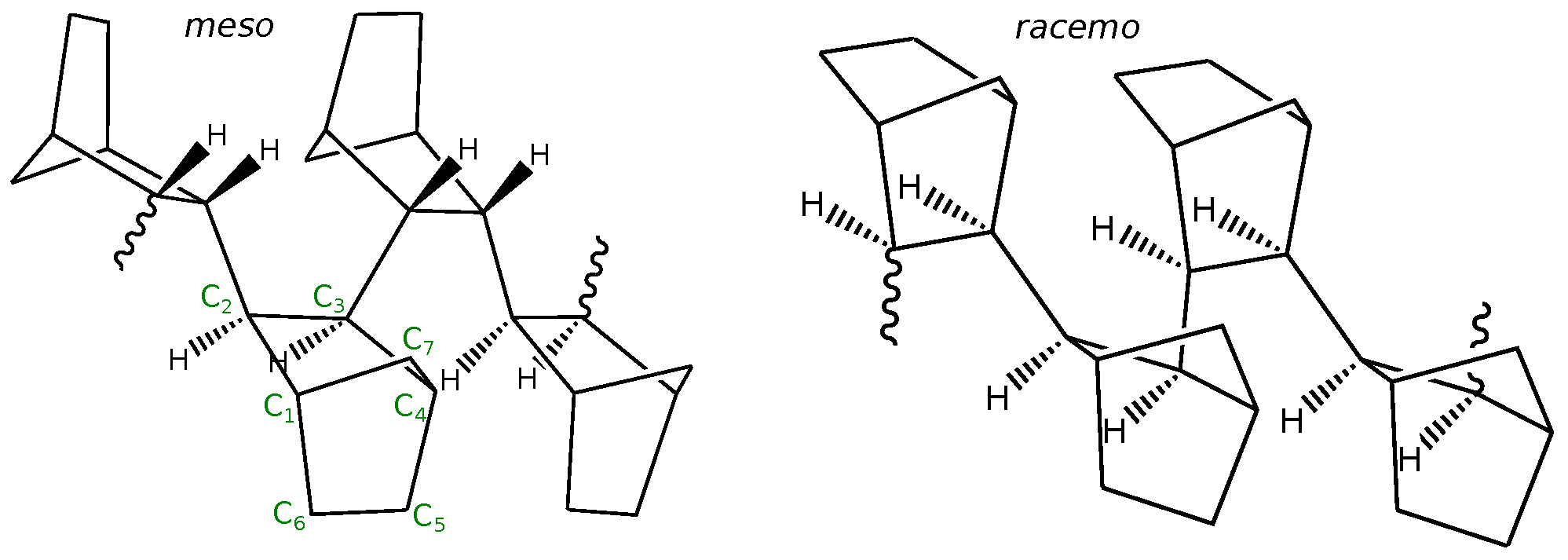
1. Introduction
2. Materials and Methods
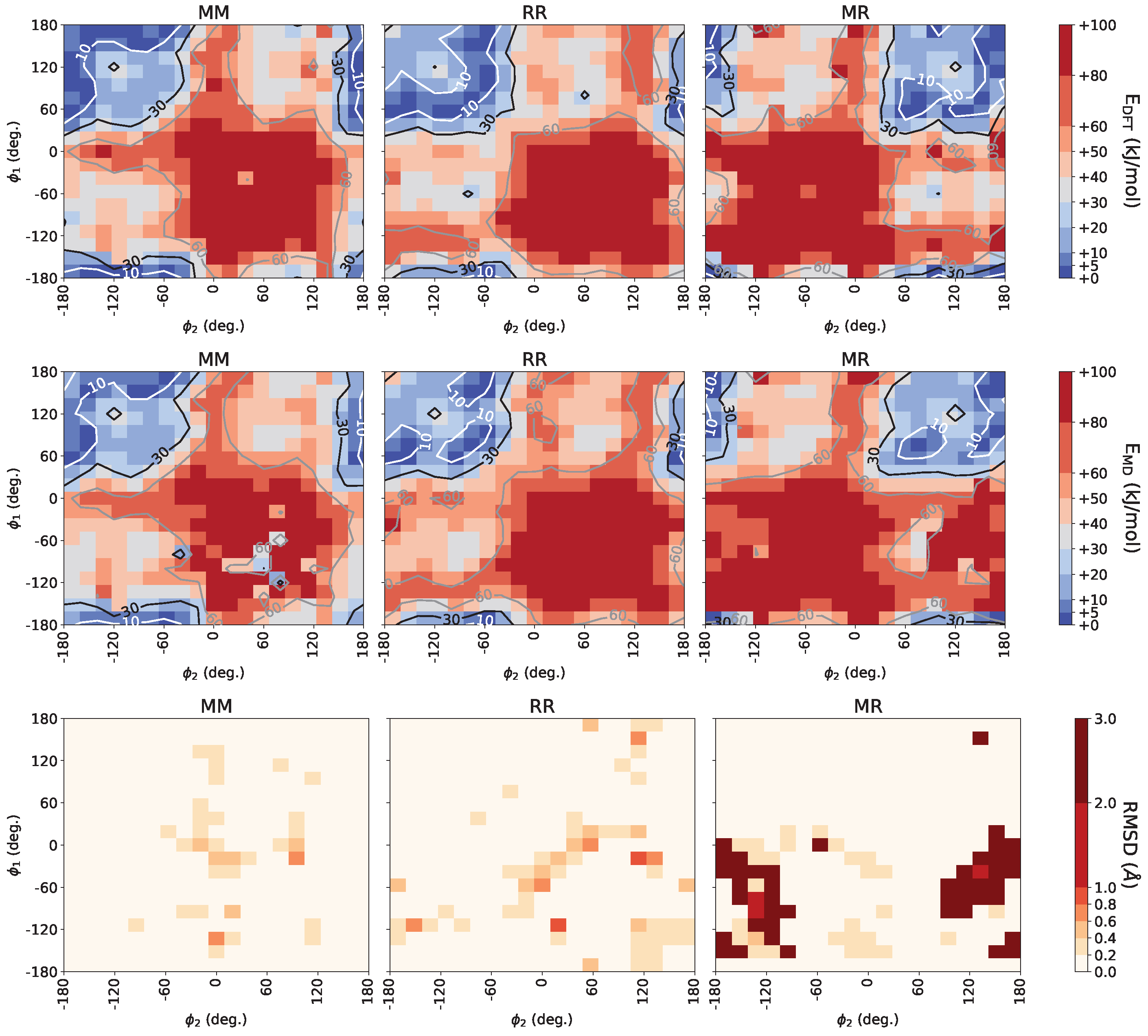
2.1. Density Functional Theory
2.2. Molecular Dynamics Simulations
| (non-bonded) | ||||||
| A (kJ/mol) | B (nm−1) | C (nm6·kJ/mol) | ||||
| C-C | ||||||
| C-H | ||||||
| H-H | ||||||
| (bond-stretching) | ||||||
| (nm) | (nm2·kJ/mol) | |||||
| C-C | 0.153 | 224,262.4 | ||||
| C-H | 0.104 | 284,512.0 | ||||
| (angle-bending) | ||||||
| (deg.) | (rad2·kJ/mol) | |||||
| C-C-C | 113.7 | 488.273 | ||||
| C-C-H | 109.2 | 313.800 | ||||
| H-C-H | 106.0 | 276.144 | ||||
| (dihedral rotation) | ||||||
(kJ/mol) | (deg.) | |||||
| C-C-C-C | 0.9791 | 0.4017 | 1.7154 | 0 | 0 | 0 |
| C-C-C-H | 0 | 0 | 0.7406 | 0 | 0 | 0 |
| H-C-C-H | 0 | 0 | 0.6904 | 0 | 0 | 0 |
| C2-C3-C2-C3 (m) | −1.3072 | 0.9035 | −3.2567 | −159.0 | 8.6 | −4.3 |
| C2-C3-C2-C3 (r) | 3.2241 | −1.2080 | −2.2806 | −0.9 | 180.0 | 1.0 |
3. Results
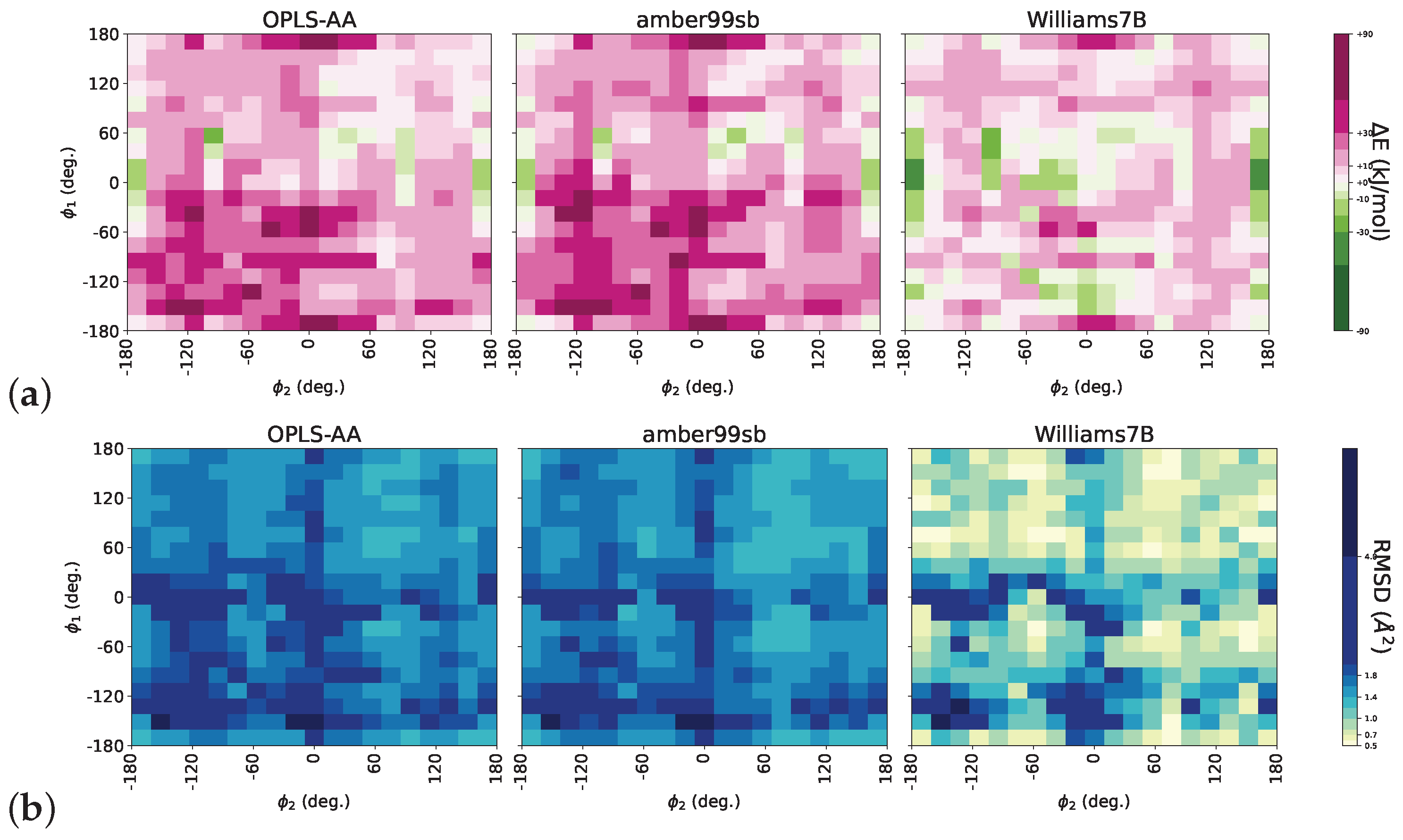
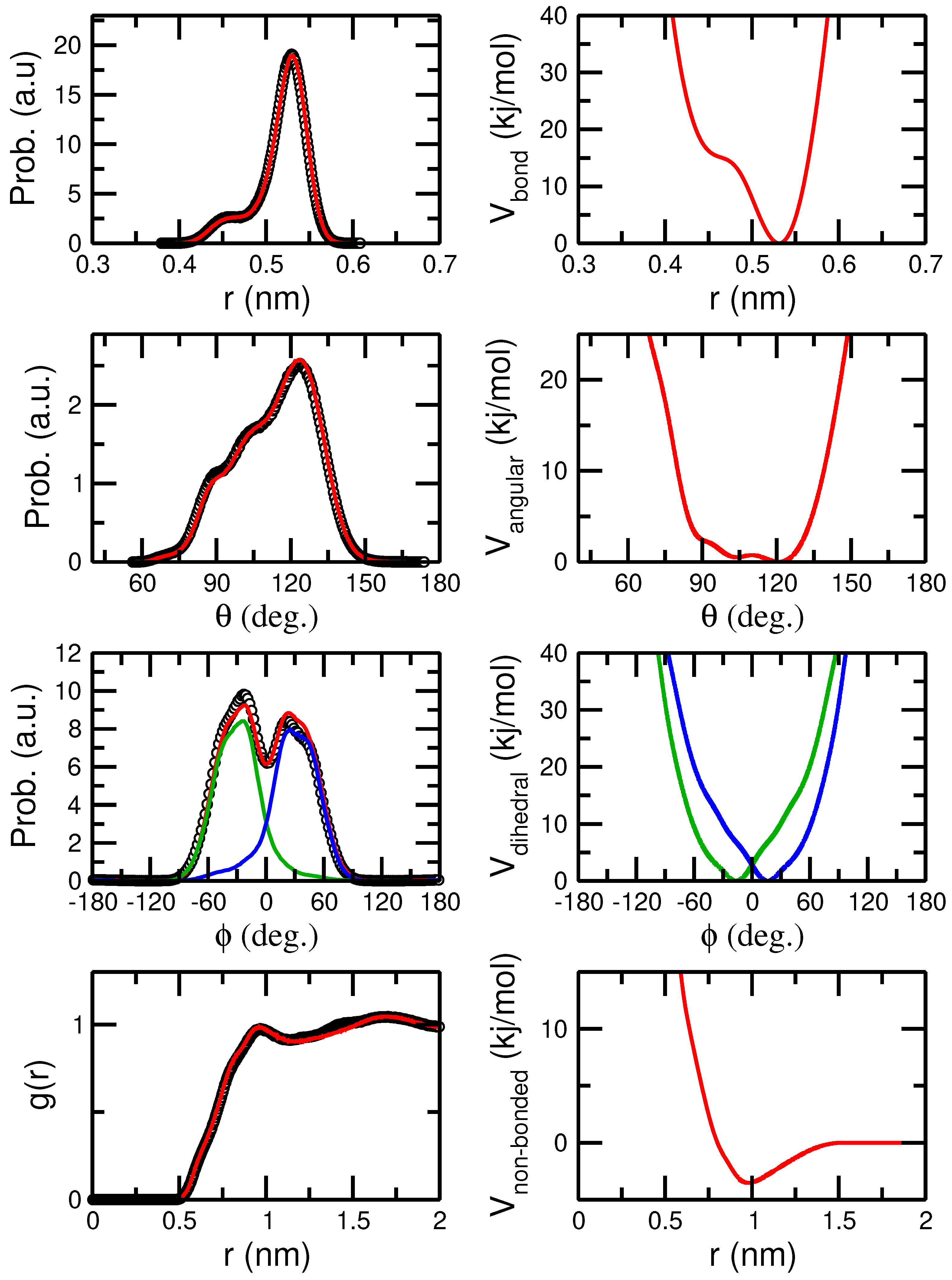
3.1. Force Field Optimization
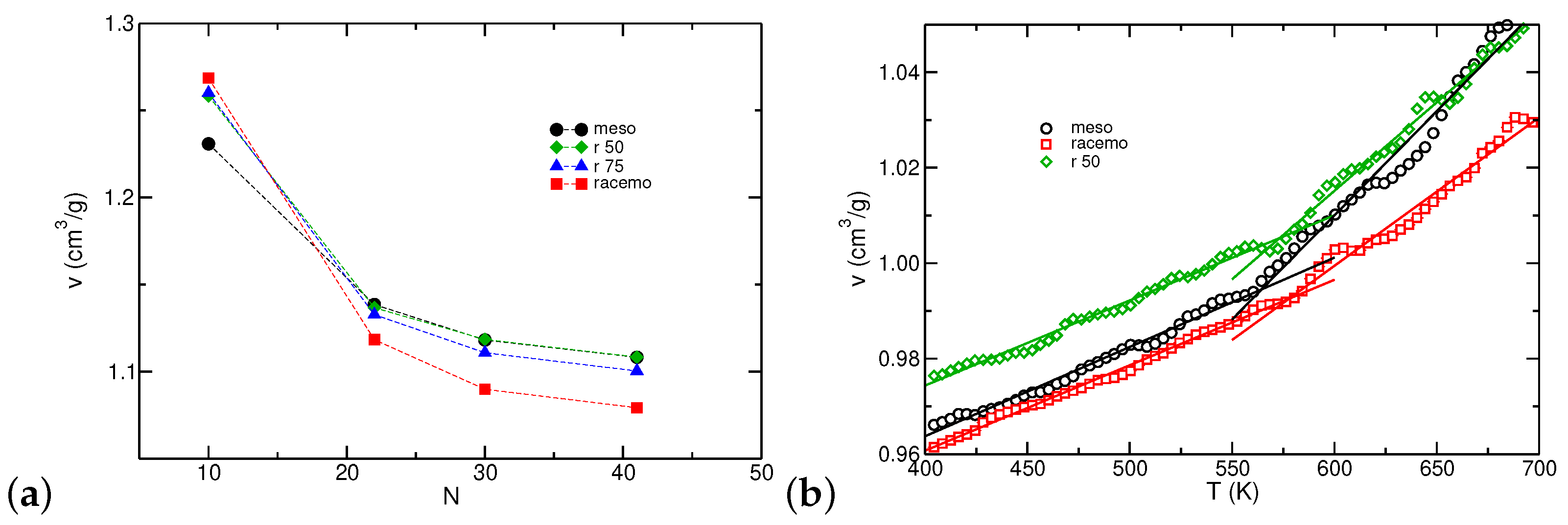
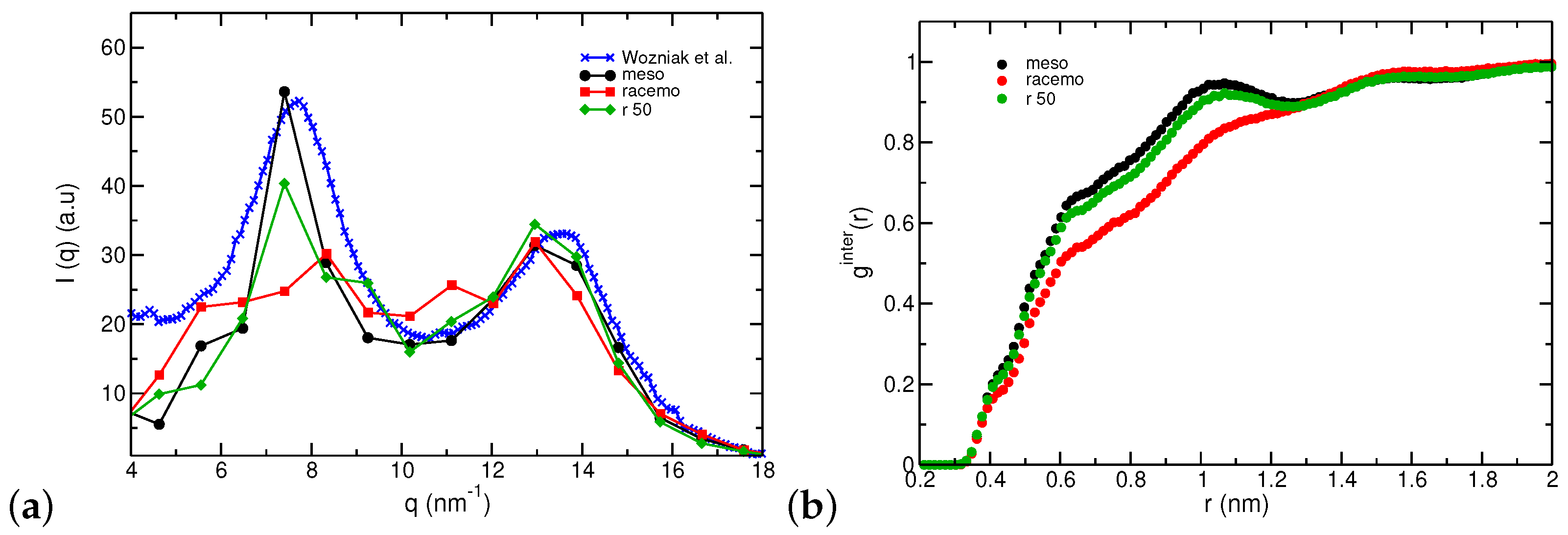
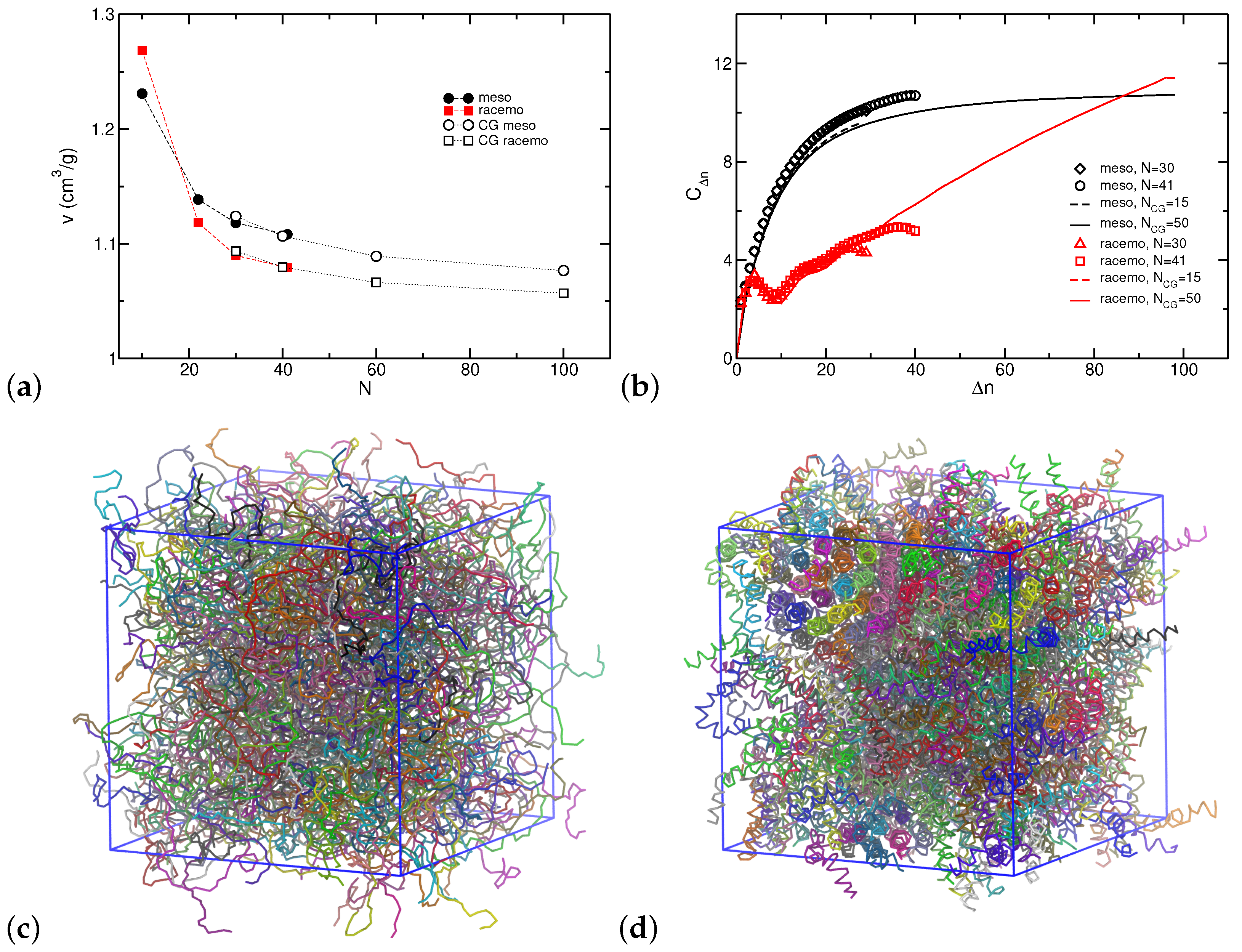
3.2. Thermodynamic and Structural Properties
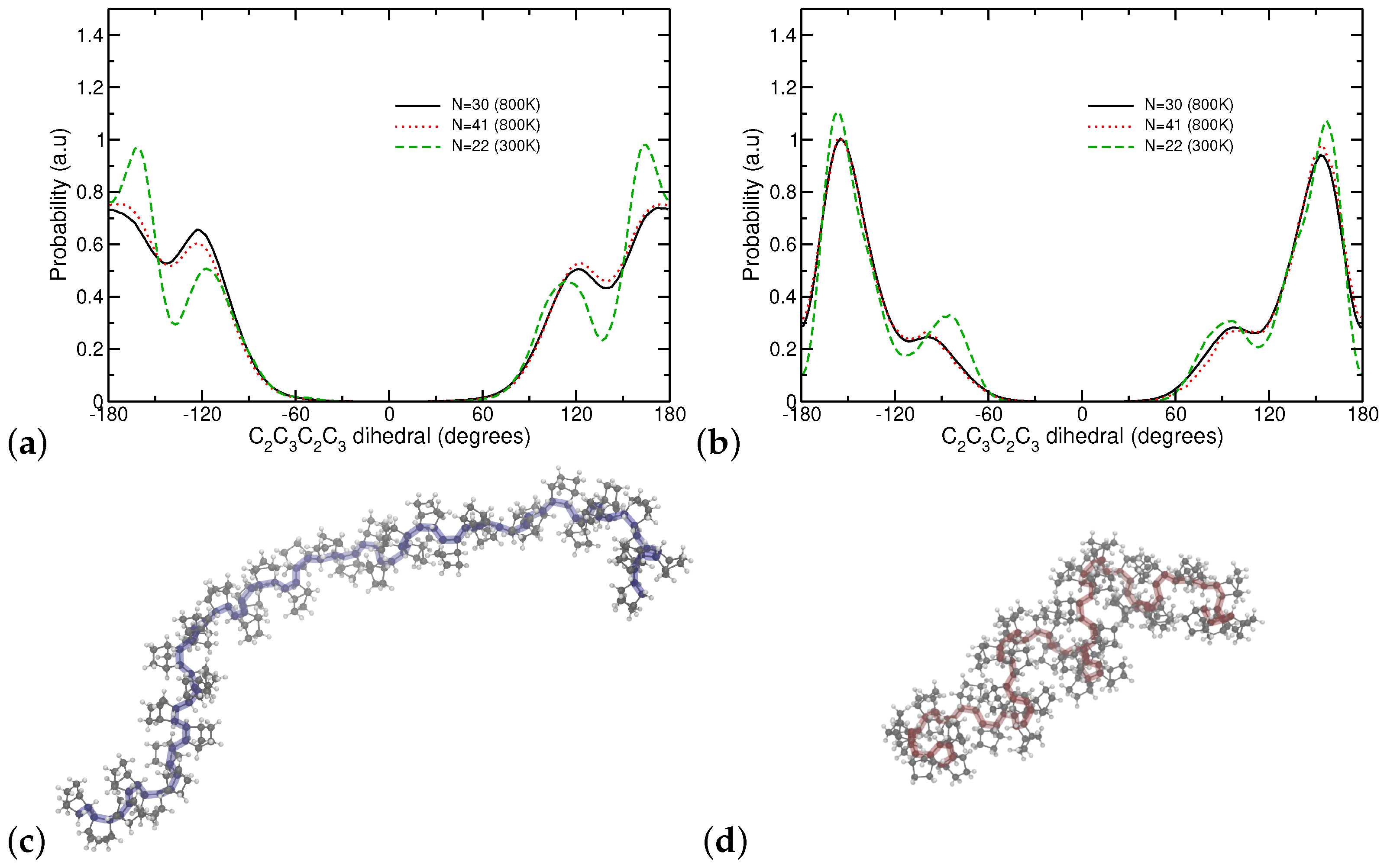
3.3. Chain Conformations
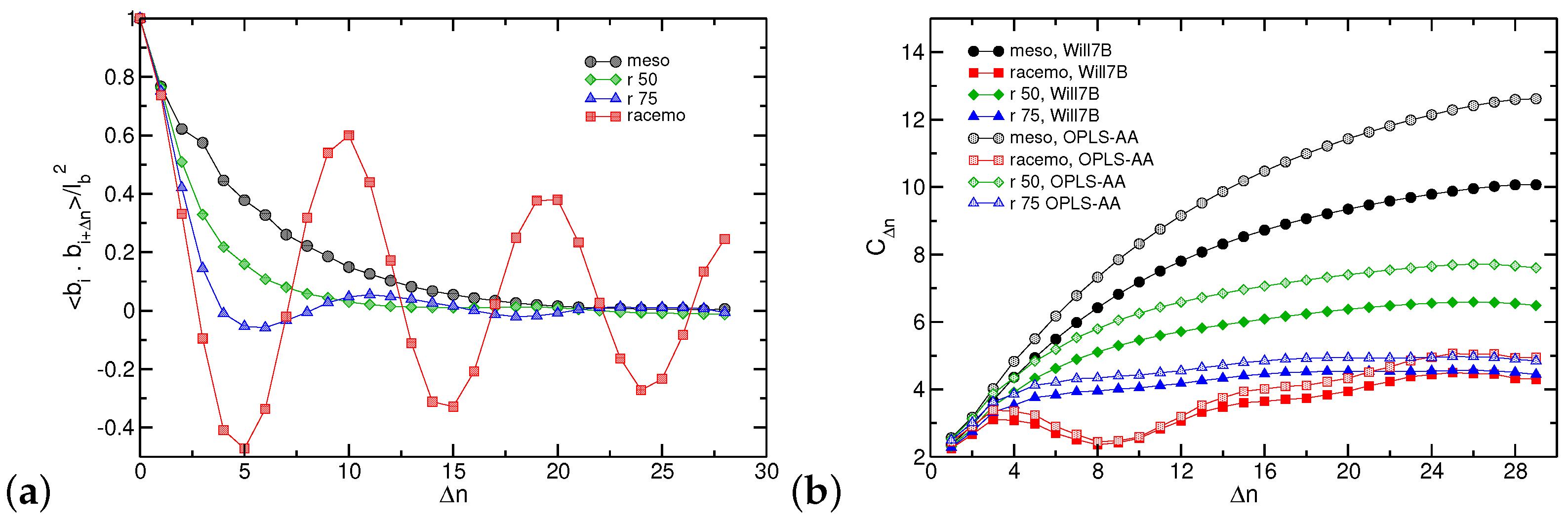
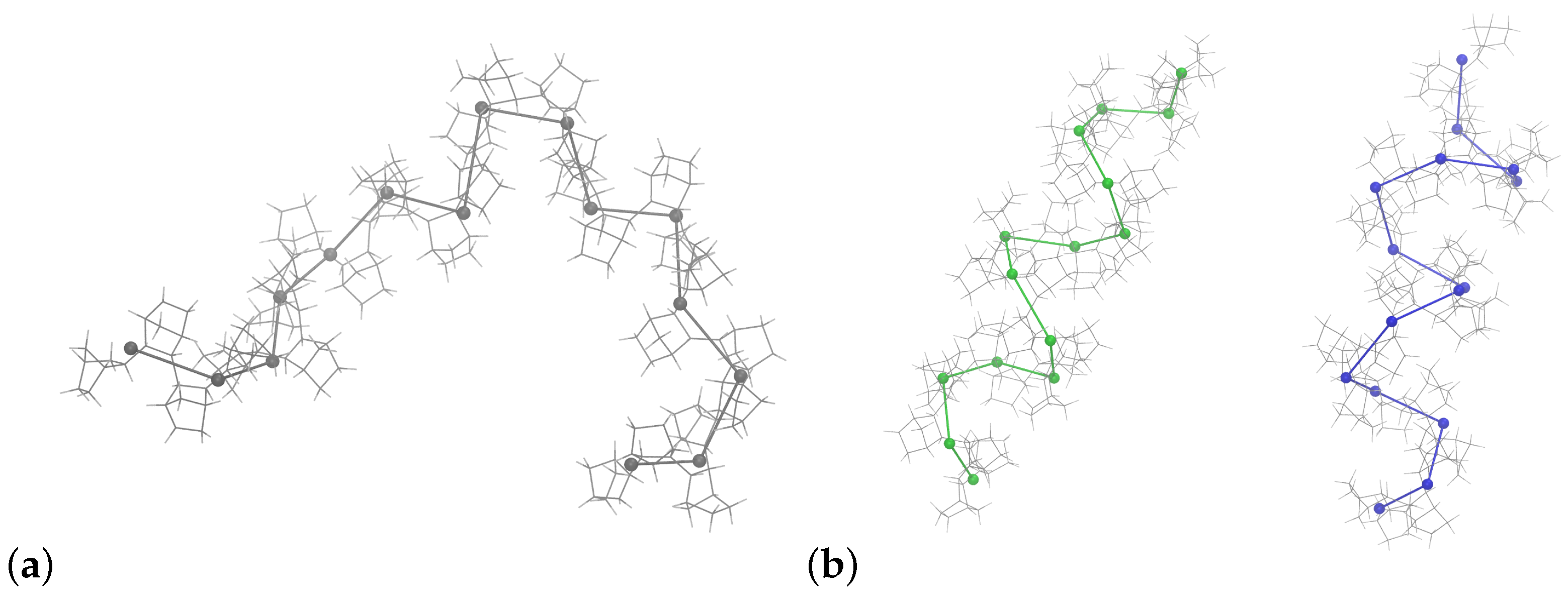
3.4. Coarse-Grained Model
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AA | All-atom |
| CG | Coarse-grained |
| DFT | Density functional theory |
| MD | Molecular dynamics |
| PNB | Vinyl-addition polynorbornene |
| RIS | Rotational isomeric state |
| Glass transition temperature |
References
- Janiak, C.; Lassahn, P.G. Metal catalysts for the vinyl polymerization of norbornene. J. Mol. Catal. A Chem. 2001, 166, 193–209. [Google Scholar] [CrossRef]
- Blank, F.; Janiak, C. Metal catalysts for the vinyl/addition polymerization of norbornene. Coord. Chem. Rev. 2009, 253, 827–861. [Google Scholar] [CrossRef]
- Ma, R.; Hou, Y.; Gao, J.; Bao, F. Recent Progress in the Vinylic Polymerization and Copolymerization of Norbornene Catalyzed by Transition Metal Catalysts. Polym. Rev. 2009, 49, 249–287. [Google Scholar] [CrossRef]
- Song, X.; Cao, L.; Tanaka, R.; Shiono, T.; Cai, Z. Optically Transparent Functional Polyolefin Elastomer with Excellent Mechanical and Thermal Properties. ACS Macro Lett. 2019, 8, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jeong, Y.L.; Love, C.; Stretz, H.A.; Stein, G.E.; Long, B.K. Design, synthesis, and characterization of vinyl-addition polynorbornenes with tunable thermal properties. Polym. Chem. 2021, 12, 5831–5841. [Google Scholar] [CrossRef]
- Gringolts, M.; Bermeshev, M.; Yampolskii, Y.; Starannikova, L.; Shantarovich, V.; Finkelshtein, E. New High Permeable Addition Poly(tricyclononenes) with Si(CH3)3 Side Groups. Synthesis, Gas Permeation Parameters, and Free Volume. Macromolecules 2010, 43, 7165–7172. [Google Scholar] [CrossRef]
- Finkelshtein, E.S.; Bermeshev, M.V.; Gringolts, M.L.; Starannikova, L.; Yampolskii, Y.P. Substituted polynorbornenes as promising materials for gas separation membranes. Russ. Chem. Rev. 2011, 80, 341. [Google Scholar] [CrossRef]
- Finkelshtein, E.; Gringolts, M.; Bermeshev, M.; Chapala, P.; Rogan, Y. Polynorbornenes. In Membrane Materials for Gas and Vapor Separation: Synthesis and Application of Silicon-Containing Polymers; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 143–221. [Google Scholar]
- Dujardin, W.; Van Goethem, C.; Steele, J.A.; Roeffaers, M.; Vankelecom, I.F.; Koeckelberghs, G. Polyvinylnorbornene gas separation membranes. Polymers 2019, 11, 704. [Google Scholar] [CrossRef]
- Wozniak, A.I.; Bermesheva, E.V.; Andreyanov, F.A.; Borisov, I.L.; Zarezin, D.P.; Bakhtin, D.S.; Gavrilova, N.N.; Ilyasov, I.R.; Nechaev, M.S.; Asachenko, A.F.; et al. Modifications of addition poly (5-vinyl-2-norbornene) and gas-transport properties of the obtained polymers. React. Funct. Polym. 2020, 149, 104513. [Google Scholar] [CrossRef]
- Wang, X.; Wilson, T.J.; Alentiev, D.; Gringolts, M.; Finkelshtein, E.; Bermeshev, M.; Long, B.K. Substituted polynorbornene membranes: A modular template for targeted gas separations. Polym. Chem. 2021, 12, 2947–2977. [Google Scholar] [CrossRef]
- Wozniak, A.I.; Bermesheva, E.V.; Borisov, I.L.; Volkov, A.V.; Petukhov, D.I.; Gavrilova, N.N.; Shantarovich, V.P.; Asachenko, A.F.; Topchiy, M.A.; Finkelshtein, E.S.; et al. Switching on/switching off solubility controlled permeation of hydrocarbons through glassy polynorbornenes by the length of side alkyl groups. J. Membr. Sci 2022, 641, 119848. [Google Scholar] [CrossRef]
- Wang, X.; Wilson, T.J.; Maroon, C.R.; Laub, J.A.; Rheingold, S.E.; Vogiatzis, K.D.; Long, B.K. Vinyl-Addition Fluoroalkoxysilyl-Substituted Polynorbornene Membranes for CO2/CH4 Separation. ACS Appl. Polym. Mater. 2022, 4, 7976–7988. [Google Scholar] [CrossRef]
- Grove, N.R.; Kohl, P.A.; Bidstrup Allen, S.A.; Jayaraman, S.; Shick, R. Functionalized polynorbornene dielectric polymers: Adhesion and mechanical properties. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 3003–3010. [Google Scholar] [CrossRef]
- Raeis-Zadeh, M.; Kohl, P.A. High-contrast, high-sensitivity aqueous base-developable polynorbornene dielectric. J. Appl. Polym. Sci. 2013, 127, 4366–4373. [Google Scholar] [CrossRef]
- He, X.; Liu, J.; Zhu, H.; Zheng, Y.; Chen, D. Novel quaternary ammonium functional addition-type norbornene copolymer as hydroxide-conductive and durable anion exchange membrane for direct methanol fuel cells. RSC Adv. 2015, 5, 63215–63225. [Google Scholar] [CrossRef]
- Mandal, M.; Huang, G.; Kohl, P.A. Anionic multiblock copolymer membrane based on vinyl addition polymerization of norbornenes: Applications in anion-exchange membrane fuel cells. J. Membr. Sci. 2019, 570, 394–402. [Google Scholar] [CrossRef]
- Mandal, M.; Huang, G.; Kohl, P.A. Highly conductive anion-exchange membranes based on cross-linked poly (norbornene): Vinyl addition polymerization. ACS Appl. Energy Mater. 2019, 2, 2447–2457. [Google Scholar] [CrossRef]
- Mandal, M.; Huang, G.; Hassan, N.U.; Mustain, W.E.; Kohl, P.A. Poly (norbornene) anion conductive membranes: Homopolymer, block copolymer and random copolymer properties and performance. J. Mater. Chem. A 2020, 8, 17568–17578. [Google Scholar] [CrossRef]
- Selhorst, R.; Gaitor, J.; Lee, M.; Markovich, D.; Yu, Y.; Treichel, M.; Olavarria Gallegos, C.; Kowalewski, T.; Kourkoutis, L.F.; Hayward, R.C.; et al. Multiblock copolymer anion-exchange membranes derived from vinyl addition polynorbornenes. ACS Appl. Energy Mater. 2021, 4, 10273–10279. [Google Scholar] [CrossRef]
- Lehmann, M.; Leonard, D.; Zheng, J.; He, L.; Tang, X.; Chen, X.C.; Lim, K.H.; Maurya, S.; Kim, Y.S.; Saito, T. Quaternized Polynorbornene Random Copolymers for Fuel Cell Devices. ACS Appl. Energy Mater. 2023, 6, 1822–1833. [Google Scholar] [CrossRef]
- Dorkenoo, K.D.; Pfromm, P.H.; Rezac, M.E. Gas transport properties of a series of highTg polynorbornenes with aliphatic pendant groups. J. Polym. Sci. Part B Polym. Phys. 1998, 36, 797–803. [Google Scholar] [CrossRef]
- Lawrence III, J.A.; Harrigan, D.J.; Maroon, C.R.; Sharber, S.A.; Long, B.K.; Sundell, B.J. Promoting acid gas separations via strategic alkoxysilyl substitution of vinyl-added poly(norbornene)s. J. Membr. Sci. 2020, 616, 118569. [Google Scholar] [CrossRef]
- He, X.; Zou, J.; Wen, Y.; Wu, B.; Zang, X.; Deng, J.; Qin, Z.; Yang, G.; Xu, J.; Chen, D. Preparation and performance of bisimidazole cationic crosslinked addition-type polynorbornene-based anion exchange membrane. Int. J. Hydrogen Energy 2022, 47, 69–80. [Google Scholar] [CrossRef]
- Goodall, B.L.; Benedikt, G.M.; McIntosh III, L.H.; Barnes, D.A. Process for Making Polymers Containing a Norbornene Repeating Unit by Addition Polymerization Using an Organo (Nickel or Palladium) Complex. U.S. Patent 5,468,819, 21 November 1995. [Google Scholar]
- Kim, E.C.; Kim, M.J.; Thi Ho, L.N.; Lee, W.; Ka, J.W.; Kim, D.G.; Shin, T.J.; Huh, K.M.; Park, S.; Kim, Y.S. Synthesis of Vinyl-Addition Polynorbornene Copolymers Bearing Pendant n-Alkyl Chains and Systematic Investigation of Their Properties. Macromolecules 2021, 54, 6762–6771. [Google Scholar] [CrossRef]
- Wilks, B.R.; Chung, W.J.; Ludovice, P.J.; Rezac, M.E.; Meakin, P.; Hill, A.J. Structural and free-volume analysis for alkyl-substituted palladium-catalyzed poly(norbornene): A combined experimental and Monte Carlo investigation. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 215–233. [Google Scholar] [CrossRef]
- Haselwander, T.F.; Heitz, W.; Krügel, S.A.; Wendorff, J.H. Polynorbornene: Synthesis, properties and simulations. Macromol. Chem. Phys. 1996, 197, 3435–3453. [Google Scholar] [CrossRef]
- Abu-Surrah, A.S.; Thewalt, U.; Rieger, B. Chiral palladium (II) complexes bearing tetradentate nitrogen ligands: Synthesis, crystal structure and reactivity towards the polymerization of norbornene. J. Organomet. Chem. 1999, 587, 58–66. [Google Scholar] [CrossRef]
- Tsujino, T.; Saegusa, T.; Furukawa, J. Polymerization of norbornene by modified Ziegler-catalysts. Makromol. Chem. 1965, 85, 71–79. [Google Scholar] [CrossRef]
- Kaminsky, W.; Bark, A.; Arndt, M. New polymers by homogenous zirconocene/aluminoxane catalysts. Makromol. Chem. Macromol. Symp. 1991, 47, 83–93. [Google Scholar] [CrossRef]
- Haselwander, T.; Heitz, W.; Maskos, M. Vinylic polymerization of norbornene by Pd (II)-catalysis in the presence of ethylene. Macromol. Rapid Commun. 1997, 18, 689–697. [Google Scholar] [CrossRef]
- Arndt, M.; Gosmann, M. Transition metal catalyzed polymerisation of norbornene. Polym. Bull. 1998, 41, 433–440. [Google Scholar] [CrossRef]
- Müller, K.; Kreiling, S.; Dehnicke, K.; Allgaier, J.; Richter, D.; Fetters, L.J.; Jung, Y.; Yoon, D.Y.; Greiner, A. Synthesis and Rheological Properties of Poly(5-n-hexylnorbornene). Macromol. Chem. Phys. 2006, 207, 193–200. [Google Scholar] [CrossRef]
- Monkenbusch, M.; Allgaier, J.; Richter, D.; Stellbrink, J.; Fetters, L.J.; Greiner, A. Nonflexible coils in solution: A neutron spin-echo investigation of alkyl-substituted polynorbornenes in tetrahydrofuran. Macromolecules 2006, 39, 9473–9479. [Google Scholar] [CrossRef]
- Arndt, M.; Engehausen, R.; Kaminsky, W.; Zoumis, K. Hydrooligomerization of cycloolefins-a view of the microstructure of polynorbornene. J. Mol. Catal. A Chem. 1995, 101, 171–178. [Google Scholar] [CrossRef]
- Ahmed, S.; Bidstrup, S.A.; Kohl, P.; Ludovice, P. Stereochemical structure-property relationships in polynorbornene from simulation. Macromol. Symp. 1998, 133, 1–10. [Google Scholar] [CrossRef]
- Deng, J.; Gao, H.; Zhu, F.; Wu, Q. Synthesis and structure of imine–N-heterocyclic carbene palladium complexes and their catalytic behavior in norbornene polymerization. Organometallics 2013, 32, 4507–4515. [Google Scholar] [CrossRef]
- Karafilidis, C.; Hermann, H.; Rufiñska, A.; Gabor, B.; Mynott, R.J.; Breitenbruch, G.; Weidenthaler, C.; Rust, J.; Joppek, W.; Brookhart, M.S.; et al. Metallocene-Catalyzed C7-Linkage in the Hydrooligomerization of Norbornene by σ-Bond Metathesis: Insight into the Microstructure of Polynorbornene. Angew. Chem. 2004, 43, 2444–2446. [Google Scholar] [CrossRef]
- Okada, M.; Nakayama, Y.; Shiono, T. Highly soluble polynorbornene prepared by an anilinonaphthoquinone-ligated nickel complex via coordination-insertion polymerization. J. Organomet. Chem. 2015, 798, 384–387. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A. DREIDING: A generic force field for molecular simulations. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Haselwander, T.F.; Heitz, W.; Krügel, S.A.; Wendorff, J. Rigid random coils: Rotationally confined chain molecules. Macromolecules 1997, 30, 5345–5351. [Google Scholar] [CrossRef]
- Krügel, S.A.; Raubacher, F.; Wendorff, J.H. Polynorbornene in the condensed state: Simulations on chain conformations and dynamics. Macromol. Chem. Phys. 1998, 199, 757–762. [Google Scholar] [CrossRef]
- Ahmed, S.; Bidstrup, S.A.; Kohl, P.; Ludovice, P. Development of a new force field for polynorbornene. J. Phys. Chem. B 1998, 102, 9783–9790. [Google Scholar] [CrossRef]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.a.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Ahmed, S.; Ludovice, P.; Kohl, P. Microstructure of 2, 3 erythro di-isotactic polynorbornene from atomistic simulation. Comput. Theor. Polym. Sci. 2000, 10, 221–233. [Google Scholar] [CrossRef]
- Chung, W.J.; Henderson, C.L.; Ludovice, P.J. RIS Model of the Helix-Kink Conformation of Erythro Diisotactic Polynobornene. Macromol. Theory Simul. 2010, 19, 421–431. [Google Scholar] [CrossRef]
- Kaminsky, W.; Noll, A. Copolymerization of norbornene and ethene with homogenous zirconocenes/methylaluminoxane catalysts. Polym. Bull. 1993, 31, 175–182. [Google Scholar] [CrossRef]
- Mi, X.; Ma, Z.; Wang, L.; Ke, Y.; Hu, Y. Homo-and Copolymerization of Norbornene and Styrene with Pd-and Ni-Based Novel Bridged Dinuclear Diimine Complexes and MAO. Macromol. Chem. Phys. 2003, 204, 868–876. [Google Scholar] [CrossRef]
- Kai, H.; Izumi, A.; Hayakawa, S.; Niemiec, J.A.; Ebner, C.; Schofield, M.; Skilskyj, D.; Rhodes, L.F. Interchain ordering structure and main chain conformation analysis of thermal stability in vinyl-addition polynorbornene. Polymer 2022, 257, 125260. [Google Scholar] [CrossRef]
- Porri, L.; Scalera, V.N.; Bagatti, M.; Famulari, A.; Meille, S.V. Titanium-Catalyzed Norbornene Oligomerization. Isolation of a Crystalline Heptamer with a 2,3-exo-Disyndiotactic Structure. Macromol. Rapid Commun. 2006, 27, 1937–1941. [Google Scholar] [CrossRef]
- Ricci, G.; Boglia, A.; Boccia, A.C.; Zetta, L.; Famulari, A.; Meille, S.V. New stereoregularity in the stereospecific polymerization of bulky strained olefins: Diheterotactic polynorbornene. Macromolecules 2008, 41, 3109–3113. [Google Scholar] [CrossRef]
- Buono, A.; Famulari, A.; Meille, S.V.; Ricci, G.; Porri, L. 2,3-exo-Disyndiotactic Polynorbornene: A crystalline polymer with tubular helical molecular structure. Macromolecules 2011, 44, 3681–3684. [Google Scholar] [CrossRef]
- Burrows, S.A.; Korotkin, I.; Smoukov, S.K.; Boek, E.; Karabasov, S. Benchmarking of molecular dynamics force fields for solid–liquid and solid–solid phase transitions in alkanes. J. Phys. Chem. B 2021, 125, 5145–5159. [Google Scholar] [CrossRef] [PubMed]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic structure calculations on workstation computers: The program system turbomole. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Valladares, D.; Yalcin, B.; Cakmak, M. Long time evolution of structural hierarchy in uniaxially stretched and retracted cross-linked natural rubber. Macromolecules 2005, 38, 9229–9242. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci 2022, 12, e1606. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on basis sets beautiful: Seasonal plantings of diffuse basis functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Klauda, J.B.; Venable, R.M.; Freites, J.A.; O’Connor, J.W.; Tobias, D.J.; Mondragon-Ramirez, C.; Vorobyov, I.; MacKerell, A.D., Jr.; Pastor, R.W. Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types. J. Phys. Chem. B 2010, 114, 7830–7843. [Google Scholar] [CrossRef] [PubMed]
- Tu, K.; Tobias, D.J.; Klein, M.L. Constant pressure and temperature molecular dynamics simulations of crystals of the lecithin fragments: Glycerylphosphorylcholine and dilauroylglycerol. J. Phys. Chem. 1995, 99, 10035–10042. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Berendsen, H.J.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Katajisto, J.; Linnolahti, M.; Haukka, M.; Pakkanen, T.A. Development of a new force field for property prediction of cyclo-olefin copolymers. J. Phys. Chem. B 2004, 108, 2168–2172. [Google Scholar] [CrossRef]
- Best, R.B.; Buchete, N.V.; Hummer, G. Are current molecular dynamics force fields too helical? Biophys. J. 2008, 95, L07–L09. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Hummer, G. Optimized molecular dynamics force fields applied to the helix- coil transition of polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef] [PubMed]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. The representation of van der Waals (vdW) interactions in molecular mechanics force fields: Potential form, combination rules, and vdW parameters. J. Am. Chem. Soc. 1992, 114, 7827–7843. [Google Scholar] [CrossRef]
- Errington, J.R.; Boulougouris, G.C.; Economou, I.G.; Panagiotopoulos, A.Z.; Theodorou, D.N. Molecular simulation of phase equilibria for water- methane and water- ethane mixtures. J. Phys. Chem. B 1998, 102, 8865–8873. [Google Scholar] [CrossRef]
- Williams, D.E. Nonbonded potential parameters derived from crystalline hydrocarbons. J. Chem. Phys. 1967, 47, 4680–4684. [Google Scholar] [CrossRef]
- Wentzel, N.; Milner, S.T. Crystal and rotator phases of n-alkanes: A molecular dynamics study. J. Chem. Phys. 2010, 132, 044901. [Google Scholar] [CrossRef] [PubMed]
- Wentzel, N.; Milner, S.T. Simulation of multiple ordered phases in C23 n-alkane. J. Chem. Phys. 2011, 134, 224504. [Google Scholar] [CrossRef]
- Wang, L.P.; Chen, J.; Van Voorhis, T. Systematic parametrization of polarizable force fields from quantum chemistry data. J. Chem. Theory Comput. 2013, 9, 452–460. [Google Scholar] [CrossRef]
- Walz, M.M.; Ghahremanpour, M.M.; Van Maaren, P.J.; Van der Spoel, D. Phase-transferable force field for alkali halides. J. Chem. Theory Comput. 2018, 14, 5933–5948. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Doxastakis, M.; Mavrantzas, V.G.; Theodorou, D.N. Detailed molecular dynamics simulation of the self-diffusion of n-alkane and cis-1,4 polyisoprene oligomer melts. J. Chem. Phys. 2002, 116, 436–446. [Google Scholar] [CrossRef]
- Brüning, R.; Samwer, K. Glass transition on long time scales. Phys. Rev. B 1992, 46, 11318. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Gee, R.H.; Boyd, R.H. Glass transition temperatures of polymers from molecular dynamics simulations. Macromolecules 1994, 27, 7781–7784. [Google Scholar] [CrossRef]
- Vollmayr, K.; Kob, W.; Binder, K. How do the properties of a glass depend on the cooling rate? A computer simulation study of a Lennard–Jones system. J. Chem. Phys. 1996, 105, 4714–4728. [Google Scholar] [CrossRef]
- Lyulin, A.V.; Balabaev, N.K.; Michels, M. Molecular-weight and cooling-rate dependence of simulated Tg for amorphous polystyrene. Macromolecules 2003, 36, 8574–8575. [Google Scholar] [CrossRef]
- Doxastakis, M.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic Monte Carlo simulation of cis-1,4 polyisoprene melts. I. Single temperature end-bridging Monte Carlo simulations. J. Chem. Phys. 2001, 115, 11339–11351. [Google Scholar] [CrossRef]
- Shahidi, N.; Chazirakis, A.; Harmandaris, V.; Doxastakis, M. Coarse-graining of polyisoprene melts using inverse Monte Carlo and local density potentials. J. Chem. Phys. 2020, 152, 124902. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Jana, P.K.; Behbahani, A.F.; Kritikos, G.; Schneider, L.; Polińska, P.; Burkhart, C.; Harmandaris, V.A.; Müller, M.; Doxastakis, M. Dynamics of Long Entangled Polyisoprene Melts via Multiscale Modeling. Macromolecules 2021, 54, 8693–8713. [Google Scholar] [CrossRef]
- Noid, W.G. Perspective: Advances, Challenges, and Insight for Predictive Coarse-Grained Models. J. Phys. Chem. B 2023, 127, 4174–4207. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.; Szukalo, R.J.; Kidder, K.M.; Lesniewski, M.C. Rigorous Progress in Coarse-Graining. Annu. Rev. Phys. Chem. 2024, 75, 21–45. [Google Scholar] [CrossRef]
- Schommers, W. Pair potentials in disordered many-particle systems: A study for liquid gallium. Phys. Rev. A 1983, 28, 3599. [Google Scholar] [CrossRef]
- Soper, A. Empirical potential Monte Carlo simulation of fluid structure. Chem. Phys. 1996, 202, 295–306. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Coarse-Graining in Polymer Simulation: From the Atomistic to the Mesoscopic Scale and Back. Chem. Phys. Chem. 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef]
- Pandey, Y.N.; Brayton, A.; Burkhart, C.; Papakonstantopoulos, G.J.; Doxastakis, M. Multiscale modeling of polyisoprene on graphite. J. Chem. Phys. 2014, 140, 054908. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Burkhart, C.; Polińska, P.; Harmandaris, V.; Doxastakis, M. Backmapping coarse-grained macromolecules: An efficient and versatile machine learning approach. J. Chem. Phys. 2020, 153, 041101. [Google Scholar] [CrossRef]
- Szukalo, R.J.; Noid, W.G. A temperature-dependent length-scale for transferable local density potentials. J. Chem. Phys. 2023, 159, 074104. [Google Scholar] [CrossRef]
- Christofi, E.; Chazirakis, A.; Chrysostomou, C.; Nicolaou, M.A.; Li, W.; Doxastakis, M.; Harmandaris, V.A. Deep convolutional neural networks for generating atomistic configurations of multi-component macromolecules from coarse-grained models. J. Chem. Phys. 2022, 157, 184903. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahidi, N.; Laub, J.A.; Vogiatzis, K.D.; Doxastakis, M. Multiscale Modeling of Vinyl-Addition Polynorbornenes: The Effect of Stereochemistry. Polymers 2024, 16, 2243. https://doi.org/10.3390/polym16162243
Shahidi N, Laub JA, Vogiatzis KD, Doxastakis M. Multiscale Modeling of Vinyl-Addition Polynorbornenes: The Effect of Stereochemistry. Polymers. 2024; 16(16):2243. https://doi.org/10.3390/polym16162243
Chicago/Turabian StyleShahidi, Nobahar, Jeffrey A. Laub, Konstantinos D. Vogiatzis, and Manolis Doxastakis. 2024. "Multiscale Modeling of Vinyl-Addition Polynorbornenes: The Effect of Stereochemistry" Polymers 16, no. 16: 2243. https://doi.org/10.3390/polym16162243
APA StyleShahidi, N., Laub, J. A., Vogiatzis, K. D., & Doxastakis, M. (2024). Multiscale Modeling of Vinyl-Addition Polynorbornenes: The Effect of Stereochemistry. Polymers, 16(16), 2243. https://doi.org/10.3390/polym16162243







