Influence of Gamma-Phase Aluminum Oxide Nanopowder and Polyester–Glass Recyclate Filler on the Destruction Process of Composite Materials Reinforced by Glass Fiber
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
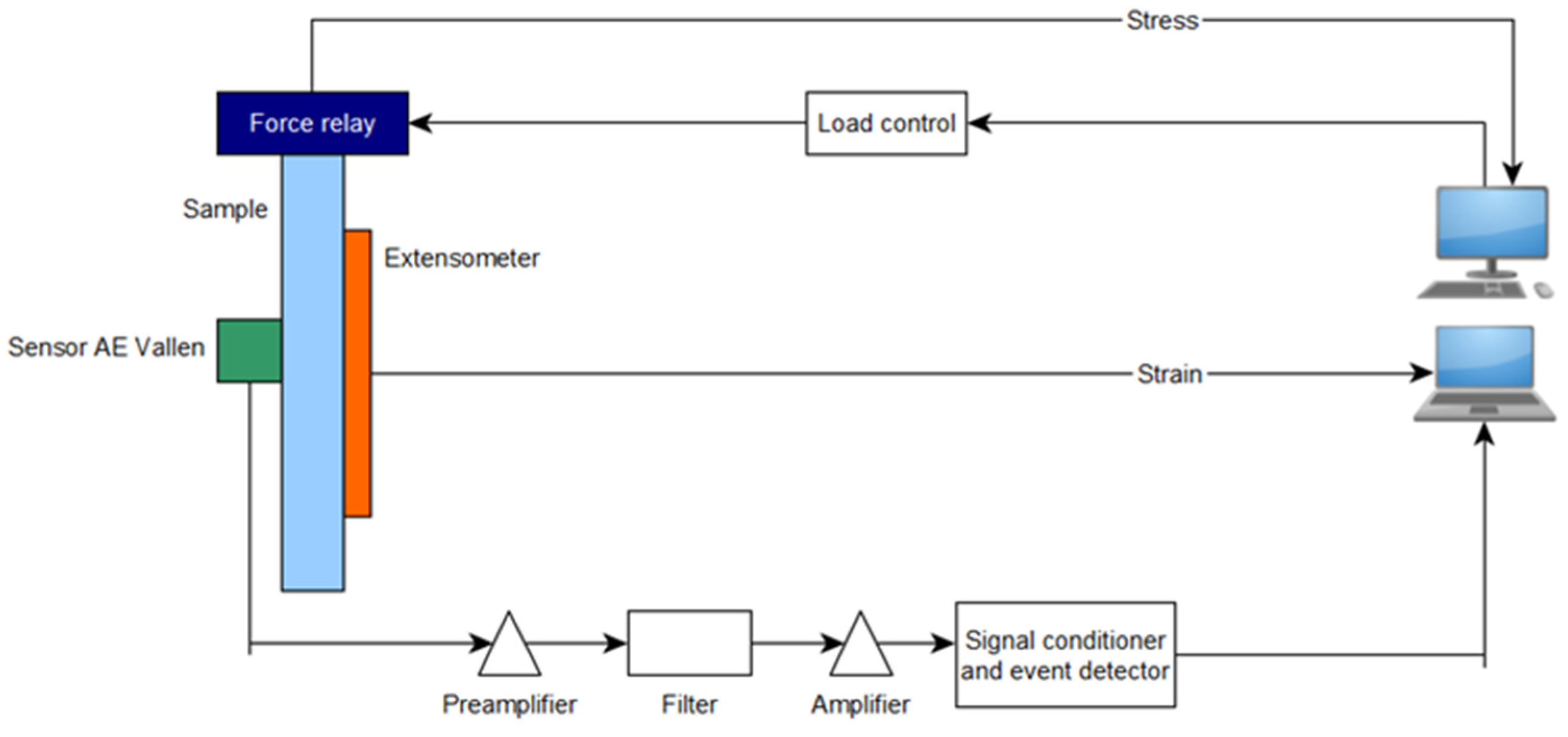
2.3. Methods
- p—probability,
- i—state.
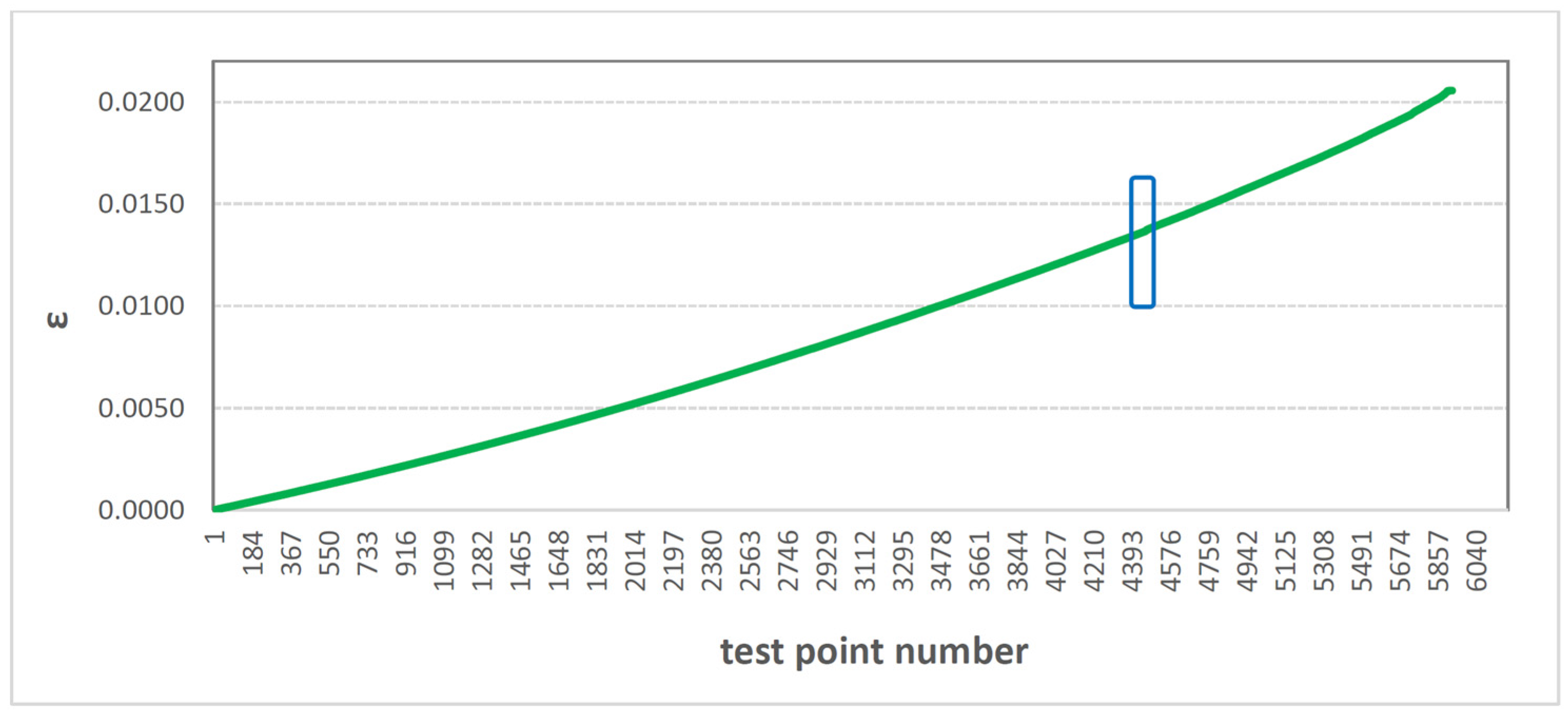
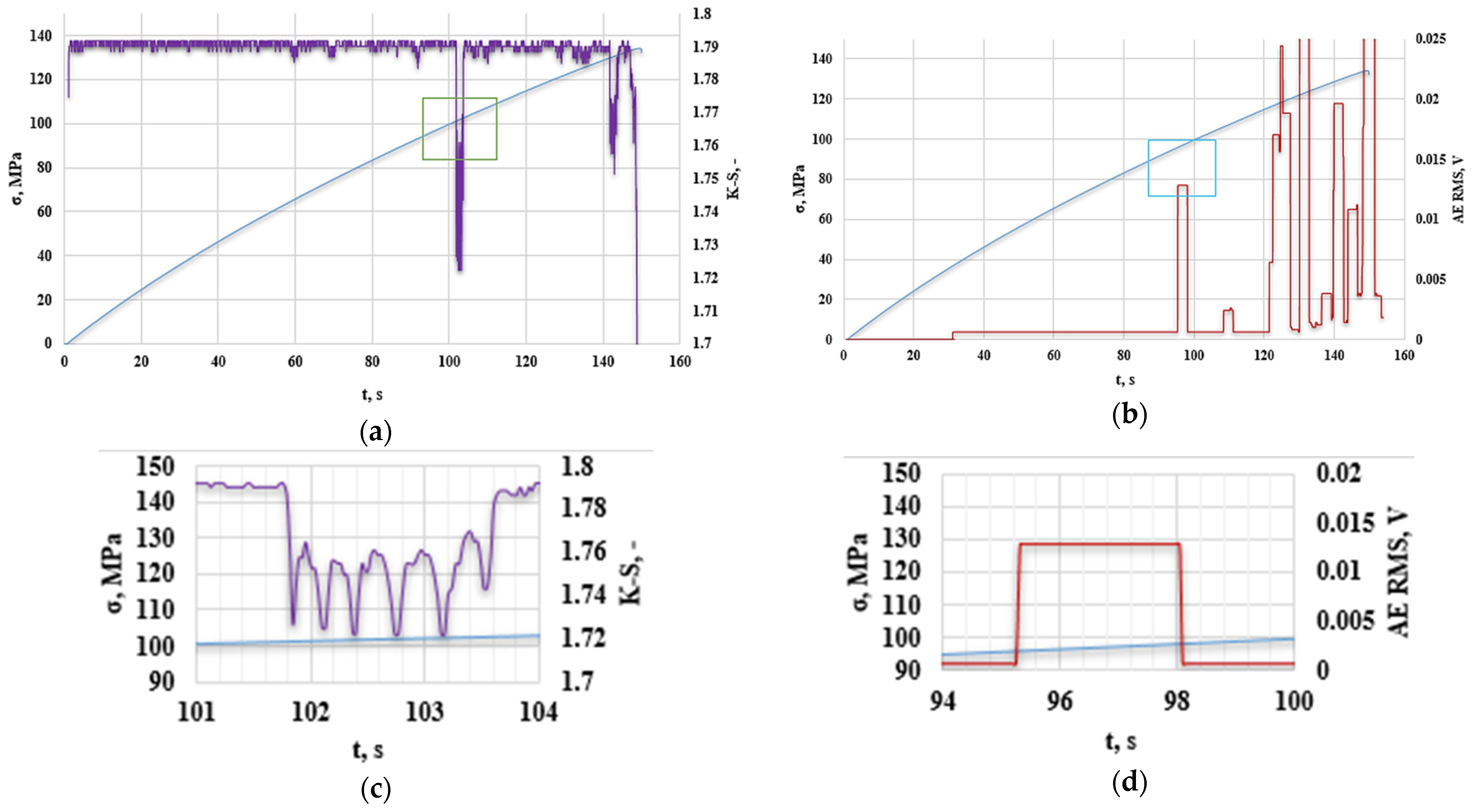
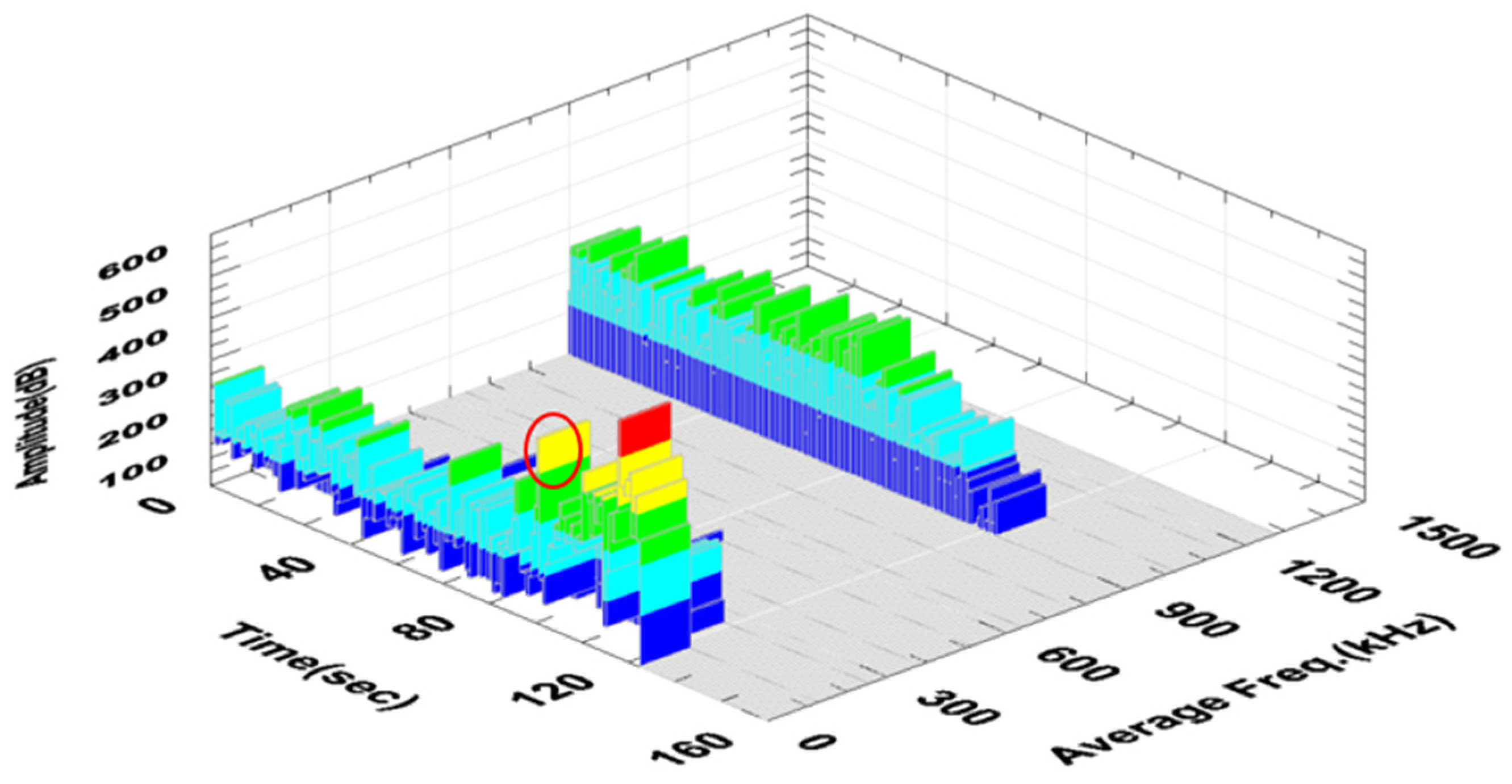
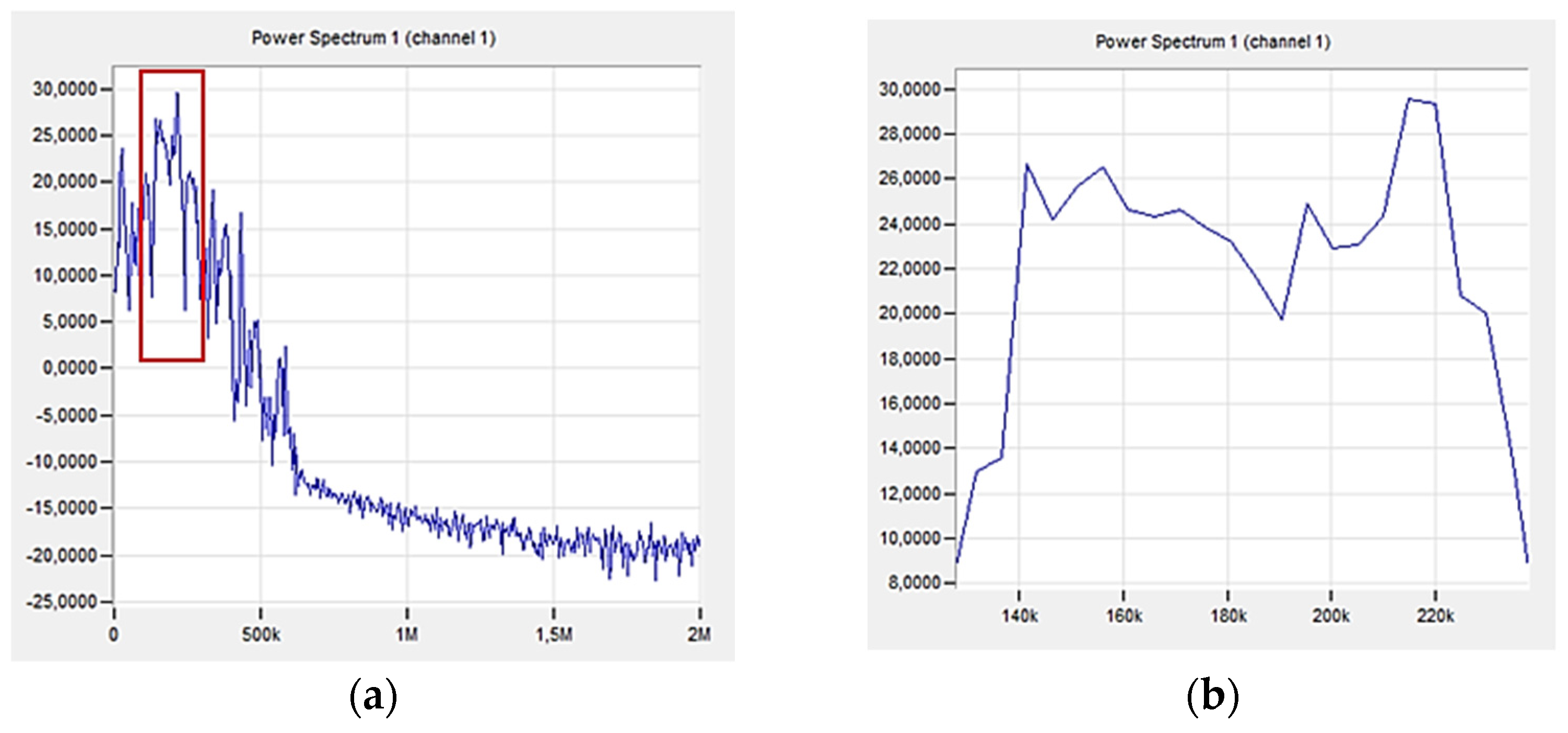
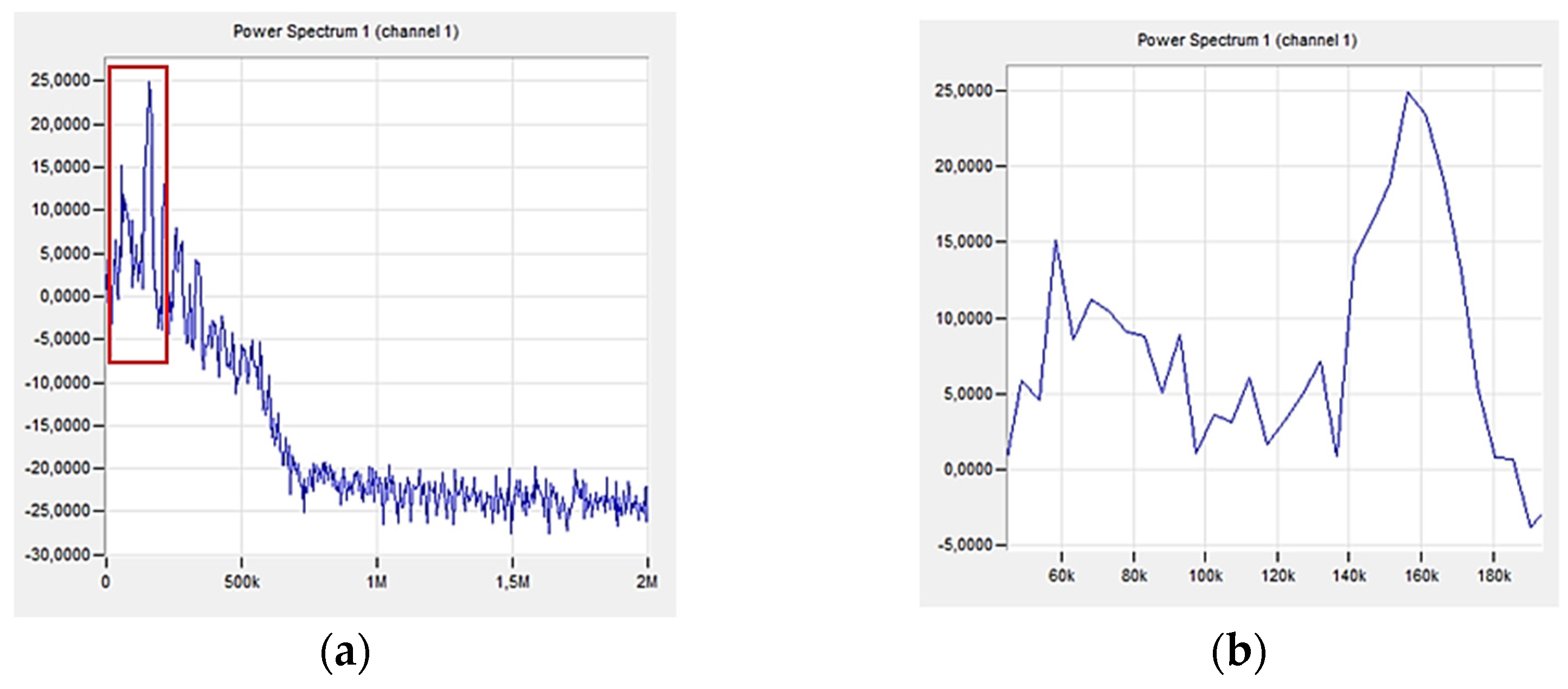
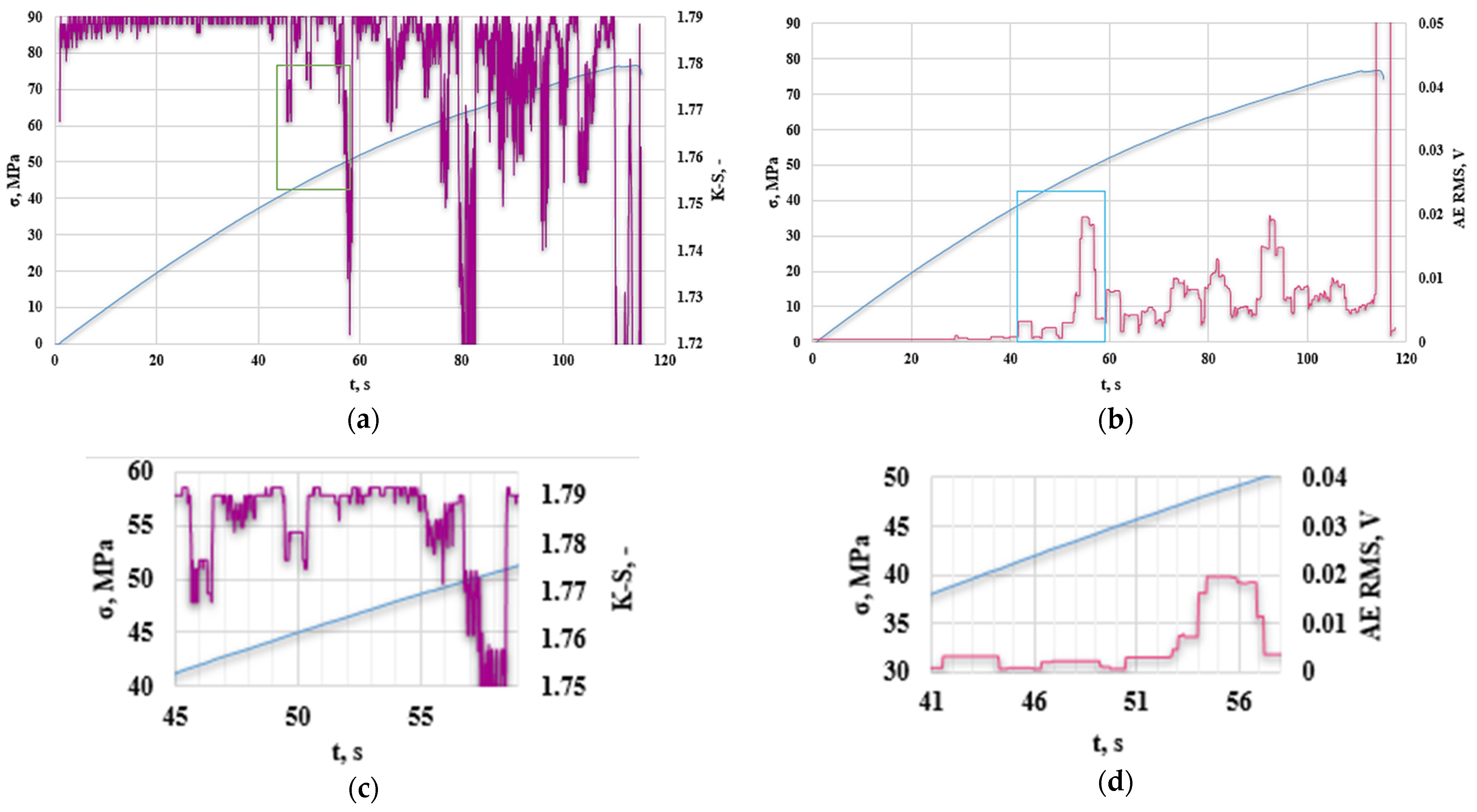
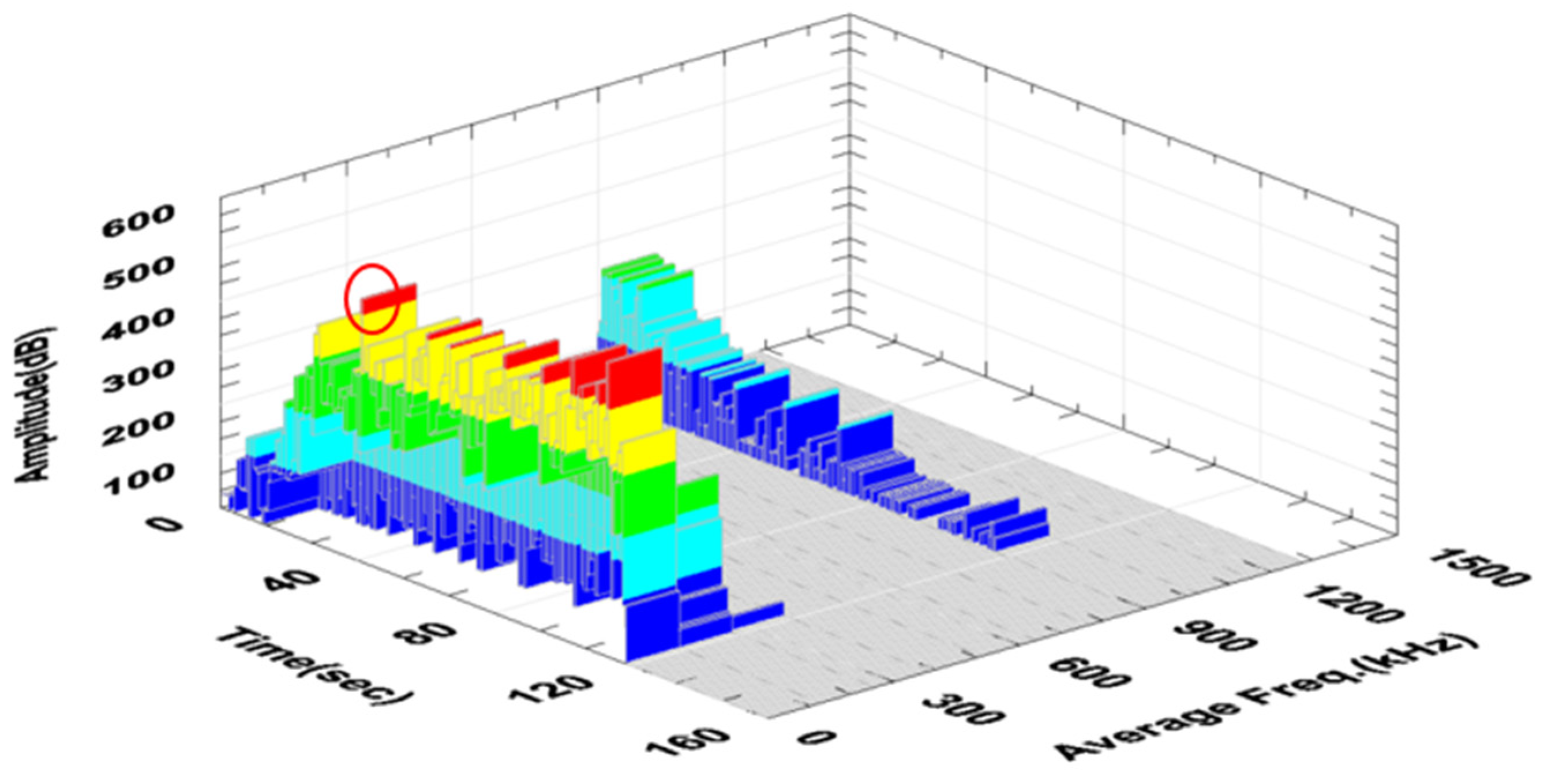
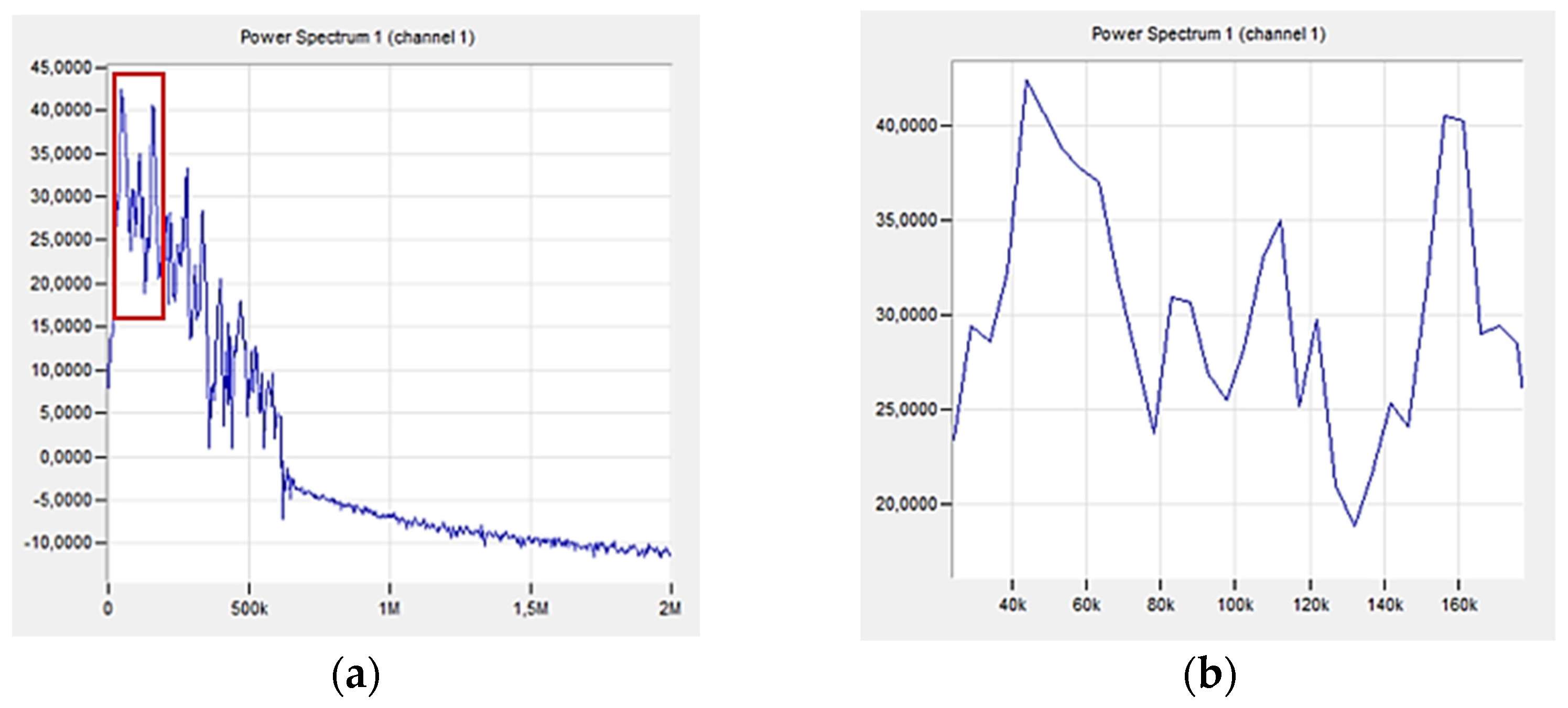
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- McConn, V.P. Launching the carbon fibre recycling industry. Reinf. Plast. 2010, 54, 33–37. [Google Scholar] [CrossRef]
- Meng, F.; McKechnie, J.; Turner, T.A.; Pickering, S.J. Energy and environmental assessment and reuse of fluidised bed recycled carbon fibres. Compos. Part A Appl. Sci. Manuf. 2017, 100, 206–214. [Google Scholar] [CrossRef]
- Veleva, V.; Bodkin, G.; Todorova, S. The need for better measurement and employee engagement to advance a circular economy: Lessons from Biogen’s “zero waste” journey. J. Clean. Prod. 2017, 154, 517–529. [Google Scholar] [CrossRef]
- Singh, S.; Ramakrishna, S.; Gupta, M.K. Towards zero waste manufacturing: A multidisciplinary review. J. Clean. Prod. 2017, 168, 1230–1243. [Google Scholar] [CrossRef]
- Kyzioł, L.; Panasiuk, K.; Barcikowski, M.; Hajdukiewicz, G. The influence of manufacturing technology on the properties of layered composites with polyester–glass recyclate additive. Prog. Rubber Plast. Recycl. Technol. 2020, 36, 18–30. [Google Scholar] [CrossRef]
- Thomason, J.; Jenkins, P.; Yang, L. Glass Fibre Strength—A Review with Relation to Composite Recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Korniejenko, K.; Kozub, B.; Bąk, A.; Balamurugan, P.; Uthayakumar, M.; Furtos, G. Tackling the Circular Economy Challenges—Composites Recycling: Used Tyres, Wind Turbine Blades, and Solar Panels. J. Compos. Sci. 2021, 5, 243. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Karl, C.W.; Gagani, A.I.; Jørgensen, J.K. Composite Material Recycling Technology—State-of-the-Art and Sustainable Development for the 2020s. J. Compos. Sci. 2021, 5, 28. [Google Scholar] [CrossRef]
- Morici, E.; Dintcheva, N.T. Recycling of Thermoset Materials and Thermoset-Based Composites: Challenge and Opportunity. Polymers 2022, 14, 4153. [Google Scholar] [CrossRef]
- Abramczyk, N.; Drewing, S.; Panasiuk, K.; Żuk, D. Application of Statistical Methods to Accurately Assess the Effect of Gamma Aluminum Oxide Nanopowder on the Hard-ness of Composite Materials with Polyester–Glass Recyclate. Materials 2022, 15, 5957. [Google Scholar] [CrossRef]
- Panasiuk, K.; Dudzik, K.; Haj-dukiewicz, G.; Abramczyk, N. Acoustic Emission and K-S Metric Entropy as Methods to Analyze the Influence of Gamma-Aluminum Oxide Nanopowder on the Destruction Process of GFRP Composite Materials. Materials 2023, 16, 7334. [Google Scholar] [CrossRef] [PubMed]
- Krlikowski, W.; Rosaniec, Z. Nanokompozyty polimerowe. Composites 2004, 4, 3–16. [Google Scholar]
- Fusco, R.; Moretti, L.; Fiore, N.; D’andrea, A. Behavior Evaluation of Bituminous Mixtures Reinforced with Nano-Sized Additives: A Review. Sustainability 2020, 12, 8044. [Google Scholar] [CrossRef]
- Spaswka, E.; Rudnik, E.; Kijeński, J. Biodegradowalne nanokompozyty polimerowe. Polimery 2006, 51, 617–626. [Google Scholar]
- No, M.A. Polymer/clay nanocomposites. Polimery 2002, 47, 326–331. [Google Scholar]
- Yariv, S.; Cross, H. Organo-Clay Complexes and Intercalations; Dekker: St. Louis, MO, USA, 2003. [Google Scholar]
- Okamoto, M. Polymer/Layered Silicate Nanocomposites; RAPRA Technology: Shrewsbury, UK, 2003. [Google Scholar]
- Rabek, J.F. Współczesna Wiedza o Polimerach; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2008. [Google Scholar]
- Barton, J.; Niemczyk, A.; Czaja, K.; Korach, Ł.; Sacher-Majewska, B. Kompozyty, biokompozyty i nanokompozyty polimerowe. Otrzymywanie, skład, właściwości I kierunkizastosowań. Chemik 2014, 68, 280–287. [Google Scholar]
- Yousri, O.M.; Abdellatif, M.H.; Bassioni, G. Effect of Al2O3 Nanoparticles on the Mechanical and Physical Properties of Epoxy Composite. Arab. J. Sci. Eng. 2018, 43, 1511–1517. [Google Scholar] [CrossRef]
- Monteserín, C.; Blanco, M.; Aranzabe, E.; Aranzabe, A.; Laza, J.M.; Larrañaga-Varga, A.; Vilas, J.L. Effects of Graphene Oxide and Chemically-Reduced Graphene Oxide on the Dynamic Mechanical Properties of Epoxy Amine Composites. Polymers 2017, 9, 449. [Google Scholar] [CrossRef] [PubMed]
- Črešnar, K.P.; Aulova, A.; Bikiaris, D.N.; Lambropoulou, D.; Kuzmič, K.; Zemljič, L.F. Incorporation of Metal-Based Nanoadditives into the PLA Matrix: Effect of Surface Properties on Antibacterial Activity and Mechanical Performance of PLA Nanoadditive Films. Molecules 2021, 26, 4161. [Google Scholar] [CrossRef]
- Smoleń, P.; Czujko, T.; Komorek, Z.; Grochala, D.; Rutkowska, A.; Osiewicz-Powęzka, M. Mechanical and Electrical Properties of Epoxy Composites Modified by Functionalized Multiwalled Carbon Nanotubes. Materials 2021, 14, 3325. [Google Scholar] [CrossRef]
- Tarfaoui, M.; Lafdi, K.; Beloufa, I.; Daloia, D.; Muhsan, A. Effect of Graphene Nano-Additives on the Local Mechanical Behavior of Derived Polymer Nanocomposites. Polymers 2018, 10, 667. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, M.E.; Khalifa, M.A.; El-Sharkawy, R.M.; Youssef, M.R. Effects of Al2O3 and BaOnano-additives on mechanical char-acteristics of high-density polyethylene. Mater. Chem. Phys. 2021, 262, 124251. [Google Scholar] [CrossRef]
- Nayak, R.K.; Mahato, K.K.; Routara, B.C.; Ray, B.C. Evaluation of mechanical properties of Al2O3 and TiO2 nano filled enhanced glass fiber reinforced polymer composites. J. Appl. Polym. Sci. 2016, 133, 44274. [Google Scholar] [CrossRef]
- Mahmoud, M.E.; El-Khatib, A.M.; El-Sharkawy, R.M.; Rashad, A.R.; Badawi, M.S.; Gepreel, M.A. Design and testing of high-density polyethylene nanocomposites filled with lead oxide micro-and nano-particles: Mechanical, thermal, and morphological properties. J. Appl. Polym. Sci. 2019, 136, 47812. [Google Scholar] [CrossRef]
- Fu, S.-Y.; Feng, X.-Q.; Lauke, B.; Mai, Y.-W. Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites. Compos. Part B Eng. 2008, 39, 933–961. [Google Scholar] [CrossRef]
- Agureev, E.; Kostikov, V.I.; Eremeeva, Z.V.; Barmin, A.A.; Savushkina, S.V.; Ivanov, B.S. Aluminum Composites with Small Nanoparticles Additions: Corrosion Resistance. Mech. Mater. Sci. Eng. 2016. [Google Scholar] [CrossRef]
- Sławski, S.; Woźniak, A.; Bazan, P.; Mrówka, M. The Mechanical and Tribological Properties of Epoxy-Based Composites Filled with Manganese-Containing Waste. Materials 2022, 15, 1579. [Google Scholar] [CrossRef] [PubMed]
- Šofer, M.; Cienciala, J.; Fusek, M.; Pavlíček, P.; Moravec, R. Damage Analysis of Composite CFRP Tubes Using Acoustic Emission Monitoring and Pattern Recognition Approach. Materials 2021, 14, 786. [Google Scholar] [CrossRef]
- Šofer, M.; Šofer, P.; Fusek, M.; Cienciala, J.; Kwiatoń, P. Adaptive approach methodology of the Ib-value estimator calculation for acoustic emission analysis of carbon fibre reinforced plastics. Eng. Fail. Anal. 2023, 19, 107264. [Google Scholar] [CrossRef]
- Šofer, M.; Šofer, P.; Pagáč, M.; Volodarskaja, A.; Babiuch, M.; Gruň, F. Acoustic Emission Signal Characterisation of Failure Mechanisms in CFRP Composites Using Dual-Sensor Approach and Spectral Clustering Technique. Polymers 2022, 15, 47. [Google Scholar] [CrossRef]
- Saeedifar, M.; Najafabadi, M.A.; Zarouchas, D.; Toudeshky, H.H.; Jalalvand, M. Clustering of interlaminar and intralaminar damages in laminated composites under indentation loading using Acoustic Emission. Compos. Part B Eng. 2018, 144, 206–219. [Google Scholar] [CrossRef]
- Sobhani, A.; Saeedifar, M.; Najafabadi, M.A.; Fotouhi, M.; Zarouchas, D. The study of buckling and post-buckling behavior of laminated composites consisting multiple delaminations using acoustic emission. Thin Walled Struct. 2018, 127, 145–156. [Google Scholar] [CrossRef]
- Šofer, M.; Kučera, P.; Mazancová, E.; Krejčí, L. Acoustic Emission and Fractographic Analysis of Seamless Steel Pressure Cylinders with Artificial Flaws Under Hydrostatic Burst Testing. J. Nondestruct. Eval. 2019, 38, 84. [Google Scholar] [CrossRef]
- Zhuang, X.; Yan, X. Investigation of damage mechanisms in self-reinforced polyethylene composites by acoustic emission. Compos. Sci. Technol. 2005, 66, 444–449. [Google Scholar] [CrossRef]
- Yu, Y.-H.; Choi, J.-H.; Kweon, J.-H.; Kim, D.-H. A study on the failure detection of composite materials using an acoustic emission. Compos. Struct. 2006, 75, 163–169. [Google Scholar] [CrossRef]
- Fotouhi, M.; Pashmforoush, F.; Ahmadi, M.; Oskouei, A.R. Monitoring the initiation and growth of delamination in composite materials using acoustic emission under qua-si-static three-point bending test. J. Reinf. Plast. Compos. 2011, 30, 1481–1493. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, S.; Chen, Y.; Liu, D.; Li, D. Acoustic Emission-Based Study to Characterize the Crack Initiation Point of Wood Fibre/HDPE Composites. Polymers 2019, 11, 701. [Google Scholar]
- Panasiuk, K.; Dudzik, K. Determining the Stages of Deformation and Destruction of Composite Materials in a Static Tensile Test by Acoustic Emission. Materials 2022, 15, 313. [Google Scholar] [CrossRef]
- Panasiuk, K.; Dudzik, K.; Hajdukiewicz, G. Acoustic Emission as a Method for Analyzing Changes and Detecting Damage in Composite Materials During Loading. Arch. Acoust. 2021, 46, 399–407. [Google Scholar] [CrossRef]
- Panasiuk, K. The use of acoustic emission signal (AE) in mechanical tests. Prz. Elektrotechniczny 2019, 95, 8–11. [Google Scholar] [CrossRef]
- Kyzioł, L.; Panasiuk, K.; Hajdukiewicz, G.; Dudzik, K. Acoustic Emission and K-S Metric Entropy as Methods for Determining Mechanical Properties of Composite Materials. Sensors 2020, 21, 145. [Google Scholar] [CrossRef] [PubMed]
- Jung, D.; Lee, J. Enhancing Reliability and Safety in Industrial Applications: Assessing the Applicability of Energy b-Value to Composites. Materials 2024, 17, 447. [Google Scholar] [CrossRef] [PubMed]
- Garbacz, G.; Kyzioł, L. Application of metric entropy to determine properties of structural materials. Polímeros 2019, 29, 1–9. [Google Scholar] [CrossRef]
- Garbacz, G.; Kyzioł, L. Application of metric entropy for results interpretation of composite materials mechanical tests. Adv. Mater. Sci. 2017, 17, 70–81. [Google Scholar] [CrossRef][Green Version]
- Kyzioł, L.; Hajdukiewicz, G. Application of the Kolmogorov-Sinai Entropy in Determining the Yield Point, as Exemplified by the EN AW-7020 Alloy. J. KONBiN 2019, 49, 241–269. [Google Scholar] [CrossRef]
- Panasiuk, K.; Kyziol, L.; Dudzik, K.; Hajdukiewicz, G. Application of the Acoustic Emission Method and Kolmogorov-Sinai Metric Entropy in Determining the Yield Point in Aluminium Alloy. Materials 2020, 13, 1386. [Google Scholar] [CrossRef]









| Sample | Resin | Glass Fiber | Gamma-Phase Aluminum Nanopowder | Polyester–Glass Recyclate |
|---|---|---|---|---|
| % | % | % | % | |
| A0R0 | 60 | 40 | 0 | 0 |
| A0R10 | 60 | 30 | 0 | 10 |
| A2R10 | 60 | 28 | 2 | 10 |
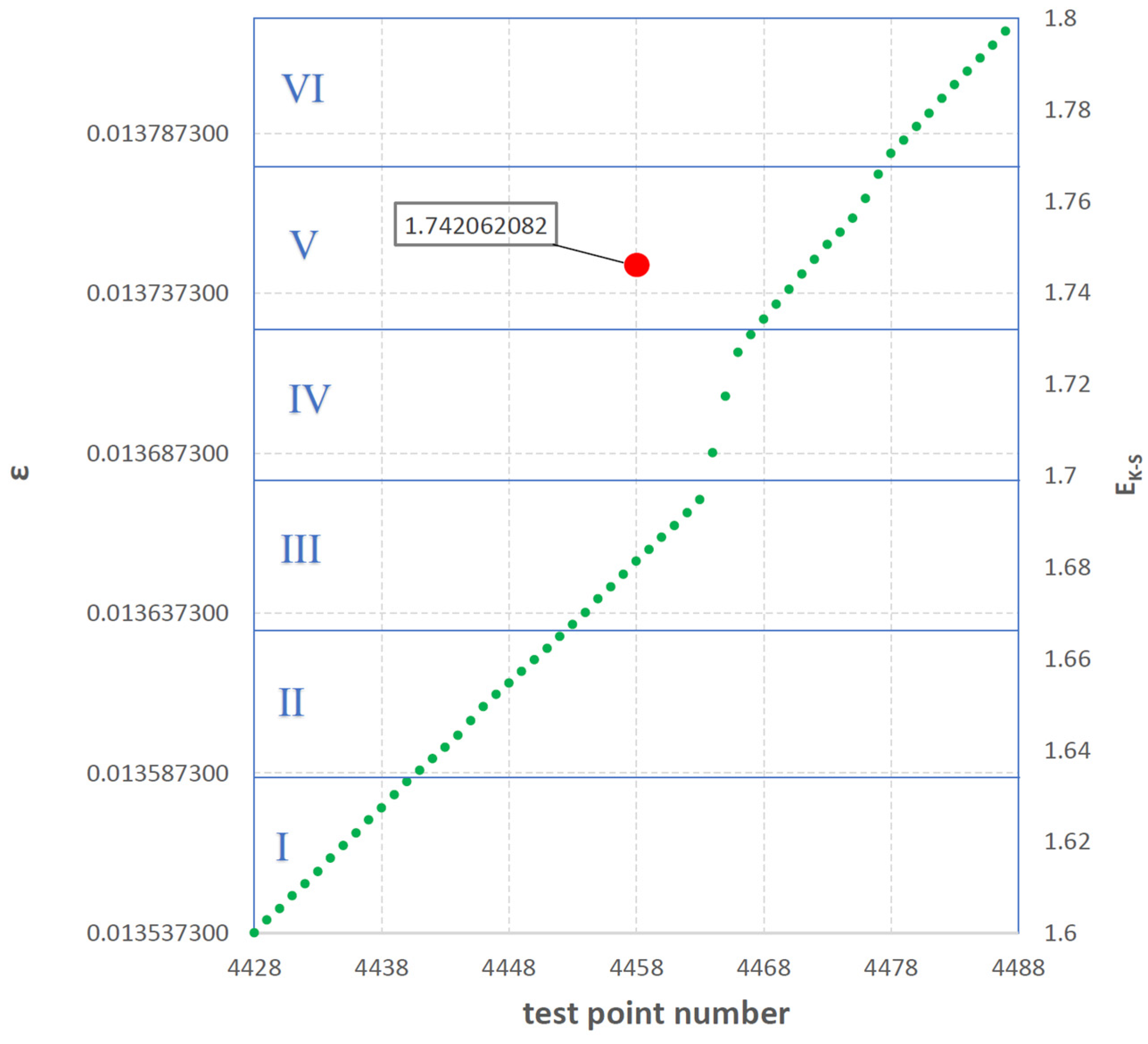
| Six Adopted Sub-Ranges of the Selected Range | ||||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
| min sub-range 0.013537400 | min sub-range 0.013585052 | min sub-range 0.013632703 | min sub-range 0.013680355 | Min sub-range 0.013728007 | Min sub-range 0.013775658 | |
| Adopted 60—digit interval from the set of extensions ε | 0.013537400 0.013541397 0.013544890 0.013548909 0.013552707 0.013556491 0.013560667 0.013564632 0.013568523 0.013572643 0.013576444 0.013580532 0.013584602 | 0.013588142 0.013591788 0.013595396 0.013599111 0.013603684 0.013608099 0.013611917 0.013615487 0.013619061 0.013622743 0.013626323 0.013630034 | 0.013633789 0.013637494 0.013641752 0.013645518 0.013649446 0.013653519 0.013657227 0.013661062 0.013664697 0.013668638 0.013672831 | 0.013687458 0.013705087 0.013718830 0.013724324 | 0.013729168 0.013733916 0.013738563 0.013743314 0.013747923 0.013752592 0.013756413 0.013760804 0.013766979 0.013774511 | 0.013781058 0.013785108 0.013789486 0.013793529 0.013798223 0.013802508 0.013806735 0.013810797 0.013814831 0.013819282 |
| max sub-range < 0.013585052 | max sub-range < 0.013632703 | max sub-range < 0.013680355 | max sub-range < 0.013728007 | max sub-range < 0.013775658 | max sub-range < 0.013823310 | |
| pi | 0.21666666 | 0.2 | 0.18333333 | 0.06666666 | 0.16666666 | 0.16666666 |
| ln pi | −1.529395205 | −1.609437912 | −1.696449289 | −2.708050201 | −1.791759469 | −1.791759469 |
| pi ln pi | −0.331368961 | −0.321887582 | −0.311015703 | −0.180536680 | −0.298626578 | −0.298626578 |
| EK-S | 1.742062082 | |||||
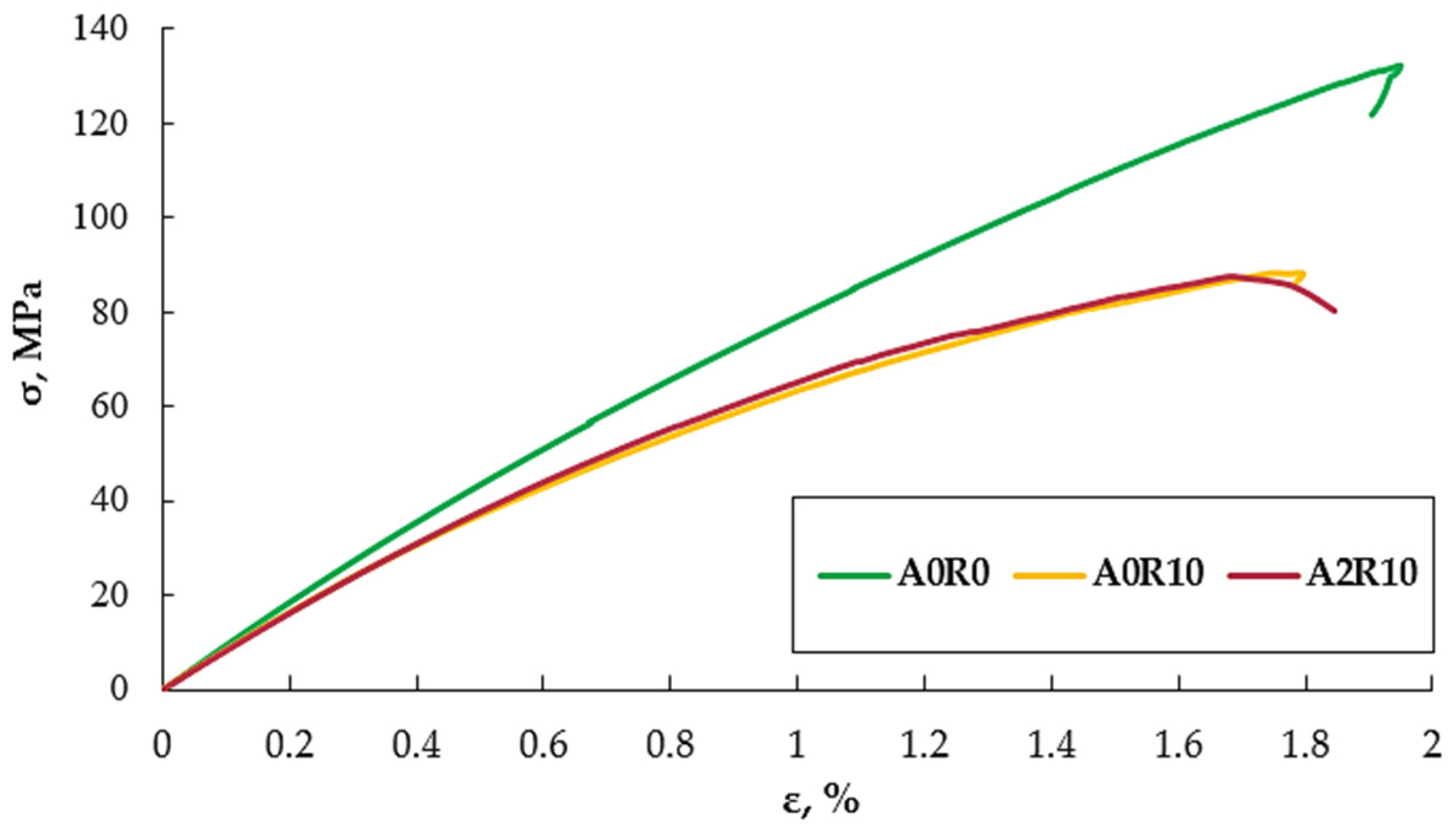
| Sample | UTS | E | ε |
|---|---|---|---|
| Mpa | Mpa | % | |
| A0R0 | 128.3 | 9169 | 1.87 |
| Standard deviation | 8.4 | 439 | 0.12 |
| A0R10 | 87.0 | 7691 | 1.67 |
| Standard deviation | 5.7 | 369 | 0.12 |
| A2R10 | 80.5 | 8057 | 1.59 |
| Standard deviation | 6.6 | 575.3 | 0.18 |
| Failure Mechanism | Amplitude | Peak Frequency |
|---|---|---|
| dB | kHz | |
| Delamination/Matrix cracking | 40–94 | 50–200 |
| Fiber/matrix debonding | 40–70 | 200–400 |
| Fiber failure | >80 | 400–600 |
| Fiber pull-out | >60 | >700 |
| Sample | Strain Value Range | Stress Value Range | UTS |
|---|---|---|---|
| % | Mpa | % | |
| A0R0 | 1.27–1.45 | 93–110 | 72 |
| A0R10 | 0.68–0.89 | 49–54 | 56 |
| A2R10 | 0.52–0.72 | 42–49 | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panasiuk, K.; Dudzik, K.; Hajdukiewicz, G.; Abramczyk, N. Influence of Gamma-Phase Aluminum Oxide Nanopowder and Polyester–Glass Recyclate Filler on the Destruction Process of Composite Materials Reinforced by Glass Fiber. Polymers 2024, 16, 2276. https://doi.org/10.3390/polym16162276
Panasiuk K, Dudzik K, Hajdukiewicz G, Abramczyk N. Influence of Gamma-Phase Aluminum Oxide Nanopowder and Polyester–Glass Recyclate Filler on the Destruction Process of Composite Materials Reinforced by Glass Fiber. Polymers. 2024; 16(16):2276. https://doi.org/10.3390/polym16162276
Chicago/Turabian StylePanasiuk, Katarzyna, Krzysztof Dudzik, Grzegorz Hajdukiewicz, and Norbert Abramczyk. 2024. "Influence of Gamma-Phase Aluminum Oxide Nanopowder and Polyester–Glass Recyclate Filler on the Destruction Process of Composite Materials Reinforced by Glass Fiber" Polymers 16, no. 16: 2276. https://doi.org/10.3390/polym16162276
APA StylePanasiuk, K., Dudzik, K., Hajdukiewicz, G., & Abramczyk, N. (2024). Influence of Gamma-Phase Aluminum Oxide Nanopowder and Polyester–Glass Recyclate Filler on the Destruction Process of Composite Materials Reinforced by Glass Fiber. Polymers, 16(16), 2276. https://doi.org/10.3390/polym16162276