Experimental Study on the Transport Properties of 12 Novel Deep Eutectic Solvents
Abstract
1. Introduction
2. Experimental Section
2.1. Experimental Reagents
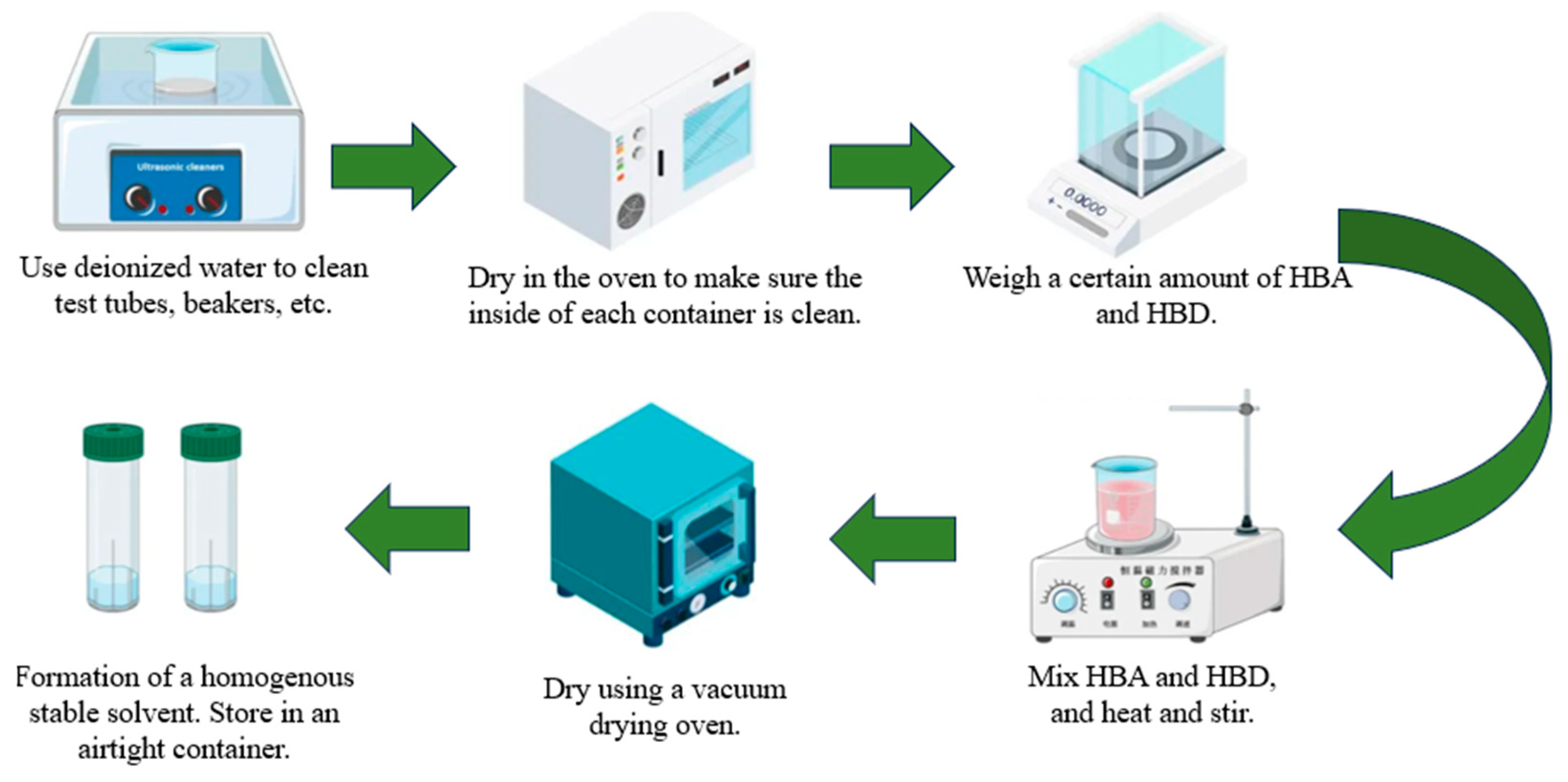
2.2. Preparation of DESs
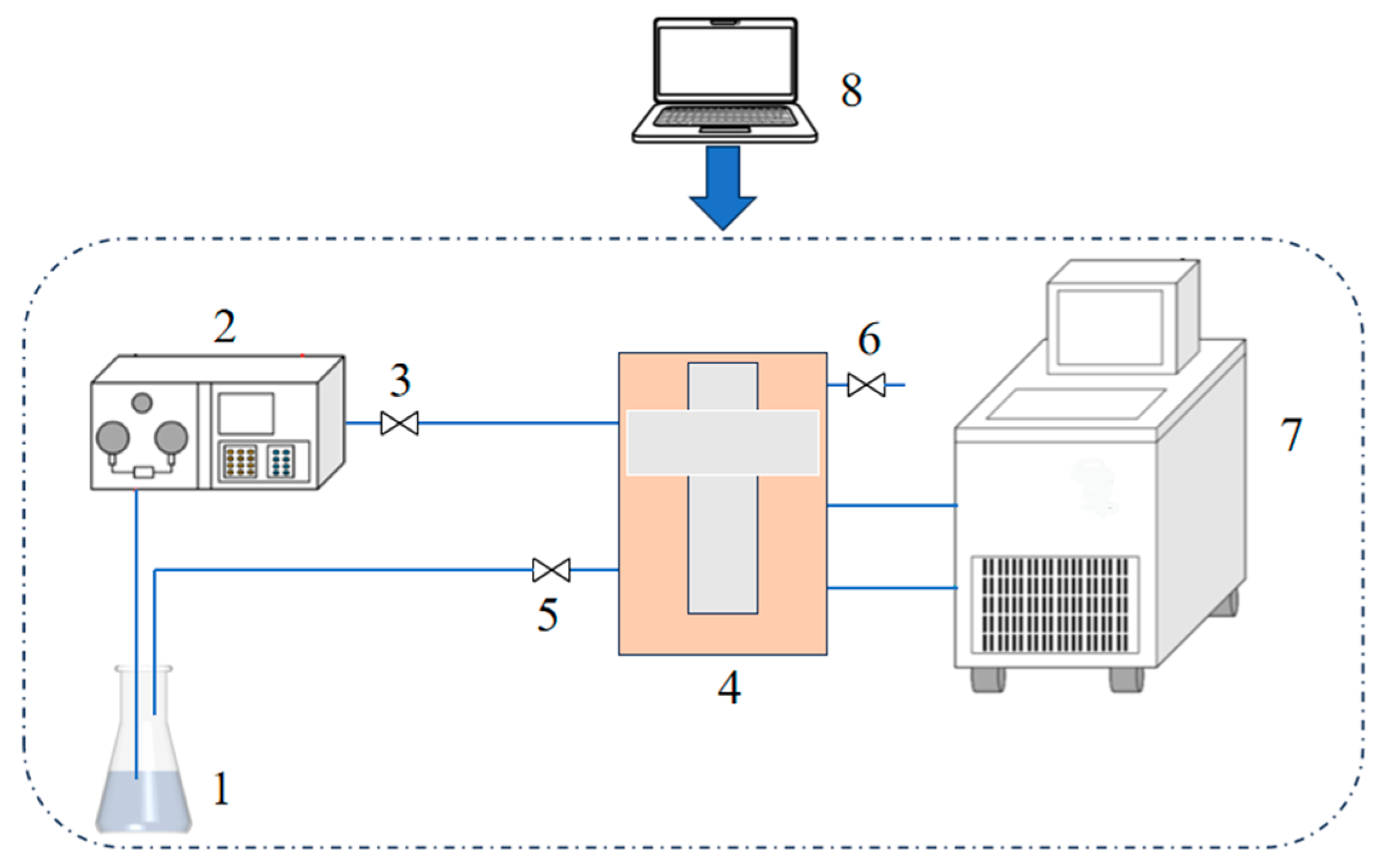
2.3. Measurement of Thermal Conductivity
2.4. Measurement of Viscosity
3. Experimental Results and Analysis
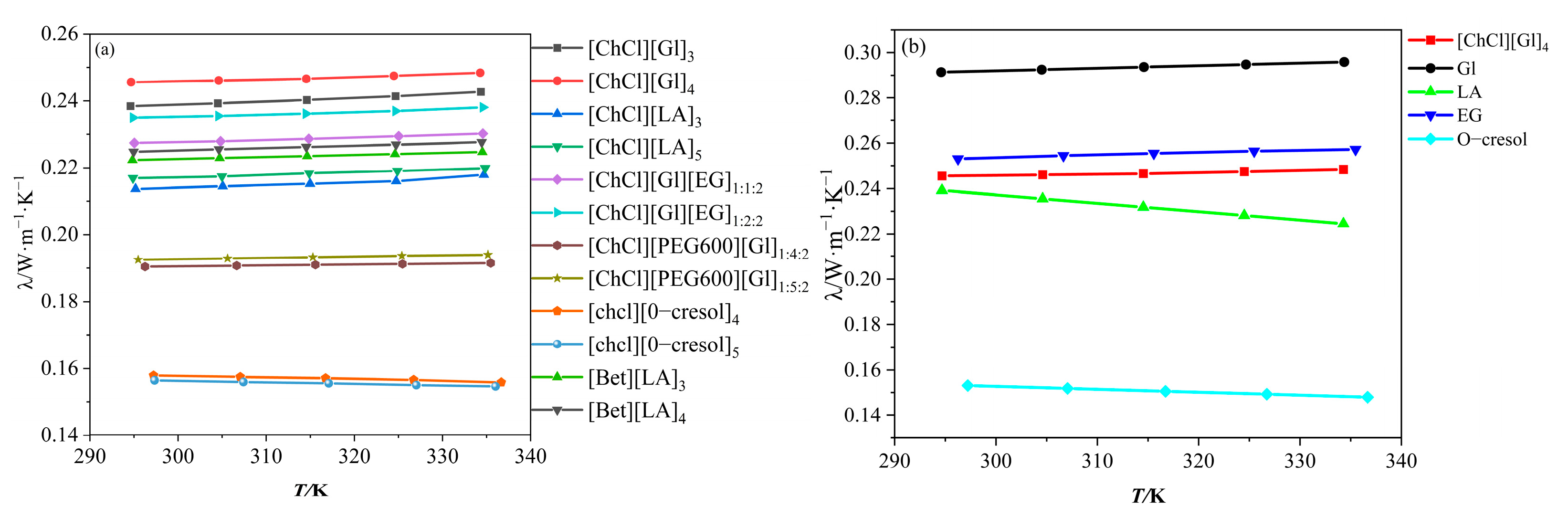
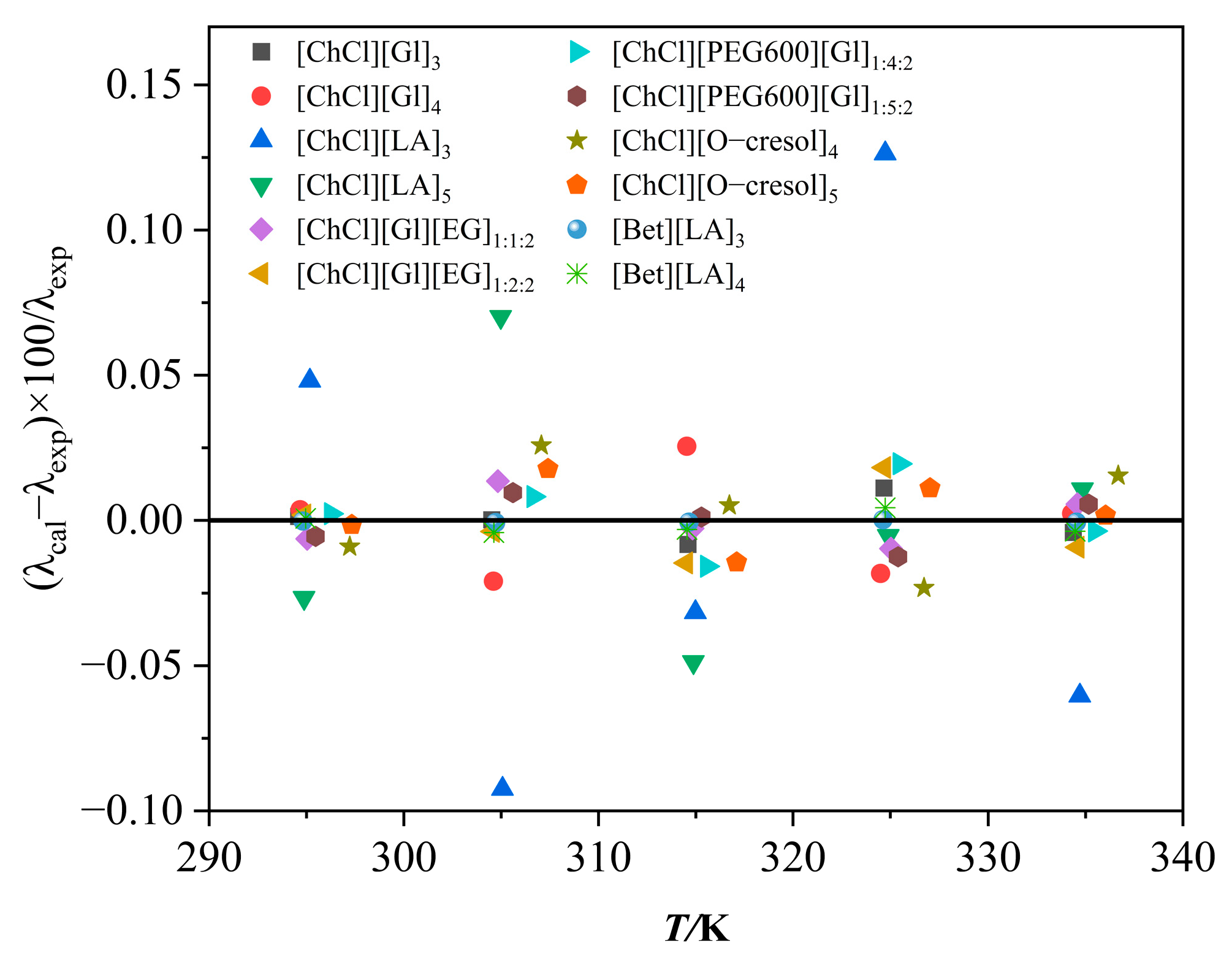
3.1. Results and Analysis of Thermal Conductivity of DESs
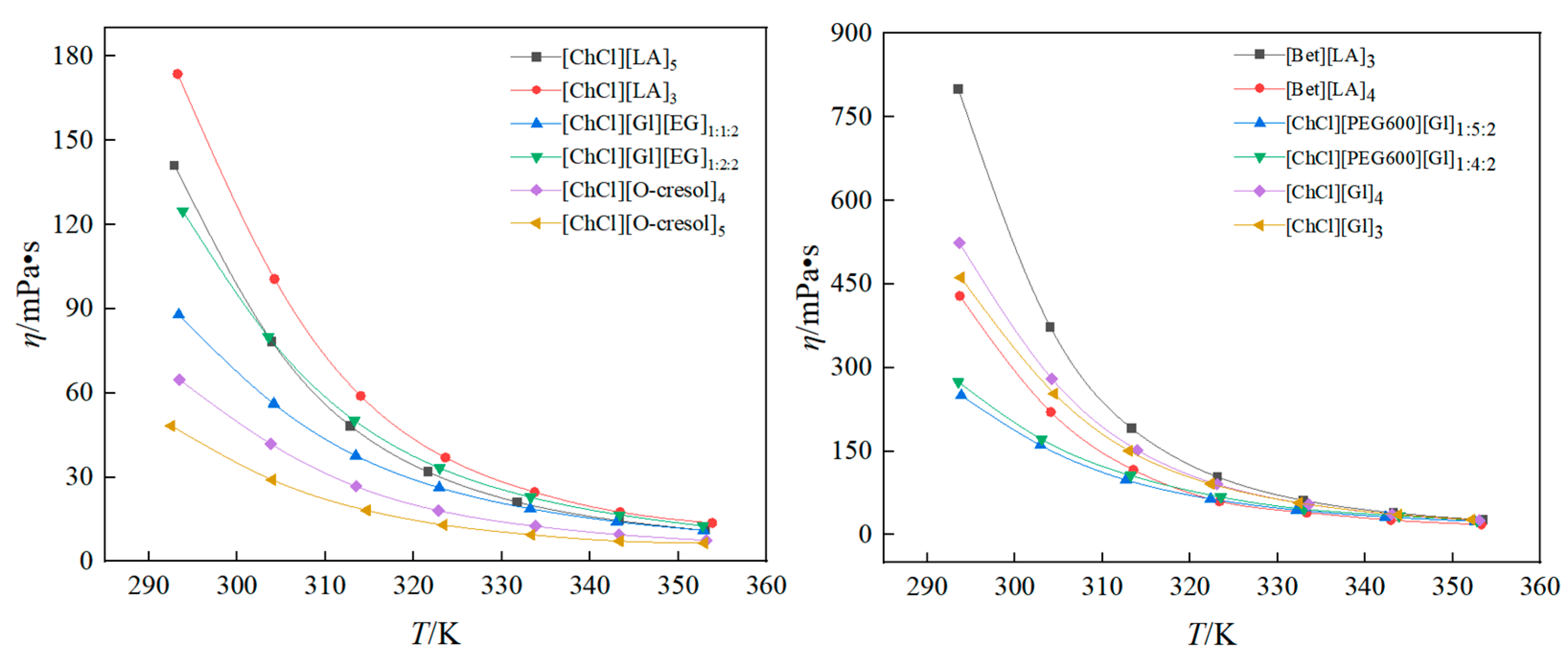
3.2. Results and Analysis of Viscosity of DESs
4. Conclusions
- (1)
- The twelve DESs appeared as homogeneous and stable liquids at room temperature, and no crystallization or precipitation was observed after 2 months of storage in a closed environment protected from light. Among them, the light yellow ChCl/O-cresol solvent slightly deepened in color, and the [ChCl][PEG600][Gl]1:5:2 solvent turned into a light white liquid.
- (2)
- The thermal conductivity of the DESs was measured using the experimental principle of the transient hot-wire method. The results showed that the thermal conductivity of the ChCl/O-cresol solvent decreased with increasing temperature, which was the opposite trend of the other ten solvents. The thermal conductivity of the [ChCl][Gl]4 solvent reached 0.2456 W·m−1·K−1 at 294 K. The thermal conductivity of the [ChCl][Gl]4 solvent was found to decrease with increasing temperature.
- (3)
- At low temperatures, the viscosities of the twelve solvents decreased significantly with increasing temperature. The selection of the HBA, HBD, or different ratios can have a dramatic effect on the viscosity of the solvents. The viscosity of [Bet][LA]3 was enhanced by 360.37% compared with that of [ChCl][Gl]3 at 293 K. At 293 K, the viscosity of [ChCl][O-cresol]5 was only 48.3 mPa·s. The activation energies of the twelve solvents were small, and all of them were in the interval of 29.36~49.31 KJ·mol−1.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Andrianov, A.; Ustinov, A.; Loginov, D. Improvement of heat exchanger efficiency by using hydraulic and thermal entrance regions. arXiv 2018, arXiv:1803.09255. [Google Scholar]
- Das, P.K. A review based on the effect and mechanism of thermal conductivity of normal nanofluids and hybrid nanofluids. J. Mol. Liq. 2017, 240, 420–446. [Google Scholar] [CrossRef]
- Jafari, K.; Fatemi, M.H.; Estellé, P. Deep eutectic solvents (DESs): A short overview of the thermophysical properties and current use as base fluid for heat transfer nanofluids. J. Mol. Liq. 2021, 321, 114752. [Google Scholar] [CrossRef]
- Dehkordi, K.G.; Karimipour, A.; Afrand, M.; Toghraie, D.; Isfahani, A.H.M. Molecular dynamics simulation concerning nanofluid boiling phenomenon affected by the external electric field: Effects of number of nanoparticles through Pt, Fe, and Au microchannels. J. Mol. Liq. 2021, 324, 114775. [Google Scholar] [CrossRef]
- Yu, W.; Xie, H.; Wang, X.; Wang, X. Significant thermal conductivity enhancement for nanofluids containing graphene nanosheets. Phys. Lett. A 2011, 375, 1323–1328. [Google Scholar] [CrossRef]
- Krishnan, A.; Gopinath, K.P.; Vo, D.V.N.; Rajagopal, M.; Nagarajan, V.; Madhav; Jayaseelan, A. Ionic liquids, deep eutectic solvents and liquid polymers as green solvents in carbon capture technologies: A review. Environ. Chem. Lett. 2020, 18, 2031–2054. [Google Scholar] [CrossRef]
- Singh, S.K.; Savoy, A.W. Ionic liquids synthesis and applications: An overview. J. Mol. Liq. 2020, 297, 112038. [Google Scholar] [CrossRef]
- Alni, A.; Cahya, A.Y.D.; Wahyuningrum, D. Synthesis of imidazolium based ionic liquids and its application as medium in cyclization reaction of diketone. Key Eng. Mater. 2019, 811, 86–91. [Google Scholar] [CrossRef]
- Maugeri, Z.; de María, P.D. Novel choline-chloride-based deep-eutectic-solvents with renewable hydrogen bond donors: Levulinic acid and sugar-based polyols. RSC Adv. 2012, 2, 421–425. [Google Scholar] [CrossRef]
- Smith, E.L.; Abbott, A.P.; Ryder, K.S. Deep eutectic solvents (DESs) and their applications. Chem. Rev. 2014, 114, 11060–11082. [Google Scholar] [CrossRef]
- Rahman, M.S.; Roy, R.; Jadhav, B.; Hossain, M.N.; Halim, M.A.; Raynie, D.E. Formulation, structure, and applications of therapeutic and amino acid-based deep eutectic solvents: An overview. J. Mol. Liq. 2021, 321, 114745. [Google Scholar] [CrossRef]
- Wang, H.; Ma, X.; Cheng, Q.; Xi, X.; Zhang, L. Deep eutectic solvent-based microwave-assisted extraction of baicalin from Scutellaria baicalensis Georgi. J. Chem. 2018, 2018, 9579872. [Google Scholar] [CrossRef]
- Landa-Castro, M.; Aldana-González, J.; de Oca-Yemha, M.G.M.; Romero-Romo, M.; Arce-Estrada, E.M.; Palomar-Pardavé, M. Ni–Co alloy electrodeposition from the cathode powder of Ni-MH spent batteries leached with a deep eutectic solvent (reline). J. Alloys Compds 2020, 830, 154650. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, X.; Wang, H.; Wang, Y.; Zhao, Y.; Ma, H.; Chai, L.; Wang, Y.; Hou, X.; Deng, T. Degradation of polycarbonate-based polyurethane via selective cleavage of carbamate and urea bonds. Polym. Degrad. Stab. 2020, 181, 109342. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, H.; Lai, S.L.; Gao, J.; Gao, L. Lignin modified by deep eutectic solvents as green, reusable, and bio-based catalysts for efficient chemical fixation of CO2. React. Funct. Polym. 2020, 149, 104502. [Google Scholar] [CrossRef]
- Li, L.; Wu, Z.; Xi, X.; Liu, B.; Cao, Y.; Xu, H.; Hu, Y. A bifunctional brønsted acidic deep eutectic solvent to dissolve and catalyze the depolymerization of alkali lignin. J. Renew. Mater. 2021, 9, 219–235. [Google Scholar] [CrossRef]
- Abbott, A.P.; Capper, G.; Davies, D.L.; Rasheed, R.K.; Tambyrajah, V. Novel solvent properties of choline chloride/urea mixtures. Chem. Commun. 2003, 70–71. [Google Scholar] [CrossRef] [PubMed]
- Abbott, A.P.; Boothby, D.; Capper, G.; Davies, D.L.; Rasheed, R.K. Deep eutectic solvents formed between choline chloride and carboxylic acids: Versatile alternatives to ionic liquids. J. Am. Chem. Soc. 2004, 126, 9142–9147. [Google Scholar] [CrossRef]
- Liu, C.; Fang, H.; Qiao, Y.; Zhao, J.; Rao, Z. Properties and heat transfer mechanistic study of glycerol/choline chloride deep eutectic solvents based nanofluids. Int. J. Heat Mass Transf. 2019, 138, 690–698. [Google Scholar] [CrossRef]
- Omar, K.A.; Sadeghi, R. Physicochemical properties of deep eutectic solvents: A review. J. Mol. Liq. 2022, 360, 119524. [Google Scholar] [CrossRef]
- Omar, K.A.; Sadeghi, R. Database of Deep Eutectic Solvents and their Physical Properties: A Review. J. Mol. Liq. 2023, 384, 121899. [Google Scholar] [CrossRef]
- Mirza, N.R.; Nicholas, N.J.; Wu, Y.; Kentish, S.; Stevens, G.W. Estimation of normal boiling temperatures, critical properties, and acentric factors of deep eutectic solvents. J. Chem. Eng. Data 2015, 60, 1844–1854. [Google Scholar] [CrossRef]
- Shaharuddin, N.A.; Abidin, S.Z. Ionic Conductivity, Dielectric, and Structural Insights of Deep Eutectic Solvent-based Polymer Electrolyte: A Review. Recent Innov. Chem. Eng. 2023, 16, 228–240. [Google Scholar] [CrossRef]
- Healy, J.; De Groot, J.; Kestin, J. The theory of the transient hot-wire method for measuring thermal conductivity. Phys. B+C 1976, 82, 392–408. [Google Scholar] [CrossRef]
- Clifford, A.; Kestin, J.; Wakeham, W.A. A further contribution to the theory of the transient hot-wire technique for thermal conductivity measurements. Phys. A Stat. Mech. Its Appl. 1980, 100, 370–374. [Google Scholar] [CrossRef]
- Roder, H.M.; Perkins, R.A.; Laesecke, A.; Nieto de Castro, C.A. Absolute steady-state thermal conductivity measurements by use of a transient hot-wire system. J. Res. Natl. Inst. Stand. Technol. 2000, 105, 221. [Google Scholar] [CrossRef] [PubMed]
- Gross, U.; Song, Y.W. Thermal conductivities of new refrigerants R125 and R32 measured by the transient hot-wire method. Int. J. Thermophys. 1996, 17, 607–619. [Google Scholar] [CrossRef]
- Kawaguchi, N.; Nagasaka, Y.; Nagashima, A. Fully automated apparatus to measure the thermal conductivity of liquids by the transient hot-wire method. Rev. Sci. Instrum. 1985, 56, 1788–1794. [Google Scholar] [CrossRef]
- Nagasaka, Y.; Nagashima, A. Precise measurements of the thermal conductivity of toluene and n-heptane by the absolute transient hot-wire method. Ind. Eng. Chem. Fund. 1981, 20, 216–220. [Google Scholar] [CrossRef]
- Murphy, T.; Varela, L.M.; Webber, G.B.; Warr, G.G.; Atkin, R. Nanostructure–thermal conductivity relationships in protic ionic liquids. J. Phys. Chem. B 2014, 118, 12017–12024. [Google Scholar] [CrossRef]
- Gautam, R.K.; Seth, D. Thermal conductivity of deep eutectic solvents. J. Therm. Anal. Calorim. 2020, 140, 2633–2640. [Google Scholar] [CrossRef]
- Dehury, P.; Singh, J.; Banerjee, T. Thermophysical and forced convection studies on (alumina+ menthol)-based deep eutectic solvents for their use as a heat transfer fluid. ACS Omega 2018, 3, 18016–18027. [Google Scholar] [CrossRef] [PubMed]
- Hansen, B.; Spittle, S.; Chen, B.; Poe, D.; Zhang, Y.; Klein, J.M.; Horton, A.; Adhikari, L.; Zelovich, T.; Doherty, B.W.; et al. Deep eutectic solvents: A review of fundamentals and applications. Chem. Rev. 2020, 121, 1232–1285. [Google Scholar] [CrossRef] [PubMed]
- Alzamel, N.O.; Alakhras, F.; Al-Arfaj, A.; Alomair, N.A.; Al-Abbad, E.; Wassel, A.A.; Ouerfelli, N. On the homographic dependence of the activation energy and the viscosity Arrhenius’ temperature for some pure fluids. Asian J. Chem. 2018, 30, 1937–1943. [Google Scholar] [CrossRef]

| Reagent Name | CAS Number | Molecular Formula | Molecular Weight (Supplier) | Purity |
|---|---|---|---|---|
| Choline chloride | 67-48-1 | C5H14ClNO | 139.62 | 98% (AR) |
| Betaine | 107-43-7 | C5H11NO2 | 117.15 | 98% (AR) |
| Glycerol | 56-81-5 | C3H8O3 | 92.09 | 99% (AR) |
| Ethylene glycol | 107-21-1 | C2H6O2 | 62.07 | 98% (AR) |
| PEG600 | 25322-68-3 | HO(CH2CH2O)nH | 600 | |
| O-cresol | 95-48-7 | C7H8O | 108.14 | 98% (AR) |
| Lactic acid | 50-21-5 | C3H6O3 | 90.08 | 85~90% (AR) |
| HBA | HBD | Molar Ratio | Abbreviation | State (293 K) | |
|---|---|---|---|---|---|
| HBA | HBD | ||||
| Choline chloride | Glycerol | 1 | 3 | [ChCl][Gl]3 | Clear liquid |
| 1 | 4 | [ChCl][Gl]4 | |||
| Choline chloride | Glycerol/Ethylene glycol | 1 | 1:2 | [ChCl][Gl][EG]1:1:2 | Clear liquid |
| 1 | 2:2 | [ChCl][Gl][EG]1:2:2 | |||
| Choline chloride | PEG600/Glycerol | 1 | 4:2 | [ChCl][PEG600][Gl]1:4:2 | Clear liquid |
| 1 | 5:2 | [ChCl][PEG600][Gl]1:5:2 | |||
| Choline chloride | O-cresol | 1 | 4 | [ChCl][O-cresol]4 | Light brown liquid |
| 1 | 5 | [ChCl][O-cresol]5 | |||
| Choline chloride | Lactic acid | 1 | 3 | [ChCl][LA]3 | Clear liquid |
| 1 | 5 | [ChCl][LA]5 | |||
| Betaine | Lactic acid | 1 | 3 | [Bet][LA]3 | Clear liquid |
| 1 | 4 | [Bet][LA]4 | |||
| T/ | λ/ | T/ | λ/ | T/ | λ/ |
|---|---|---|---|---|---|
| K | W·m−1·K−1 | K | W·m−1·K−1 | K | W·m−1·K−1 |
| [ChCl][Gl]3 | [ChCl][Gl]4 | [ChCl][LA]3 | |||
| 294.59 | 0.2385 | 294.67 | 0.2456 | 295.17 | 0.2137 |
| 304.51 | 0.2393 | 304.61 | 0.2461 | 305.07 | 0.2145 |
| 314.60 | 0.2403 | 314.54 | 0.2466 | 314.98 | 0.2152 |
| 324.67 | 0.2414 | 324.49 | 0.2475 | 324.74 | 0.2160 |
| 334.36 | 0.2427 | 334.28 | 0.2484 | 334.70 | 0.2179 |
| [ChCl][LA]5 | [ChCl][Gl][EG]1:1:2 | [ChCl][Gl][EG]1:2:2 | |||
| 294.88 | 0.2169 | 295.04 | 0.2274 | 294.89 | 0.2350 |
| 304.98 | 0.2174 | 304.83 | 0.2279 | 304.58 | 0.2355 |
| 314.88 | 0.2184 | 314.84 | 0.2286 | 314.50 | 0.2362 |
| 324.89 | 0.2191 | 325.03 | 0.2294 | 324.68 | 0.2370 |
| 334.84 | 0.2199 | 334.58 | 0.2302 | 334.59 | 0.2381 |
| [ChCl][PEG600][Gl]1:4:2 | [ChCl][PEG600][Gl]1:5:2 | [ChCl][O-cresol]4 | |||
| 296.25 | 0.1904 | 295.47 | 0.1925 | 297.22 | 0.1579 |
| 306.65 | 0.1907 | 305.61 | 0.1929 | 307.06 | 0.1575 |
| 315.58 | 0.1910 | 315.29 | 0.1933 | 316.73 | 0.1571 |
| 325.47 | 0.1912 | 325.39 | 0.1937 | 326.73 | 0.1566 |
| 335.48 | 0.1915 | 335.16 | 0.1940 | 336.67 | 0.1559 |
| [ChCl][O-cresol]5 | [Bet][LA]3 | [Bet][LA]4 | |||
| 297.33 | 0.1565 | 294.82 | 0.2223 | 294.95 | 0.2248 |
| 307.41 | 0.1560 | 304.72 | 0.2229 | 304.63 | 0.2255 |
| 317.10 | 0.1556 | 314.65 | 0.2235 | 314.55 | 0.2262 |
| 327.04 | 0.1551 | 324.62 | 0.2241 | 324.73 | 0.2269 |
| 336.02 | 0.1547 | 334.53 | 0.2247 | 334.46 | 0.2276 |
| DES | A | B | C | r2 |
|---|---|---|---|---|
| [ChCl][Gl]3 | −4.19084 × 10−4 | 8.33701 × 10−7 | 0.28961 | 0.999 |
| [ChCl][Gl]4 | −4.89096 × 10−4 | 8.89908 × 10−7 | 0.31246 | 0.999 |
| [ChCl][LA]3 | −9.60836 × 10−4 | 1.68473 × 10−6 | 0.35063 | 0.986 |
| [ChCl][LA]5 | −6.61081 × 10−5 | 2.27432 × 10−7 | 0.21656 | 0.994 |
| [ChCl][Gl][EG]1:1:2 | −2.63097 × 10−4 | 5.31426 × 10−7 | 0.25875 | 0.999 |
| [ChCl][Gl][EG]1:2:2 | −4.93418 × 10−4 | 9. 93418 × 10−7 | 0.30165 | 0.999 |
| [ChCl][PEG600][Gl]1:4:2 | 7.51905 × 10−5 | −7.50958 × 10−8 | 0.17472 | 0.997 |
| [ChCl][PEG600][Gl]1:5:2 | 1.23432 × 10−4 | −1.34945 × 10−7 | 0.1678 | 0.999 |
| [ChCl][O-cresol]4 | 2.64003 × 10−4 | −4.94921 × 10−7 | 0.12314 | 0.998 |
| [ChCl][O-cresol]5 | −5.1071 × 10−5 | 7.38161 × 10−9 | 0.17103 | 0.999 |
| [Bet][LA]3 | 6.20657 × 10−5 | −2.62959 × 10−9 | 0.20423 | 1 |
| [Bet][LA]4 | 8.24401 × 10−5 | −1.8784 × 10−8 | 0.20212 | 0.999 |
| T/ | η/ | T/ | η/ | T/ | η/ |
|---|---|---|---|---|---|
| K | mPa·s | K | mPa·s | K | mPa·s |
| [ChCl][Gl]3 | [ChCl][Gl]4 | [ChCl][LA]3 | |||
| 293.80 | 461.5 | 293.62 | 524.1 | 293.25 | 173.6 |
| 304.50 | 253.3 | 304.22 | 279.8 | 304.22 | 100.6 |
| 313.04 | 150.9 | 313.95 | 152.1 | 313.98 | 59.0 |
| 322.34 | 91.7 | 323.07 | 90.9 | 323.59 | 37.0 |
| 332.43 | 57.6 | 333.54 | 54.9 | 333.71 | 24.7 |
| 343.83 | 36.3 | 343.03 | 37.1 | 343.39 | 17.6 |
| 352.19 | 27.1 | 353.04 | 26.2 | 353.83 | 13.7 |
| [ChCl][LA]5 | [ChCl][Gl][EG]1:1:2 | [ChCl][Gl][EG]1:2:2 | |||
| 292.90 | 141.0 | 293.37 | 87.9 | 293.82 | 124.8 |
| 303.95 | 78.3 | 304.13 | 56.2 | 303.54 | 80.0 |
| 312.84 | 48.2 | 313.44 | 37.7 | 313.28 | 50.2 |
| 321.63 | 31.9 | 322.89 | 26.3 | 322.95 | 33.3 |
| 331.75 | 21.2 | 333.20 | 18.8 | 333.25 | 22.9 |
| 343.33 | 14.5 | 343.02 | 14.2 | 343.35 | 16.6 |
| 353.07 | 11.1 | 352.84 | 11.1 | 352.78 | 12.7 |
| [ChCl][PEG600][Gl]1:4:2 | [ChCl][PEG600][Gl]1:5:2 | [ChCl][O-cresol]4 | |||
| 293.52 | 274.3 | 293.86 | 250.1 | 293.43 | 64.8 |
| 303.04 | 171.5 | 302.88 | 160.9 | 303.80 | 41.9 |
| 313.20 | 106.8 | 312.66 | 98.6 | 313.46 | 26.8 |
| 323.51 | 68.0 | 322.34 | 64.4 | 322.81 | 18.1 |
| 333.02 | 46.2 | 332.15 | 44.7 | 333.80 | 12.6 |
| 343.85 | 34.1 | 342.29 | 32.2 | 343.30 | 9.6 |
| 352.79 | 25.8 | 352.51 | 24.4 | 353.20 | 7.5 |
| [ChCl][O-cresol]5 | [Bet][LA]3 | [Bet][LA]4 | |||
| 292.54 | 48.3 | 293.53 | 799.2 | 293.68 | 428.4 |
| 303.98 | 29.1 | 304.05 | 372.5 | 304.09 | 220.3 |
| 314.68 | 18.2 | 313.33 | 190.8 | 313.52 | 116.6 |
| 323.41 | 13.0 | 323.12 | 104 | 323.35 | 60.2 |
| 333.38 | 9.5 | 332.93 | 62.1 | 333.31 | 39.9 |
| 343.34 | 7.3 | 343.23 | 39.4 | 342.92 | 26.7 |
| 352.95 | 6.5 | 353.49 | 26.8 | 353.27 | 18.7 |
| DES | η0/(mPa·s) | Eη/(kJ·mol−1) | r2 |
|---|---|---|---|
| [ChCl][Gl]3 | 1.3781 × 10−5 | 42.26 | 0.998 |
| [ChCl][Gl]4 | 7.0270 × 10−7 | 44.16 | 0.997 |
| [ChCl][LA]3 | 4.0445 × 10−5 | 37.14 | 0.995 |
| [ChCl][LA]5 | 3.7587 × 10−5 | 36.70 | 0.995 |
| [ChCl][Gl][EG]1:1:2 | 3.4969 × 10−4 | 30.26 | 0.998 |
| [ChCl][Gl][EG]1:2:2 | 1.2114 × 10−4 | 33.76 | 0.998 |
| [ChCl][PEG600][Gl]1:4:2 | 1.8643 × 10−4 | 34.57 | 0.997 |
| [ChCl][PEG600][Gl]1:5:2 | 1.6930 × 10−4 | 34.60 | 0.997 |
| [ChCl][O-cresol]4 | 1.4793 × 10−4 | 31.62 | 0.996 |
| [ChCl][O-cresol]5 | 2.5616 × 10−4 | 29.36 | 0.987 |
| [Bet][LA]3 | 1.2290 × 10−6 | 49.31 | 0.995 |
| [Bet][LA]4 | 2.5023 × 10−6 | 46.12 | 0.993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Pan, Y.; Gao, D.; Qu, H. Experimental Study on the Transport Properties of 12 Novel Deep Eutectic Solvents. Polymers 2024, 16, 1946. https://doi.org/10.3390/polym16131946
Fan J, Pan Y, Gao D, Qu H. Experimental Study on the Transport Properties of 12 Novel Deep Eutectic Solvents. Polymers. 2024; 16(13):1946. https://doi.org/10.3390/polym16131946
Chicago/Turabian StyleFan, Jing, Yuting Pan, Dazhi Gao, and Hongwei Qu. 2024. "Experimental Study on the Transport Properties of 12 Novel Deep Eutectic Solvents" Polymers 16, no. 13: 1946. https://doi.org/10.3390/polym16131946
APA StyleFan, J., Pan, Y., Gao, D., & Qu, H. (2024). Experimental Study on the Transport Properties of 12 Novel Deep Eutectic Solvents. Polymers, 16(13), 1946. https://doi.org/10.3390/polym16131946





