Optimization of Cohesive Parameters in the Interfacial Transition Zone of Rubberized Concrete Based on the Response Surface Method
Abstract
1. Introduction
2. Model Building
2.1. Detailed Model Geometry Generation
2.2. Constitutive Model of Concrete
2.3. Modeling of Cohesive Elements in ITZs
2.4. Model Calculations
2.4.1. Model Loads
2.4.2. Peak Load
2.4.3. Fatigue Life
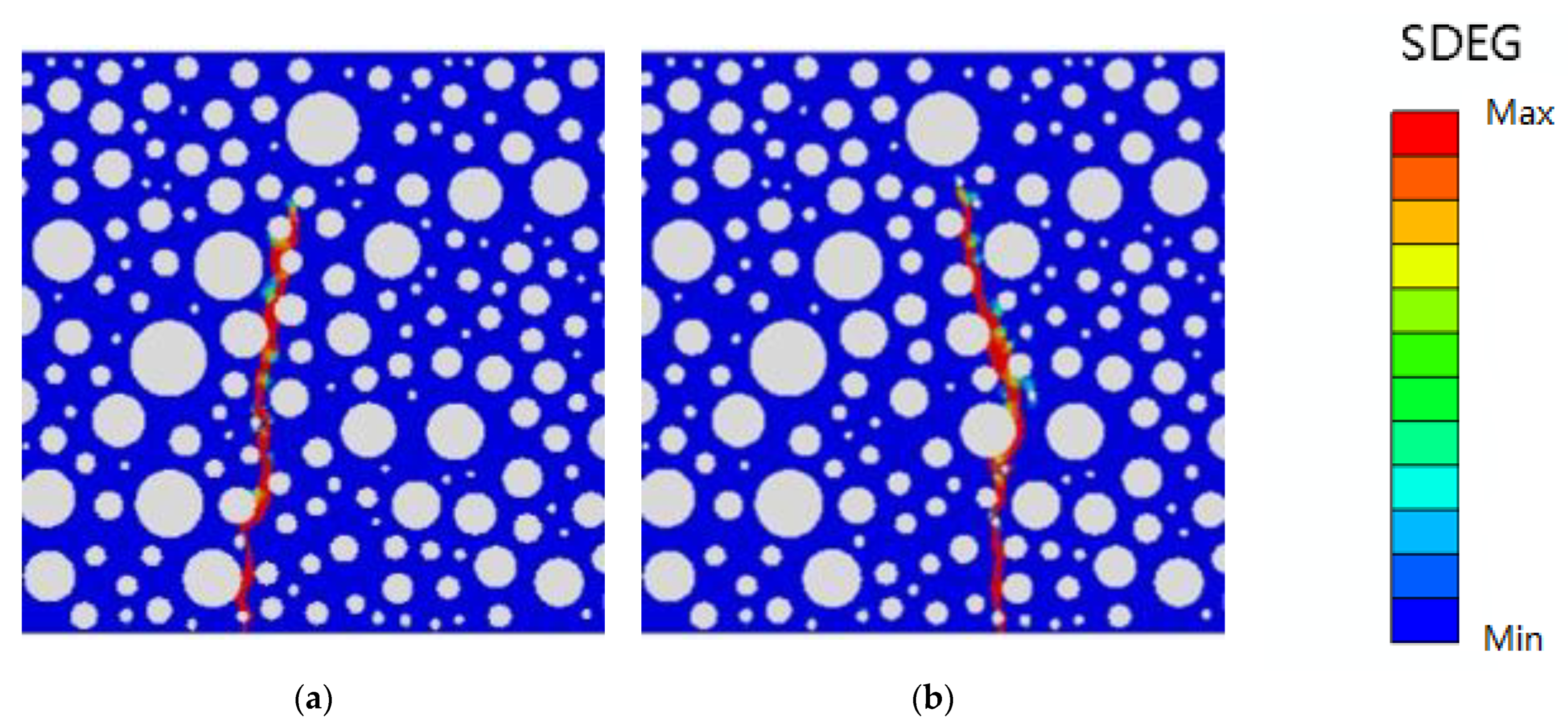
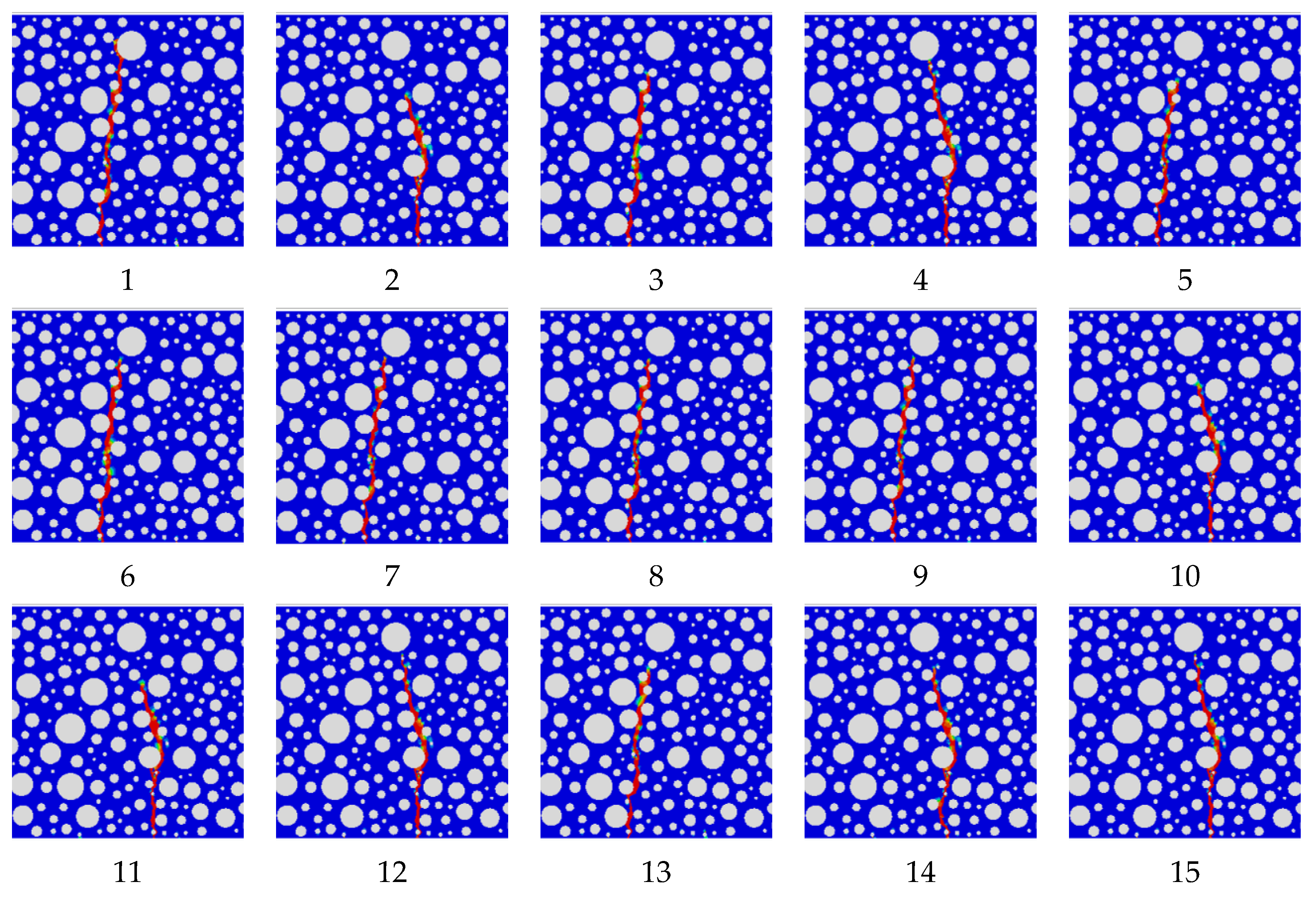
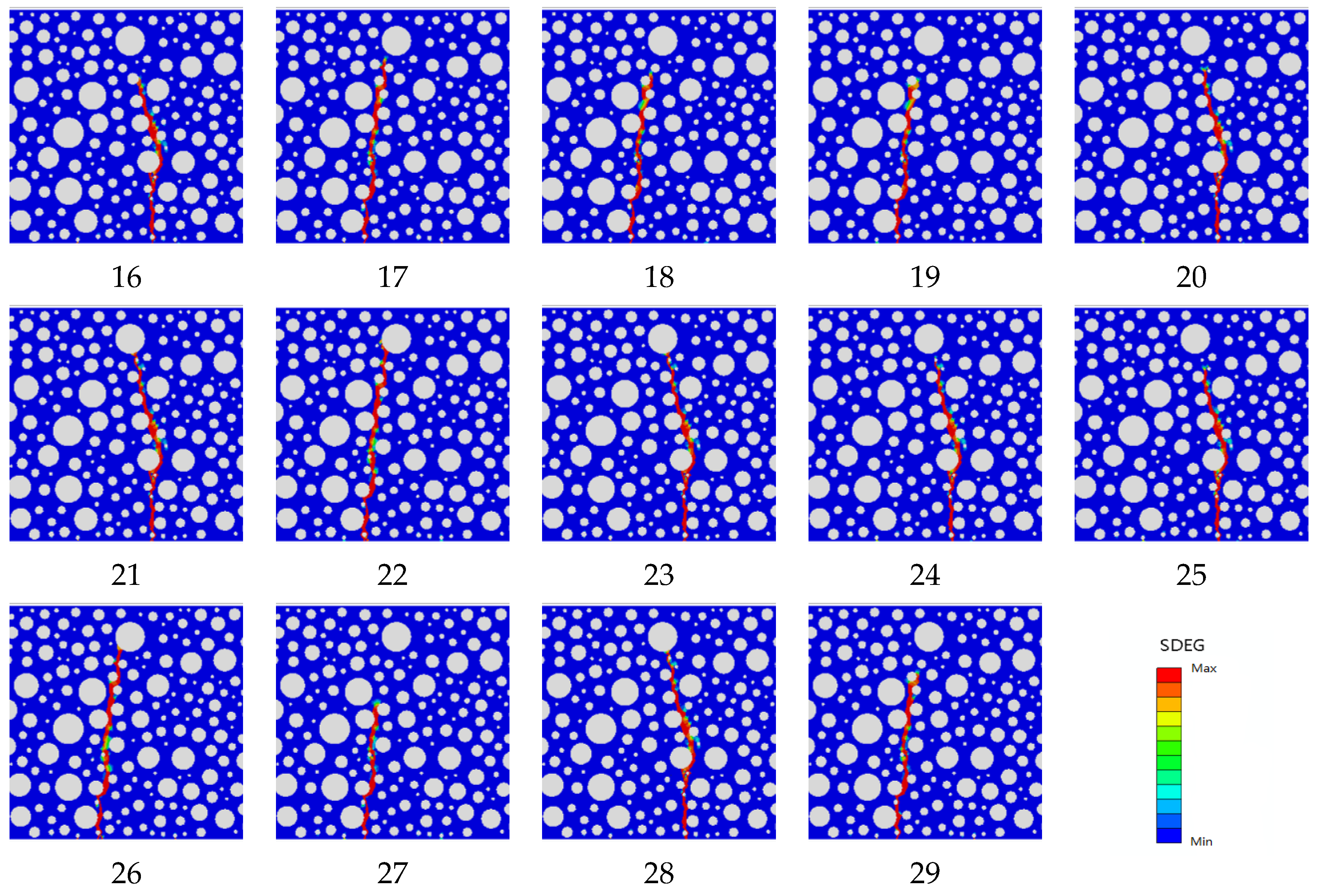
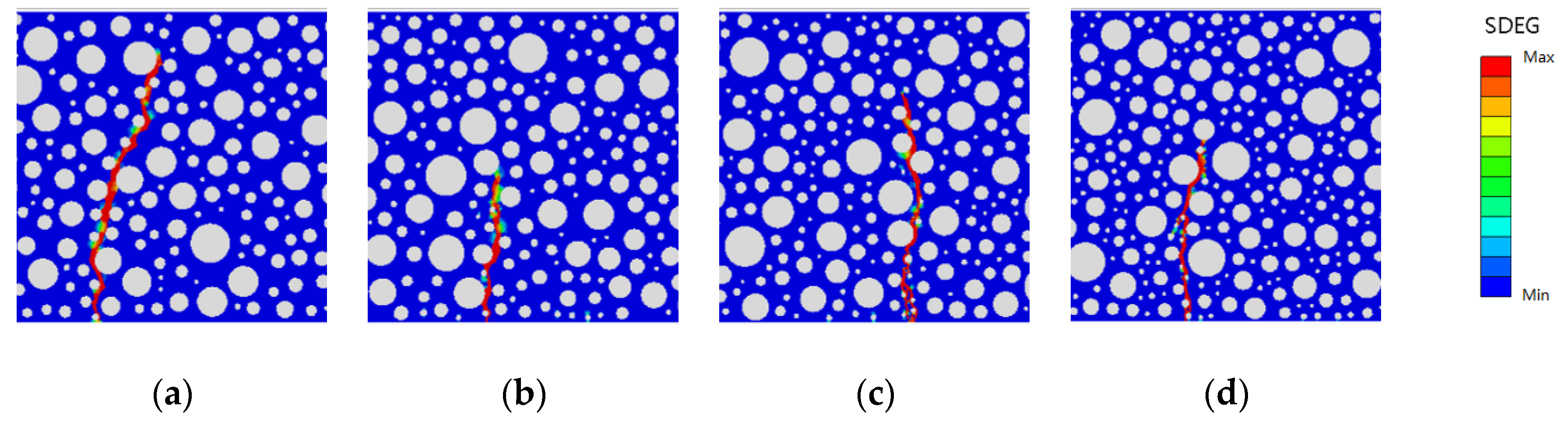
2.4.4. Forms of Damage
3. Cohesive Parameter Optimization
3.1. Monofactor Analysis
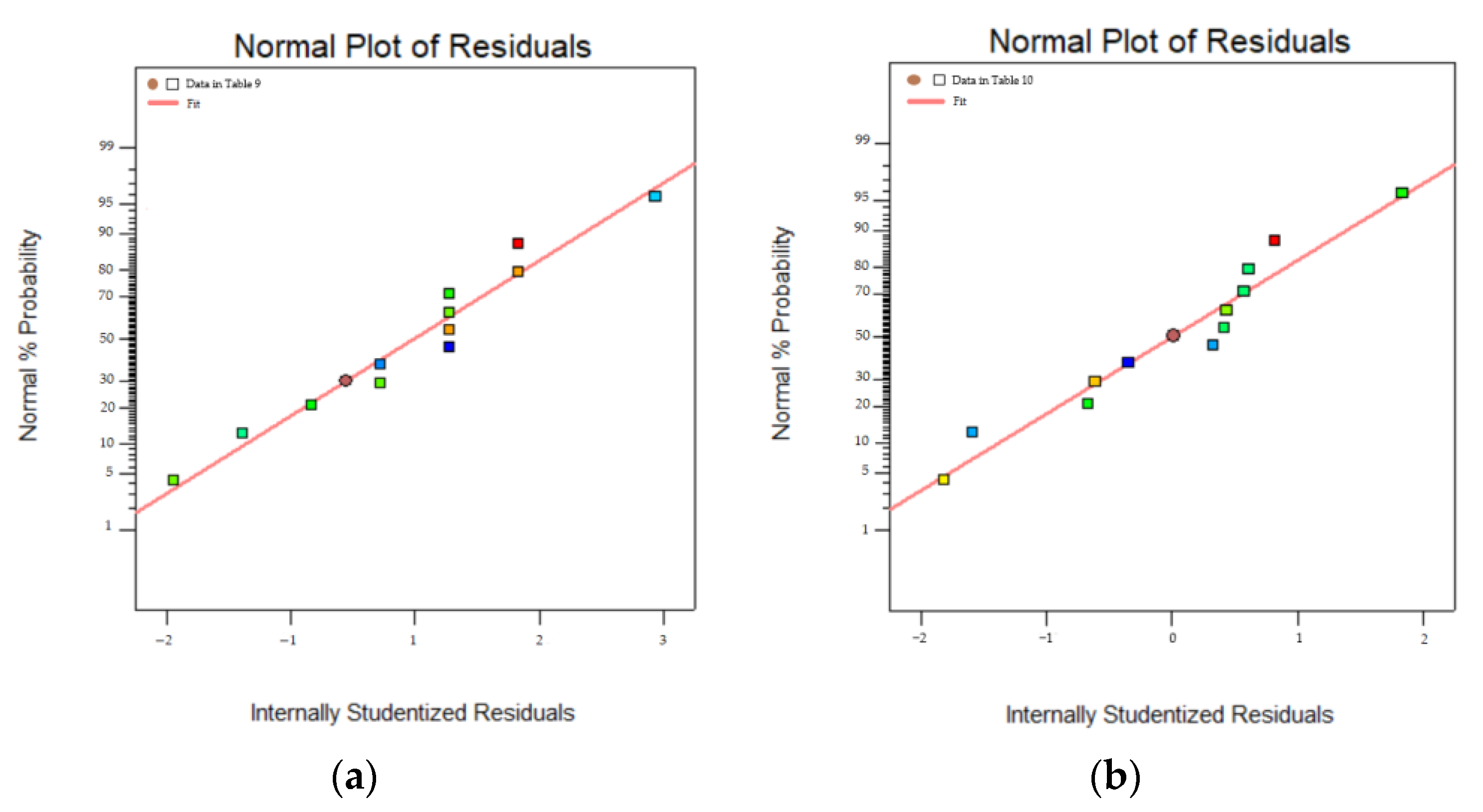
3.2. Plackett–Burman Design
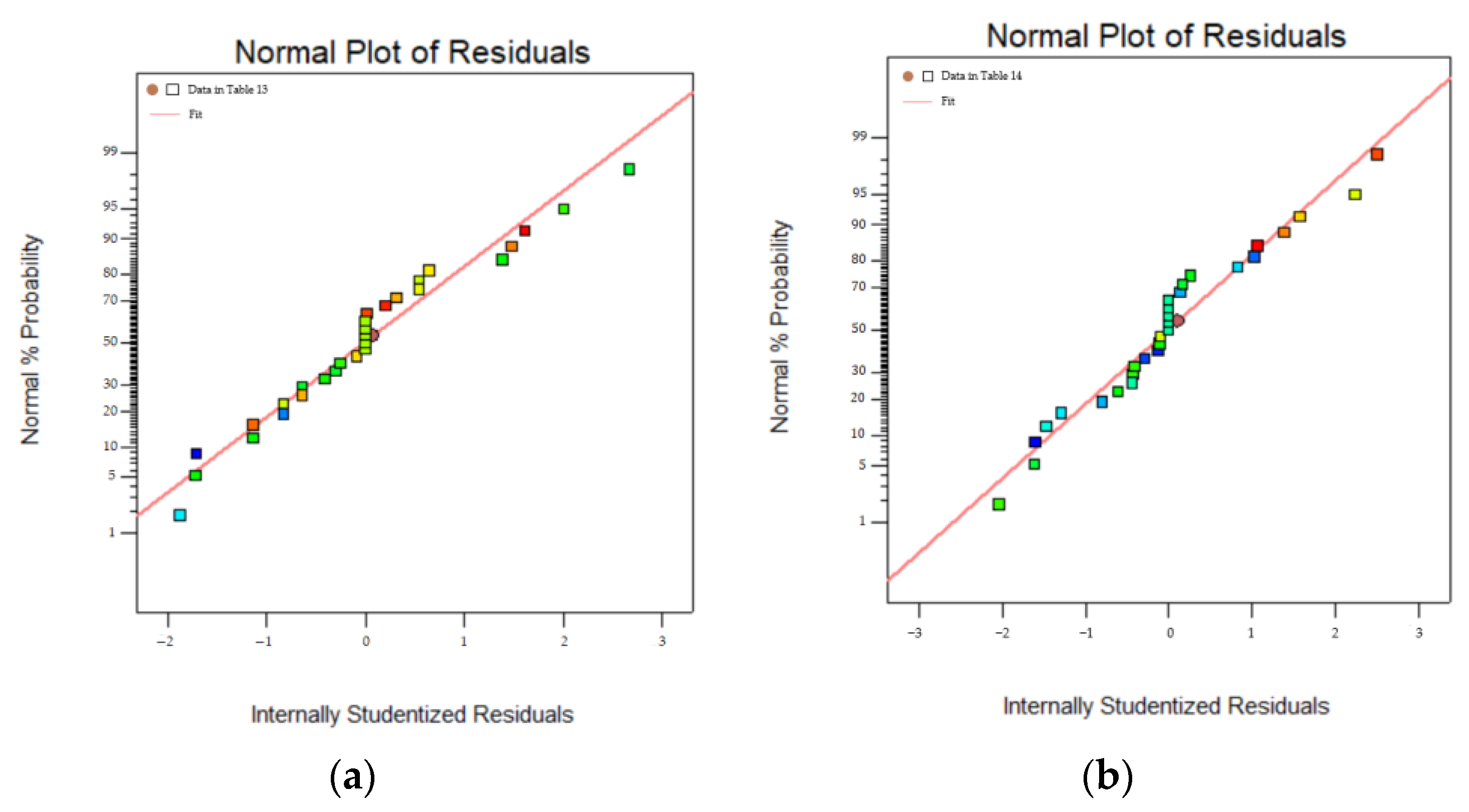
3.3. Response Surface Method Optimization
3.4. Optimization of Rubber-Mortar Interface Parameters
4. Numerical Simulation of Rubber-Mortar Interface Cohesive Parameters after Optimization
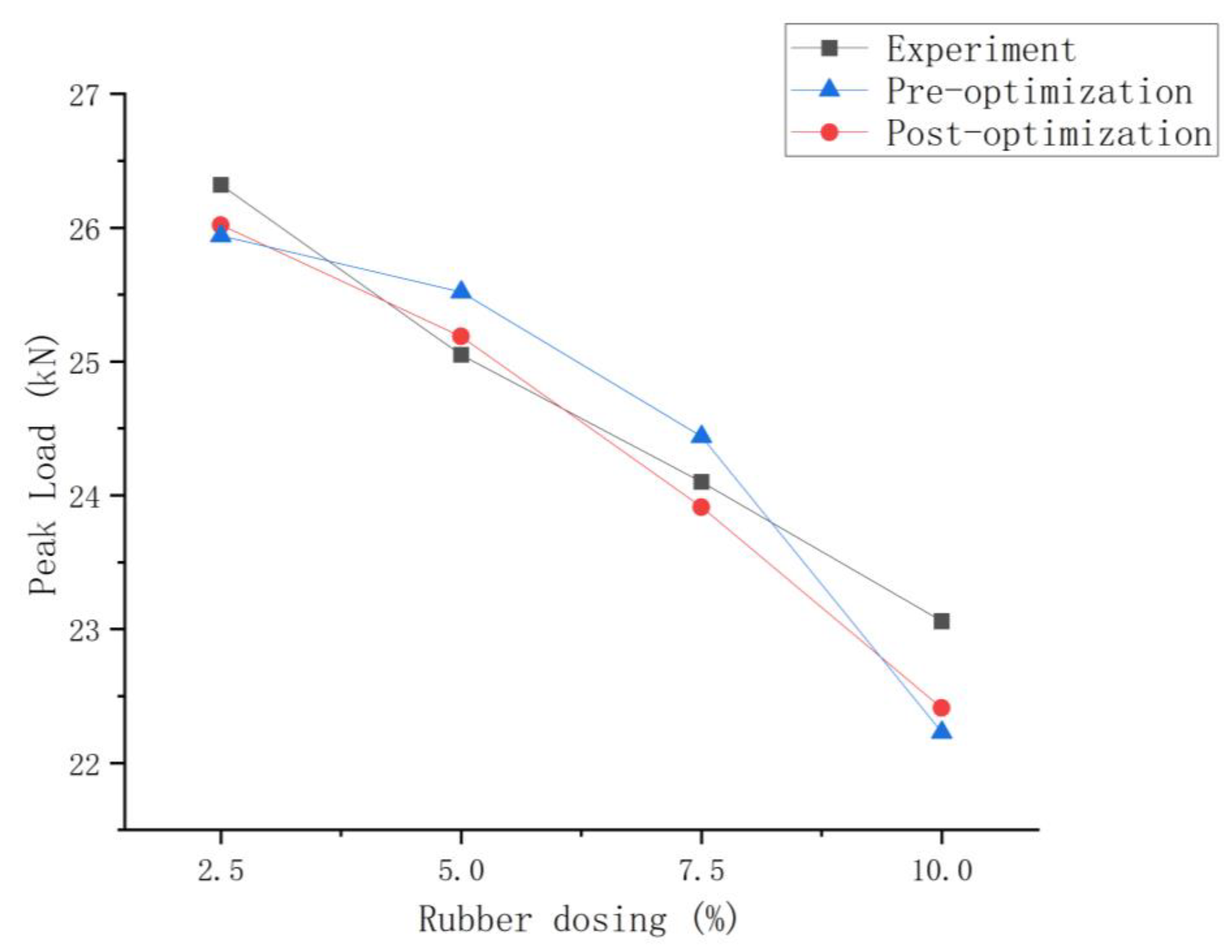
4.1. Peak Load after Optimization of rubber-mortar Interface Parameters
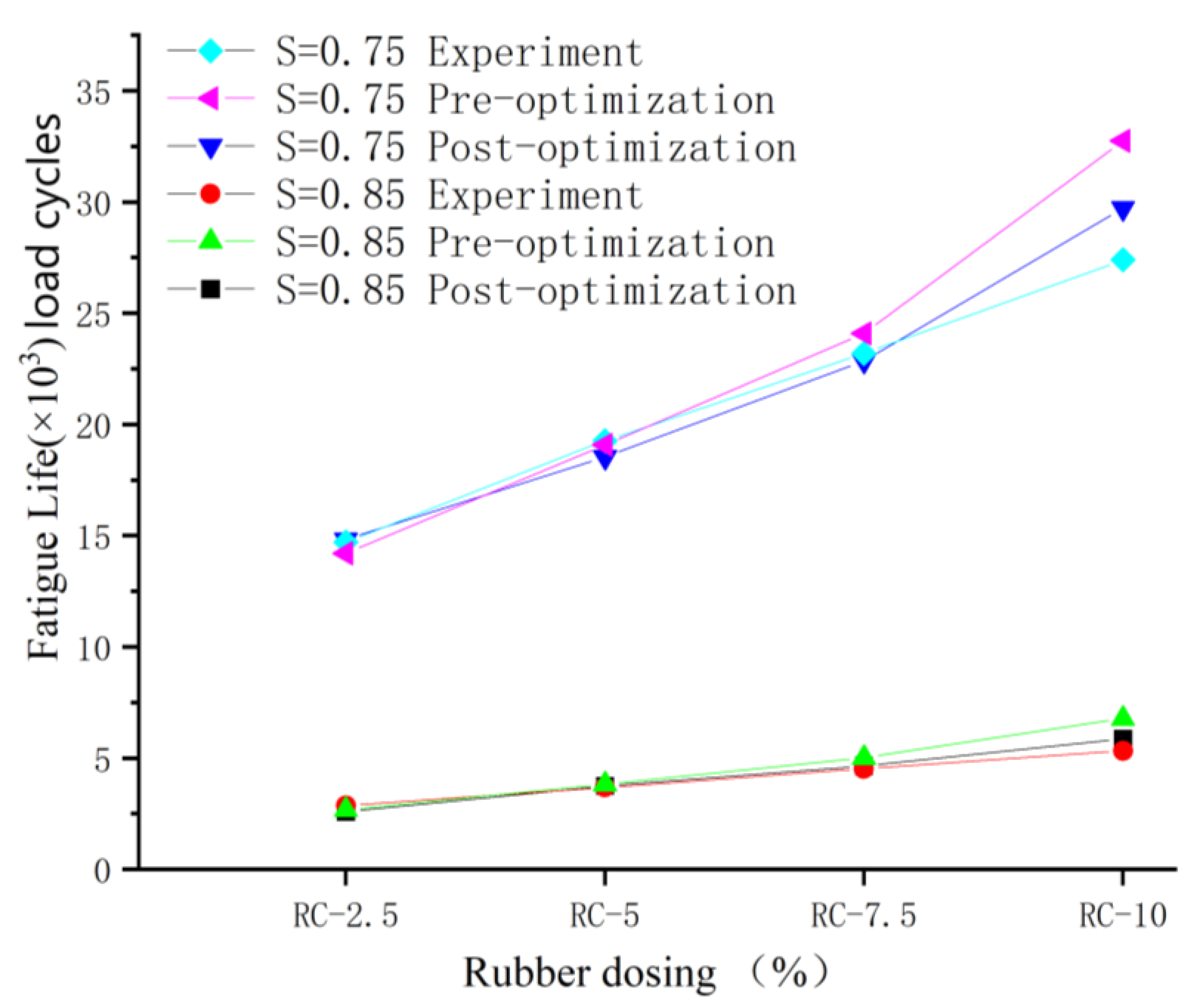
4.2. Fatigue Life after Optimization of Rubber-Mortar Interface Cohesive Parameters
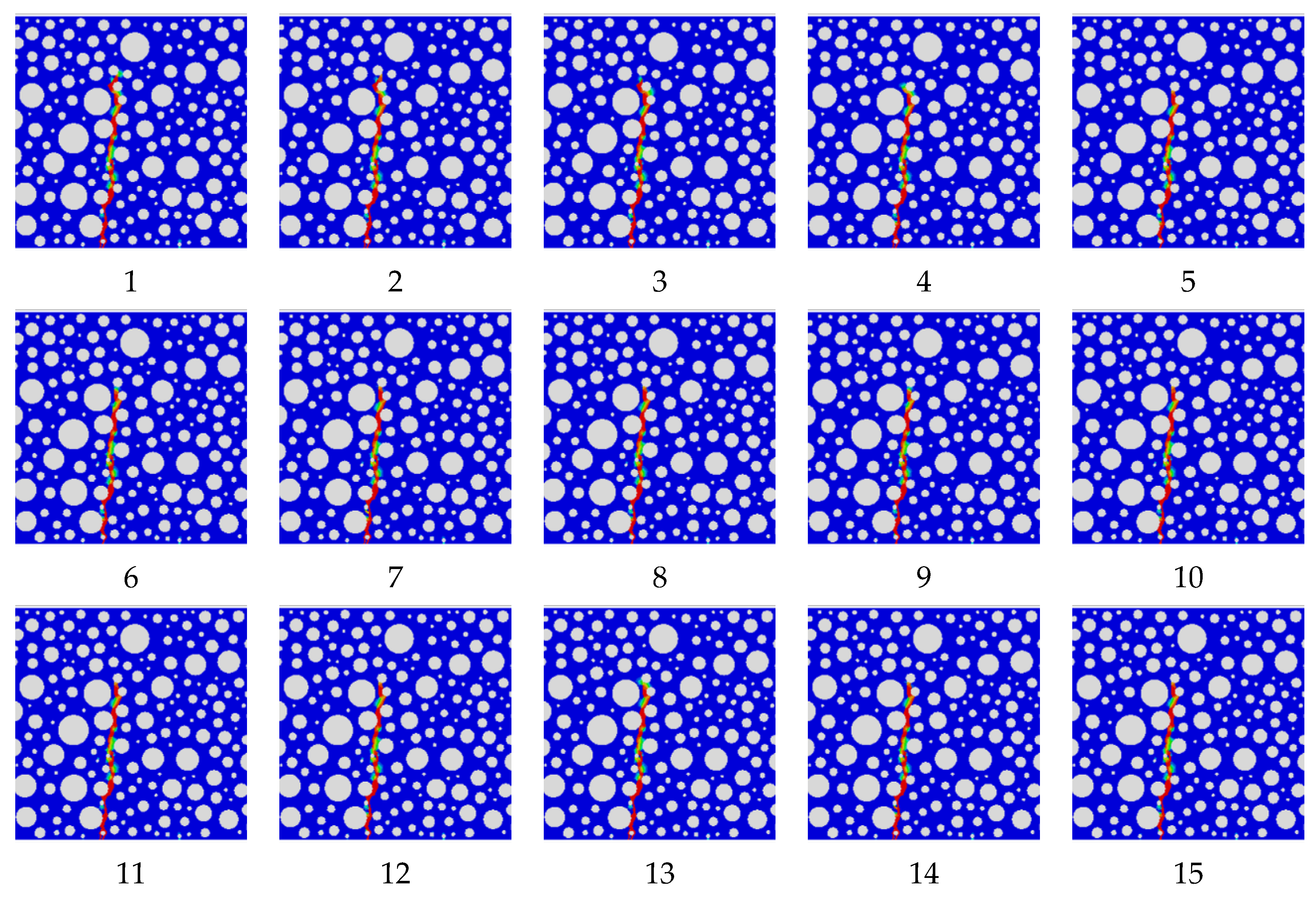
4.3. Damage Forms after Optimization of Rubber-Mortar Interface Cohesive Parameters
5. Discussion
5.1. Influence of Rubber-Mortar Interface Parameters
5.2. Optimization of Rubber-Mortar Interface Cohesive Parameters
5.3. Potential Applications and Developments
6. Conclusions
- A new numerical model containing plastic damage theory and cohesive element in the ITZ is adopted.
- The response surface method is used to analyze and optimize the rubber-mortar interfacial cohesive parameters of the new numerical model.
- An optimal rubber-mortar interfacial cohesive parameter combination is obtained, featuring a normal modulus of 29,300 MPa, tangential modulus of 11,000 MPa, normal strength of 2.57 MPa, and tangential strength of 8.6 MPa.
- It is found that, after optimizing the cohesive parameters, error values of the peak load and fatigue life at different stress levels decrease significantly.
- The failure form conforms to the actual situation, and the effect of the SDEG contour map is also better.
- In the rubber concrete models with rubber contents of 2.5%, 7.5%, and 10%, errors between simulation and experiment results under the optimal setting of the cohesive parameters at the rubber-mortar interface are all within a reasonable range.
- This set of optimized cohesive parameters has fully verified its feasibility and wide applicability in the cohesive model of rubber concrete, which can effectively improve the accuracy of this type of numerical simulation results.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, F.; Zheng, W.; Li, L.; Feng, W.; Ning, G. Mechanical and Fatigue Performance of Rubber Concrete. Constr. Build. Mater. 2013, 47, 711–719. [Google Scholar] [CrossRef]
- Yang, C.; Yang, M. Effect of modification mode on mechanical properties of rubberized concrete. J. Shenyang Univ. 2012, 24, 78–81. [Google Scholar]
- Yang, M. Research on Basic Mechanical Properties of Waste Rubber Concrete. Master’s Thesis, Shenyang University, Shenyang, China, 2012. [Google Scholar]
- Yuan, Q.; Feng, L.; Yuan, B. Effects of rubber particle size and admixture on concrete properties. People’s Yellow River 2013, 35, 111–113. [Google Scholar]
- Zheng, W. Experimental Study on Fatigue Performance of Rubberized Concrete. Master’s Thesis, Guangdong University of Technology, Guangdong, China, 2011. [Google Scholar]
- Fan, K. Research on Impact and Abrasion Resistance of Rubberized Concrete. Master’s Thesis, Tianjin University, Tianjin, China, 2010. [Google Scholar]
- Chen, G. Research on Impact Resistance of Rubberized Concrete. Master’s Thesis, Guangdong University of Technology, Guangdong, China, 2011. [Google Scholar]
- Hao, D.; Huang, X.; Li, H. Numerical Simulation of the Effect of Freeze-Thaw Cycles on the Axial Compression Strength of Rubber Concrete. Materials 2023, 16, 4460. [Google Scholar] [CrossRef]
- Raza, A.; Elhadi, K.M.; Abid, M. Structural performance of FRP composite b ars reinforced rubberized concrete compressive members: Tests and numerical modeling. Heliyon 2024, 10, e26222. [Google Scholar] [CrossRef]
- Qin, X.; Xu, Q. Study on fine-scale parameters of concrete direct shear test based on discrete element simulation. Hydropower Energy Sci. 2023, 41, 156–160. [Google Scholar]
- Hu, J. Numerical simulation of concrete strength under different test block heights. J. Anhui Archit. 2023, 30, 93–94+113. [Google Scholar]
- Chen, L.; Cheng, Y.; Zhou, W. Research on the mechanical properties of long-age concrete based on the lattice model. J. Wuhan Univ. (Eng. Ed.) 2022, 55, 238–246. [Google Scholar]
- Lu, D.; Gao, Y.; Wang, G. A near-field dynamics approach to reinforced concrete interfaces. J. Mech. 2023, 55, 403–416. [Google Scholar]
- Deng, W.; Li, H.; Wu, K. Peri Dynamics Simulation of Concrete Under Compression Based on Meso-Scale Model. J. Hubei Univ. Technol. 2019, 39, 86–91. [Google Scholar]
- You, Q.; Wang, W.; Nan, C. Research on the construction method of concrete fine view model based on CT image. J. Railw. Sci. Eng. 2023, 20, 3385–3395. [Google Scholar]
- An, R.; Li, Y.; Chen, G. Macroscopic model-based study of tensile stiffening effect of FRP-reinforced fiber-concrete beams. Compos. Sci. Eng. 2023, 2, 67–74. [Google Scholar]
- Wang, L.; Wang, C.; Zhang, Y.; Ma, A. Study on Fatigue Damage Process of Rubberized Cement Concrete by Acoustic Emission Technique. J. Southeast Univ. Nat. Sci. Ed. 2009, 39, 3. [Google Scholar]
- Kachkouch, F.Z.; Noberto, C.C.; Babadopulos, L.F.D.A.L.; Melo, A.R.S.; Machado, A.M.L.; Sebaibi, N.; Boukhelf, F.; El Mendili, Y. Fatigue Behavior of Concrete: A Literature Review on the Main Relevant Parameters. J. Constr. Build. Mater. 2022, 338, 127510. [Google Scholar] [CrossRef]
- He, J.; Lei, D.; Gao, Z. Research progress on the testing method of mechanical properties of concrete interfacial transition zone. Exp. Mech. 2022, 37, 805–820. [Google Scholar]
- Gaedicke, C.; Roesler, J.; Evangelista, F. Three-dimensional cohesive crack model prediction of the flexural capacity of concrete slabs on soil. Eng. Fract. Mech. 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Víctor, R.; Marta, S.; Flora, F.; Juan, M. Self-Compacting Concrete Manufactured with Recycled Concrete Aggregate: An Overview. J. Clean. Prod. 2020, 262, 121362. [Google Scholar]
- Zhang, B.; Nadimi, S.; Eissa, A. Modeling fracturing process using cohesive interface elements: Theoretical verification and experimental validation. Constr. Build. Mater. 2023, 365, 130132. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Wang, J.; Jivkov, A.P.; Dirk, L.; Engelberg, Q.; Li, M. Parametric Study of Cohesive ITZ in Meso-Scale Concrete Model. Procedia Struct. Integr. 2019, 23, 167–172. [Google Scholar] [CrossRef]
- Goncalves, D.J.S.; Moura, D.C. Application of interface of interface finite elements to three-dimensional progressive failure analysis of adhesive joints. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 479–486. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Dong, Y.; Su, C.; Qiao, P. An improved mesoscale damage model for quasi-brittle fracture analysis of concrete with ordinary state-based peridynamics. Theor. Appl. Fract. Mech. 2021, 112, 102829. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.P.; Costa, J. Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: Definition of interlaminar strengths and elastic stiffness. Compos. Struct. 2010, 92, 1857–1864. [Google Scholar] [CrossRef]
- Dimitri, R.; Trullo, M. Coupled cohesive zone models for mixed-mode fracture: A comparative study. Eng. Fract. Mech. 2015, 148, 145–179. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1987, 25, 299–326. [Google Scholar] [CrossRef]
- Zhong, G.; Guo, Y.; Li, L.; Liu, F. Analysis of Mechanical Performance of Crumb Rubber Concrete by Different Aggregate Shape under Uniaxial Compression on Me soscopic. Key Eng. Mater. 2011, 462–463, 219–222. [Google Scholar] [CrossRef]
- Schlangen, E.; Van Mier, J.G.M. Simple lattice model for numerical simulation of fracture of concrete materials and structures. Mater. Struct. 1992, 25, 534–542. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.; Kamel, M.M.A.; Ying, L. Mesomechanical Properties of Concrete with Different Shapes and Replacement Ratios of Recycled Aggregate Based on Base Force Element Method. Struct. Concr. 2019, 20, 1425–1437. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, X.; Shi, C. A review on the formation and improvement of the transition zone at the interface between cement paste and aggregate in concrete. Mater. Her. 2023, 37, 106–117. [Google Scholar]
- Xiao, J.; Li, W.; Sun, Z.; David, A.L.; Surendra, P.S. Properties of Interfacial Transition Zones in Recycled Aggregate Concrete Tested by Nanoindentation. Cem. Concr. Compos. 2013, 37, 276–292. [Google Scholar] [CrossRef]
- Kim, S.M.; Abu Al-Rub, R.K. Meso-scale computational modeling of the plastic-damage response of cementitious composites. Cem. Concr. Res. 2011, 41, 339–358. [Google Scholar] [CrossRef]
- Li, W.; Xiao, J.; Corr, D.J.; Shah, S.P. Numerical Modeling on the Stress-Strain Response and Fracture of Modeled Recycled Aggregate Concrete. Eng. Mater. Sci. 2013, 1, 749–759. [Google Scholar]
- Liu, Y. Fatigue Test and Life Prediction of Pre-Treated. Master’s Thesis, North China University of Water Resources and Electric Power, Zhengzhou, China, 2020. [Google Scholar]
- Pei, X. Numerical simulation of fatigue life of rubber concrete on the mesoscale. Polymers 2023, 15, 2048. [Google Scholar] [CrossRef]

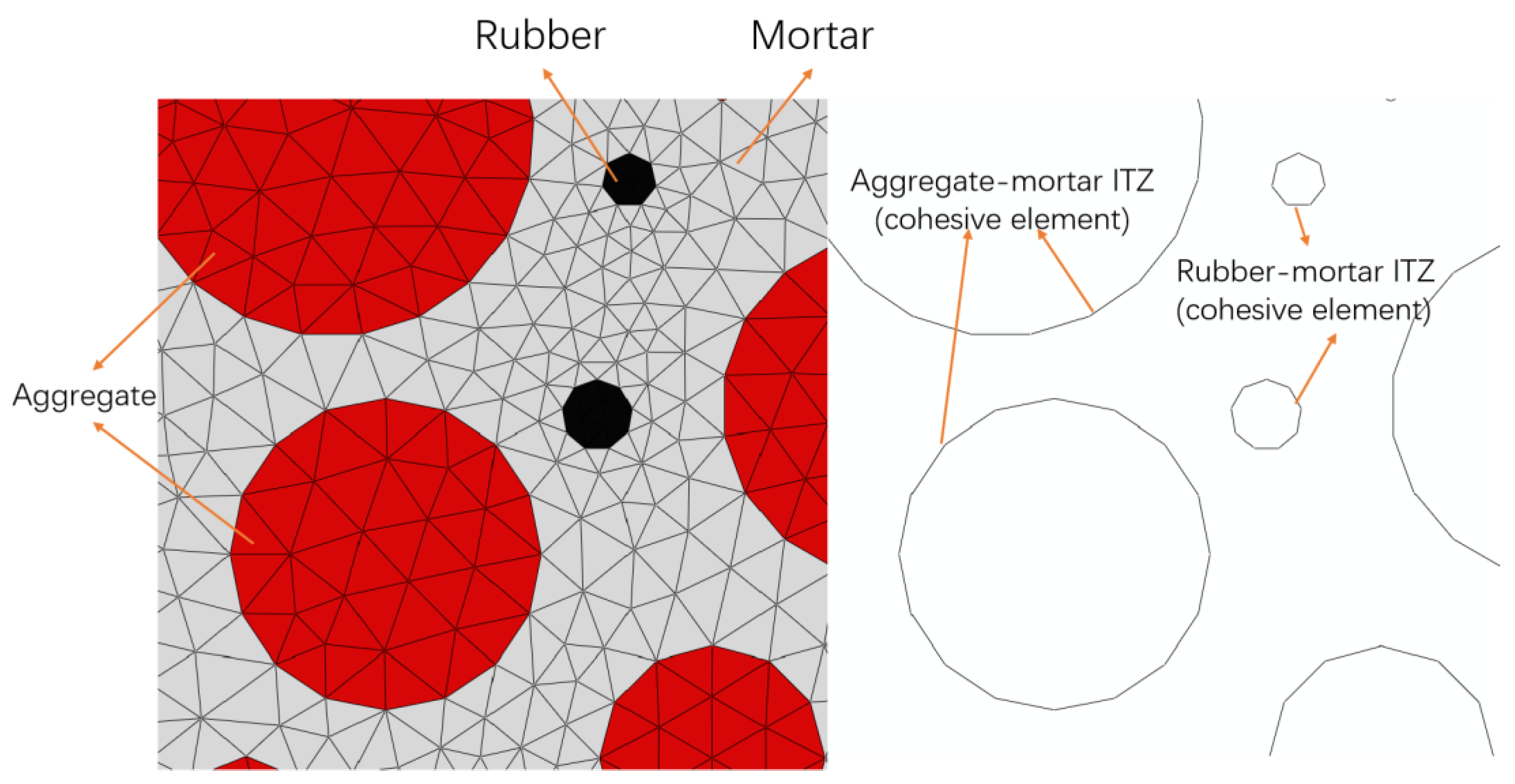
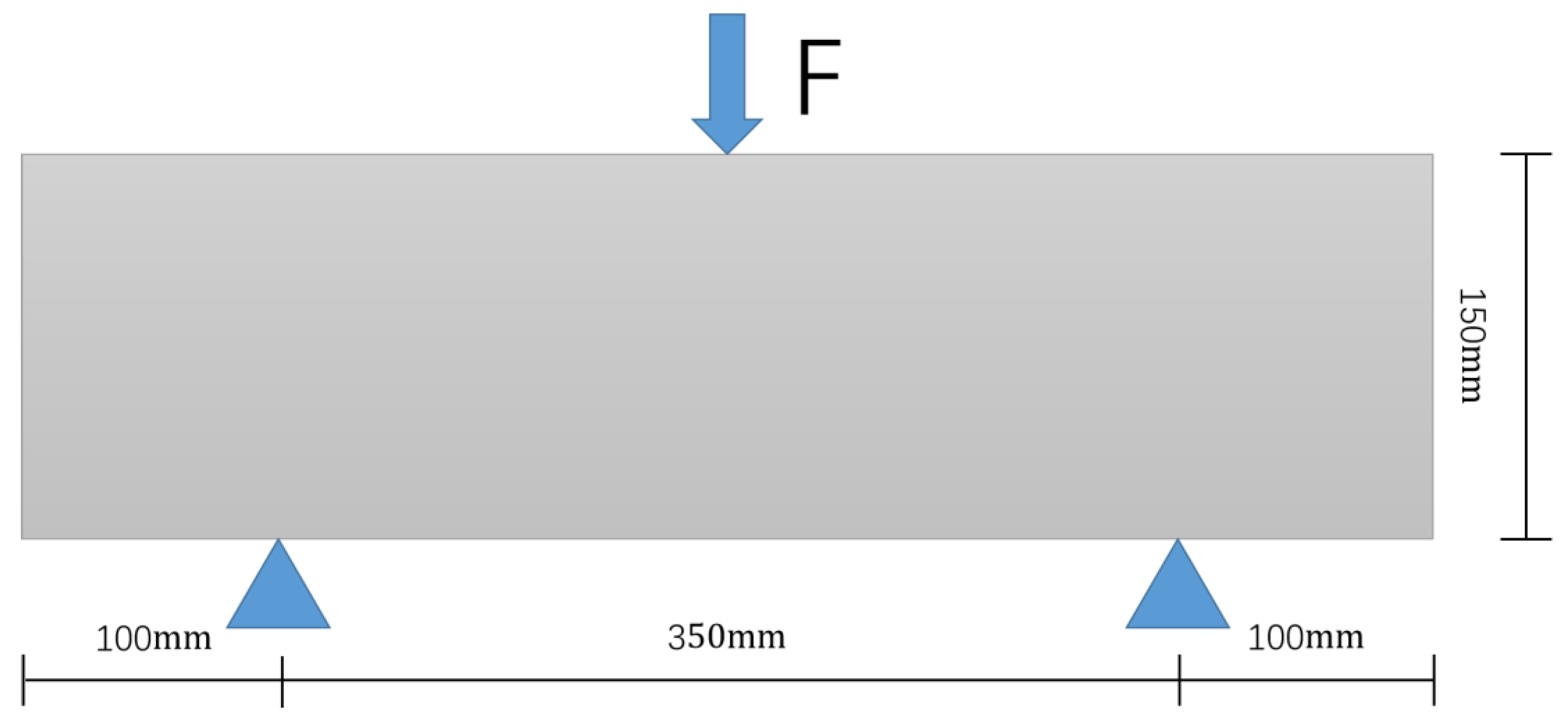
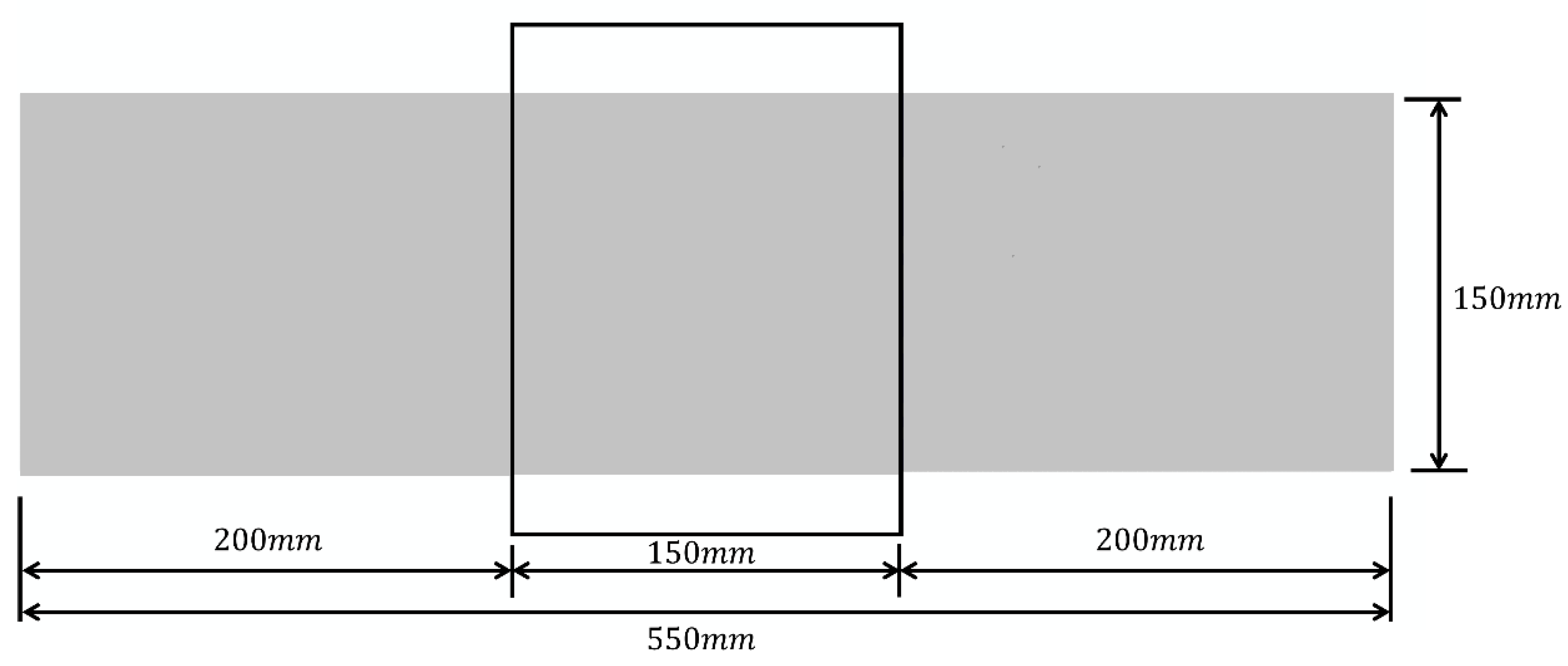
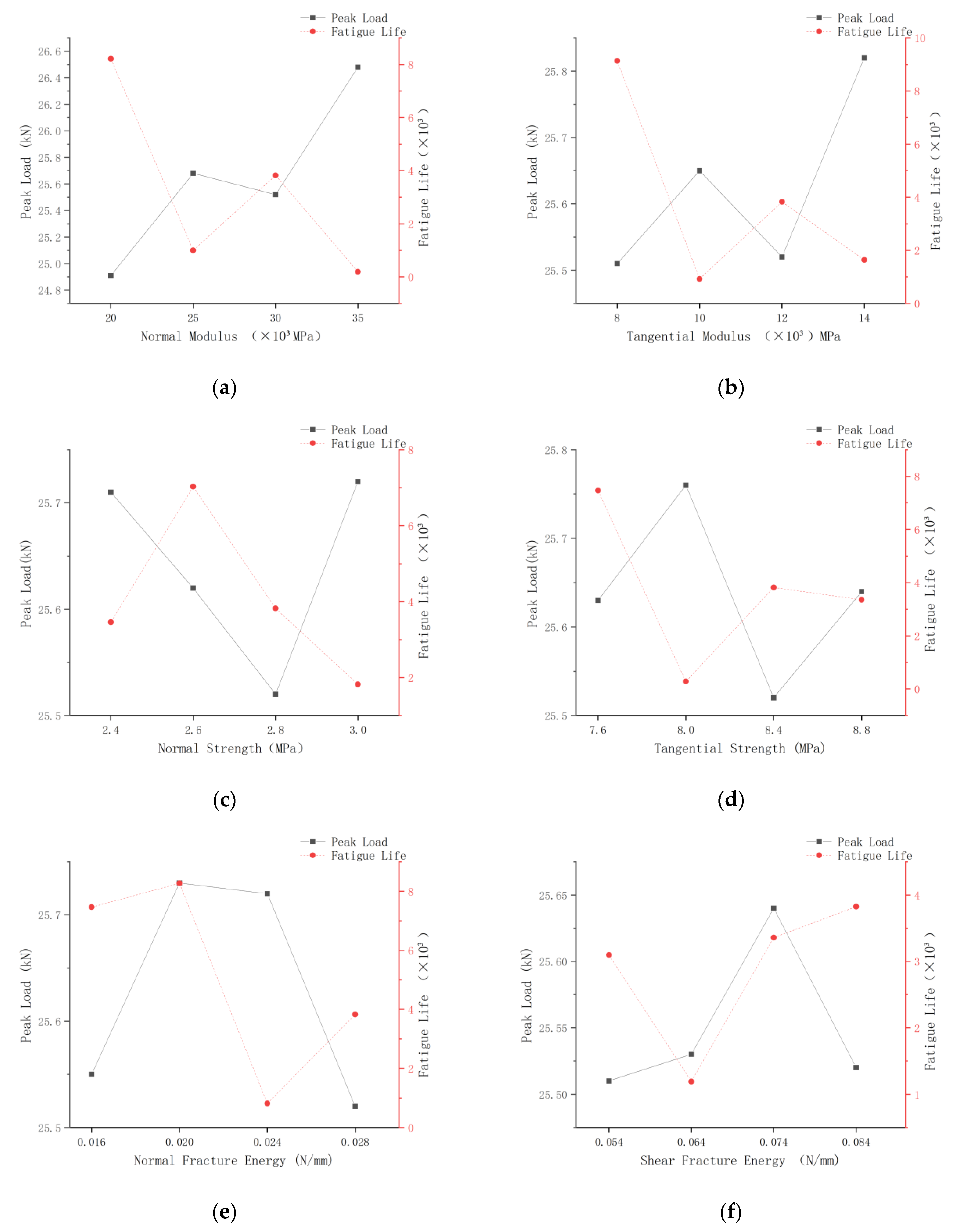




| Rubber Replacement Rate (%) | 5–10 mm (mm2) | 10–15 mm (mm2) | 15–20 mm (mm2) | Rubber (mm2) |
|---|---|---|---|---|
| 5 | 12,547 | 8851 | 5612 | 1537 |
| Type | Normal Strength (MPa) | Tangential Strength (MPa) | Normal Fracture Energy (N/mm) | Shear Fracture Energy (N/mm) |
|---|---|---|---|---|
| Aggregate-mortar ITZ | 3.1 | 9 | 0.03 | 0.09 |
| rubber-mortar ITZ | 2.8 | 8.4 | 0.028 | 0.084 |
| Experimental Peak Load (kN) | Simulated Peak Load (kN) | Error (%) |
|---|---|---|
| 25.05 | 25.52 | 1.88 |
| Type | S = 0.75 | S = 0.85 |
|---|---|---|
| Experiment (load cycles) | 18,555 | 3671 |
| Simulation (load cycles) | 19,081 | 3824 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Normal Fracture Energy (N/mm) | Shear Fracture Energy (N/mm) |
|---|---|---|---|---|---|
| 20,000 | 8000 | 2.4 | 7.6 | 0.016 | 0.054 |
| 25,000 | 10,000 | 2.6 | 8 | 0.02 | 0.064 |
| 30,000 | 12,000 | 2.8 | 8.4 | 0.024 | 0.074 |
| 35,000 | 14,000 | 3 | 8.8 | 0.028 | 0.084 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Normal Fracture Energy (N/mm) | Shear Fracture Energy (N/mm) |
|---|---|---|---|---|---|
| 30,000 | 12,000 | 2.8 | 8.4 | 0.024 | 0.074 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Normal Fracture Energy (N/mm) | Shear Fracture Energy (N/mm) |
|---|---|---|---|---|---|
| 27,000 | 11,000 | 2.5 | 7.8 | 0.022 | 0.07 |
| 32,000 | 13,000 | 2.9 | 8.6 | 0.03 | 0.09 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Normal Fracture Energy (N/mm) | Shear Fracture Energy (N/mm) | Peak Load (kN) | Fatigue Life (Load Cycles) |
|---|---|---|---|---|---|---|---|
| 32,000 | 13,000 | 2.5 | 7.8 | 0.02 | 0.09 | 25.33 | 3071 |
| 27,000 | 11,000 | 2.5 | 7.8 | 0.02 | 0.07 | 25.02 | 7812 |
| 32,000 | 13,000 | 2.5 | 8.6 | 0.03 | 0.09 | 25.33 | 3087 |
| 32,000 | 11,000 | 2.9 | 8.6 | 0.02 | 0.09 | 25.12 | 6889 |
| 32,000 | 13,000 | 2.9 | 7.8 | 0.02 | 0.07 | 25.4 | 1744 |
| 27,000 | 13,000 | 2.9 | 7.8 | 0.03 | 0.09 | 25.23 | 4836 |
| 27,000 | 13,000 | 2.5 | 8.6 | 0.03 | 0.07 | 25.22 | 5037 |
| 32,000 | 11,000 | 2.9 | 8.6 | 0.03 | 0.07 | 25.19 | 5634 |
| 32,000 | 11,000 | 2.5 | 7.8 | 0.03 | 0.07 | 25.18 | 5882 |
| 27,000 | 11,000 | 2.5 | 8.6 | 0.02 | 0.09 | 24.97 | 9733 |
| 27,000 | 13,000 | 2.9 | 8.6 | 0.02 | 0.07 | 25.22 | 4913 |
| 27,000 | 11,000 | 2.9 | 7.8 | 0.03 | 0.09 | 25.09 | 8178 |
| Variables | Sum of Squares of Variables | Variable Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Normal Modulus | 0.053 | 1 | 0.053 | 133.33 | <0.0001 |
| Tangential Modulus | 0.11 | 1 | 0.11 | 280.33 | <0.0001 |
| Normal Strength | 3.33 | 1 | 3.33 | 8.33 | 0.0343 |
| Tangential Strength | 3.33 | 1 | 3.33 | 8.33 | 0.0343 |
| Normal Fracture Energy | 2.7 | 1 | 2.7 | 6.75 | 0.0484 |
| Shear Fracture Energy | 2.13 | 1 | 2.13 | 5.33 | 0.069 |
| Variables | Sum of Squares of Variables | Variable Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Normal Modulus | 1.68 | 1 | 1.68 | 197.29 | <0.0001 |
| Tangential Modulus | 3.83 | 1 | 3.83 | 449.64 | <0.0001 |
| Normal Strength | 4.91 | 1 | 4.91 | 5.77 | 0.0615 |
| Tangential Strength | 1.18 | 1 | 1.18 | 13.9 | 0.0136 |
| Normal Fracture Energy | 1.9 | 1 | 1.9 | 2.22 | 0.196 |
| Shear Fracture Energy | 1.9 | 1 | 1.9 | 22.27 | 0.0052 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) |
|---|---|---|---|
| 27,000 | 11,000 | 2.5 | 7.8 |
| 29,500 | 12,000 | 2.7 | 8.2 |
| 32,000 | 13,000 | 2.9 | 8.6 |
| Group | Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Peak Load (kN) | Fatigue Life (Load Cycles) |
|---|---|---|---|---|---|---|
| 1 | 27,000 | 12,000 | 2.5 | 8.2 | 25.018 | 6591 |
| 2 | 27,000 | 12,000 | 2.7 | 8.6 | 25.223 | 3791 |
| 3 | 27,000 | 13,000 | 2.7 | 8.2 | 25.13 | 5057 |
| 4 | 32,000 | 13,000 | 2.7 | 8.2 | 25.215 | 4897 |
| 5 | 32,000 | 11,000 | 2.7 | 8.2 | 25.306 | 2654 |
| 6 | 29,500 | 11,000 | 2.7 | 8.6 | 25.243 | 3517 |
| 7 | 32,000 | 12,000 | 2.7 | 8.6 | 25.294 | 2814 |
| 8 | 29,500 | 12,000 | 2.9 | 7.8 | 25.257 | 3326 |
| 9 | 29,500 | 12,000 | 2.9 | 8.6 | 25.317 | 2499 |
| 10 | 29,500 | 12,000 | 2.7 | 8.2 | 25.2 | 4101 |
| 11 | 32,000 | 12,000 | 2.9 | 8.2 | 25.283 | 2968 |
| 12 | 29,500 | 12,000 | 2.7 | 8.2 | 25.2 | 4101 |
| 13 | 29,500 | 13,000 | 2.5 | 8.2 | 25.126 | 5115 |
| 14 | 27,000 | 11,000 | 2.7 | 8.2 | 25.132 | 5034 |
| 15 | 29,500 | 12,000 | 2.7 | 8.2 | 25.2 | 4101 |
| 16 | 32,000 | 12,000 | 2.5 | 8.2 | 25.147 | 5822 |
| 17 | 29,500 | 11,000 | 2.7 | 7.8 | 25.161 | 4632 |
| 18 | 29,500 | 13,000 | 2.7 | 8.6 | 25.145 | 5857 |
| 19 | 27,000 | 12,000 | 2.7 | 7.8 | 25.163 | 4608 |
| 20 | 29,500 | 12,000 | 2.5 | 7.8 | 24.974 | 7188 |
| 21 | 29,500 | 12,000 | 2.7 | 8.2 | 25.2 | 4101 |
| 22 | 29,500 | 11,000 | 2.5 | 8.2 | 25.146 | 4843 |
| 23 | 29,500 | 12,000 | 2.7 | 8.2 | 25.2 | 4101 |
| 24 | 29,500 | 13,000 | 2.7 | 7.8 | 25.045 | 6219 |
| 25 | 29,500 | 13,000 | 2.9 | 8.2 | 25.237 | 3599 |
| 26 | 27,000 | 12,000 | 2.9 | 8.2 | 25.218 | 6860 |
| 27 | 32,000 | 12,000 | 2.7 | 7.8 | 25.274 | 4088 |
| 28 | 29,500 | 11,000 | 2.9 | 8.2 | 25.257 | 3328 |
| 29 | 29,500 | 12,000 | 2.5 | 8.6 | 25.15 | 4784 |
| Variables | Sum of Squares of Variables | Variable Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Normal Modulus _(A) | 0.034 | 1 | 0.034 | 17.68 | 0.0009 |
| Tangential Modulus _(B) | 9.46 | 1 | 9.46 | 4.98 | 0.0425 |
| Normal Strength _(C) | 0.085 | 1 | 0.085 | 44.55 | <0.0001 |
| Tangential Strength _(D) | 0.02 | 1 | 0.02 | 10.44 | 0.006 |
| AB | 1.98 | 1 | 1.98 | 1.04 | 0.3247 |
| AC | 1.02 | 1 | 1.02 | 0.54 | 0.475 |
| AD | 4 | 1 | 4 | 0.21 | 0.6534 |
| BC | 0 | 1 | 0 | 0 | 1 |
| BD | 1.64 | 1 | 1.64 | 8.42 | 0.9282 |
| CD | 3.36 | 1 | 3.36 | 1.77 | 0.2046 |
| A2 | 1.29 | 1 | 1.29 | 0.68 | 0.4244 |
| B2 | 1.91 | 1 | 1.91 | 1.01 | 0.3329 |
| C2 | 2.61 | 1 | 2.61 | 1.37 | 0.2612 |
| D2 | 1.2 | 1 | 1.2 | 0.063 | 0.8057 |
| Variables | Sum of Squares of Variables | Variable Degree of Freedom | Mean Square | F | p |
|---|---|---|---|---|---|
| Normal Modulus _(A) | 6.31 | 1 | 6.31 | 7.41 | 0.0165 |
| Tangential Modulus _(B) | 3.78 | 1 | 3.78 | 4.44 | 0.0535 |
| Normal Strength _(C) | 1.15 | 1 | 1.15 | 13.55 | 0.0025 |
| Tangential Strength _(D) | 3.85 | 1 | 3.85 | 4.53 | 0.0516 |
| AB | 1.23 | 1 | 1.23 | 1.45 | 0.2488 |
| AC | 2.44 | 1 | 2.44 | 2.87 | 0.1126 |
| AD | 52,212.25 | 1 | 52,212.25 | 0.061 | 0.8079 |
| BC | 0.25 | 1 | 0.25 | 2.94 | 0.9996 |
| BD | 1.42 | 1 | 1.42 | 0.17 | 0.6893 |
| CD | 6.22 | 1 | 6.22 | 0.73 | 0.407 |
| A2 | 4.40 | 1 | 4.40 | 0.52 | 0.484 |
| B2 | 2.76 | 1 | 2.76 | 0.32 | 0.5778 |
| C2 | 1.48 | 1 | 1.48 | 1.74 | 0.2083 |
| D2 | 4995 | 1 | 4995 | 5.87 | 0.94 |
| Normal Modulus (MPa) | Tangential Modulus (MPa) | Normal Strength (MPa) | Tangential Strength (MPa) | Expected Peak Load (kN) | Expected Fatigue Life (Load Cycles) |
|---|---|---|---|---|---|
| 29,300 | 11,000 | 2.57 | 8.6 | 25.194 | 3684 |
| Peak Load (kN) | Fatigue Life (Load Cycles) | |
|---|---|---|
| Expected value | 25.194 | 3684 |
| Experimental value | 25.05 | 3671 |
| Simulated value | 25.187 | 3744 |
| RC–2.5 | RC–5 | RC–7.5 | RC–10 | |
|---|---|---|---|---|
| Experiment (kN) | 26.32 | 25.05 | 24.1 | 23.06 |
| Pre-optimization (kN) | 25.94 | 25.52 | 24.44 | 22.23 |
| Pre-optimization error | −1.44% | 1.88% | 1.41% | −3.6% |
| Post-optimization (kN) | 26.02 | 25.187 | 23.913 | 22.41 |
| Post-optimization error | −1.14% | 0.55% | −0.78% | −2.82% |
| RC–2.5 | RC–5 | RC–7.5 | RC–10 | |
|---|---|---|---|---|
| Experiment (load cycles) | 2870 | 3684 | 4521 | 5330 |
| Pre-optimization (load cycles) | 2678 | 3824 | 5018 | 6779 |
| Pre-optimization error | −6.69% | 3.8% | 10.99% | 27.2% |
| Post-optimization (load cycles) | 2588 | 3744 | 4651 | 5861 |
| Post-optimization error | −9.83% | 1.98% | 2.88% | 9.97% |
| RC–2.5 | RC–5 | RC–7.5 | RC–10 | |
|---|---|---|---|---|
| Experiment (load cycles) | 14,706 | 19,265 | 23,188.5 | 27,403 |
| Pre-optimization (load cycles) | 14,208 | 19,081 | 24,085 | 32,742 |
| Pre-optimization error | −3.39% | −0.96% | 3.87% | 19.48% |
| Post-optimization (load cycles) | 14,823 | 18,534 | 22,859 | 29,724 |
| Post-optimization error | 0.80% | −3.79% | −1.42% | 8.47% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Min, K.; Pei, X.; Li, H.; Cao, Z.; Yang, Z.; Hao, D.; Li, W.; Liu, C.; Wu, K. Optimization of Cohesive Parameters in the Interfacial Transition Zone of Rubberized Concrete Based on the Response Surface Method. Polymers 2024, 16, 1579. https://doi.org/10.3390/polym16111579
Min K, Pei X, Li H, Cao Z, Yang Z, Hao D, Li W, Liu C, Wu K. Optimization of Cohesive Parameters in the Interfacial Transition Zone of Rubberized Concrete Based on the Response Surface Method. Polymers. 2024; 16(11):1579. https://doi.org/10.3390/polym16111579
Chicago/Turabian StyleMin, Kai, Xianfeng Pei, Houmin Li, Zhou Cao, Zijiang Yang, Dingyi Hao, Wenchao Li, Cai Liu, and Keyang Wu. 2024. "Optimization of Cohesive Parameters in the Interfacial Transition Zone of Rubberized Concrete Based on the Response Surface Method" Polymers 16, no. 11: 1579. https://doi.org/10.3390/polym16111579
APA StyleMin, K., Pei, X., Li, H., Cao, Z., Yang, Z., Hao, D., Li, W., Liu, C., & Wu, K. (2024). Optimization of Cohesive Parameters in the Interfacial Transition Zone of Rubberized Concrete Based on the Response Surface Method. Polymers, 16(11), 1579. https://doi.org/10.3390/polym16111579







