Strain Effect on Dielectricity of Elastic Thermoplastic Polyurethanes
Abstract
1. Introduction
2. Materials and Methods
2.1. Dielectric Elastomers
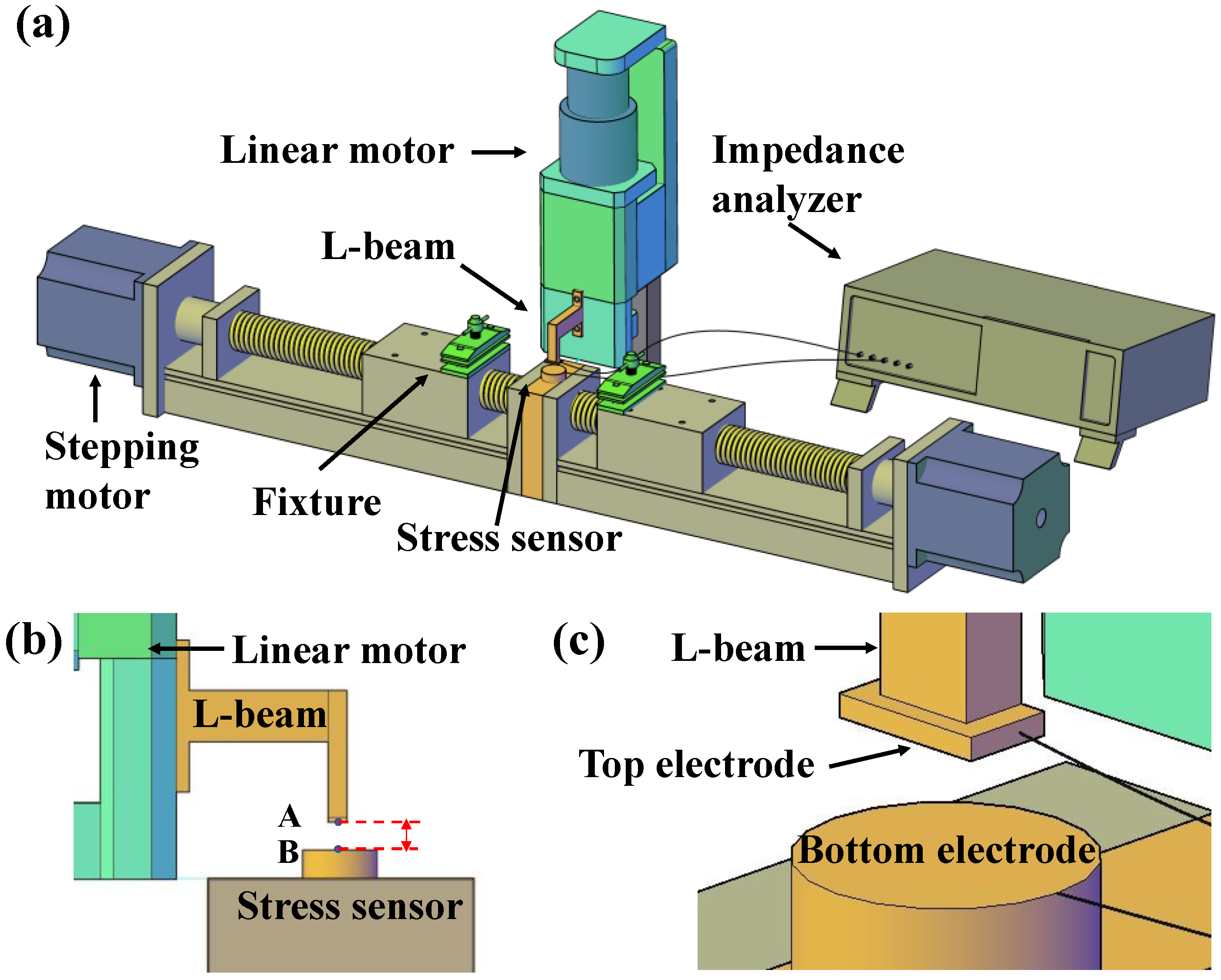
2.2. Experimental Setup
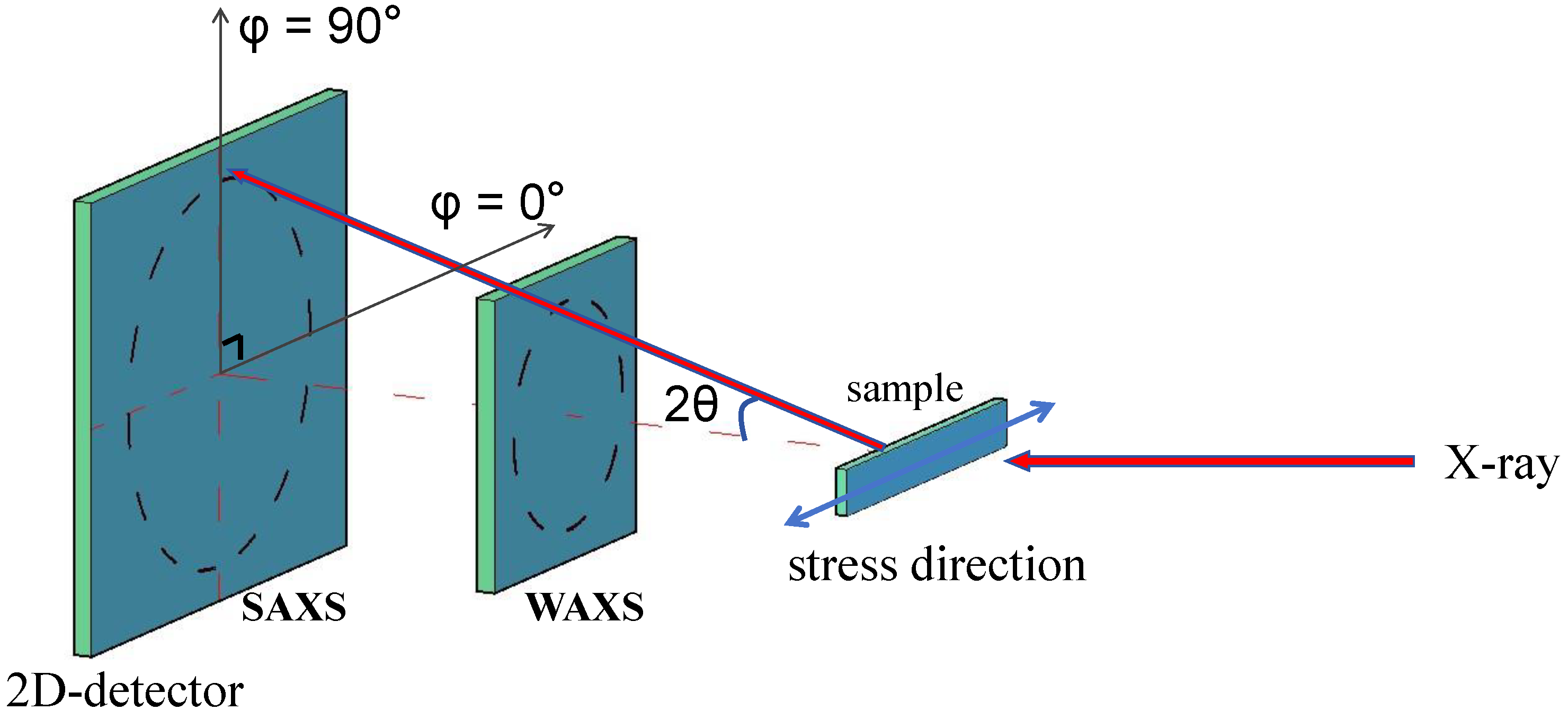
2.3. Characterization
3. Results
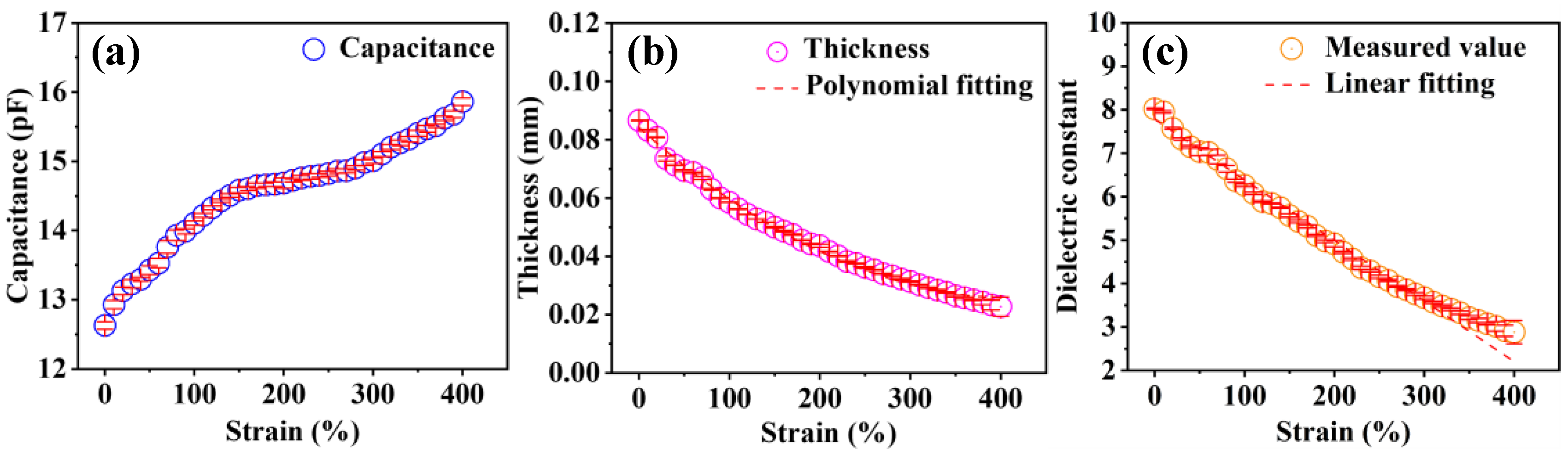
3.1. Variation in the Dielectric Constant of TPU under Tensile Strain
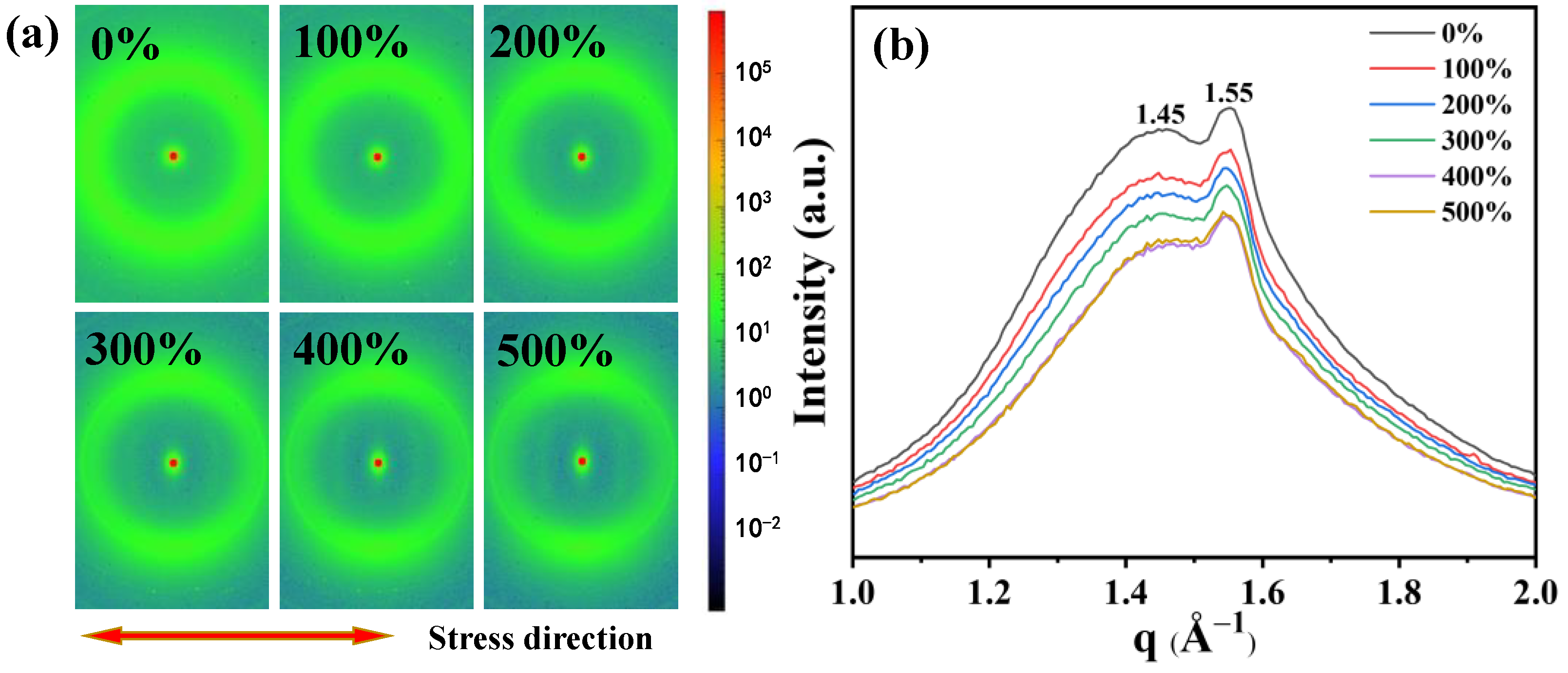
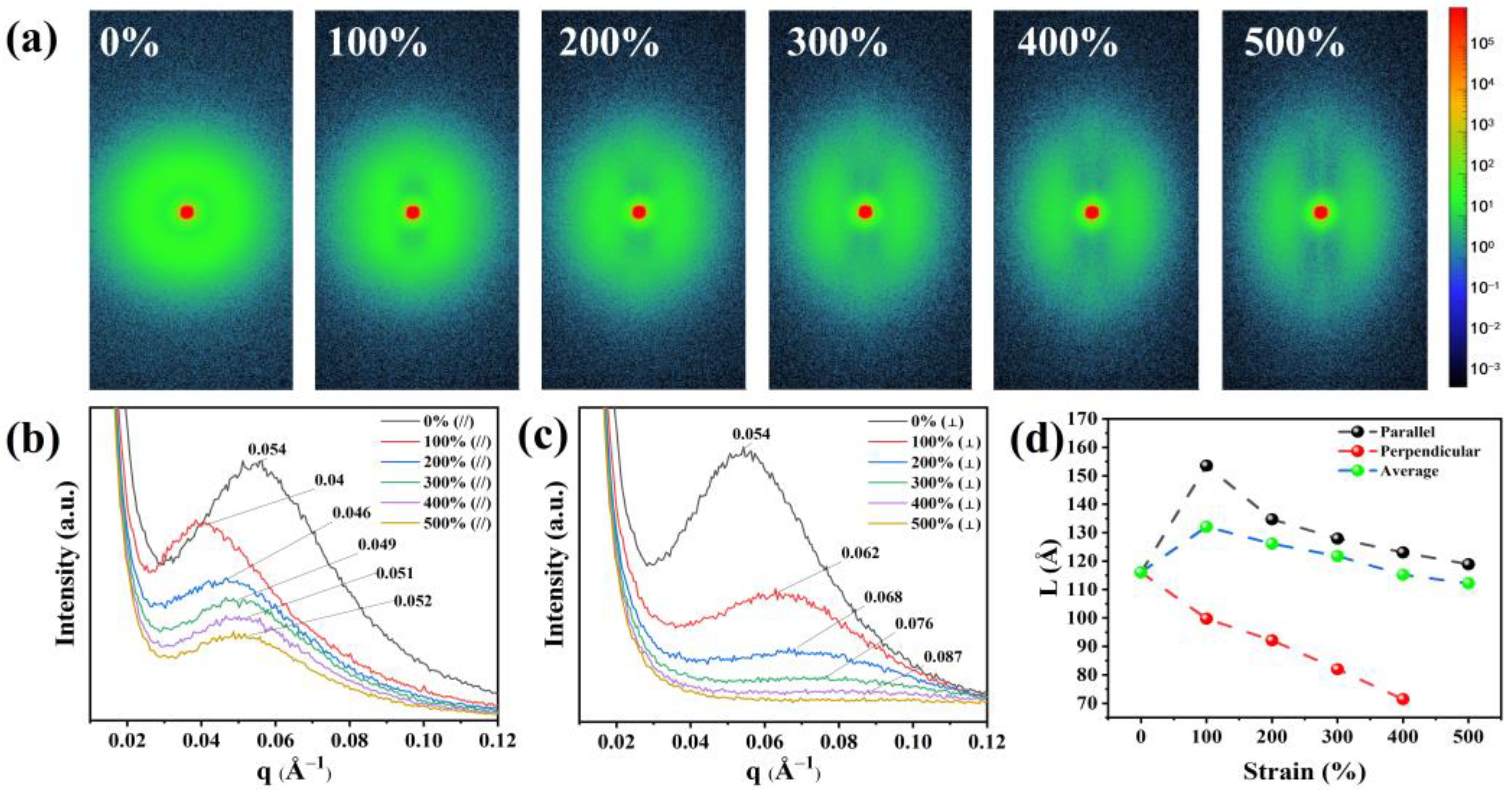
3.2. Orientation Behavior of TPU during Tensile Strain
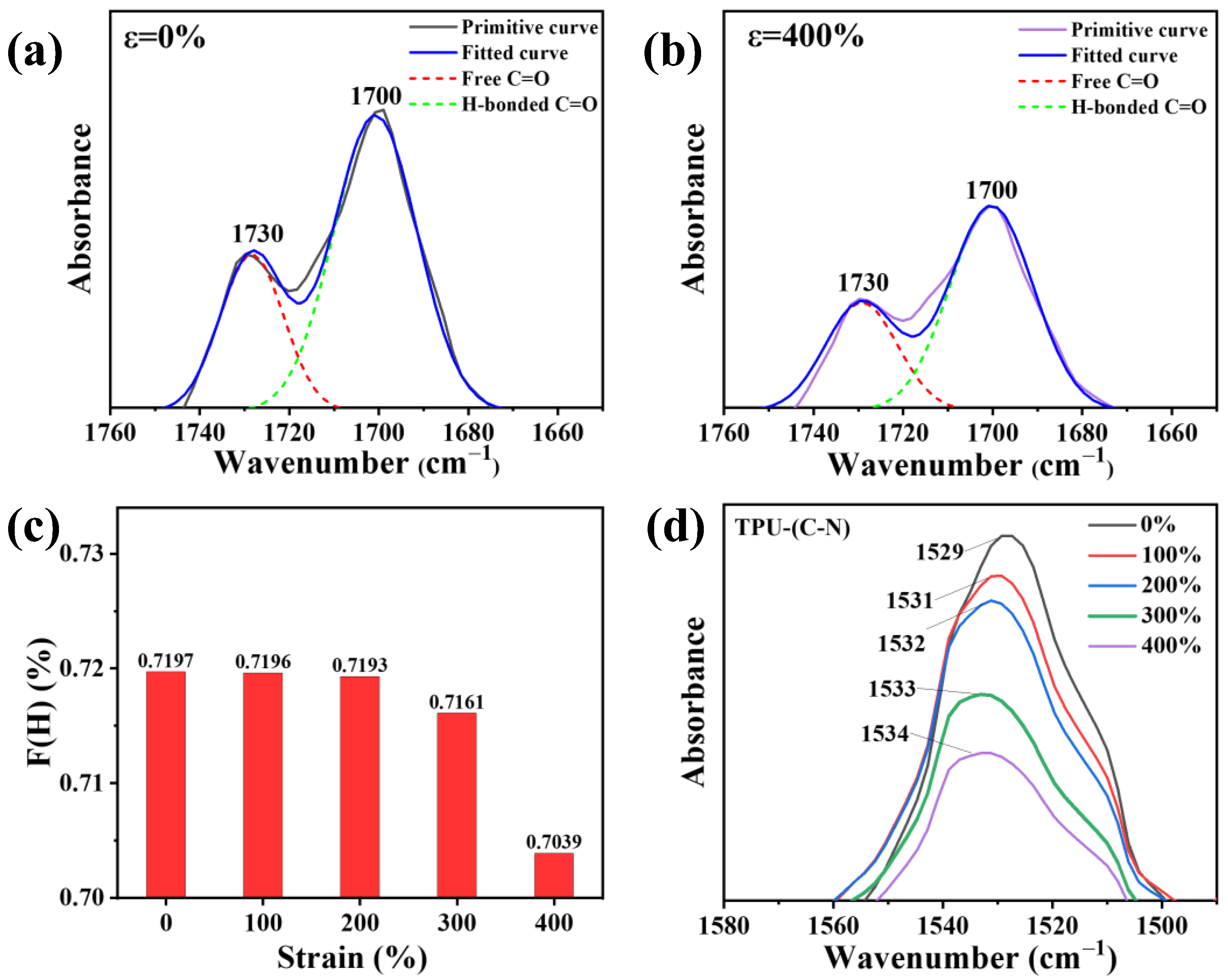
3.3. Changes in Hydrogen Bonding under Tensile Strain
3.4. Variation in the Molecular Chain Long Period during Stretching
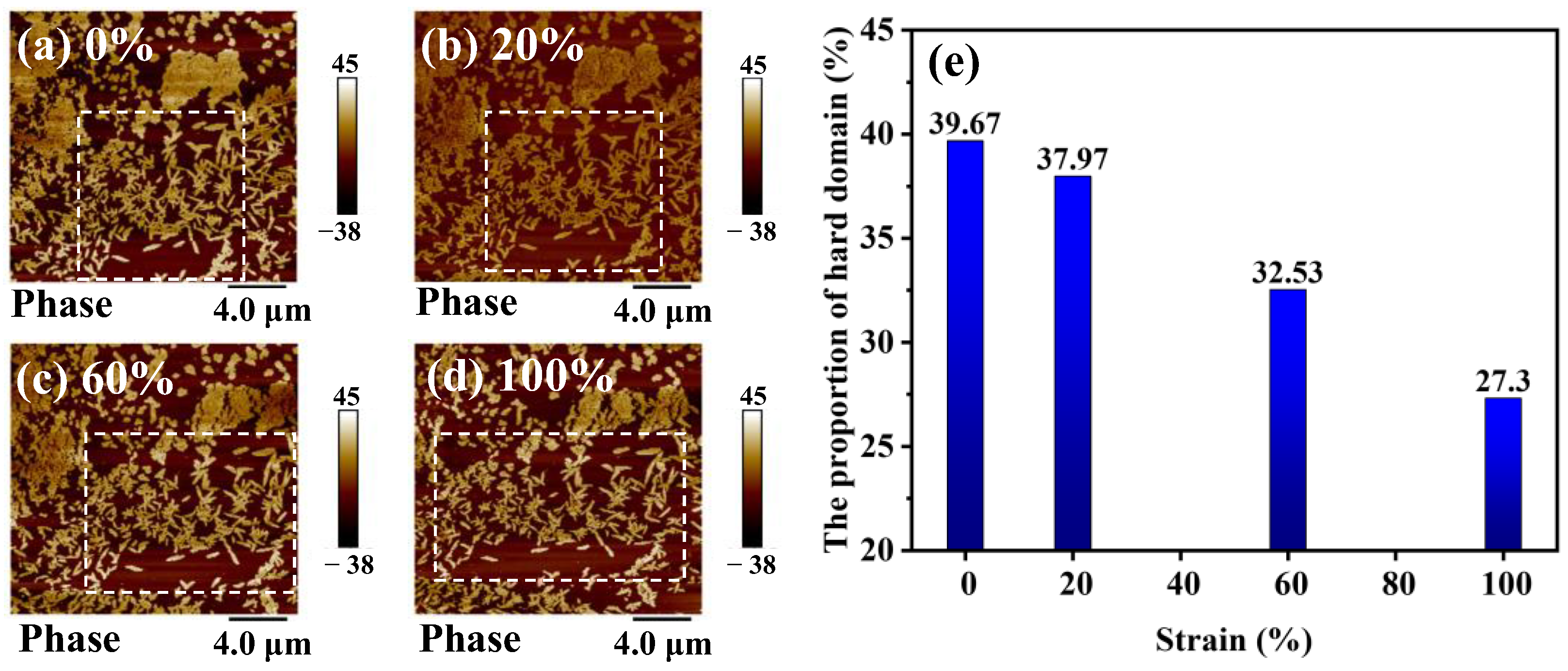
3.5. Characterization of TPU Microphase Separation
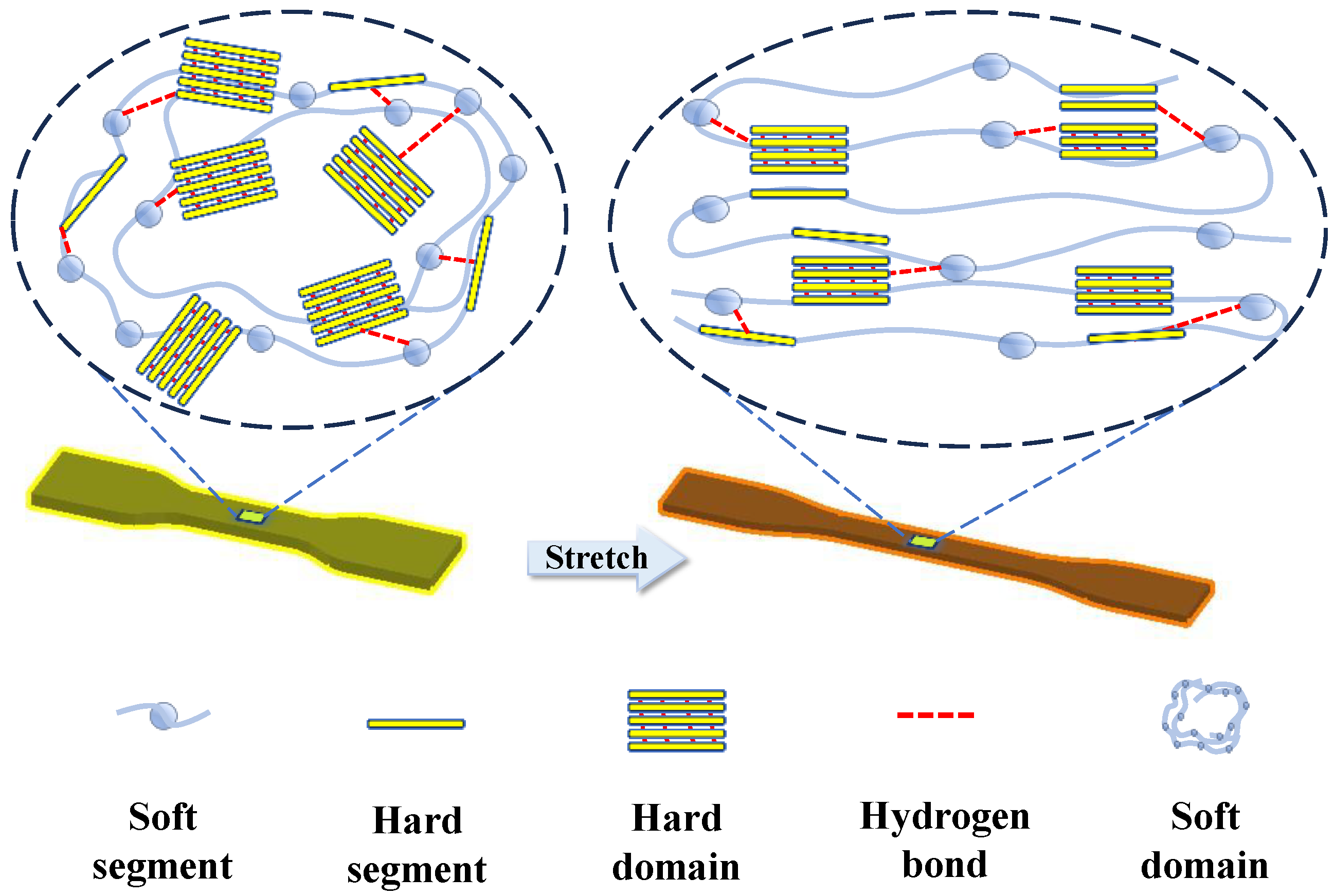
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abramson, A.; Chan, C.T.; Khan, Y.; Mermin-Bunnell, A.; Matsuhisa, N.; Fong, R.; Shad, R.; Hiesinger, W.; Mallick, P.; Gambhir, S.S.; et al. A flexible electronic strain sensor for the real-time monitoring of tumor regression. Sci. Adv. 2022, 8, eabn6550. [Google Scholar] [CrossRef] [PubMed]
- Hu, Q.; Zhu, S.; Gu, C.; Liu, S.; Zeng, M.; Wu, Y. Ultrashort 15-nm flexible radio frequency ITO transistors enduring mechanical and temperature stress. Sci. Adv. 2022, 8, eade4075. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yan, S.; Cao, J.; Chen, H.; Liu, B.; Xie, J.; Shu, Y.; Wang, F.; Wang, A.; Dong, J.; et al. High performance flexible Sn-Pb mixed perovskite solar cells enabled by a crosslinking additive. NPJ Flex. Electron. 2023, 7, 18. [Google Scholar] [CrossRef]
- Zhu, Q.-B.; Li, B.; Yang, D.-D.; Liu, C.; Feng, S.; Chen, M.-L.; Sun, Y.; Tian, Y.-N.; Su, X.; Wang, X.-M.; et al. A flexible ultrasensitive optoelectronic sensor array for neuromorphic vision systems. Nat. Commun. 2021, 12, 1798. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Liu, Y.; Zhou, Y.; Man, Q.; Hu, C.; Asghar, W.; Li, F.; Yu, Z.; Shang, J.; Liu, G.; et al. A skin-inspired tactile sensor for smart prosthetics. Sci. Robot. 2018, 3, eaat0429. [Google Scholar] [CrossRef] [PubMed]
- Phadkule, S.S.; Sarma, S. Progress in nanocomposite based flexible temperature sensors: A review. Meas. Sens. 2023, 27, 100692. [Google Scholar] [CrossRef]
- Ma, H.D.; Hou, J.D.; Xiao, X.; Wan, R.T.; Ge, G.; Zheng, W.Q.; Chen, C.; Cao, J.; Wang, J.Y.; Liu, C.; et al. Self-healing electrical bioadhesive interface for electrophysiology recording. J. Colloid Interface Sci. 2024, 654, 639–648. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Zhong, Y.; Xu, H.; Qin, K.; Guo, X.; Hu, Y.; Zhu, P.; Qu, Y.; Yan, D.; Li, Z.; et al. Self-protection soft fluidic robots with rapid large-area self-healing capabilities. Nat. Commun. 2023, 14, 6430. [Google Scholar] [CrossRef] [PubMed]
- Onyenucheya, B.; Allen, J.; Pierre, K.; Zirnheld, J.; Burke, K. Dielectric Elastomers: An Investigation in Strain Dependent Electrostatic Pressure of Soft Compliant Dielectric. In Proceedings of the 2019 IEEE Pulsed Power & Plasma Science (PPPS), Orlando, FL, USA, 23–29 June 2019; pp. 1–4. [Google Scholar]
- Lotfiani, A.; Yi, X.; Shao, Z.; Zhao, H.; Parkestani, A.N. Analytical modeling and optimization of a corrugated soft pneumatic finger considering the performance of pinch and power grasps. Extreme Mech. Lett 2021, 44, 101215. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.-J.; Zhao, H. Speeding up soft pneumatic actuators through pressure and flow dynamics modeling and optimization. Extrem. Mech. Lett. 2022, 57, 101914. [Google Scholar] [CrossRef]
- Pramanik, B.; Sahu, R.K.; Bhaumik, S.; Patra, K.; Pandey, A.K.; Setua, D.K. Experimental study on permittivity of acrylic dielectric elastomer. In Proceedings of the 2012 IEEE 10th International Conference on the Properties and Applications of Dielectric Materials, Bangalore, India, 24–28 July 2012; pp. 1–4. [Google Scholar]
- Troels, A.; Kogler, A.; Baumgartner, R.; Kaltseis, R.; Keplinger, C.; Schwoediauer, R.; Graz, I.; Bauer, S. Stretch dependence of the electrical breakdown strength and dielectric constant of dielectric elastomers. Smart Mater. Struct. 2013, 22, 104012. [Google Scholar] [CrossRef]
- Diaz-Calleja, R.; Riande, E. Comments on the influence of stretching on the permittivity of dielectric elastomers. Smart Mater. Struct. 2013, 22, 038001. [Google Scholar] [CrossRef]
- Choi, H.; Jung, K.; Nguyen, C.; Jung, M.; Koo, I.; Koo, I.; Lee, J.; Lee, J.; Nam, J.; Cho, M.; et al. Effects of prestrain on behavior of dielectric elastomer actuator. In Proceedings of the Smart Structures and Materials 2005: Electroactive Polymer Actuators and Devices (EAPAD) International Society for Optics and Photonics, San Diego, CA, USA, 7–10 March 2005; Volume 5759. [Google Scholar]
- Kofod, G.; Sommer-Larsen, P.; Kornbluh, R.; Pelrine, R. Actuation Response of Polyacrylate Dielectric Elastomers. J. Intell. Mater. Syst. Struct. 2003, 14, 787–793. [Google Scholar] [CrossRef]
- Zeng, C.; Gao, X.S. Effect of the deformation dependent permittivity on the actuation of a pre-stretched circular dielectric actuator. Mech. Res. Commun 2019, 101, 103420. [Google Scholar] [CrossRef]
- Kumar, A.; Patra, K. Proposal of a generic constitutive model for deformation-dependent dielectric constant of dielectric elastomers. Environ. Sci. Technol. 2021, 24, 1347–1360. [Google Scholar] [CrossRef]
- Vu-Cong, T.; Nguyen-Thi, N.; Jean-Mistral, C.; Sylvestre, A. How does static stretching decrease the dielectric constant of VHB 4910 elastomer? In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) 2014, San Diego, CA, USA, 10–13 March 2014; Volume 9056. [Google Scholar]
- Srivastava, A.K.; Basu, S. Exploring the performance of a dielectric elastomer generator through numerical simulations. Sens. Actuator A Phys. 2021, 319, 112401. [Google Scholar] [CrossRef]
- Hong, W.; Liang, Y.; Xining, Z.; Ang, M.H.J. Permittivity, loss factor and Cole-Cole model of acrylic materials for dielectric elastomers. Results Phys. 2021, 29, 104781. [Google Scholar]
- Ahmad, D.; Patra, K. Experimental and theoretical analysis of laterally pre-stretched pure shear deformation of dielectric elastomer. Polym. Test. 2019, 75, 291–297. [Google Scholar] [CrossRef]
- Huang, W.; Kang, G. Experimental study on uniaxial ratchetting of VHB 4910 dielectric elastomer. Polym. Test. 2022, 109, 107557. [Google Scholar] [CrossRef]
- Schlögl, T.; Leyendecker, S. A polarisation based approach to model the strain dependent permittivity of dielectric elastomers. Sens. Actuator A Phys. 2017, 267, 156–163. [Google Scholar] [CrossRef]
- Li, B.; Chen, H.; Qiang, J.; Zhou, J. A model for conditional polarization of the actuation enhancement of a dielectric elastomer. Soft Matter 2012, 8, 311–317. [Google Scholar] [CrossRef]
- Jimenez, S.M.A.; McMeeking, R.M. Deformation dependent dielectric permittivity and its effect on actuator performance and stability. Int. J. Nonlin. Mech. 2013, 57, 183–191. [Google Scholar] [CrossRef]
- Friedberg, I.Z.; de Botton, G. Electroelasticity of copolymer networks. J. Mech. Phys. Solids 2023, 175, 105295. [Google Scholar] [CrossRef]
- Jean-Mistral, C.; Sylvestre, A.; Basrour, S.; Chaillout, J.J. Dielectric properties of polyacrylate thick films used in sensors and actuators. Smart Mater. Struct. 2010, 19, 075019. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, R.; Xiao, Q.; Guo, H.; Wang, Z.; Li, X.; Chen, J.; Zhu, J. Asynchronous fracture of hierarchical microstructures in hard domain of thermoplastic polyurethane elastomer: Effect of chain extender. Polymer 2018, 138, 242–254. [Google Scholar] [CrossRef]
- Zheng, M.-S.; Zha, J.-W.; Yang, Y.; Han, P.; Hu, C.-H.; Wen, Y.-Q.; Dang, Z.-M. Polyurethane induced high breakdown strength and high energy storage density in polyurethane/poly(vinylidene fluoride) composite films. Appl. Phys. Lett. 2017, 110, 252902. [Google Scholar] [CrossRef]
- Lorenzini, R.G.; Kline, W.M.; Wang, C.C.; Ramprasad, R.; Sotzing, G.A. The rational design of polyurea & polyurethane dielectric materials. Polymer 2013, 54, 3529–3533. [Google Scholar]
- Yuan, W.; Yang, J.; Yin, F.; Li, Y.; Ye, Y. Flexible and stretchable MXene/Polyurethane fabrics with delicate wrinkle structure design for effective electromagnetic interference shielding at a dynamic stretching process. Compos. Commun. 2020, 19, 90–98. [Google Scholar] [CrossRef]
- Ueda, Y.; Tanaka, M.; Nakanotani, H.; Adachi, C. A polar transition of spontaneous orientation polarization in organic amorphous thin films. Chem. Phys. Lett 2023, 833, 140915. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Pöselt, E.; Eling, B.; Wang, Z. Melting behavior of polymorphic MDI/BD-block TPU investigated by using in-situ SAXS/WAXS and FTIR techniques. Hydrogen bonding formation causing the inhomogeneous melt. Polym. Test. 2021, 96, 107065. [Google Scholar] [CrossRef]
- Lee, H.S.; Wang, Y.K.; Hsu, S.L. Spectroscopic analysis of phase separation behavior of model polyurethanes. Macromolecules 1987, 20, 2089–2095. [Google Scholar] [CrossRef]
- Sánchez-Adsuar, M.S. Influence of the composition on the crystallinity and adhesion properties of thermoplastic polyurethane elastomers. Int. J. Adhes 2000, 20, 291–298. [Google Scholar] [CrossRef]
- Cheng, B.-X.; Gao, W.-C.; Ren, X.-M.; Ouyang, X.-Y.; Zhao, Y.; Zhao, H.; Wu, W.; Huang, C.-X.; Liu, Y.; Liu, X.-Y.; et al. A review of microphase separation of polyurethane: Characterization and applications. Polym. Test. 2022, 107, 107489. [Google Scholar] [CrossRef]
- Atawa, B.; Maneval, L.; Alcouffe, P.; Sudre, G.; David, L.; Sintes-Zydowicz, N.; Beyou, E.; Serghei, A. In-situ coupled mechanical/electrical investigations on conductive TPU/CB composites: Impact of thermo-mechanically induced structural reorganizations of soft and hard TPU domains on the coupled electro-mechanical properties. Polymer 2022, 256, 125147. [Google Scholar] [CrossRef]
- Jia, Y.; Yue, X.; Wang, Y.; Yan, C.; Zheng, G.; Dai, K.; Liu, C.; Shen, C. Multifunctional stretchable strain sensor based on polydopamine/reduced graphene oxide/electrospun thermoplastic polyurethane fibrous mats for human motion detection and environment monitoring. Compos. Part B Eng. 2020, 183, 107696. [Google Scholar] [CrossRef]
- Oprea, S. Effect of the hard-segment structure on the dielectric relaxation of crosslinked polyurethanes. J. Appl. Polym. Sci. 2011, 119, 2196–2204. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, H.; Xie, Y.; Bao, X.; Pan, L.; Zhao, D.; Chen, J.; Zou, M.; Tian, T.; Li, R. Strain Effect on Dielectricity of Elastic Thermoplastic Polyurethanes. Polymers 2024, 16, 1465. https://doi.org/10.3390/polym16111465
Wang Y, Yang H, Xie Y, Bao X, Pan L, Zhao D, Chen J, Zou M, Tian T, Li R. Strain Effect on Dielectricity of Elastic Thermoplastic Polyurethanes. Polymers. 2024; 16(11):1465. https://doi.org/10.3390/polym16111465
Chicago/Turabian StyleWang, Yubo, Huali Yang, Yali Xie, Xilai Bao, Lili Pan, Dan Zhao, Jinxia Chen, Mengting Zou, Tian Tian, and Runwei Li. 2024. "Strain Effect on Dielectricity of Elastic Thermoplastic Polyurethanes" Polymers 16, no. 11: 1465. https://doi.org/10.3390/polym16111465
APA StyleWang, Y., Yang, H., Xie, Y., Bao, X., Pan, L., Zhao, D., Chen, J., Zou, M., Tian, T., & Li, R. (2024). Strain Effect on Dielectricity of Elastic Thermoplastic Polyurethanes. Polymers, 16(11), 1465. https://doi.org/10.3390/polym16111465







