Simulation and Experimental Study of the Isothermal Thermogravimetric Analysis and the Apparent Alterations of the Thermal Stability of Composite Polymers
Abstract
1. Introduction
2. Materials and Methods
3. Theoretical Analysis
3.1. General Concepts
- (1)
- Recently, the latent limit of detection of TGA was reported [20]. Briefly, by the subtraction of the blank TGA measurement we can take into account the error that is introduced in the measurement due to the buoyancy which is exerted on the pan. However, the buoyancy exerted on the sample always influences the TGA signal (that is, the apparent mass sample which is equal to the real mass minus buoyancy) and introduces an additional error in the detection and quantification limits of TGA [20]. Typically, the fillers that are used in polymer composites have higher densities than those of the polymers. Thus, the pure and the composite polymers have a non-negligible difference in density. Due to the different density, the buoyancy exerted on the pure and composite polymers is different, thus the limit of detection and quantification is different. In other words, due to the difference in density, the detection and quantification of mass loss appears to be different and causes an apparent difference in the thermal stability.
- (2)
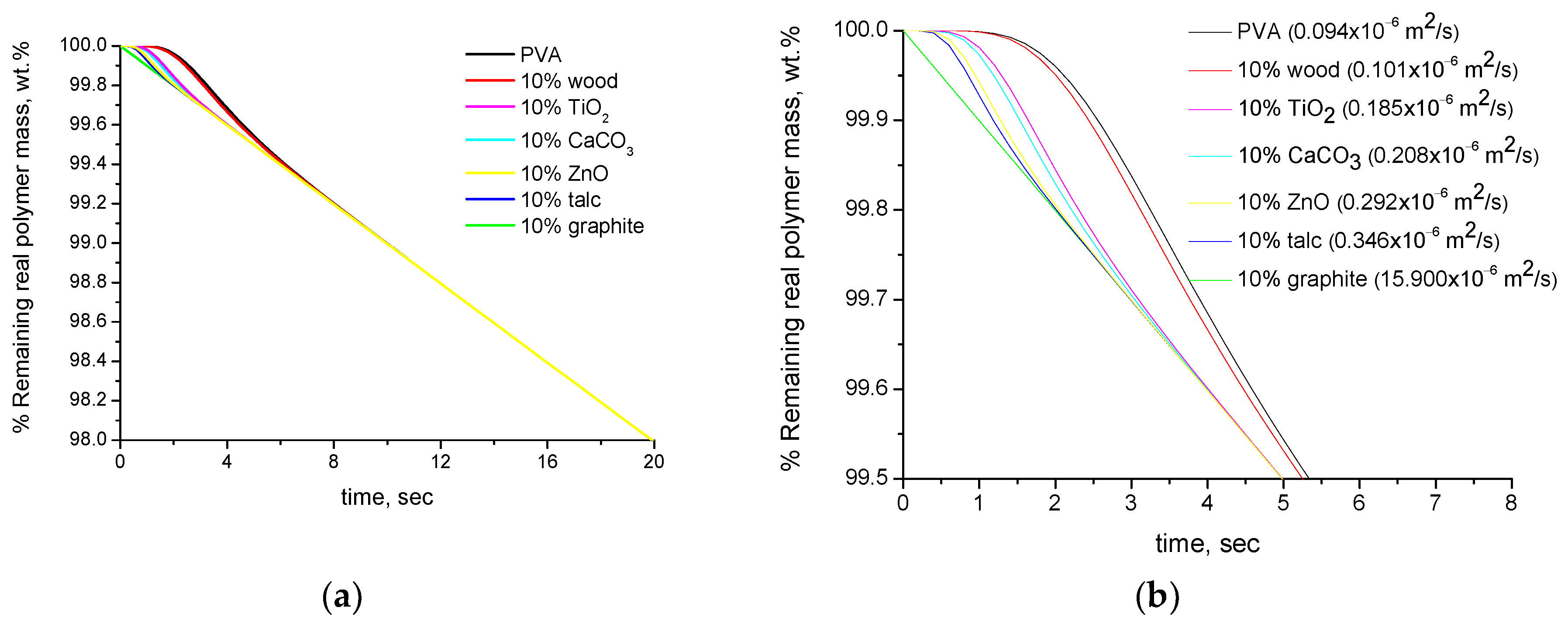
- It is widely known that in TGA, the measured temperature is not the actual temperature of the sample but the temperature of the purge gas near the sample. In addition, the sample does not have a uniform temperature but instead a temperature gradient exists within the sample. In general, such effects are well-known, e.g., that a thicker sample will exhibit a more intense temperature gradient than a thinner sample. The temperature gradient does not depend only on the dimensions of the sample but also on its thermal diffusivity (which in turn depends on the thermal conductivity, density and specific heat capacity). Thus, fillers with high and low thermal diffusivity are expected to cause, respectively, a faster and slower heating of the composite material. This is an actual and not an apparent effect, e.g., if a composite material with low thermal diffusivity is exposed in a real application at high temperature, it will be heated slower than the pure polymer. However, it is not accurate to claim that the composite material exhibits increased thermal stability. If there is no interaction between the polymer and the filler, or the compatibility arises from entopic reasons (as discussed in Section 1), the polymer will degrade at the same temperature both in the pure form and the composite material. Put simply, due to the lower thermal diffusivity of the composite material, the polymer will reach this temperature slower. In an isothermal TGA measurement, this will be observed as degradation of the composite at higher times than the pure polymer. In a non-isothermal TGA measurement, since the actual temperature of the sample is not measured, this will be observed as degradation of the composite at higher temperatures. In both cases, this may be (erroneously) interpreted as an actual increase of the thermal stability.
- (3)
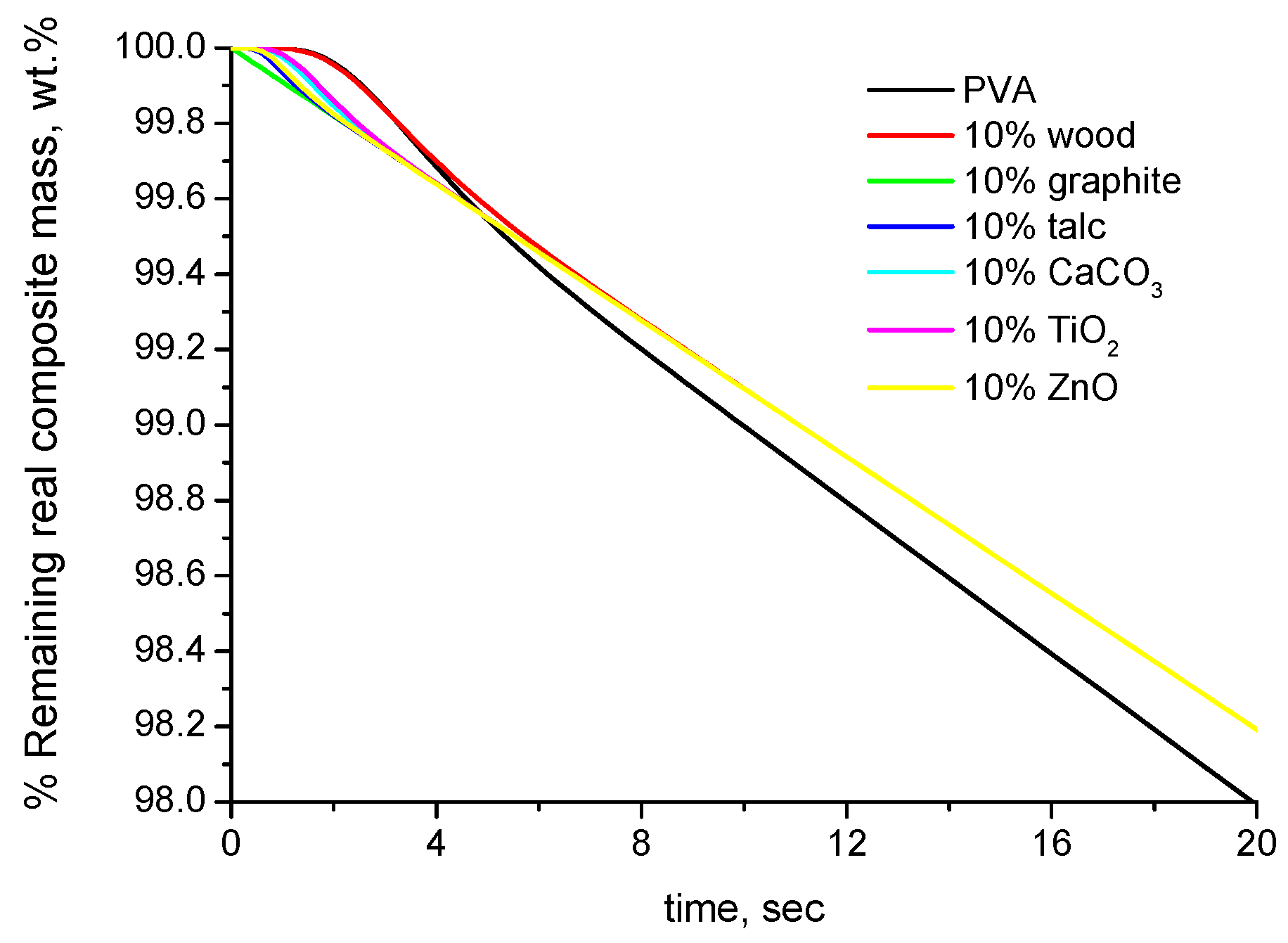
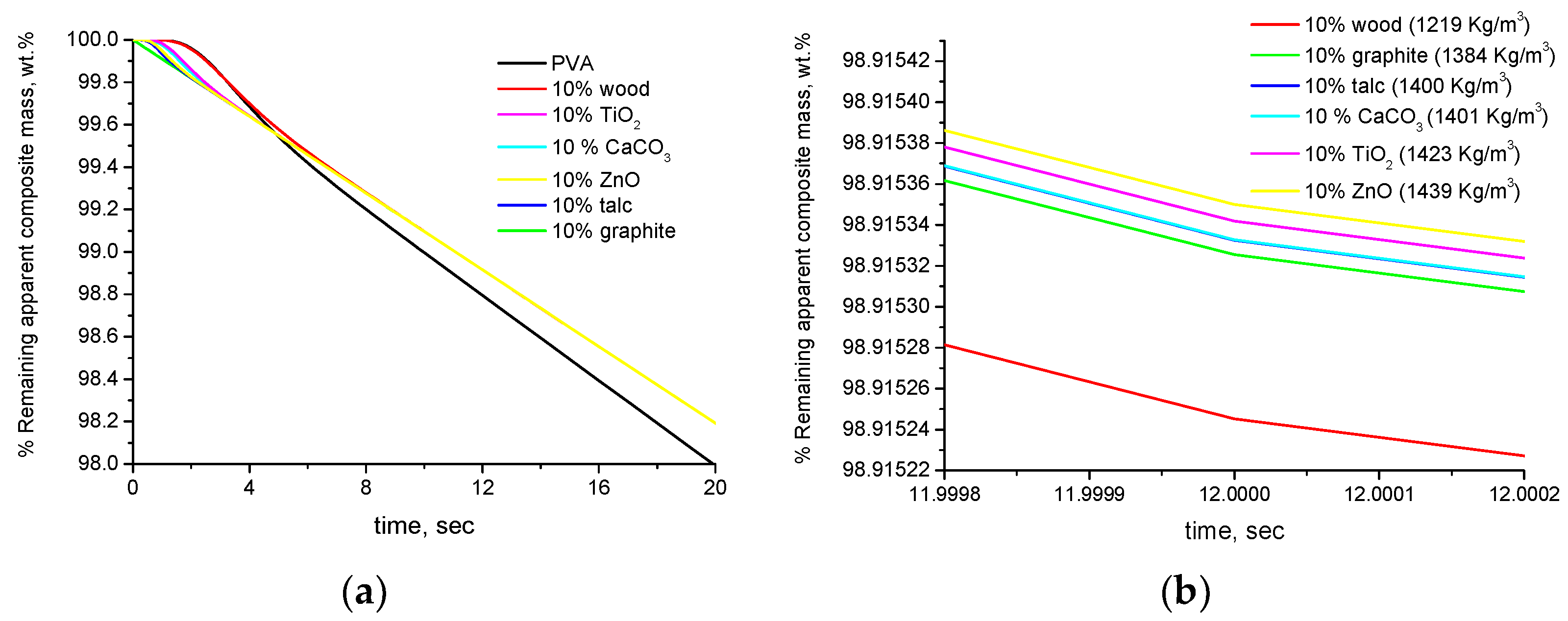
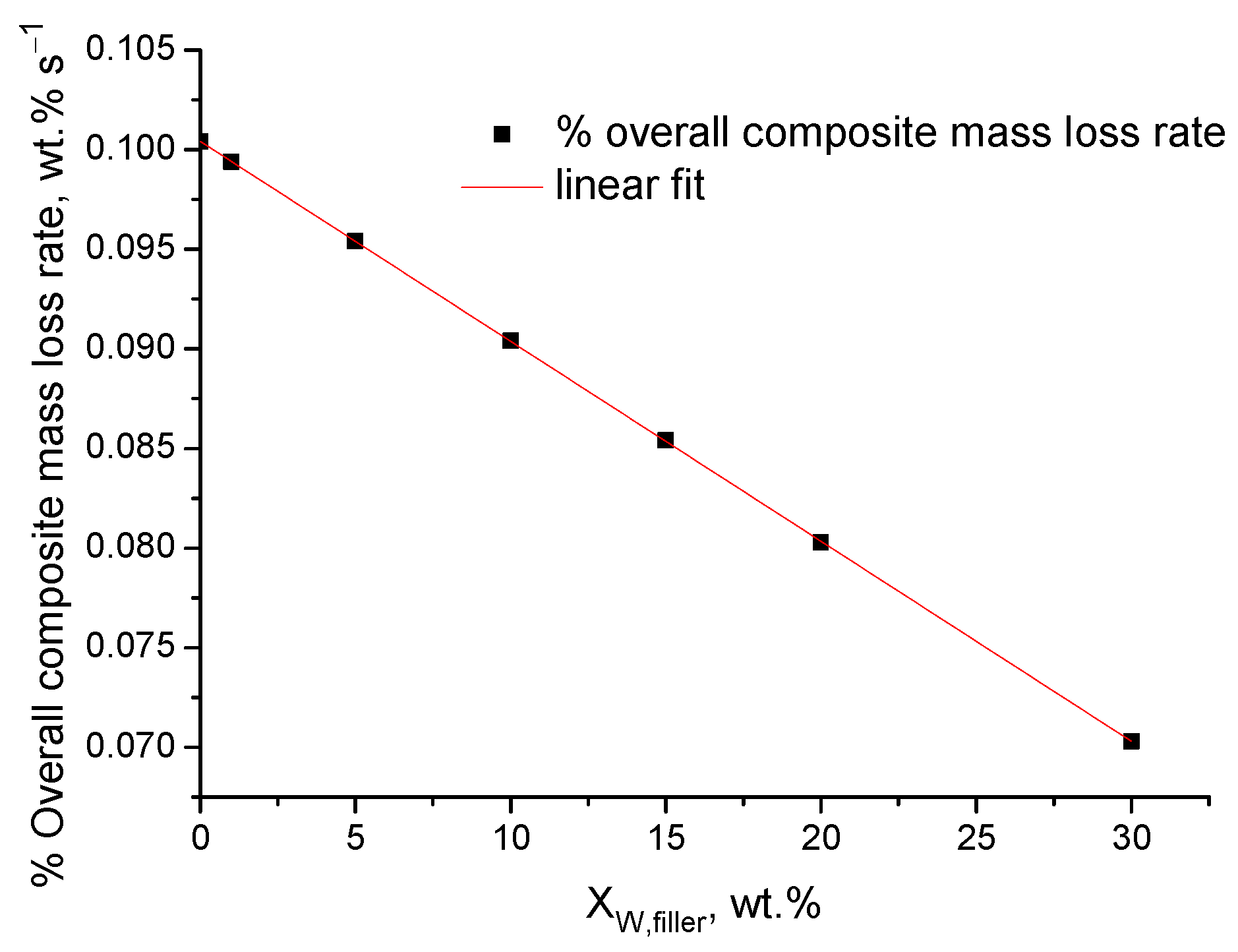
- The mass loss (or the remaining mass) of the composite materials, conventionally, is expressed per overall composite mass and not per degradable (polymer) mass of the composite. This can cause an apparent alteration of the thermal stability for the following reason: For sake of simplicity, this will be discussed through an example. If the mass sample of the pure polymer that is used for the TGA measurement is 5 mg with a scale readability of 0.01 mg, then, by excluding any other sources of error/uncertainty, the minimum % detectable mass loss is 100 × 0.01/5 = 0.2%. If the mass of the composite is also 5 mg, then the minimum detectable % mass loss is again 0.2%. However, this is true only if the mass loss arises from the overall mass sample. However, in the composite material, e.g., with 20% inorganic (non-degradable) filler, the mass loss is not due to the overall mass sample (5 mg) but only due to the degradable (polymer) mass, i.e., 5 − 5 × 0.2 = 4 mg. Thus, in the composite material, the absolute mass loss of 0.01 mg that is due to the 4 mg of degradable mass is expressed and reduced with respect to the overall mass of 5 mg. Since both measurements are conducted with the same readability, in the case of the composite material, the actual minimum detectable % mass loss is 100 × 0.01/4 = 0.25%. In other words, the TGA has the same sensitivity in detecting absolute mass loss but is less sensitive in detecting relative (%) mass loss in the composite material. This causes the composite material to appear more thermally stable than the pure polymer if the mass loss is expressed per overall mass of the composite.
3.2. Modelling
- (1)
- The weight, buoyancy and drag force of the TGA pan are not taken into account since their effect can be eliminated by the subtraction of the empty pan measurement.
- (2)
- The drag force that is exerted on the sample is considered to be low and to have a negligible effect on the TGA signal, and thus it is not taken into account in the modelling equations.
- (3)
- There is no interaction between the polymer and the filler and thus the degradation profile and degradation temperature of the polymer are the same both in the neat and composite form; that is, the same equation describes the degradation profile of the real mass loss of the neat and composite polymer.
- (4)
- The density, the specific heat capacity and the thermal conductivity of the polymer and the additive do not change with temperature.
- (5)
- The density, the specific heat capacity and the thermal conductivity of the polymer do not change due to degradation. This assumption may be considered to be valid for low degrees of degradation. For this reason, the simulated results will be presented for low degrees of degradation, namely, up to 2% mass loss (98% remaining mass).
4. Results and Discussion
4.1. Simulation Results
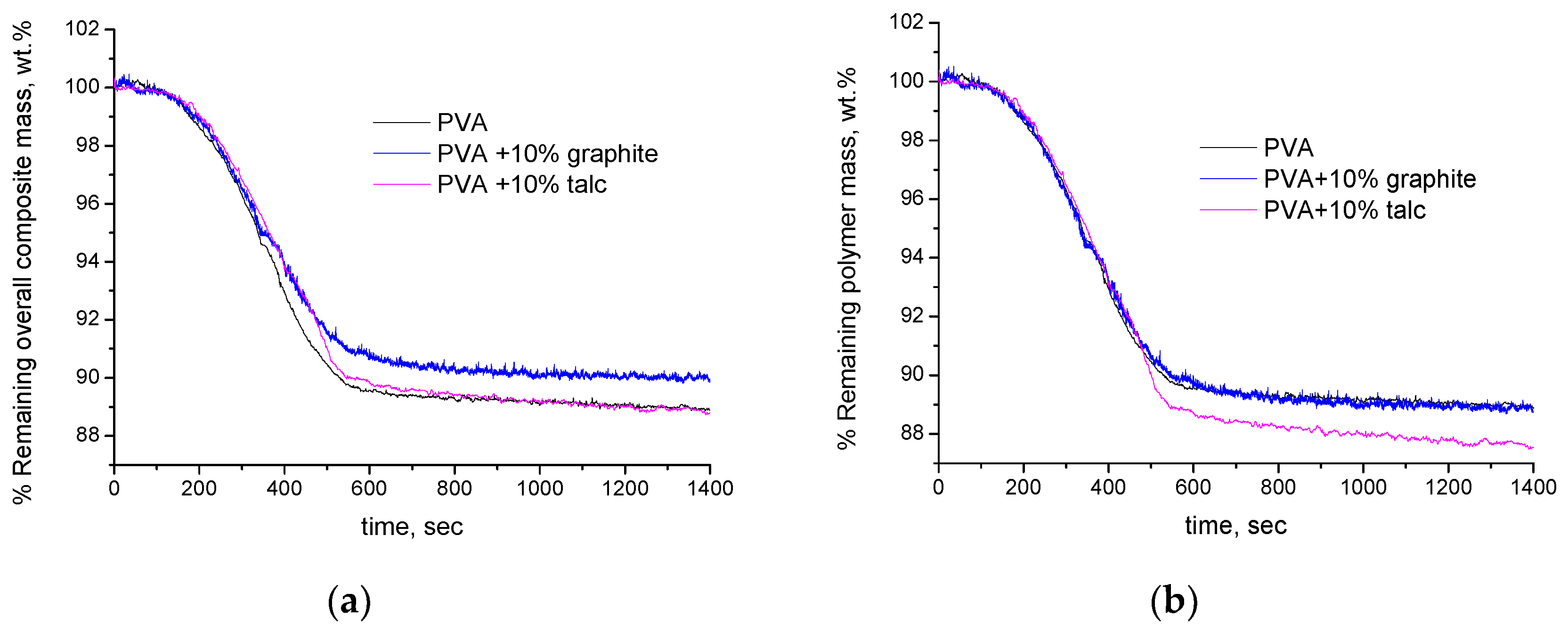
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chi, Y.; Maitland, E.; Pascall, M.A. The effect of citric acid concentrations on the mechanical, thermal, and structural properties of starch edible films. Int. J. Food Sci. Technol. 2024, 59, 1801–1813. [Google Scholar] [CrossRef]
- Jendrzejewska, I.; Goryczka, T.; Pietrasik, E.; Klimontko, J.; Jampilek, J. X-ray and Thermal Analysis of Selected Drugs Containing Acetaminophen. Molecules 2020, 25, 5909. [Google Scholar] [CrossRef] [PubMed]
- Vasileiadou, A.; Zoras, S.; Iordanidis, A. Biofuel potential of compost-like output from municipal solid waste: Multiple analyses of its seasonal variation and blends with lignite. Energy 2021, 236, 121457. [Google Scholar] [CrossRef]
- Xu, J.; Li, T.; Yan, T.; Chao, J.; Wang, R. Dehydration kinetics and thermodynamics of magnesium chloride hexahydrate for thermal energy storage. Sol. Energy Mater. Sol. Cells 2021, 219, 110819. [Google Scholar] [CrossRef]
- Pellenz, L.; de Oliveira, C.R.S.; da Silva Júnior, A.H.; da Silva, L.J.S.; da Silva, L.; de Souza, A.A.U.; de Souza, S.M.D.A.G.U.; Borba, F.H.; da Silva, A. A comprehensive guide for characterization of adsorbent materials. Sep. Purif. Technol. 2023, 305, 122435. [Google Scholar] [CrossRef]
- Gao, J.-F.; Fang, D.-L.; Wang, Z.-B.; Yang, P.-H.; Chen, C.-S. Preparation and electrical properties of copper–nickel manganite ceramic derived from mixed oxalate. Sens. Actuators A Phys. 2007, 135, 472–475. [Google Scholar] [CrossRef]
- Borghetti, G.S.; Carini, J.P.; Honorato, S.B.; Ayala, A.P.; Moreira, J.C.F.; Bassani, V.L. Physicochemical properties and thermal stability of quercetin hydrates in the solid state. Thermochim. Acta 2012, 539, 109–114. [Google Scholar] [CrossRef]
- Sahoo, K.; Biswas, A.; Nayak, J. Effect of synthesis temperature on the UV sensing properties of ZnO-cellulose nanocomposite powder. Sens. Actuators A Phys. 2017, 267, 99–105. [Google Scholar] [CrossRef]
- Chen, D.; Tiwari, S.K.; Ma, Z.; Wen, J.; Liu, S.; Li, J.; Wei, F.; Thummavichai, K.; Yang, Z.; Zhu, Y.; et al. Phase Behavior and Thermo-Mechanical Properties of IF-WS2 Reinforced PP–PET Blend-Based Nanocomposites. Polymers 2020, 12, 2342. [Google Scholar] [CrossRef]
- Barra, G.; Guadagno, L.; Raimondo, M.; Santonicola, M.G.; Toto, E.; Ciprioti, S.V. Comprehensive Review on the Thermal Stability Assessment of Polymers and Composites for Aeronautics and Space Applications. Polymers 2023, 15, 3786. [Google Scholar] [CrossRef]
- Chrissafis, K.; Bikiaris, D. Can nanoparticles really enhance thermal stability of polymers? Part I: An overview on thermal decomposition of addition polymers. Thermochim. Acta 2011, 523, 1–24. [Google Scholar] [CrossRef]
- Bikiaris, D. Can nanoparticles really enhance thermal stability of polymers? Part II: An overview on thermal decomposition of polycondensation polymers. Thermochim. Acta 2011, 523, 25–45. [Google Scholar] [CrossRef]
- Okada, A.; Usuki, A. The chemistry of polymer-clay hybrids. Mater. Sci. Eng. C 1995, 3, 109–115. [Google Scholar] [CrossRef]
- Vaia, R.A.; Giannelis, E.P. Lattice Model of Polymer Melt Intercalation in Organically-Modified Layered Silicates. Macromolecules 1997, 30, 7990–7999. [Google Scholar] [CrossRef]
- Manias, E.; Touny, A.; Wu, L.; Strawhecker, K.; Lu, B.; Chung, T.C. Polypropylene/Montmorillonite Nanocomposites. Review of the Synthetic Routes and Materials Properties. Chem. Mater. 2001, 13, 3516–3523. [Google Scholar] [CrossRef]
- Stuart, B. Infrared Spectroscopy: Fundamentals and Applications; John Wiley and Sons Ltd.: West Sussex, UK, 2004. [Google Scholar]
- Cremer, D.; Wu, A.; Larsson, A.; Kraka, E. Some Thoughts about Bond Energies, Bond Lengths, and Force Constants. Mol. Model. Annu. 2000, 6, 396–412. [Google Scholar] [CrossRef]
- Zavitsas, A.A. Quantitative relationship between bond dissociation energies, infrared stretching frequencies, and force constants in polyatomic molecules. J. Phys. Chem. 1987, 91, 5573–5577. [Google Scholar] [CrossRef]
- Roger, M.R. (Ed.) Handbook of Wood Chemistry and Wood Composites; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Vyazovkin, S. Isoconversional Kinetics of Thermally Stimulated Processes; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Tsioptsias, C. On the specific heat and mass loss of thermochemical transition. Chem. Thermodyn. Therm. Anal. 2022, 8, 100082. [Google Scholar] [CrossRef]
- Tsioptsias, C. On the latent limit of detection of thermogravimetric analysis. Measurement 2022, 204, 112136. [Google Scholar] [CrossRef]
- Nist Chemistry Webbook. 2024. Available online: https://webbook.nist.gov/ (accessed on 10 April 2024).
- CRC Handbook of Chemistry and Physics, 97th ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, USA, 2017.
- Sundararajan, P.R. Polymer Data Handbook; Oxford University Press, Inc.: Oxford, UK, 1999. [Google Scholar]
- Niemz, P.; Sonderegger, W.; Keplinger, T.; Jiang, J.; Lu, J. Springer Handbook of Wood Science and Technology; Springer Nature: Cham, Switzerland, 2023. [Google Scholar]
- Tsioptsias, C.; Fardis, D.; Ntampou, X.; Tsivintzelis, I.; Panayiotou, C. Thermal Behavior of Poly(vinyl alcohol) in the Form of Physically Crosslinked Film. Polymers 2023, 15, 1843. [Google Scholar] [CrossRef]
- Tsioptsias, C.; Leontiadis, K.; Messaritakis, S.; Terzaki, A.; Xidas, P.; Mystikos, K.; Tzimpilis, E.; Tsivintzelis, I. Experimental Investigation of Polypropylene Composite Drawn Fibers with Talc, Wollastonite, Attapulgite and Single-Wall Carbon Nanotubes. Polymers 2022, 14, 260. [Google Scholar] [CrossRef] [PubMed]


| Material | d, kg/m3 | Cp, J/g·K | k, W/m·K | a, m2/s |
|---|---|---|---|---|
| PVA | 1329 [25] | 1.6 [25] | 0.2 [25] | 9.41 × 10−8 |
| Wood | 700 [26] | 1.45 [26] | 0.17 [26] | 1.68 × 10−7 |
| Graphite | 2200 | 1.17 | 541.61 | 2.10 × 10−4 |
| Talc | 2700 | 0.85 | 10.6 | 4.63 × 10−6 |
| CaCO3 (Calcite) | 2720 | 1.02 | 5.05 | 1.82 × 10−6 |
| TiO2 | 3900 | 0.68 | 5.6 | 2.11 × 10−6 |
| ZnO | 5600 | 0.62 | 17 | 4.90 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsioptsias, C.; Zacharis, A.K. Simulation and Experimental Study of the Isothermal Thermogravimetric Analysis and the Apparent Alterations of the Thermal Stability of Composite Polymers. Polymers 2024, 16, 1454. https://doi.org/10.3390/polym16111454
Tsioptsias C, Zacharis AK. Simulation and Experimental Study of the Isothermal Thermogravimetric Analysis and the Apparent Alterations of the Thermal Stability of Composite Polymers. Polymers. 2024; 16(11):1454. https://doi.org/10.3390/polym16111454
Chicago/Turabian StyleTsioptsias, Costas, and Alexandros K. Zacharis. 2024. "Simulation and Experimental Study of the Isothermal Thermogravimetric Analysis and the Apparent Alterations of the Thermal Stability of Composite Polymers" Polymers 16, no. 11: 1454. https://doi.org/10.3390/polym16111454
APA StyleTsioptsias, C., & Zacharis, A. K. (2024). Simulation and Experimental Study of the Isothermal Thermogravimetric Analysis and the Apparent Alterations of the Thermal Stability of Composite Polymers. Polymers, 16(11), 1454. https://doi.org/10.3390/polym16111454







