Prediction Distribution Model of Moisture Content in Laminated Wood Components
Abstract
1. Introduction
2. Analogy of Unsteady Heat Transfer and Humidity Transfer
3. Establishment of Humidity Field Distribution Model
3.1. General Analytical Solution of Humidity Transfer Control Equation
3.2. Distribution of Moisture Content in Time
3.3. Spatial Distribution of Moisture Content
4. Validation of Humidity Field Distribution Model
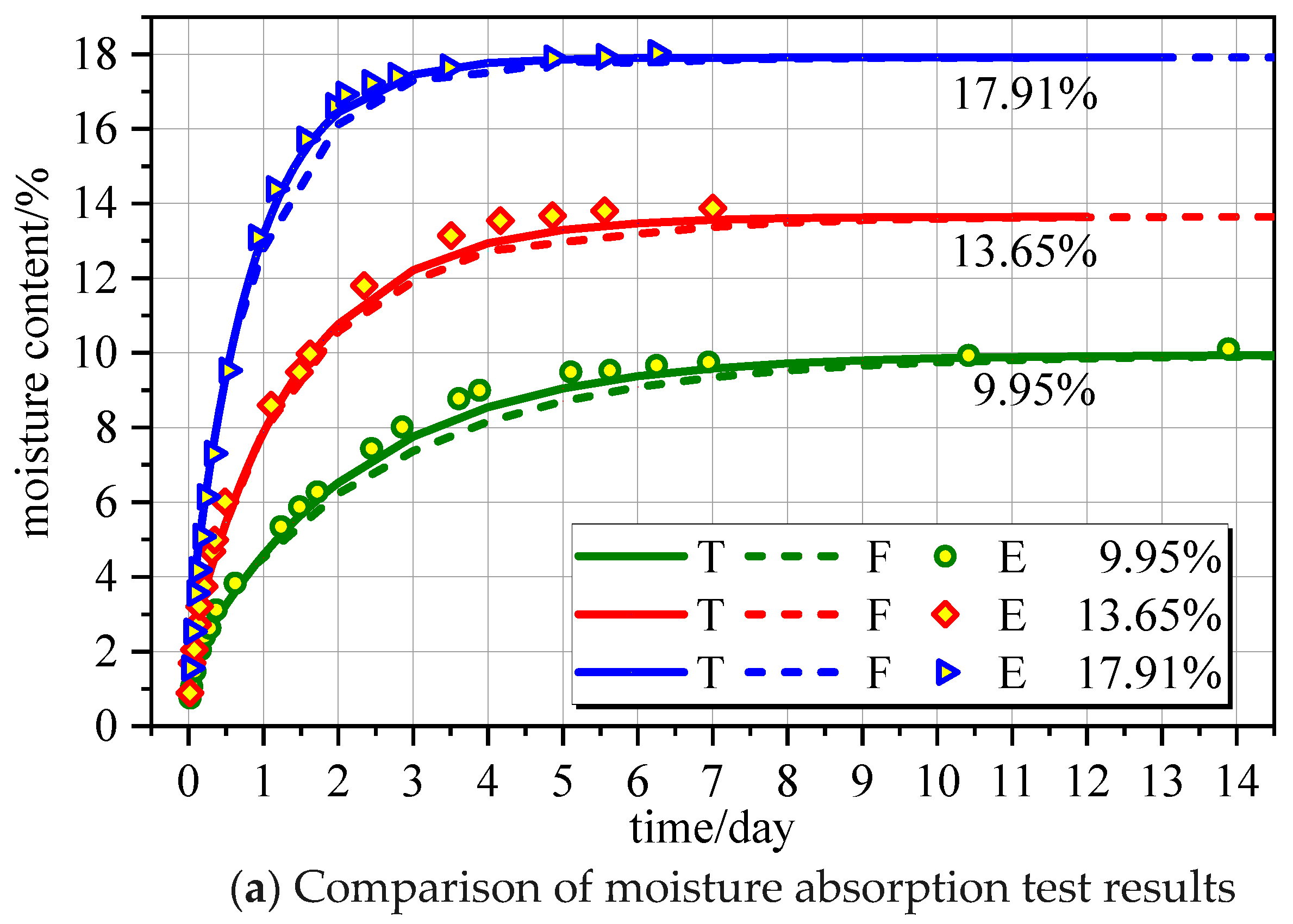
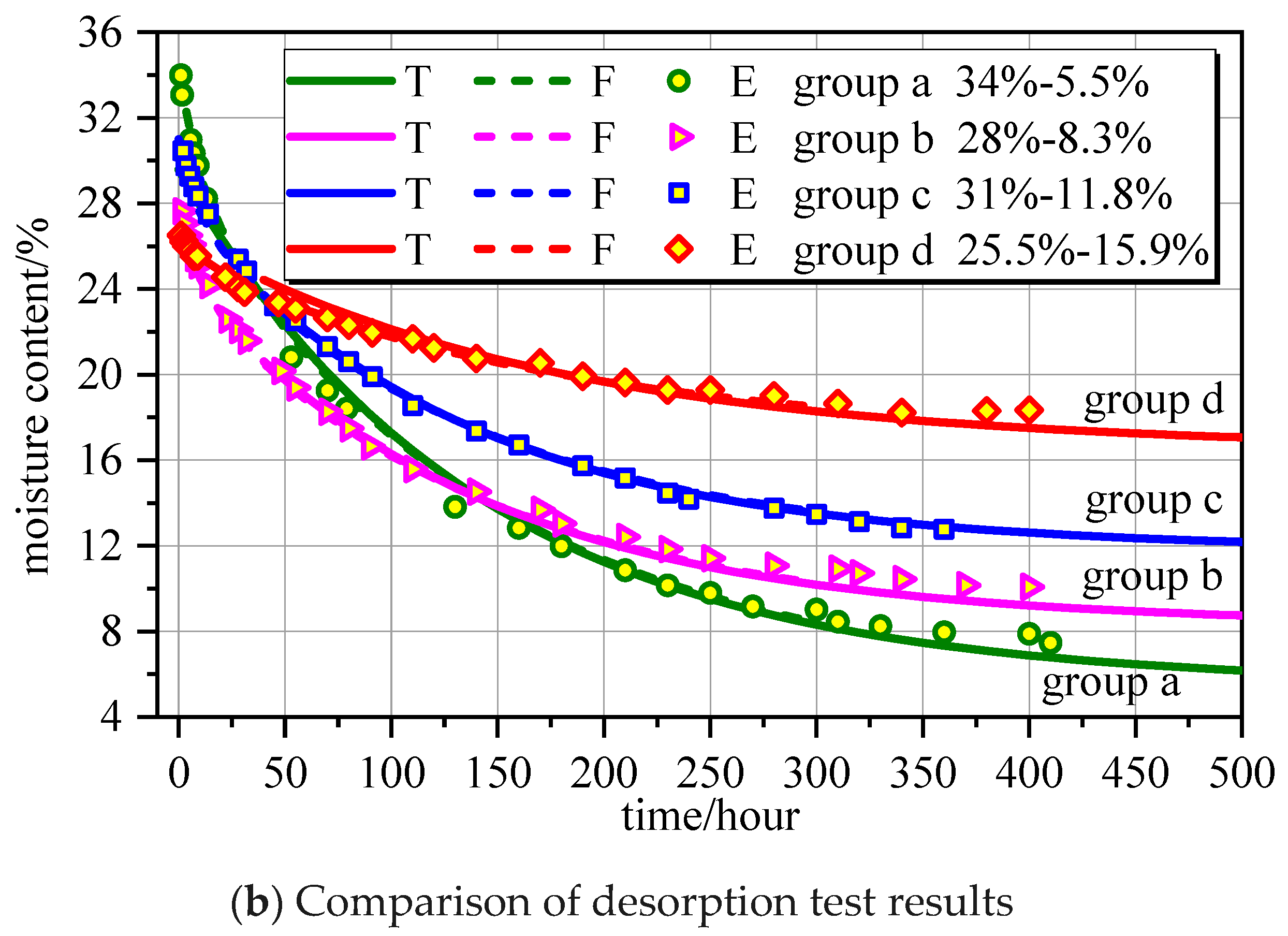
4.1. Related Test
4.2. Finite Element Analysis
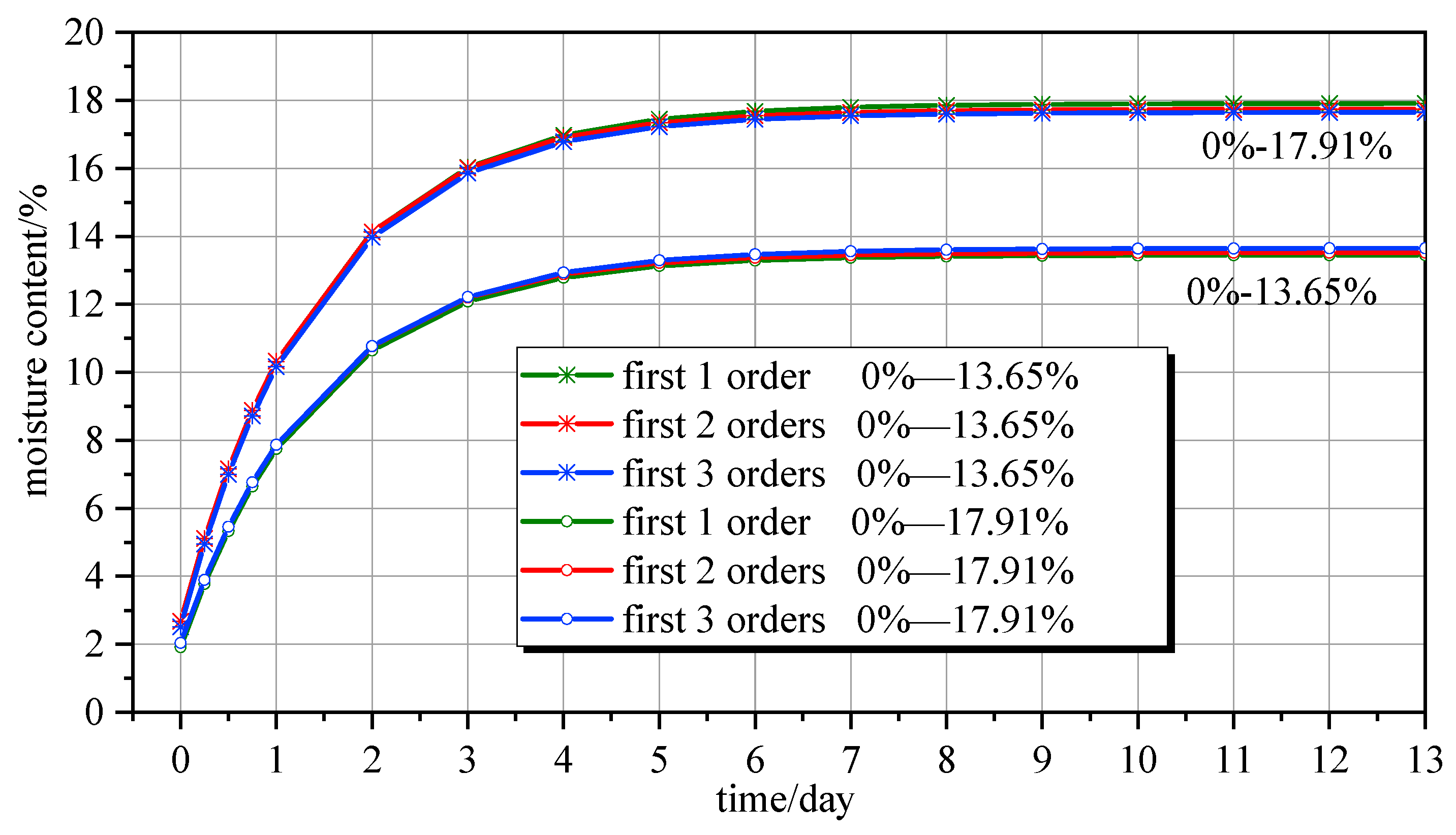
4.3. Moisture Content Changes over Time
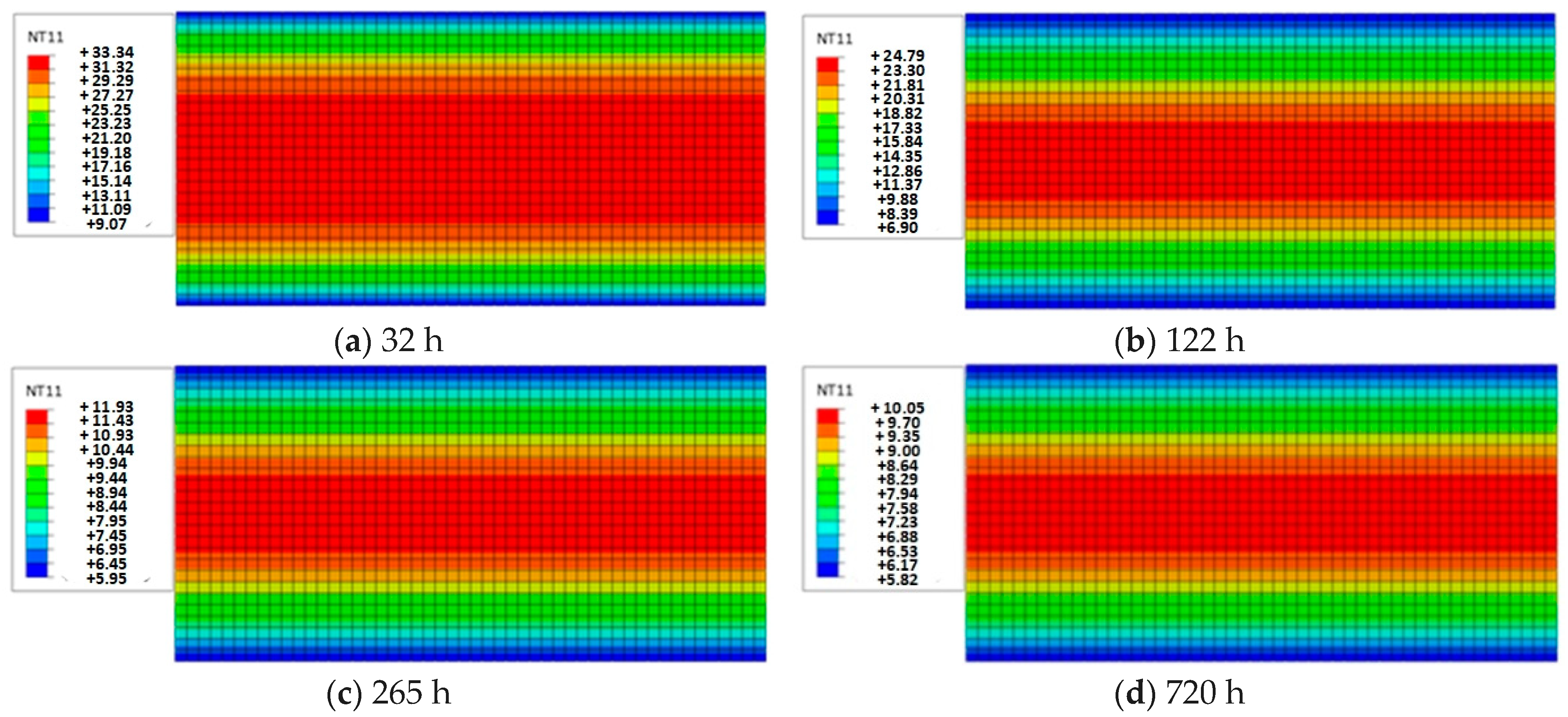
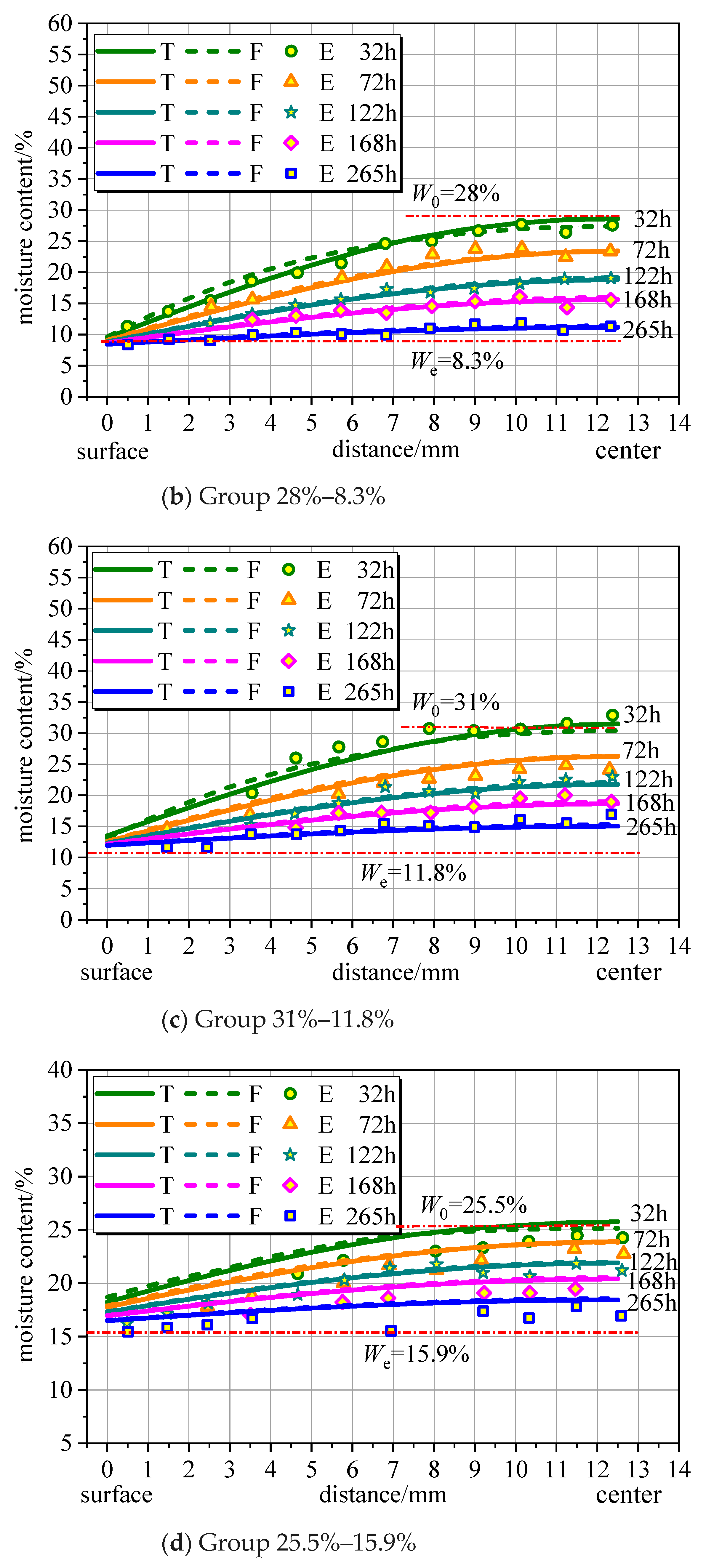
4.4. Moisture Content Changes in Space
5. Discussion
5.1. Solution of the Characteristic Equation
5.2. Moisture Gradient
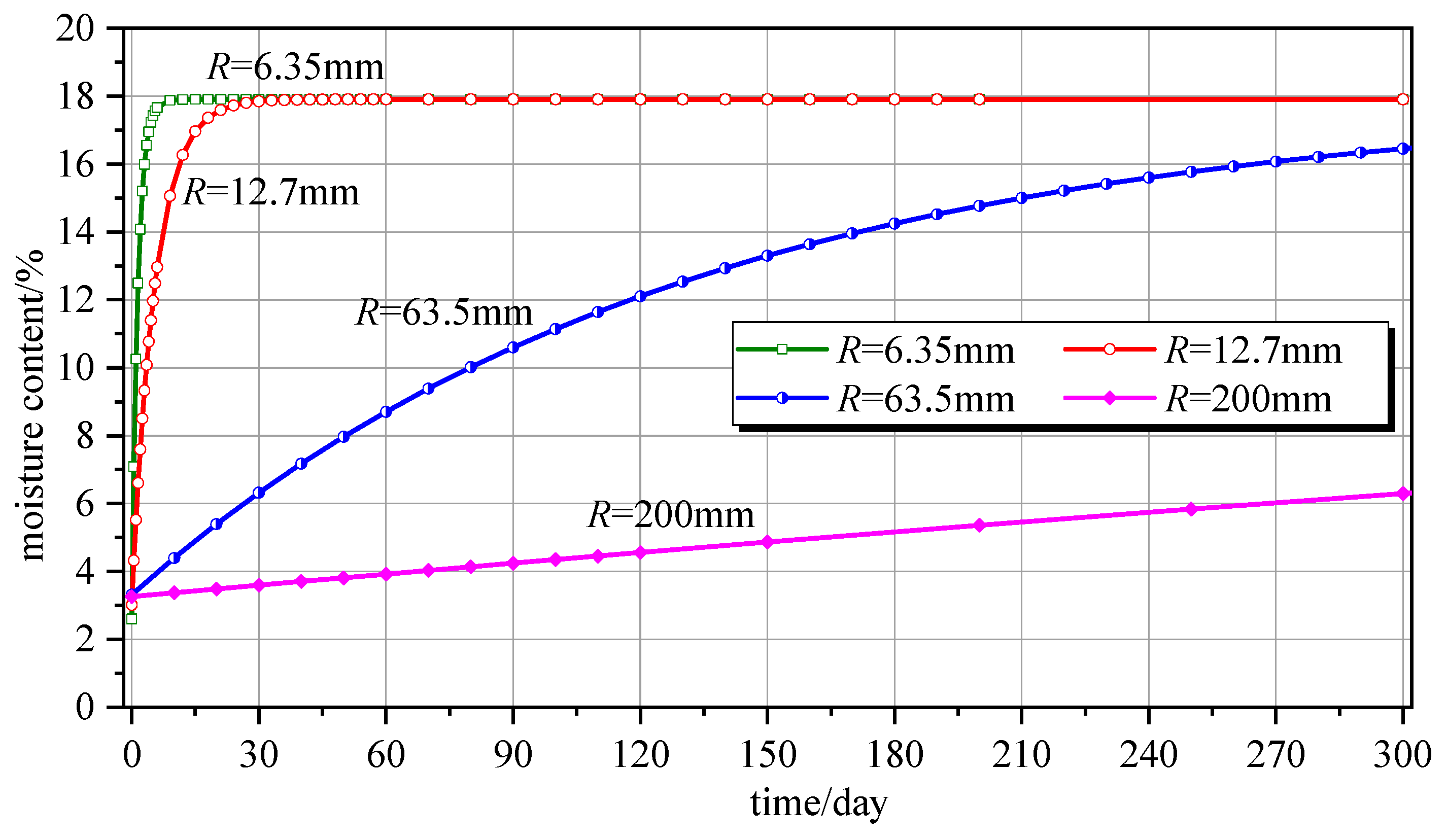
5.3. Component Dimensions
6. Conclusions
- (1)
- The theory of food drying can be applied to the calculation of wood moisture content.
- (2)
- The established moisture content model and optimized calculation formula can be used to determine the moisture content of laminated wood components at any time and position, which can improve the convenience of future experiments and wood inspection.
- (3)
- Meanwhile, the speed at which the outer side of the wooden component reaches equilibrium moisture content is much greater than that of the inner side. Even after hundreds of hours, the internal moisture content of the wood does not reach equilibrium.
- (4)
- Regarding the humidity field model or moisture content prediction formula for laminated wood components, the first one or two orders are recommended for the root of the characteristic equation to meet the accuracy requirements.
- (5)
- Regardless of moisture absorption or desorption, the greater the difference in moisture content, the greater the speed at which equilibrium moisture content is achieved.
- (6)
- The distribution of moisture content varies greatly among different component sizes and at different positions of the same size.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| r(mm) | The radial distance from the position of any point to the center |
| R(mm) | Half of the radial length R |
| J | The first kind of Bessel function |
| μn | The solution of the characteristic equation |
| ν | The Bessel function series of the first type |
| T(K) | Temperature |
| Ti(K) | Initial temperature |
| Te(K) | Ambient temperature |
| Ts(K) | Surface temperature of the object |
| Dimensionless relative temperature | |
| α(m2/s) | Thermal conductivity |
| h(W/m2/K) | Surface heat exchange coefficient |
| Biot number of heat transfer | |
| Fourier number | |
| W(%) | Moisture content |
| Wi(%) | Initial moisture content |
| We(%) | Equilibrium moisture content |
| Ws(%) | Surface moisture content |
| Dimensionless relative moisture content | |
| D(m2/s) | Water diffusion coefficient |
| S(m/s) | Surface humidity divergence coefficient |
| Biot number of humidity transfer | |
| Fourier number | |
| t | the time |
| ER, ET, EL | Radial/tangential/longitudinal elastic modulus |
| ft,R, ft,T, ft,L | Radial/tangential/longitudinal tensile strength in cross-section |
| fc,R, fc,T, fc,L | Radial/tangential/longitudinal compressive strength in cross-section |
| αR, αT, αL | Radial/tangential/longitudinal shrinkage and swelling coefficient |
| vRT, vRL, vTL | Poisson ratio of different directions |
| GRT, GRL, GTL | Shear modulus of different directions |
References
- Li, H.; Wang, P.; Zhao, Q.; Ou, J.; Liu, J.; Wang, Z.; Qiu, H.; Zuo, T. Experimental and numerical study on timber-to-bamboo scrimber connection with self-tapping screws. Constr. Build. Mater. 2024, 411, 134225. [Google Scholar] [CrossRef]
- Rahman, A.; Marufuzzaman, M.; Street, J.; Wooten, J.; Gude, V.G.; Buchanan, R.; Wang, H. A comprehensive review on wood chip moisture content assessment and prediction. Renew. Sustain. Energy Rev. 2024, 189, 113843. [Google Scholar] [CrossRef]
- Fu, W.-L.; Guan, H.-Y.; Kei, S. Effects of Moisture Content and Grain Direction on the Elastic Properties of Beech Wood Based on Experiment and Finite Element Method. Forests 2021, 12, 610. [Google Scholar] [CrossRef]
- Li, Y.; Cao, J. A Guide to the Uses of Treated Wood; China Architecture & Building Press: Beijing, China, 2006. [Google Scholar]
- Schwarze, F.W.; Spycher, M. Resistance of thermo-hygro-mechanically densified wood to colonisation and degradation by brown-rot fungi. Holzforschung 2005, 59, 358–363. [Google Scholar] [CrossRef]
- Liu, J. Relationship between Moisture and Strain Behavior during the Drying Process of Ulmus Pumila. Ph.D. Thesis, Inner Mongolia Agricultural University, Hohhot, China, 2023. [Google Scholar]
- Gao, X. Fatigue of Wood Subjected to Cyclic Moisture-Induced Stress Perpendicular to Grain. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Zhao, J. Research on Drying Characteristics and Check within White Birch Disks. Master’s Thesis, Northeast Forestry University, Harbin, China, 2013. [Google Scholar]
- Barański, J.; Suchta, A.; Barańska, S.; Klement, I.; Vilkovská, T.; Vilkovský, P. Wood Moisture-Content Measurement Accuracy of Impregnated and Nonimpregnated Wood. Sensors 2021, 21, 7033. [Google Scholar] [CrossRef] [PubMed]
- Chomcharn, A.; Skaar, C. Dynamic sorption and hygroexpansion of wood wafers exposed to sinusoidally varying humidity. Wood Sci. Technol. 1983, 17, 259–277. [Google Scholar] [CrossRef]
- Yang, T.; Ma, E. Dynamic sorption and hygroexpansion of wood by humidity cyclically changing effect. J. Funct. Mater. 2013, 24, 3576–3580. [Google Scholar]
- Time, B. Studies on hygroscopic moisture in Norway spruce (Picea abies). Part 1: Sorption measurements of spruce exposed to cyclic step changes in relative humidity. Eur. J. Wood Wood Products. 2002, 4, 271–276. [Google Scholar] [CrossRef]
- Time, B. Studies on hygroscopic moisture in Norway spruce (Picea abies). Part 2: Modelling of transient moisture transport and hysteresis in wood. Eur. J. Wood Wood Products. 2002, 4, 405–410. [Google Scholar] [CrossRef]
- Fan, C.; Wang Linan, P.J. Measures to control seasoning checks of wood used for the repair of the ancient wooden towers in Yingxian County, Shanxi Province. J. Beijing For. Univ. 2006, 01, 98–102. [Google Scholar]
- Jiang, X.; Song, J.; Xia, P. Numerical Simulation of Temperature and Moisture Diffusion during Wave Drying of Birch. For. Eng. 2022, 38, 34–51. [Google Scholar]
- Arends, T.; Barakat, A.J.; Pel, L. Moisture transport in pine wood during one-sided heating studied by NMR. Exp. Therm. Fluid Sci. 2018, 99, 259–271. [Google Scholar] [CrossRef]
- Baronas, R.; Ivanauskas, F.; Juodeikient, I. Modelling of moisture movement in wood during outdoor storage. Nonlinear Anal. Model. Control 2001, 6, 3–14. [Google Scholar] [CrossRef]
- Duan, R.; Wang, Y.; Zhao, L.; Zhou, X. Prediction of Wood Moisture Content Based onTHz Time-Domain Spectroscopy. Bioresources 2022, 17, 4745–4762. [Google Scholar] [CrossRef]
- Chen, K. The Study on Decay and Shrinkage Cracks of Timber Components. Ph.D. Thesis, Southeast University, Nanjing, China, 2019. [Google Scholar]
- Fu, Z.; Wang, H.; Li, J.; Lu, Y. Determination of Moisture Content and Shrinkage Strain during Wood Water Loss with Electrochemical Method. Polymers 2022, 14, 778. [Google Scholar] [CrossRef]
- Fukui, T.; Yanase, Y.; Fujii, Y. Moisture content estimation of green softwood logs of three species based on measurements of fexural vibration. J. Wood Sci. 2023, 69, 32. [Google Scholar] [CrossRef]
- Awais, M.; Altgen, M.; Ma, M.; Belt, T.; Rautkari, L. Quantitative rediction of moisture content distribution in acetylated wood using near-infrared hyperspectral imaging. J. Mater. Sci. 2022, 57, 3419–3429. [Google Scholar] [CrossRef]
- Fragiacomo, M.; Fortino, S.; Tononi, D.; Usardi, I.; Toratti, T. Moisture-induced stresses perpendicular to grain in cross-sections of timber members exposed to different climates. Eng. Struct. 2011, 33, 3071–3078. [Google Scholar] [CrossRef]
- Lü, J.; Tu, D.; Hu, C.; Wang, X.; Wang, Q.; Zhou, Q. Measurement of Wood Moisture Content Distribution by X-ray Method Based on Control Volume Shrinkage Model. Sci. Sivae Sin. 2023, 59, 76–84. [Google Scholar]
- Kang, W.; Lee, N.-H.; Choi, J.-H. A radial distribution of moistures and tangential strains within a larch log cross section during radio-frequency/vacuum drying. Holz Als Roh-Und Werkstoff. 2004, 62, 59–63. [Google Scholar] [CrossRef]
- Jia, D.; Afzal Muhammad, T. Modeling of moisture diffusion in microwave drying of hardwood. Dry. Technol. 2007, 25, 449–454. [Google Scholar] [CrossRef]
- Zhan, J.; Gu, J.; Ai, M. Transverse Drying Stress of White Birch Wood during Drying. J. Northeast For. Univ. 2005, 04, 25–28. [Google Scholar]
- Chen, K.; Qiu, H.; Sun, M.; Lam, F. Experimental and numerical study of moisture distribution and shrinkage crack propagation in cross section of timber members. Constr. Build. Mater. 2019, 221, 219–231. [Google Scholar] [CrossRef]
- Adebiyi, G.A. A single expression for the solution of the one-dimensional transient conduction equation for the simple regular shaped solids. J. Heat Transf. 1995, 117, 158–160. [Google Scholar] [CrossRef]
- Simpson, W.T.; Liu, J.Y. Dependence of the water vapor diffusion coefficient of aspen on moisture content. Wood Sci. Technol. 1991, 26, 9–21. [Google Scholar] [CrossRef]
- Simpson, W.T. Determination and use of moisture diffusion coefficient to characterize dring of northern red oak. Wood Sci. Technol. 1993, 27, 409–420. [Google Scholar] [CrossRef]
- Sun, M. Experimental Research on Shrinkage Crack Development of Timber Structural Members. Master’s Thesis, Southeast University, Nanjing, China, 2018. [Google Scholar]


| Heat Transfer | Humidity Transfer | ||
|---|---|---|---|
| Temperature | T(K) | Moisture content | W(%) |
| Initial temperature | Ti | Initial moisture content | Wi |
| Ambient temperature | Te | Equilibrium moisture content | We |
| Surface temperature of the object | Ts | Surface moisture content | Ws |
| Dimensionless relative temperature | Dimensionless relative moisture content | ||
| Thermal conductivity | α(m2/s) | Water diffusion coefficient | D(m2/s) |
| Surface heat exchange coefficient | h(W/m2/K) | Surface humidity divergence coefficient | S(m/s) |
| Biot number of heat transfer | Biot number of humidity transfer | ||
| Fourier number | Fourier number | ||
| Heat Transfer | Humidity Transfer | |
|---|---|---|
| Cartesian coordinates | ||
| Cylindrical coordinates | ||
| Spherical coordinates |
| Group | Specimen Thickness (mm) | W0 (%) | We (%) | Test Type | Specimen Type (mm × mm × mm) | D (mm2/h) | S (mm/h) | Bi (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 2R = 12.7 | 0 | 0.0269 | absorption | 76 × 146 × 12.7 | 0.377 | 1.88 | 28.7663 |
| 2 | 2R = 12.7 | 0 | 0.0506 | absorption | 76 × 146 × 12.7 | 0.505 | 2.01 | 20.5863 |
| 3 | 2R = 12.7 | 0 | 0.0750 | absorption | 76 × 146 × 12.7 | 0.685 | 2.57 | 17.4727 |
| 4 | 2R = 12.7 | 0 | 0.0995 | absorption | 76 × 146 × 12.7 | 0.918 | 3.39 | 15.2670 |
| 5 | 2R = 12.7 | 0 | 0.1216 | absorption | 76 × 146 × 12.7 | 1.21 | 3.65 | 11.3061 |
| 6 | 2R = 12.7 | 0 | 0.1365 | absorption | 76 × 146 × 12.7 | 1.47 | 4.12 | 9.9475 |
| 7 | 2R = 12.7 | 0 | 0.1622 | absorption | 76 × 146 × 12.7 | 2.01 | 5.35 | 8.3676 |
| 8 | 2R = 12.7 | 0 | 0.1791 | absorption | 76 × 146 × 12.7 | 2.48 | 6.61 | 7.7873 |
| a | 2R = 25.0 | 0.34 | 0.055 | desorption | 50 × 50 × 25 | 1.3805 | 2.3456 | 21.2386 |
| b | 2R = 25.0 | 0.28 | 0.083 | desorption | 50 × 50 × 25 | 1.3553 | 3.3653 | 31.0376 |
| c | 2R = 25.0 | 0.31 | 0.118 | desorption | 50 × 50 × 25 | 1.4069 | 3.2301 | 28.6983 |
| d | 2R = 25.0 | 0.255 | 0.159 | desorption | 50 × 50 × 25 | 1.3956 | 0.6234 | 5.5831 |
| Directions | Elastic Modulus (MPa) | Compressive Strength (MPa) | Tensile Strength (MPa) | Shrinkage/Swelling Coefficient (%) |
|---|---|---|---|---|
| R | ER = 1048 (16.1%) | fc,R = 3.07 (12.23%) | ft,R = 3.07 (12.23%) | αR = 0.139 |
| T | ET = 594 (22.7%) | fc,T = 2.67 (13.44%) | ft,T = 2.67 (13.44%) | αT = 0.255 |
| L | EL = 12,888 (6.9%) | fc,L = 36.25 (10.43%) | ft,L = 36.25 (10.43%) | αL = 0.019 |
| Directions | Poisson ratio | Shear modulus (MPa) | ||
| RT | vRT = 0.43 | GRT = 232 | ||
| RL | vRL = 0.03 | GRT = 967 | ||
| TL | vTL = 0.02 | GRT = 773 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, P.; Han, J.; Guo, S.; Di, J.; Han, X. Prediction Distribution Model of Moisture Content in Laminated Wood Components. Polymers 2024, 16, 1453. https://doi.org/10.3390/polym16111453
Tian P, Han J, Guo S, Di J, Han X. Prediction Distribution Model of Moisture Content in Laminated Wood Components. Polymers. 2024; 16(11):1453. https://doi.org/10.3390/polym16111453
Chicago/Turabian StyleTian, Panpan, Jianhong Han, Shangjie Guo, Jun Di, and Xia Han. 2024. "Prediction Distribution Model of Moisture Content in Laminated Wood Components" Polymers 16, no. 11: 1453. https://doi.org/10.3390/polym16111453
APA StyleTian, P., Han, J., Guo, S., Di, J., & Han, X. (2024). Prediction Distribution Model of Moisture Content in Laminated Wood Components. Polymers, 16(11), 1453. https://doi.org/10.3390/polym16111453





