1. Introduction
A polymer solution consists of a molecularly dispersed polymer in a low molecular weight solvent. Above a critical concentration
c*, the macromolecules begin to interact just like in a polymer melt, but at much higher mobility. In the ideal case of monodisperse and sufficiently long flexible chain polymers, polymer solutions exhibit viscoelastic properties which are universal [
1,
2,
3]. For such model polymer solutions, under isobaric conditions, two state variables such as polymer concentration and solvent quality are sufficient to define their properties at equilibrium or quasi-equilibrium. Solvent quality is a measure of polymeric chain segment–segment interactions mediated through a solvent. In the dilute limit, the mean radius of gyration of a molecular chain is scaled with the molecular weight,
M, as
, where
ν is a characteristic scaling exponent; 0.50 in θ solvents, and 0.588 in good solvents. The longest relaxation time is scaled as
, where
is the relaxation time of a Kuhn monomer,
is the Zimm model accounting for hydrodynamic interactions and
is the Rouse model for eligible hydrodynamic effects. The terminal modulus and the zero shear viscosity are scaled with the molecular weight and polymer concentration
c, as
and
. All flexible chain polymers would follow such a universal scaling law, no matter how different in their chemical monomers. The complicity of polymer segment–segment thermodynamic and hydrodynamic interactions mediated with solvents is casted into a simple scaling theory, which captures the fundamental physics of polymer solutions very well.
The conformations of individual polymer chains start to overlap at an increased concentration, starting at
, above which the solutions are in the semidilute concentration range. Polymer dynamics in a semidilute solution involve multiple length and time scales and become much more complicated than those in a dilute solution. The polymer structure is characterized by its correlation length
[
2]. Below the correlation scale, the structure and dynamic properties exhibit the characteristics of dilute solutions. On a larger scale, the interchain interactions are screened, and the dynamic properties of polymer solutions behave like those of polymer melts. The properties of an unentangled polymer in semidilute solutions could be predicted by the Rouse model as
,
and
. For monodisperse entangled polymer solutions, the reptation model predicts
,
and
[
3]. These classical relations were derived for model polymers with linear flexible chains of uniform and infinite length. The scaling exponent depends on concentration range and solvent quality as could be validated by experiments with a range of model polymer solutions [
4]. Again, the dynamic theory gives reasonably good predictions for the rheological properties of concentrated polymer solutions in which polymer chains are well entangled. However, those dynamic scaling theories cannot account for many practical factors deviated from the model polymer fluids such as finite length of a polymer chain, polydispersity, variation of solvent quality between a good solvent and θ-solvent, ionic strength, possible phase transitions in different temperatures and concentrations, etc. (hereafter called non-model polymers). This poses the question: Do solutions of non-model polymers also exhibit a well-defined power law concentration dependence, especially over semidilute and entangled concentration regions? If so, how can the concentration scaling exponents be estimated in an unambiguous way despite of all the complicated factors involved?
This paper focuses on the concentration scaling analysis of linear viscoelasticity of non-model polymer solutions above their overlap concentration,
c/c* > 1, semidilute entangled and concentrated solutions. Frequency-dependent, dynamic moduli
G′ and
G″ from small amplitude oscillation shear (SAOS) experiments are analyzed using time–concentration superposition (TCS). As known from time–temperature superposition (TTS) [
5], the shifting of
G′ and
G″ data can be separated in a frequency shift
aT and a modulus shift
bT, which has its equivalent, now, in
ac and
bc for TCS. We will determine the concentration shift factors
ac (c/c*) and
bc (
c/
c*) in search of an unambiguous way to estimate the concentration scaling exponents of non-model polymer solutions in comparison to the universal properties known for model polymer solutions. The shift factor of the complex viscosity,
bc/
ac, is also included. Equivalently to TTS, TCS is shown to expand the experimental frequency window of the SAOS data. This has been studied experimentally with a typical non-model polymer solution. The results were compared to data available from other laboratories that have not yet been analyzed in this way.
3. Results
Linear viscoelastic properties of polymer solutions are strongly affected by the level of polymer loading as exemplified by the 18M PAAm–sucrose–water solution shown in
Figure 1a. At high polymer concentrations, the internal dynamics slow down and the dynamic moduli
G′(
ω,
c/c*),
G″(
ω,
c/c*) increase their value. The slowing of characteristic times is not visible immediately because of the fixed frequency range. It requires the time–concentration shifting with its increased width of the frequency window due to gains from the additional slow modes in the highly concentrated solution samples. Such time–concentration superposition, if possible, merges all data into a single pair of dynamic moduli
G′(
ω,
cref/c*),
G″(
ω,
cref/c*). They belong to the solution at reference composition
cref/c*, abbreviated as
G′ref,
G″ref in the following.
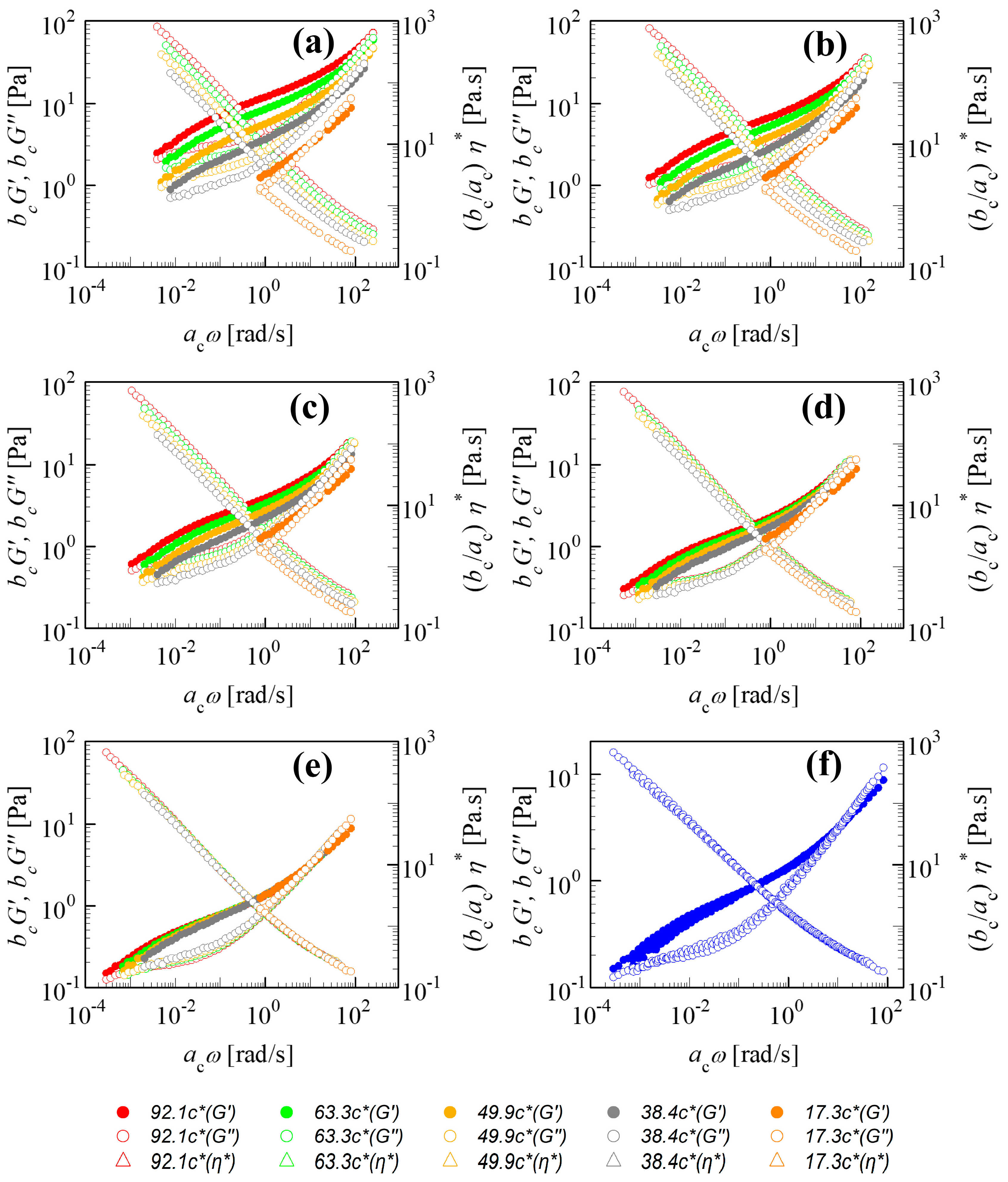
Figure 1a–f demonstrate the TCS shifting for the linear viscoelastic properties of the 18M PAAm–sucrose–water solution with respect to Rouse dynamics. The unshifted experimental data define the starting condition for the shifting, as in
Figure 1a. The lowest concentration
cref = 17.3
c* was chosen here to serve as a reference state providing the frequency-dependent
G′ref and
G″ref in the relatively narrow frequency window of the SAOS experiment. These values for
cref = 17.3
c* are fixed during the shifting while the higher
c/
c* moduli become shifted to the left and down thereby widening the frequency window. Stepwise progress of the shifting is pictured as a sequence. When the shifting is complete, the rescaled moduli superimpose on
G′ref and
G″ref of the reference state and a set of master curves is generated. These master curves belong to
cref = 17.3
c* but can now be shifted to other concentrations.
The shift direction depends on a solution’s concentration with respect to the reference state: for
c/
cref < 1,
bc is positive and
ac is negative and for
c/
cref > 1, the signs change and
bc < 1 and
ac > 1. Since TCS in
Figure 1 is based on the lowest concentration, all shifting occurs to one side.
The shifted
G′ and
G″ are not so well superimposed in the low-frequency region. This has commonly been observed in the other polymer solutions [
9,
10,
11,
12,
13].
Figure 2 shows three-dimensional plots of
G′ and
G″ against concentration and frequency for the 18M PAAm–sucrose–water ternary solution, the 18M PAAm–water binary solution [
11] and the monodisperse polybutadiene (PB) in phenyloctane (PHO) binary solution [
4] before and after TCS shifting. The three-dimensional curves are also projected on the G′- or G″-Freq plane of the three-dimensional plots in order to show the outcomes of TCS superposition clearly. As shown in
Figure 2a, it is evident that there is a frequency window, either in the frequency region or the low-frequency region, over which the concentration scaling of
G′ and
G″ exhibits a dynamic similarity with the same power law exponent. However, the scaling exponents are significantly different between the high-frequency region and the low-frequency region, indicating the existence of different dynamic mechanisms corresponding to Rouse dynamics and terminal entanglement dynamics, respectively. Similarly, as shown in
Figure 2b,c, the terminal entanglement dynamics dominate over a much wider frequency window, which extends several orders of the magnitude for the 18M PAAm–water solution and the PB–PHO solution.
However, by closely examining those
G′ and
G″ curves in the relatively high frequency, it is also evident that the data are not perfectly superimposed. The apparent superposition discrepancy simply reflects the fact that dynamics with well-separated time and length scales would follow different dynamic similarity, respectively, in terms of concentration scaling. As long as the
G′ and
G″ data with various concentrations could be superimposed over a certain range of frequency (no matter how narrow it would be), the dynamic similarity would hold under the corresponding dynamics with its own characteristic time and length scale. The superposition discrepancy in other dynamics over different time and length scales is irrelevant to the dynamics being considered. According to the dynamic scaling theory [
1,
2,
3], the characteristic times of Rouse dynamics are well separated from the characteristic time of the entanglement dynamics, and the ratio between the reptation time and the Rouse time is proportional to the length of the polymer chain. Therefore, the concentration scaling of Rouse dynamics should also be different from the terminal flow dynamics dominated by the entanglement dynamics. As such, TCS could only be realized either in the Rouse dynamic regime or in the terminal entanglement dynamic regime. Alternatively, the same linear viscoelastic data of
Figure 1a and
Figure 2a could also be superimposed with respect to the terminal dynamic regime. The results are shown in
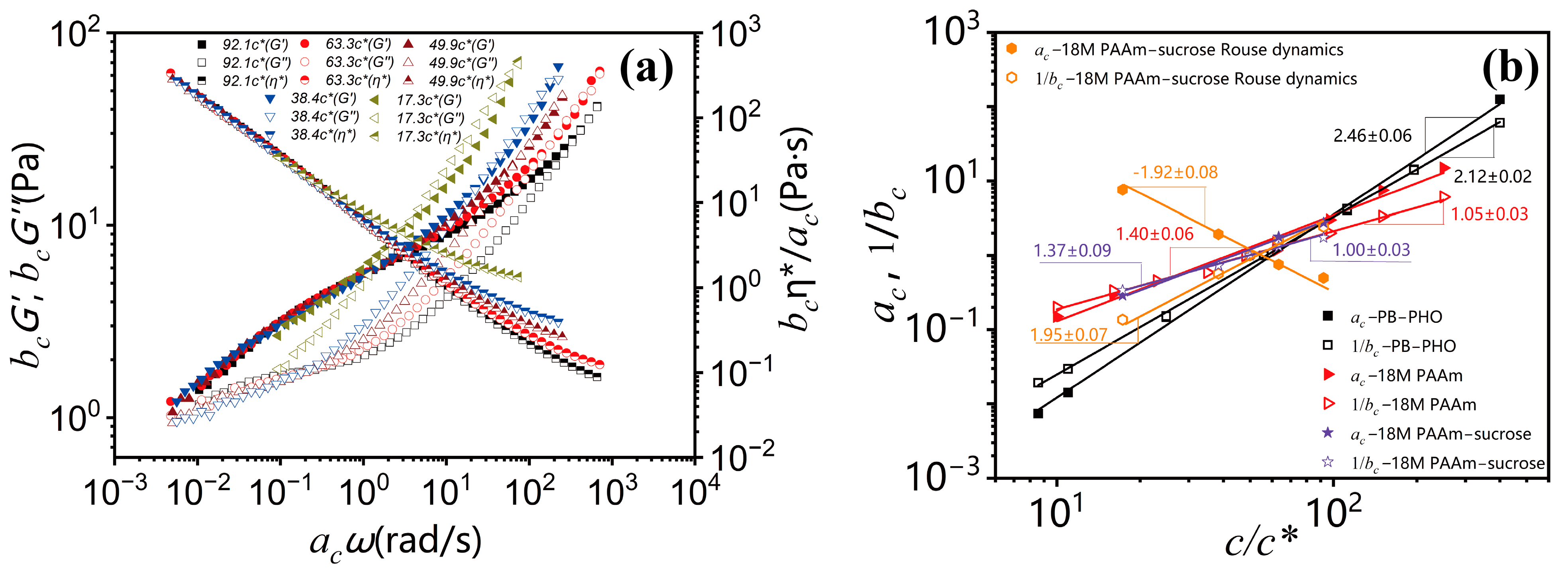
Figure 3a. Note that due to the same reason, the better superimposed linear viscoelastic data of the 18M PAAm–sucrose–water ternary solutions over the terminal dynamic regime would inevitably result in the less well superimposed high-frequency data. Although the outcome of TCS might not look perfect, the resulting shift factors could be related to a power law concentration scaling as
The concentration scaling of the shifting factors
ac is equivalent to the concentration scaling of either the terminal relaxation time or the Rouse relaxation time, respectively. The time–concentration shift effectively amounts to a multiplication of the dynamic moduli
G′(
ω,
c) and
G″(
ω,
c) with the above modulus shift factor
bc and a multiplication of the experimental frequency with the above
ac as
The concentration shifting also applies to the complex viscosity. It superimposes the viscosity data (any concentration within range) onto a reference viscosity function:
Typical viscosity shifting is shown in
Figure 1b–f and
Figure 3a. Shifting involves rescaling of complex viscosity data:
The viscosity shifting gains from both shift factors,
ac and
bc, and hence is larger than the shifting of
G′ or
G″ as
Obviously, as long as a power law concentration scaling on linear viscoelastic properties of polymer solutions exists, TCS is a robust way to estimate their scaling exponents.
As shown in
Figure 3b, the concentration scaling of the horizontal shifting factor
ac and the vertical shifting factor
bc over the terminal entanglement dynamics and Rouse dynamics for 18M PAAm–sucrose–water ternary solutions is compared with the concentration scaling of the terminal entanglement dynamics for 18M PAAm–water binary solution [
11] and monodisperse PB–PHO binary solution [
4]. The concentration scaling of the 18M PAAm–water ternary solutions over the terminal entanglement dynamics is in excellent agreement with those of the 18M PAAm–water binary solutions. It shows that the solvent quality of 60
wt.% sucrose and water mixture is very similar to that of pure water. However, the power law concentration scaling exponent of the shifting factor
ac over Rouse dynamics shows a negative sign. It reflects the fact that the characteristic relaxation time over Rouse dynamics is decreased with the increase in polymer concentration, likely due to the screening effect of segment–segment interactions in polymer solutions. The estimated concentration scaling exponents
and
for PB–PHO, 18M PAAm binary and ternary solutions are listed in
Table 1 along with the results of other binary polymer solutions obtained from the TCS procedure over the terminal entanglement dynamic regime. The concentration scaling of complex viscosity is equivalent to the scaling of the shifting factors
ac/
bc. As shown in
Figure 4, they all exhibit a well-defined power law concentration scaling.
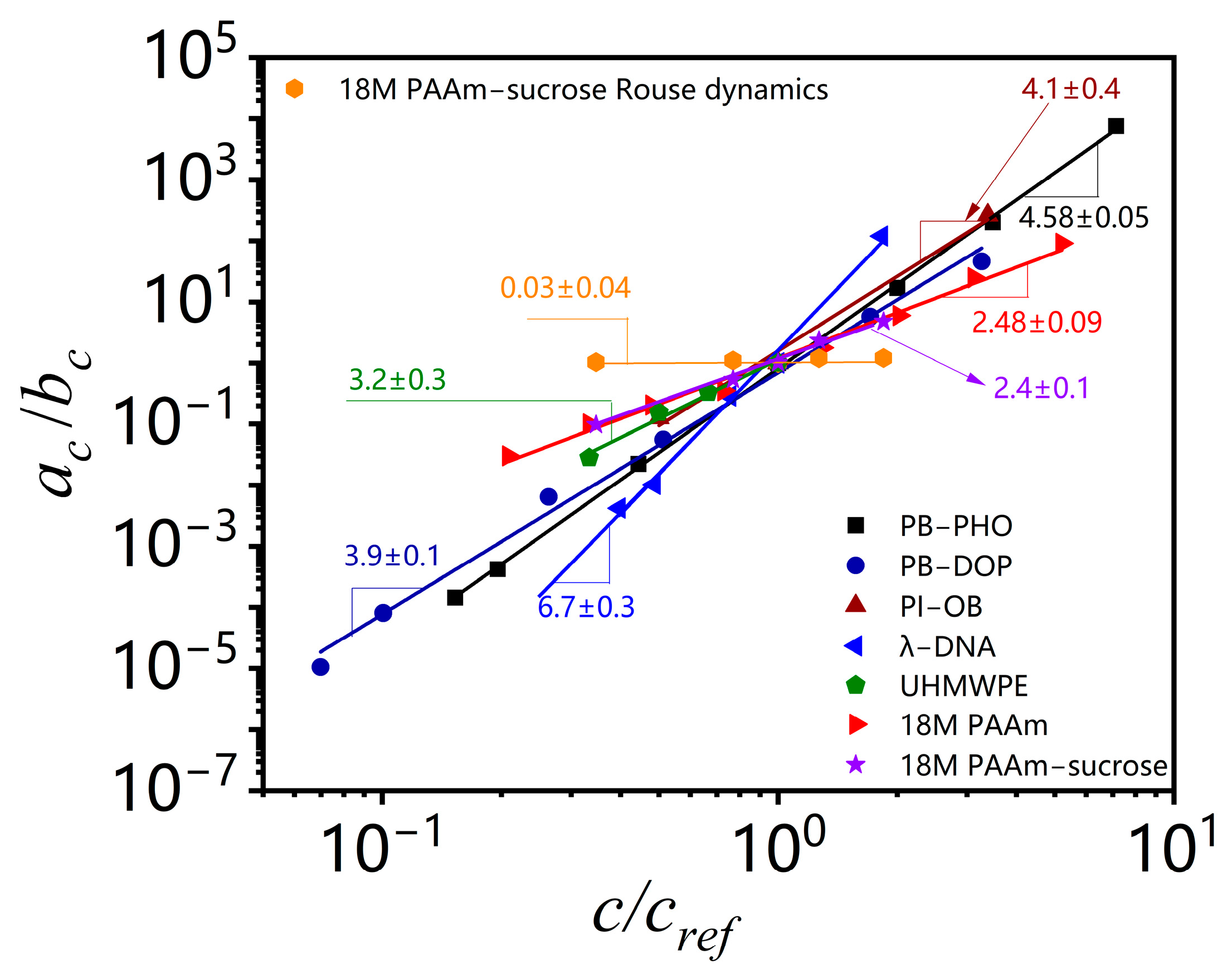
Table 1 also lists the estimated concentration scaling exponent (
α −
β) for all the polymer solutions analyzed here. The convolution of shift factors in the viscosity shift obscures its meaning and makes it hard to draw conclusions about concentration effects on other viscoelastic material functions.
4. Discussion
There is still considerable ambiguity in predicting the power law concentration scaling exponent of linear viscoelastic properties of entangled polymer solutions. Under single-parameter scaling approximation proposed by de Gennes [
2] and the scaling of the zero shear viscosity with molecular weight as
, the single-parameter scaling theory predicts
for polymer in θ solvent solution and
for polymer in good solvent solution. On the other hand, under the two-parameter scaling approximation [
14], which accounts for a possible difference in concentration dependence of the tube diameter and the correlation length, the two-parameter scaling theory estimates the concentration scaling exponents of the zero shear viscosity for θ solvent as 5.2 and good solvent polymer solutions as 4.5, respectively. The same scaling exponent (4.5) of the zero shear viscosity is found for good solvent PB–PHO solutions and θ solvent PB–DOP solutions [
4]. Although the dynamic scaling theory could give a reasonably consistent prediction to the concentration scaling of the zero shear viscosity of the above model polymer solutions and the results are also in quite good agreement with those estimated by the TCS procedure, there are still significant discrepancies in the estimated concentration scaling exponent of the reptation time and terminal modulus.
Table 1 lists the outcomes of the TCS analysis for a range of non-model polymer solutions, along with the model polymer solutions. The results show that the concentration scaling is very sensitive to the actual dependence of correlation length, tube diameter, reptation time, terminal modulus, and viscosity on solvent quality, finite molecular length and polydispersity, possible changes of equilibrium phase or thermodynamic state with concentration at a certain temperature, etc. Under a marginal solvent quality between good and θ conditions, the concentration scaling of the zero shear viscosity for PI–OB solutions sets between good solvent PB–PHO solution and θ solvent PB–DOP solutions. The scaling exponents of its terminal entanglement time and terminal modulus are out of the range between the two limits defined by PB–PHO and PB–DOP solutions. The concentration scaling of Welan solutions is similar to that of PI–OB solutions. The effect of polymer chain length is evident, in addition to solvent quality. The effect is much more pronounced to the concentration scaling of the terminal entanglement time for completely monodisperse ultrahigh molecular weight λ-DNA, resulting in a higher scaling exponent of the zero shear viscosity. The different Kuhn length and finite size of those polymers might also be important factors that cause different concentration scaling. TCS results of highly polydisperse UHMWPE, 18M PAAm binary and ternary solutions also show a general trend that the polydispersity could significantly reduce the concentration scaling exponents of the terminal entanglement time and the zero shear viscosity. At present, no unified theory can quantitatively account for all the effects deviated from the model polymer solutions. The present work illustrates that TCS could implicitly account for all the above effects for non-model as well as model polymer solutions and also for colloidal suspensions, as reported in a recent study that the power law concentration scaling exponent depends on colloidal interactions mediated with solvent and is sensitive to equilibrium phase behavior of colloidal suspensions [
15].
5. Conclusions
The concentration shift was analyzed using the same framework as JD Ferry’s time–temperature superposition. Surprisingly, power law scaling was found far above the overlap concentration. Unlike time–temperature superposition, both shifts are substantial, with the vertical shift sometimes being as large as the time shift, or even larger. The data analysis presented here indicates that TCS is a powerful alternative method to estimate the concentration scaling of linear viscoelastic properties of polymer solutions. It can account for actual solvent quality, flexibility of the molecular chain, molecular weight, and distribution. It can also identify the concentration range where power law scaling may or may not exist and estimate the concentration scaling exponents of linear viscoelastic properties unambiguously. Moreover, the dependence of scaling exponents over the concentration region indicates possible different dynamic similarity and corresponding structural features, e.g., from the Zimm dynamics for dilute polymer solutions, the Rouse dynamics for concentrated but unentangled polymer solutions, to the reptation dynamics for highly entangled polymer solutions and possible phase transitions of liquid crystalline polymer solutions. Hence, this method is significant in predicting and optimizing engineering for non-model polymer solutions.
The relatively “clean” exponent values of α ≈ 5/2 and β ≈ −2 for monodisperse PB–PHO solutions, α ≈ 3/2 and β ≈ −1 for highly polydisperse 18M PAAm aqueous solutions, and α ≈ −2 and β ≈ −2 for highly polydisperse 18M PAAm–sucrose–water solutions must be considered coincidental at this level of information. Further experiments are needed to explore the generality of these values for classes of polymer solutions with shared characteristics such as solvent quality, molecular interaction, distance from any type of equilibrium phase transition, etc. This framework provides a starting point for such exploration.