Prediction of Stress–Strain Curves for HFRP Composite Confined Brick Aggregate Concrete under Axial Load
Abstract
1. Introduction
2. Experimental Setup
2.1. Test Matrix
2.2. Properties of Materials
2.3. Strengthening Process
2.4. Instrumentation and Loading Setup
3. Experimental Results
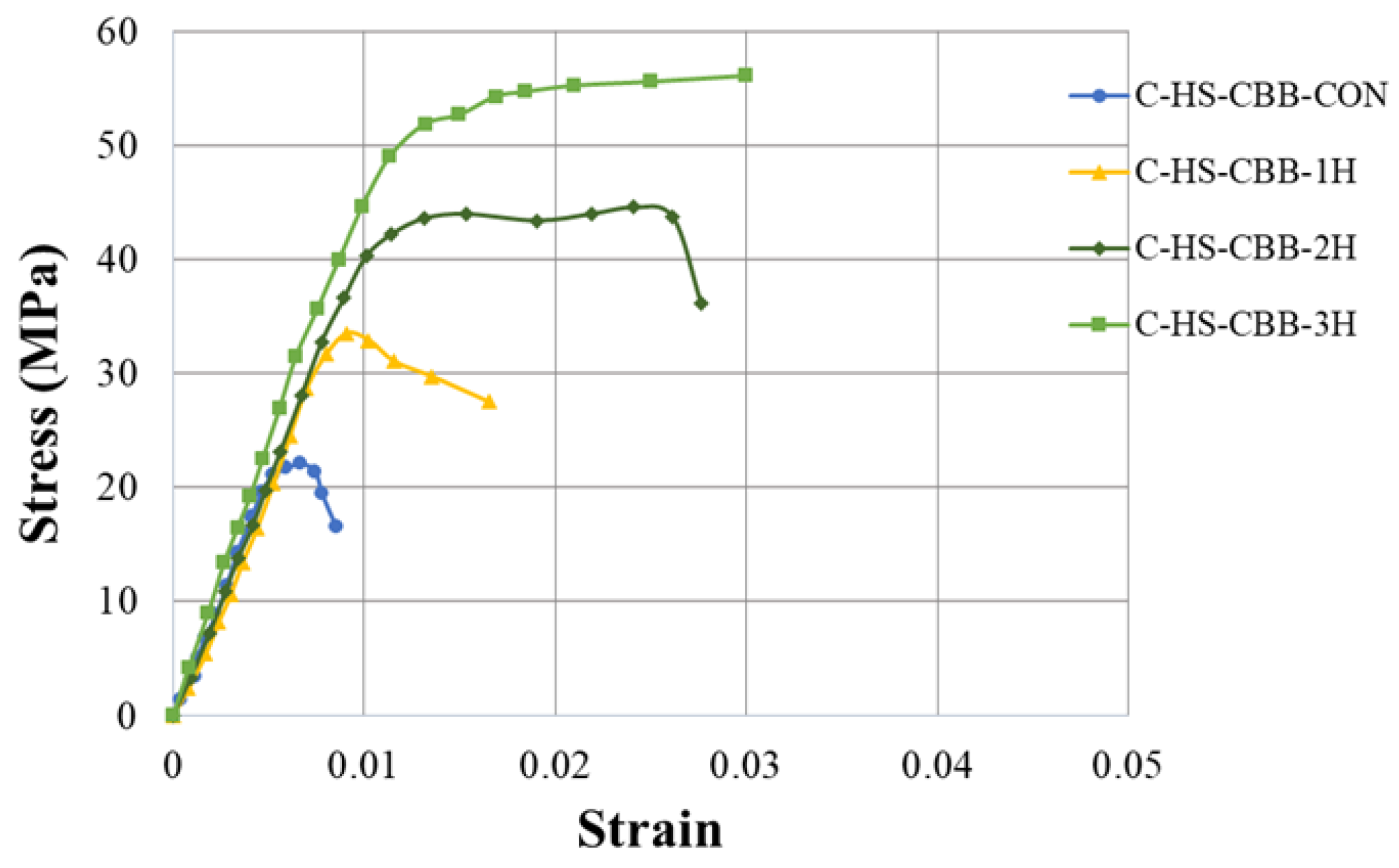
3.1. Axial Stress–Strain Response
3.2. Hemp Rope Layers Effect on Type-1 and Type-2 Concrete
3.3. Failure Pattern of Specimens
4. Comparison with Analytical Models
4.1. Detail of Existing Models
4.2. Performance of Existing Models
5. Proposed Approach to Predict Compressive Stress–Strain Curves of Hemp-Confined Concrete
5.1. Ultimate Compressive Strength
5.2. Ultimate Compressive Strain
5.3. Prediction of Compressive Stress–Strain Response of HFRP-Confined Concrete
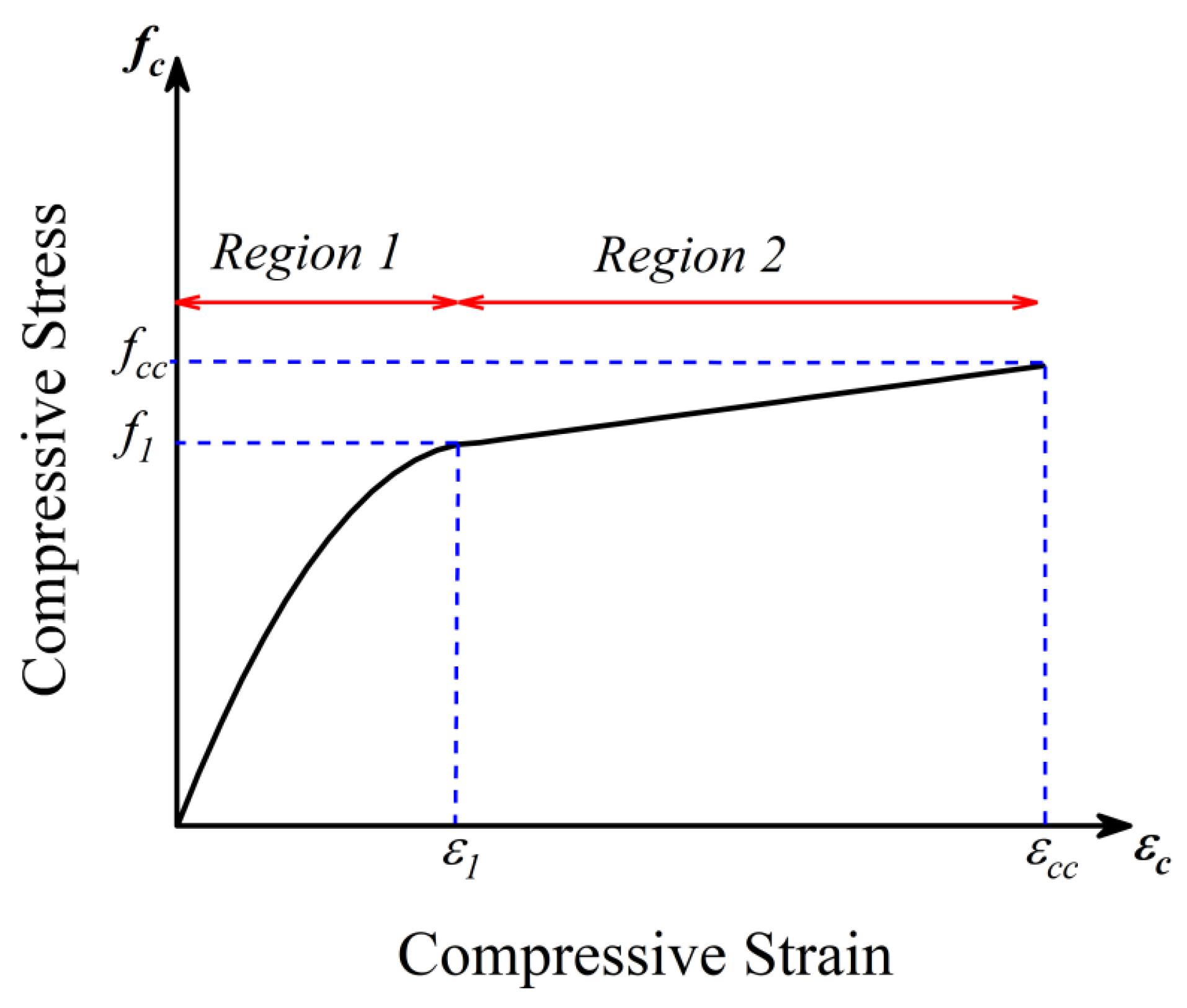
5.3.1. Compressive Stress vs. Strain Response in Region 1
5.3.2. Compressive Stress vs. Strain Response in Region 2
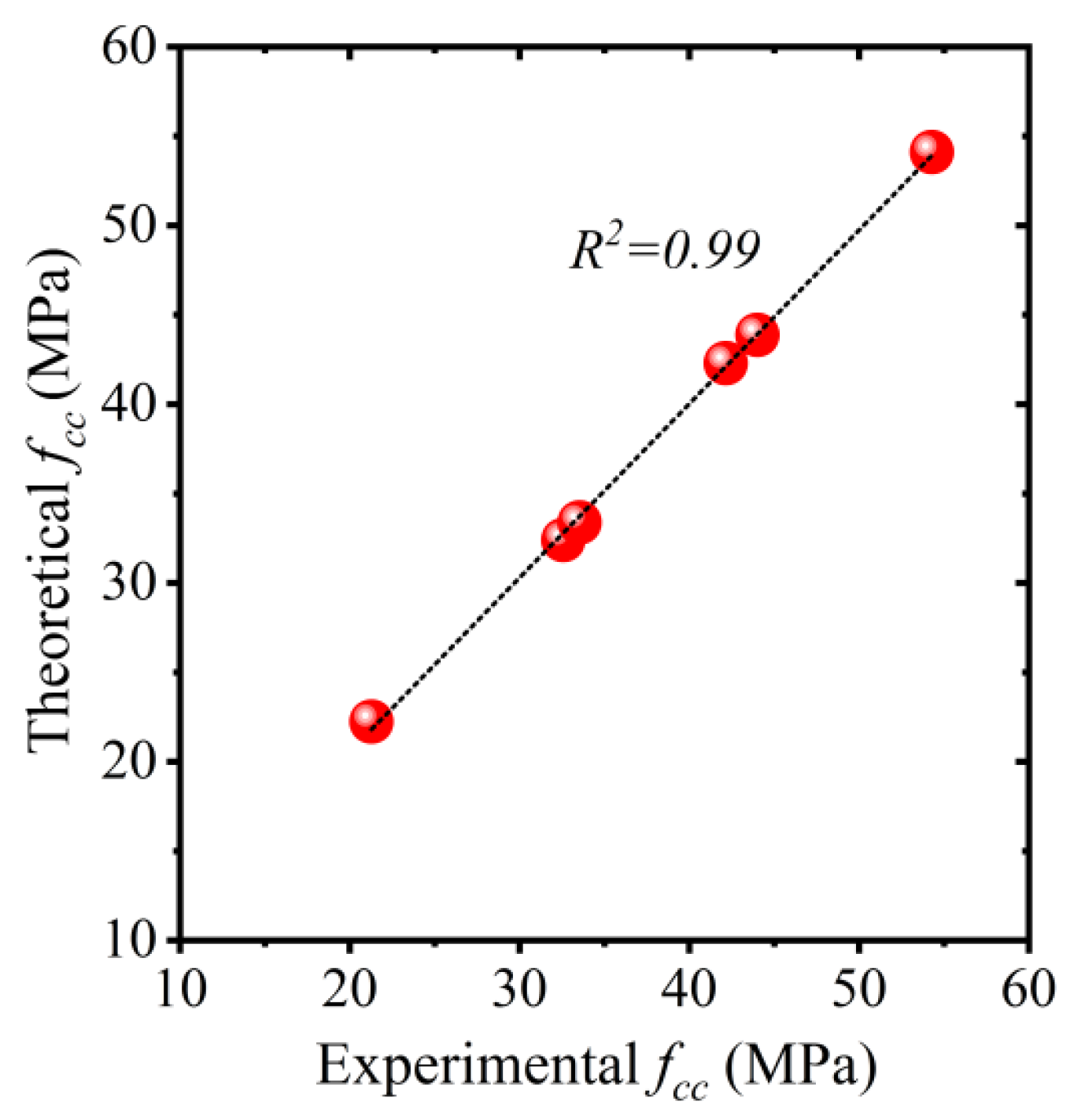
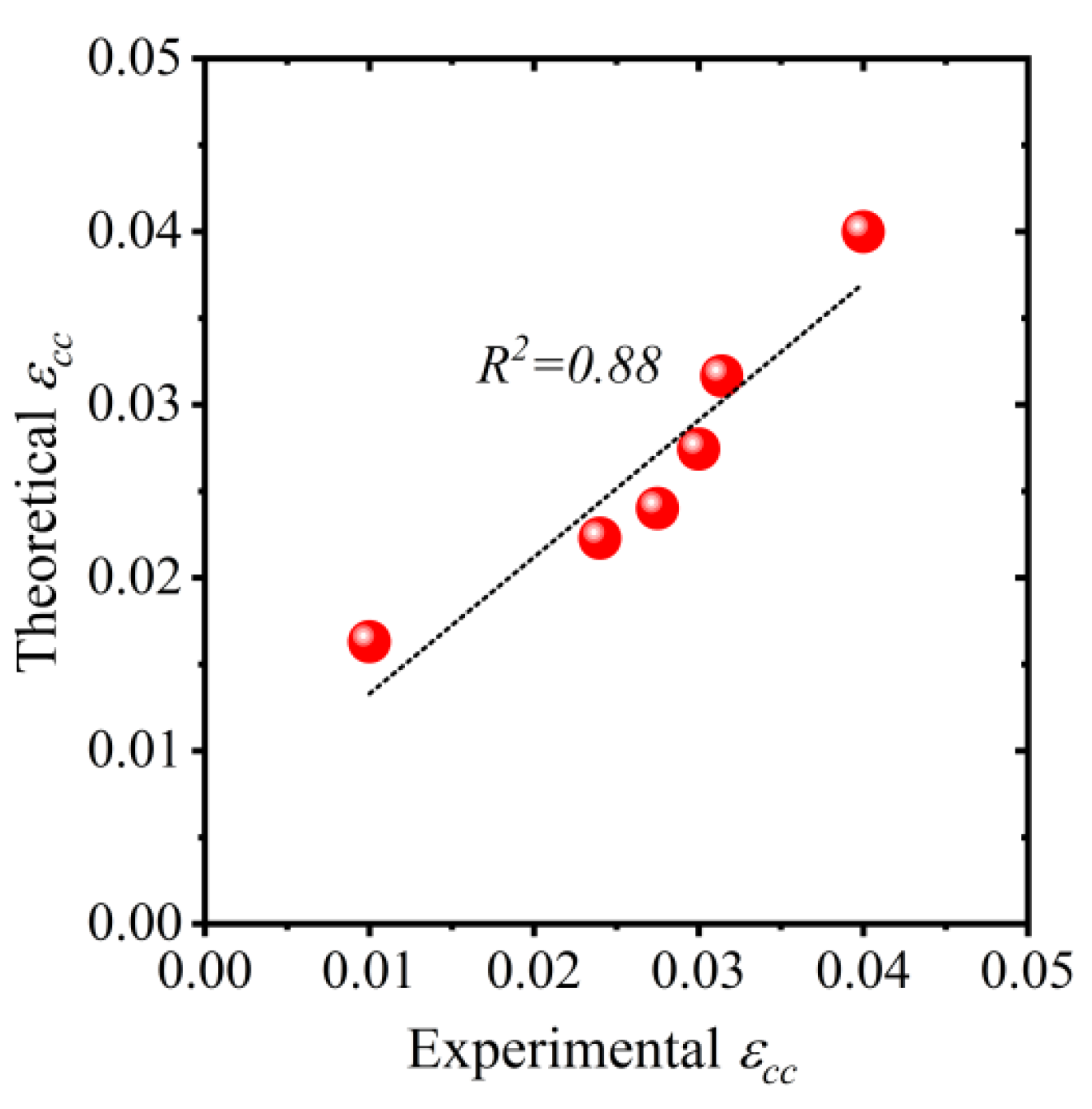
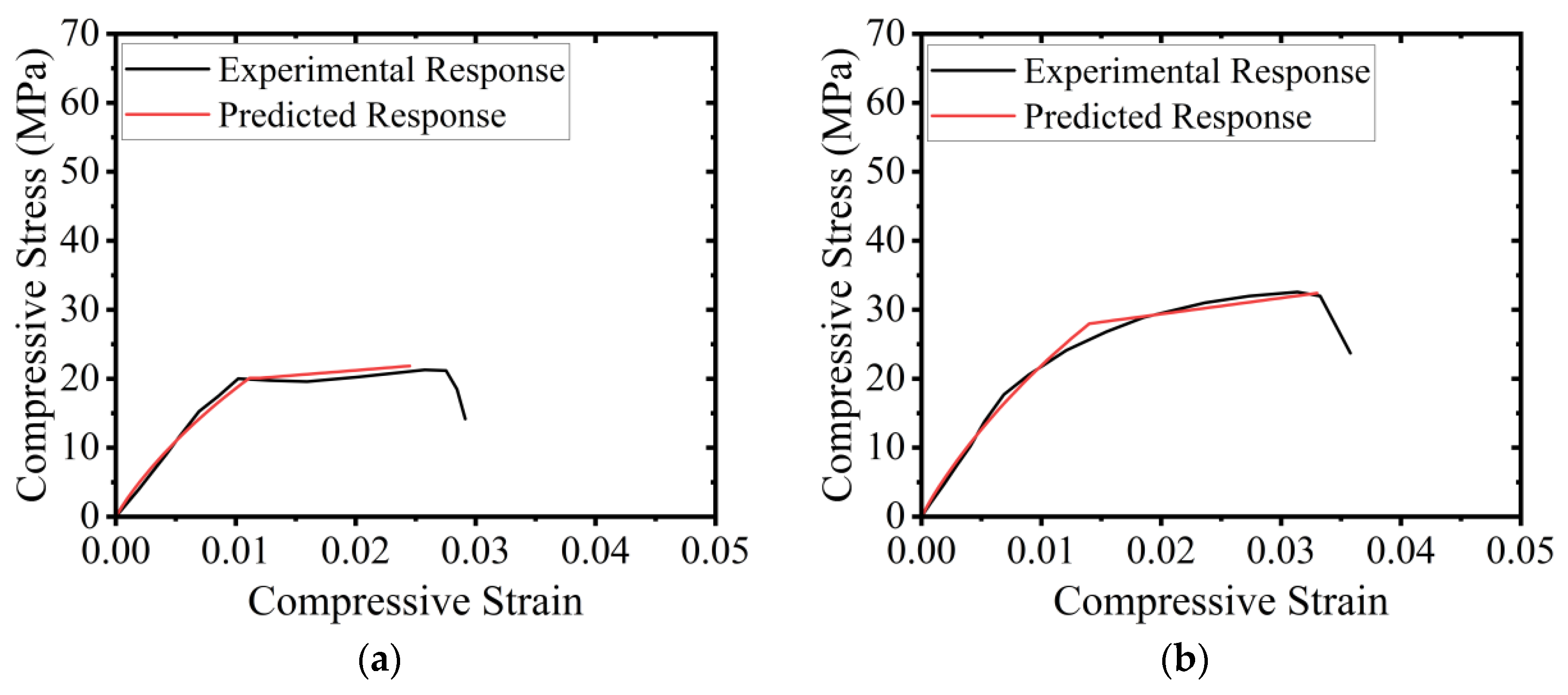
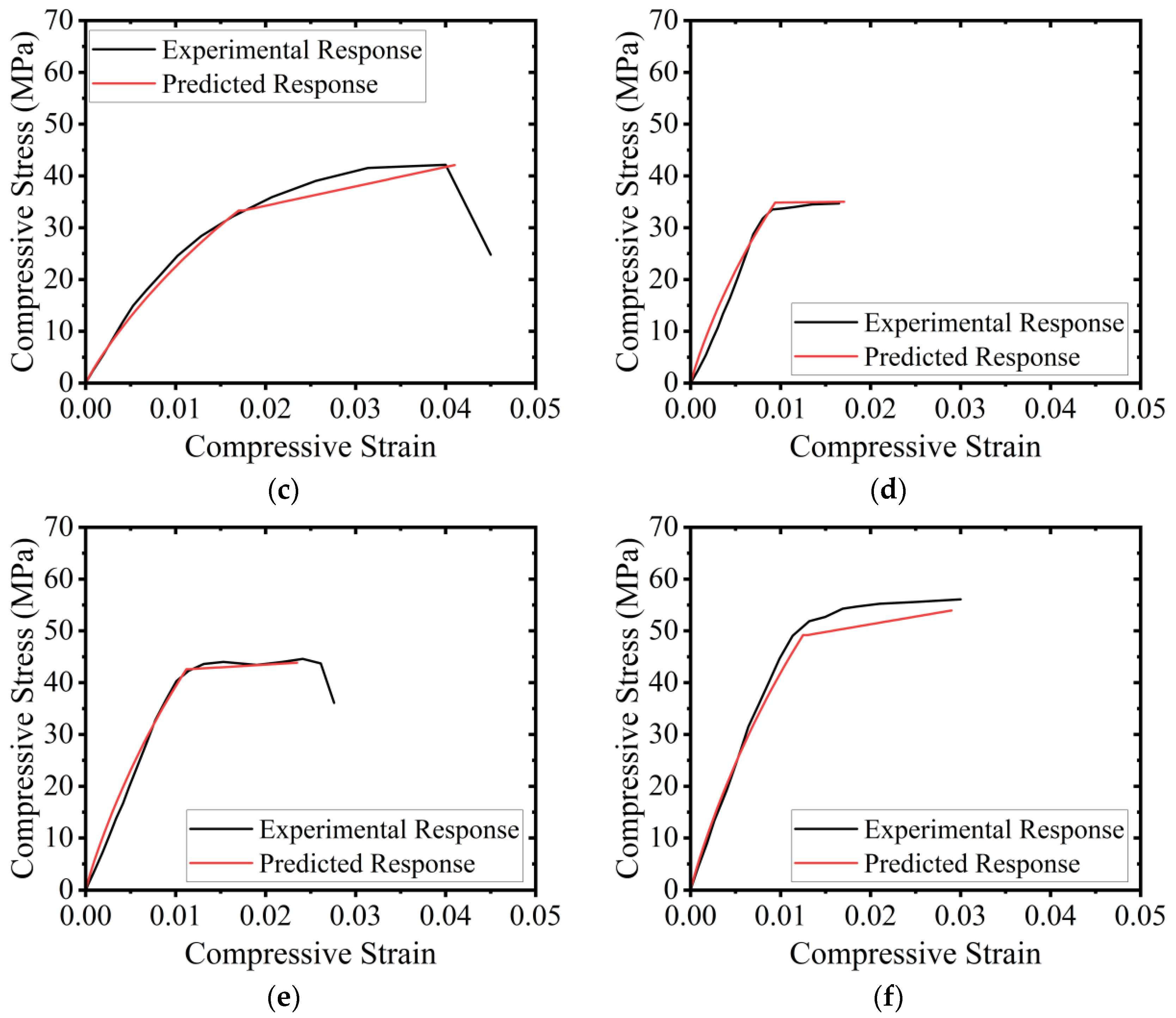
5.3.3. Comparison of Predicted vs. Experimental Stress–Strain Curves
6. Conclusions
- Specimens confined with hemp ropes exhibited a bilinear stress–strain response. Contrary to control specimens, the axial ductility was significantly improved as a result of the hemp fiber rope confinement. The peak axial strength and the corresponding strain in Type-1, as well as Type-2 concrete, increased with the increase in the number of hemp rope layers. Furthermore, the maximum compressive strength and strain were observed in the case of the 3-layer confinement. The improvement in the ultimate compressive strength and strain was more pronounced as the compressive strength of unstrengthened concrete decreased. Improvements of up to 272% and 457% in the ultimate compressive strength and strain were observed due to hemp confinement.
- The ultimate compressive strength and strain were predicted in this research work using existing analytical stress–strain models. Several models were shown to reasonably predict the compressive strengths. However, none of the models could accurately predict peak strain. Therefore, it was found necessary to propose expressions for predicting the characteristic points on the compressive stress–strain envelope of HFRP-confined RAC.
- Nonlinear regression analysis was conducted to propose expressions to predict the ultimate compressive strength and strain of HFRP-confined concrete constructed by partial replacement of natural coarse aggregates by recycled fired-clay brick aggregates. In addition, expressions for the compressive stress and strain at the end of the initial stiff branch were also proposed. The proposed expressions resulted in good agreement with the experimental results.
- An analytical procedure was proposed to predict the stress–strain curves of HFRP-confined concrete constructed by partial replacement of natural coarse aggregates by recycled fired-clay brick aggregates. The compressive stress–strain curves of HFRP-confined RAC were idealized into two branches, i.e., a parabolic branch followed by a linear branch. The proposed regression expressions were utilized to trace the full compressive stress–strain curves of HFRP-confined RAC. A close agreement was found between the experimental and analytically predicted stress-strain curves.
- The results of this study could be used in multiple areas of civil and structural engineering, especially where there is a need to strengthen and or retrofit existing buildings. In addition, the developed models can be utilized for the design and analysis of reinforced concrete structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bribián, I.Z.; Capilla, A.V.; Usón, A.A. Life Cycle Assessment of Building Materials: Comparative Analysis of Energy and Environmental Impacts and Evaluation of the Eco-Efficiency Improvement Potential. Build. Environ. 2011, 46, 1133–1140. [Google Scholar] [CrossRef]
- Xiao, J. Recycled Aggregate Concrete Structures, 1st ed.; Springer Tracts in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 978-3-662-53985-9. [Google Scholar]
- Zhu, L.; Zhu, Z. Reuse of Clay Brick Waste in Mortar and Concrete. Adv. Mater. Sci. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Martins, R.O.G.; de Alvarenga, R.C.S.S.A.; Pedroti, L.G.; de Oliveira, A.F.; Mendes, B.C.; de Azevedo, A.R.G. Assessment of the Durability of Grout Submitted to Accelerated Carbonation Test. Constr. Build. Mater. 2018, 159, 261–268. [Google Scholar] [CrossRef]
- Liu, Q.; Singh, A.; Xiao, J.; Li, B.; Tam, V.W. Workability and Mechanical Properties of Mortar Containing Recycled Sand from Aerated Concrete Blocks and Sintered Clay Bricks. Resour. Conserv. Recycl. 2020, 157, 104728. [Google Scholar] [CrossRef]
- Rodsin, K.; Joyklad, P.; Hussain, Q.; Mohamad, H.; Buatik, A.; Zhou, M.; Chaiyasarn, K.; Nawaz, A.; Mehmood, T.; Elnemr, A. Behavior of Steel Clamp Confined Brick Aggregate Concrete Circular Columns Subjected to Axial Compression. Case Stud. Constr. Mater. 2022, 16, e00815. [Google Scholar] [CrossRef]
- Rodsin, K. Confinement Effects of Glass FRP on Circular Concrete Columns Made with Crushed Fired Clay Bricks as Coarse Aggregates. Case Stud. Constr. Mater. 2021, 15, e00609. [Google Scholar] [CrossRef]
- Manfredi, S.; Pant, R.; Pennington, D.W.; Versmann, A. Supporting Environmentally Sound Decisions for Waste Management with LCT and LCA. Int. J. Life Cycle Assess. 2011, 16, 937–939. [Google Scholar] [CrossRef]
- Debieb, F.; Kenai, S. The Use of Coarse and Fine Crushed Bricks as Aggregate in Concrete. Constr. Build. Mater. 2008, 22, 886–893. [Google Scholar] [CrossRef]
- Yang, J.; Du, Q.; Bao, Y. Concrete with Recycled Concrete Aggregate and Crushed Clay Bricks. Constr. Build. Mater. 2011, 25, 1935–1945. [Google Scholar] [CrossRef]
- Nováková, I.; Mikulica, K. Properties of Concrete with Partial Replacement of Natural Aggregate by Recycled Concrete Aggregates from Precast Production. Procedia Eng. 2016, 151, 360–367. [Google Scholar] [CrossRef]
- González, J.S.; Gayarre, F.L.; Pérez, C.L.C.; Ros, P.S.; López, M.A.S. Influence of Recycled Brick Aggregates on Properties of Structural Concrete for Manufacturing Precast Prestressed Beams. Constr. Build. Mater. 2017, 149, 507–514. [Google Scholar] [CrossRef]
- Jiang, T.; Wang, X.M.; Zhang, W.P.; Chen, G.M.; Lin, Z.H. Behavior of FRP-Confined Recycled Brick Aggregate Concrete under Monotonic Compression. J. Compos. Constr. 2020, 24, 04020067. [Google Scholar] [CrossRef]
- Amin, M.N.; Iqtidar, A.; Khan, K.; Javed, M.F.; Shalabi, F.I.; Qadir, M.G. Comparison of machine learning approaches with traditional methods for predicting the compressive strength of rice husk ash concrete. Crystals 2021, 11, 779. [Google Scholar] [CrossRef]
- Medina, C.; Zhu, W.; Howind, T.; De Rojas, M.I.S.; Frías, M. Influence of Mixed Recycled Aggregate on the Physical—Mechanical Properties of Recycled Concrete. J. Clean. Prod. 2014, 68, 216–225. [Google Scholar] [CrossRef]
- Cachim, P.B. Mechanical Properties of Brick Aggregate Concrete. Constr. Build. Mater. 2009, 23, 1292–1297. [Google Scholar] [CrossRef]
- Liu, Q.; Xiao, J.; Singh, A. Crack Propagation and Failure Characteristics of Modeled Concrete with Natural and Brick Aggregates. J. Renew. Mater. 2021, 9, 1309–1327. [Google Scholar] [CrossRef]
- Khalaf, F.M.; DeVenny, A.S. Recycling of Demolished Masonry Rubble as Coarse Aggregate in Concrete: Review. J. Mater. Civ. Eng. 2004, 16, 331–340. [Google Scholar] [CrossRef]
- Huang, Y.; Xiao, J.; Zhang, C. Theoretical Study on Mechanical Behavior of Steel Confined Recycled Aggregate Concrete. J. Constr. Steel. Res. 2012, 76, 100–111. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Aslam, F.; Ahmad, A.; Al-Faiad, M.A. Comparison of Prediction Models Based on Machine Learning for the Compressive Strength Estimation of Recycled Aggregate Concrete. Materials 2022, 15, 3430. [Google Scholar] [CrossRef]
- Shah, M.I.; Amin, M.N.; Khan, K.; Niazi, M.S.K.; Aslam, F.; Alyousef, R.; Javed, M.F.; Mosavi, A. Performance Evaluation of Soft Computing for Modeling the Strength Properties of Waste Substitute Green Concrete. Sustainability 2021, 13, 2867. [Google Scholar] [CrossRef]
- Amin, M.N.; Ahmad, W.; Khan, K.; Sayed, M.M. Mapping Research Knowledge on Rice Husk Ash Application in Concrete: A Scientometric Review. Materials 2022, 15, 3431. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.T.; Teng, J.G. FRP-Strengthened RC Beams. I: Review of Debonding Strength Models. Eng. Struct. 2002, 24, 385–395. [Google Scholar] [CrossRef]
- Wei, Y.; Zhang, Y.; Chai, J.; Wu, G.; Dong, Z. Experimental Investigation of Rectangular Concrete-Filled Fiber Reinforced Polymer (FRP)-Steel Composite Tube Columns for Various Corner Radii. Compos. Struct. 2020, 244, 112311. [Google Scholar] [CrossRef]
- Wei, Y.; Xu, P.; Zhang, Y.; Wang, G.; Zheng, K. Compressive Behaviour of FRP-Steel Wire Mesh Composite Tubes Filled with Seawater and Sea Sand Concrete. Constr. Build. Mater. 2022, 314, 125608. [Google Scholar] [CrossRef]
- Amin, M.N.; Iqbal, M.; Khan, K.; Qadir, M.G.; Shalabi, F.I.; Jamal, A. Ensemble Tree-Based Approach towards Flexural Strength Prediction of FRP Reinforced Concrete Beams. Polymers 2022, 14, 1303. [Google Scholar] [CrossRef]
- Liang, J.; Lin, S.; Ahmed, M. Axial Behavior of Carbon Fiber-Reinforced Polymer–Confined Recycled Aggregate Concrete-Filled Steel Tube Slender Square Columns. Adv. Struct. Eng. 2021, 24, 3507–3518. [Google Scholar] [CrossRef]
- Chen, G.M.; He, Y.H.; Jiang, T.; Lin, C.J. Behavior of CFRP-Confined Recycled Aggregate Concrete under Axial Compression. Constr. Build. Mater. 2016, 111, 85–97. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Y.; Miao, K.; Li, B. A Novel Seawater and Sea Sand Concrete-Filled FRP-Carbon Steel Composite Tube Column: Cyclic Axial Compression Behaviour and Modelling. Eng. Struct. 2022, 252, 113531. [Google Scholar] [CrossRef]
- Wei, Y.; Bai, J.; Zhang, Y.; Miao, K.; Zheng, K. Compressive Performance of High-Strength Seawater and Sea Sand Concrete-Filled Circular FRP-Steel Composite Tube Columns. Eng. Struct. 2021, 240, 112357. [Google Scholar] [CrossRef]
- Chaiyasarn, K.; Hussain, Q.; Joyklad, P.; Rodsin, K. New Hybrid Basalt/E-Glass FRP Jacketing for Enhanced Confinement of Recycled Aggregate Concrete with Clay Brick Aggregate. Case Stud. Constr. Mater. 2021, 14, e00507. [Google Scholar] [CrossRef]
- Yinh, S.; Hussain, Q.; Joyklad, P.; Chaimahawan, P.; Rattanapitikon, W.; Limkatanyu, S.; Pimanmas, A. Strengthening Effect of Natural Fiber Reinforced Polymer Composites (NFRP) on Concrete. Case Stud. Constr. Mater. 2021, 15, e00653. [Google Scholar] [CrossRef]
- Sen, T.; Reddy, H.N.J. Efficacy of Bio Derived Jute FRP Composite Based Technique for Shear Strength Retrofitting of Reinforced Concrete Beams and Its Comparative Analysis with Carbon and Glass FRP Shear Retrofitting Schemes. Sustain. Cities Soc. 2014, 13, 105–124. [Google Scholar] [CrossRef]
- Li, Y.; Mai, Y.W.; Ye, L. Sisal Fibre and Its Composites: A Review of Recent Developments. Compos. Sci. Technol. 2000, 60, 2037–2055. [Google Scholar] [CrossRef]
- Alam, M.A.; Al Riyami, K. Shear Strengthening of Reinforced Concrete Beam Using Natural Fibre Reinforced Polymer Laminates. Constr. Build. Mater. 2018, 162, 683–696. [Google Scholar] [CrossRef]
- Bambach, M.R. Compression Strength of Natural Fibre Composite Plates and Sections of Flax, Jute and Hemp. Thin-Walled Struct. 2017, 119, 103–113. [Google Scholar] [CrossRef]
- Hussain, Q.; Ruangrassamee, A.; Tangtermsirikul, S.; Joyklad, P. Behavior of Concrete Confined with Epoxy Bonded Fiber Ropes under Axial Load. Constr. Build. Mater. 2020, 263, 120093. [Google Scholar] [CrossRef]
- Fragoudakis, R.; Gallagher, J.A.; Kim, V. A Computational Analysis of the Energy Harvested by Gfrp and Nfrp Laminated Beams Under Cyclic Loading. Procedia Eng. 2017, 200, 221–228. [Google Scholar] [CrossRef]
- Ghalieh, L.; Awwad, E.; Saad, G.; Khatib, H.; Mabsout, M. Concrete Columns Wrapped with Hemp Fiber Reinforced Polymer—An Experimental Study. Procedia Eng. 2017, 200, 440–447. [Google Scholar] [CrossRef]
- Joyklad, P.; Yooprasertchai, E.; Rahim, A.; Ali, N.; Chaiyasarn, K.; Hussain, Q. Sustainable and Low-Cost Hemp FRP Composite Confinement of B-Waste Concrete. Sustainability 2022, 14, 7673. [Google Scholar] [CrossRef]
- ASTM C1314-21; Standard Test Method for Compressive Strength Of Masonry Prisms. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM C140/C140M-22a; Standard Test Methods for Sampling and Testing Concrete Masonry Units and Related Units. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM A931-18; Standard Test Method for Tension Testing of Wire Ropes and Strand. ASTM International: West Conshohocken, PA, USA, 2018.
- ASTM E8/E8M-13; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2013.
- Qi, Y.; Xie, L.; Bai, Y.; Liu, W.; Fang, H. Axial Compression Behaviours of Pultruded GFRP–Wood Composite Columns. Sensors 2019, 19, 755. [Google Scholar] [CrossRef]
- Hussain, Q.; Ruangrassamee, A.; Tangtermsirikul, S.; Joyklad, P.; Wijeyewickrema, A.C. Low-Cost Fiber Rope Reinforced Polymer (FRRP) Confinement of Square Columns with Different Corner Radii. Buildings 2021, 11, 355. [Google Scholar] [CrossRef]
- Ghernouti, Y.; Rabehi, B. FRP-Confined Short Concrete Columns under Compressive Loading: Experimental and Modeling Investigation. J. Reinf. Plast. Compos. 2010, 30, 241–255. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A. Compressive Strength Models of FRP-Confined Concrete. In Proceedings of the 1st Asia-Pacific Conference on FRP in Structures: APFIS 2007, Hong Kong, China, 12–14 December 2007; Volume 1, pp. 175–180. [Google Scholar]
- Olsen, N.H. Uniaxial Stress-Strain Curves of High Strength Concrete. Dan. Tek. Hojsk. Afd. Baerende Konstr. Ser. R 1990, 97, 209–215. [Google Scholar]
- Lam, L.; Teng, J.G. Strength Models for Fiber-Reinforced Plastic-Confined Concrete. J. Struct. Eng. 2002, 128, 612–623. [Google Scholar] [CrossRef]
- Lu, X.; Hsu, C.T.T. Behavior of High Strength Concrete with and without Steel Fiber Reinforcement in Triaxial Compression. Cem. Concr. Res. 2006, 36, 1679–1685. [Google Scholar] [CrossRef]
- Légeron, F.; Paultre, P. Uniaxial Confinement Model for Normal- and High-Strength Concrete Columns. J. Struct. Eng. 2003, 129, 241–252. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Papanicolaou, C.G.; Zissimopoulos, P.; Laourdekis, T. Concrete Confinement with Textile-Reinforced Mortar Jackets. ACI Struct. J. 2006, 103, 28–37. [Google Scholar] [CrossRef]
- Akiyama, M.; Suzuki, M.; Frangopol, D.M. Stress-Averaged Strain Model for Confined High-Strength Concrete. ACI Struct. J. 2010, 107, 179–188. [Google Scholar] [CrossRef]
- Benzaid, R.; Mesbah, H.; Chikh, N.E. FRP-Confined Concrete Cylinders: Axial Compression Experiments and Strength Model. J. Reinf. Plast. Compos. 2010, 29, 2469–2488. [Google Scholar] [CrossRef]
- Scott, B.D.; Park, R.; Priestley, M.J.N. Stress-Strain Behavior of Concrete Confined by Overlapping Hoops at Low and High Strain Rates. ACI J. Proc. 1982, 79, 13–27. [Google Scholar] [CrossRef]
- Harajli, M.H. Axial Stress–Strain Relationship for FRP Confined Circular and Rectangular Concrete Columns. Cem. Concr. Compos. 2006, 28, 938–948. [Google Scholar] [CrossRef]










| Specimen Name | Coarse Aggregate Replacement (%) | Number of Hemp Fiber Rope Layers | Number of Specimens |
|---|---|---|---|
| C-LS-CBB-CON | 50% | None | 2 |
| C-LS-CBB-1H | 50% | 1 | 2 |
| C-LS-CBB-2H | 50% | 2 | 2 |
| C-LS-CBB-3H | 50% | 3 | 2 |
| C-HS-CBB-CON | 50% | None | 2 |
| C-HS-CBB-1H | 50% | 1 | 2 |
| C-HS-CBB-2H | 50% | 2 | 2 |
| C-HS-CBB-3H | 50% | 3 | 2 |
| Mix Materials (kg/m3) | Type-1 Concrete | Type-2 Concrete |
|---|---|---|
| Cement | 242 | 444 |
| Natural coarse aggregates | 605 | 504 |
| Fine aggregates | 726 | 605 |
| Fired-clay brick aggregates | 605 | 504 |
| Property | Value |
|---|---|
| Tensile Strength (MPa) | 50 |
| Elongation (%) | 2.5 |
| Flexural Strength (MPa) | 75 |
| Curing Time (hours) | 6–10 |
| Specimen Name | Ultimate Strain | Increase in Ultimate Strain (%) | Compressive Strength (MPa) | Increase in Strength (%) |
|---|---|---|---|---|
| C-LS-CBB-CON | 0.0072 | - | 11.340 | - |
| C-LS-CBB-1H | 0.0275 | 258 | 21.280 | 88 |
| C-LS-CBB-2H | 0.0314 | 337 | 32.580 | 187 |
| C-LS-CBB-3H | 0.0400 | 457 | 42.160 | 272 |
| C-HS-CBB-CON | 0.0070 | - | 22.105 | - |
| C-HS-CBB-1H | 0.0100 | 51 | 33.535 | 52 |
| C-HS-CBB-2H | 0.0240 | 262 | 44.012 | 99 |
| C-HS-CBB-3H | 0.0300 | 350 | 54.294 | 146 |
| Study | Stress Equation | Strain Equation |
|---|---|---|
| Ghernouti and Rabehi [47] | ||
| Al-Salloum [48] | ||
| Candappa et al. [49] | ||
| Lam and Teng [50] | ||
| Lu and Hsu [51] | ||
| Legeron and Paultre [52] | ||
| Triantafillou et al. [53] | ||
| Akiyama et al. [54] | ||
| Benzaid et al. [55] |
| Study | Specimen | (exp) (MPa) | (Theoretical) (MPa) | (exp) | (Theoretical) |
|---|---|---|---|---|---|
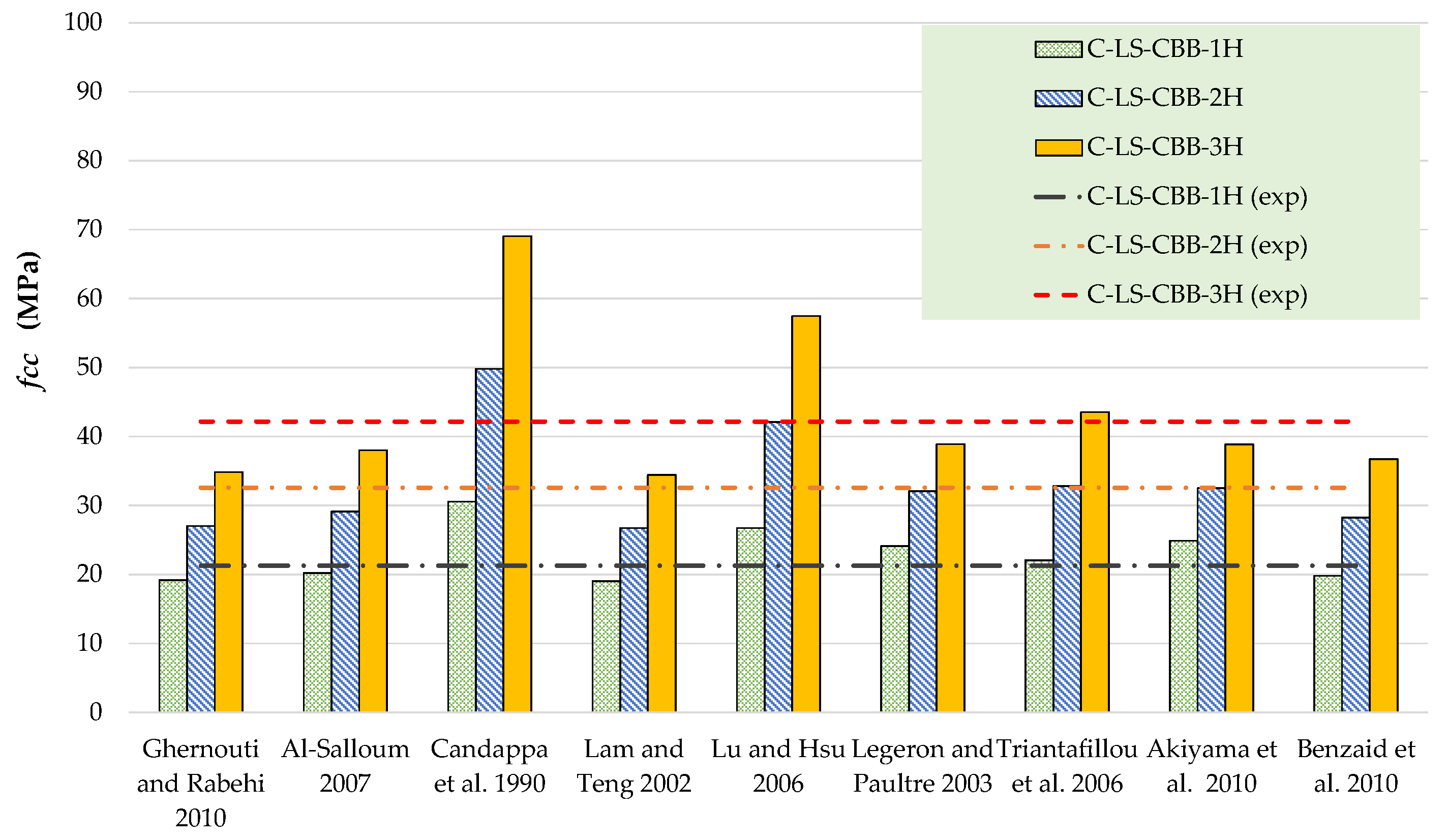
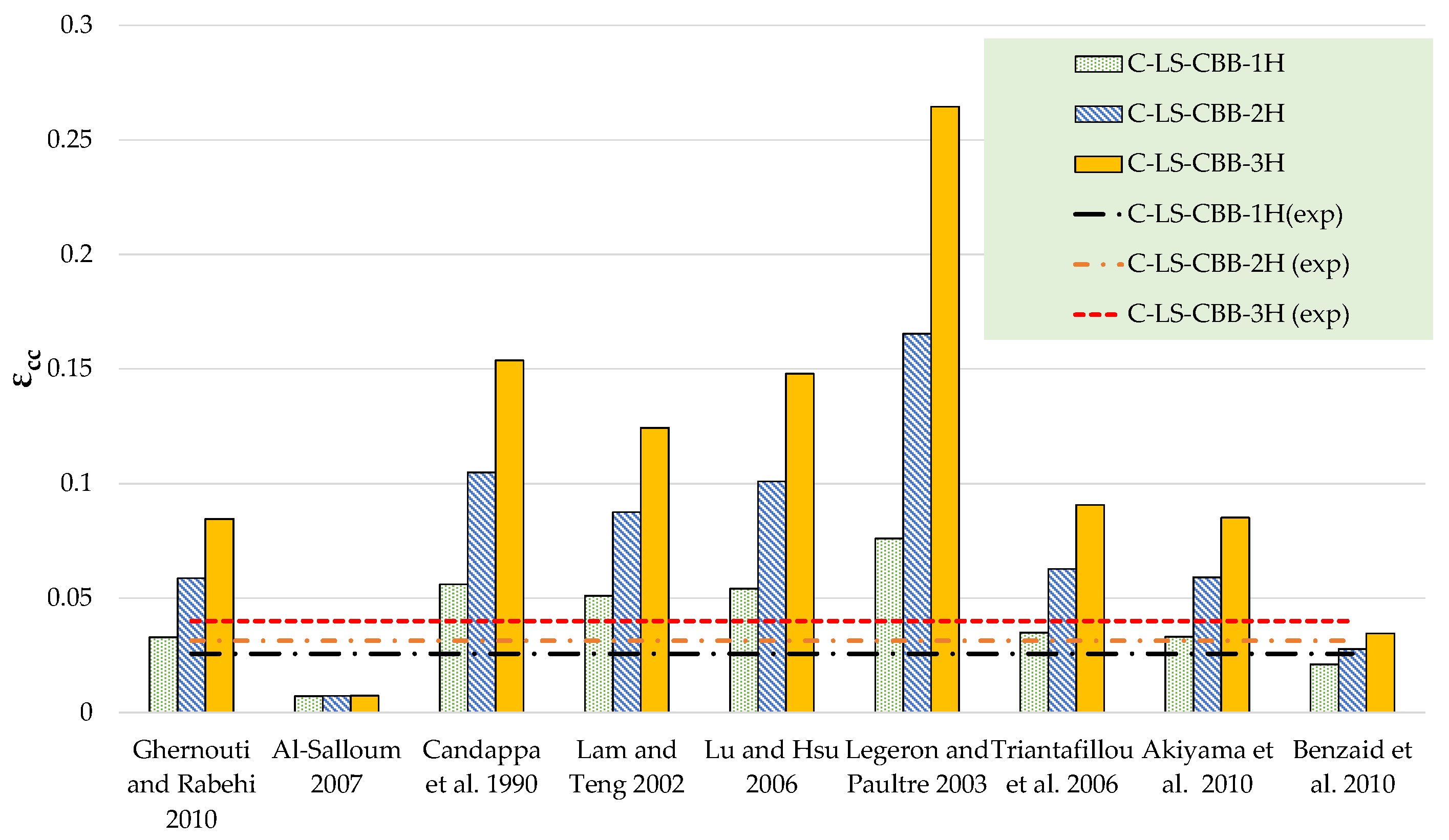
| Ghernouti and Rabehi [47] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 19.18 27.02 34.86 | 0.0257 0.0314 0.0400 | 0.0329 0.0587 0.0845 |
| Al-Salloum [48] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 20.23 29.12 38.02 | 0.0257 0.0314 0.0400 | 0.0072 0.0073 0.0074 |
| Candappa et al. [49] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 30.57 49.81 69.04 | 0.0257 0.0314 0.0400 | 0.0560 0.1049 0.1537 |
| Lam and Teng [50] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 19.03 26.72 34.42 | 0.0257 0.0314 0.0400 | 0.0510 0.0876 0.1243 |
| Lu and Hsu [51] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 26.72 42.11 57.50 | 0.0257 0.0314 0.0400 | 0.0541 0.1010 0.1479 |
| Legeron and Paultre [52] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 24.11 32.08 38.89 | 0.0257 0.0314 0.0400 | 0.0760 0.1654 0.2645 |
| Triantafillou et al. [53] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 22.07 32.80 43.54 | 0.0257 0.0314 0.0400 | 0.0350 0.0628 0.0906 |
| Akiyama et al. [54] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 24.86 32.51 38.86 | 0.0257 0.0314 0.0400 | 0.0331 0.0591 0.0851 |
| Benzaid et al. [55] | C-LS-CBB-1H C-LS-CBB-2H C-LS-CBB-3H | 21.28 32.58 42.16 | 19.80 28.26 36.73 | 0.0257 0.0314 0.0400 | 0.0211 0.0278 0.0346 |
| Study | Specimen | (exp) (MPa) | (Theoretical) (MPa) | (exp) | (Theoretical) |
|---|---|---|---|---|---|
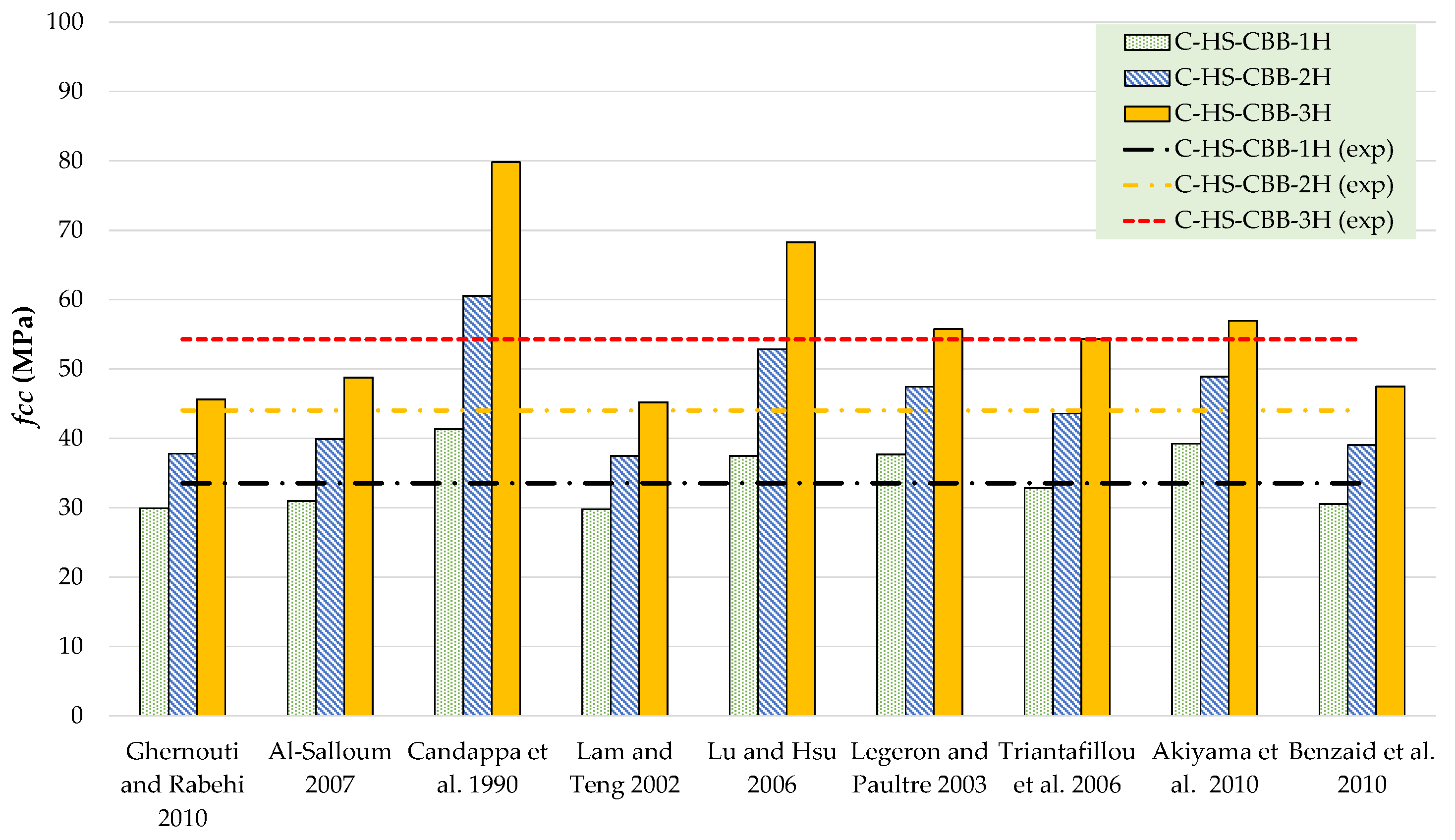
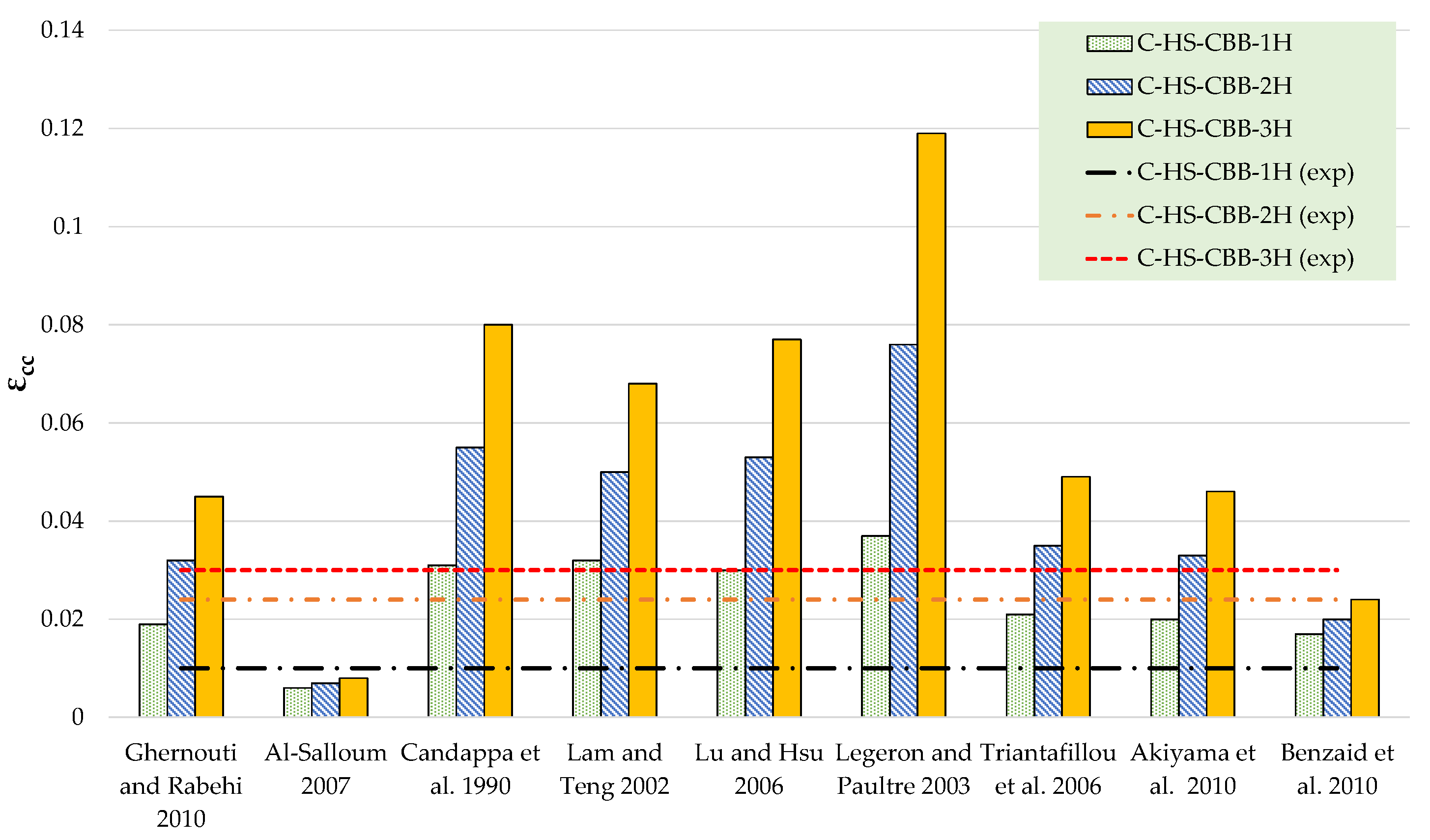
| Ghernouti and Rabehi [47] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 29.94 37.78 45.62 | 0.010 0.024 0.030 | 0.019 0.032 0.045 |
| Al-Salloum [48] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 30.99 39.89 48.78 | 0.010 0.024 0.030 | 0.006 0.007 0.008 |
| Candappa et al. [49] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 41.34 60.57 79.81 | 0.010 0.024 0.030 | 0.031 0.055 0.080 |
| Lam and Teng [50] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 29.79 37.49 45.18 | 0.010 0.024 0.030 | 0.032 0.050 0.068 |
| Lu and Hsu [51] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 37.49 52.88 68.27 | 0.010 0.024 0.030 | 0.030 0.053 0.077 |
| Legeron and Paultre [52] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 37.70 47.44 55.76 | 0.010 0.024 0.030 | 0.037 0.076 0.119 |
| Triantafillou et al. [53] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 32.83 43.57 54.30 | 0.010 0.024 0.030 | 0.021 0.035 0.049 |
| Akiyama et al. [54] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 39.22 48.90 56.94 | 0.010 0.024 0.030 | 0.020 0.033 0.046 |
| Benzaid et al. [55] | C-HS-CBB-1H C-HS-CBB-2H C-HS-CBB-3H | 33.535 44.012 54.294 | 30.56 39.03 47.49 | 0.010 0.024 0.030 | 0.017 0.020 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saingam, P.; Ejaz, A.; Ali, N.; Nawaz, A.; Hussain, Q.; Joyklad, P. Prediction of Stress–Strain Curves for HFRP Composite Confined Brick Aggregate Concrete under Axial Load. Polymers 2023, 15, 844. https://doi.org/10.3390/polym15040844
Saingam P, Ejaz A, Ali N, Nawaz A, Hussain Q, Joyklad P. Prediction of Stress–Strain Curves for HFRP Composite Confined Brick Aggregate Concrete under Axial Load. Polymers. 2023; 15(4):844. https://doi.org/10.3390/polym15040844
Chicago/Turabian StyleSaingam, Panumas, Ali Ejaz, Nazam Ali, Adnan Nawaz, Qudeer Hussain, and Panuwat Joyklad. 2023. "Prediction of Stress–Strain Curves for HFRP Composite Confined Brick Aggregate Concrete under Axial Load" Polymers 15, no. 4: 844. https://doi.org/10.3390/polym15040844
APA StyleSaingam, P., Ejaz, A., Ali, N., Nawaz, A., Hussain, Q., & Joyklad, P. (2023). Prediction of Stress–Strain Curves for HFRP Composite Confined Brick Aggregate Concrete under Axial Load. Polymers, 15(4), 844. https://doi.org/10.3390/polym15040844