Study on Self-Humidification in PEMFC with Crossed Flow Channels and an Ultra-Thin Membrane
Abstract
:1. Introduction
2. Model Descriptions
2.1. Geometric Model
2.2. Model Assumptions
- (1)
- The flow in the flow channel is regarded as laminar flow [40];
- (2)
- The reaction gases are ideal and incompressible;
- (3)
- The water generated by the reaction in the CL is membrane water [41];
- (4)
- The porous media is assumed to be isotropic and uniform;
- (5)
- The crossover of the hydrogen permeation phenomenon in MEM is ignored [42];
- (6)
- Ignoring the influence of gravity.
2.3. Governing Equations
2.4. Water Transport
2.5. Numerical Methodology and Boundary Conditions
2.6. Model Verification
3. Experiment
3.1. Experimental Equipment
3.2. Experimental Methods
4. Results and Discussion
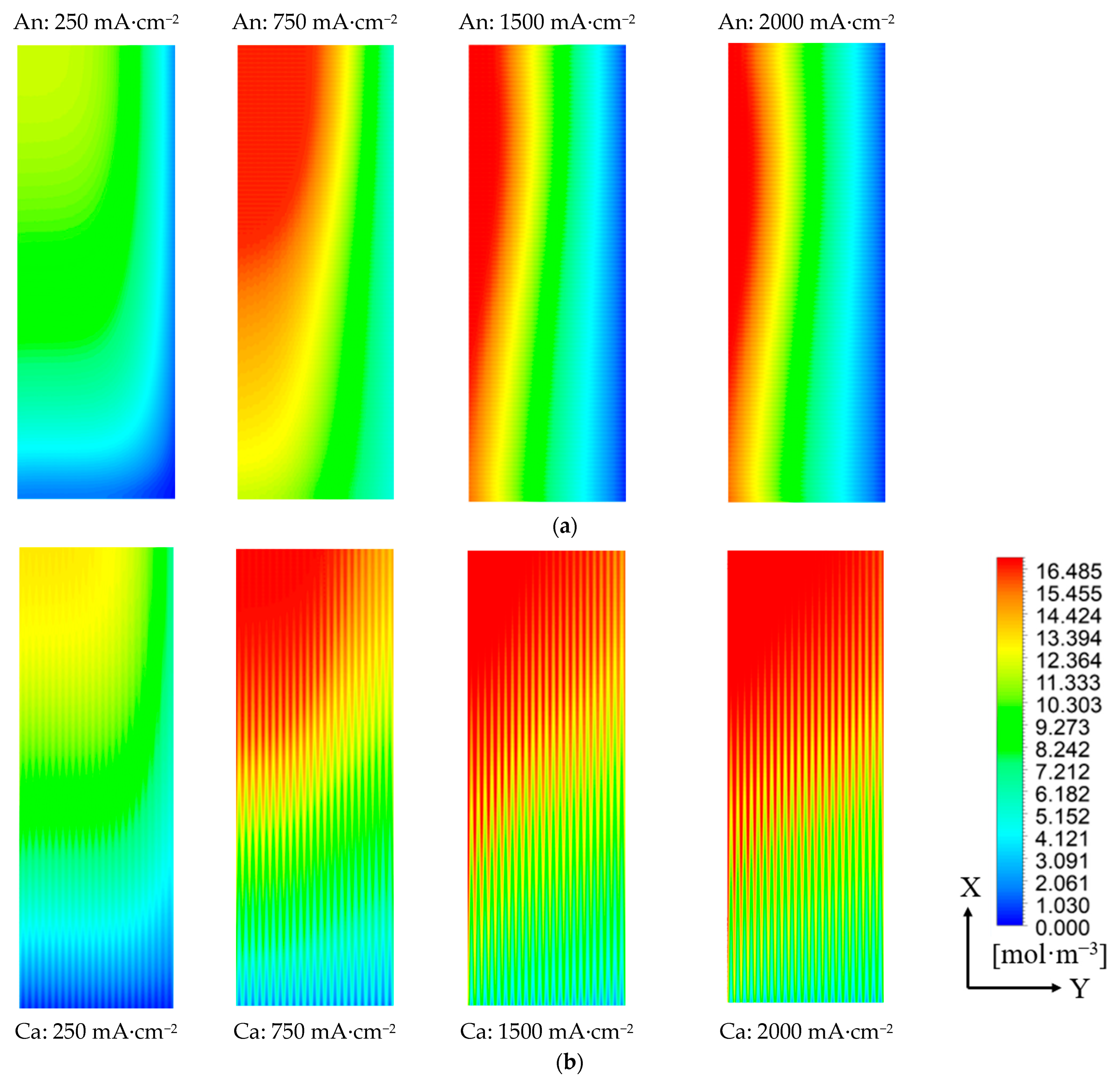
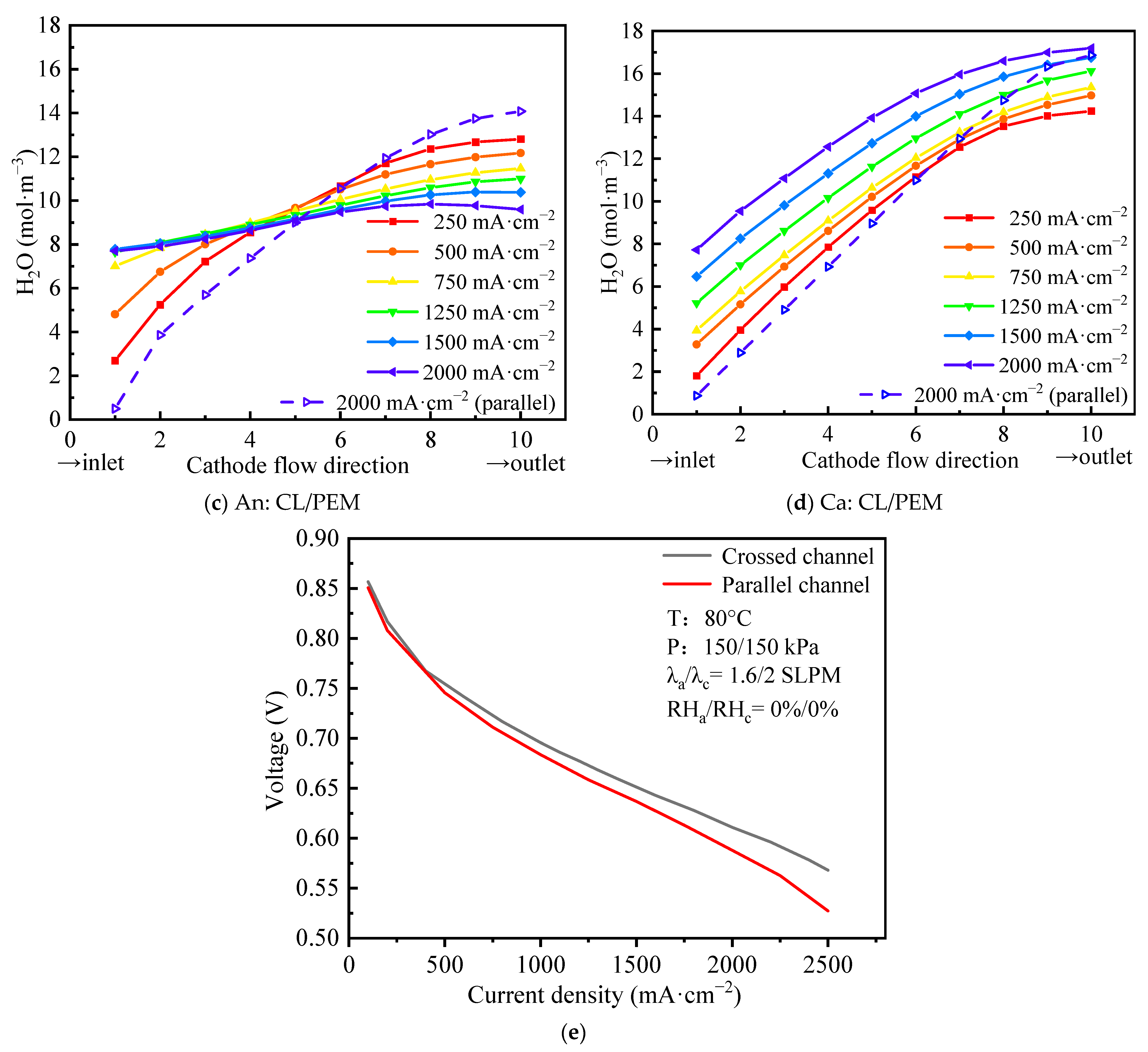
4.1. Effects of the Crossed Channel on Water Distribution
4.2. Effects of RHa on Cell Performance
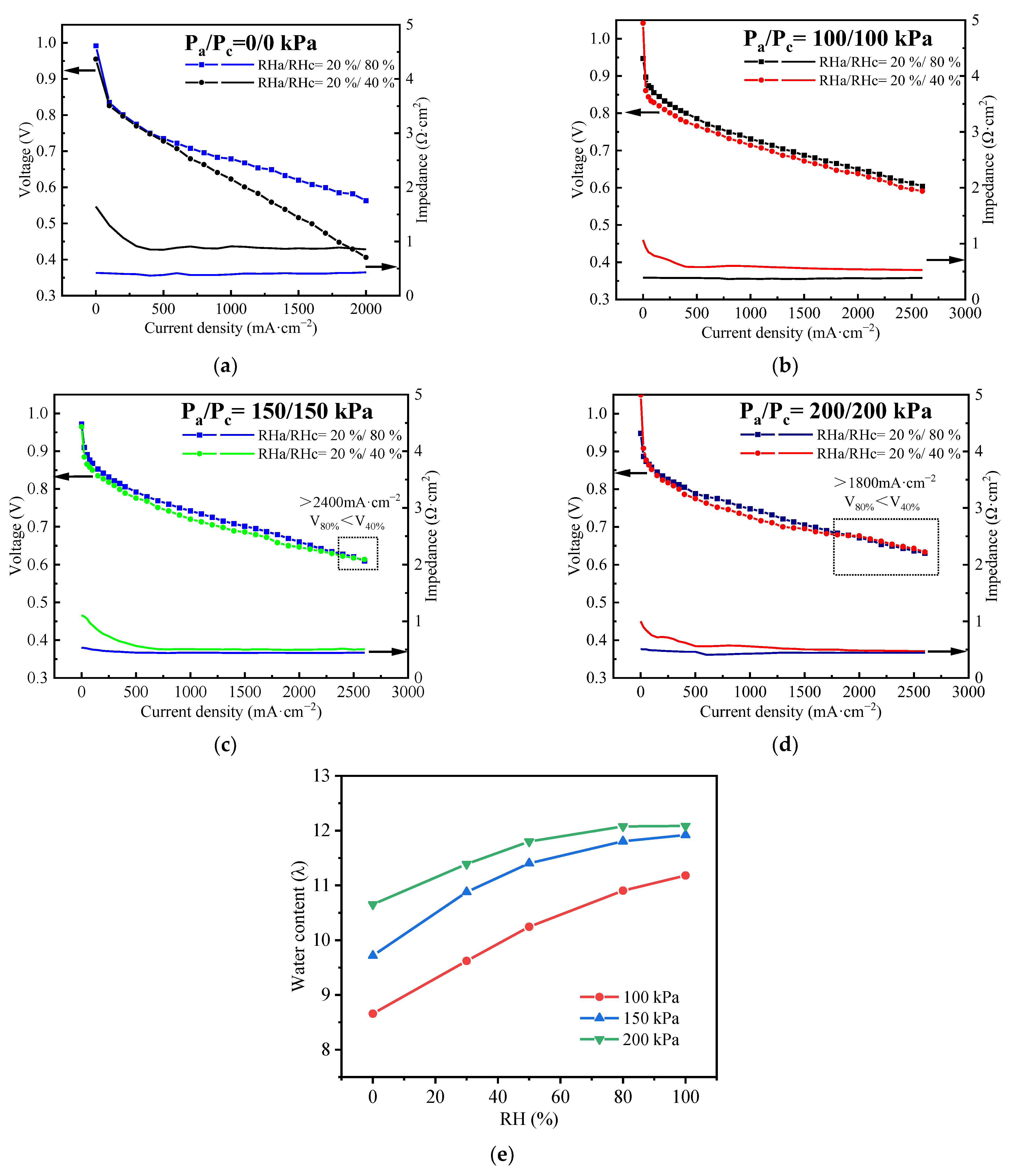
4.3. Effects of Pressure on Self-Humidification
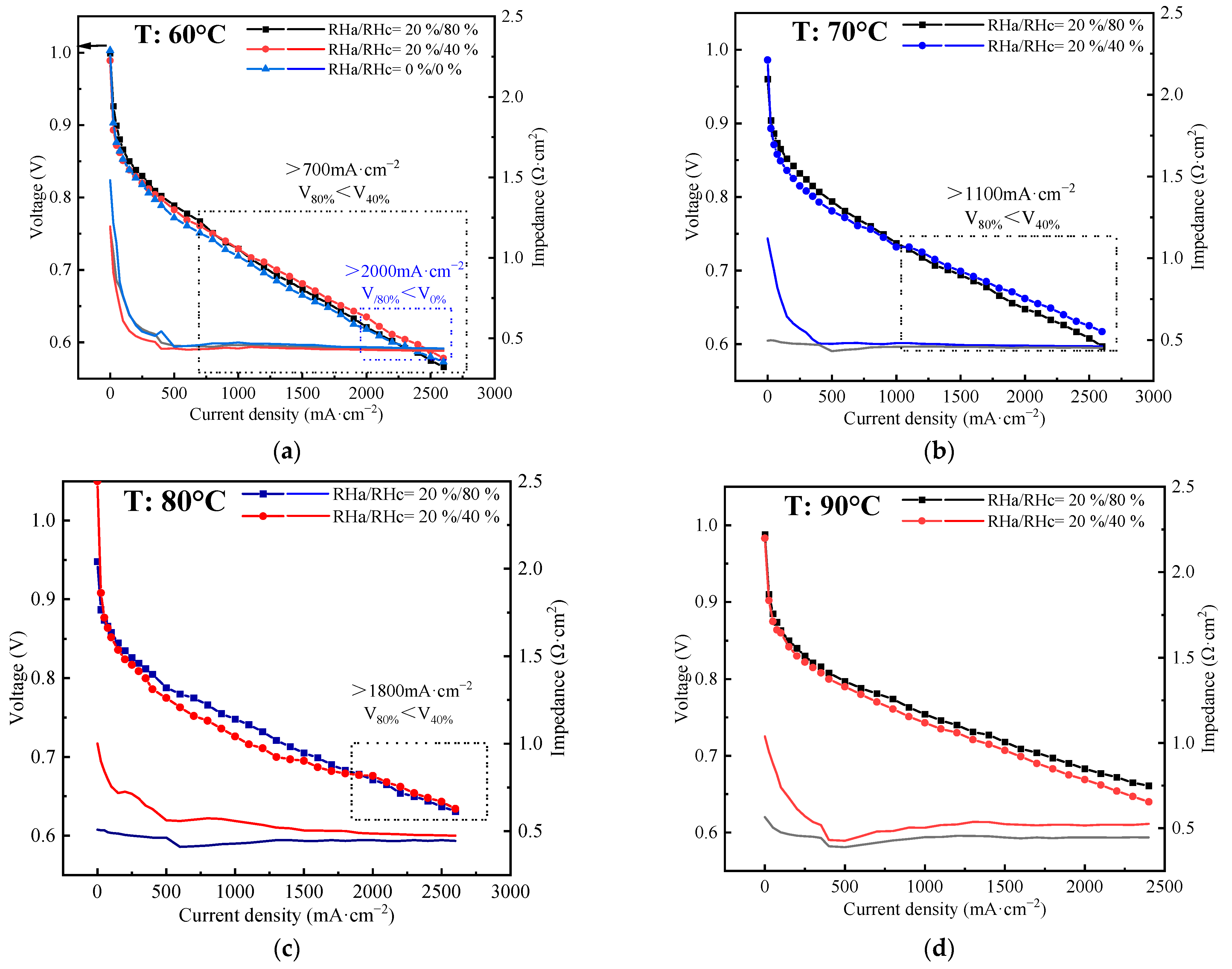
4.4. Effects of Temperature on Self-Humidification
4.5. Crossover Points
5. Conclusions
- (1)
- When operated under no humidity conditions, for the FC with crossed channels and an ultra-thin membrane, the uniformity of water distribution is improved, and the water concentration is increased compared with the parallel channel counter-flow configuration cell. Therefore, the cell can achieve better performance without humidifiers than the parallel channel cell. Meanwhile, increasing the current density can also improve the water concentration and the uniformity of water distribution.
- (2)
- The anode is insensitive to the change of RHa under most OCs because the anode water is mainly transported from the cathode by back diffusion, which can be improved by the ultra-thin membrane. This is verified by the measured performance of the stack operated at Pa/Pc = 100/100 kPa, T = 80 °C, and RHc = 100%, and the performance difference between with and without anode humidification can be ignored, which is ≤3% at all current densities and is ≤1% when the density is ≥800 mA·cm−2. Consequently, the external humidification on the anode can be removed.
- (3)
- Increasing the back pressure leads to an increase in water content in PEM and an increase in oxygen concentration in CL, which results in a decrease in impedance and an increase in performance at low/no humidification. Therefore, increasing the back pressure is beneficial to achieve self-humidification.
- (4)
- It is more difficult for the stack to achieve self-humidification at higher temperatures because the sulfonate group tends to lose water. However, increasing back pressure can compensate for the negative effect of increasing temperature. Self-humidification can be achieved for the stack operated at 60–90 °C with a suitable back pressure in the range of 100–200 kPa.
- (5)
- It is observed that with an increase in current density, there is a gradual convergence and crossing of the voltage at RHa/RHc = 20%/40% with that at RHa/RHc = 20%/80%, and the crossover point, even for RHa/RHc = 0%, occurs at 2000 mA·cm−2, 60 °C, and 200 kPa. Below the current density of the crossover point, the stack’s performance is inferior at lower RH due to membrane unsaturation. Conversely, the stack’s performance is inferior at higher RH due to flooding. Furthermore, the crossover point appears only with the achievement of successful self-humidification, and the current density of the point decreases with increasing pressure and decreasing temperature.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| cp | constant pressure specific heat, J mol−1 K−1 | φ | potential, V |
| Dλ | diffusivity, m2 s−1 | χ | velocity ratio of liquid water to gas in the flow channel |
| Di | multi-component diffusivity, m2 s−1 | ||
| F | Farady’s constant, 96,485 C mol−1 | ||
| EW | the equivalent mass of PEM, g mol−1 | Superscripts | |
| i | current density, A m−2 | eff | effective |
| keff | thermal conductivity, W m−1 K−1 | ref | reference |
| kion | proton conductivity, S m−1 | T | thermal |
| kele | electron conductivity, S m−1 | ||
| M | molecular weight, kg mol−1 | Subscripts | |
| n | number | a | anode |
| nd | electro-osmotic drag coefficient | c | condensation |
| p | pressure, Pa | ca | cathode |
| R | ideal gas constant, 8.314 J mol−1 K−1 | Cl | catalyst layer |
| RH | relative humidity | d | electro-osmotic drag |
| S | source term | d | dissolved water |
| s | liquid water saturation | e | evaporation |
| T | temperature, K | ele | electron |
| velocity, m s−1 | eq | equilibrium | |
| g | gaseous water | ||
| Greek | i | species i | |
| κ | permeability, m2 | ion | ion |
| λ | water content | j | species j |
| μ | viscosity, Pa s | k | species k |
| ρ | density, kg m−3 | l | liquid water |
| ε | porosity | liq | liquid water |
| δ | thickness, m | mem | membrane |
| γc | condensation rate coefficient | mw | membrane water |
| γe | evaporation rate coefficient | sat | saturation |
| γ | exchange rate coefficient | λ | membrane water |
References
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next Generation of Proton-Exchange Membrane Fuel Cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Elwan, H.A.; Mamlouk, M.; Scott, K. A Review of Proton Exchange Membranes Based on Protic Ionic Liquid/Polymer Blends for Polymer Electrolyte Membrane Fuel Cells. J. Power Sources 2021, 484, 229197. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Vezzù, K.; Pagot, G.; Cavinato, G.; Nale, A.; Herve Bang, Y.; Di Noto, V. Hybrid Inorganic-Organic Proton-Conducting Membranes Based on SPEEK Doped with WO3 Nanoparticles for Application in Vanadium Redox Flow Batteries. Electrochim. Acta 2019, 309, 311–325. [Google Scholar] [CrossRef]
- Kongkanand, A.; Mathias, M.F. The Priority and Challenge of High-Power Performance of Low-Platinum Proton-Exchange Membrane Fuel Cells. J. Phys. Chem. Lett. 2016, 7, 1127–1137. [Google Scholar] [CrossRef] [PubMed]
- Sharaf, O.Z.; Orhan, M.F. An Overview of Fuel Cell Technology: Fundamentals and Applications. Renew. Sustain. Energy Rev. 2014, 32, 810–853. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, L.; Xu, L.; Zhang, X.; Wang, Z.; Zhao, G.; Hu, Z.; Li, J.; Ouyang, M. Water Management Issues during Load Cycling under High Temperature and Low Humidity Conditions Relevant for Heavy-Duty Applications of PEMFC. eTransportation 2023, 18, 100285. [Google Scholar] [CrossRef]
- Kim, J.H.; Cho, E.A.; Jang, J.H.; Kim, H.J.; Lim, T.H.; Oh, I.H.; Ko, J.J.; Oh, S.C. Effects of Cathode Inlet Relative Humidity on PEMFC Durability during Startup–Shutdown Cycling. J. Electrochem. Soc. 2010, 157, B633. [Google Scholar] [CrossRef]
- Chang, Y.; Qin, Y.; Yin, Y.; Zhang, J.; Li, X. Humidification Strategy for Polymer Electrolyte Membrane Fuel Cells—A Review. Appl. Energy 2018, 230, 643–662. [Google Scholar] [CrossRef]
- Mirfarsi, S.H.; Parnian, M.J.; Rowshanzamir, S. Self-Humidifying Proton Exchange Membranes for Fuel Cell Applications: Advances and Challenges. Processes 2020, 8, 1069. [Google Scholar] [CrossRef]
- Park, H. Effect of the Hydrophilic and Hydrophobic Characteristics of the Gas Diffusion Medium on Polymer Electrolyte Fuel Cell Performance under Non-Humidification Condition. Energy Convers. Manag. 2014, 81, 220–230. [Google Scholar] [CrossRef]
- Kong, I.M.; Choi, J.W.; Kim, S.I.; Lee, E.S.; Kim, M.S. Experimental Study on the Self-Humidification Effect in Proton Exchange Membrane Fuel Cells Containing Double Gas Diffusion Backing Layer. Appl. Energy 2015, 145, 345–353. [Google Scholar] [CrossRef]
- Lin, R.; Chen, L.; Zheng, T.; Tang, S.; Yu, X.; Dong, M.; Hao, Z. Interfacial Water Management of Gradient Microporous Layer for Self-Humidifying Proton Exchange Membrane Fuel Cells. Int. J. Heat Mass Transf. 2021, 175, 121340. [Google Scholar] [CrossRef]
- Koh, B.-S.; Yoo, J.-H.; Jang, E.-K.; Jothi, V.R.; Jung, C.-Y.; Yi, S.C. Fabrication of Highly Effective Self-Humidifying Membrane Electrode Assembly for Proton Exchange Membrane Fuel Cells via Electrostatic Spray Deposition. Electrochem. Commun. 2018, 93, 76–80. [Google Scholar] [CrossRef]
- Liu, J.; Yin, Y.; Zhang, J.; Zhang, T.; Zhang, X.; Chen, H. Mechanical Degradation of Catalyst Layer under Accelerated Relative Humidity Cycling in a Polymer Electrolyte Membrane Fuel Cell. J. Power Sources 2021, 512, 230487. [Google Scholar] [CrossRef]
- Oh, K.; Kwon, O.; Son, B.; Lee, D.H.; Shanmugam, S. Nafion-Sulfonated Silica Composite Membrane for Proton Exchange Membrane Fuel Cells under Operating Low Humidity Condition. J. Membr. Sci. 2019, 583, 103–109. [Google Scholar] [CrossRef]
- Ren, H.; Meng, X.; Lin, Y.; Shao, Z. Structural Stability of Catalyst Ink and Its Effects on the Catalyst Layer Microstructure and Fuel Cell Performance. J. Power Sources 2022, 517, 230698. [Google Scholar] [CrossRef]
- Cha, D.; Jeon, S.W.; Yang, W.; Kim, D.; Kim, Y. Comparative Performance Evaluation of Self-Humidifying PEMFCs with Short-Side-Chain and Long-Side-Chain Membranes under Various Operating Conditions. Energy 2018, 150, 320–328. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Z.; Liu, X.; Wu, W.-T. Modeling of PEM Fuel Cell with Thin MEA under Low Humidity Operating Condition. Appl. Energy 2019, 242, 1513–1527. [Google Scholar] [CrossRef]
- Huang, H.; Xu, S.; Zhang, L.; Fan, J.; Li, H.; Wang, H. A Self-Humidifying Proton Exchange Membrane Embedded with Phosphonic Acid-Functionalized Mesoporous Silica Nanoparticles That Has Excellent Dispersion and Water Retention. Sustain. Energy Fuels 2021, 5, 230–245. [Google Scholar] [CrossRef]
- Xie, Z.; Tian, L.; Zhang, W.; Ma, Q.; Xing, L.; Xu, Q.; Khotseng, L.; Su, H. Enhanced Low-Humidity Performance of Proton Exchange Membrane Fuel Cell by Incorporating Phosphoric Acid-Loaded Covalent Organic Framework in Anode Catalyst Layer. Int. J. Hydrogen Energy 2021, 46, 10903–10912. [Google Scholar] [CrossRef]
- Shin, S.; Maiyalagan, T.; Jothi, V.R.; Jung, C.Y.; Yi, S.C. Numerical Analysis on Transport Properties of Self-Humidifying Dual Catalyst Layer via 3-D Reconstruction Technique. Int. J. Hydrogen Energy 2021, 46, 14639–14650. [Google Scholar] [CrossRef]
- Hou, S.; Wang, H.; Ren, J.; Yao, C.; Shi, L.; Liao, S. Enhanced Low-Humidity Performance of Proton-Exchange Membrane Fuel Cell by Introducing Hydrophilic CNTs in Membrane Electrode Assembly. Prog. Nat. Sci. Mater. Int. 2022, 32, 150–156. [Google Scholar] [CrossRef]
- Angayarkanni, R.; Ganesan, A.; Dhelipan, M.; Karthikeyan, S.; Mani, N.; Thiyagarajan, P. Self-Humidified Operation of a PEM Fuel Cell Using a Novel Silica Composite Coating Method. Int. J. Hydrogen Energy 2022, 47, 4827–4837. [Google Scholar] [CrossRef]
- Ren, G.; Qu, Z.; Wang, X.; Zhang, J. Liquid Water Transport and Mechanical Performance of Electrospun Gas Diffusion Layers. Int. J. Green Energy 2022, 19, 210–218. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Xie, Z.; Guo, X.; Yang, T.; Li, Z.; Tu, M.; Rao, H. High Performance and Self-Humidifying of Novel Cross-Linked and Nanocomposite Proton Exchange Membranes Based on Sulfonated Polysulfone. Nanomaterials 2022, 12, 841. [Google Scholar] [CrossRef]
- Tong, G.; Xu, X.; Yuan, Q.; Yang, Y.; Tang, W.; Sun, X. Simulation Study of Proton Exchange Membrane Fuel Cell Cross-convection Self-humidifying Flow Channel. Int. J. Energy Res. 2021, 45, 4036–4047. [Google Scholar] [CrossRef]
- Wang, Z.; Zhan, Z.; Tan, J.; Pan, M. Water transport law of fuel cell membranes at different current densities. Chin. Sci. Bull. 2019, 64, 2254–2261. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, B.; Lei, X.; Ming, P.; Li, B.; Lei, Y.; Yang, D.; Zhang, C. Droplets Dynamics Theory and Micro-Flow Field Experiments of Improving Self-Humidifying Feature and Maximum Power Density in Fuel Cells. Chem. Eng. J. 2022, 429, 131974. [Google Scholar] [CrossRef]
- Lian, Y.; You, C.; Zhu, Z.; Zhu, X.; Li, X.; Zhou, W. Preparation and Performance of a Self-Humidifying Fuel Cell Using a Fiber Sintered Sheet as Flow Field. J. Power Sources 2022, 536, 231513. [Google Scholar] [CrossRef]
- Lian, Y.; Zhu, Z.; You, C.; Lin, L.; Lin, F.; Lin, L.; Huang, Y.; Zhou, W. Structural Optimization of Fiber Porous Self-Humidifying Flow Field Plates Applied to Proton Exchange Membrane Fuel Cells. Energy 2023, 271, 127034. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, G.; Jiao, K. Characteristics of PEMFC Operating at High Current Density with Low External Humidification. Energy Convers. Manag. 2017, 150, 763–774. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, L.; Fang, C.; Jiang, H.; Li, J.; Ouyang, M. Study on Voltage Clamping and Self-Humidification Effects of Pem Fuel Cell System with Dual Recirculation Based on Orthogonal Test Method. Int. J. Hydrogen Energy 2018, 43, 16268–16278. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, L.; Zhao, X.; Li, J.; Hu, Z.; Fang, C.; Hu, J.; Guo, D.; Ouyang, M. Comparison of Self-Humidification Effect on Polymer Electrolyte Membrane Fuel Cell with Anodic and Cathodic Exhaust Gas Recirculation. Int. J. Hydrogen Energy 2020, 45, 3108–3122. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, Z.; Tong, S. Effect of Cathode Recirculation on High Potential Limitation and Self-Humidification of Hydrogen Fuel Cell System. J. Power Sources 2020, 468, 228388. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, Z.; Tong, S.; Cheng, Z. Self-Humidifying Effect of Air Self-Circulation System for Proton Exchange Membrane Fuel Cell Engines. Renew. Energy 2021, 164, 1143–1155. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, S.; Guo, S. High-Potential Control for Durability Improvement of the Vehicle Fuel Cell System Based on Oxygen Partial Pressure Regulation under Low-Load Conditions. Int. J. Hydrogen Energy 2022, 47, 32607–32627. [Google Scholar] [CrossRef]
- Li, Q.; Gong, J.; Peng, S.; Lu, S.; Sui, P.-C.; Djilali, N.; Xiang, Y. Theoretical Design Strategies of Bipolar Membrane Fuel Cell with Enhanced Self-Humidification Behavior. J. Power Sources 2016, 307, 358–367. [Google Scholar] [CrossRef]
- Heo, P.; Kim, M.; Ko, H.; Nam, S.Y.; Kim, K. Self-Humidifying Membrane for High-Performance Fuel Cells Operating at Harsh Conditions: Heterojunction of Proton and Anion Exchange Membranes Composed of Acceptor-Doped SnP2O7 Composites. Membranes 2021, 11, 776. [Google Scholar] [CrossRef]
- Wang, J.; Wang, B.; Tongsh, C.; Miao, T.; Cheng, P.; Wang, Z.; Du, Q.; Jiao, K. Combining Proton and Anion Exchange Membrane Fuel Cells for Enhancing the Overall Performance and Self-Humidification. Chem. Eng. J. 2022, 428, 131969. [Google Scholar] [CrossRef]
- Corda, G.; Fontanesi, S.; d’Adamo, A. Methodology for PEMFC CFD Simulation Including the Effect of Porous Parts Compression. Int. J. Hydrogen Energy 2022, 47, 14658–14673. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water Transport in Polymer Electrolyte Membrane Fuel Cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Li, S.; Sundén, B. Effects of Gas Diffusion Layer Deformation on the Transport Phenomena and Performance of PEM Fuel Cells with Interdigitated Flow Fields. Int. J. Hydrogen Energy 2018, 43, 16279–16292. [Google Scholar] [CrossRef]
- Jiang, P.; Zhan, Z.; Zhang, D.; Wang, C.; Zhang, H.; Pan, M. Two-Dimensional Simulation of the Freezing Characteristics in PEMFCs during Cold Start Considering Ice Crystallization Kinetics. Polymers 2022, 14, 3203. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Zhan, Z.; Zhang, H.; Du, Q.; Chen, X.; Xiang, X.; Wen, X.; Pan, M. Effects of Cathode GDL Gradient Porosity Distribution along the Flow Channel Direction on Gas–Liquid Transport and Performance of PEMFC. Polymers 2023, 15, 1629. [Google Scholar] [CrossRef] [PubMed]
- Ji, M.; Wei, Z. A Review of Water Management in Polymer Electrolyte Membrane Fuel Cells. Energies 2009, 2, 1057–1106. [Google Scholar] [CrossRef]
- Wallnöfer-Ogris, E.; Pertl, P.; Trattner, A. Quasi-Stationary UI-Characteristic Model of a PEM Fuel Cell–Evaluating the Option of Self-Humidifying Operation. Int. J. Hydrogen Energy 2020, 45, 32464–32477. [Google Scholar] [CrossRef]
- He, X.; Zhan, Z.; Zhang, H.; Shua, L.; Sui, P.C.; Xu, L. The Optimal Control of PEM Fuel Cell Operating at Large Current Density Based on Water Balance. J. Eng. Thermophys. 2017, 38, 1994–2000. [Google Scholar]
- Tang, X.; Zhang, Y.; Xu, S. Experimental Study of PEM Fuel Cell Temperature Characteristic and Corresponding Automated Optimal Temperature Calibration Model. Energy 2023, 283, 128456. [Google Scholar] [CrossRef]
- Luo, Z.; Chang, Z.; Zhang, Y.; Liu, Z.; Li, J. Electro-Osmotic Drag Coefficient and Proton Conductivity in Nafion® Membrane for PEMFC. Int. J. Hydrogen Energy 2010, 35, 3120–3124. [Google Scholar] [CrossRef]
- Li, Y.; Pei, P.; Wu, Z.; Ren, P.; Jia, X.; Chen, D.; Huang, S. Approaches to Avoid Flooding in Association with Pressure Drop in Proton Exchange Membrane Fuel Cells. Appl. Energy 2018, 224, 42–51. [Google Scholar] [CrossRef]
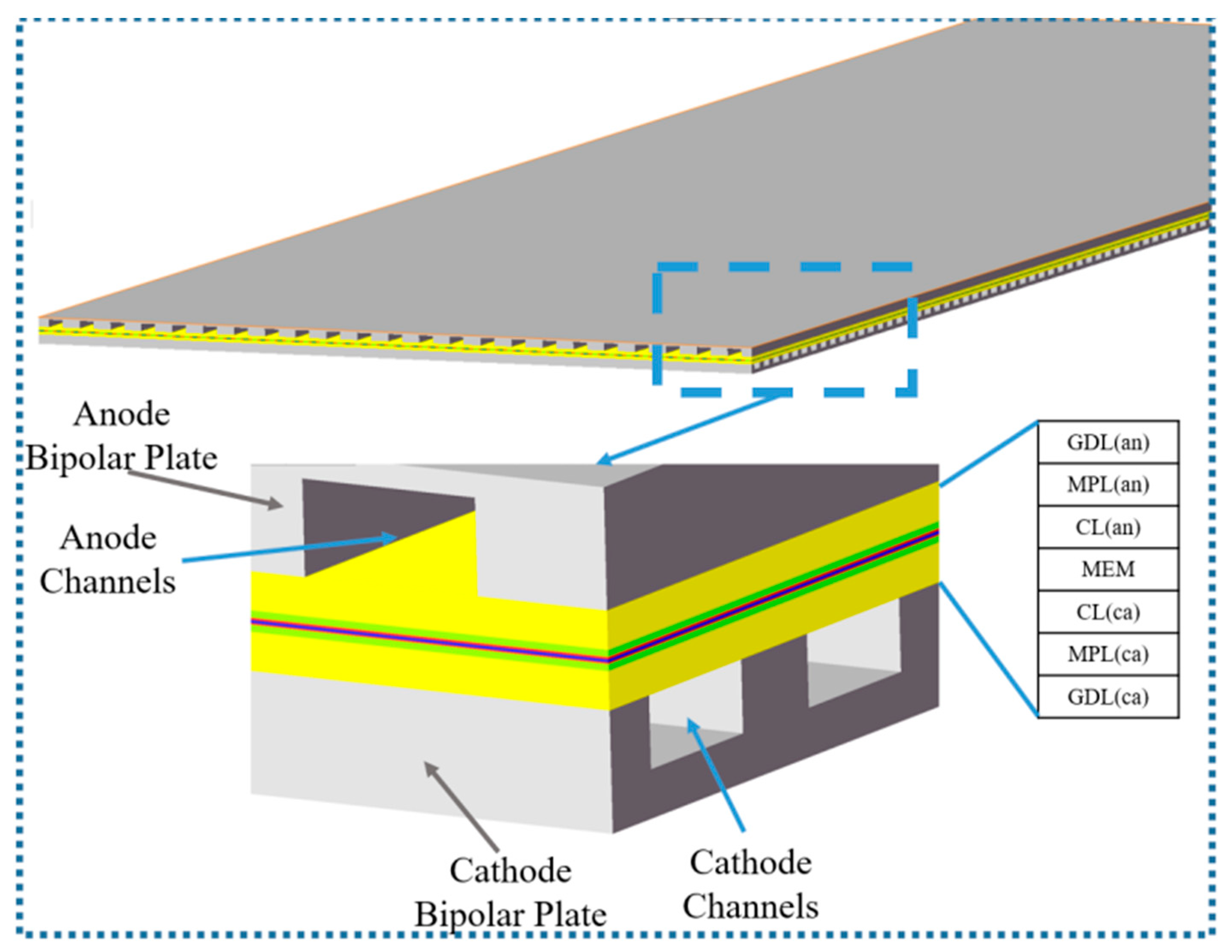
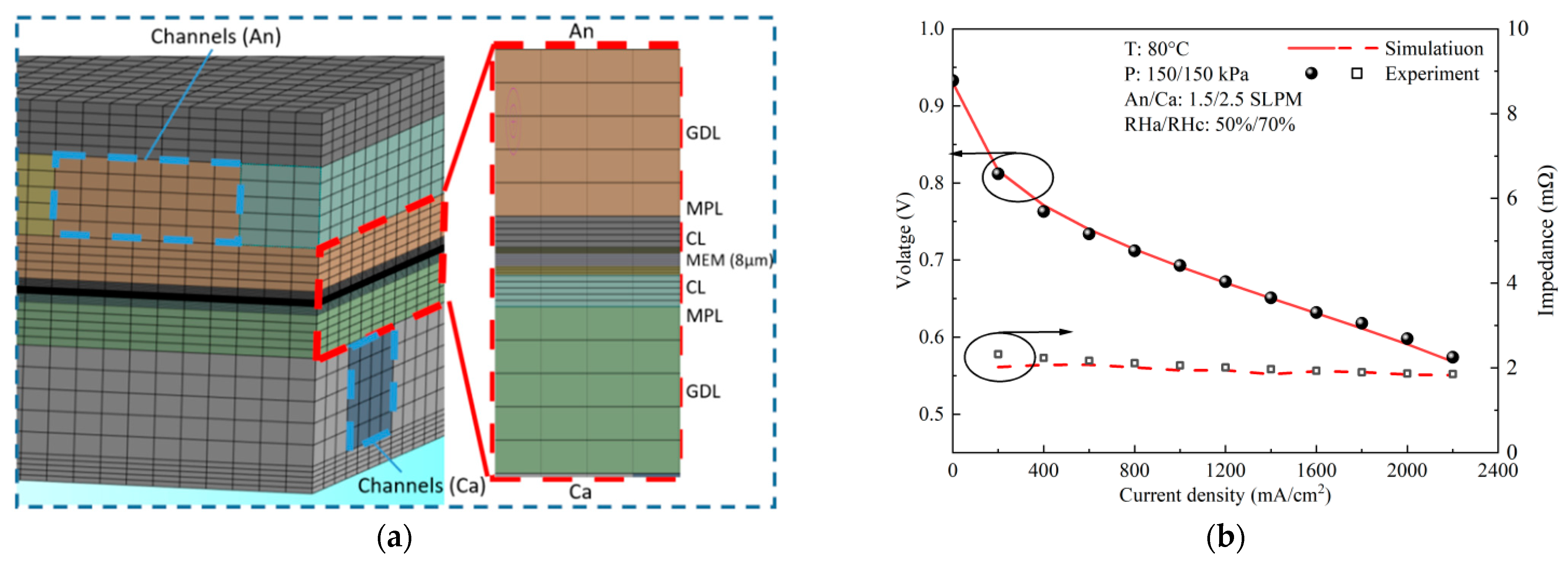


| Geometric Parameters | Values (mm) |
|---|---|
| BP thickness | 0.5 |
| Cathode channel length/width/height | 120.1/0.8/0.4 |
| Anode channel length/width/height | 41.6/0.7/0.3 |
| Anode/cathode rib width | 0.5/1 |
| GDL thickness | 0.16 |
| MPL thickness | 0.03 |
| Cathode/anode CL thickness | 0.009/0.006 |
| MEM thickness | 0.008 |
| Value | |
|---|---|
| Open-circuit voltage (V) | 1.15 |
| Temperature (K) | 353.15 |
| Anode/cathode outlet pressure (kPa) | 150/150 |
| Anode/cathode stoichiometry | 2/1.6 |
| Active area (cm2) | 49.6614 |
| GDL/MPL/CL contact angle (deg) | 130/140/120 |
| GDL/MPL/CL porosity | 0.7/0.6/0.5 |
| GDL/MPL/CL/PEM permeability(m2) | 8 × 10−12/5 × 10−13/3 × 10−14/1 × 10−18/0 |
| GDL/MPL/CL density (kg·m−3) | 440/440/1000 |
| GDL/MPL/CL specific heat capacity (J·kg−1·K−1) | 710/710/3300 |
| GDL/MPL/CL thermal conductivity (W·m−1·K−1) | 1.7/1.7/8 |
| GDL/MPL/CL electrical conductivity (S·m−1) | 5000/5000/1000 |
| Surface/volume ratio in CL (m−1) | 200,000 |
| PEM equivalent mass (kg·kmol−1) | 1100 |
| Anode/cathode exchange current density (mA·cm−2) | 10,000/10 |
| Grid Number | Current Density (mA·cm−2) | Voltage (V) | Calculated Time (h) | |
|---|---|---|---|---|
| Case 1 | 8,243,664 | 2000 | 0.612416 | 60 |
| Case 2 | 10,991,552 | 2000 | 0.613369 | 72 |
| Case 3 | 13,739,440 | 2000 | 0.613764 | 84 |
| Case 4 | 18,985,408 | 2000 | 0.613349 | 144 |
| Temperature (°C) | Back Pressure (Gauge Pressure, kPa) | |||
|---|---|---|---|---|
| Anode | Cathode | |||
| 60 | 200 | 200 | ||
| 70 | 200 | 200 | ||
| 80 | 0 | 0 | ||
| 100 | 100 | |||
| 150 | 150 | |||
| 200 | 200 | |||
| 90 | 200 | 200 | ||
| Flux | RH (%) | |||
| Anode | 1.6 SLPM | 0 | 20 | 20 |
| Cathode | 2 SLPM | 0 | 40 | 80 |
| Temperature (°C) | Pressure (kPa) | Self-Humidification (Yes or No) | Current Density of Crossover Point (mA·cm−2) |
|---|---|---|---|
| An/Ca | |||
| 60 | 200/200 | Yes | 700 (2000 at RH = 0%) |
| 70 | 200/200 | Yes | 1100 |
| 80 | 0/0 | No | No cross |
| 100/100 | Yes | No cross | |
| 150/150 | Yes | 2400 | |
| 200/200 | Yes | 1800 | |
| 90 | 200/200 | No | No cross |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chen, X.; Xiang, X.; Zhang, H.; Huang, Z.; Huang, X.; Zhan, Z. Study on Self-Humidification in PEMFC with Crossed Flow Channels and an Ultra-Thin Membrane. Polymers 2023, 15, 4589. https://doi.org/10.3390/polym15234589
Wang C, Chen X, Xiang X, Zhang H, Huang Z, Huang X, Zhan Z. Study on Self-Humidification in PEMFC with Crossed Flow Channels and an Ultra-Thin Membrane. Polymers. 2023; 15(23):4589. https://doi.org/10.3390/polym15234589
Chicago/Turabian StyleWang, Chenlong, Xiaosong Chen, Xin Xiang, Heng Zhang, Zhiping Huang, Xinhao Huang, and Zhigang Zhan. 2023. "Study on Self-Humidification in PEMFC with Crossed Flow Channels and an Ultra-Thin Membrane" Polymers 15, no. 23: 4589. https://doi.org/10.3390/polym15234589
APA StyleWang, C., Chen, X., Xiang, X., Zhang, H., Huang, Z., Huang, X., & Zhan, Z. (2023). Study on Self-Humidification in PEMFC with Crossed Flow Channels and an Ultra-Thin Membrane. Polymers, 15(23), 4589. https://doi.org/10.3390/polym15234589







