A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture
Abstract
1. Introduction
2. Calculation Section
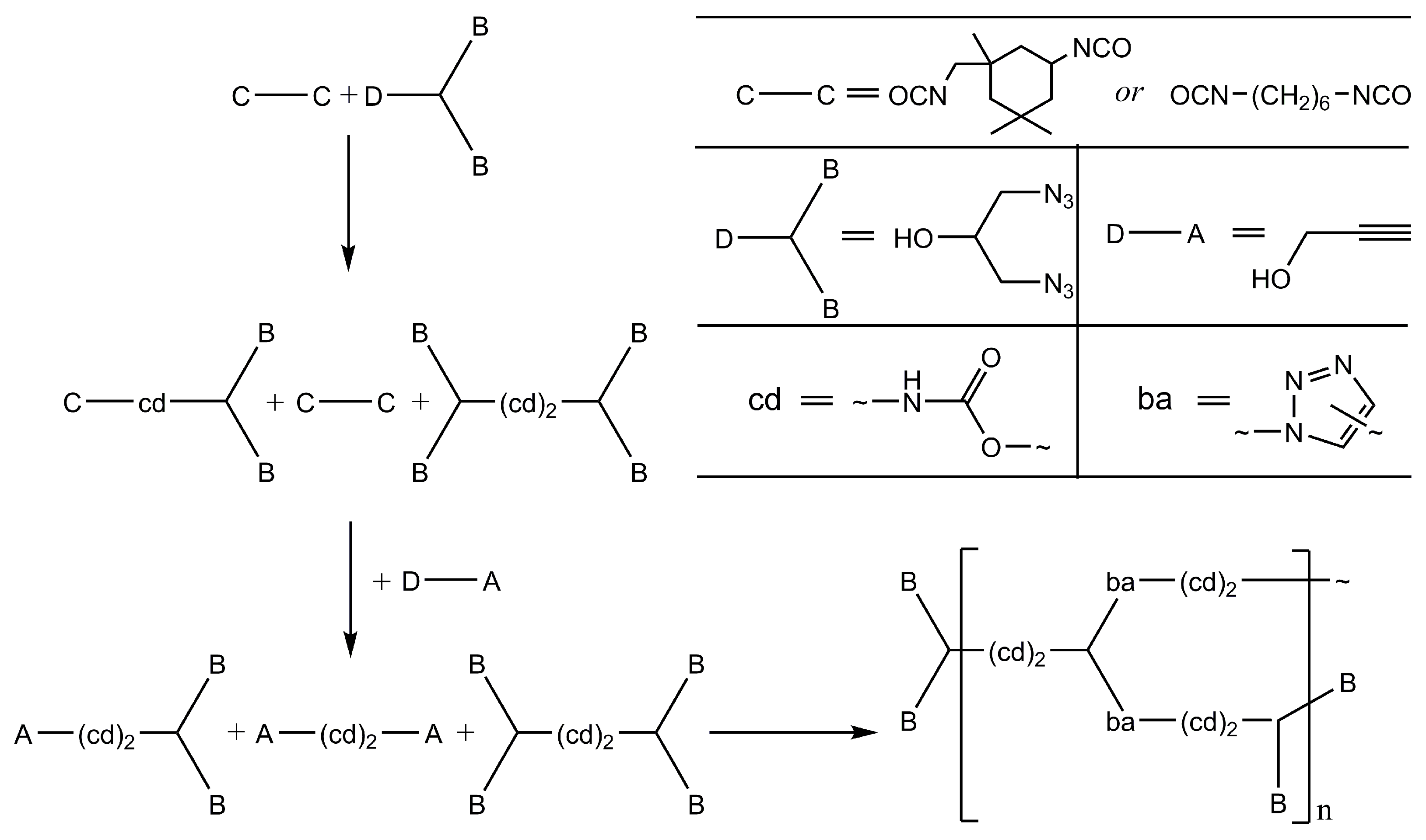
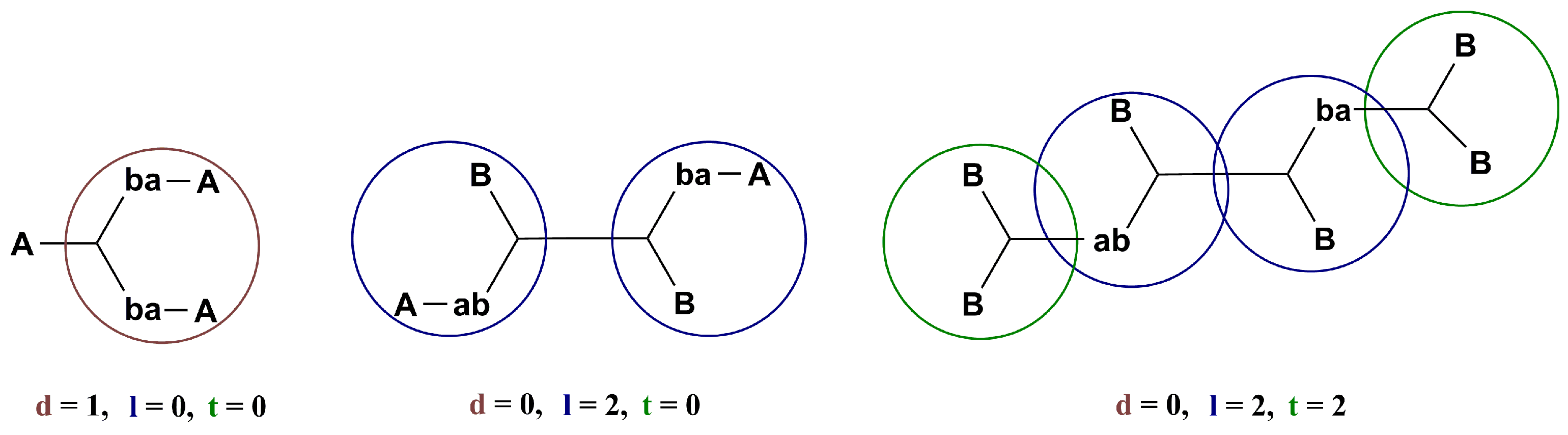
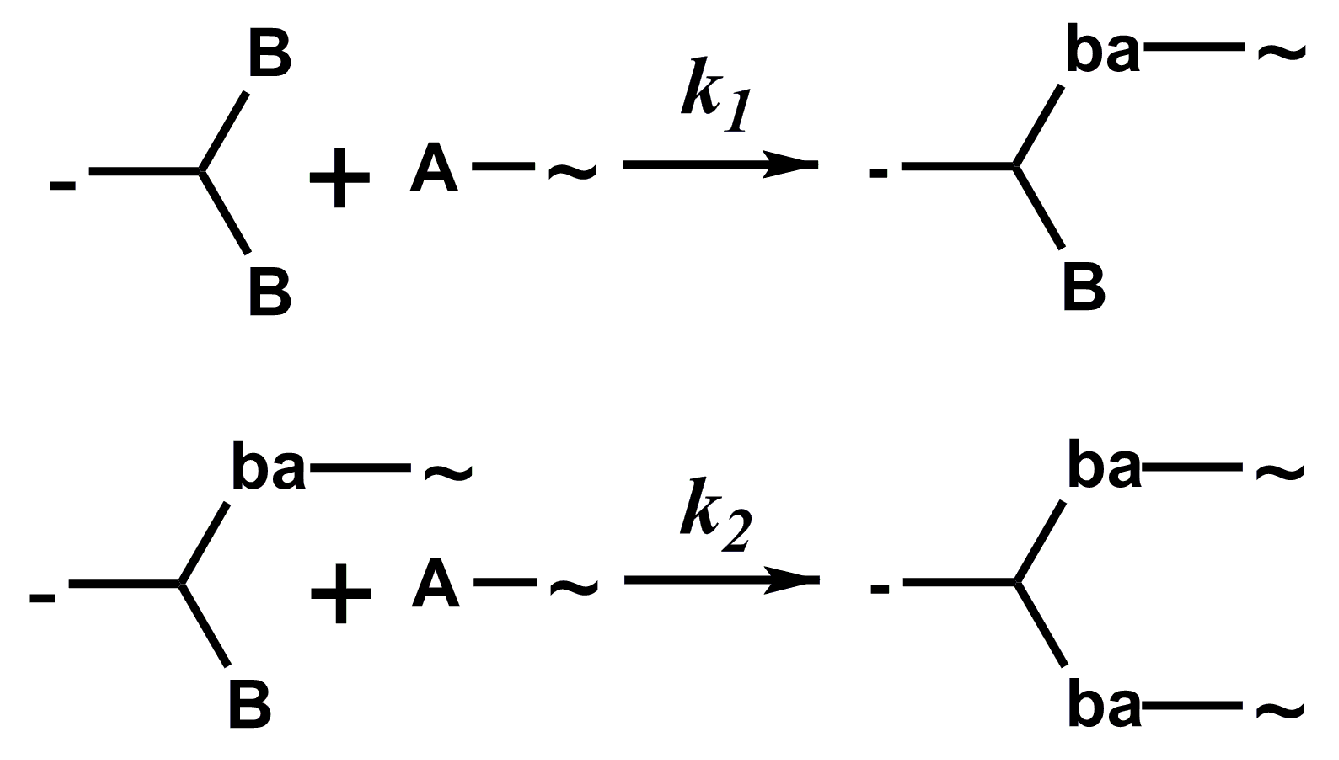
2.1. Design of the Kinetic–Structural Model
- Flory assumption, i.e., function group reactivity is independent of the chain length;
- System homogeneity;
- No solvent impact.
2.2. Verification of the Kinetic—Structural Model
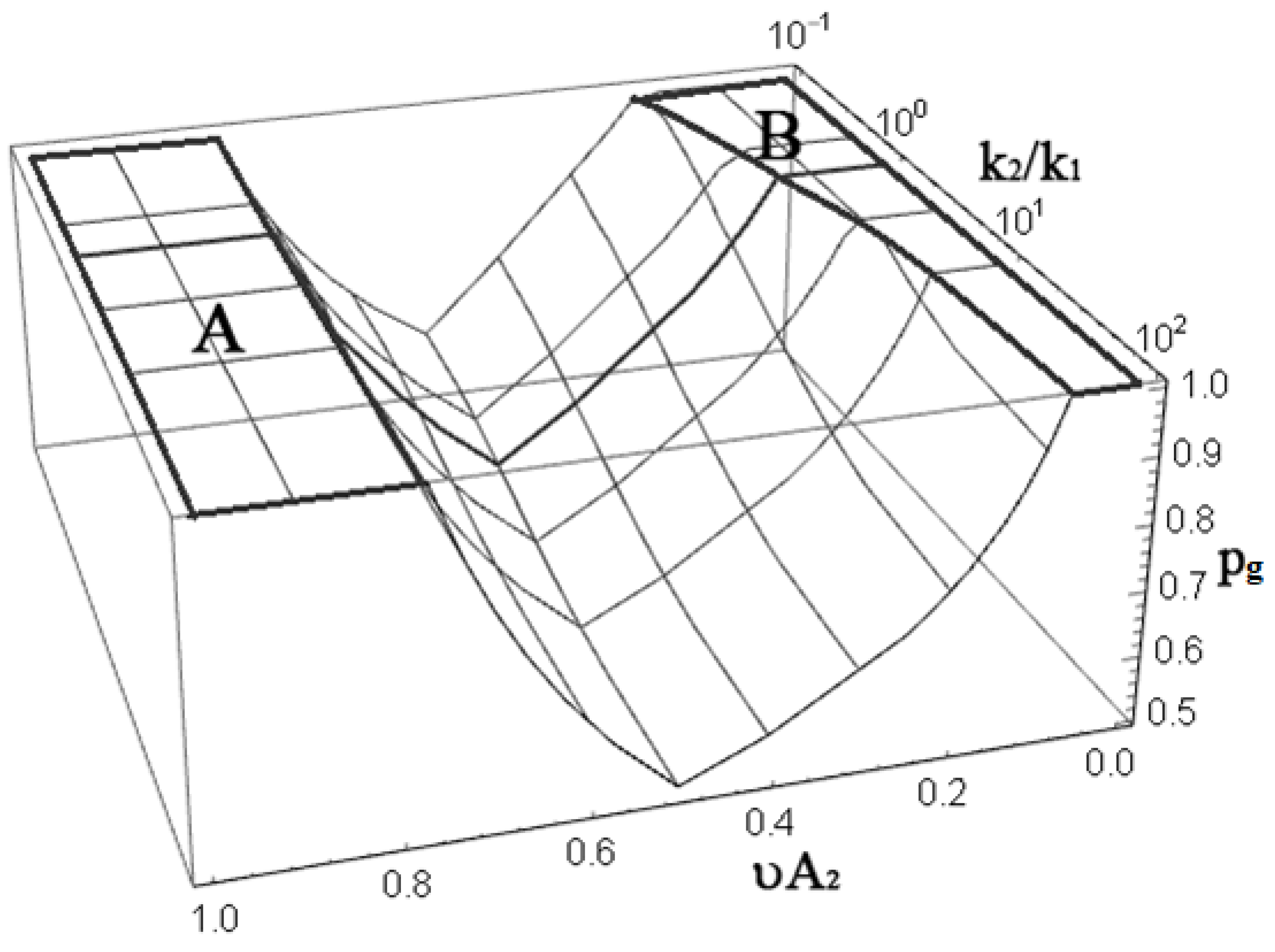
3. Results and Discussion
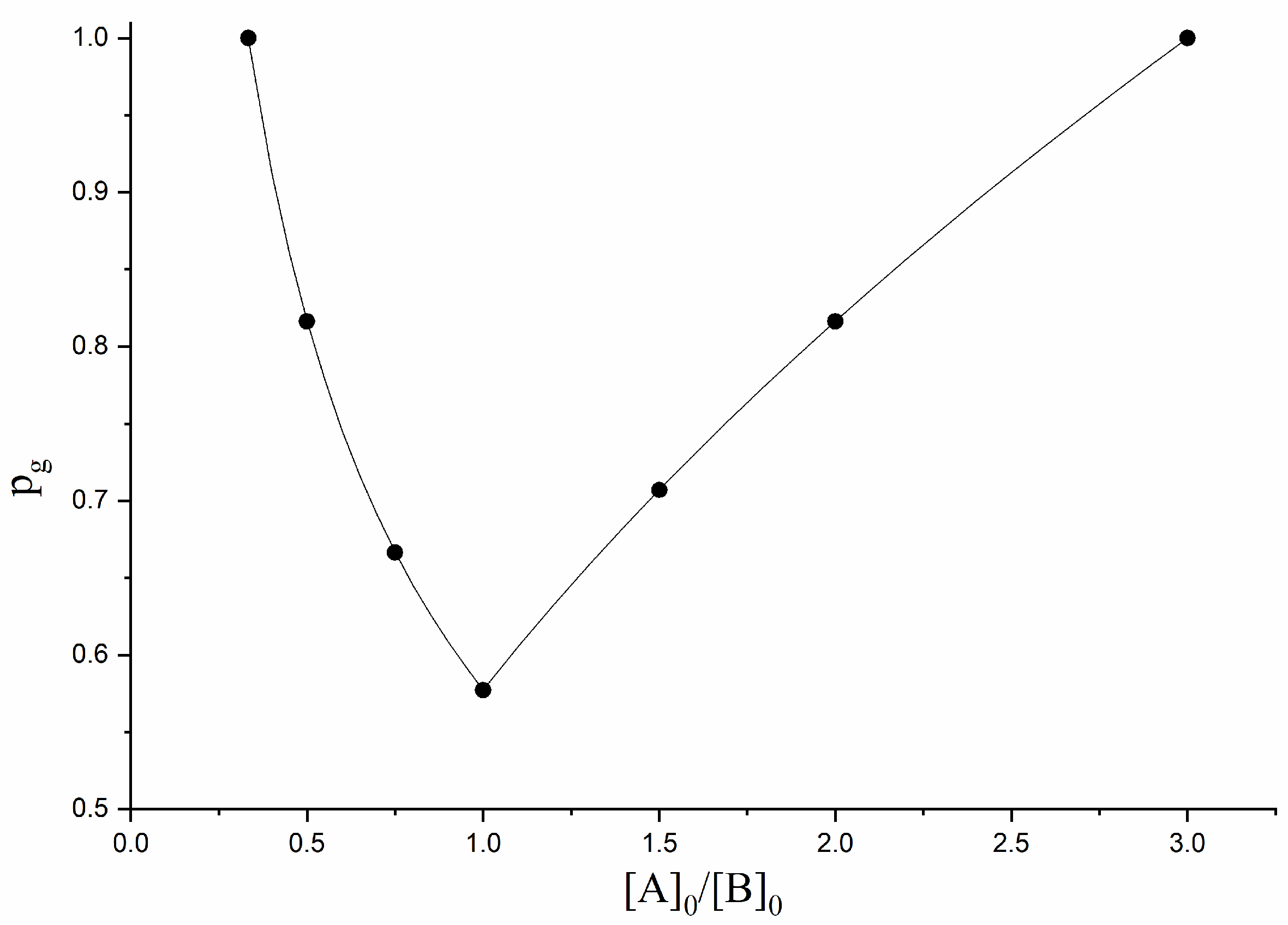
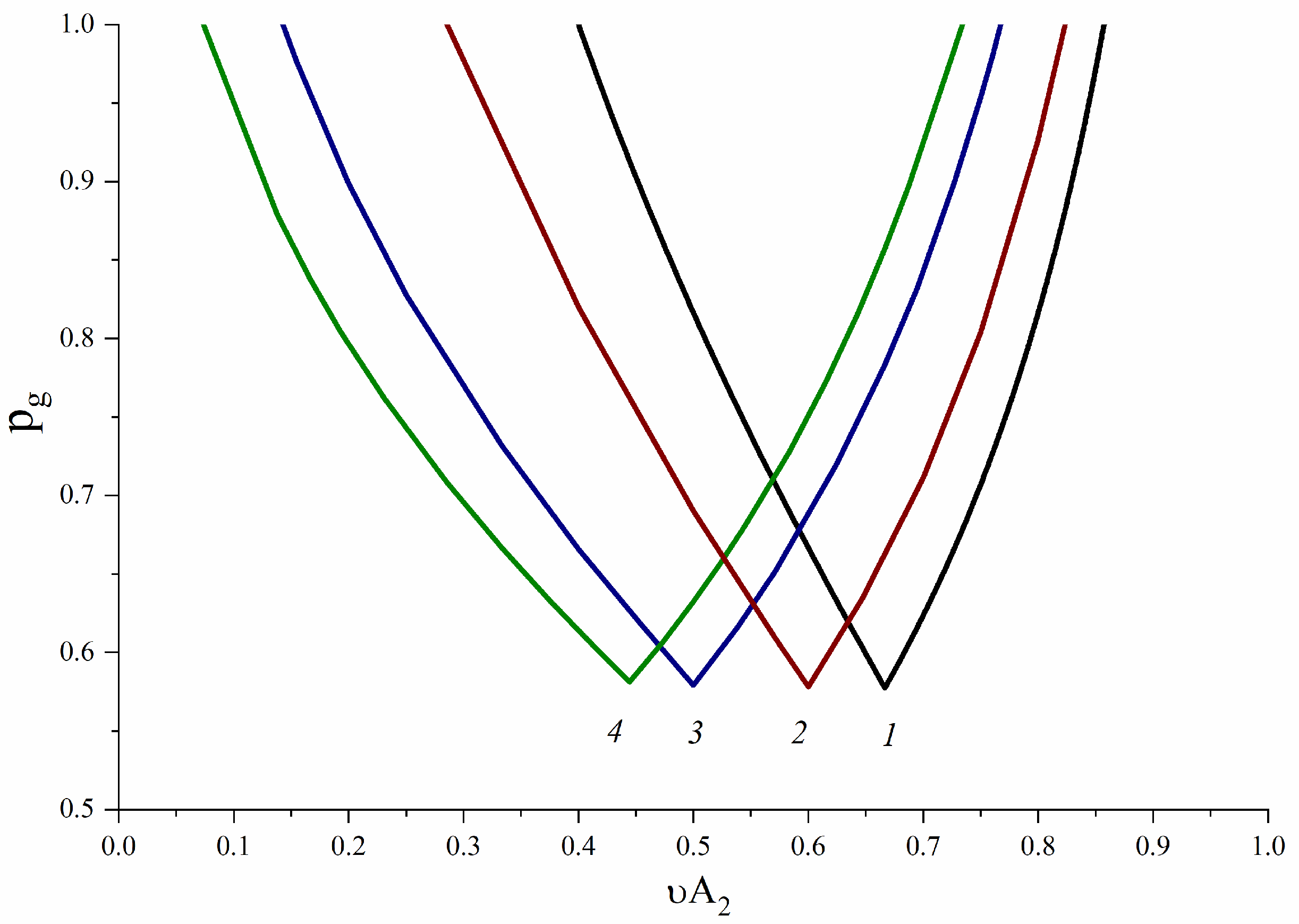
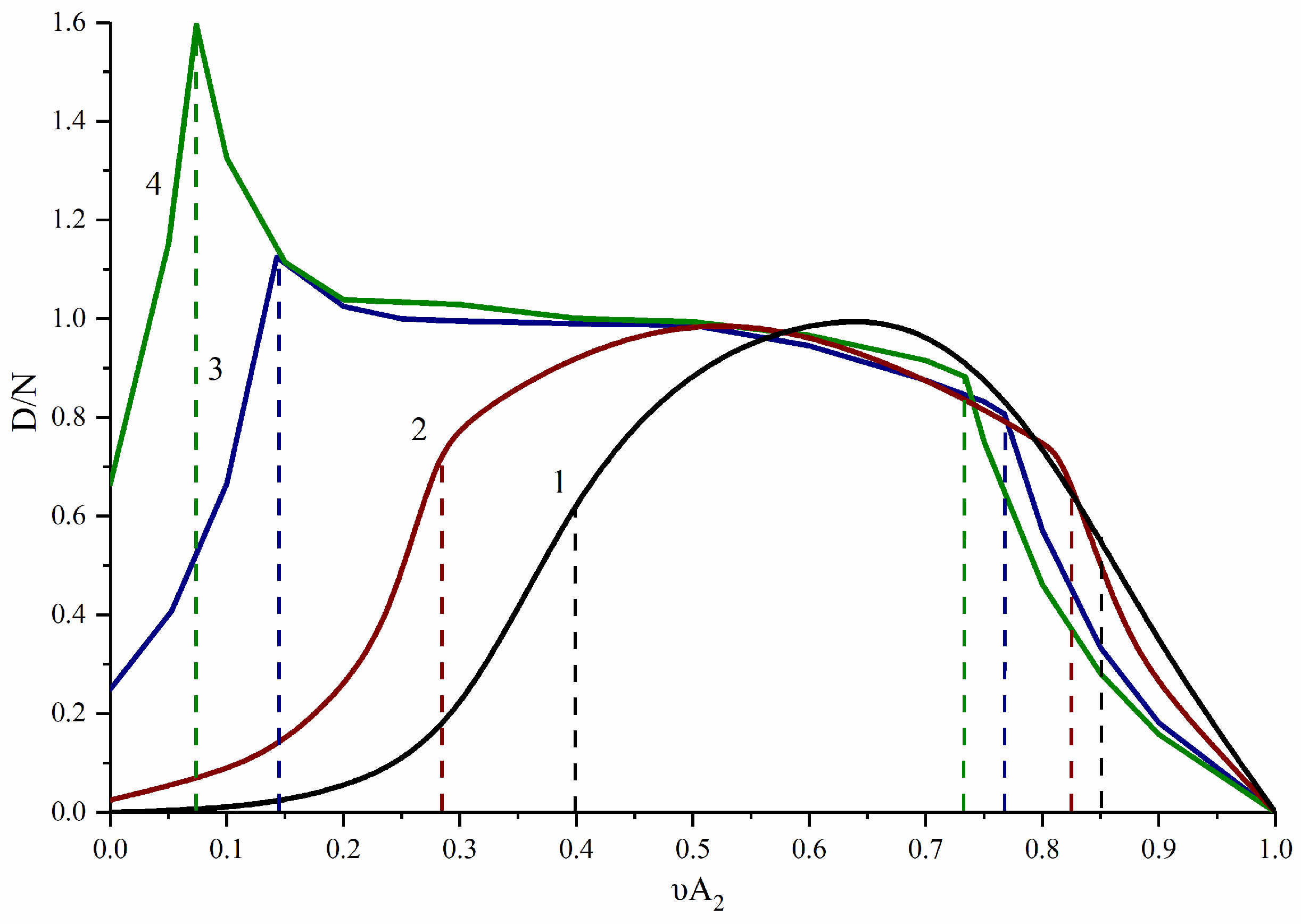
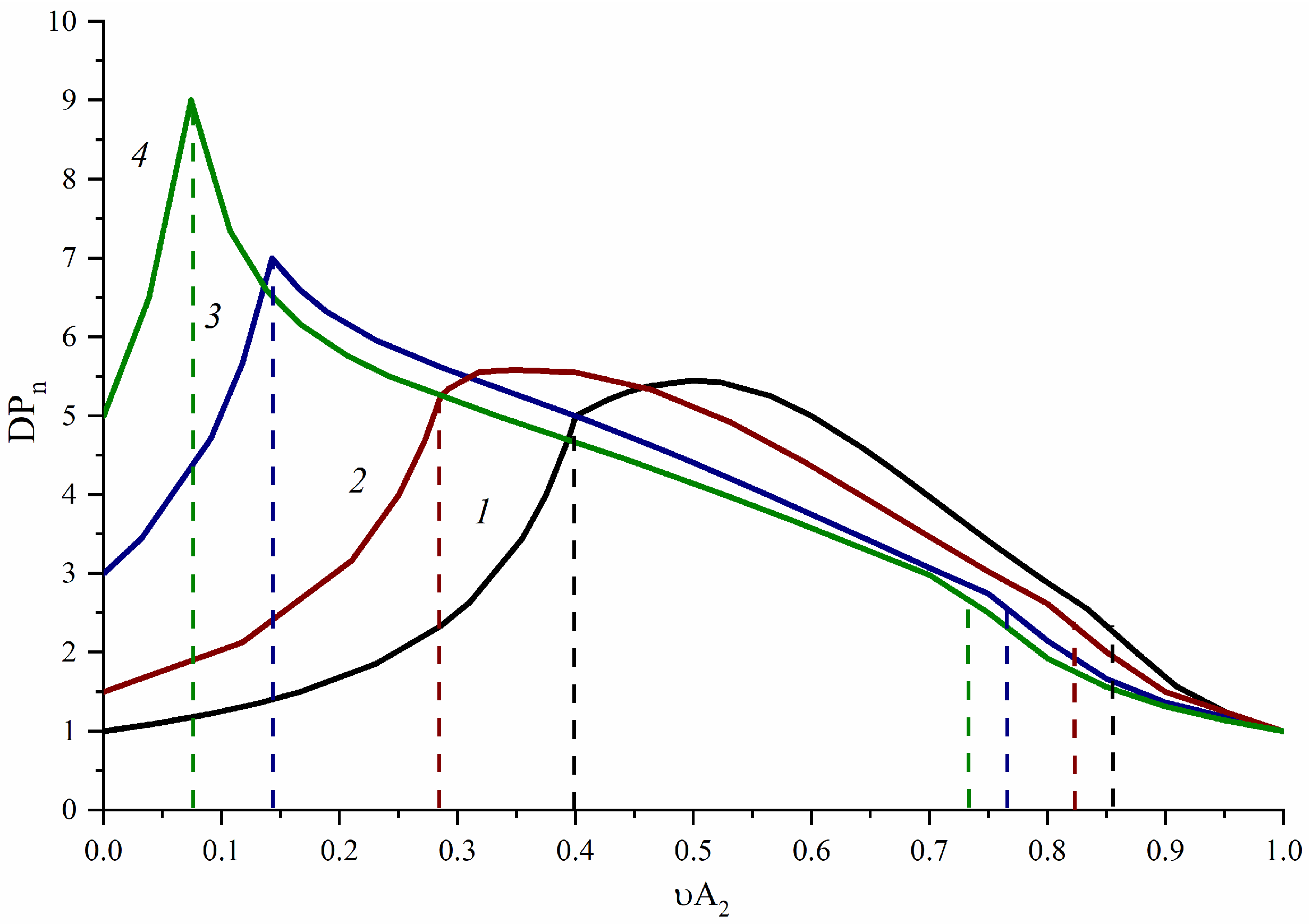
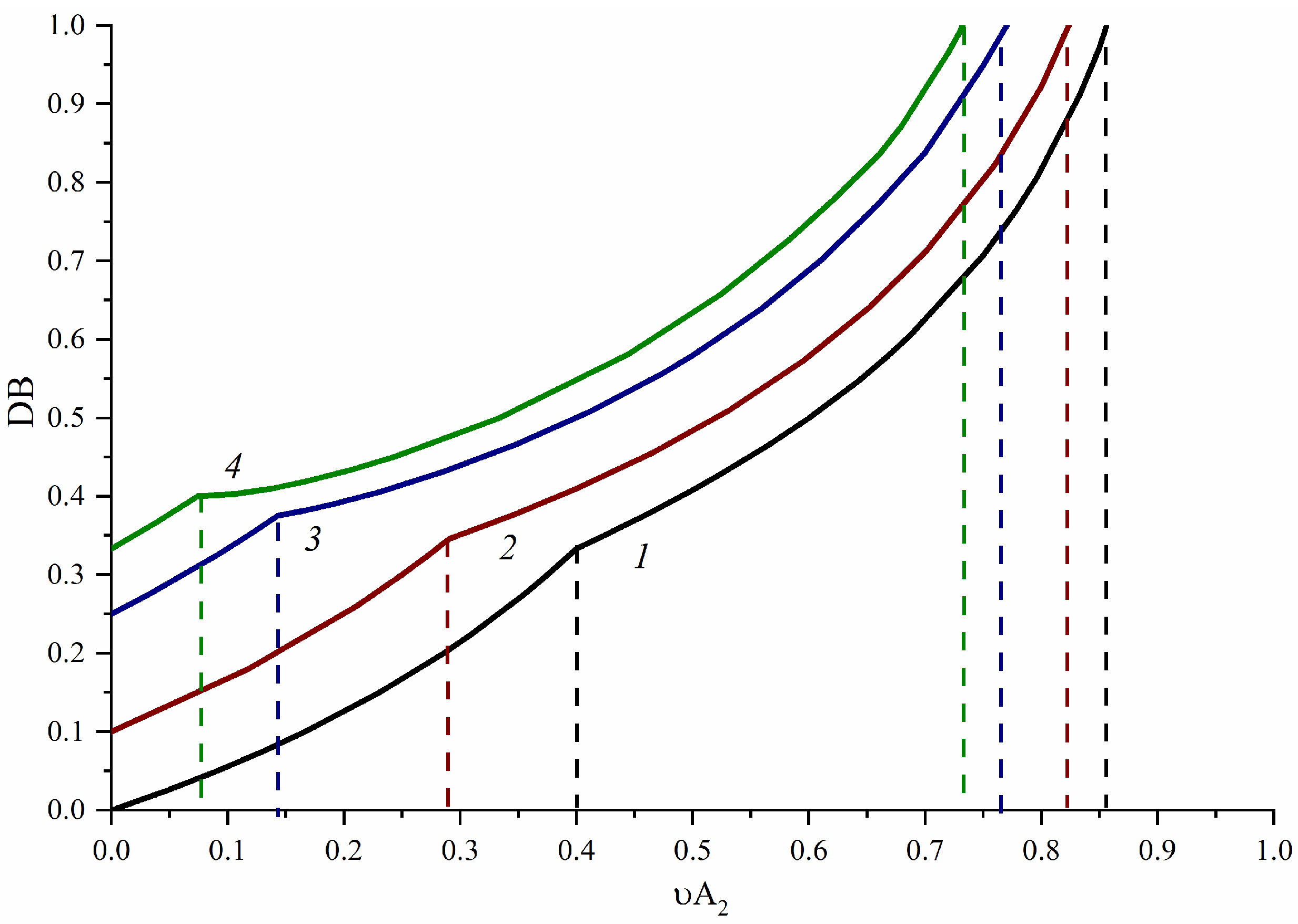
3.1. A2-Type Monomer Effects
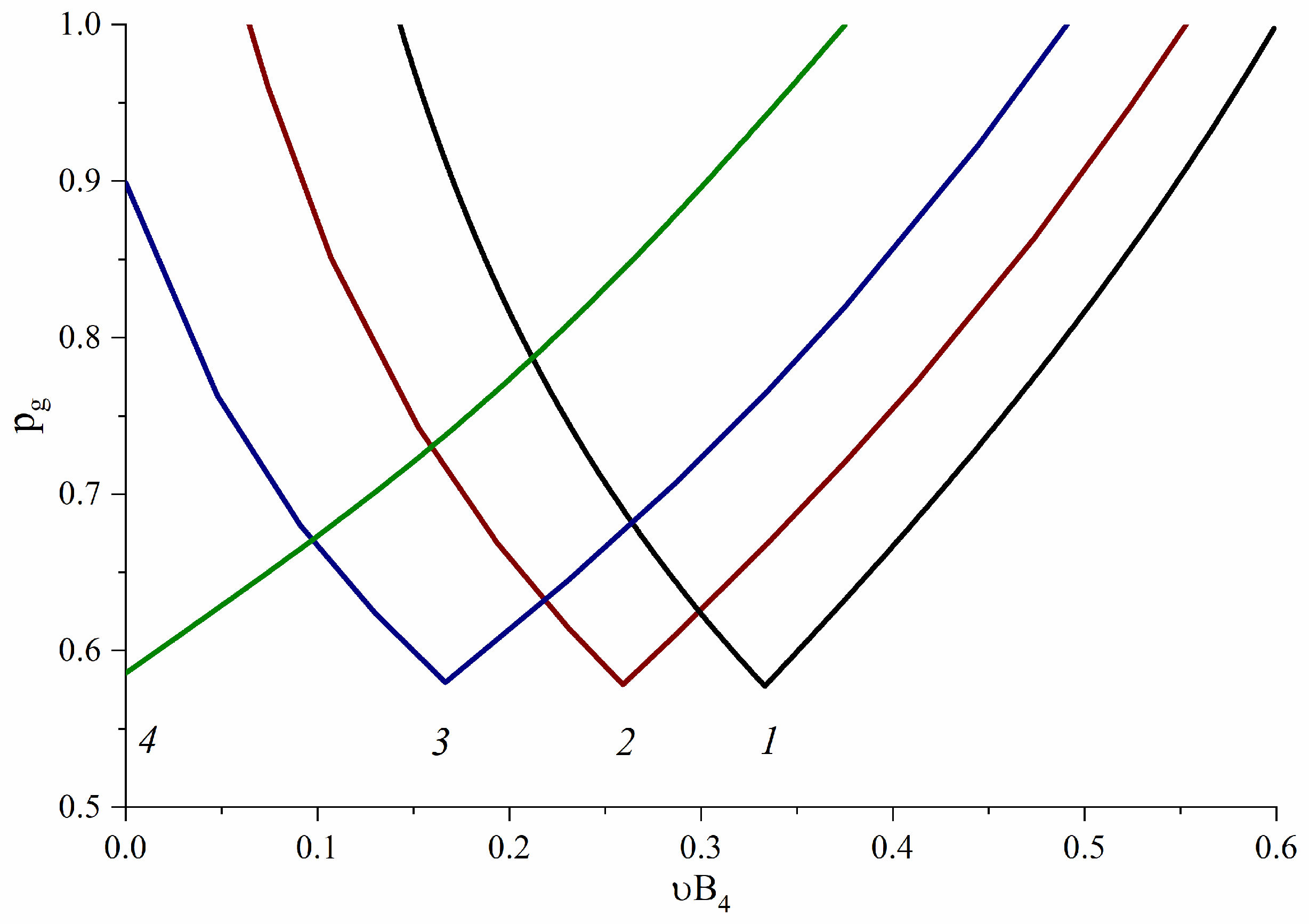
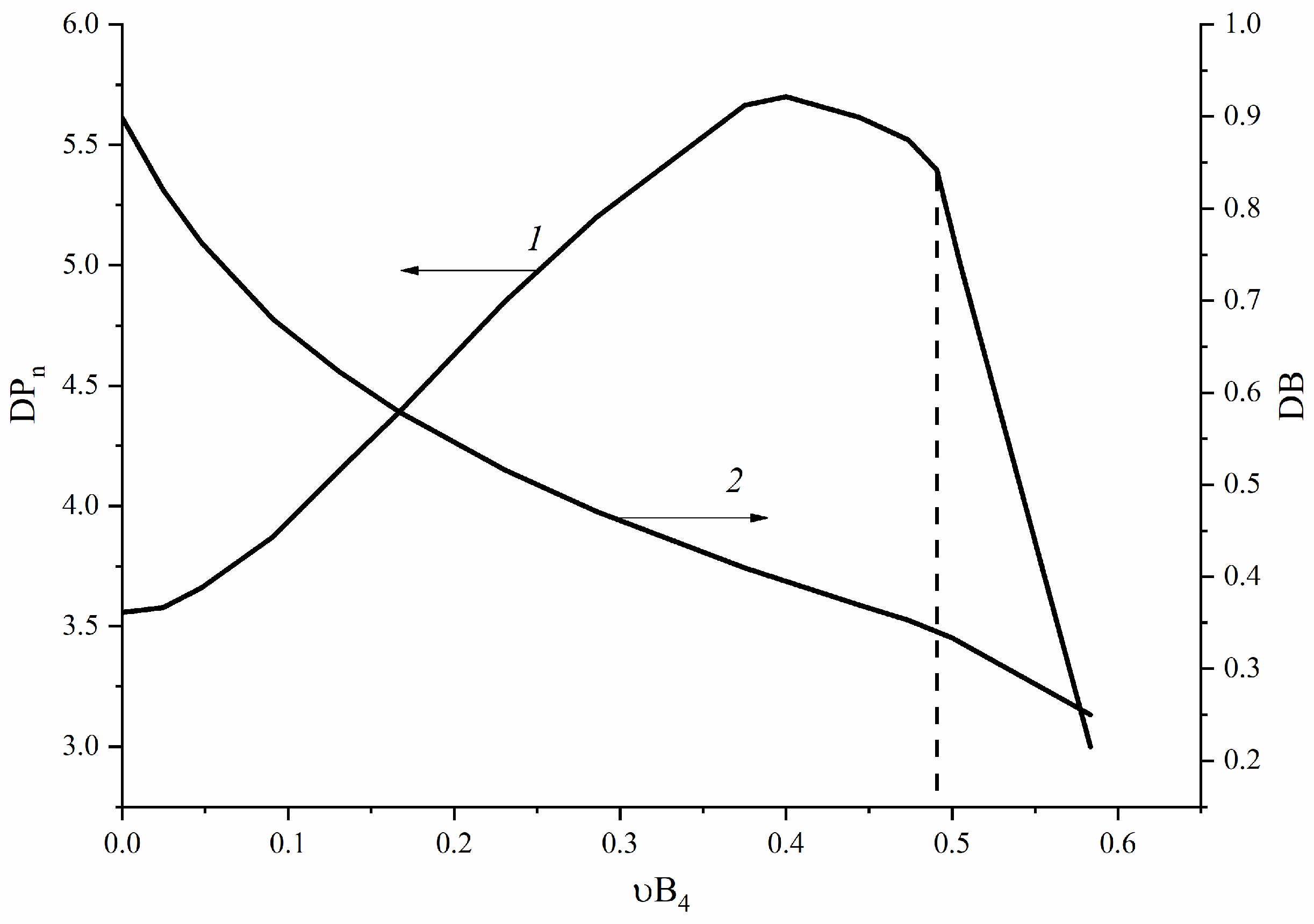
3.2. B4-Type Monomer Effects
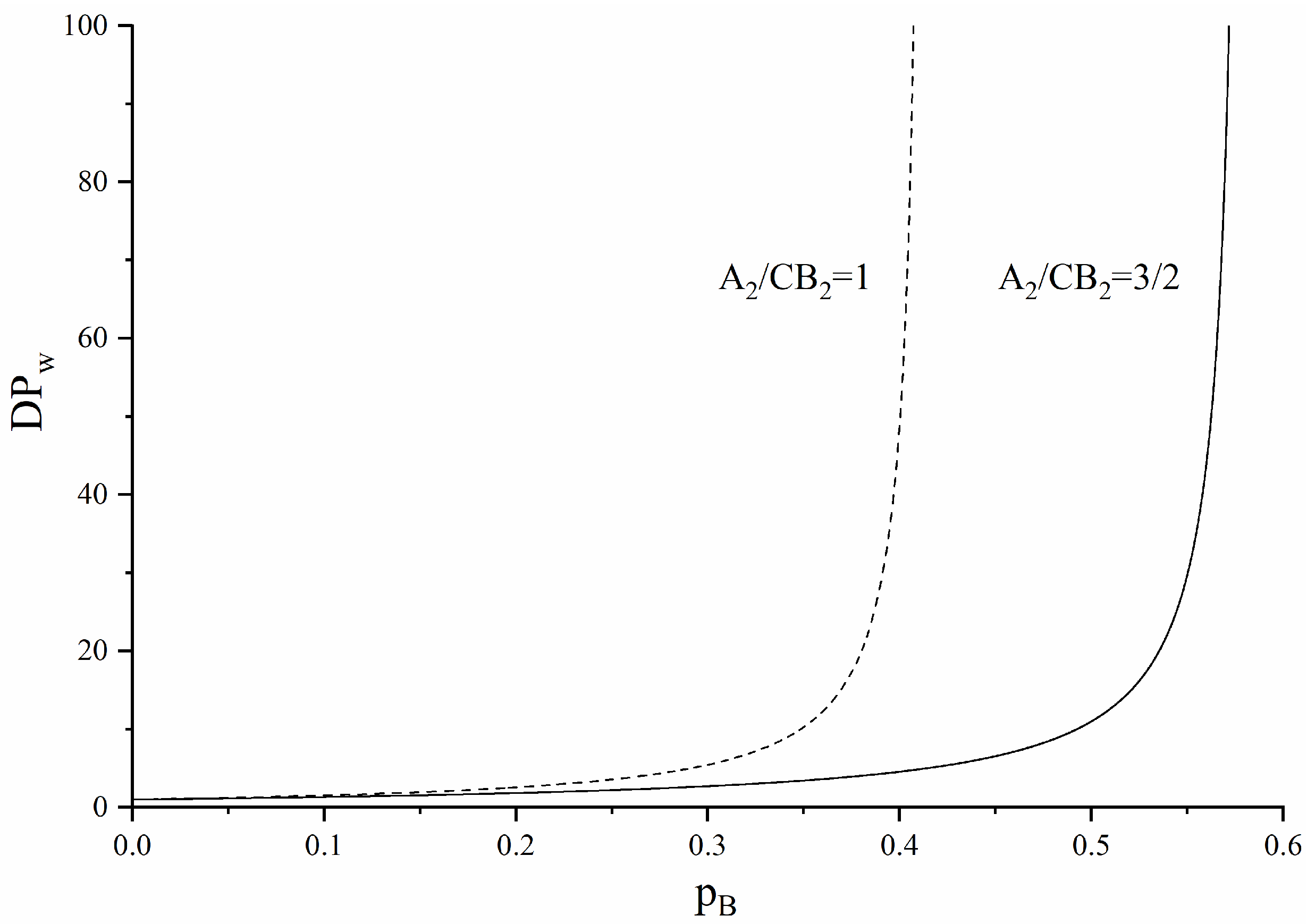
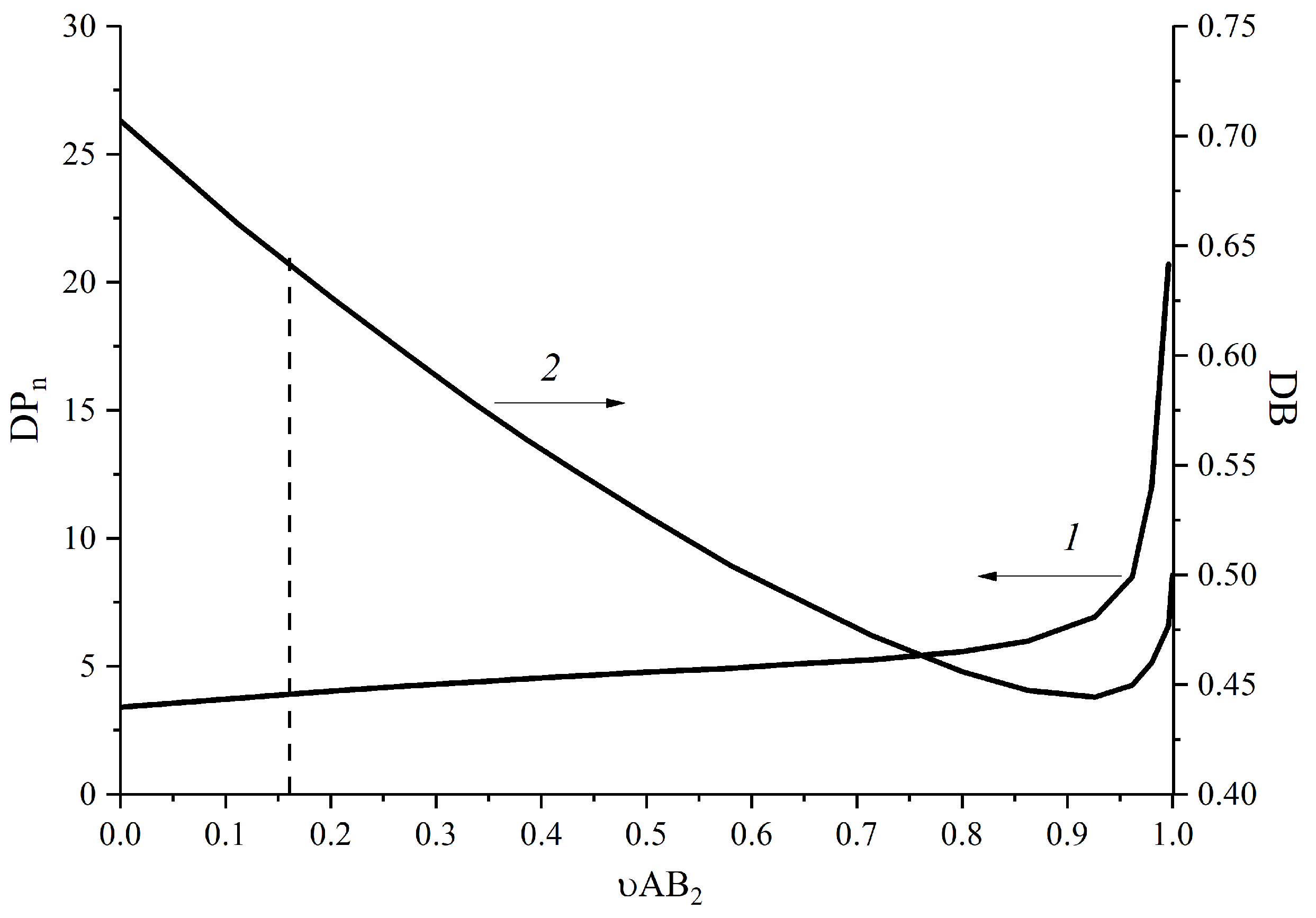
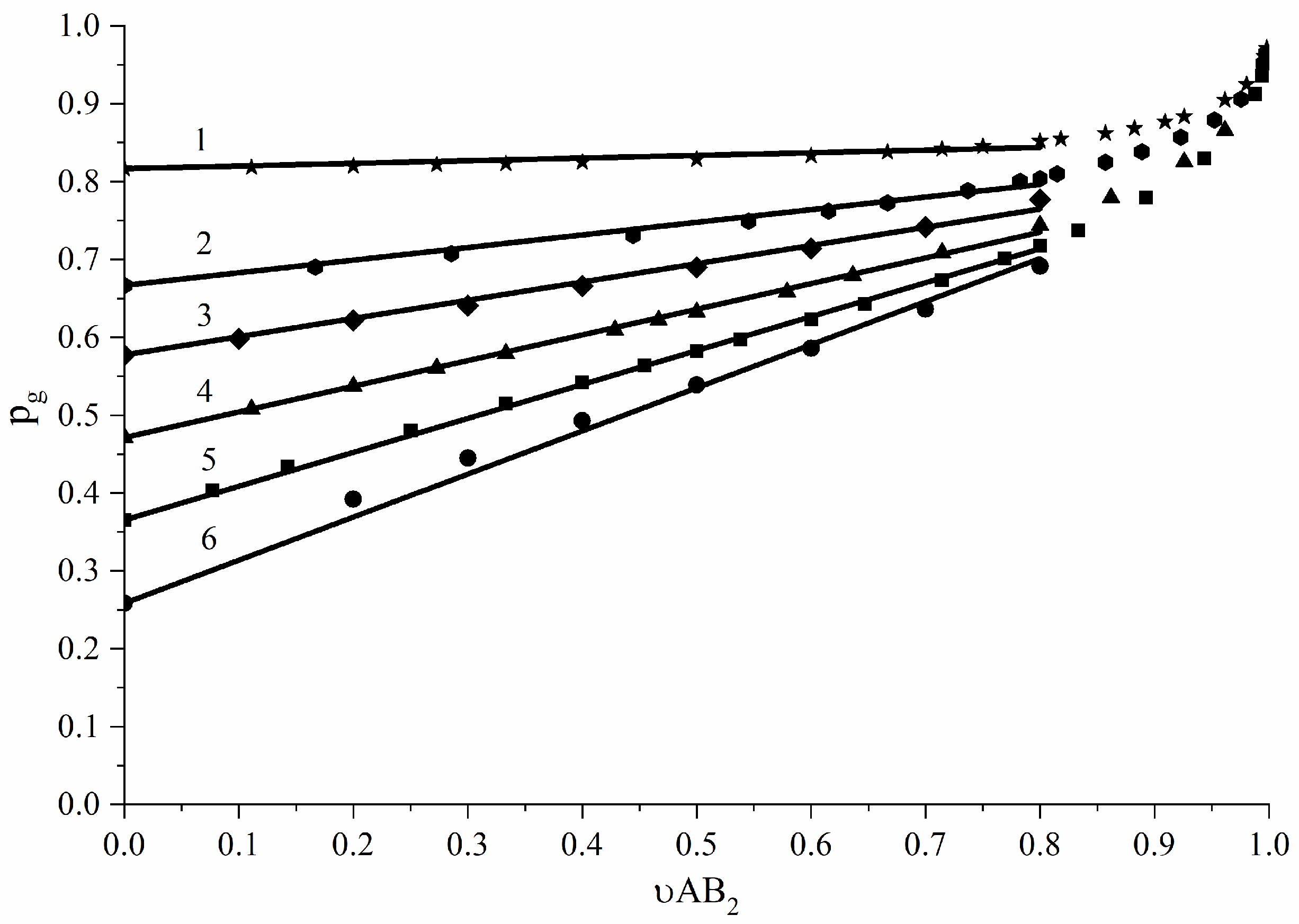
3.3. AB2-Type Monomer Effects
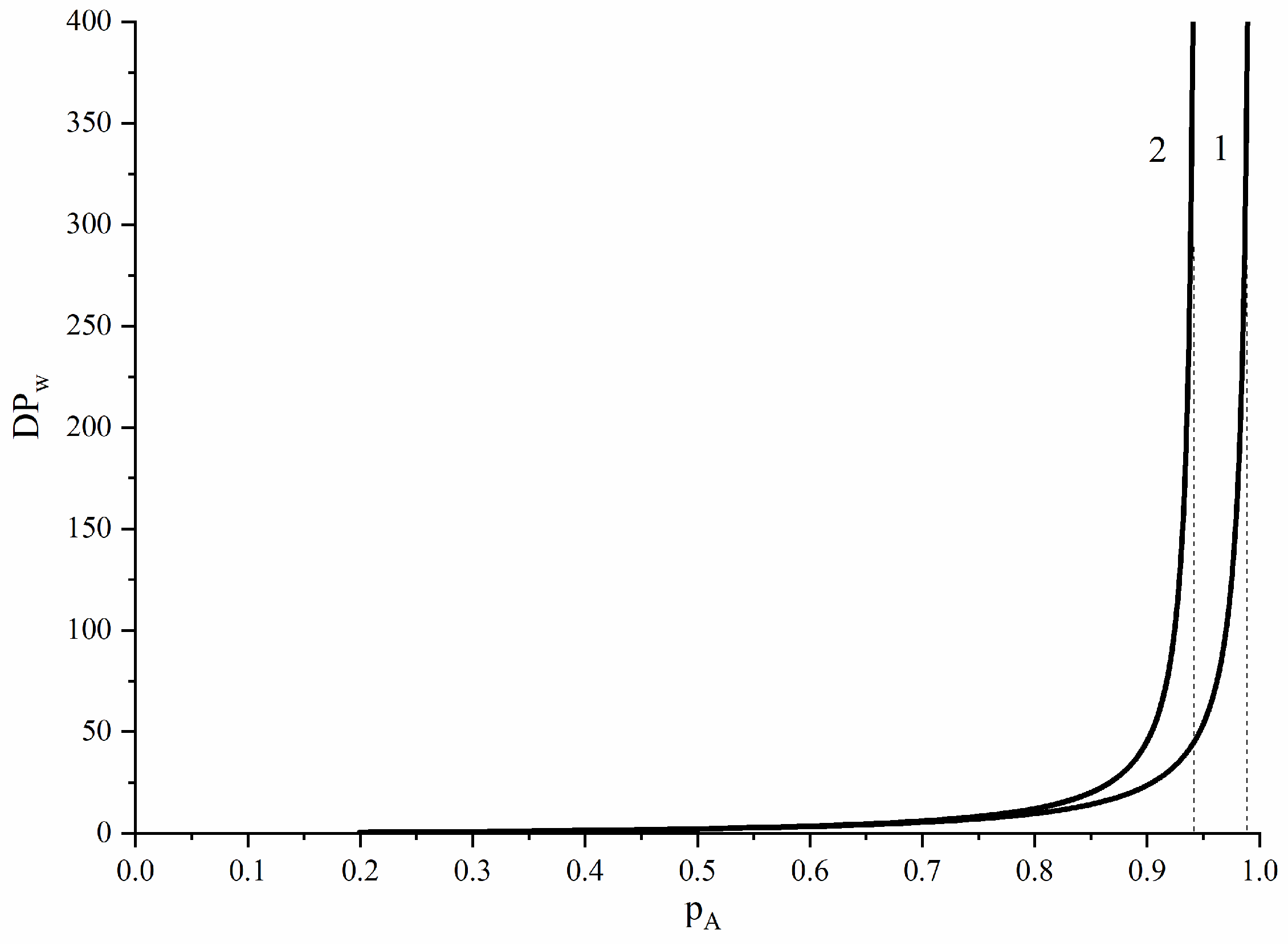
3.4. Substitution Effects
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
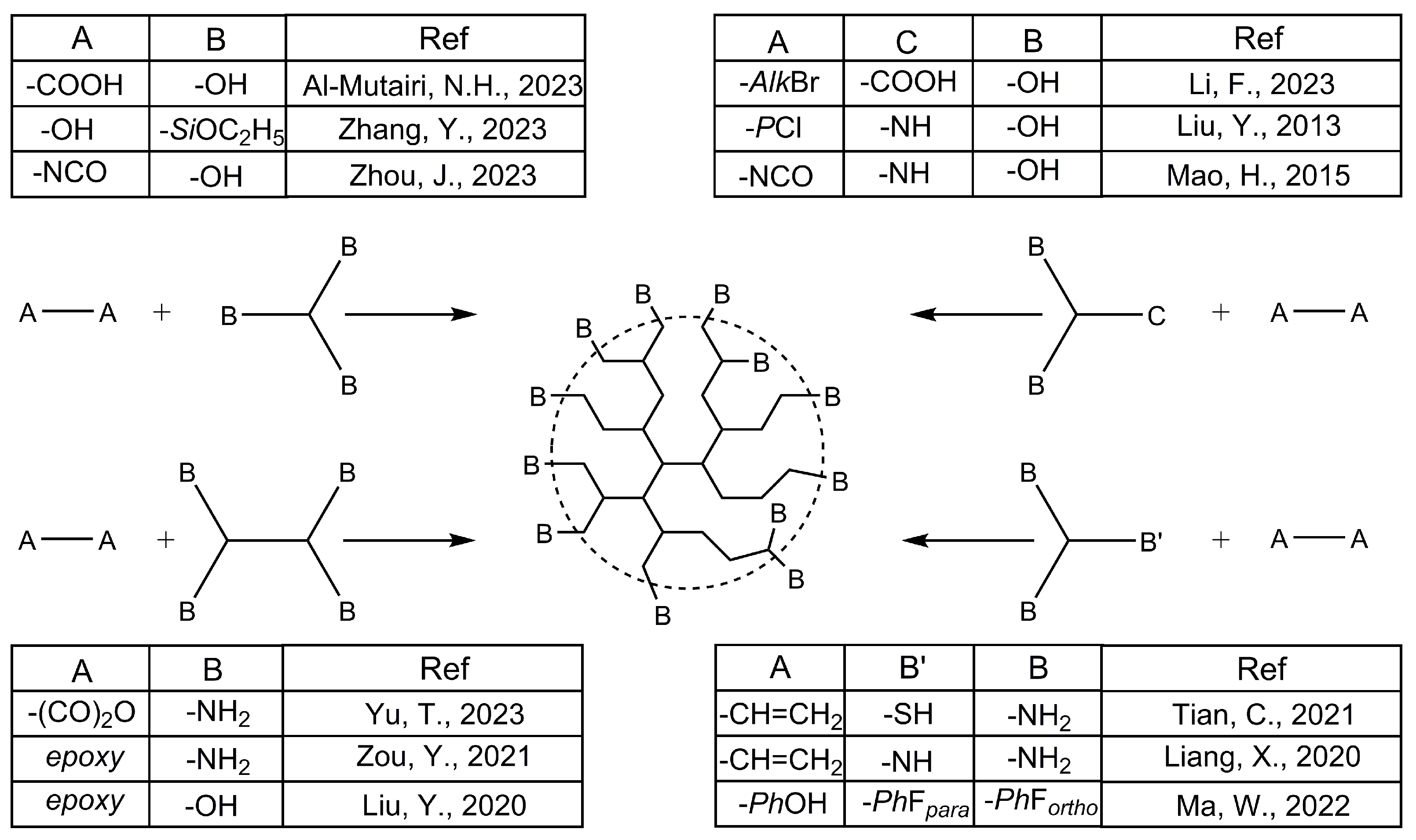
- Kaiser, T.; Frey, H. Hyperbranched Polymer Architectures: From Flory’s AB(f-1) Polycondensates to Controlled Structures. Polymer 2020, 211, 123113. [Google Scholar] [CrossRef]
- Jeon, I.-Y.; Noh, H.-J.; Baek, J.-B. Hyperbranched Macromolecules: From Synthesis to Applications. Molecules 2018, 23, 657. [Google Scholar] [CrossRef]
- Caminade, A.-M.; Yan, D.; Smith, D.K. Dendrimers and Hyperbranched Polymers. Chem. Soc. Rev. 2015, 44, 3870–3873. [Google Scholar] [CrossRef]
- Thompson, M.; Scholz, C. Highly Branched Polymers Based on Poly(Amino Acid)s for Biomedical Application. Nanomaterials 2021, 11, 1119. [Google Scholar] [CrossRef]
- Saadati, A.; Hasanzadeh, M.; Seidi, F. Biomedical Application of Hyperbranched Polymers: Recent Advances and Challenges. TrAC Trends Anal. Chem. 2021, 142, 116308. [Google Scholar] [CrossRef]
- Liu, J.; Wu, W. Dendronized Hyperbranched Polymer: A New Architecture for Second-Order Nonlinear Optics. Symmetry 2022, 14, 882. [Google Scholar] [CrossRef]
- Zang, X.; Liu, H.; Li, Q.; Li, Z.; Li, Z. A TCBD-Based AB 2 -Type Second-Order Nonlinear Optical Hyperbranched Polymer Prepared by a Facile Click-Type Postfunctionalization. Polym. Chem. 2020, 11, 5493–5499. [Google Scholar] [CrossRef]
- Rafiq, M.; Chen, Z.; Tang, H.; Hu, Z.; Zhang, X.; Xing, Y.; Li, Y.; Huang, F. Water–Alcohol-Soluble Hyperbranched Polyelectrolytes and Their Application in Polymer Solar Cells and Photocatalysis. ACS Appl. Polym. Mater. 2020, 2, 12–18. [Google Scholar] [CrossRef]
- Bathula, C.; Appiagyei, A.B.; Yadav, H.; K, A.K.; Ramesh, S.; Shrestha, N.K.; Shinde, S.; Kim, H.S.; Kim, H.S.; Reddy, L.V.; et al. Facile Synthesis of Triphenylamine Based Hyperbranched Polymer for Organic Field Effect Transistors. Nanomaterials 2019, 9, 1787. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Yu, B.; Jiang, S.-D.; Song, L.; Hu, Y.; Wang, B. Hyper-Branched Polymer Grafting Graphene Oxide as an Effective Flame Retardant and Smoke Suppressant for Polystyrene. J. Hazard. Mater. 2015, 300, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Täuber, K.; Marsico, F.; Wurm, F.R.; Schartel, B. Hyperbranched Poly(Phosphoester)s as Flame Retardants for Technical and High Performance Polymers. Polym. Chem. 2014, 5, 7042–7053. [Google Scholar] [CrossRef]
- Jikei, M.; Kakimoto, M. Hyperbranched Polymers: A Promising New Class of Materials. Prog. Polym. Sci. 2001, 26, 1233–1285. [Google Scholar] [CrossRef]
- Petrov, A.O.; Karpov, S.V.; Malkov, G.V.; Shastin, A.V.; Badamshina, E.R. New Non-Symmetric Azido-Diacetylenic s-Triazine Monomer for Polycycloaddition. Mendeleev Commun. 2022, 32, 464–466. [Google Scholar] [CrossRef]
- Voit, B.I.; Lederer, A. Hyperbranched and Highly Branched Polymer Architectures—Synthetic Strategies and Major Characterization Aspects. Chem. Rev. 2009, 109, 5924–5973. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. VI. Branched Polymers Containing A—R—B f-1 Type Units. J. Am. Chem. Soc. 1952, 74, 2718–2723. [Google Scholar] [CrossRef]
- Hölter, D.; Burgath, A.; Frey, H. Degree of Branching in Hyperbranched Polymers. Acta Polym. 1997, 48, 30–35. [Google Scholar] [CrossRef]
- Yates, C.R.; Hayes, W. Synthesis and Applications of Hyperbranched Polymers. Eur. Polym. J. 2004, 40, 1257–1281. [Google Scholar] [CrossRef]
- Voit, B. Hyperbranched Polymers—All Problems Solved after 15 Years of Research? J. Polym. Sci. Part A Polym. Chem. 2005, 43, 2679–2699. [Google Scholar] [CrossRef]
- Chen, H.; Kong, J. Hyperbranched Polymers from A 2 + B 3 Strategy: Recent Advances in Description and Control of Fine Topology. Polym. Chem. 2016, 7, 3643–3663. [Google Scholar] [CrossRef]
- Liu, C.; Xie, X.; Kong, X.; Zhang, Q.; Yang, J.; Yang, J.; Wang, W. A Removable, Antibacterial and Strong Adhesive Based on Hyperbranched Catechol Polymers. Mater. Lett. 2022, 316, 132019. [Google Scholar] [CrossRef]
- Kricheldorf, H.R. Hyperbranched Cyclic and Multicyclic Polymers by “a 2 + b 4 ” Polycondensations. J. Polym. Sci. Part A Polym. Chem. 2009, 47, 1971–1987. [Google Scholar] [CrossRef]
- Shibasaki, Y.; Sasahara, R.; Hoshino, Y.; Tsukamoto, T.; Suzuki, E.; Oishi, Y. Reactivity-Controlled Synthesis of A2 + B3 Type Soluble Hyperbranched Polymers from Aromatic Diamines and Cyanuryl Chloride via a Coupled Monomer Method. Mater. Today Commun. 2020, 24, 101043. [Google Scholar] [CrossRef]
- Al-Mutairi, N.H.; Al-Zubiedy, A.; Al-Zuhairi, A.J. Preparation and Characterization of a Novel Hyperbranched Polyester Polymers Using A2+B3 Monomers. Prod. Eng. Arch. 2023, 29, 28–36. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuan, J.; Hu, J.; Tian, Z.; Feng, W.; Yan, H. Toward Understanding the Cross-linking from Molecular Chains to Aggregates by Engineering Terminals of Supramolecular Hyperbranched Polysiloxane. Aggregate 2023, e404. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, G.; Niu, Z.; Li, X.; Zhao, J.; Li, X. Hyperbranched Waterborne Polyurethane Solid–Solid Phase Change Material for Thermal Energy Storage in Thermal Management Fabric. Fibers Polym. 2023, 24, 413–422. [Google Scholar] [CrossRef]
- Yu, T.; Yao, H.; Liu, H.; Guan, S. High-Performance Fluorescent/Electroactive (A4+B2)-Type Hyperbranched Polyimide with AIE-Enhanced Electroflourochromic Behavior. Dye. Pigment. 2023, 214, 111207. [Google Scholar] [CrossRef]
- Zou, Y.; Li, L.; Li, Y.; Chen, S.; Xie, X.; Jin, X.; Wang, X.; Ma, C.; Fan, G.; Wang, W. Restoring Cardiac Functions after Myocardial Infarction–Ischemia/Reperfusion via an Exosome Anchoring Conductive Hydrogel. ACS Appl. Mater. Interfaces 2021, 13, 56892–56908. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Li, S.; Chen, C.; Xu, L.; Huang, P.; Liu, F.; Su, Y.; Qi, M.; Yu, C.; et al. In Situ Supramolecular Polymerization-Enhanced Self-Assembly of Polymer Vesicles for Highly Efficient Photothermal Therapy. Nat. Commun. 2020, 11, 1724. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Guo, X.; Wang, Y.; Jin, M. From Soft Hyperbranched Polymers to Hard Crosslinkers: UV Curable Macromers That Contained Oxetane on and around Hyperbranched Frameworks. Eur. Polym. J. 2023, 192, 112074. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, N.; Li, F.; Chen, P. Synthesis and Properties of a Novel Hyperbranched Polyphosphoramidate Using an A 2 + CB 2 Approach. Polym. Int. 2013, 62, 390–396. [Google Scholar] [CrossRef]
- Mao, H.; Qiang, S.; Yang, F.; Zhao, C.; Wang, C.; Yin, Y. Synthesis of Blocked and Branched Waterborne Polyurethanes for Pigment Printing Applications. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Tian, C.; Zhou, K.-C.; Lu, Y.-F.; Li, J.-J.; Yao, Y.; Tao, X.-F.; Zhuang, Q.-X.; Xie, Y.-F.; Lin, S.-L. Hyperbranched Azopolymer with Quadruple Responsibility. Chin. J. Polym. Sci. 2021, 39, 1169–1176. [Google Scholar] [CrossRef]
- Liang, X.; Li, X.; Gao, X.; Zhang, Y.; Wei, W.; Liu, X. Fabrication of Unimolecular Micelle-Based Nanomedicines from Hyperbranched Polymers Containing Both Terminal and Internal Reactive Groups. Polymer 2020, 202, 122716. [Google Scholar] [CrossRef]
- Ma, W.; Wang, X.; Chen, W.; Chen, Y. Improved the Surface Properties of Carbon Fiber through Hyperbranched Polyaryletherketone Sizing. Polym. Compos. 2022, 43, 1948–1960. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. I. Gelation 1. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Zhou, D.; Cutlar, L.; Gao, Y.; Wang, W.; O’Keeffe-Ahern, J.; McMahon, S.; Duarte, B.; Larcher, F.; Rodriguez, B.J.; Greiser, U.; et al. The Transition from Linear to Highly Branched Poly(β-Amino Ester)s: Branching Matters for Gene Delivery. Sci. Adv. 2016, 2, e1600102. [Google Scholar] [CrossRef]
- Zhou, D.; Gao, Y.; Aied, A.; Cutlar, L.; Igoucheva, O.; Newland, B.; Alexeeve, V.; Greiser, U.; Uitto, J.; Wang, W. Highly Branched Poly(β-Amino Ester)s for Skin Gene Therapy. J. Control. Release 2016, 244, 336–346. [Google Scholar] [CrossRef]
- Gurunathan, T.; Mohanty, S.; Nayak, S.K. Hyperbranched Polymers for Coating Applications: A Review. Polym. Plast. Technol. Eng. 2016, 55, 92–117. [Google Scholar] [CrossRef]
- Cheng, W.; Wu, D.; Liu, Y. Michael Addition Polymerization of Trifunctional Amine and Acrylic Monomer: A Versatile Platform for Development of Biomaterials. Biomacromolecules 2016, 17, 3115–3126. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Jia, Z.; Yan, D. Theoretical Investigation on the Polyaddition of A2 and CB2 Monomers with Non-Equal Reactivity. Polymer 2009, 50, 5608–5612. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, D. Kinetic Treatment for the Copolycondensation of A2 and CB2 Monomers with Non-Equal Reactivity. Polymer 2011, 52, 5387–5392. [Google Scholar] [CrossRef]
- Karpov, S.V.; Perepelitsina, E.O.; Malkov, G.V. Synthesis of New Branched Urethane-Triazole Polymers. Polym. Sci. Ser. B 2014, 56, 298–306. [Google Scholar] [CrossRef]
- Karpov, S.V.; Iakunkov, A.; Akkuratov, A.V.; Petrov, A.O.; Perepelitsina, E.O.; Malkov, G.V.; Badamshina, E.R. One-Pot Synthesis of Hyperbranched Polyurethane-Triazoles with Controlled Structural, Molecular Weight and Hydrodynamic Characteristics. Polymers 2022, 14, 4514. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Kong, J. 100% Hyperbranched Polymers via the Acid-Catalyzed Friedel–Crafts Aromatic Substitution Reaction. Polym. Chem. 2016, 7, 5226–5232. [Google Scholar] [CrossRef]
- Emamikia, M.; Barikani, M.; Bakhshandeh, G. Study of Negative Substitution and Monomer Self-condensation Effects on Molar Mass and Structural Characteristics of Hyperbranched Polyesters Originating from a High-functionality Core. Polym. Int. 2015, 64, 521–529. [Google Scholar] [CrossRef]
- Testud, B.; Pintori, D.; Grau, E.; Taton, D.; Cramail, H. Hyperbranched Polyesters by Polycondensation of Fatty Acid-Based AB n -Type Monomers. Green Chem. 2017, 19, 259–269. [Google Scholar] [CrossRef]
- Cheng, K.-C.; Chuang, T.-H.; Tsai, T.-H.; Guo, W.; Su, W.-F. First Shell Substitution Effects on Hyperbranched Polymers Formed from Monomers and with End-Capping Molecules. Eur. Polym. J. 2009, 45, 2942–2950. [Google Scholar] [CrossRef]
- De Keer, L.; Kilic, K.I.; Van Steenberge, P.H.M.; Daelemans, L.; Kodura, D.; Frisch, H.; De Clerck, K.; Reyniers, M.-F.; Barner-Kowollik, C.; Dauskardt, R.H.; et al. Computational Prediction of the Molecular Configuration of Three-Dimensional Network Polymers. Nat. Mater. 2021, 20, 1422–1430. [Google Scholar] [CrossRef]
- Jin, J.; Yang, Y.-N.; Zhou, Y.-N.; Luo, Z.-H. In Silico Tracking of Topological Variations in Hyperbranched Polymers Synthesis. Macromolecules 2023, 56, 6589–6599. [Google Scholar] [CrossRef]
- Villada, J.T.; Lyngdoh, G.A.; Paswan, R.; Oladipo, B.; Das, S. Evaluating the Adhesion Response of Acrylonitrile-Butadiene-Styrene (ABS)/Thermoplastic Polyurethane (TPU) Fused Interface Using Multiscale Simulation and Experiments. Mater. Des. 2023, 232, 112155. [Google Scholar] [CrossRef]
- Cheng, K.-C. Model of Hyperbranched Polymers Prepared via Polymerization of AB2 and Core C3 Monomers in a Continuous-Stirred Tank Reactor. Chem. Eng. Res. Des. 2020, 155, 40–47. [Google Scholar] [CrossRef]
- Zhao, Z.-F.; Yao, N.; Li, H.-J.; Zhang, Q.; Wang, H.-J. Average Properties of the Self-Condensing Vinyl Polymerization System of Comonomers with Any Initial Size Distribution. J. Polym. Res. 2023, 30, 422. [Google Scholar] [CrossRef]
- Gu, F.; Li, J.-T.; Hong, X.-Z.; Wang, H.-J. A Unified Theoretical Treatment on Statistical Properties of the Semi-Batch Self-Condensing Vinyl Polymerization System. Chin. J. Polym. Sci. 2021, 39, 1510–1520. [Google Scholar] [CrossRef]
- Cheng, K.; Cheng, P.; Wang, P. Hyperbranched Polyurethane Acrylates Synthesized via Copolymerization of Monomers A 2 and B 3 with Monofunctional Compound BR Added Gradually at Different Rates. Polym. Eng. Sci. 2020, 60, 1138–1145. [Google Scholar] [CrossRef]
- Irzhak, V.I. A Structural Characteristic of Hyperbranched Polymers. Polym. Sci. Ser. B 2009, 51, 143–148. [Google Scholar] [CrossRef]
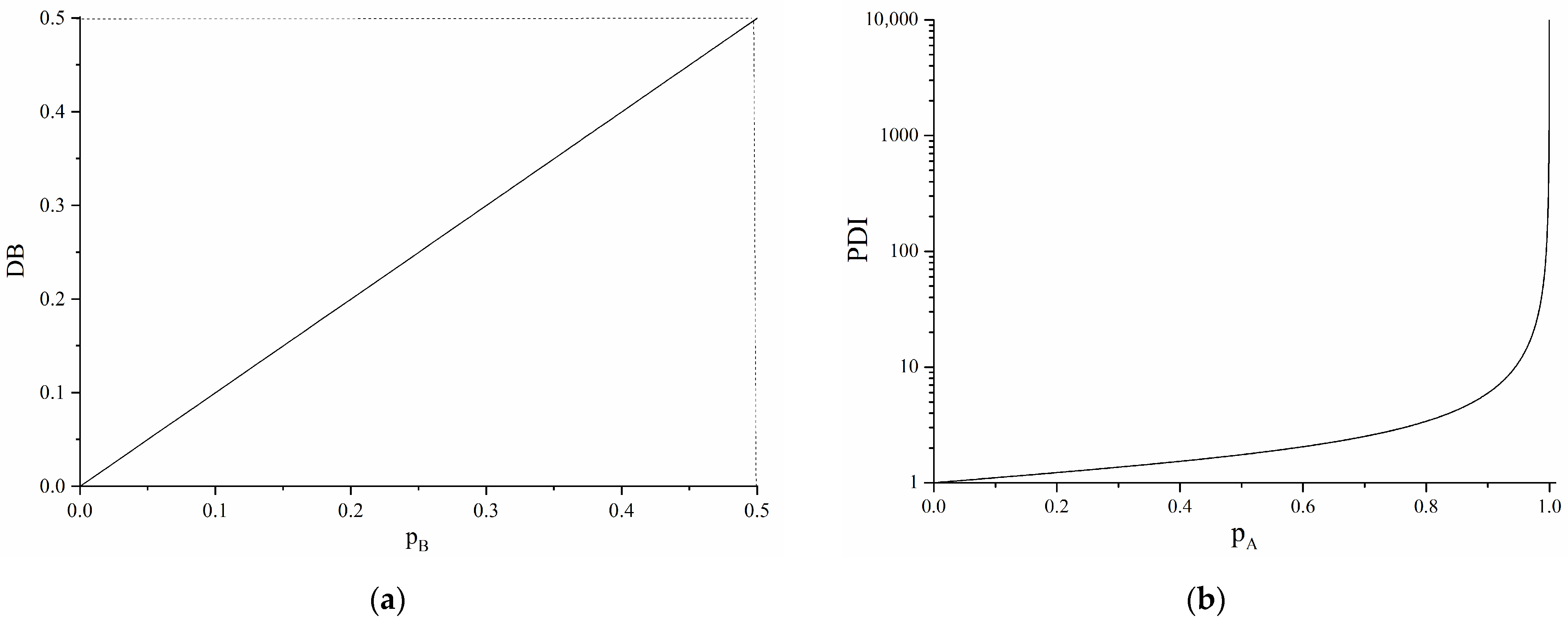

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karpov, S.V.; Iakunkov, A.; Chernyaev, D.A.; Kurbatov, V.G.; Malkov, G.V.; Badamshina, E.R. A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture. Polymers 2024, 16, 426. https://doi.org/10.3390/polym16030426
Karpov SV, Iakunkov A, Chernyaev DA, Kurbatov VG, Malkov GV, Badamshina ER. A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture. Polymers. 2024; 16(3):426. https://doi.org/10.3390/polym16030426
Chicago/Turabian StyleKarpov, Sergei V., Artem Iakunkov, Dmitry A. Chernyaev, Vladimir G. Kurbatov, Georgiy V. Malkov, and Elmira R. Badamshina. 2024. "A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture" Polymers 16, no. 3: 426. https://doi.org/10.3390/polym16030426
APA StyleKarpov, S. V., Iakunkov, A., Chernyaev, D. A., Kurbatov, V. G., Malkov, G. V., & Badamshina, E. R. (2024). A Theoretical Investigation of the Polyaddition of an AB2+A2+B4 Monomer Mixture. Polymers, 16(3), 426. https://doi.org/10.3390/polym16030426






