Pyrolysis Kinetics Analysis and Prediction for Carbon Fiber-Reinforced Epoxy Composites
Abstract
:1. Introduction
2. Theory
2.1. Kinetic Analysis
2.2. Model of Pyrolysis Prediction
3. Experimental Section
3.1. Materials
3.2. Experimental Procedures
4. Results and Discussion
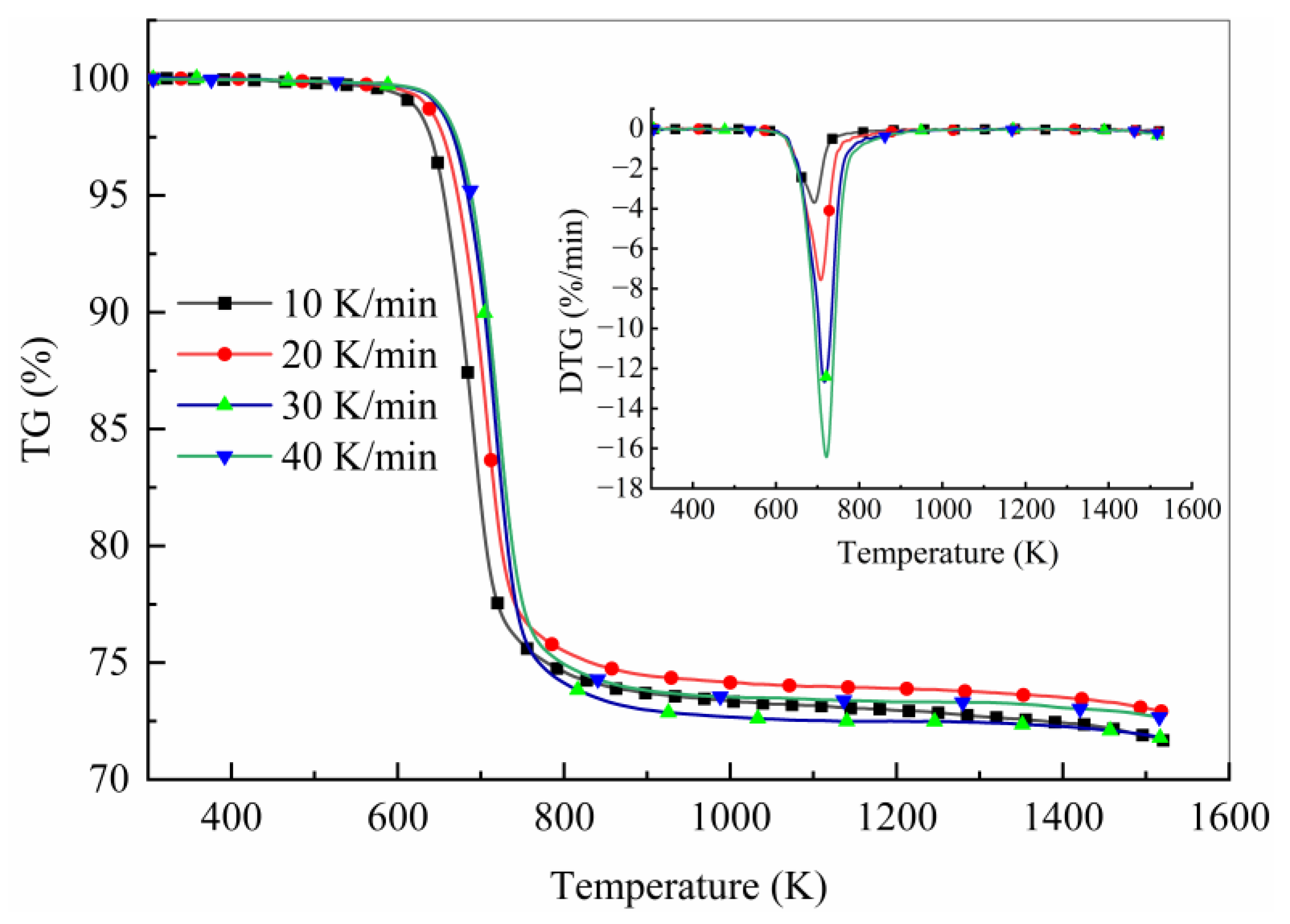
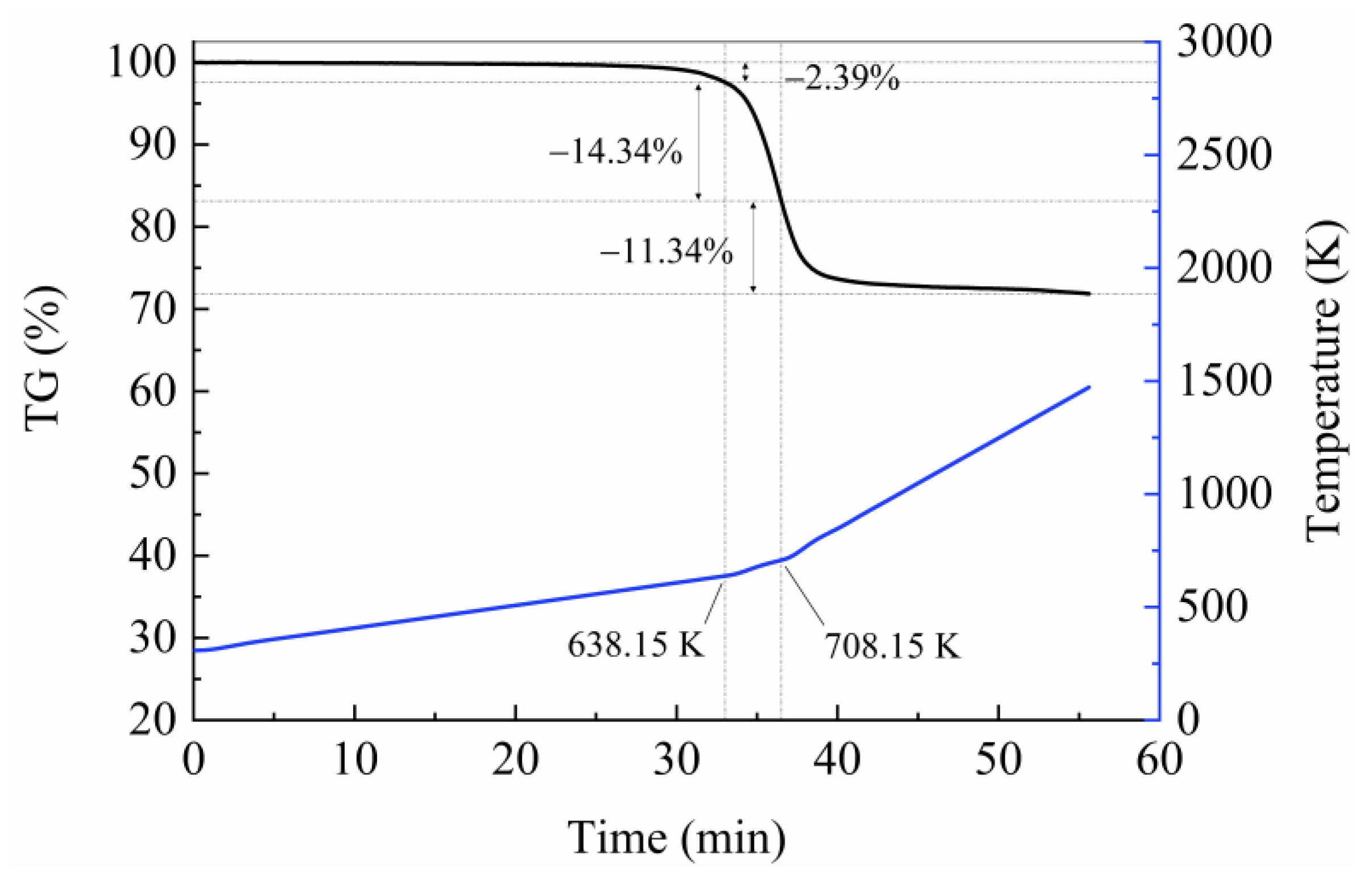
4.1. Thermal Decomposition Data Analysis
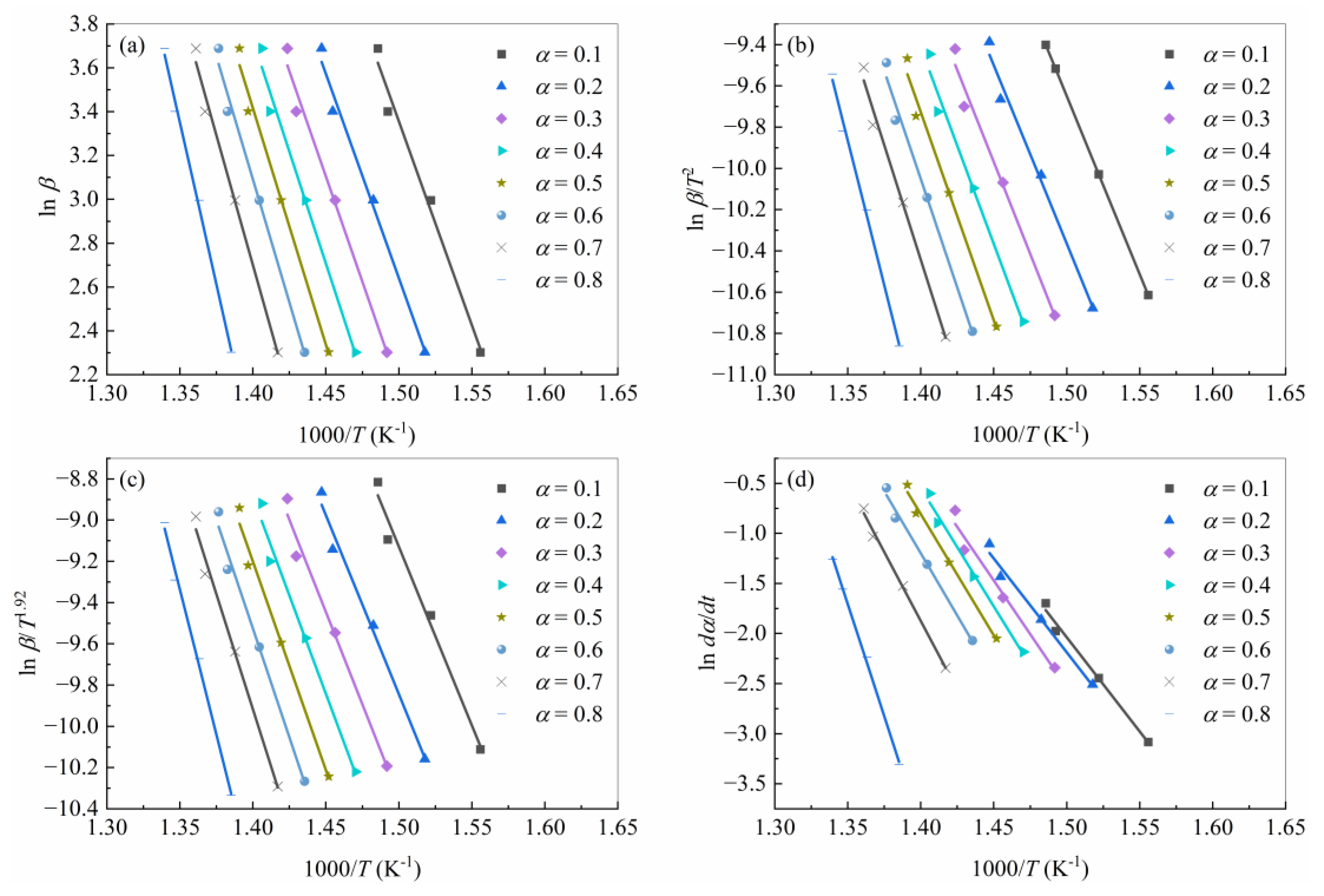
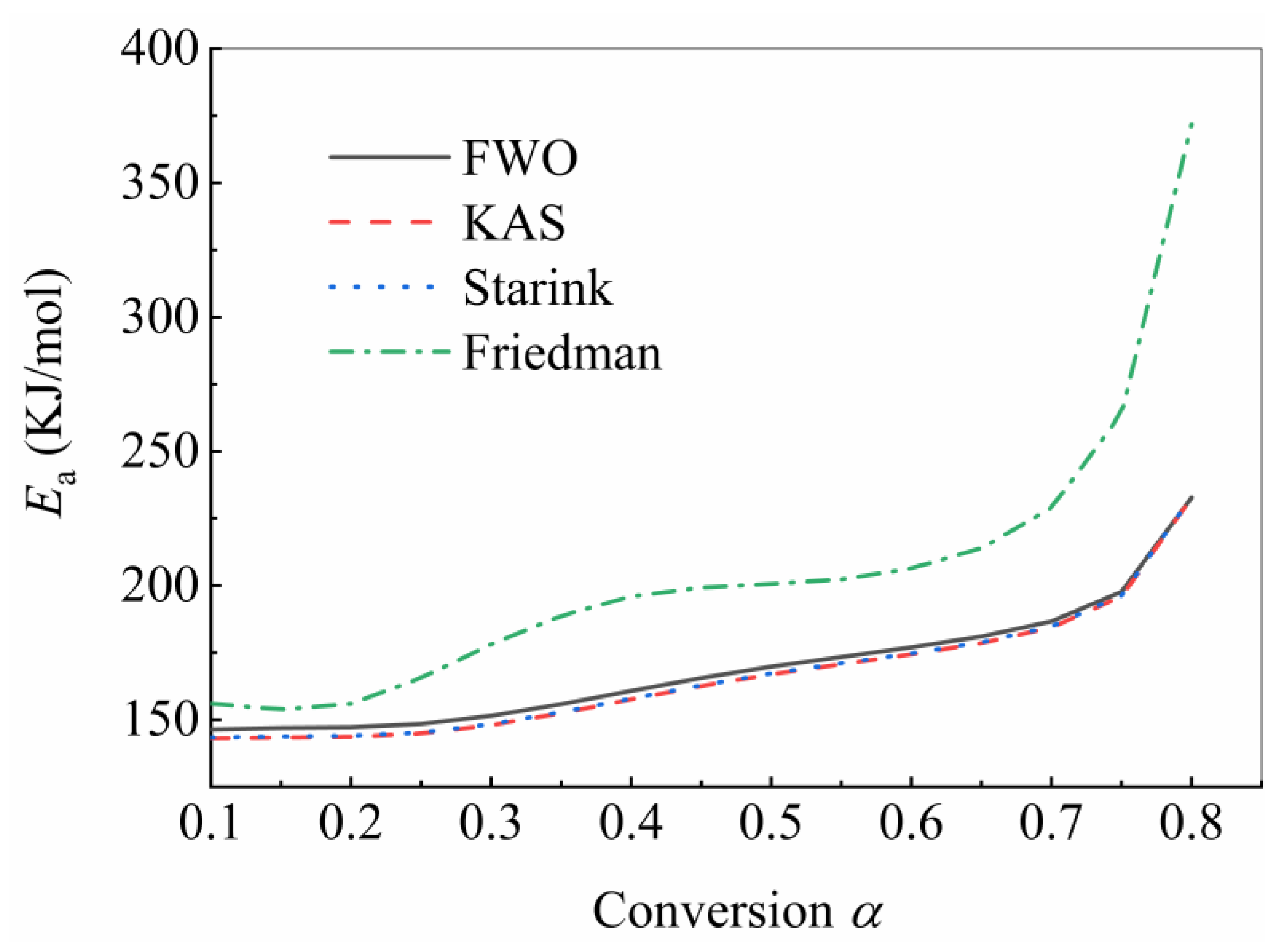
4.2. Determination of Kinetic Triplet
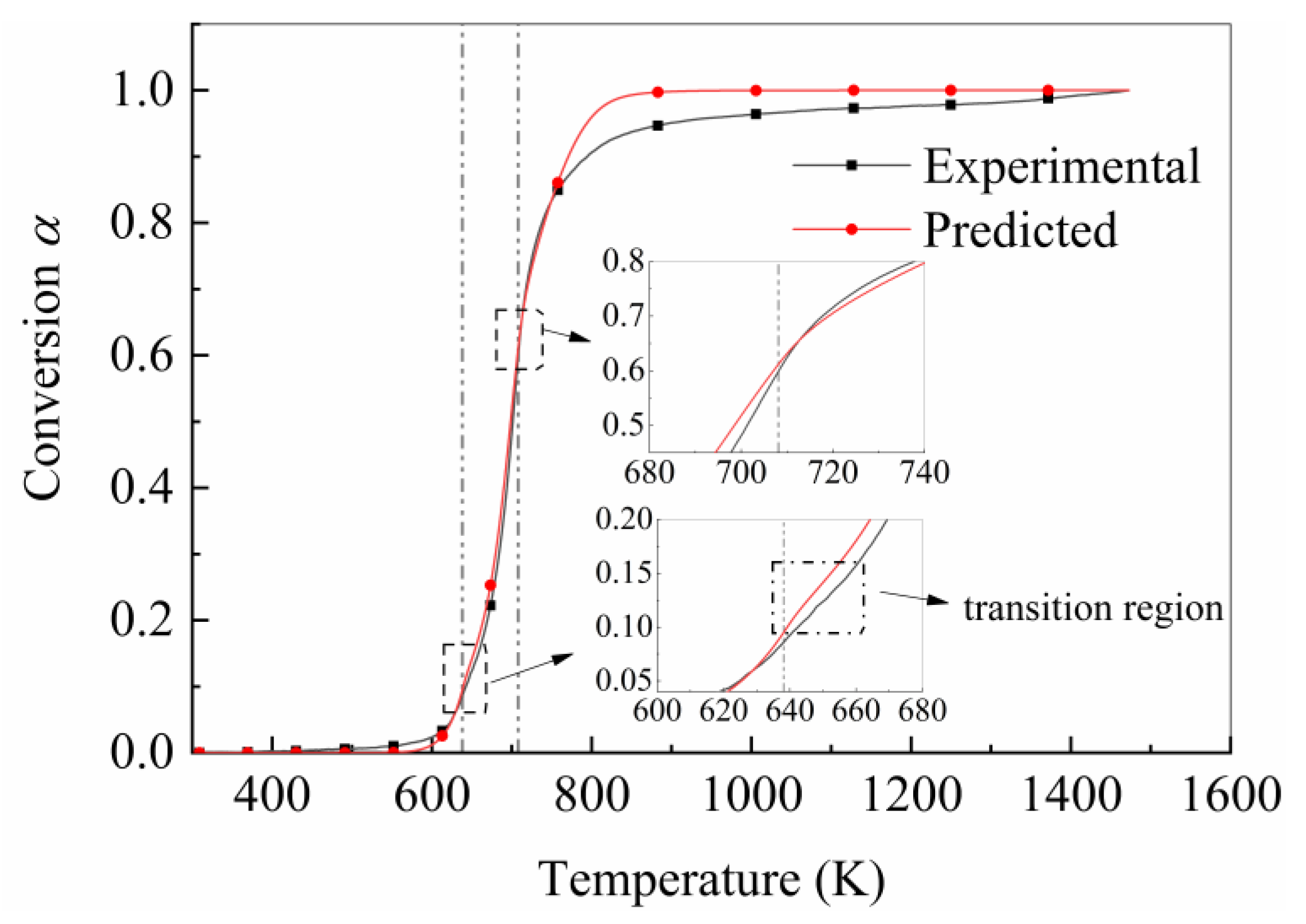
4.3. Validation of Pyrolysis Prediction Model
4.4. Influence of Time Step on Prediction Accuracy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mouritz, A.P.; Mathys, Z.; Gibson, A.G. Heat release of polymer composites in fire. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1040–1054. [Google Scholar] [CrossRef]
- Domingo, R. Aviation Maintenance Technician Handbook-Airframe, Volume 1; FAA-H-8083-31A; US Department of Transportation: Oklahoma City, OK, USA, 2018. [Google Scholar]
- Hirano, Y.; Katsumata, S.; Iwahori, Y.; Todoroki, A. Artificial lightning testing on graphite/epoxy composite laminate. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1461–1470. [Google Scholar] [CrossRef]
- Gou, J.; Tang, Y.; Liang, F.; Zhao, Z.; Firsich, D.; Fielding, J. Carbon nanofiber paper for lightning strike protection of composite materials. Compos. Part B Eng. 2010, 41, 192–198. [Google Scholar] [CrossRef]
- Lee, J.; Gharghabi, P.; Boushab, D.; Ricks, T.M.; Lacy, T.E.; Pittman, C.U.; Mazzola, M.S.; Velicki, A. Artificial lightning strike tests on PRSEUS panels. Compos. Part B Eng. 2018, 154, 467–477. [Google Scholar] [CrossRef]
- Wang, F.; Ma, X.; Zhang, Y.; Jia, S. Lightning damage testing of aircraft composite-reinforced panels and its metal protection structures. Appl. Sci. 2018, 8, 1791. [Google Scholar] [CrossRef]
- Tranchard, P.; Duquesne, S.; Samyn, F.; Estèbe, B.; Bourbigot, S. Kinetic analysis of the thermal decomposition of a carbon fibre-reinforced epoxy resin laminate. J. Anal. Appl. Pyrolysis. 2017, 126, 14–21. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Huang, G.; Liu, H.; Yang, S.; Zhang, A. Thermal degradation behaviors and reaction mechanism of carbon fibre-epoxy composite from hydrogen tank by TG-FTIR. J. Hazard. Mater. 2018, 357, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Sihn, S.; Ehlert, G.J.; Roy, A.K.; Vernon, J.P. Identifying unified kinetic model parameters for thermal decomposition of polymer matrix composites. J. Compos. Mater. 2019, 53, 2875–2890. [Google Scholar] [CrossRef]
- Sihn, S.; Ehlert, G.J.; Roy, A.K.; Vernon, J.P. A unified kinetic model for multistage thermal decomposition of polymer matrix composites in air. Mater. Today Commun. 2020, 24, 101095. [Google Scholar] [CrossRef]
- Carpier, Y.; Alia, A.; Vieille, B.; Barbe, F. Experiments based analysis of thermal decomposition kinetics model. Case of carbon fibers PolyPhenylene Sulfide composites. Polym. Degrad. Stab. 2021, 186, 109525. [Google Scholar] [CrossRef]
- Li, H.; Wang, N.; Han, X.; Yuan, H.; Xie, J. Mechanism identification and kinetics analysis of thermal degradation for carbon fiber/epoxy resin. Polymers 2021, 13, 569. [Google Scholar] [CrossRef] [PubMed]
- Zheng, F.; Ren, Z.; Xu, B.; Wan, K.; Cai, J.; Yang, J.; Zhang, T.; Wang, P.; Niu, B.; Zhang, Y.; et al. Elucidating multiple-scale reaction behaviors of phenolic resin pyrolysis via TG-FTIR and ReaxFF molecular dynamics simulations. J. Anal. Appl. Pyrolysis. 2021, 157, 105222. [Google Scholar] [CrossRef]
- Gibson, A.G.; Wu, Y.S.; Chandler, H.W.; Wilcox, J.A.D.; Bettess, P. Model for the thermal performance of thick composite laminates in hydrocarbon fires. Rev. L'institute Fr. Pet. 1995, 50, 69–74. [Google Scholar] [CrossRef]
- Henderson, J.B.; Wiebelt, J.A.; Tant, M.R. A Model for the Thermal Response of Polymer Composite Materials with Experimental Verification. J. Compos. Mater. 1985, 19, 579–595. [Google Scholar] [CrossRef]
- Dodds, N.; Gibson, A.G.; Dewhurst, D.; Davies, J.M. Fire behaviour of composite laminates. Compos. Part A Appl. Sci. Manuf. 2000, 31, 689–702. [Google Scholar] [CrossRef]
- Galgano, A.; Di Blasi, C.; Branca, C.; Milella, E. Thermal response to fire of a fibre-reinforced sandwich panel: Model formulation, selection of intrinsic properties and experimental validation. Polym. Degrad. Stab. 2009, 94, 1267–1280. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Feih, S.; Kandare, E.; Mathys, Z.; Gibson, A.G.; Jardin, P.E.D.; Case, S.W.; Lattimer, B.Y. Review of fire structural modelling of polymer composites. Compos. Part A Appl. Sci. Manuf. 2009, 40, 1800–1814. [Google Scholar] [CrossRef]
- Zhuge, J.; Gou, J.; Chen, R.H.; Kapat, J. Finite element modeling of post-fire flexural modulus of fiber reinforced polymer composites under constant heat flux. Compos. Part A Appl. Sci. Manuf. 2012, 43, 665–674. [Google Scholar] [CrossRef]
- Rizk, G.; Nahas, R.; Khalil, K.; Challita, G.; Legrand, V.; Casari, P.; Jacquemin, F. Durability of composite assemblies under extreme conditions: Thermomechanical damage prediction of a double-lap bonded composite assembly subject to impact and high temperature. Compos. Struct. 2019, 213, 58–70. [Google Scholar] [CrossRef]
- Li, H.; Wang, N.; Han, X.; Fan, B.; Feng, Z.; Guo, S. Simulation of thermal behavior of glass fiber/phenolic composites exposed to heat flux on one side. Materials 2020, 13, 421. [Google Scholar] [CrossRef]
- Loh, T.W.; Kandare, E.; Nguyen, K.T.Q. The effect of thickness on the compression failure of composite laminates in fire. Compos. Struct. 2022, 286, 115334. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Isoconversional kinetic analysis of thermally stimulated processes in polymers. Macromol. Rapid Commun. 2006, 27, 1515–1532. [Google Scholar] [CrossRef]
- Feih, S.; Mathys, Z.; Gibson, A.G.; Mouritz, A.P. Modelling the compression strength of polymer laminates in fire. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2354–2365. [Google Scholar] [CrossRef]
- Kandare, E.; Kandola, B.K.; McCarthy, E.D.; Myler, P.; Edwards, G.; Jifeng, Y.; Wang, Y.C. Fiber-reinforced epoxy composites exposed to high temperature environments. Part II: Modeling mechanical property degradation. J. Compos. Mater. 2011, 45, 1511–1521. [Google Scholar] [CrossRef]
- Summers, P.T.; Lattimer, B.Y.; Case, S.; Feih, S. Predicting compression failure of composite laminates in fire. Compos. Part A Appl. Sci. Manuf. 2012, 43, 773–782. [Google Scholar] [CrossRef]
- Anjang, A.; Chevali, V.S.; Kandare, E.; Mouritz, A.P.; Feih, S. Tension modelling and testing of sandwich composites in fire. Compos. Struct. 2014, 113, 437–445. [Google Scholar] [CrossRef]
- FWang, S.; Ding, N.; Liu, Z.Q.; Ji, Y.Y.; Yue, Z.F. Ablation damage characteristic and residual strength prediction of carbon fiber/epoxy composite suffered from lightning strike. Compos. Struct. 2014, 117, 222–233. [Google Scholar] [CrossRef]
- FWang, S.; Yu, X.S.; Jia, S.Q.; Li, P. Experimental and numerical study on residual strength of aircraft carbon/epoxy composite after lightning strike. Aerosp. Sci. Technol. 2018, 75, 304–314. [Google Scholar] [CrossRef]
- Flynn, J.H. Thermal analysis kinetics—Past, present and future. Thermochim. Acta 1992, 203, 519–526. [Google Scholar] [CrossRef]
- Flynn, J.H. The “Temperature Integral”—Its use and abuse. Thermochim. Acta 1997, 300, 83–92. [Google Scholar] [CrossRef]
- Bai, Y.; Keller, T. Time dependence of material properties of frp composites in fire. J. Compos. Mater. 2009, 43, 2469–2484. [Google Scholar] [CrossRef]
- Dong, Q.; Guo, Y.; Sun, X.; Jia, Y. Coupled electrical-thermal-pyrolytic analysis of carbon fiber/epoxy composites subjected to lightning strike. Polymer 2015, 56, 385–394. [Google Scholar] [CrossRef]
- Dong, Q.; Guo, Y.; Chen, J.; Yao, X.; Yi, X.; Ping, L.; Jia, Y. Influencing factor analysis based on electrical-thermal-pyrolytic simulation of carbon fiber composites lightning damage. Compos. Struct. 2016, 140, 1–10. [Google Scholar] [CrossRef]
- Dong, Q.; Wan, G.; Ping, L.; Guo, Y.; Yi, X.; Jia, Y. Coupled thermal-mechanical damage model of laminated carbon fiber/resin composite subjected to lightning strike. Compos. Struct. 2018, 206, 185–193. [Google Scholar] [CrossRef]
- Dong, Q.; Wan, G.; Guo, Y.; Zhang, L.; Wei, X.; Yi, X.; Jia, Y. Damage analysis of carbon fiber composites exposed to combined lightning current components D and C. Compos. Sci. Technol. 2019, 179, 1–9. [Google Scholar] [CrossRef]
- Kamiyama, S.; Hirano, Y.; Ogasawara, T. Delamination analysis of CFRP laminates exposed to lightning strike considering cooling process. Compos. Struct. 2018, 196, 55–62. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: Basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. General treatment of the thermogravimetry of polymers. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1966, 70, 487. [Google Scholar] [CrossRef]
- Flynn, J.H. The isoconversional method for determination of energy of activation at constant heating rates. J. Therm. Anal. 1983, 27, 95–102. [Google Scholar] [CrossRef]
- Akahira, T.; Sunose, T. Method of determining activation deterioration constant of electrical insulating materials. Res. Rep. Chiba Inst. Technol. (Sci. Technol.) 1971, 16, 22–31. [Google Scholar]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Criado, J.M. Kinetic analysis of DTG data from master curves. Thermochim. Acta 1978, 24, 186–189. [Google Scholar] [CrossRef]
- Pérez-Maqueda, L.A.; Ortega, A.; Criado, J.M. The use of master plots for discriminating the kinetic model of solid state reactions from a single constant-rate thermal analysis (CRTA) experiment. Thermochim. Acta 1996, 277, 165–173. [Google Scholar] [CrossRef]
- Das, P.; Tiwari, P. Thermal degradation kinetics of plastics and model selection. Thermochim. Acta 2017, 654, 191–202. [Google Scholar] [CrossRef]
- Málek, J. A computer program for kinetic analysis of non-isothermal thermoanalytical data. Thermochim. Acta 1989, 138, 337–346. [Google Scholar] [CrossRef]
- Málek, J. The kinetic analysis of non-isothermal data. Thermochim. Acta 1992, 200, 257–269. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Sbirrazzuoli, N. Mechanism and kinetics of epoxy-amine cure studied by differential scanning calorimetry. Macromolecules 1996, 29, 1867–1873. [Google Scholar] [CrossRef]
- Granado, L.; Sbirrazzuoli, N. Isoconversional computations for nonisothermal kinetic predictions. Thermochim. Acta 2021, 697, 2–7. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.A.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
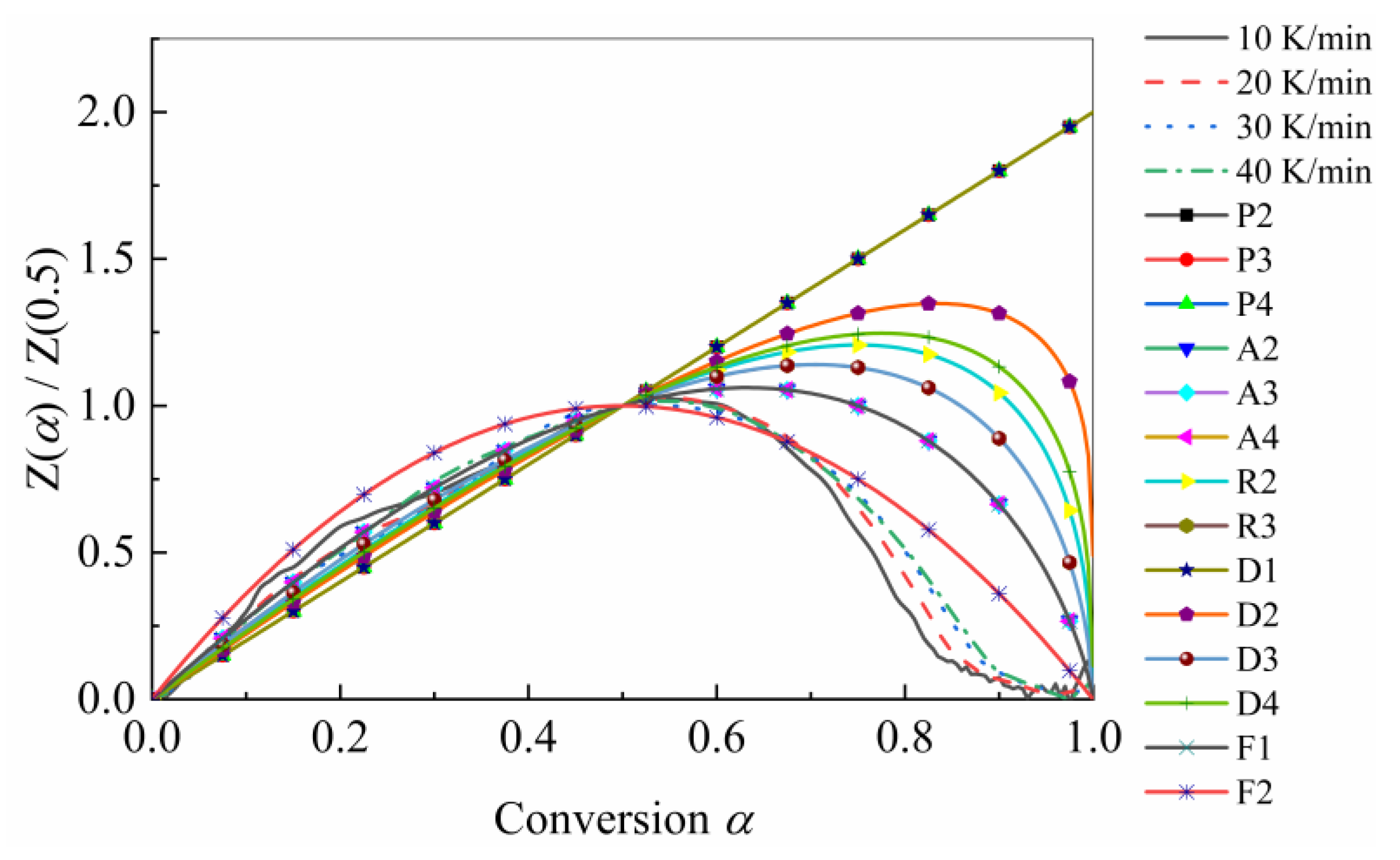



| Reaction Model | Model Code | f (α) | g (α) |
|---|---|---|---|
| Power law | P2 | ||
| Power law | P3 | ||
| Power law | P4 | ||
| Avrami–Erofeyev | A2 | ||
| Avrami–Erofeyev | A3 | ||
| Avrami–Erofeyev | A4 | ||
| Contracting cylinder | R2 | ||
| Contracting sphere | R3 | ||
| One-dimensional diffusion | D1 | ||
| Two-dimensional diffusion | D2 | ||
| Three-dimensional diffusion | D3 | ||
| Ginstling–Brounshtein | D4 | ||
| First-order | F1 | ||
| Second-order | F2 | ||
| Third-order | F3 |
| Method | Expression | ||
|---|---|---|---|
| Isoconversional methods | Differential | Friedman | |
| Integral | Flynn–Wall–Ozawa (FWO) | ||
| Kissinger–Akahira–Sunose (KAS) | |||
| Starink |
| Heating Rate | Isoconversional Method | (kJ/mol) | (min−1) | f (α) | |
|---|---|---|---|---|---|
| Equation (3) (Differential) | Equation (8) (Málek) | ||||
| 10 K/min | FWO | 146.4–232.7 | |||
| KAS | 143.1–232.6 | ||||
| Starink | 143.4–232.9 | ||||
| Friedman | 156.0–371.9 | ||||
| 20 K/min | FWO | 146.4–232.7 | |||
| KAS | 143.1–232.6 | ||||
| Starink | 143.4–232.9 | ||||
| Friedman | 156.0–371.9 | ||||
| 30 K/min | FWO | 146.4–232.7 | |||
| KAS | 143.1–232.6 | ||||
| Starink | 143.4–232.9 | ||||
| Friedman | 156.0–371.9 | ||||
| 40 K/min | FWO | 146.4–232.7 | |||
| KAS | 143.1–232.6 | ||||
| Starink | 143.4–232.9 | ||||
| Friedman | 156.0–371.9 | ||||
| Isoconversional Method | (kJ/mol) | (min−1) | f (α) |
|---|---|---|---|
| Equation (3) (Differential) | |||
| FWO | 169.80 | ||
| KAS | 166.94 | ||
| Starink | 167.27 | ||
| Friedman | 200.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, P.; Zhang, J.; Li, H.; Mou, H.; Feng, Z.; Xie, J. Pyrolysis Kinetics Analysis and Prediction for Carbon Fiber-Reinforced Epoxy Composites. Polymers 2023, 15, 4533. https://doi.org/10.3390/polym15234533
Xiao P, Zhang J, Li H, Mou H, Feng Z, Xie J. Pyrolysis Kinetics Analysis and Prediction for Carbon Fiber-Reinforced Epoxy Composites. Polymers. 2023; 15(23):4533. https://doi.org/10.3390/polym15234533
Chicago/Turabian StyleXiao, Pei, Jingyi Zhang, Han Li, Haolei Mou, Zhenyu Feng, and Jiang Xie. 2023. "Pyrolysis Kinetics Analysis and Prediction for Carbon Fiber-Reinforced Epoxy Composites" Polymers 15, no. 23: 4533. https://doi.org/10.3390/polym15234533
APA StyleXiao, P., Zhang, J., Li, H., Mou, H., Feng, Z., & Xie, J. (2023). Pyrolysis Kinetics Analysis and Prediction for Carbon Fiber-Reinforced Epoxy Composites. Polymers, 15(23), 4533. https://doi.org/10.3390/polym15234533





