Structure Strengthening Phenomena of Gluten Matrices under Different Stress Types
Abstract
:1. Introduction
2. Materials and Methods
2.1. Strain Hardening Index from Biaxial Extension
2.2. Strain Hardening from Shear
2.3. Statistical Analysis
3. Results and Discussion
3.1. Biaxial Extension
3.2. Shear Experiments
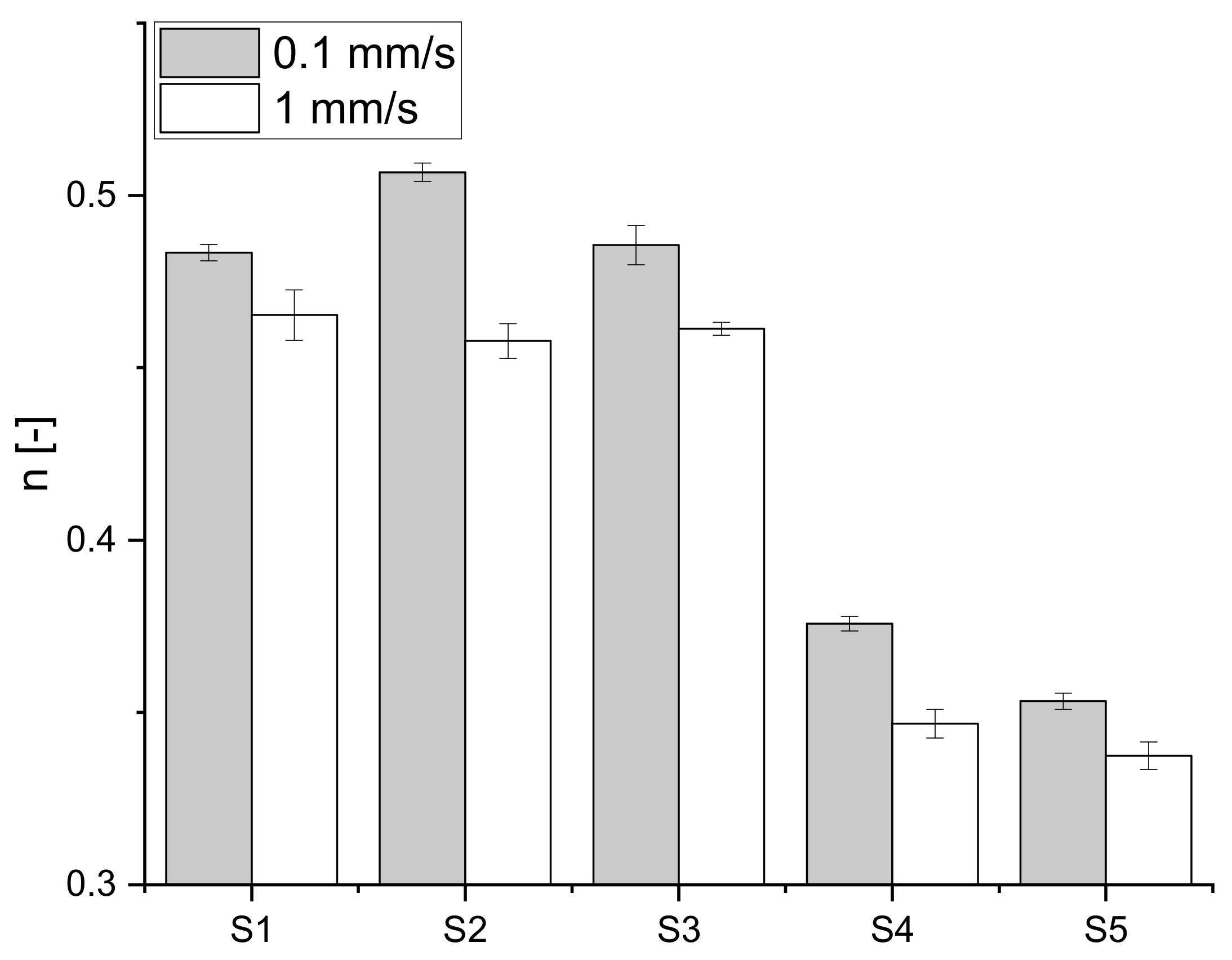
3.2.1. Dependency of the Strain Hardening Exponent on Deformation Speed
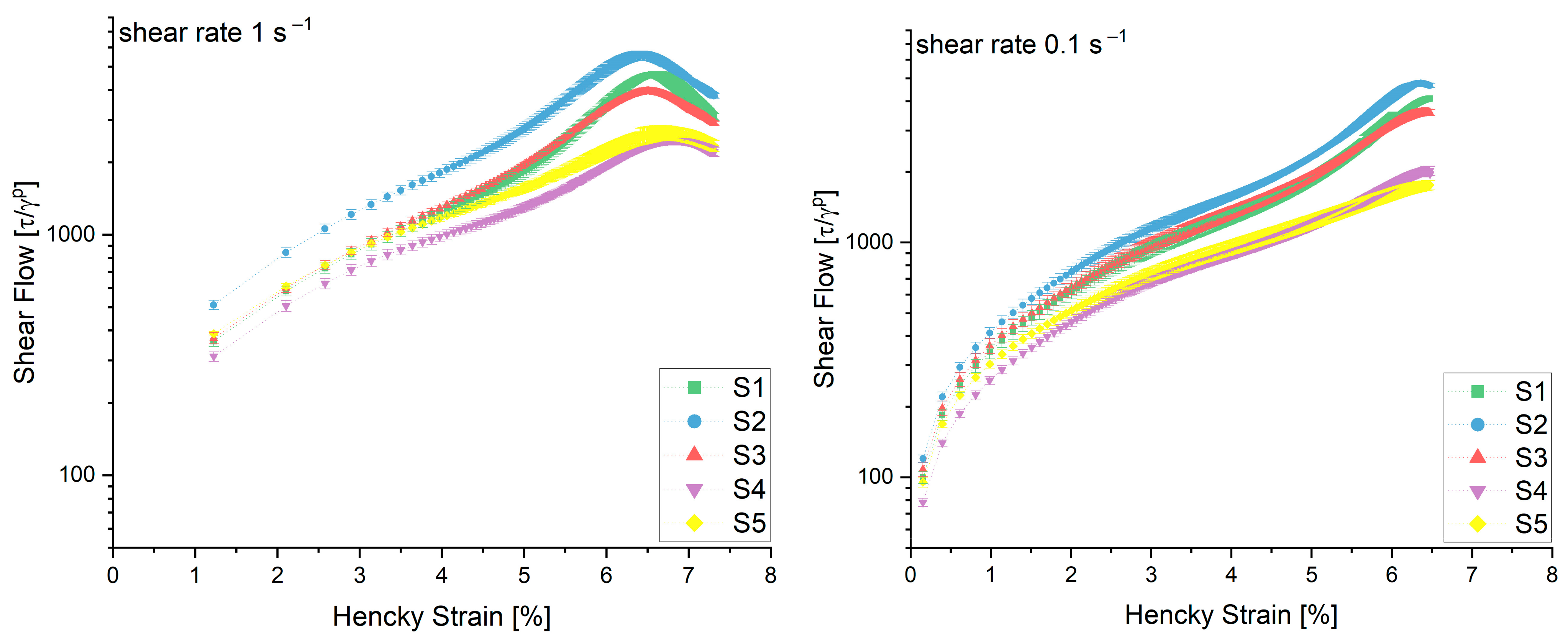
3.2.2. Increase in the Shear Flow Depending on Hencky Strain and Flour Composition
3.3. Correlation Analysis of Flour and Dough Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Delcour, J.A.; Joye, I.J.; Pareyt, B.; Wilderjans, E.; Brijs, K.; Lagrain, B. Wheat Gluten Functionality as a Quality Determinant in Cereal-Based Food Products. Annu. Rev. Food Sci. Technol. 2012, 3, 469–492. [Google Scholar] [CrossRef]
- Vensel, W.H.; Tanaka, C.K.; Altenbach, S.B. Protein composition of wheat gluten polymer fractions determined by quantitative two-dimensional gel electrophoresis and tandem mass spectrometry. Proteome Sci. 2014, 12, 8. [Google Scholar] [CrossRef] [PubMed]
- McCann, T.H.; Day, L. Effect of sodium chloride on gluten network formation, dough microstructure and rheology in relation to breadmaking. J. Cereal Sci. 2013, 57, 444–452. [Google Scholar] [CrossRef]
- Delcour, J.A.; Hoseney, R.C. Principles of Cereal Science and Technology, 3rd ed.; American Association of Cereal Chemists, Inc.: St. Paul, MN, USA, 1998. [Google Scholar]
- Van Vliet, T. Strain hardening as an indicator of bread-making performance: A review with discussion. J. Cereal Sci. 2008, 48, 1–9. [Google Scholar] [CrossRef]
- Mann, G.; Allen, H.; Morell, M.K.; Nath, Z.; Martin, P.; Oliver, J.; Cullis, B.; Smith, A. Comparison of small-scale and large-scale extensibility of dough produced from wheat flour. Aust. J. Agric. Res. 2005, 56, 1387–1394. [Google Scholar] [CrossRef]
- Van Vliet, T.; Janssen, A.; Bloksma, A.; Walstra, P. Strain Hardening of Dough as a Requirement for Gas Retention. J. Texture Stud. 1992, 23, 439–460. [Google Scholar] [CrossRef]
- Wikströma, K.; Bohlinb, L. Extensional flow studies of wheat Flour Dough. J. Cereal Sci. 1999, 29, 217–226. [Google Scholar]
- Stading, M.; Bohlin, L. Contraction flow measurements of extensional properties. Anu. Trans. Nord. Rheol. Soc. 2001, 8, 181–185. [Google Scholar]
- Amend, T.; Belitz, H.-D. Microstructural Studies of Gluten and a Hypothesis on Dough Formation. Food Struct. 1991, 10, 1. Available online: https://digitalcommons.usu.edu/foodmicrostructure/vol10/iss4/1 (accessed on 5 June 2023).
- Mohammed, M.A.P.; Tarleton, E.; Charalambides, M.N.; Williams, J.G. Mechanical characterization and micromechanical modeling of bread dough. J. Rheol. 2013, 57, 249–272. [Google Scholar] [CrossRef]
- Amemiya, J.; Menjivar, J. Comparison of small and large deformation measurements to characterize the rheology of wheat flour doughs. J. Food Eng. 1992, 16, 91–108. [Google Scholar] [CrossRef]
- Meerts, M.; Cardinaels, R.; Oosterlinck, F.; Courtin, C.M.; Moldenaers, P. The Interplay Between the Main Flour Constituents in the Rheological Behaviour of Wheat Flour Dough. Food Bioprocess Technol. 2016, 10, 249–265. [Google Scholar] [CrossRef]
- Kartsovnik, V.I.; Volchenkov, D. Elastic Entropic Forces in Polymer Deformation. Entropy 2022, 24, 1260. [Google Scholar] [CrossRef] [PubMed]
- Meerts, M.; Cardinaels, R.; Oosterlinck, F.; Courtin, C.M.; Moldenaers, P. Contributions of the main flour constituents to dough rheology, and implications for dough quality and its assessment. Adv. Mater. TechConnect Briefs 2016, 3, 23–26. [Google Scholar]
- Vidal, L.M.; Braun, A.; Jekle, M.; Becker, T. Micro-Scale Shear Kneading—Gluten Network Development under Multiple Stress–Relaxation Steps and Evaluation via Multiwave Rheology. Polymers 2022, 14, 846. [Google Scholar] [CrossRef] [PubMed]
- Tietze, S.; Jekle, M.; Becker, T. Advances in the development of wheat dough and bread by means of shearing. J. Food Eng. 2019, 247, 136–143. [Google Scholar] [CrossRef]
- Vidal, L.M.; Wittkamp, T.; Benz, J.P.; Jekle, M.; Becker, T. A dynamic micro-scale dough foaming and baking analysis—Comparison of dough inflation based on different leavening agents. Food Res. Int. 2023, 164, 112342. [Google Scholar] [CrossRef]
- Vidal, L.M.; Ewigmann, H.; Schuster, C.; Alpers, T.; Scherf, K.A.; Jekle, M.; Becker, T. Microscopic analysis of gluten network development under shear load—Combining confocal laser scanning microscopy with rheometry. J. Texture Stud. 2023, 1–10. [Google Scholar] [CrossRef]
- Chatraei, S.; Macosko, C.W.; Winter, H.H. Lubricated Squeezing Flow: A New Biaxial Extensional Rheometer. J. Rheol. 1981, 25, 433–443. [Google Scholar] [CrossRef]
- Rouillé, J.; Della Valle, G.; Lefebvre, J.; Sliwinski, E.; Vanvliet, T. Shear and extensional properties of bread doughs affected by their minor components. J. Cereal Sci. 2005, 42, 45–57. [Google Scholar] [CrossRef]
- Kokelaar, J.; van Vliet, T.; Prins, A. Strain Hardening Properties and Extensibility of Flour and Gluten Doughs in Relation to Breadmaking Performance. J. Cereal Sci. 1996, 24, 199–214. [Google Scholar] [CrossRef]
- Alpers, T.; Tauscher, V.; Steglich, T.; Becker, T.; Jekle, M. The Self-Enforcing Starch–Gluten System—Strain–Dependent Effects of Yeast Metabolites on the Polymeric Matrix. Polymers 2020, 13, 30. [Google Scholar] [CrossRef] [PubMed]
- Jødal, A.-S.S.; Larsen, K.L. Investigation of the relationships between the alveograph parameters. Sci. Rep. 2021, 11, 5349. [Google Scholar] [CrossRef] [PubMed]
- Kitoko, V.; Keentok, M.; Tanner, R.I. Study of shear and elongational flow of solidifying polypropylene melt for low deformation rates. Korea Aust. Rheol. J. 2003, 15, 63–73. [Google Scholar]
- Tanner, R.I.; Qi, F.; Dai, S.-C. Bread dough rheology and recoil: I. Rheology. J. Non-Newton. Fluid Mech. 2008, 148, 33–40. [Google Scholar] [CrossRef]
- Winter, H.H.; Mours, M. Rheology of Polymers Near Liquid-Solid Transitions. Adv. Polym. Sci. 1997, 134, 164–234. [Google Scholar] [CrossRef]
- Pipkin, A.C. Lectures on Viscoelasticity Theory; Springer Science and Business Media LLC: Dordrecht, The Netherlands, 1986; ISBN 9780387097237. [Google Scholar]
- Dobraszczyk, B.J.; Smewing, J.; Albertini, M.; Maesmans, G.; Schofield, J.D. Extensional Rheology and Stability of Gas Cell Walls in Bread Doughs at Elevated Temperatures in Relation to Breadmaking Performance. Cereal Chem. 2003, 80, 218–224. [Google Scholar] [CrossRef]
- Alpers, T.; Becker, T.; Jekle, M. Strain-dependent assessment of dough’s polymer structure and functionality during the baking process. PLoS ONE 2023, 18, e0282670. [Google Scholar] [CrossRef]
- Nicolle, S.; Vezin, P.; Palierne, J.-F. A strain-hardening bi-power law for the nonlinear behaviour of biological soft tissues. J. Biomech. 2010, 43, 927–932. [Google Scholar] [CrossRef]
- Lindborg, K.M.; Trägårdh, C.; Eliasson, A.-C.; Dejmek, P. Time-Resolved Shear Viscosity of Wheat Flour Doughs—Effect of Mixing, Shear Rate, and Resting on the Viscosity of Doughs of Different Flours. Cereal Chem. 1997, 74, 49–55. [Google Scholar] [CrossRef]
- Bonilla, J.C.; Erturk, M.Y.; Schaber, J.A.; Kokini, J.L. Distribution and function of LMW glutenins, HMW glutenins, and gliadins in wheat doughs analyzed with ‘in situ’ detection and quantitative imaging techniques. J. Cereal Sci. 2020, 93, 102931. [Google Scholar] [CrossRef]
- Bonilla, J.C.; Schaber, J.A.; Bhunia, A.K.; Kokini, J.L. Mixing dynamics and molecular interactions of HMW glutenins, LMW glutenins, and gliadins analyzed by fluorescent co-localization and protein network quantification. J. Cereal Sci. 2019, 89, 102792. [Google Scholar] [CrossRef]
- Jankiewicz, M. The Protein Complex of Bread Dough as an Interacting System. Mol. Nutr. Food Res. 1975, 19, 775–783. [Google Scholar] [CrossRef]
- Gupta, R.; Shepherd, K.; MacRitchie, F. Genetic control and biochemical properties of some high molecular weight albumins in bread wheat. J. Cereal Sci. 1991, 13, 221–235. [Google Scholar] [CrossRef]

| Flour | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| Protein (g/100g) | 14.86 ± 0.06 | 14.29 ± 0.03 | 14.22 ± 0.01 | 11.79 ± 0.03 | 11.77 ± 0.05 |
| ω5-Gliadin | 3.9 | 3.6 | 3.9 | 3.9 | 3.3 |
| ω1,2-Gliadin | 3.8 | 3.8 | 4 | 3.9 | 3.5 |
| α-Gliadin | 31.2 | 33 | 32.2 | 32.3 | 29.6 |
| γ-Gliadin | 20.8 | 20.4 | 20.6 | 22.1 | 21.4 |
| HMW-GS | 8.6 | 8.6 | 8.1 | 5.9 | 6.6 |
| LMW-GS | 19.9 | 19.3 | 18.7 | 17.5 | 19 |
| DDT | Network Connectivity | TNoJ | Peak Shear Flow 0.1 1/s | Peak Shear Flow 1 1/s | K 0.1 mm/s | n 0.1 mm/s | K 1 mm/s | n 1 mm/s | SHI 0.1 mm/s | SHI 1 mm/s | Gliadine | Glutenine | Albumine /Globuline | Omega 5 | Omega 1,2 | Alpha | Gamma | Omega b | HMW | LMW | Volume Increase in Baking Trials | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DDT | 1 | |||||||||||||||||||||
| Network Connectivity | 0.19 | 1 | ||||||||||||||||||||
| TNoJ | 0.90 | 0.24 | 1 | |||||||||||||||||||
| Peak Shear Flow 0.1 1/s | 0.63 | 0.35 | 0.88 | 1 | ||||||||||||||||||
| Peak Shear Flow 1 1/s | 0.54 | 0.48 | 0.82 | 0.98 | 1 | |||||||||||||||||
| K 0.1 mm/s | −0.43 | 0.05 | −0.71 | −0.88 | −0.82 | 1 | ||||||||||||||||
| n 0.1 mm/s | 0.77 | 0.18 | 0.85 | 0.86 | 0.79 | −0.84 | 1 | |||||||||||||||
| K 1 mm/s | −0.94 | −0.07 | −0.94 | −0.78 | −0.68 | 0.70 | −0.92 | 1 | ||||||||||||||
| n 1 mm/s | 0.84 | 0.30 | 0.98 | 0.95 | 0.90 | −0.80 | 0.91 | −0.92 | 1 | |||||||||||||
| SHI 0.1 mm/s | 0.90 | 0.02 | 0.90 | 0.78 | 0.67 | −0.75 | 0.95 | −0.99 | 0.90 | 1 | ||||||||||||
| SHI 1 mm/s | 0.51 | 0.12 | 0.70 | 0.87 | 0.82 | −0.94 | 0.94 | −0.75 | 0.81 | 0.81 | 1 | |||||||||||
| Gliadine | −0.06 | −0.77 | 0.09 | 0.21 | 0.09 | −0.63 | 0.32 | −0.23 | 0.14 | 0.32 | 0.49 | 1 | ||||||||||
| Glutenine | 0.76 | 0.69 | 0.87 | 0.86 | 0.87 | −0.53 | 0.75 | −0.74 | 0.89 | 0.69 | 0.62 | −0.30 | 1 | |||||||||
| Albumine/Globuline | −0.67 | −0.09 | −0.88 | −0.95 | −0.89 | 0.96 | −0.93 | 0.86 | −0.94 | −0.88 | −0.94 | −0.45 | −0.72 | 1 | ||||||||
| Omega 5 | 0.51 | −0.60 | 0.49 | 0.39 | 0.23 | −0.67 | 0.68 | −0.70 | 0.49 | 0.76 | 0.65 | 0.80 | 0.08 | −0.65 | 1 | |||||||
| Omega 1,2 | 0.48 | −0.68 | 0.54 | 0.39 | 0.23 | −0.61 | 0.48 | −0.62 | 0.48 | 0.65 | 0.44 | 0.76 | 0.05 | −0.61 | 0.87 | 1 | ||||||
| Alpha | 0.10 | −0.46 | 0.40 | 0.58 | 0.51 | −0.87 | 0.51 | −0.40 | 0.46 | 0.47 | 0.69 | 0.88 | 0.09 | −0.72 | 0.69 | 0.75 | 1 | |||||
| Gamma | −0.65 | −0.50 | −0.87 | −0.88 | −0.89 | 0.59 | −0.60 | 0.65 | −0.87 | −0.59 | −0.53 | 0.15 | −0.90 | 0.74 | −0.06 | −0.25 | −0.30 | 1 | ||||
| Omega b | 0.96 | 0.25 | 0.97 | 0.82 | 0.74 | −0.64 | 0.89 | −0.98 | 0.95 | 0.95 | 0.70 | 0.05 | 0.85 | −0.84 | 0.54 | 0.50 | 0.29 | −0.77 | 1 | |||
| HMW | 0.78 | 0.52 | 0.94 | 0.94 | 0.94 | −0.69 | 0.81 | −0.81 | 0.97 | 0.78 | 0.72 | −0.08 | 0.97 | −0.85 | 0.24 | 0.27 | 0.31 | −0.94 | 0.90 | 1 | ||
| LMW | 0.61 | 0.89 | 0.64 | 0.63 | 0.69 | −0.23 | 0.54 | −0.52 | 0.67 | 0.46 | 0.39 | −0.60 | 0.93 | −0.44 | −0.22 | −0.30 | −0.26 | −0.74 | 0.66 | 0.81 | 1 | |
| Volume Increase in Baking Trials | 0.49 | −0.13 | 0.78 | 0.84 | 0.77 | −0.88 | 0.89 | −0.66 | 0.65 | 0.66 | 0.70 | 0.53 | 0.52 | −0.88 | 0.55 | 0.74 | 0.83 | −0.75 | 0.65 | 0.71 | 0.18 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidal, L.M.; Alpers, T.; Becker, T. Structure Strengthening Phenomena of Gluten Matrices under Different Stress Types. Polymers 2023, 15, 4491. https://doi.org/10.3390/polym15234491
Vidal LM, Alpers T, Becker T. Structure Strengthening Phenomena of Gluten Matrices under Different Stress Types. Polymers. 2023; 15(23):4491. https://doi.org/10.3390/polym15234491
Chicago/Turabian StyleVidal, Leonhard Maria, Thekla Alpers, and Thomas Becker. 2023. "Structure Strengthening Phenomena of Gluten Matrices under Different Stress Types" Polymers 15, no. 23: 4491. https://doi.org/10.3390/polym15234491
APA StyleVidal, L. M., Alpers, T., & Becker, T. (2023). Structure Strengthening Phenomena of Gluten Matrices under Different Stress Types. Polymers, 15(23), 4491. https://doi.org/10.3390/polym15234491







