Coarse-Grained Molecular Dynamics Simulation of Polycarbonate Deformation: Dependence of Mechanical Performance by the Effect of Spatial Distribution and Topological Constraints
Abstract
1. Introduction
2. Methodology
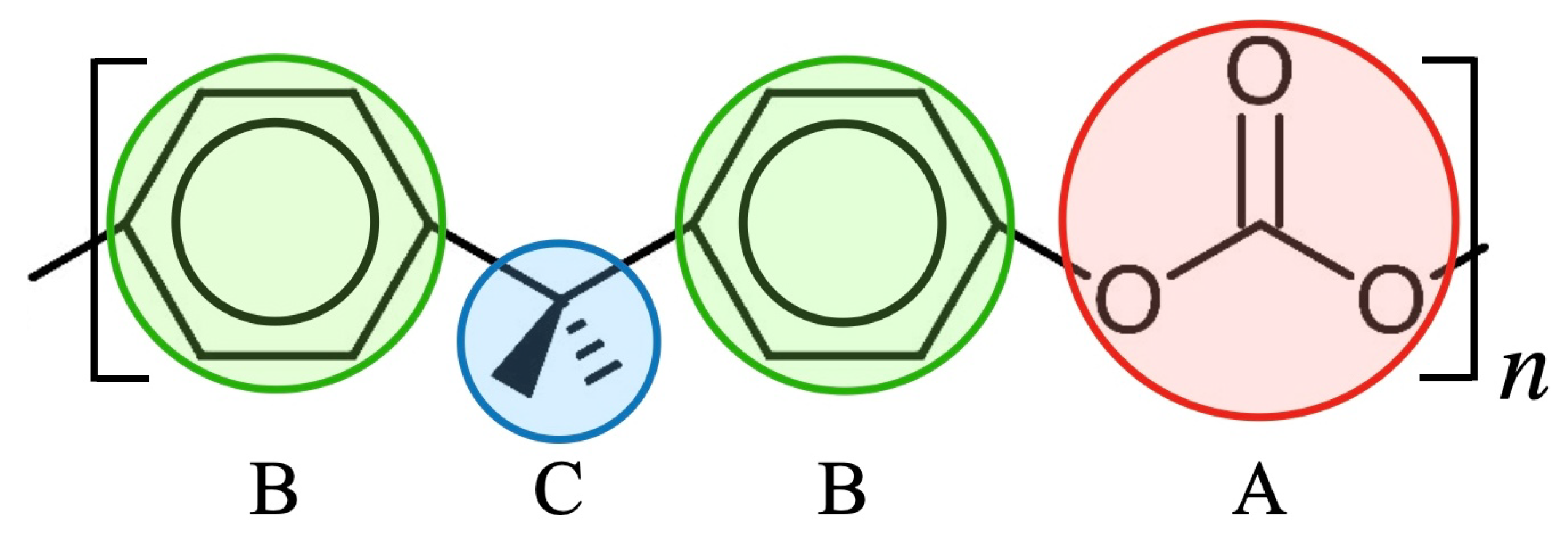
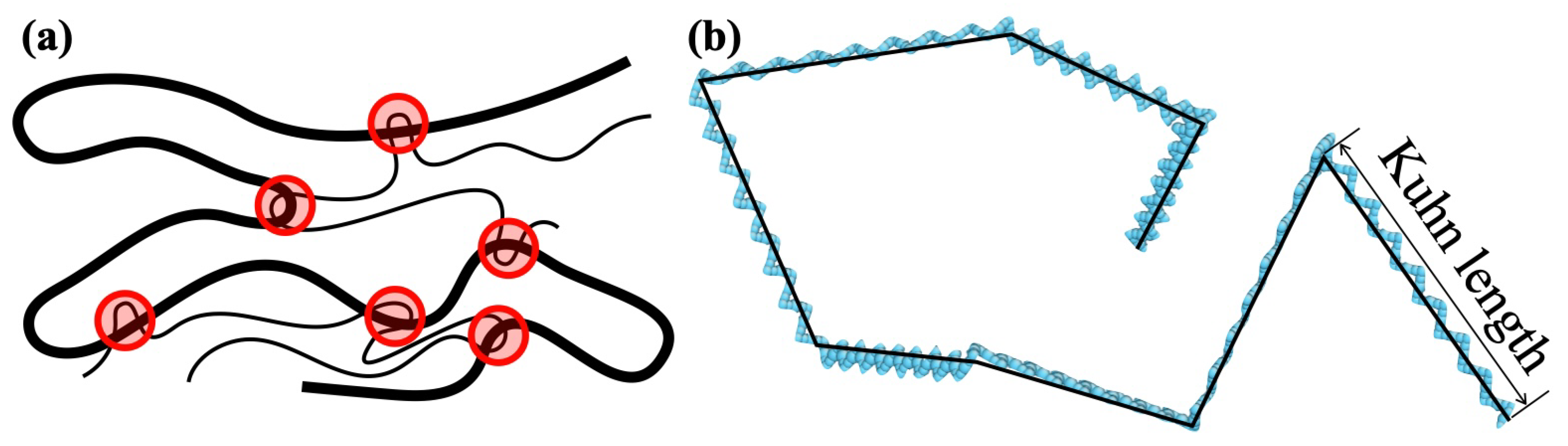
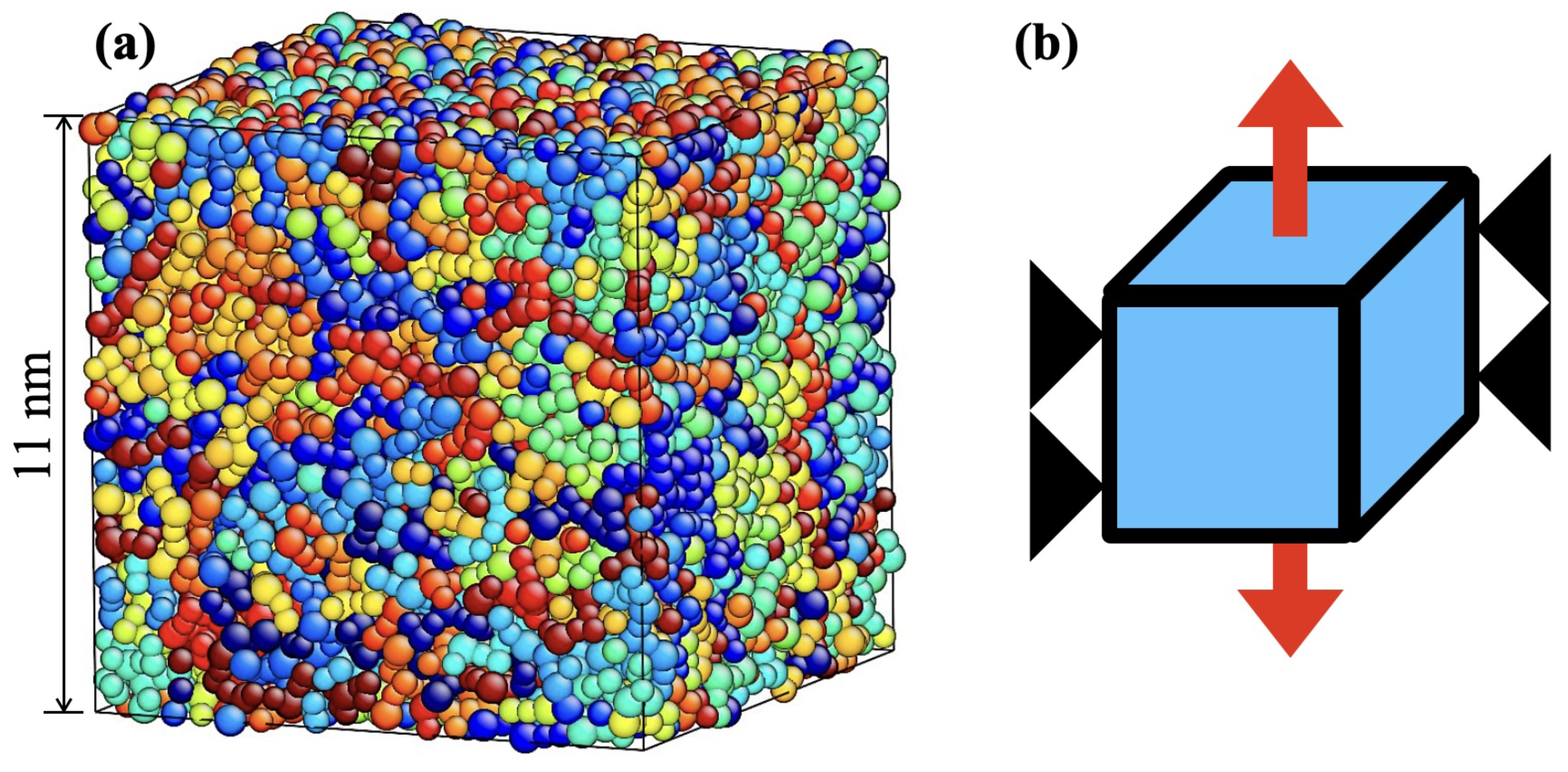
2.1. Coarse-Grained Particle Model
2.2. Initial Structure Preparation
2.3. Conditions for Deformation Analysis
3. Results and Discussion
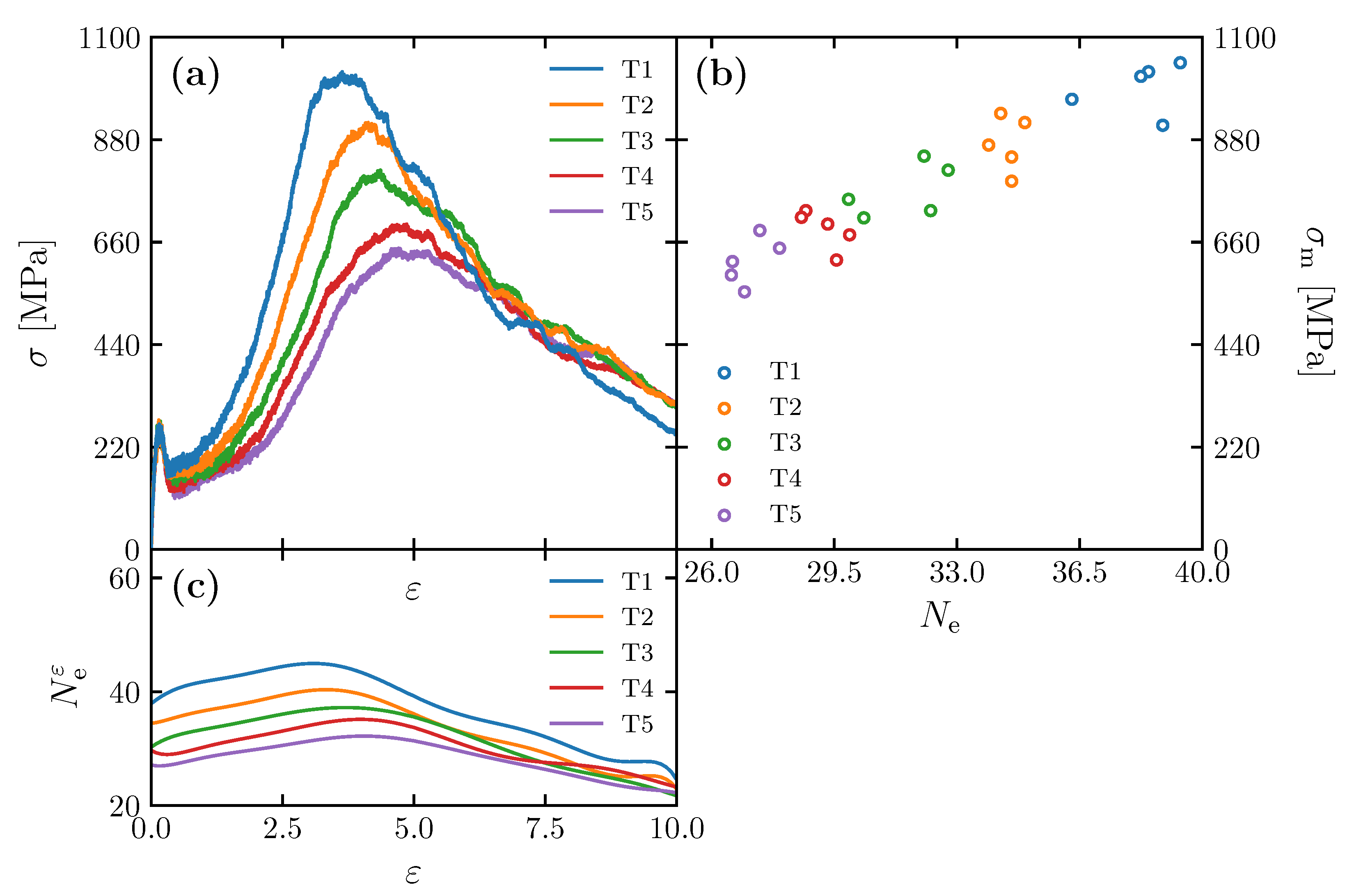
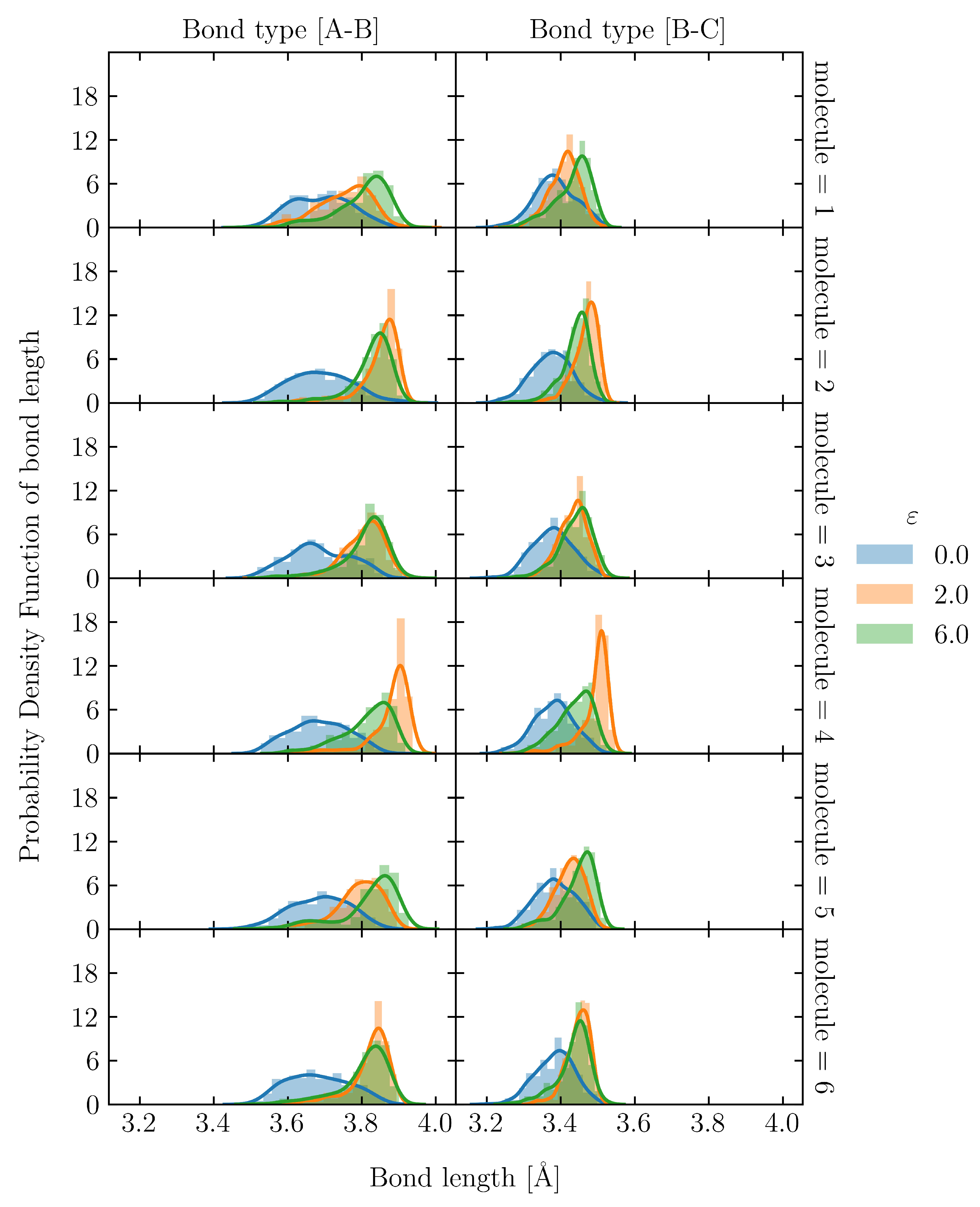
3.1. Effect of the Number of Entanglement Points per Molecule on Maximum Stress
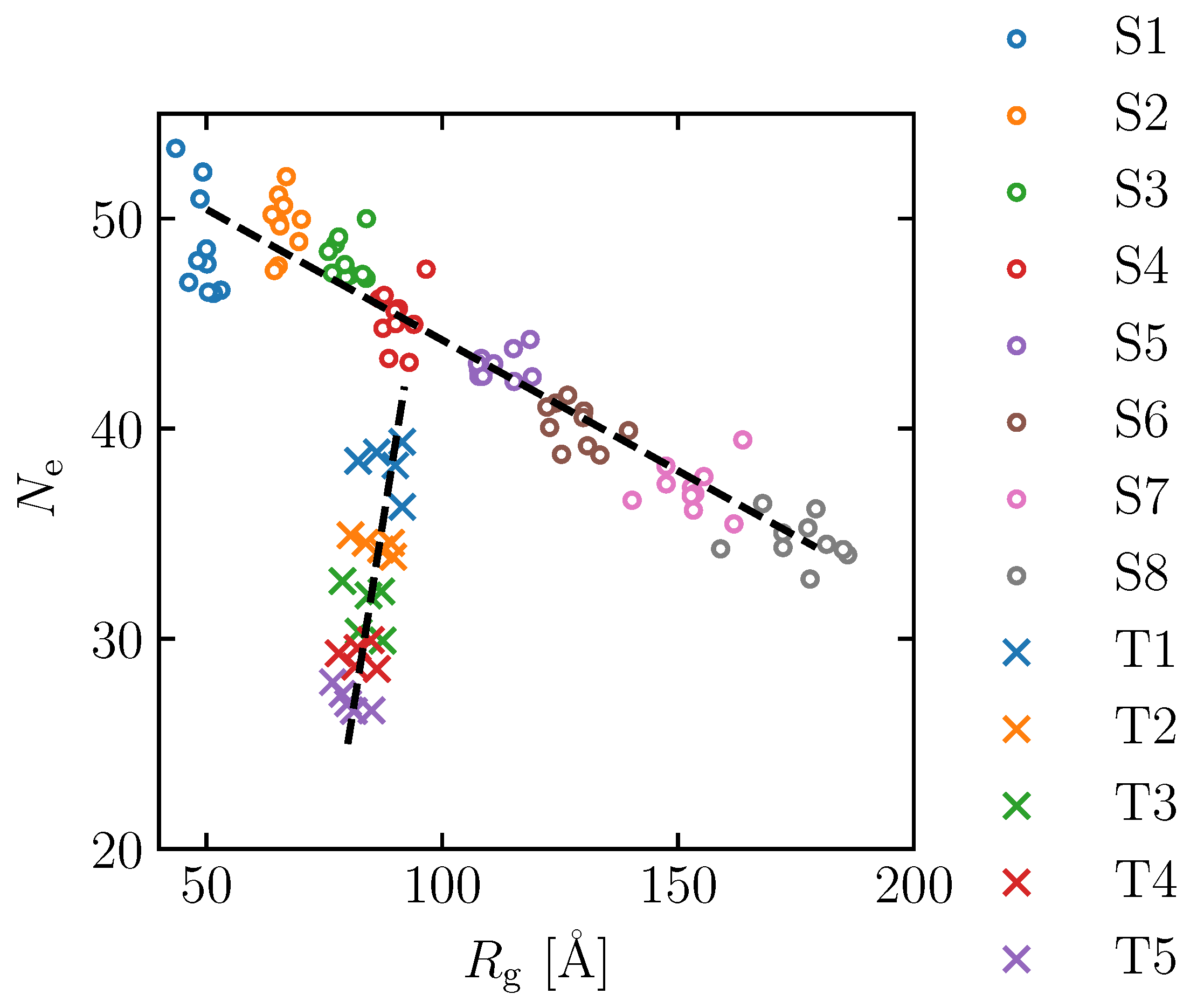
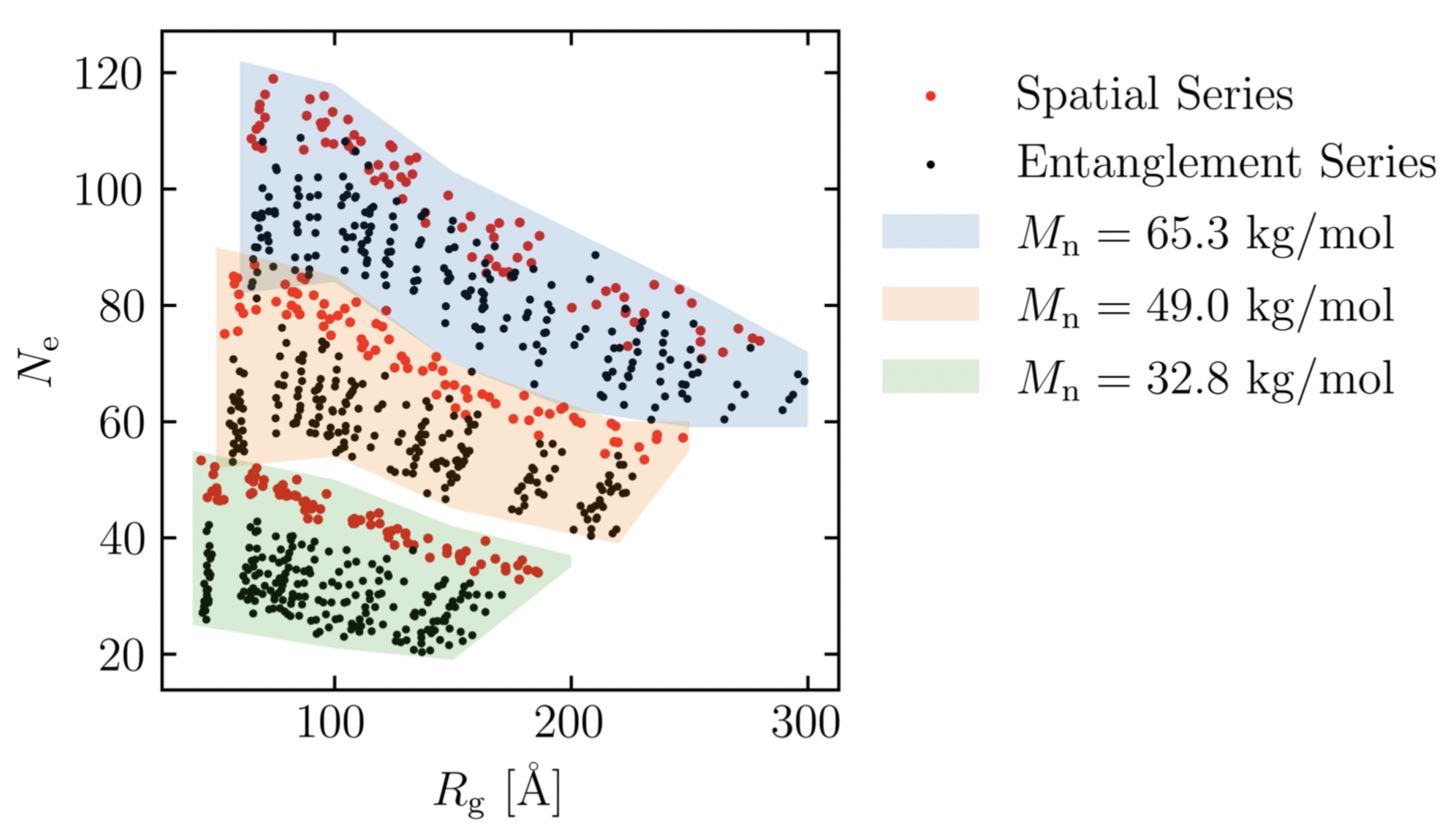
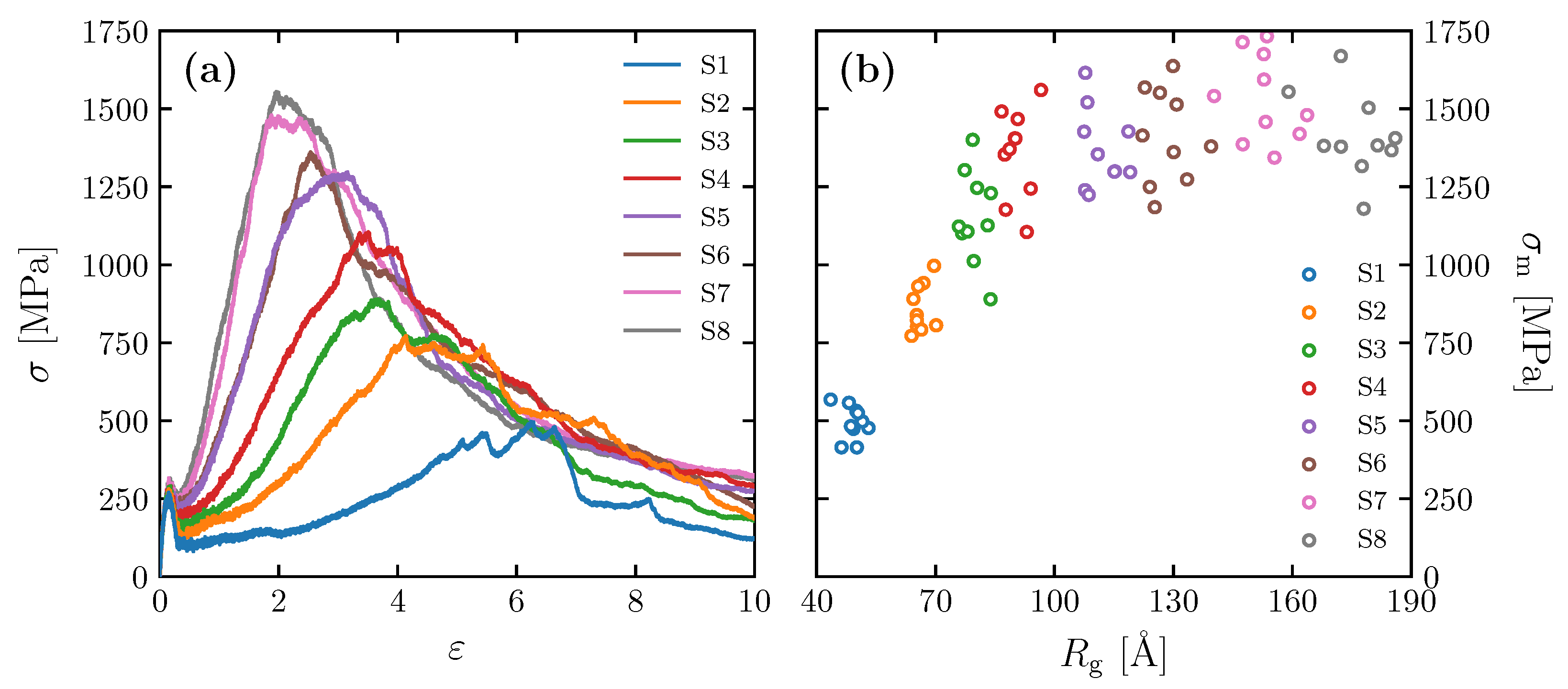
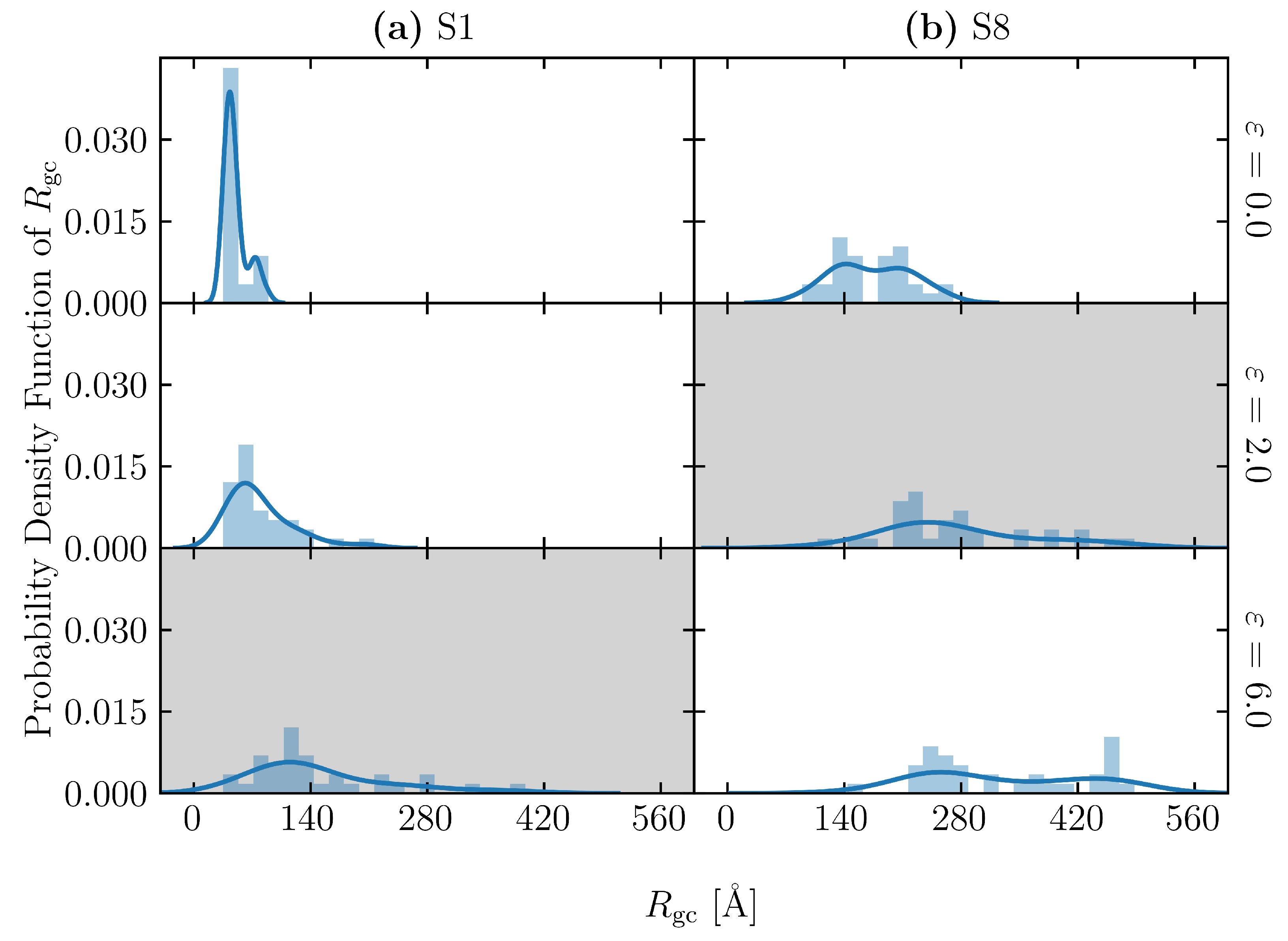
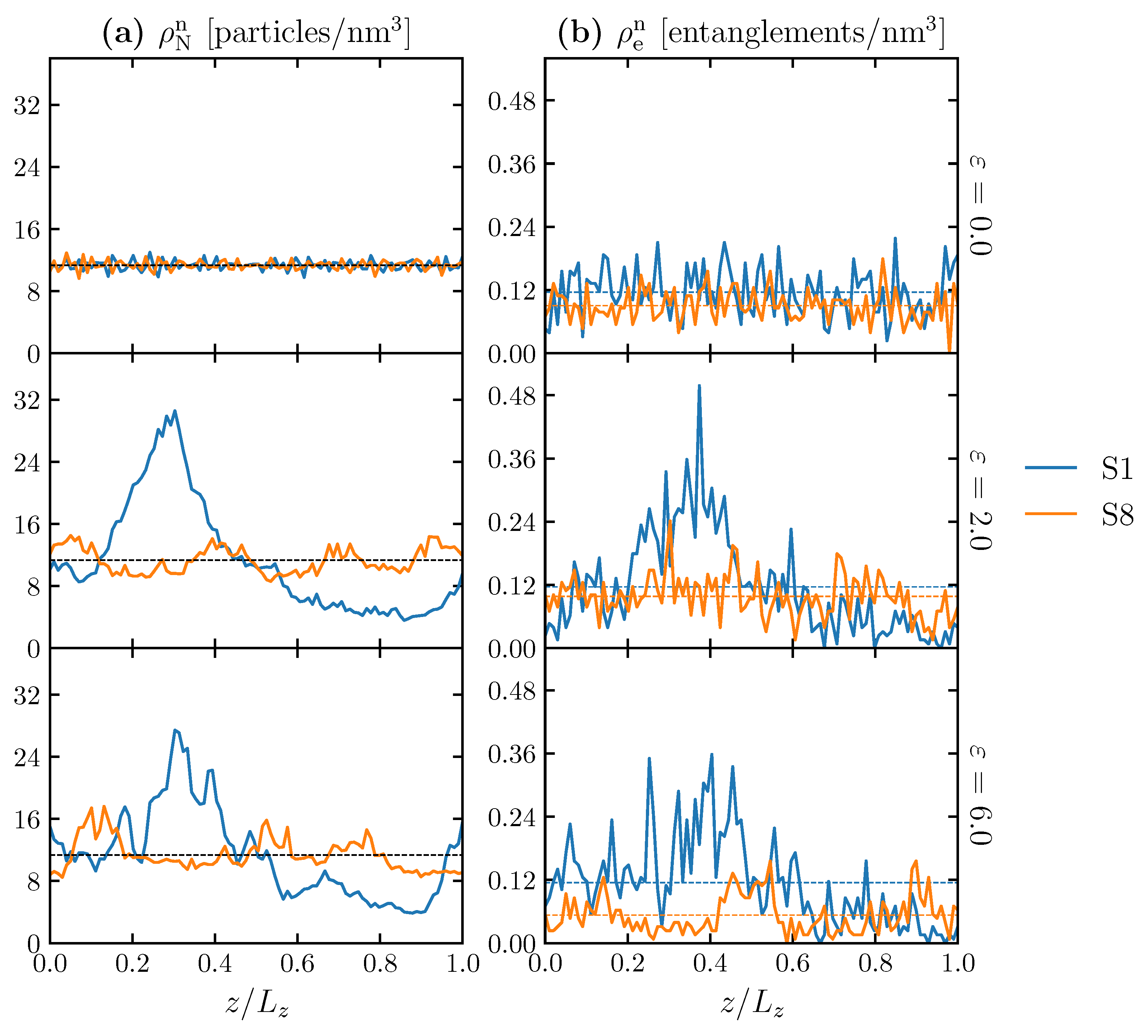
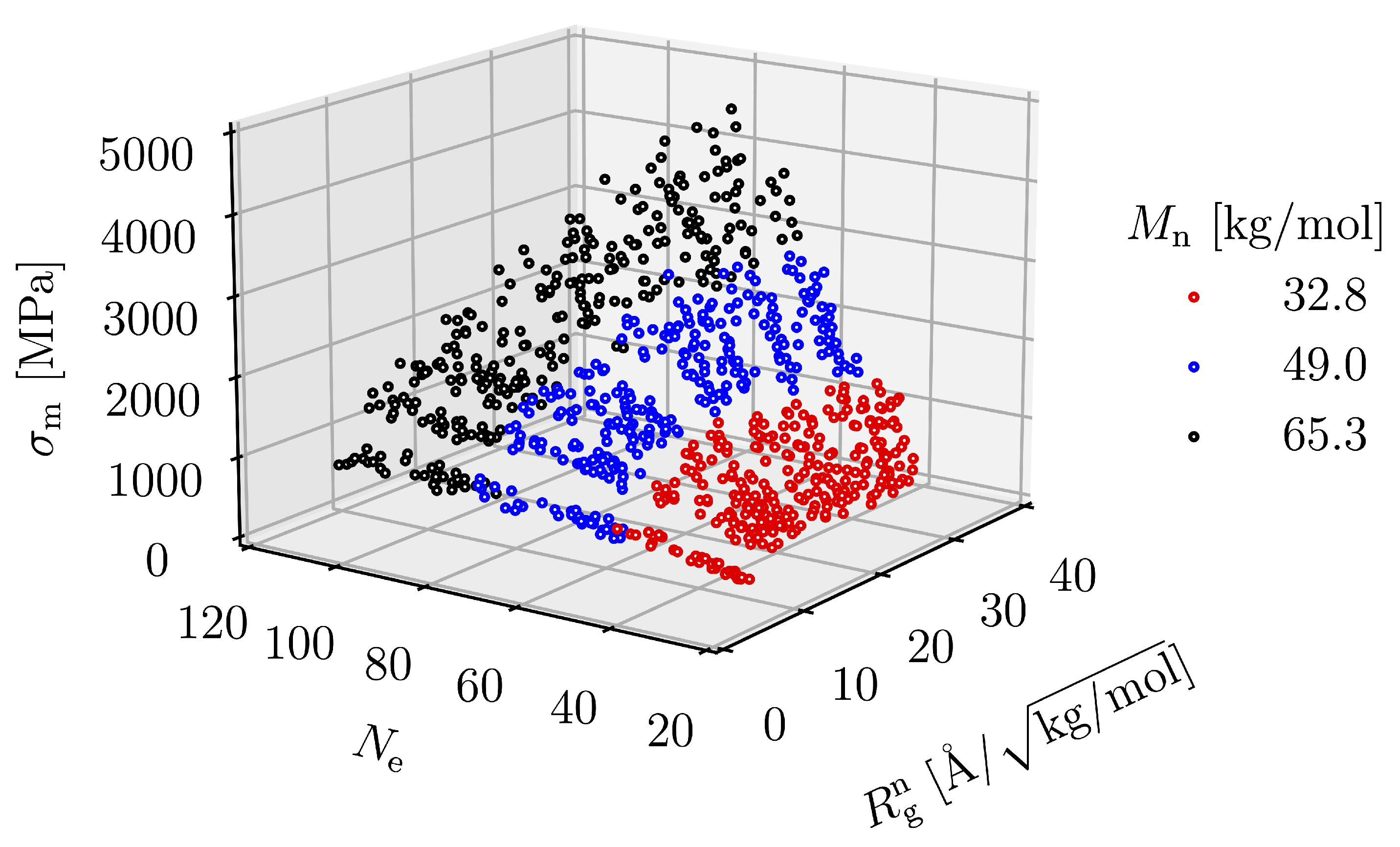
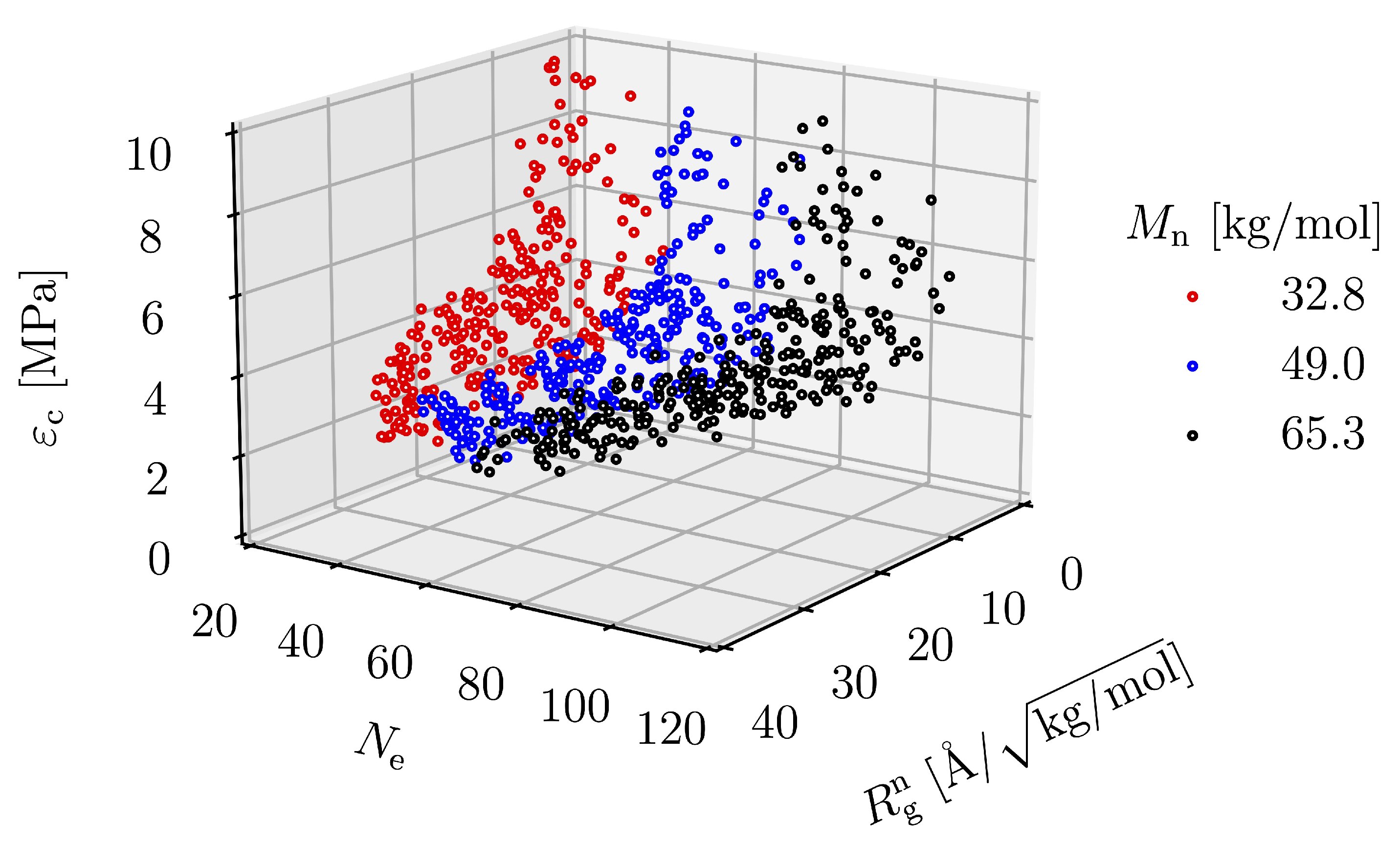
3.2. Effect of Spatial Distribution of Molecules on Maximum Stress
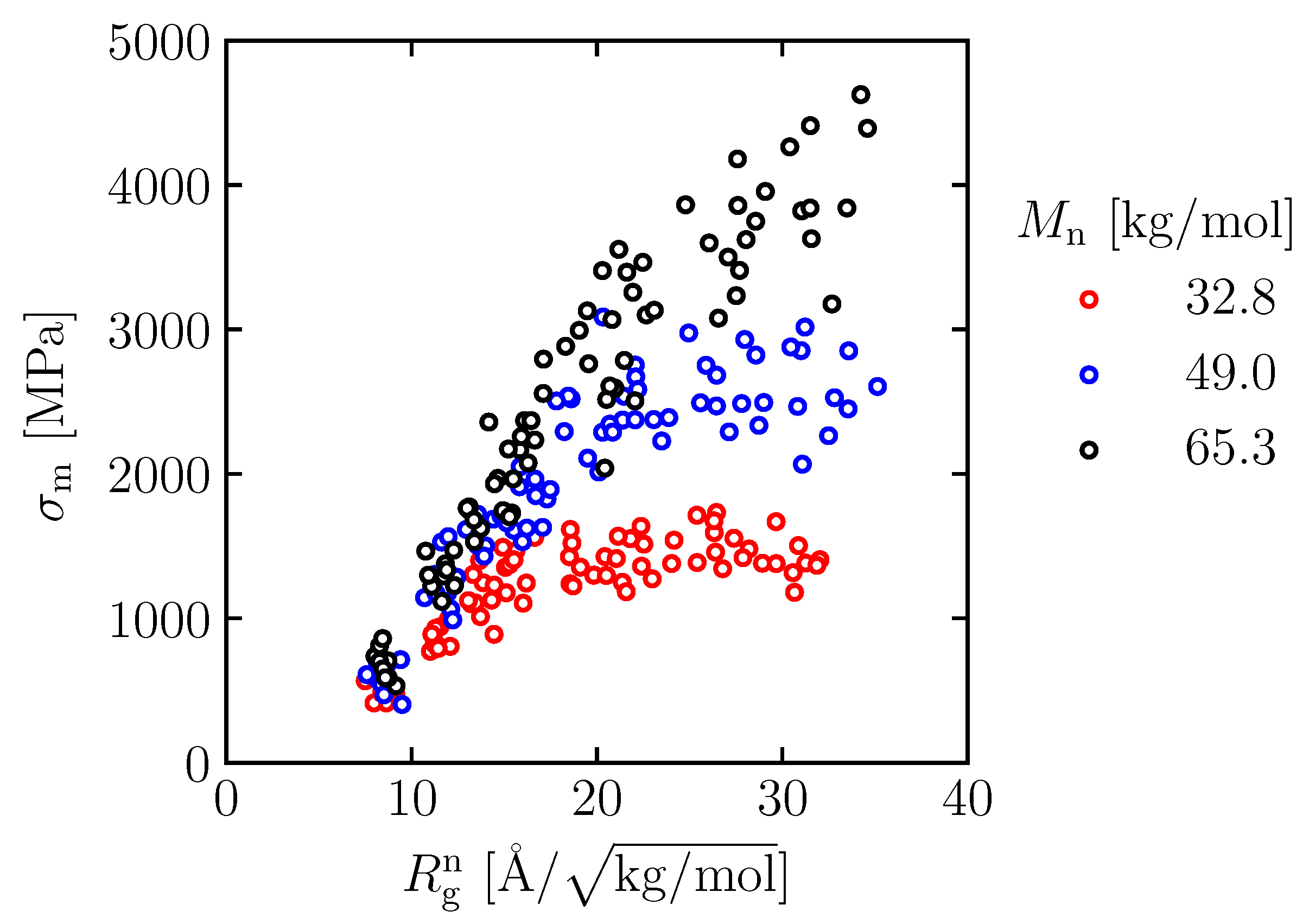
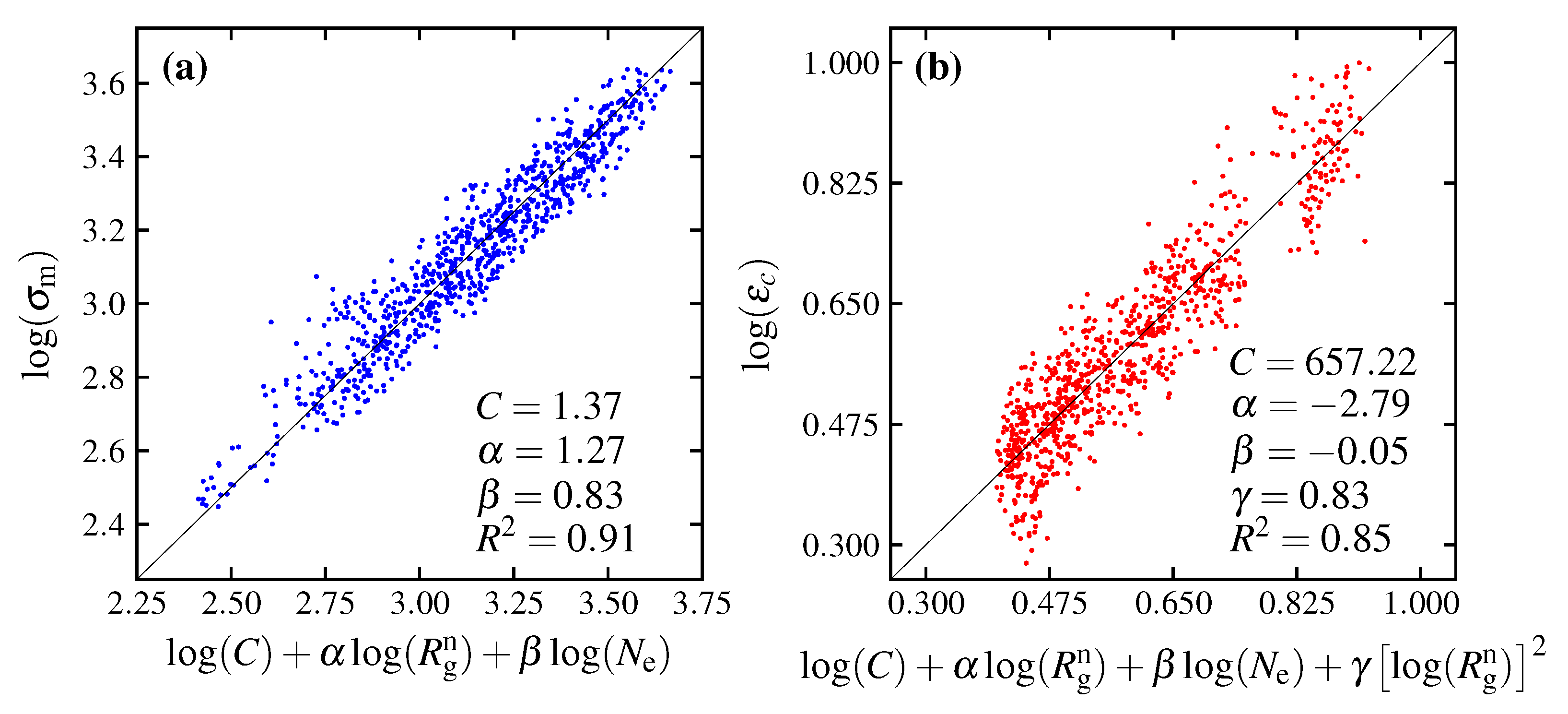
3.3. Equation Relating Number of Entanglement and Radius of Gyration to Maximum Stress
3.4. Equation Relating Number of Entanglement and Radius of Gyration to Critical Strain
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Davis, A.; Golden, J.H. Stability of Polycarbonate. J. Macromol. Sci. Part C Polym. Rev. 1969, 3, 49–68. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, X.; Song, M.; Wu, S. A study on the relationship between polycarbonate microstructure and performance as determined by a combined experimental and molecular dynamics simulation method. e-Polymers 2014, 14, 407–415. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, Y. Introduction. In Mechanical Properties of Polycarbonate: Experiment and Modeling for Aeronautical and Aerospace Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. xi–xxvii. ISBN 9781785483134. [Google Scholar] [CrossRef]
- Inoue, M.; Ito, N.; Fukami, T.; Takagi, M. Anisotropy in Mechanical Properties of Injection Molded Thermoplastics. J. Soc. Mater. Sci. Jpn. 1967, 16, 716–722. [Google Scholar] [CrossRef]
- Wu, S. Chain structure, phase morphology, and toughness relationships in polymers and blends. Polym. Eng. Sci. 1990, 30, 753–761. [Google Scholar] [CrossRef]
- Fujimoto, K.; Tang, Z.; Shinoda, W.; Okazaki, S. All-atom molecular dynamics study of impact fracture of glassy polymers. I: Molecular mechanism of brittleness of PMMA and ductility of PC. Polymer 2019, 178, 121570. [Google Scholar] [CrossRef]
- Umeno, Y.; Kubo, A.; Albina, J.-M. Coarse-grained molecular dynamics simulation of deformation and fracture in polycarbonate: Effect of molar mass and entanglement. Theor. Appl. Fract. Mech. 2020, 109, 102699. [Google Scholar] [CrossRef]
- Pitman, G.L.; Ward, I.M. Effect of molecular weight on craze shape and fracture toughness in polycarbonate. Polymer 1979, 20, 896–902. [Google Scholar] [CrossRef]
- Tang, Z.; Fujimoto, K.; Okazaki, S. All-atom molecular dynamics study of impact fracture of glassy polymers. II: Microscopic origins of stresses in elasticity, yielding, and strain hardening. Polymer 2020, 207, 122908. [Google Scholar] [CrossRef]
- Baschnagel, J.; Binder, K.; Paul, W.; Laso, M.; Suter, U.W.; Batoulis, I.; Jilge, W.; Bürger, T. On the construction of coarse-grained models for linear flexible polymer chains: Distribution functions for groups of consecutive monomers. J. Chem. Phys. 1991, 95, 6014–6025. [Google Scholar] [CrossRef]
- Kubo, A.; Albina, J.-M.; Umeno, Y. Construction of master yield stress curves for polycarbonate: A coarse-grained molecular dynamics study. Polymer 2019, 177, 84–90. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive Path Networks Generated by Annealing and Geometrical Methods: Insights into Differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two- and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Karayiannis, N.; Kröger, M. Combined Molecular Algorithms for the Generation, Equilibration and Topological Analysis of Entangled Polymers: Methodology and Performance. Int. J. Mol. Sci. 2009, 10, 5054–5089. [Google Scholar] [CrossRef] [PubMed]
- Benhamou, M.; Mahoux, G. Long polymers in good solvent: ϵ-expansion of the ratio of the radius of gyration to the end to end distance. J. Phys. Lett. 1985, 46, 689–693. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Li, J. AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. Eng. 2003, 11, 173–177. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Mahajan, D.K.; Singh, B.; Basu, S. Void nucleation and disentanglement in glassy amorphous polymers. Phys. Rev. E. 2010, 82, 011803. [Google Scholar] [CrossRef]
- Makke, A.; Perez, M.; Rottler, J.; Lame, O.; Barrat, J.-L. Predictors of Cavitation in Glassy Polymers under Tensile Strain: A Coarse-Grained Molecular Dynamics Investigation. Macromol. Theory Simul. 2011, 20, 1022–1344. [Google Scholar] [CrossRef]
- Jatin; Sudarkodi, V.; Basu, S. Investigations into the origins of plastic flow and strain hardening in amorphous glassy polymers. Int. J. Plast. 2014, 56, 139–155. [Google Scholar] [CrossRef]
- Jiang, Y.; Luo, B.; Cheng, X. Enhanced Thermal Stability of Thermoplastic Polymer Nanostructures for Nanoimprint Lithography. Materials 2019, 12, 545. [Google Scholar] [CrossRef] [PubMed]

| Kuhn Segment Length (Monomers) | [Å] | ||
|---|---|---|---|
| S1 (2) | 51.52 | 45.94 | 5.37 |
| S2 (4) | 64.03 | 47.94 | 5.30 |
| S3 (6) | 83.88 | 46.16 | 6.79 |
| S4 (8) | 93.05 | 49.22 | 5.87 |
| S5 (12) | 119.09 | 42.47 | 5.84 |
| S6 (16) | 130.36 | 40.44 | 6.32 |
| S7 (24) | 163.73 | 39.47 | 5.92 |
| S8 (32) | 179.26 | 36.25 | 6.62 |
| Annealing (Time) | [Å] | ||
|---|---|---|---|
| T1 (10 ns) | 86.14 | 38.25 | 5.08 |
| T2 (20 ns) | 83.78 | 34.56 | 5.50 |
| T3 (30 ns) | 82.31 | 30.34 | 5.43 |
| T4 (40 ns) | 82.04 | 29.56 | 5.92 |
| T5 (50 ns) | 80.04 | 26.94 | 5.85 |
| Molecular Weight [kg/mol] | Number of CG Particles (Each Molecule) | Number of Molecules (Each Cell) | Total CG Particles in a Cell |
|---|---|---|---|
| 32.8 | 515 (128-mers) | 32 | 16,480 |
| 49.0 | 771 (192-mers) | 22 | 16,962 |
| 65.3 | 1027 (256-mers) | 16 | 16,432 |
| (sd) [particles/nm] | (sd) [entanglements/nm] | |||
|---|---|---|---|---|
| S1 | S8 | S1 | S8 | |
| 0.0 | 11.33 (0.65) | 11.33 (0.62) | 0.116 (0.046) | 0.090 (0.030) |
| 2.0 | 11.33 (7.19) | 11.33 (1.61) | 0.116 (0.095) | 0.098 (0.040) |
| 6.0 | 11.33 (5.71) | 11.33 (2.04) | 0.114 (0.084) | 0.053 (0.036) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leelaprachakul, T.; Kubo, A.; Umeno, Y. Coarse-Grained Molecular Dynamics Simulation of Polycarbonate Deformation: Dependence of Mechanical Performance by the Effect of Spatial Distribution and Topological Constraints. Polymers 2023, 15, 43. https://doi.org/10.3390/polym15010043
Leelaprachakul T, Kubo A, Umeno Y. Coarse-Grained Molecular Dynamics Simulation of Polycarbonate Deformation: Dependence of Mechanical Performance by the Effect of Spatial Distribution and Topological Constraints. Polymers. 2023; 15(1):43. https://doi.org/10.3390/polym15010043
Chicago/Turabian StyleLeelaprachakul, Tatchaphon, Atsushi Kubo, and Yoshitaka Umeno. 2023. "Coarse-Grained Molecular Dynamics Simulation of Polycarbonate Deformation: Dependence of Mechanical Performance by the Effect of Spatial Distribution and Topological Constraints" Polymers 15, no. 1: 43. https://doi.org/10.3390/polym15010043
APA StyleLeelaprachakul, T., Kubo, A., & Umeno, Y. (2023). Coarse-Grained Molecular Dynamics Simulation of Polycarbonate Deformation: Dependence of Mechanical Performance by the Effect of Spatial Distribution and Topological Constraints. Polymers, 15(1), 43. https://doi.org/10.3390/polym15010043







