Electric Field Improvement for High-Voltage Bushings
Abstract
1. Introduction
2. Materials and Methods
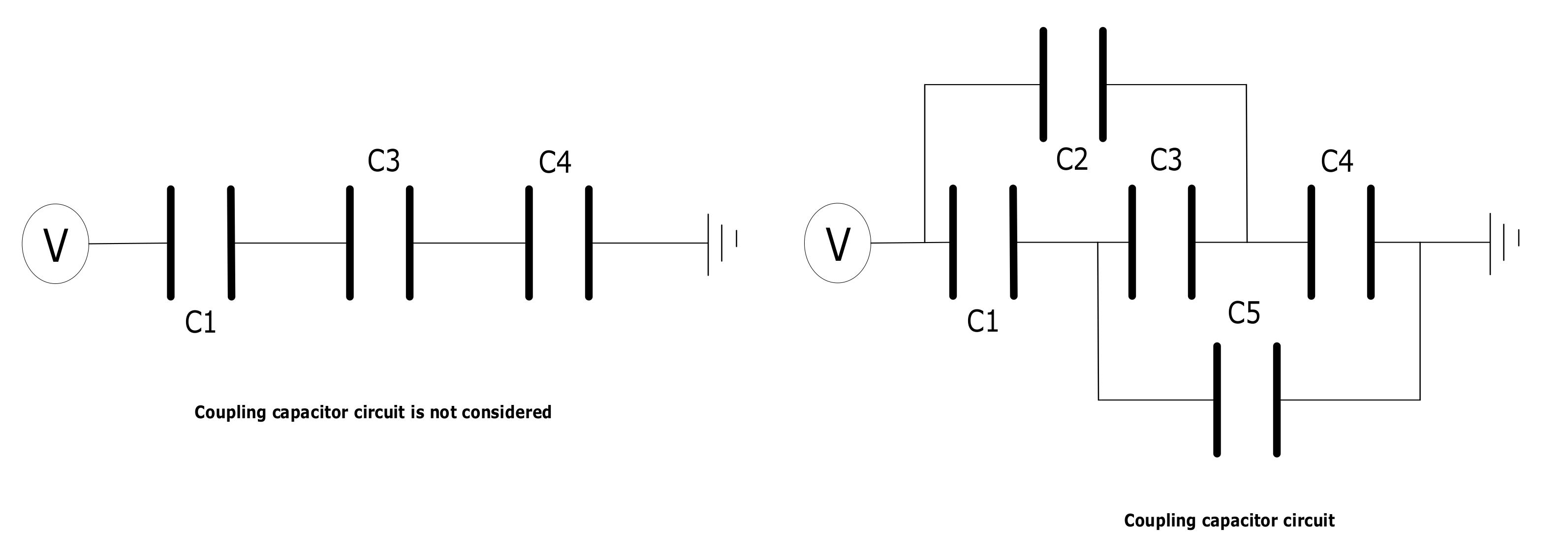
2.1. Theory
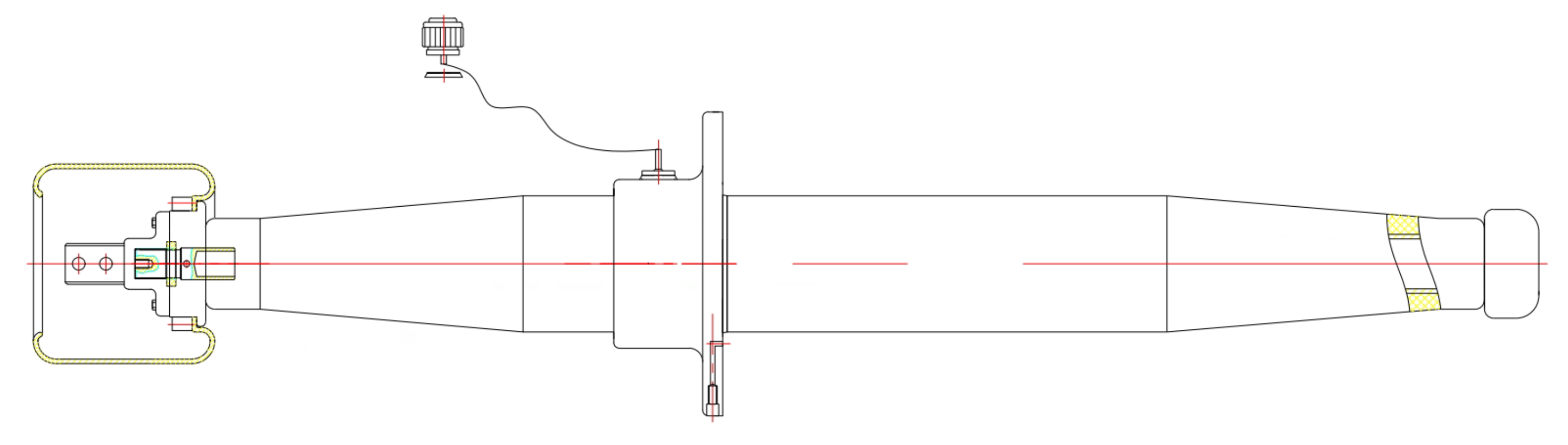
2.2. Geometric Modeling and Materials
2.3. Boundary Conditions and Meshing
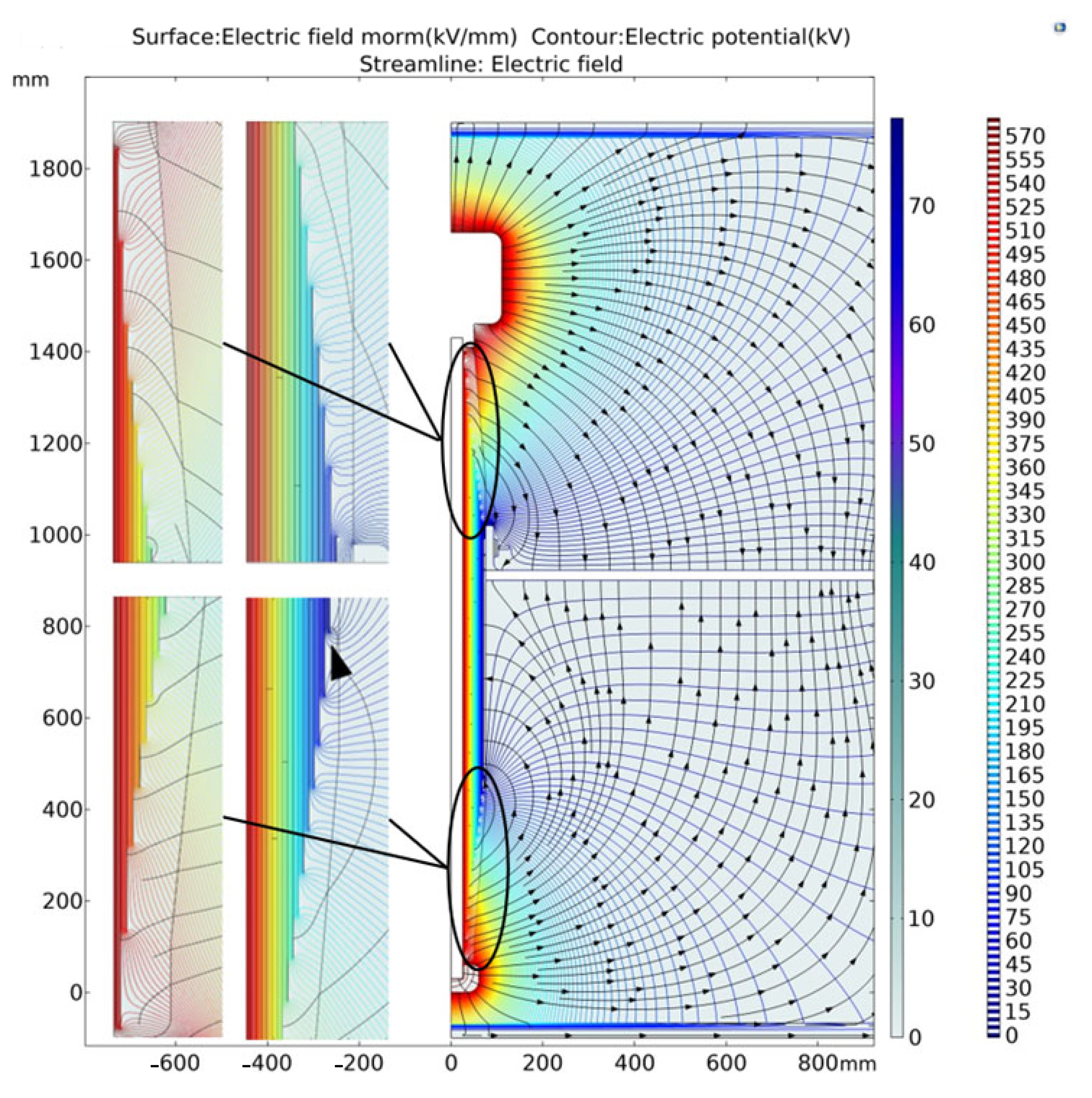
3. Results and Discussion
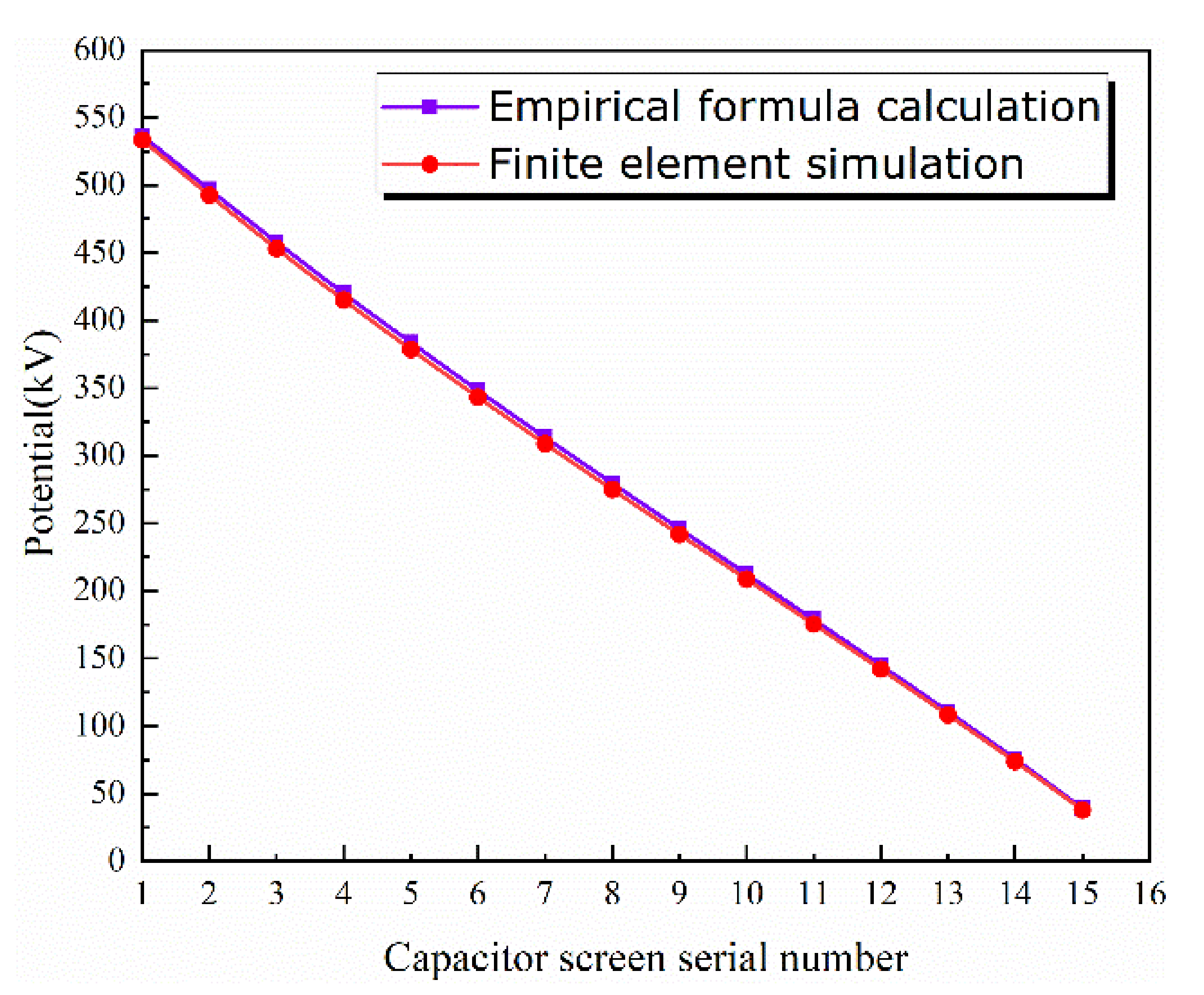
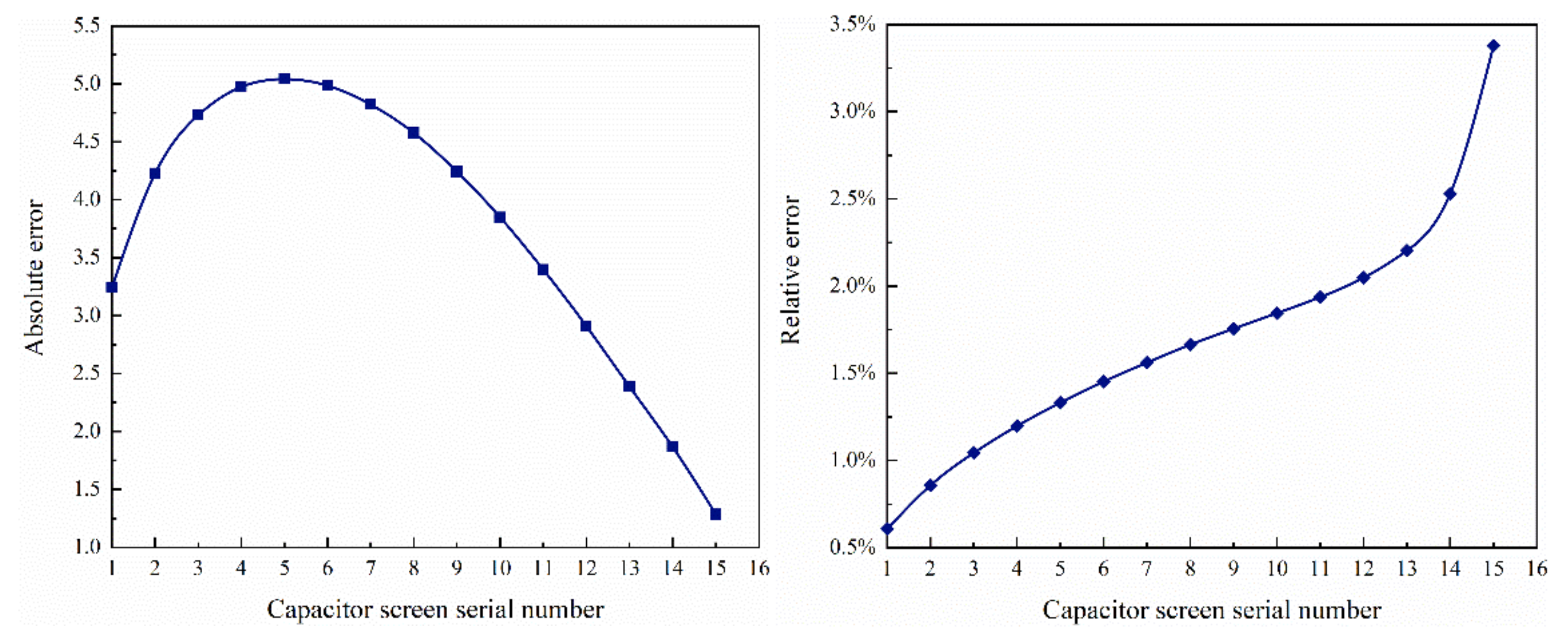
3.1. Comparison between Classical Calculation Method and COMSOL Simulation Results
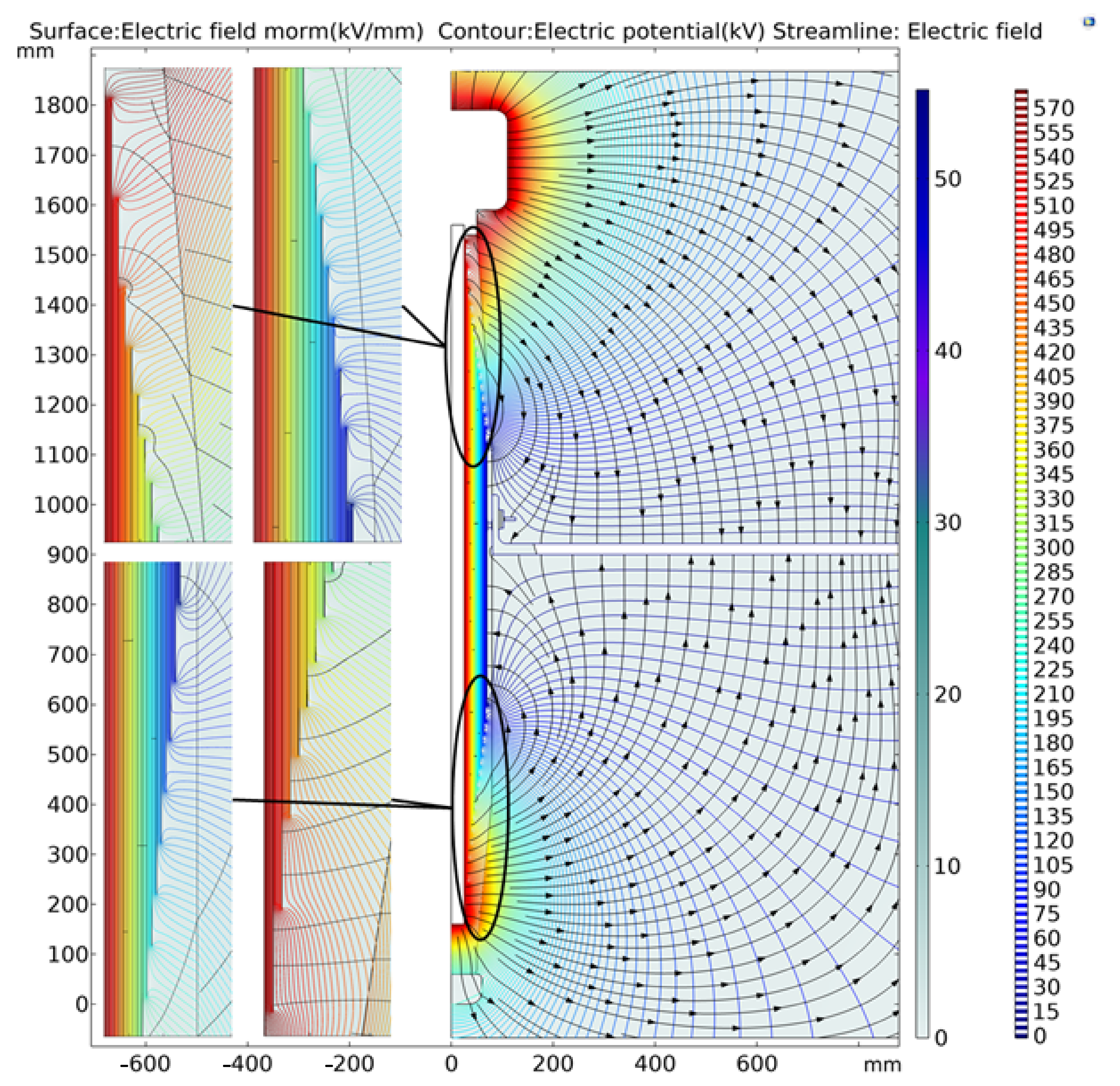
3.2. Effect of Dielectric Constant of Epoxy Resin on Results
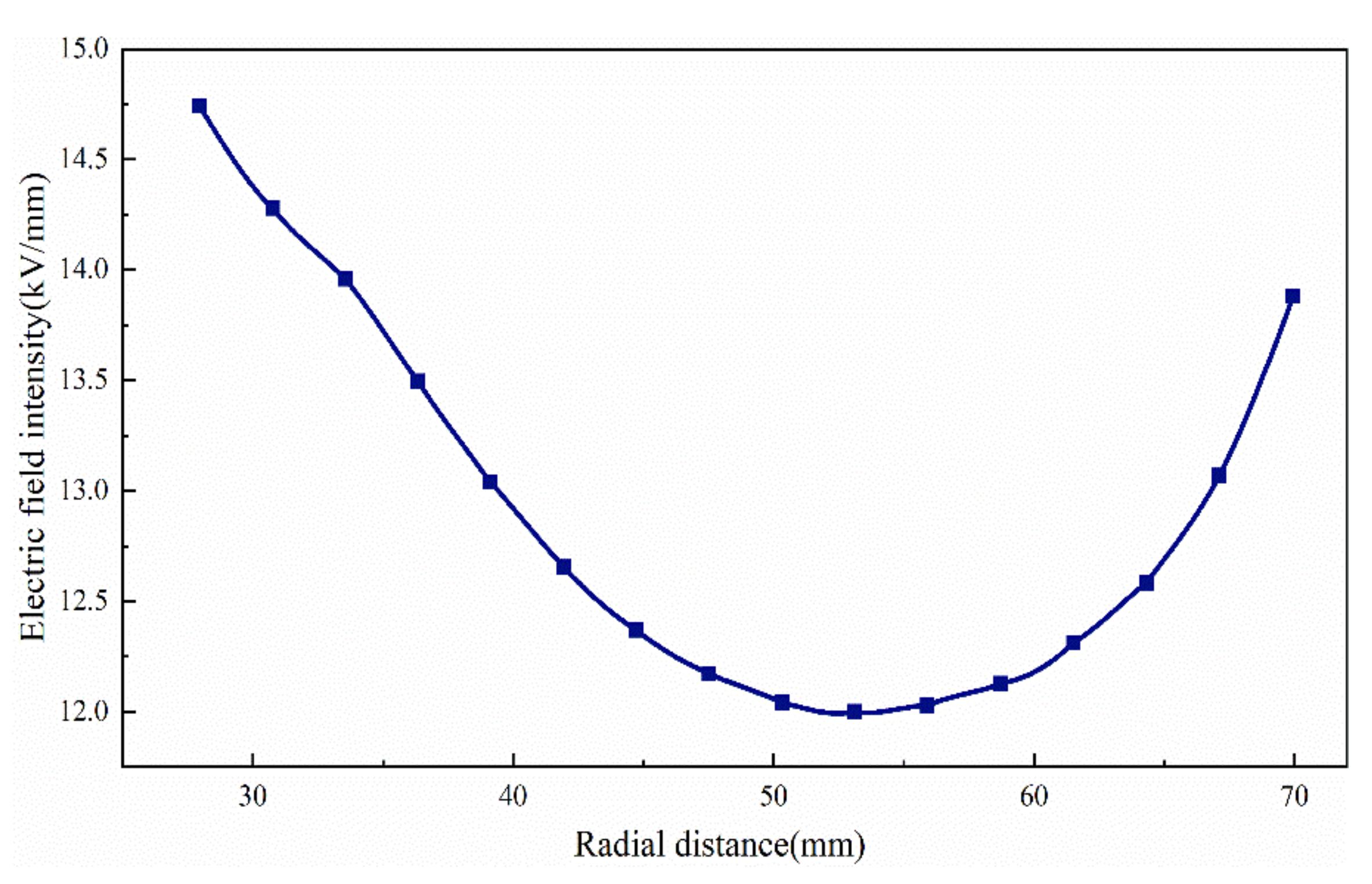
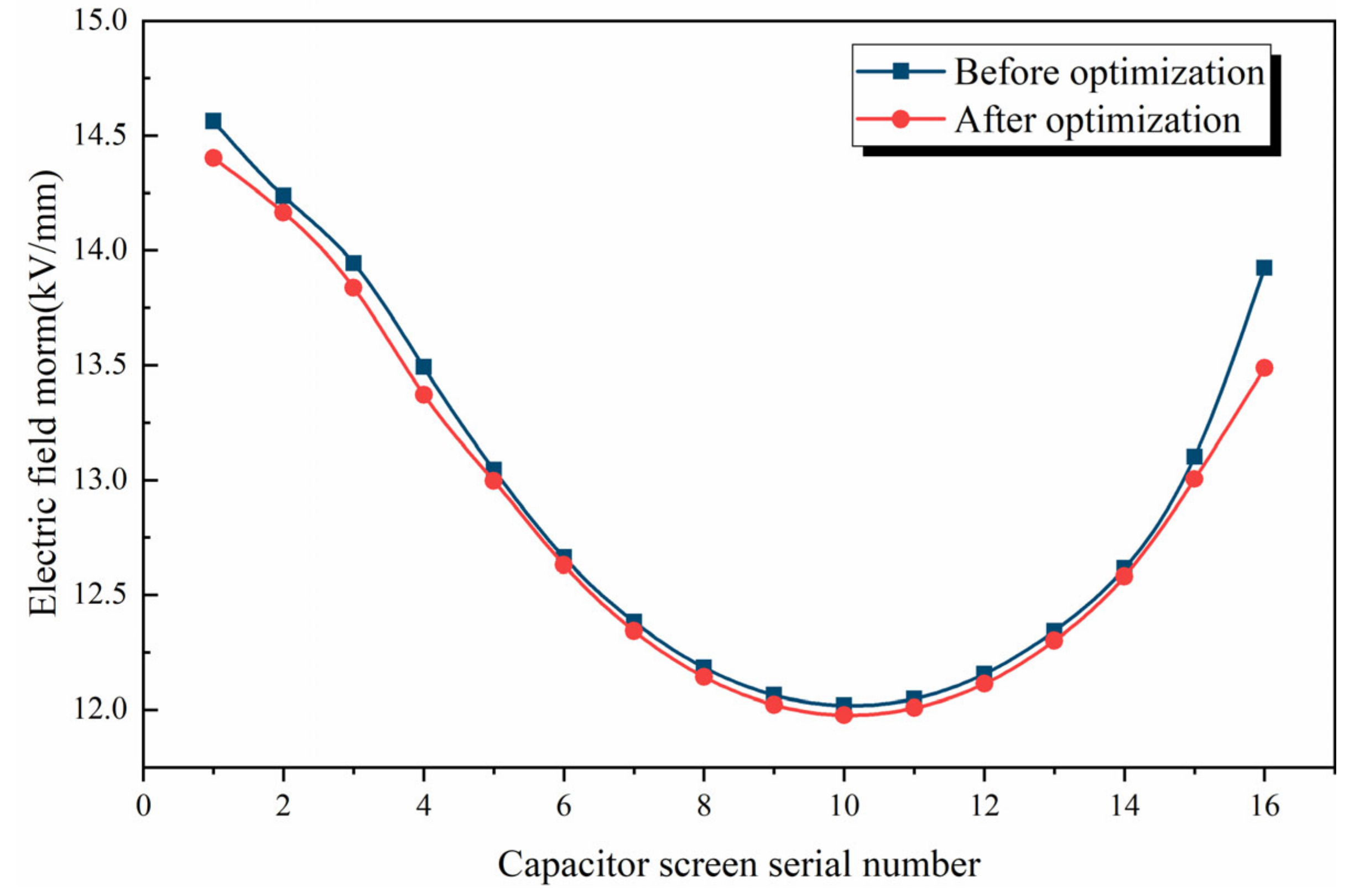
3.3. Optimal Design of Size Structure
4. Conclusions
- By comparing the potential inside the capacitor screen with the traditional design scheme, it is proved that the simulation physical field setting is accurate, has high correlation with the actual parameters, and that the modeling effect is good. The relative error is basically below 2.5%.
- The modeling shows the comprehensive field strength distribution, equipotential line, and radial and axial field strength distribution of the bushing. The electric field between the electrodes of each layer of the bushing capacitor screen is relatively uniform, and there are obvious changes at the electrode plate.
- The dielectric constant of the internal insulating material filled around the bushing capacitor screen will change under the actual operating conditions. Take the normal dielectric constant 5.5 and the aging dielectric constant 30 for analysis and judgment. It can be seen that the influence of the increase in dielectric constant on the electric field strength of the bushing first decreases and then increases. That is, the increase in dielectric constant caused by factors such as humidity and aging will affect the actual operation of the bushing and the risk of leakage.
- The improved optimization design based on the simulation model can improve the electric field distribution and size by increasing the radial length of the bushing on the premise of meeting the insulation requirements. This has practical guiding significance.
5. Acknowledgment
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, H.; Lei, Y.; Chen, D.; Wang, P. Numerical calculation and optimization design of electric field of wall bushing in medium voltage C-GIS. High Voltage. Appar. 2001, 3, 6–8. [Google Scholar]
- Yang, J.; Liu, Y.; Cao, X. Simulation calculation and experimental analysis of stress controlled casing electric field improved by nonlinear dielectric. Insul. Mater. 2003, 5, 29–31. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, Z. Electric field calculation and analysis of composite high voltage bushing. High Volt. Technol. 2004, 3, 17–18, 21. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, C.; Li, Y.; Lu, F.; Tan, X. Grounding inner shield to SF_6 study on the influence of casing electric field distribution. J. North China Electr. Power Univ. 2007, 6, 11–14. [Google Scholar]
- Di, Q.; Shi, Y.; Yang, F. Calculation and analysis of electric field of 145 kV composite bushing. Electr. Manuf. 2008, 9, 57–59. [Google Scholar]
- Liu, X.; Zhao, Y.; Wen, J. Numerical calculation of electric field and insulation analysis of outgoing bushing of EHV circuit breaker. J. Shenyang Univ. Technol. 2008, 1, 28–31, 54. [Google Scholar]
- Zhong, J.; Han, S.; Zhang, Y. Design calculation and analysis of UHV composite casing. Electr. Manuf. 2008, 2, 62–64. [Google Scholar]
- Chen, J.; Xie, P.; Peng, F.; Liang, W. Test of rain flash proof umbrella skirt for high voltage bushing of 500 kV main transformer. China South. Power Grid Technol. 2012, 6, 23–26. [Google Scholar] [CrossRef]
- Yu, Q.; Ma, Z.; Shi, R. 40.5 kV box-type gas-insulated switchgear through wall bushing electric field analysis and design optimization. Huatong Technol. 2005, 3, 7–10. [Google Scholar]
- Wang, D.; Ruan, J.; Du, Z.; Ruan, X.; Yang, B.; Wang, Y. Numerical solution of field potential and electric field intensity inside valve hall of DC converter station by sub-model method. Power Grid Technol. 2011, 35, 158–163. [Google Scholar] [CrossRef]
- Wang, J.; Peng, Z.; Liu, P.; Wu, H.; Wei, X. Analysis of surface electric field of voltage equalizing shielding fittings in valve hall of ± 1100 kV UHV converter station. High Volt. Technol. 2015, 41, 3728–3736. [Google Scholar] [CrossRef]
- Cao, W.; Shen, W.; He, B.; Wu, K. Structural design for dc bushing core based on the material life. IEEE Trans. Dielectr. Electr. Insul. 2013, 20, 281–288. [Google Scholar] [CrossRef]
- Wen, Z. Optimal Calculation of Electric Field of Transformer Bushing Capacitor Core Based on Agent Model. Electrotechnics 2018, 9, 1–2. [Google Scholar]
- Zhang, S.; Peng, Z.; Peng, L.; Wei, H.U.; Wang, H. Electro-thermal Coupling Model for Computation of Radial Temperature and Electric Field of Resin Impregnated Paper High Voltage Direct Current Bushing. Proc. CSEE 2013, 33, 191–200. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, Z.; Liu, P.; Li, N. Design and dielectric characteristics of the ±1100 kV UHVDC wall bushing in china. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 409–419. [Google Scholar] [CrossRef]
- Zhang, S.; Peng, Z.; Liu, P. Inner insulation structure optimization of UHV RIP oil-SF6 bushing using electro-thermal simulation and advanced equal margin design method. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 1768–1777. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, J.; Zhang, H.; Liu, D. Research on key technology of high voltage bushing equalizing ball structure of EHV AC transformer. High Volt. Appar. 2016, 52, 126–129, 135. [Google Scholar] [CrossRef]
- Wang, Q.; Liao, J.; Tian, H.; Liu, P.; Peng, Z. Regularity analysis of the temperature distribution of epoxy impregnated paper converter transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3254–3264. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, X.; Tian, H.; Liu, P.; Peng, Z. A novel dissipating heat structure of converter transformer RIP bushings based on 3-D electromagnetic-fluid-thermal analysis. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1938–1946. [Google Scholar] [CrossRef]
- Yang, J.; Yang, X.; Ma, Q.; Chen, X.; Chen, B.; Liu, M. Three dimensional simulation of bushing electric field distribution of ± 800 kV converter transformer. Hydropower Energy Sci. 2018, 36, 188–191. [Google Scholar]
- Wang, D.; Zhou, L.; Yang, Z.; Liao, W.; Wang, L.; Guo, L. Simulation for Transient Moisture Distribution and Effects on the Electric Field in Stable Condition: 110 kV Oil-Immersed Insulation Paper Bushing. IEEE Access 2019, 7, 162991–163002. [Google Scholar] [CrossRef]
- Chen, M.; Liu, X.; Sun, Y.; Wu, Z.; Tang, H. Influence of material volume conductivity on electric field and surface charge of RIP valve-side bushing core under DC electro-thermal coupling stress. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 164–171. [Google Scholar] [CrossRef]
- Jin, L.; Guo, Y.; Xue, Y.; Zhao, B.; Chen, J. Electric field analysis and structure optimization for high voltage insulation bushing. Gaoya Dianqi/High Volt. Appar. 2015, 51, 7–12, 18. [Google Scholar] [CrossRef]
- Hesamzadeh, M.R.; Hosseinzadeh, N.; Wolfs, P. An Advanced Optimal Approach for High Voltage AC Bushing Design. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 461–466. [Google Scholar] [CrossRef]
- Dai, Q.; Qi, B.; Zhuo, R.; Li, C.; Tian, Y.; Fu, M. Electric Field Simulation and Optimization Methods of Capacitor Core Foil Edge of Oil-Impregnated Paper Bushing. Dianwang Jishu/Power Syst. Technol. 2017, 41, 1683–1688. [Google Scholar] [CrossRef]
- Rowland, S.M.; Schurch, R.; Pattouras, M.; Li, Q. Application of FEA to image-based models of electrical trees with uniform conductivity. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 1537–1546. [Google Scholar] [CrossRef]
- Li, Q.; Shuttleworth, R.; Dupere, I.; Zhang, G.; Rowland, S.M.; Morris, R.S. FEA modelling of a water droplet vibrating in an electric field. In Proceedings of the IEEE International Symposium on Electrical Insulation (ISEI), San Juan, PR, USA, 10–13 June 2012; pp. 449–453. [Google Scholar]
- Li, Q.; Shuttleworth, R.; Zhang, G.; Rowland, S.M.; Morris, R.S. On calculating surface potential gradient of overhead line conductors. In Proceedings of the Conference Record of the 2012 IEEE International Symposium on Electrical Insulation (ISEI), San Juan, PR, USA, 10–13 June 2012; pp. 540–544. [Google Scholar]
- Peesapati, V.; Zachariades, C.; Li, Q.; Rowland, S.M.; Cotton, I.; Green, P.R.; Allison, F.; Chambers, D. 3D Electric field computation of a composite cross-arm. In Proceedings of the Conference Record of the 2012 IEEE International Symposium on Electrical Insulation (ISEI), San Juan, PR, USA, 10–13 June 2012; pp. 464–468. [Google Scholar]
- Peesapati, V.; Zachariades, C.; Li, Q.; Rowland, S.M.; Cotton, I.; Allison, F.; Chambers, D.; Rhodes, P. Electric field computation for a 400 kV composite cross-arm. In Proceedings of the 2012 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Montreal, QC, USA, 14–17 October 2012; pp. 790–793. [Google Scholar]
- Li, Q.; Rowland, S.M.; Shuttleworth, R. Calculating the Surface Potential Gradient of Overhead Line Conductors. IEEE Trans. Power Deliv. 2015, 30, 43–52. [Google Scholar] [CrossRef]
- Li, Q.; Rowland, S.M.; Dupere, I.; Morris, R. The impact of water droplet vibration on corona inception on conductors under 50 Hz AC fields. IEEE Trans. Power Deliv. 2018, 33, 2428–2436. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, J.; Bu, S.; Li, Q.; Terzija, V.J.; Rowland, S.M. The Development of Low-Current Surface Arcs Under Clean and Salt-Fog Conditions in Electricity Distribution Networks. IEEE Access 2018, 6, 15835–15843. [Google Scholar] [CrossRef]

| Unit Type | Quantity | Grid Parameters | Statistical Information |
|---|---|---|---|
| Triangular element | 423,659 | Number of units | 423,659 |
| Edge element | 34,064 | Grid area | 1,976,000 |
| Vertex element | 183 | Minimum unit mass | 0.06276 |
| Average unit mass | 0.8478 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Li, Q.; Xu, S.; Liu, R.; Dong, M.; Ying, S.; Tian, J.; Xin, W.; Haddad, M.; Jiang, X. Electric Field Improvement for High-Voltage Bushings. Polymers 2023, 15, 40. https://doi.org/10.3390/polym15010040
Li L, Li Q, Xu S, Liu R, Dong M, Ying S, Tian J, Xin W, Haddad M, Jiang X. Electric Field Improvement for High-Voltage Bushings. Polymers. 2023; 15(1):40. https://doi.org/10.3390/polym15010040
Chicago/Turabian StyleLi, Li, Qi Li, Shuxin Xu, Rui Liu, Manling Dong, Si Ying, Jieyuan Tian, Wanpeng Xin, Manu Haddad, and Xingliang Jiang. 2023. "Electric Field Improvement for High-Voltage Bushings" Polymers 15, no. 1: 40. https://doi.org/10.3390/polym15010040
APA StyleLi, L., Li, Q., Xu, S., Liu, R., Dong, M., Ying, S., Tian, J., Xin, W., Haddad, M., & Jiang, X. (2023). Electric Field Improvement for High-Voltage Bushings. Polymers, 15(1), 40. https://doi.org/10.3390/polym15010040







