Fractional Coupling of Primary and Johari–Goldstein Relaxations in a Model Polymer
Abstract
1. Introduction
2. Model and Numerical Methods
3. Results
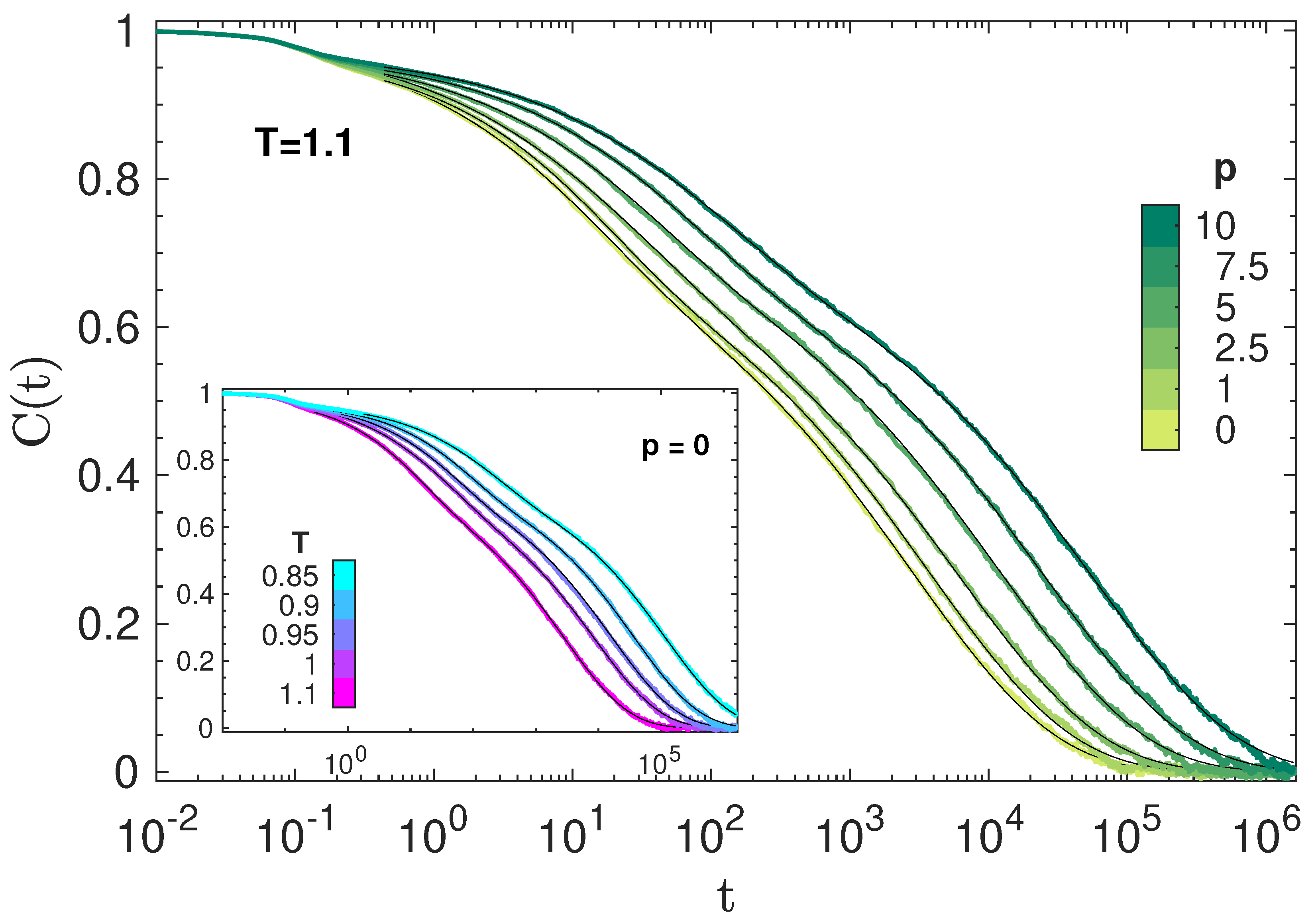
3.1. Bond Correlation Function
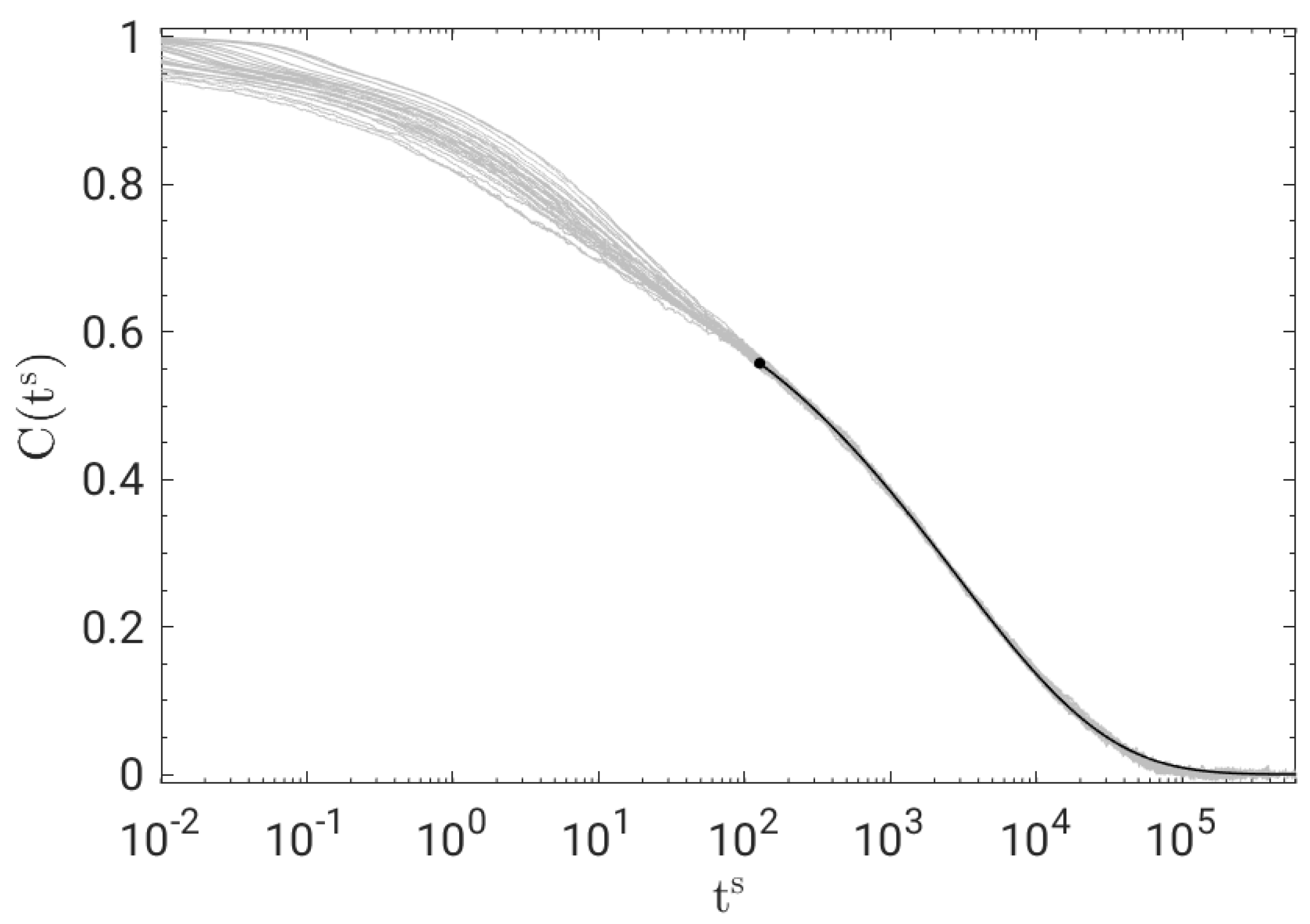
3.2. Time Temperature and Pressure Superposition of Primary Relaxation
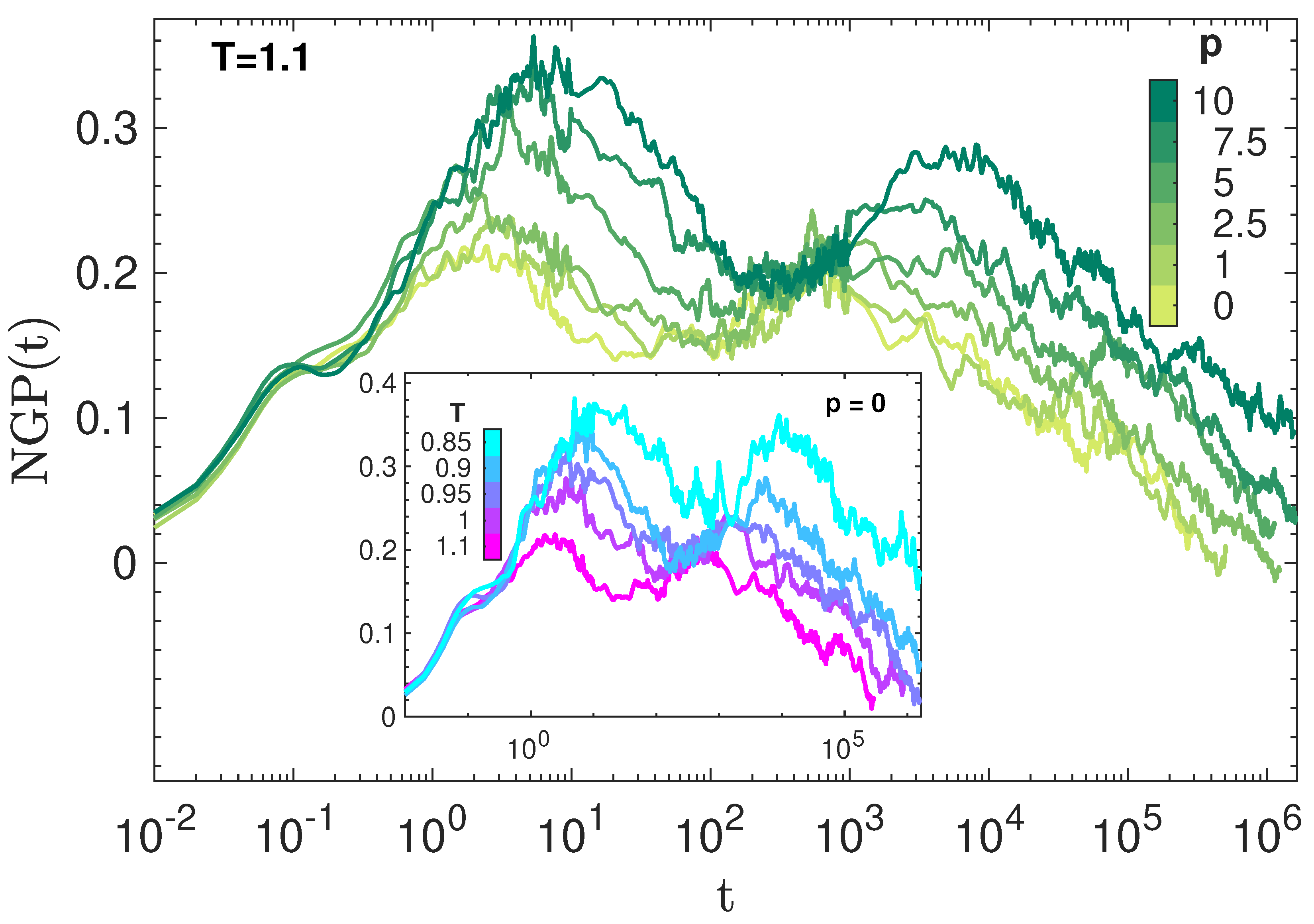
3.3. Dynamic Heterogeneity
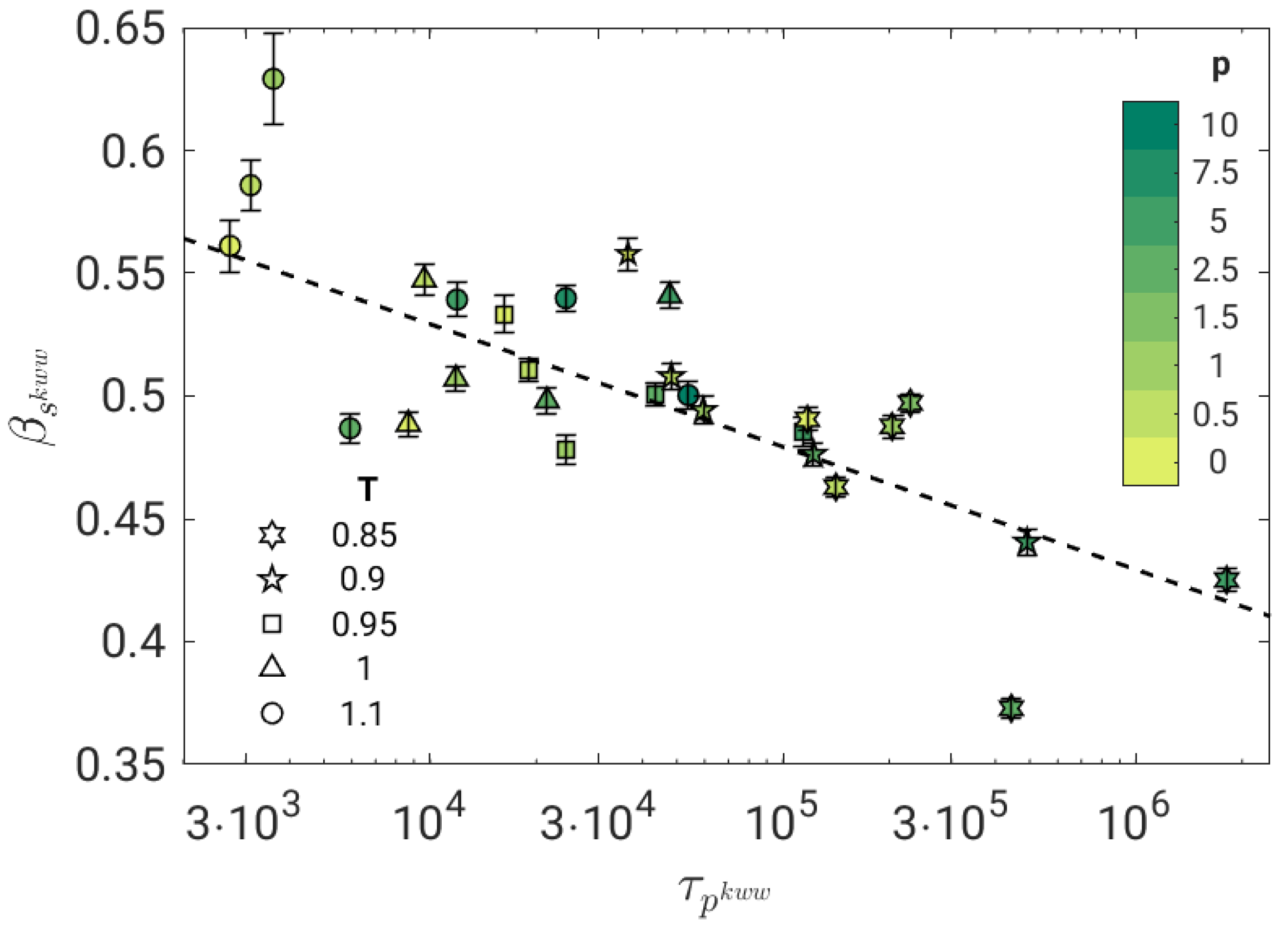
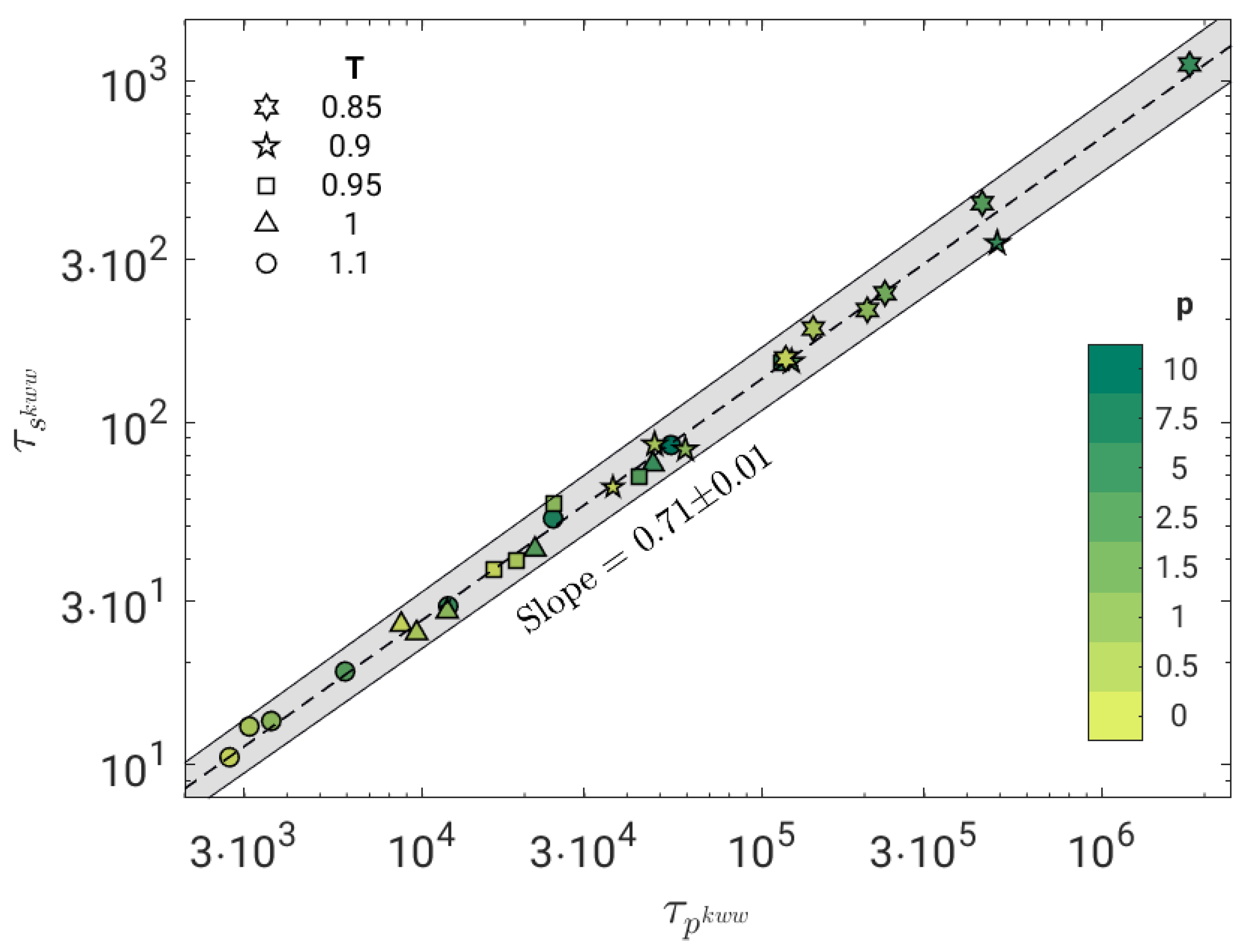
3.4. Fractional Coupling of Primary and JG Relaxations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCF | Bond correlation function |
| CM | Coupling model |
| DH | Dynamical heterogeneity |
| JG | Johari–Goldstein |
| KWW | Kohlrausch–Williams–Watts |
| LJ | Lennard–Jones |
| MD | Molecular dynamics |
| NGP | Non-Gaussian parameter |
| NPT | Constant number of monomers N, constant pressure P and constant temperature T |
| NVT | Constant number of monomers N, constant volume V and constant temperature T |
| TTPS | Time–temperature–pressure superposition |
References
- Debenedetti, P.G. Metastable Liquids; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- McCrum, N.G.; Read, B.E.; Williams, G. Anelastic and Dielectric Effects in Polymeric Solids; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Johari, G.P.; Goldstein, M. Viscous Liquids and the Glass Transition. II. Secondary Relaxations in Glasses of Rigid Molecules. J. Chem. Phys. 1970, 53, 2372. [Google Scholar] [CrossRef]
- Ngai, K.L. Relation between some secondary relaxations and the α relaxations in glass-forming materials according to the coupling model. J. Chem. Phys. 1998, 109, 6982–6994. [Google Scholar] [CrossRef]
- Ngai, K.L.; Paluch, M. Classification of secondary relaxation in glass-formers based on dynamic properties. J. Chem. Phys. 2004, 120, 857–873. [Google Scholar] [CrossRef]
- Capaccioli, S.; Paluch, M.; Prevosto, D.; Wang, L.M.; Ngai, K.L. Many-Body Nature of Relaxation Processes in Glass-Forming Systems. J. Phys. Chem. Lett. 2012, 3, 735–743. [Google Scholar] [CrossRef]
- Cicerone, M.T.; Zhong, Q.; Tyagi, M. Picosecond Dynamic Heterogeneity, Hopping, and Johari-Goldstein Relaxation in Glass-Forming Liquids. Phys. Rev. Lett. 2014, 113, 117801. [Google Scholar] [CrossRef]
- Yu, H.-B.; Richert, R.; Samwer, K. Structural rearrangements governing Johari-Goldstein relaxations in metallic glasses. Sci. Adv. 2017, 3, 1701577. [Google Scholar] [CrossRef]
- Boyd, R.H.; Breitling, S.M. The Conformational Analysis of Crankshaft Motions in Polyethylene. Macromolecules 1974, 7, 855–862. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.D.; Yoon, D.Y. Static and Dynamic Properties of a n-C100H202 Melt from Molecular Dynamics Simulations. Macromolecules 1997, 30, 7772–7780. [Google Scholar] [CrossRef]
- Meier, R.J.; Struik, L. Atomistic modelling study of relaxation processes in polymers: The β-relaxation in polyvinylchloride. Polymer 1998, 39, 31–38. [Google Scholar] [CrossRef]
- Goldstein, M. The past, present, and future of the Johari–Goldstein relaxation. J. Non-Cryst. Solids 2011, 357, 249–250. [Google Scholar] [CrossRef]
- Johari, G.P. Source of JG-Relaxation in the Entropy of Glass. J. Phys. Chem. B 2019, 123, 3010–3023. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D. Relationship between the α- and β-relaxation processes in amorphous polymers: Insight from atomistic molecular dynamics simulations of 1,4-polybutadiene melts and blends. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 627–643. [Google Scholar] [CrossRef]
- Karmakar, S.; Dasgupta, C.; Sastry, S. Short-Time Beta Relaxation in Glass-Forming Liquids Is Cooperative in Nature. Phys. Rev. Lett. 2016, 116, 085701. [Google Scholar] [CrossRef]
- Ngai, K.L.; Capaccioli, S.; Paluch, M.; Wang, L. Clarifying the nature of the Johari-Goldstein β-relaxation and emphasising its fundamental importance. Philos. Mag. 2020, 100, 2596–2613. [Google Scholar] [CrossRef]
- Johari, G.P. Glass Transition and Secondary Relaxations in Molecular Liquids and Crystals. Ann. N. Y. Acad. Sci. 1976, 279, 117–140. [Google Scholar] [CrossRef]
- Bershtein, V.; Egorov, V.; Egorova, L.; Ryzhov, V. The role of thermal analysis in revealing the common molecular nature of transitions in polymers. Thermochim. Acta 1994, 238, 41–73. [Google Scholar] [CrossRef]
- Böhmer, R.; Diezemann, G.; Geil, B.; Hinze, G.; Nowaczyk, A.; Winterlich, M. Correlation of Primary and Secondary Relaxations in a Supercooled Liquid. Phys. Rev. Lett. 2006, 97, 135701. [Google Scholar] [CrossRef]
- Goldstein, M. Communications: Comparison of activation barriers for the Johari–Goldstein and alpha relaxations and its implications. J. Chem. Phys. 2010, 132, 041104. [Google Scholar] [CrossRef]
- Cicerone, M.T.; Tyagi, M. Metabasin transitions are Johari-Goldstein relaxation events. J. Chem. Phys. 2017, 146, 054502. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, Z.Y.; Guan, P.F.; Yu, H.B.; Wang, W.H.; Ngai, K.L. Invariance of the relation between α relaxation and β relaxation in metallic glasses to variations of pressure and temperature. Phys. Rev. B 2020, 102, 094205. [Google Scholar] [CrossRef]
- Sillescu, H. Heterogeneity at the glass transition: A review. J. Non-Cryst. Solids 1999, 243, 81–108. [Google Scholar] [CrossRef]
- Ediger, M.D. Spatially heterogeneous dynamics in supercooled liquids. Annu. Rev. Phys. Chem. 2000, 51, 99–128. [Google Scholar] [CrossRef]
- Richert, R. Heterogeneous dynamics in liquids: Fluctuations in space and time. J. Phys. Condens. Matter 2002, 14, R703–R738. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Karmakar, S.; Dasgupta, C.; Sastry, S. Length scales in glass-forming liquids and related systems: A review. Rep. Prog. Phys. 2015, 79, 016601. [Google Scholar] [CrossRef]
- Tracht, U.; Wilhelm, M.; Heuer, A.; Feng, H.; Schmidt-Rohr, K.; Spiess, H.W. Length Scale of Dynamic Heterogeneities at the Glass Transition Determined by Multidimensional Nuclear Magnetic Resonance. Phys. Rev. Lett. 1998, 81, 2727–2730. [Google Scholar] [CrossRef]
- Colmenero, J.; Alvarez, F.; Arbe, A. Self-motion and the α relaxation in a simulated glass-forming polymer: Crossover from Gaussian to non-Gaussian dynamic behavior. Phys. Rev. E 2002, 65, 041804. [Google Scholar] [CrossRef]
- Napolitano, S.; Capponi, S.; Vanroy, B. Glassy dynamics of soft matter under 1D confinement: How irreversible adsorption affects molecular packing, mobility gradients and orientational polarization in thin films. Eur. Phys. J. E 2013, 36, 61. [Google Scholar] [CrossRef]
- Napolitano, S.; Glynos, E.; Tito, N.B. Glass transition of polymers in bulk, confined geometries, and near interfaces. Rep. Prog. Phys. 2017, 80, 036602. [Google Scholar] [CrossRef]
- Weeks, E.R.; Crocker, J.C.; Levitt, A.C.; Schofield, A.; Weitz, D.A. Three-Dimensional Direct Imaging of Structural Relaxation Near the Colloidal Glass Transition. Science 2000, 287, 627–631. [Google Scholar] [CrossRef] [PubMed]
- Fragiadakis, D.; Roland, C.M. Role of structure in the α and β dynamics of a simple glass-forming liquid. Phys. Rev. E 2017, 95, 022607. [Google Scholar] [CrossRef] [PubMed]
- Puosi, F.; Tripodo, A.; Malvaldi, M.; Leporini, D. Johari–Goldstein Heterogeneous Dynamics in a Model Polymer. Macromolecules 2021, 54, 2053–2058. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 3rd ed.; Academic Press: New York, NY, USA, 2006. [Google Scholar]
- Zorn, R. Deviation from Gaussian behavior in the self-correlation function of the proton motion in polybutadiene. Phys. Rev. B 1997, 55, 6249–6259. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Kröger, M. Simple models for complex nonequilibrium fluids. Phys. Rep. 2004, 390, 453–551. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Available online: http://lammps.sandia.gov (accessed on 30 October 2022).
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Richter, D.; Monkenbusch, M.; Arbe, A.; Colmenero, J.; Farago, B. Dynamic structure factors due to relaxation processes in glass-forming polymers. Phys. B Condens. Matter 1997, 241–243, 1005–1012. [Google Scholar] [CrossRef]
- Tölle, A. Neutron scattering studies of the model glass former ortho-terphenyl. Rep. Prog. Phys. 2001, 64, 1473–1532. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Roland, C.M. Dynamic correlations and heterogeneity in the primary and secondary relaxations of a model molecular liquid. Phys. Rev. E 2014, 89, 052304. [Google Scholar] [CrossRef]
- Tripodo, A.; Puosi, F.; Malvaldi, M.; Capaccioli, S.; Leporini, D. Coincident Correlation between Vibrational Dynamics and Primary Relaxation of Polymers with Strong or Weak Johari-Goldstein Relaxation. Polymers 2020, 12, 761. [Google Scholar] [CrossRef] [PubMed]
- Barbieri, A.; Campani, E.; Capaccioli, S.; Leporini, D. Molecular dynamics study of the thermal and the density effects on the local and the large-scale motion of polymer melts: Scaling properties and dielectric relaxation. J. Chem. Phys. 2004, 120, 437–453. [Google Scholar] [CrossRef] [PubMed]
- Bedrov, D.; Smith, G.D. Molecular dynamics simulation study of the α and β-relaxation processes in a realistic model polymer. Phys. Rev. E 2005, 71, 050801. [Google Scholar] [CrossRef] [PubMed]
- Bedrov, D.; Smith, G.D. Secondary Johari–Goldstein relaxation in linear polymer melts represented by a simple bead-necklace model. J. Non-Cryst. Solids 2011, 357, 258–263. [Google Scholar] [CrossRef]
- De Michele, C.; Leporini, D. Viscous flow and jump dynamics in molecular supercooled liquids. I. Translations. Phys. Rev. E 2001, 63, 036701. [Google Scholar] [CrossRef]
- Williams, G. Molecular aspects of multiple dielectric relaxation processes in solid polymers. In Proceedings of the Electric Phenomena in Polymer Science. In Advances in Polymer Science; Springer: Berlin/Heidelberg, Germany, 1979; pp. 59–92. [Google Scholar]
- Williams, G. Dielectric relaxation spectroscopy of polymers revealing dynamics in isotropic and anisotropic stationary systems and changes in molecular mobility in non-stationary systems. Polymer 1994, 35, 1915–1922. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Roland, C.M. Characteristics of the Johari-Goldstein process in rigid asymmetric molecules. Phys. Rev. E 2013, 88, 042307. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Roland, C.M. Rotational dynamics of simple asymmetric molecules. Phys. Rev. E 2015, 91, 022310. [Google Scholar] [CrossRef]
- Chang, I.; Fujara, F.; Geil, B.; Heuberger, G.; Mangel, T.; Sillescu, H. Translational and rotational molecular motion in supercooled liquids studied by NMR and forced Rayleigh scattering. J. Non-Cryst. Solids 1994, 172–175, 248–255. [Google Scholar] [CrossRef]
| T∖p | 0 | 0.5 | 1 | 1.5 | 2.5 | 5 | 7.5 | 10 |
|---|---|---|---|---|---|---|---|---|
| 1.1 | ||||||||
| 1 | ||||||||
| 0.95 | ||||||||
| 0.9 | ||||||||
| 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massa, C.A.; Puosi, F.; Leporini, D. Fractional Coupling of Primary and Johari–Goldstein Relaxations in a Model Polymer. Polymers 2022, 14, 5560. https://doi.org/10.3390/polym14245560
Massa CA, Puosi F, Leporini D. Fractional Coupling of Primary and Johari–Goldstein Relaxations in a Model Polymer. Polymers. 2022; 14(24):5560. https://doi.org/10.3390/polym14245560
Chicago/Turabian StyleMassa, Carlo Andrea, Francesco Puosi, and Dino Leporini. 2022. "Fractional Coupling of Primary and Johari–Goldstein Relaxations in a Model Polymer" Polymers 14, no. 24: 5560. https://doi.org/10.3390/polym14245560
APA StyleMassa, C. A., Puosi, F., & Leporini, D. (2022). Fractional Coupling of Primary and Johari–Goldstein Relaxations in a Model Polymer. Polymers, 14(24), 5560. https://doi.org/10.3390/polym14245560







