Tactile Sensing Using Magnetic Foam
Abstract
:1. Introduction
2. Materials and Methods
2.1. Magnetic Foam Composite Preparation
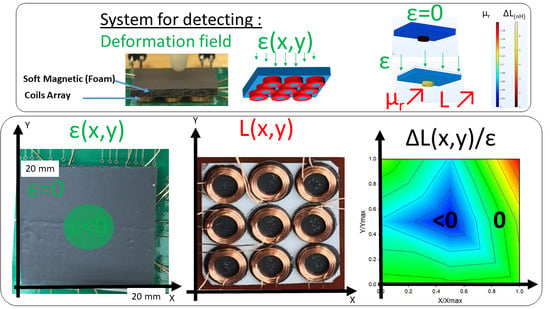
2.2. Sensing Device
2.3. Mechanical Testing
2.4. Magnetic Characterization
3. Results
3.1. FTIR
3.2. Mechanical Test
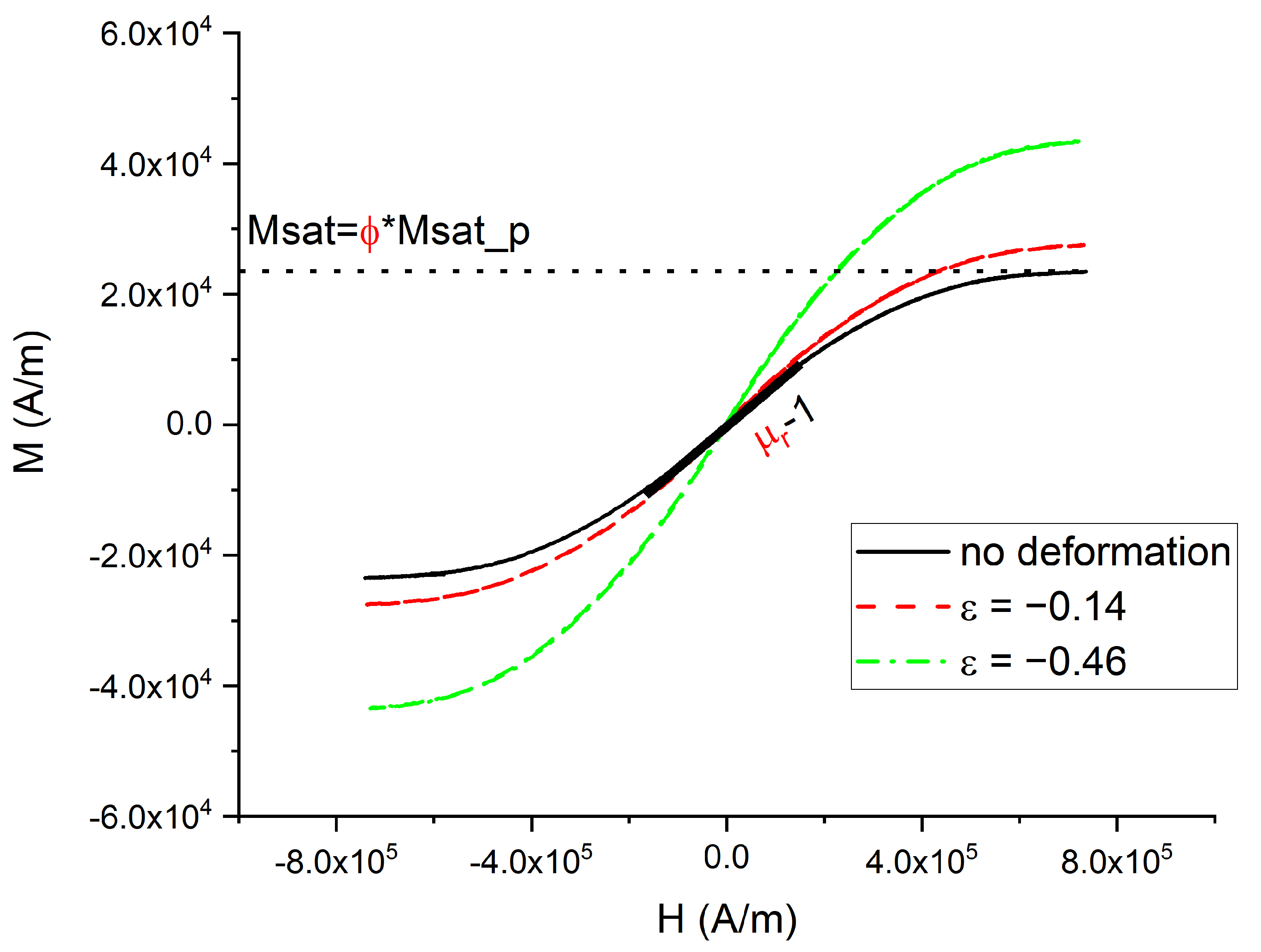
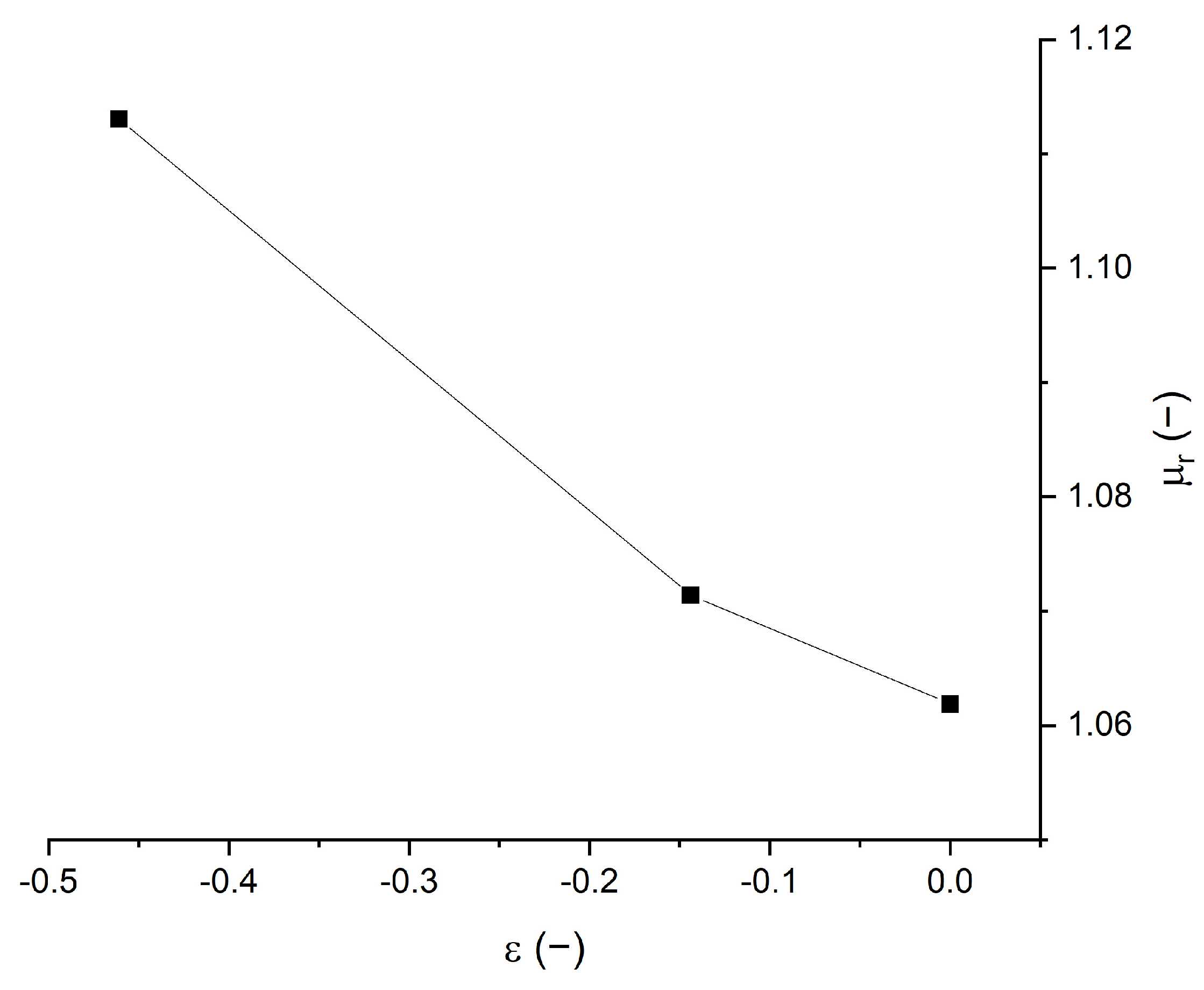
3.3. Magnetization Loop
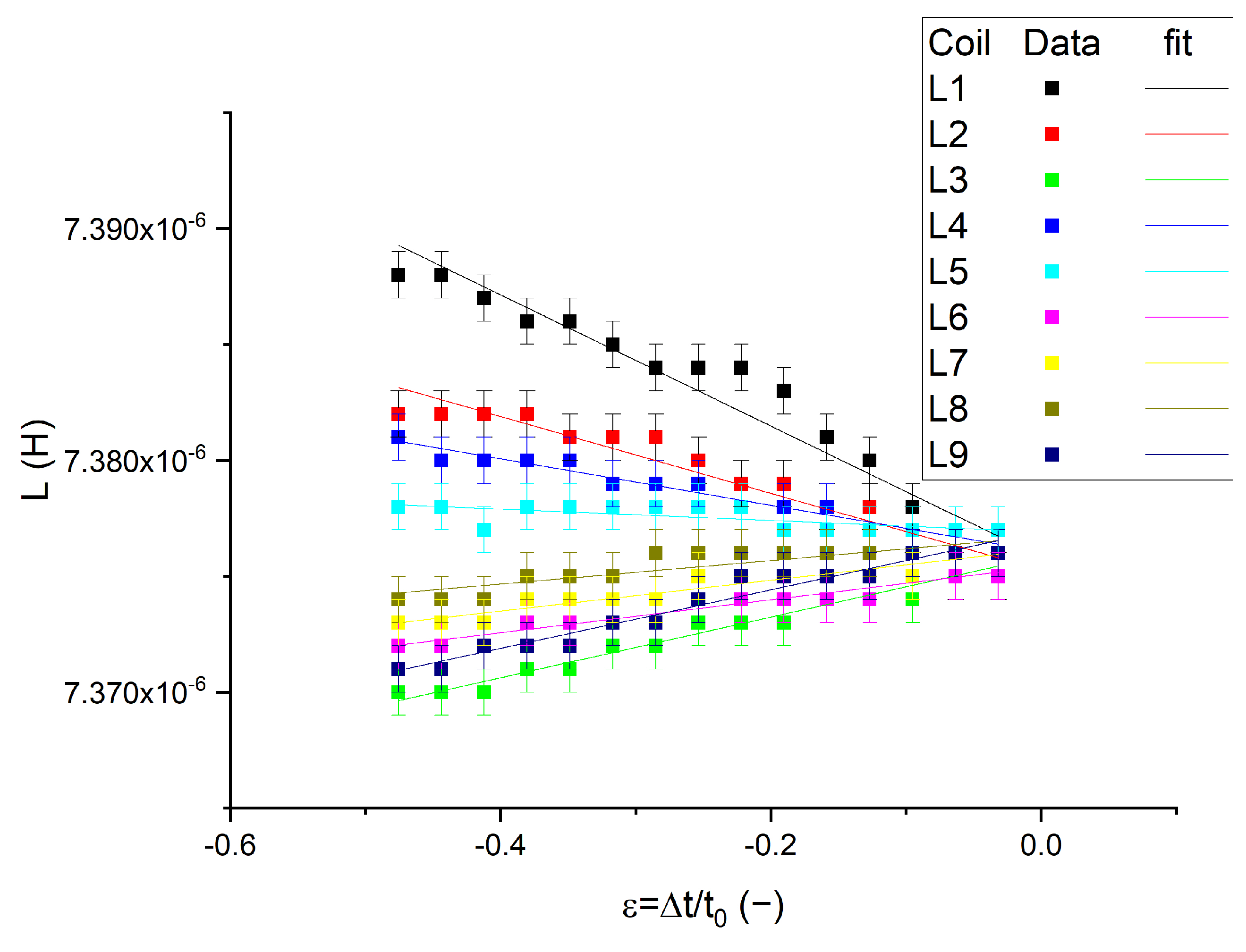
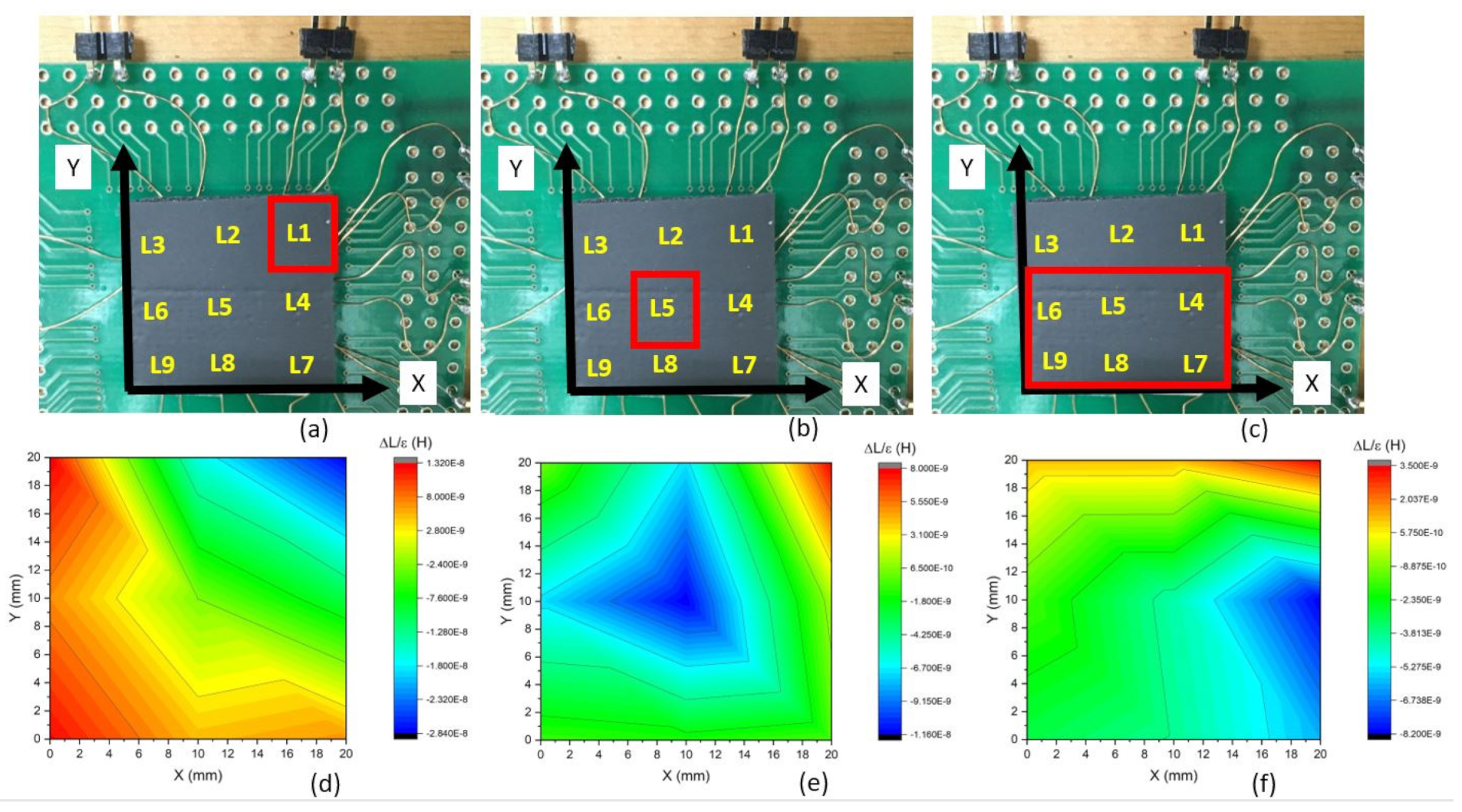
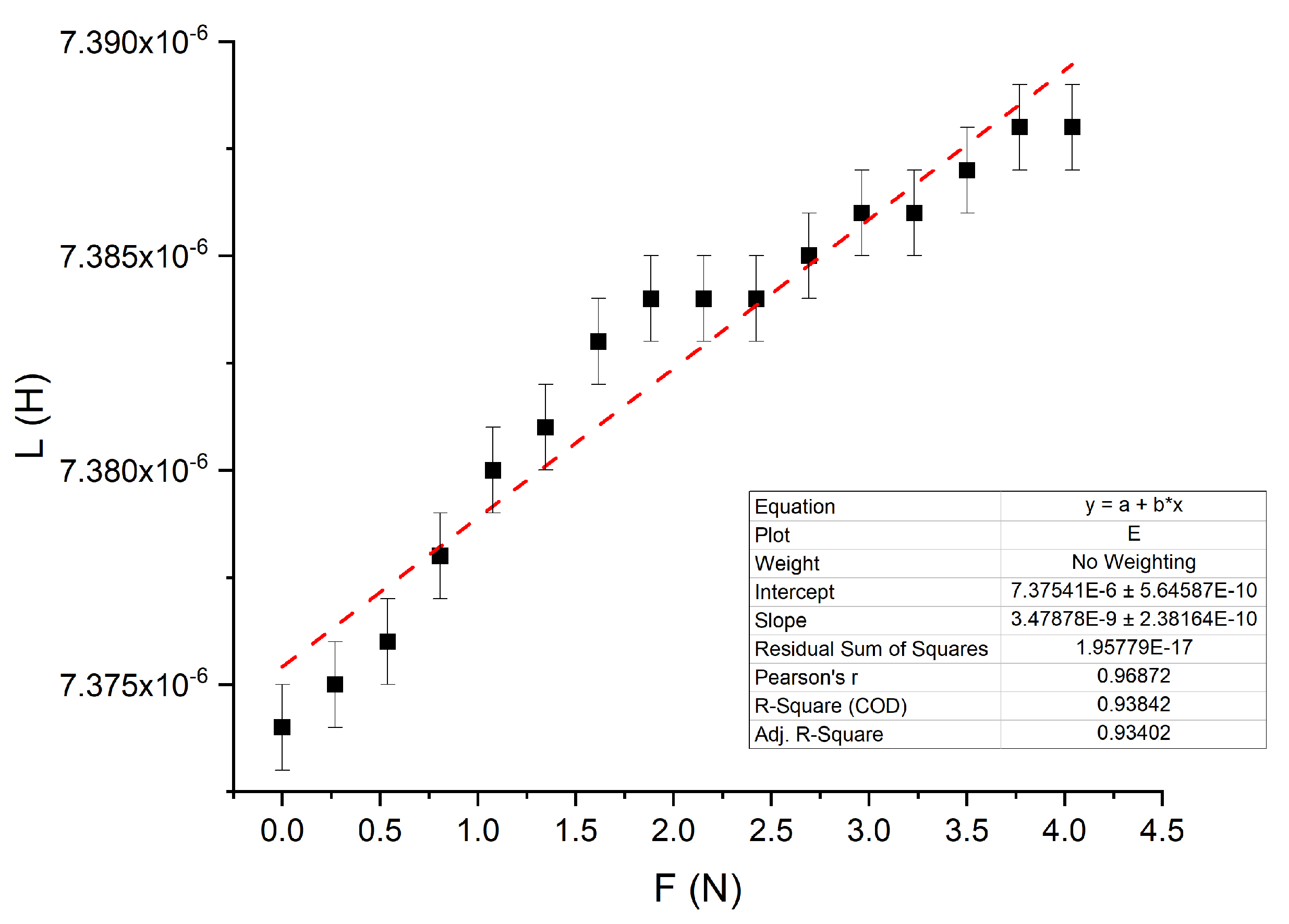
3.4. Sensing Array
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miriyev, A.; Stack, K.; Lipson, H. Soft material for soft actuators. Nat. Commun. 2017, 8, 596. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.H.; Lee, K.T.; Kim, H.J.; Wu, R.; Kim, J.S.; Song, S.H. Smart Soft Composite: An Integrated 3D Soft Morphing Structure Using Bend–Twist Coupling of Anisotropic Materials. Int. J. Precis. Manuf. 2012, 13, 631–634. [Google Scholar] [CrossRef]
- Dalmas, F.; Dendievel, R.; Chazeau, L.; Cavaille, J.Y.; Gauthier, C. Carbon nanotube-filled polymer composites. Numerical simulation of electrical conductivity in three-dimensional entangled fibrous networks. Acta Mater. 2006, 54, 2923–2931. [Google Scholar] [CrossRef]
- Cvek, M.; Kultalkova, E.; Moucka, R.; Urbanek, P.; Sedlacik, M. Lightweight, transparent piezoresistive sensors conceptualized as anisotropic magnetorheological elastomers: A durability study. Int. J. Mech. Sci. 2020, 183, 105816. [Google Scholar] [CrossRef]
- Ren, Z.; Hu, W.; Dong, X.; Sitti, M. Multi-functional soft-bodied jellyfish-like swimming. Nat. Commun. 2019, 10, 2703. [Google Scholar] [CrossRef]
- Kawasetsu, A.; Horii, T.; Ishihara, H.; Asada, M. Flexible Tri-Axis Tactile Sensor Using Spiral Inductor and Magnetorheological Elastomer. IEEE Sens. J. 2018, 18, 5834–5841. [Google Scholar] [CrossRef]
- Kawasetsu, A.; Horii, T.; Ishihara, H.; Asada, M. Mexican-hat-like Response in a flexible Tactile Sensor Using a Magnetorheological Elastomer. Sensors 2018, 18, 587. [Google Scholar] [CrossRef] [Green Version]
- Alkhalaf, A.; Hooshiar, A.; Dargahi, J. Composite magnetorheological elastomers for tactile displays: Enhanced MR-effect through bi-layer composition. Compos. Part B 2020, 190, 107888. [Google Scholar] [CrossRef]
- Kovacik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Alasfar, R.H.; Ahzi, S.; Barth, N.; Kochkodan, V.; Khraisheh, M.; Koç, M. A Review on the Modeling of the Elastic Modulus and Yield Stress of Polymers and Polymer Nanocomposites: Effect of Temperature, Loading Rate and Porosity. Polymers 2022, 14, 360. [Google Scholar] [CrossRef]
- Widdle, R.D., Jr.; Bajaj, A.K.; Davies, P. Measurement of the Poisson’s ratio of flexible polyurethane foam and its influence on a uniaxial compression model. Int. J. Eng. Sci. 2008, 46, 31–49. [Google Scholar] [CrossRef]
- Phadtare, V.D.; Parale, V.G.; Lee, K.Y.; Kim, T.; Puri, V.R.; Park, H.H. Flexible and lightweight Fe3O4/polymer foam composites for microwave-absorption applications. J. Alloys Compd. 2019, 805, 120–129. [Google Scholar] [CrossRef]
- Makarov, D. Energy supply from magnetoelastic composites. Nat. Mater. 2021, 20, 1588–1600. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhao, X.; Xu, J.; Fang, Y.; Chen, G.; Song, Y.; Li, S.; Chen, J. Giant magnetoelastic effect in soft systems for bioelectronics. Nat. Mater. 2021, 20, 1670–1676. [Google Scholar] [CrossRef] [PubMed]
- Diguet, G.; Sebald, G.; Nakano, M.; Lallart, M.; Cavaille, J.Y. Magnetic behavior of Magneto-Rheological Foam under Uniaxial Compression Strain. Smart Mater. Struct. 2022, 31, 025018. [Google Scholar] [CrossRef]
- ImageJ. Available online: https://imagej.nih.gov/ij/ (accessed on 21 December 2021).
- Ju, B.X.; Yu, M.; Fu, J.; Yang, Q.; Liu, X.Q.; Zheng, X. A novel porous magnetorheological elastomer: Preparation and evaluation. Smart Mater. Struct. 2012, 21, 035001. [Google Scholar] [CrossRef]
- Girão, P.S.; Ramos, P.M.P.; Postolache, O.; Pereira, J.M.D. Tactile sensors for robotic applications. Measurement 2013, 46, 1257–1271. [Google Scholar] [CrossRef]
- Rodrigues, P.V.; Ramoa, B.; Machado, A.V.; Cardiff, P.; Nóbrega, J.M. Assessing the Compressive and Impact Behavior of Plastic Safety Toe Caps through Computational Modelling. Polymers 2021, 13, 4332. [Google Scholar] [CrossRef]
- Su, J.; Zhang, Q.M.; Kinm, C.H.; Capps, R. Effects of transitional phenomena on the electric field induced strain–electrostrictive response of a segmented polyurethane elastomer. J. Appl. Polym.Sci. 1998, 65, 1363–1370. [Google Scholar] [CrossRef]
- Li, C.; Liu, J.; Li, J.; Huang, Q.; Xu, H. Studies of 4,40-diphenylmethane diisocyanate (MDI)/1,4-butanediol (BDO) based TPUs by in situ and moving-window two-dimensional correlation infrared spectroscopy: Understanding of multiple DSC endotherms from intermolecular interactions and motions level. Polymer 2012, 53, 5423–5435. [Google Scholar] [CrossRef]
- Sarier, N.; Onder, E. Thermal characteristics of polyurethane foams incorporated with phase change materials. Thermochim. Acta 2007, 454, 90–98. [Google Scholar] [CrossRef]
- Du Tremolet de Lacheisserie, E.; Gignoux, D.; Schlenker, M. Magnetism-Materials and Application; Springer: New York, NY, USA, 2002. [Google Scholar]
- Garnett, J.C.M. Colours in metal glasses and in metallic films. Phil. Trans. R. Soc. A 1904, 203, 385–420. [Google Scholar] [CrossRef] [Green Version]



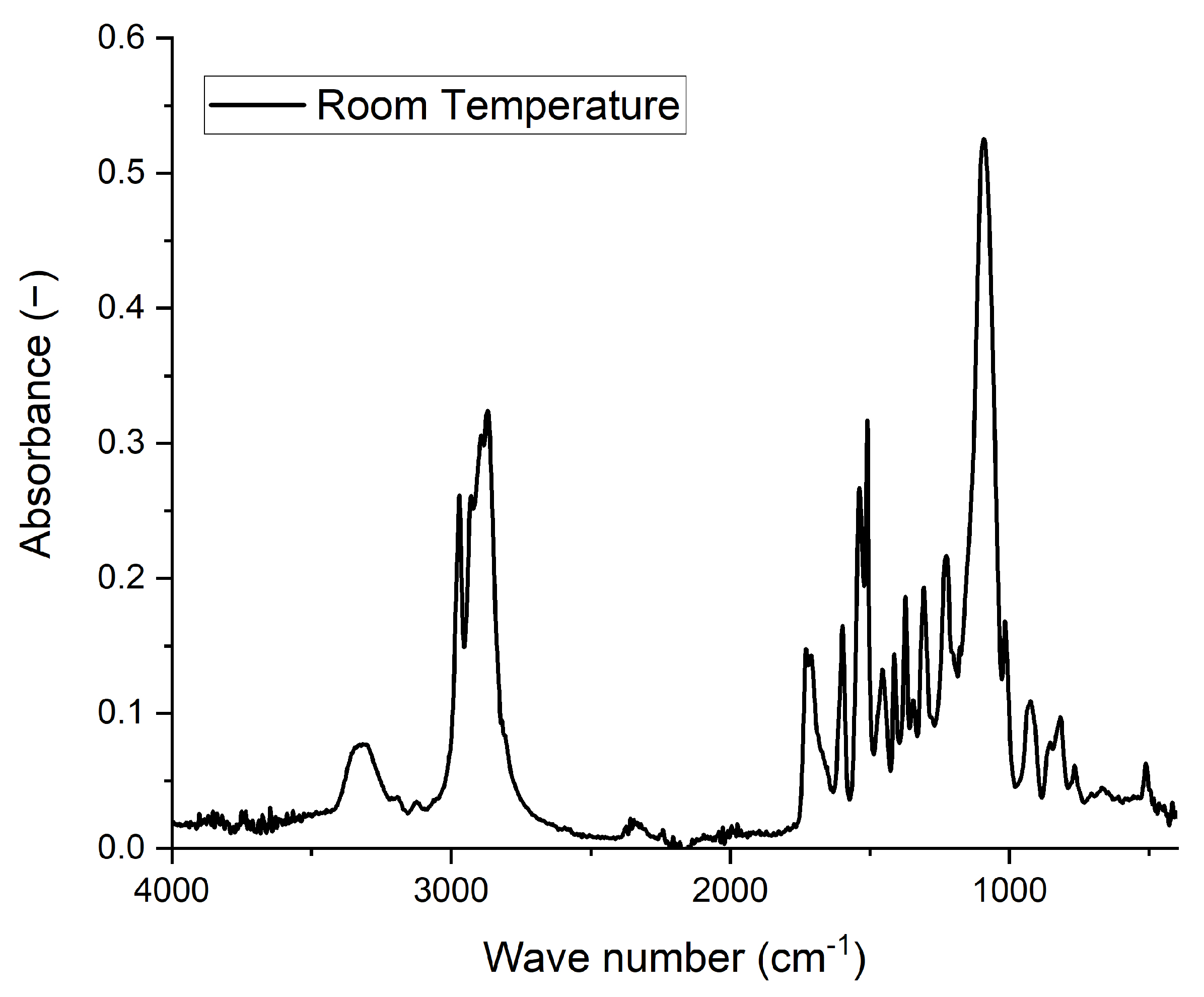


| Wavenumber (cm−1) | Vibration Group | Vibration Type |
|---|---|---|
| 3440 | Free N-H | Stretching 1,2 |
| 3330 | H-bonded N-H | Stretching 1,2 |
| 2890 | CH2 | Asymmetry stretching 2 |
| 2850 | CH2 | Symmetry stretching 2 |
| 1709 | Free C=O | Stretching 1 |
| 1728 | H-bonded C=O | Stretching 1 |
| 1597 | Benzene ring | Framework vibration 2 |
| 1537 | N-H | Bending 2 |
| 1412 | CH2 | Bending 2,3 |
| 1373 | CN | Stretching 3 |
| 1225 | CO | Stretching 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diguet, G.; Froemel, J.; Muroyama, M.; Ohtaka, K. Tactile Sensing Using Magnetic Foam. Polymers 2022, 14, 834. https://doi.org/10.3390/polym14040834
Diguet G, Froemel J, Muroyama M, Ohtaka K. Tactile Sensing Using Magnetic Foam. Polymers. 2022; 14(4):834. https://doi.org/10.3390/polym14040834
Chicago/Turabian StyleDiguet, Gildas, Joerg Froemel, Masanori Muroyama, and Koichi Ohtaka. 2022. "Tactile Sensing Using Magnetic Foam" Polymers 14, no. 4: 834. https://doi.org/10.3390/polym14040834
APA StyleDiguet, G., Froemel, J., Muroyama, M., & Ohtaka, K. (2022). Tactile Sensing Using Magnetic Foam. Polymers, 14(4), 834. https://doi.org/10.3390/polym14040834