Data-Driven Modelling of Polyethylene Recycling under High-Temperature Extrusion
Abstract
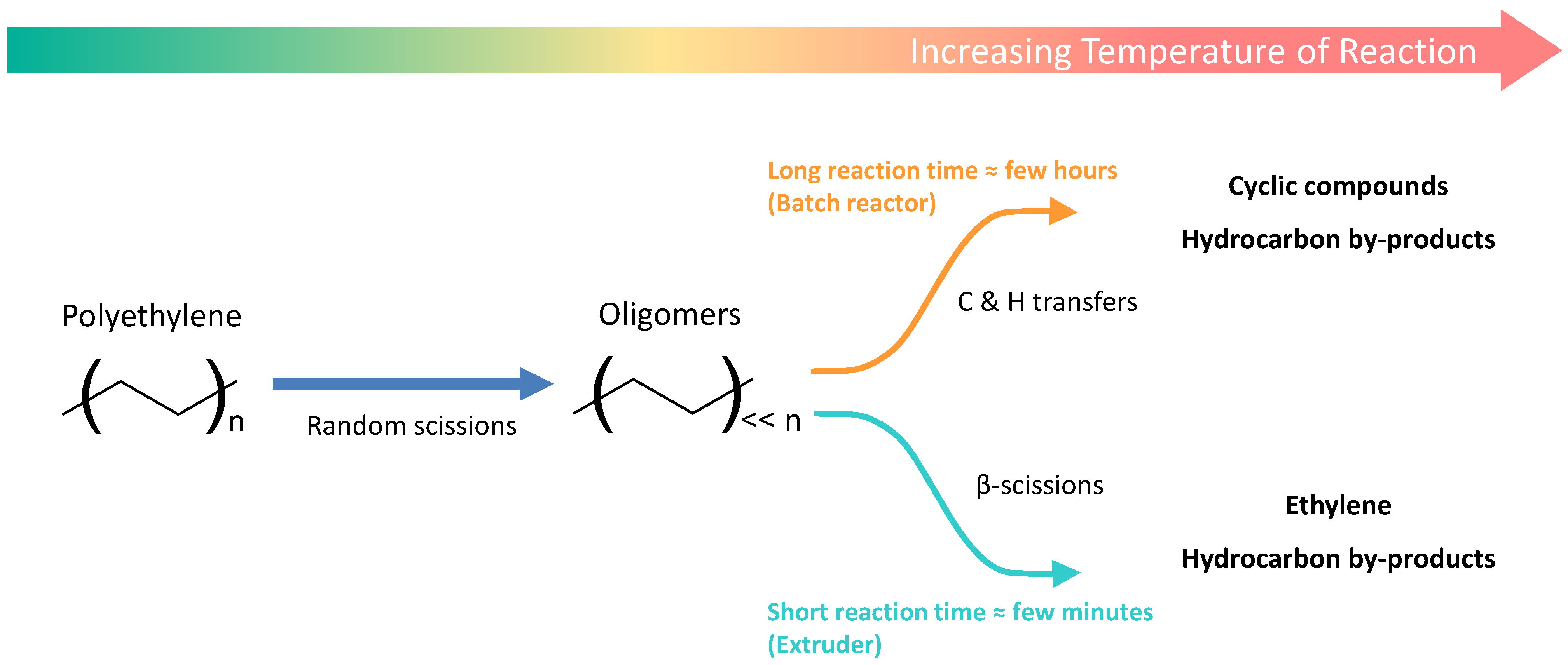
:1. Introduction
2. Experimental Section
2.1. Materials and Extrusion
2.2. Characterizations
2.3. Theoretical Methodologies
2.3.1. Determination of Mw from Viscoelastic Behaviour
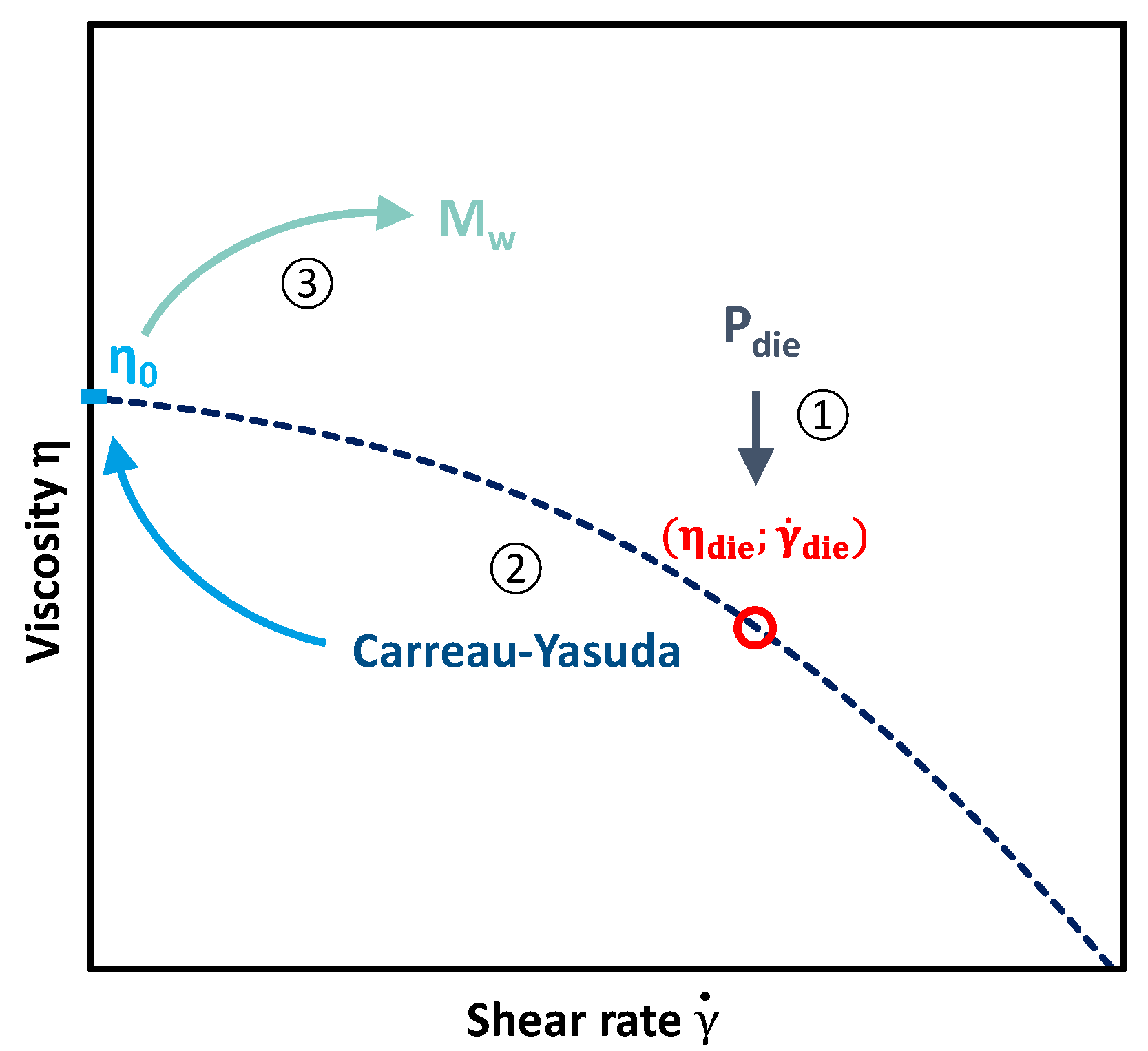
2.3.2. Determination of Mw from Measured Die Pressure
3. Modelling and Machine Learning
3.1. Simulation
3.2. Machine-Learning
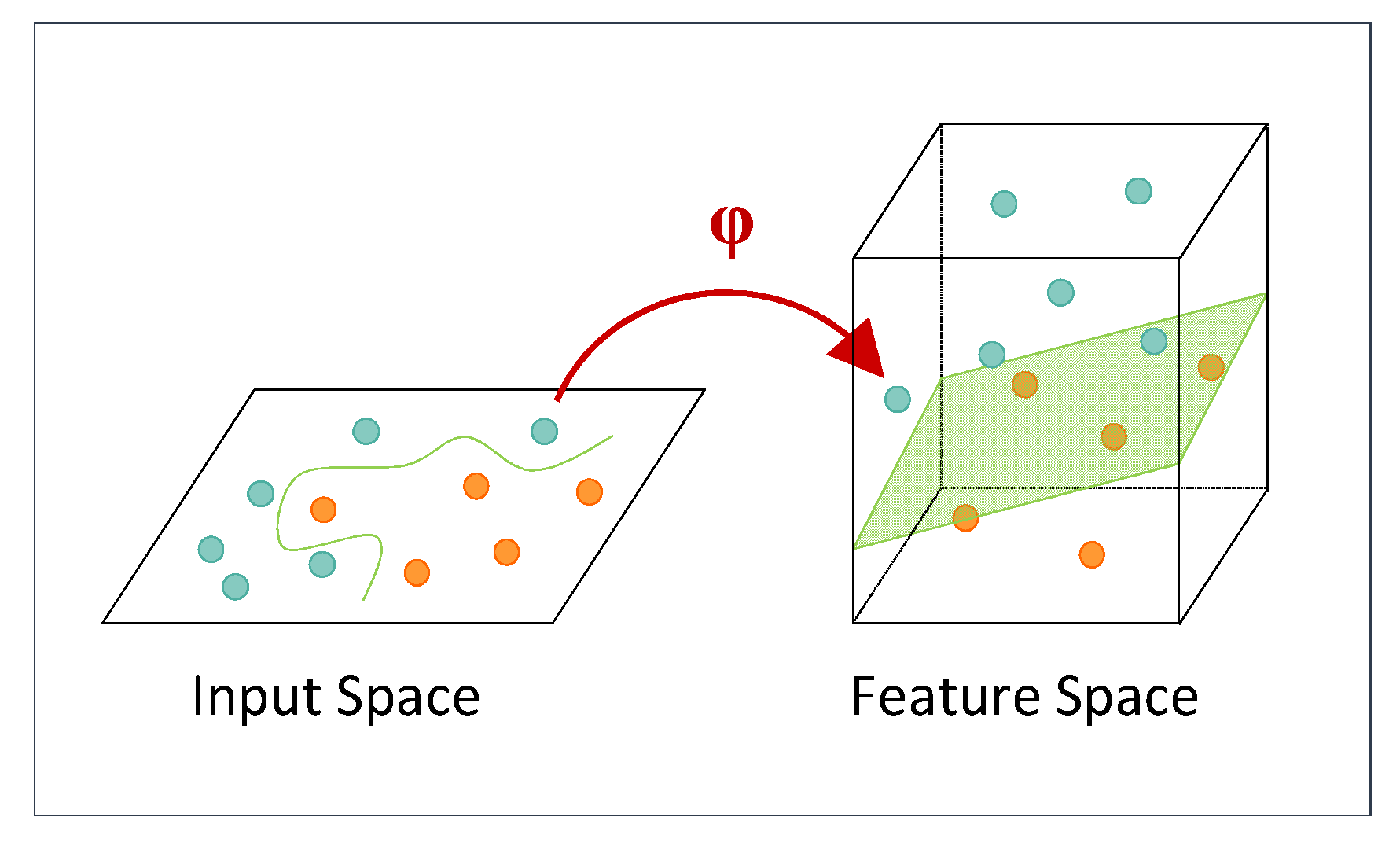
3.2.1. Support Vector Machine Regression—SVR
3.2.2. Sparsed Proper Generalized Decomposition—sPGD
3.2.3. Stochastic Methods
4. Results and Discussion
4.1. Comparison of Estimated and Measured Viscosities
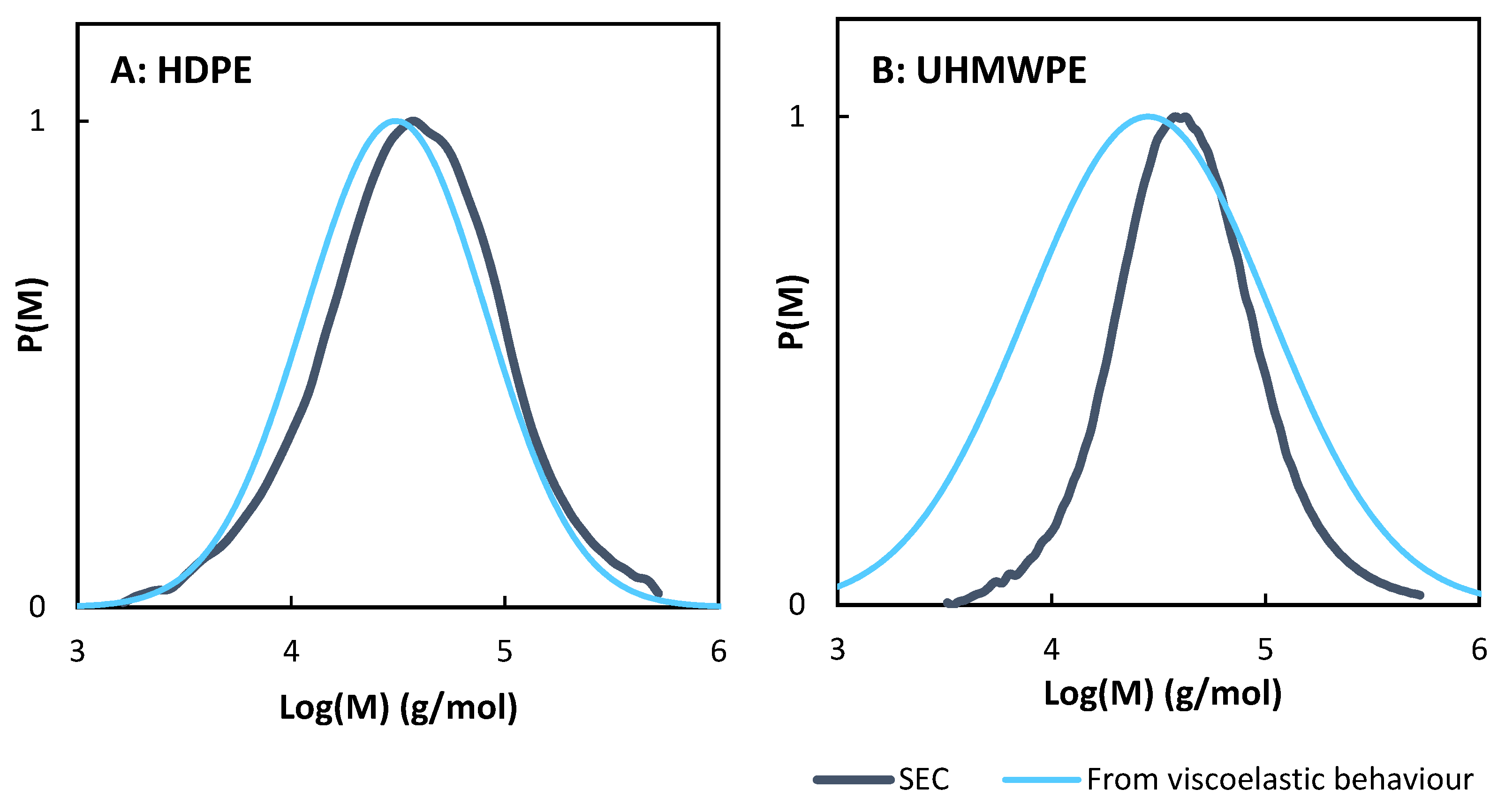
4.2. Molecular Weight Distribution
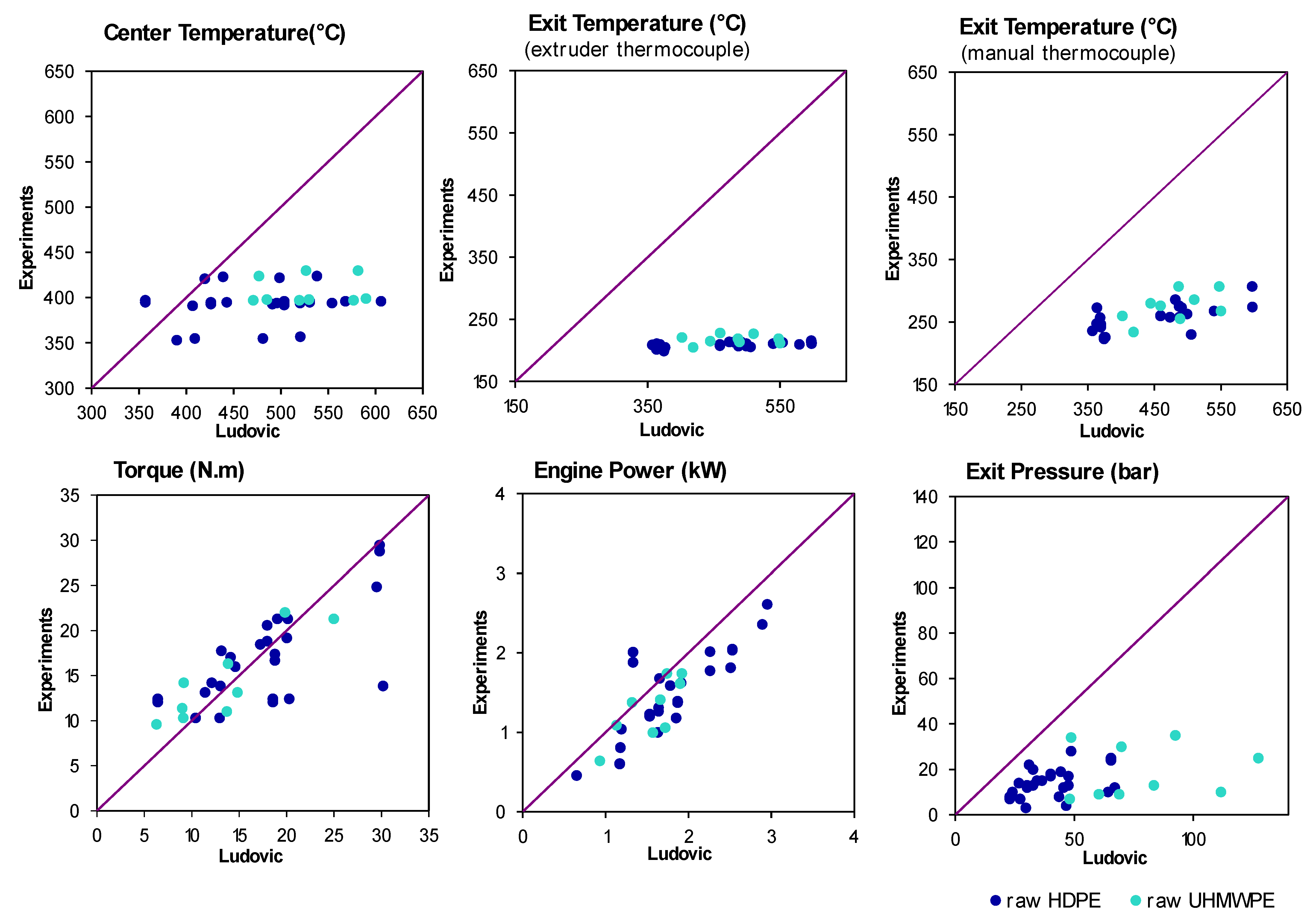
4.3. Ludovic® Simulation
4.4. Data-Based Modelling
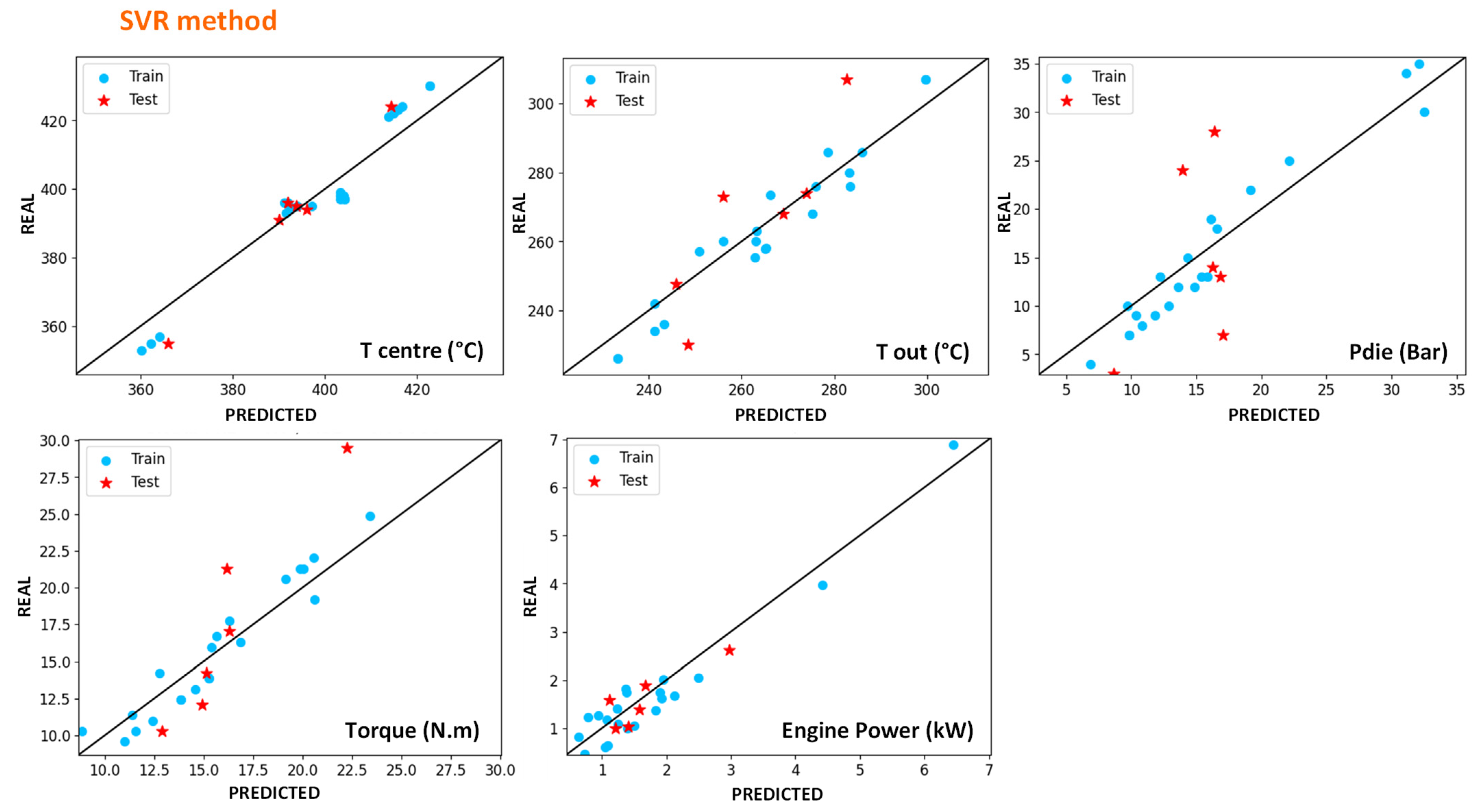
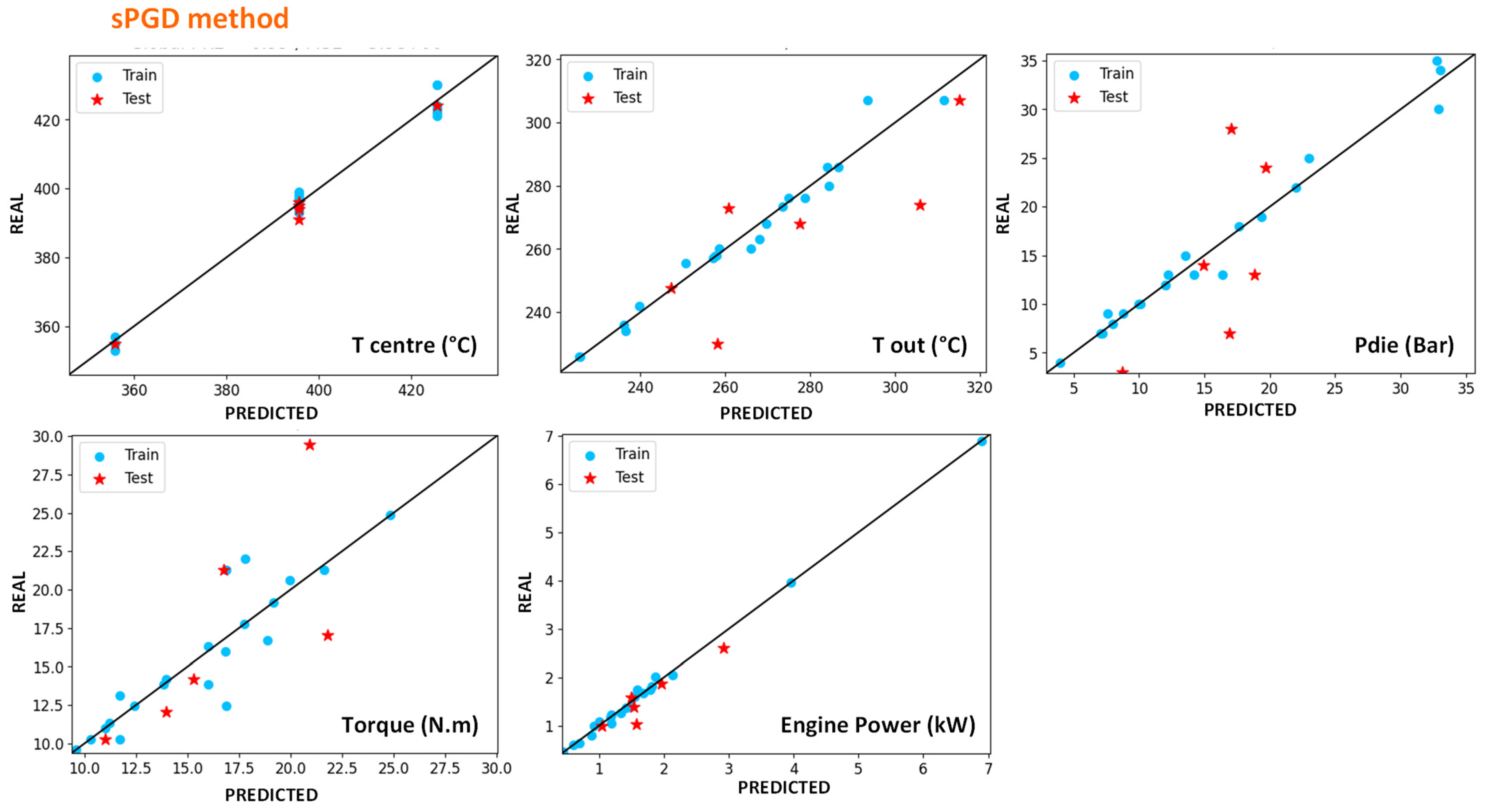
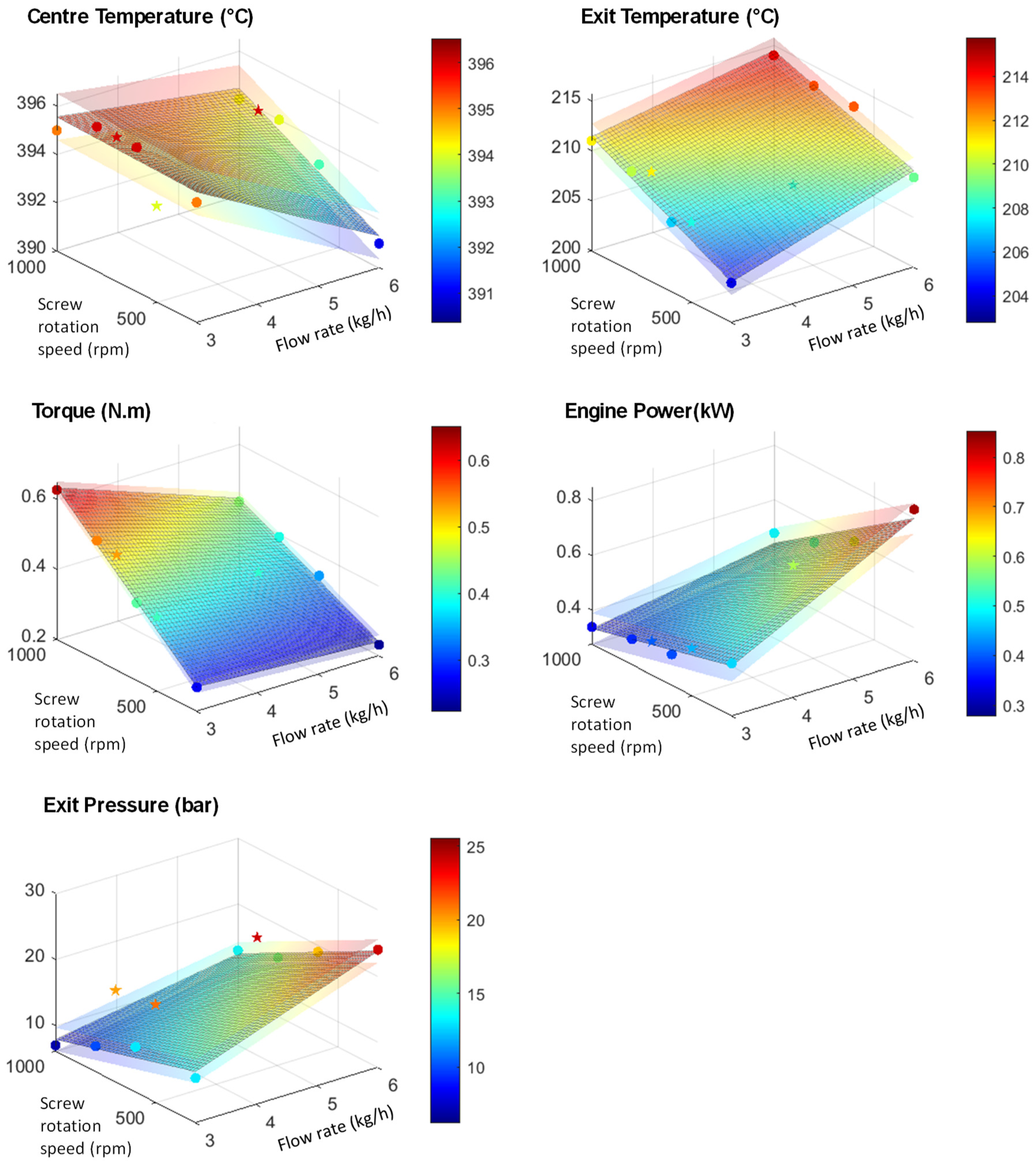
4.4.1. Modelling of In-Line Measures with Machine-Learning Methods
4.4.2. Modelling of Viscosity and Molecular Weight
4.4.3. Stochastic Models
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detail of Data’s
| Process Inputs | Extrusion in-Line Measurements | |||||||
|---|---|---|---|---|---|---|---|---|
| PE Type | Q (kg/h) | N (rpm) | Tmax (°C) | Torque (N·m) | Pe (Bar) | Tc (°C) | Engine Power (kW) | Te (°C) |
| HDPE | 3 | 300 | 350 | 21.3 | 28 | 355 | 1.04 | 248 |
| HDPE | 3 | 600 | 350 | 17.7 | 22 | 357 | 1.68 | 273 |
| HDPE | 6 | 300 | 350 | 13.8 | 12 | 353 | 3.97 | 236 |
| HDPE | 6 | 600 | 350 | 12.4 | 12 | 355 | 6.89 | 258 |
| HDPE | 1 | 300 | 390 | 10.3 | 7 | 395 | 0.46 | 226 |
| HDPE | 3 | 300 | 390 | 16.7 | 13 | 395 | 0.81 | 242 |
| HDPE | 3 | 300 | 390 | 17.4 | 17 | 393 | 0.81 | 247 |
| HDPE | 3 | 500 | 390 | 16.0 | 15 | 394 | 1.23 | 260 |
| HDPE | 3 | 500 | 390 | 16.0 | 15 | 394 | 1.20 | 261 |
| HDPE | 3 | 600 | 390 | 13.8 | 12 | 395 | 1.31 | 263 |
| HDPE | 3 | 700 | 390 | 14.2 | 14 | 396 | 1.59 | 268 |
| HDPE | 3 | 1000 | 390 | 12.4 | 8 | 397 | 2.01 | 274 |
| HDPE | 5 | 600 | 390 | 20.6 | 18 | 396 | 2.01 | 276 |
| HDPE | 6 | 300 | 390 | 28.7 | 25 | 391 | 0.69 | 273 |
| HDPE | 6 | 600 | 390 | 21.3 | 19 | 393 | 1.02 | 286 |
| HDPE | 6 | 1000 | 390 | 17.0 | 20 | 396 | 0.38 | 307 |
| HDPE | 3 | 300 | 420 | 12.4 | 4 | 423 | 0.60 | 226 |
| HDPE | 3 | 600 | 420 | 10.3 | 3 | 424 | 1.00 | 230 |
| HDPE | 6 | 300 | 420 | 24.8 | 10 | 421 | 0.59 | 257 |
| HDPE | 6 | 600 | 420 | 19.2 | 8 | 422 | 1.81 | 258 |
| UHMWPE | 1 | 300 | 390 | 13.1 | 25 | 397 | 0.64 | 260 |
| UHMWPE | 1 | 600 | 390 | 11.4 | 13 | 398 | 1.09 | 276 |
| UHMWPE | 1 | 1000 | 390 | 9.6 | 9 | 399 | 1.38 | 286 |
| UHMWPE | 3 | 400 | 390 | 22.0 | 35 | 398 | 1.41 | 280 |
| UHMWPE | 3 | 600 | 390 | 16.3 | 30 | 397 | 1.74 | 307 |
| UHMWPE | 3 | 1000 | 390 | 14.2 | 34 | 397 | 1.74 | 307 |
| UHMWPE | 3 | 300 | 420 | 21.3 | 10 | 424 | 1.00 | 234 |
| UHMWPE | 3 | 600 | 420 | 11.0 | 9 | 430 | 1.06 | 256 |
| UHMWPE | 3 | 1000 | 420 | 10.3 | 7 | 430 | 1.61 | 268 |
| Process Inputs | Ludovic® Simulation | |||||||
|---|---|---|---|---|---|---|---|---|
| Polymer | Q (kg/h) | N (rpm) | Tmax (°C) | Torque (N·m) | Te (°C) | Tc (°C) | Pe (bar) | Engine Power (kW) |
| HDPE | 3 | 300 | 350 | 19.0 | 363 | 409 | 49 | 1.19 |
| HDPE | 3 | 600 | 350 | 13.1 | 491 | 520 | 31 | 1.65 |
| HDPE | 6 | 300 | 350 | 30.2 | 357 | 390 | 67 | 1.90 |
| HDPE | 6 | 600 | 350 | 20.3 | 473 | 481 | 45 | 2.55 |
| HDPE | 1 | 300 | 390 | 10.4 | 376 | 443 | 27 | 0.65 |
| HDPE | 3 | 300 | 390 | 18.7 | 369 | 426 | 47 | 1.18 |
| HDPE | 3 | 500 | 390 | 14.6 | 459 | 496 | 34 | 1.53 |
| HDPE | 3 | 500 | 390 | 14.6 | 459 | 496 | 34 | 1.53 |
| HDPE | 3 | 600 | 390 | 13.0 | 499 | 530 | 30 | 1.64 |
| HDPE | 3 | 700 | 390 | 12.1 | 539 | 568 | 27 | 1.78 |
| HDPE | 3 | 800 | 390 | 11.4 | 579 | 606 | 24 | 1.91 |
| HDPE | 3 | 1000 | 390 | 6.4 | 597 | 356 | 23 | 1.33 |
| HDPE | 5 | 600 | 390 | 17.9 | 487 | 503 | 40 | 2.26 |
| HDPE | 6 | 300 | 390 | 29.8 | 363 | 407 | 65 | 1.87 |
| HDPE | 6 | 600 | 390 | 20.1 | 481 | 491 | 44 | 2.53 |
| HDPE | 6 | 800 | 390 | 17.2 | 553 | 554 | 36 | 2.89 |
| HDPE | 6 | 1000 | 390 | 14.1 | 597 | 520 | 32 | 2.95 |
| HDPE | 3 | 300 | 420 | 18.5 | 374 | 439 | 47 | 1.17 |
| HDPE | 3 | 600 | 420 | 12.9 | 505 | 538 | 30 | 1.63 |
| HDPE | 6 | 300 | 420 | 29.5 | 368 | 419 | 64 | 1.85 |
| HDPE | 6 | 600 | 420 | 20.0 | 488 | 498 | 43 | 2.51 |
| UHMWPE | 1 | 300 | 390 | 14.8 | 402 | 471 | 127 | 0.93 |
| UHMWPE | 1 | 600 | 390 | 9.0 | 459 | 530 | 83 | 1.13 |
| UHMWPE | 1 | 1000 | 390 | 6.3 | 510 | 590 | 60 | 1.32 |
| UHMWPE | 3 | 400 | 390 | 19.8 | 444 | 485 | 92 | 1.66 |
| UHMWPE | 3 | 600 | 390 | 13.8 | 486 | 519 | 70 | 1.74 |
| UHMWPE | 3 | 1000 | 390 | 9.2 | 547 | 577 | 49 | 1.92 |
| UHMWPE | 3 | 300 | 420 | 25.0 | 419 | 477 | 112 | 1.57 |
| UHMWPE | 3 | 600 | 420 | 13.7 | 488 | 527 | 69 | 1.72 |
| UHMWPE | 3 | 1000 | 420 | 9.1 | 550 | 581 | 48 | 1.90 |
| Process Inputs | Zero Shear-Rate Viscosities | Molecular Weights (Inverse Rheology) | Mw (From Die Pressure) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Polymer | Q (kg/h) | N (rpm) | T (°C) | η0 from Die Pressure (Pa·s) | η0 Rheometer (Pa·s) | Mw (g/mol) | Mz (g/mol) | Mn (g/mol) | Mw (g/mol) |
| HDPE | 3 | 300 | 350 | 2.6 × 104 | 3.2 × 104 | 1.1 × 105 | 5.0 × 105 | 2.4 × 104 | 1.1 × 105 |
| HDPE | 3 | 600 | 350 | 1.3 × 104 | 2.1 × 104 | 9.1 × 104 | 4.3 × 105 | 1.9 × 104 | 8.6 × 104 |
| HDPE | 6 | 300 | 350 | 1.1 × 104 | 3.5 × 104 | 1.0 × 105 | 5.2 × 105 | 1.9 × 104 | 8.3 × 104 |
| HDPE | 6 | 600 | 350 | 1.1 × 104 | 1.3 × 104 | 8.4 × 104 | 3.7 × 105 | 1.9 × 104 | 8.2 × 104 |
| HDPE | 3 | 300 | 390 | 6.4 × 103 | 3.2 × 103 | 6.0 × 104 | 1.5 × 105 | 2.4 × 104 | 7.0 × 104 |
| HDPE | 6 | 300 | 390 | 7.4 × 103 | 3.4 × 103 | 7.1 × 104 | 2.2 × 105 | 2.3 × 104 | 7.3 × 104 |
| HDPE | 6 | 600 | 390 | 4.0 × 103 | 2.5 × 103 | 6.4 × 104 | 2.0 × 105 | 2.0 × 104 | 6.1 × 104 |
| HDPE | 6 | 1000 | 390 | 1.4 × 103 | 1.2 × 103 | 5.4 × 104 | 1.5 × 105 | 1.9 × 104 | 4.5 × 104 |
| HDPE | 3 | 300 | 420 | 3.5 × 102 | 9.0 × 101 | 2.8 × 104 | 5.9 × 104 | 1.3 × 104 | 3.0 × 104 |
| HDPE | 3 | 600 | 420 | 2.2 × 102 | 1.0 × 102 | 2.9 × 104 | 5.9 × 104 | 1.4 × 104 | 2.6 × 104 |
| HDPE | 6 | 300 | 420 | 8.1 × 102 | 3.5 × 102 | 4.1 × 104 | 9.3 × 104 | 1.8 × 104 | 3.8 × 104 |
| HDPE | 6 | 600 | 420 | 5.2 × 102 | 3.1 × 102 | 3.9 × 104 | 8.7 × 104 | 1.8 × 104 | 3.4 × 104 |
| UHMWPE | 1 | 300 | 390 | 7.4 × 104 | 5.0 × 104 | 1.2 × 105 | 1.4 × 106 | 9.6 × 103 | 1.4 × 105 |
| UHMWPE | 1 | 600 | 390 | 1.3 × 104 | 5.4 × 104 | 1.1 × 105 | 8.8 × 105 | 1.3 × 104 | 8.6 × 104 |
| UHMWPE | 1 | 1000 | 390 | 5.8 × 103 | 1.0 × 104 | 6.6 × 104 | 3.5 × 105 | 1.2 × 104 | 6.8 × 104 |
| UHMWPE | 3 | 400 | 390 | 5.3 × 104 | 7.0 × 103 | 1.6 × 105 | 1.5 × 106 | 1.6 × 104 | 1.3 × 105 |
| UHMWPE | 3 | 600 | 390 | 3.1 × 104 | 1.0 × 105 | 1.6 × 105 | 3.4 × 106 | 5.8 × 103 | 1.1 × 105 |
| UHMWPE | 3 | 1000 | 390 | 4.8 × 104 | 2.9 × 104 | 1.2 × 105 | 8.7 × 105 | 1.5 × 104 | 1.3 × 105 |
| UHMWPE | 3 | 300 | 420 | 1.9 × 103 | 3.1 × 103 | 6.3 × 104 | 2.4 × 105 | 1.6 × 104 | 4.9 × 104 |
| UHMWPE | 3 | 600 | 420 | 1.5 × 103 | 4.2 × 103 | 6.8 × 104 | 2.6 × 105 | 1.8 × 104 | 4.6 × 104 |
| UHMWPE | 3 | 1000 | 420 | 9.4 × 102 | 1.9 × 103 | 5.8 × 104 | 2.0 × 105 | 1.7 × 104 | 4.6 × 104 |
References
- PlascticEurope-Association of Plastics Manufactures, Plastics—The Facts 2020. PlasticEurope 2020, 1–64. Available online: https://www.plasticseurope.org/en/resources/publications/4312-plastics-facts-2020 (accessed on 2 June 2021).
- Al-Salem, S.M.; Lettieri, P.; Baeyens, J. Recycling and recovery routes of plastic solid waste (PSW): A review. Waste Manag. 2009, 29, 2625–2643. [Google Scholar] [CrossRef] [PubMed]
- Meran, C.; Ozturk, O.; Yuksel, M. Examination of the possibility of recycling and utilizing recycled polyethylene and polypropylene. Mater. Des. 2008, 29, 701–705. [Google Scholar] [CrossRef]
- Gu, F.; Guo, J.; Zhang, W.; Summers, P.A.; Hall, P. From waste plastics to industrial raw materials: A life cycle assessment of mechanical plastic recycling practice based on a real-world case study. Sci. Total Environ. 2017, 601–602, 1192–1207. [Google Scholar] [CrossRef]
- Pinheiro, L.A.; Chinelatto, M.A.; Canevarolo, S.V. The role of chain scission and chain branching in high density polyethylene during thermo-mechanical degradation. Polym. Degrad. Stab. 2004, 86, 445–453. [Google Scholar] [CrossRef]
- Mastellone, M.L.; Perugini, F.; Ponte, M.; Arena, U. Fluidized bed pyrolysis of a recycled polyethylene. Polym. Degrad. Stab. 2002, 76, 479–487. [Google Scholar] [CrossRef]
- Basfar, A.A.; Idriss Ali, K.M. Natural weathering test for films of various formulations of low density polyethylene (LDPE) and linear low density polyethylene (LLDPE). Polym. Degrad. Stab. 2006, 91, 437–443. [Google Scholar] [CrossRef]
- Al-Salem, S.M. Influence of natural and accelerated weathering on various formulations of linear low density polyethylene (LLDPE) films. Mater. Des. 2009, 30, 1729–1736. [Google Scholar] [CrossRef]
- Benoit, N.; González-Núñez, R.; Rodrigue, D. High density polyethylene degradation followed by closedloop recycling. Prog. Rubber, Plast. Recycl. Technol. 2017, 33, 17–37. [Google Scholar] [CrossRef]
- Salomão, R.; Pandolfelli, V.C. Anti-spalling fibers for refractory castables: A potential application for recycling drinking straws. Ceram. Int. 2020, 46, 14262–14268. [Google Scholar] [CrossRef]
- Adhikary, K.B.; Pang, S.; Staiger, M.P. Dimensional stability and mechanical behaviour of wood-plastic composites based on recycled and virgin high-density polyethylene (HDPE). Compos. Part B Eng. 2008, 39, 807–815. [Google Scholar] [CrossRef]
- Lei, Y.; Wu, Q.; Yao, F.; Xu, Y. Preparation and properties of recycled HDPE/natural fiber composites. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1664–1674. [Google Scholar] [CrossRef]
- Christakopoulos, F.; Troisi, E.; Friederichs, N.; Vermant, J.; Tervoort, T.A. “Tying the Knot”: Enhanced Recycling through Ultrafast Entangling across Ultrahigh Molecular Weight Polyethylene Interfaces. Macromolecules 2021, 54, 9452–9460. [Google Scholar] [CrossRef]
- Kulkarni, G.S. Introduction to Polymer and Their Recycling Techniques; Elsevier Inc.: Amsterdam, The Netherlands, 2018; ISBN 9780323511346. [Google Scholar]
- Kaminsky, W.; Schlesselmann, B.; Simon, C. Olefins from polyolefins and mixed plastics by pyrolysis. J. Anal. Appl. Pyrolysis 1995, 32, 19–27. [Google Scholar] [CrossRef]
- Mccaffrey, C.; Cooper, C.; Kamal, M.R. Thermolysis of Polyethylene/Polystyrene Mixtures. J. Appl. Polym. Sci. 1996, 60, 2133–2140. [Google Scholar] [CrossRef]
- Bockhorn, H.; Hornung, A.; Hornung, U. Stepwise pyrolysis for raw material recovery from plastic waste. J. Anal. Appl. Pyrolysis 1998, 46, 1–13. [Google Scholar] [CrossRef]
- Horvat, N.; Ng, F.T.T. Tertiary polymer recycling: Study of polyethylene thermolysis as a first step to synthetic diesel fuel. Fuel 1999, 78, 459–470. [Google Scholar] [CrossRef]
- Nishino, J.; Itoh, M.; Fujiyoshi, H.; Uemichi, Y. Catalytic degradation of plastic waste into petrochemicals using Ga-ZSM-5. Fuel 2008, 87, 3681–3686. [Google Scholar] [CrossRef]
- Del Remedio Hernández, M.; García, Á.N.; Marcilla, A. Catalytic flash pyrolysis of HDPE in a fluidized bed reactor for recovery of fuel-like hydrocarbons. J. Anal. Appl. Pyrolysis 2007, 78, 272–281. [Google Scholar] [CrossRef]
- Achilias, D.S.; Roupakias, C.; Megalokonomos, P.; Lappas, A.A.; Antonakou, V. Chemical recycling of plastic wastes made from polyethylene (LDPE and HDPE) and polypropylene (PP). J. Hazard. Mater. 2007, 149, 536–542. [Google Scholar] [CrossRef]
- Buekens, A.G.; Huang, H. Catalytic plastics cracking for recovery of gasoline-range hydrocarbons from municipal plastic wastes. Resour. Conserv. Recycl. 1998, 23, 163–181. [Google Scholar] [CrossRef]
- Guy, L.; Fixari, B. Waxy polyethylenes from solution thermolysis of high density polyethylene: Inert and H-donor solvent dilution effect. Polymer 1999, 40, 2845–2857. [Google Scholar] [CrossRef]
- Scheirs, J.; Kaminsky, W. Recycling and Pyrolysis of Waste Plastics: Converting Waste Plastics into Diesel and Other Fuels; Scheirs, J., Kaminsky, W., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; Volume 3, ISBN 0-470-02152-7. [Google Scholar]
- Vollmer, I.; Jenks, M.J.F.; Roelands, M.C.P.; White, R.J.; van Harmelen, T.; de Wild, P.; van der Laan, G.P.; Meirer, F.; Keurentjes, J.T.F.; Weckhuysen, B.M. Beyond Mechanical Recycling: Giving New Life to Plastic Waste. Angew. Chem.-Int. Ed. 2020, 59, 15402–15423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manas, D.; Manas, M.; Mizera, A.; Navratil, J.; Ovsik, M.; Tomanova, K.; Sehnalek, S. Use of irradiated polymers after their lifetime period. Polymers 2018, 10, 641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manas, D.; Manas, M.; Mizera, A.; Stoklasek, P.; Navratil, J.; Sehnalek, S.; Drabek, P. The high density polyethylene composite with recycled radiation cross-linked filler of rHDPEx. Polymers 2018, 10, 1361. [Google Scholar] [CrossRef] [Green Version]
- Elmanovich, I.V.; Stakhanov, A.I.; Kravchenko, E.I.; Stakhanova, S.V.; Pavlov, A.A.; Ilyin, M.M.; Kharitonova, E.P.; Gallyamov, M.O.; Khokhlov, A.R. Chemical recycling of polyethylene in oxygen-enriched supercritical CO2. J. Supercrit. Fluids 2021, 181, 105503. [Google Scholar] [CrossRef]
- Inderthal, H.; Tai, S.L.; Harrison, S.T.L. Non-Hydrolyzable Plastics—An Interdisciplinary Look at Plastic Bio-Oxidation. Trends Biotechnol. 2021, 39, 12–23. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, D.; Wei, N. Enzyme discovery and engineering for sustainable plastic recycling. Trends Biotechnol. 2022, 40, 22–37. [Google Scholar] [CrossRef]
- Castéran, F.; Ibanez, R.; Argerich, C.; Delage, K.; Chinesta, F.; Cassagnau, P. Application of Machine Learning Tools for the Improvement of Reactive Extrusion Simulation. Macromol. Mater. Eng. 2020, 305, 2000375. [Google Scholar] [CrossRef]
- Ibañez, R.; Casteran, F.; Argerich, C.; Ghnatios, C.; Hascoet, N.; Ammar, A.; Cassagnau, P.; Chinesta, F. On the Data-Driven Modeling of Reactive Extrusion. Fluids 2020, 5, 94. [Google Scholar] [CrossRef]
- Cassagnau, P.; Montfort, J.P.; Marin, G.; Monge, P. Rheology of polydisperse polymers: Relationship between intermolecular interactions and molecular weight distribution. Rheol. Acta 1993, 32, 156–167. [Google Scholar] [CrossRef]
- Des Cloizeaux, J.; Jannik, G. Polymers in Solution Their Modelling and Structure; Oxford University Press: Oxford, UK, 1990; ISBN 0-19-852036-0. [Google Scholar]
- Vega, J.F.; Rastogi, S.S.; Peters, G.G.; Meijer, H.E.H. Rheology and reptation of linear polymers. Ultrahigh molecular weight chain dynamics in the melt. J. Rheol. 2004, 48, 663–678. [Google Scholar] [CrossRef] [Green Version]
- Wasserman, S.H.; Graessley, W.W. Prediction of linear viscoelastic response for entangled polyolefin melts from molecular weight distribution. Polym. Eng. Sci. 1996, 36, 852–861. [Google Scholar] [CrossRef]
- Rochefort, W.E.; Smith, G.G.; Rachapudy, H.; Raju, V.R.; Graessley, W.W. Properties of amorphous and crystallizable hydrocarbon polymers. II. Rheology of linear and star-branched polybutadiene. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1197–1210. [Google Scholar] [CrossRef]
- Wood-Adams, P.M.; Dealy, J.M.; DeGroot, A.W.; Redwine, O.D. Effect of molecular structure on the viscoelastic behavior of epoxy resin. Kobunshi Ronbunshu 1976, 33, 19–27. [Google Scholar] [CrossRef]
- Vergnes, B.; Della Valle, G.; Delamare, L. A global computer software for polymer flows in corotating twin screw extruders. Polym. Eng. Sci. 1998, 38, 1781–1792. [Google Scholar] [CrossRef]
- Fel, E.; Massardier, V.; Mélis, F.; Vergnes, B.; Cassagnau, P. Residence time distribution in a high shear twin screw extruder. Int. Polym. Process. 2014, 29, 71–80. [Google Scholar] [CrossRef]
- Berzin, F.; Tara, A.; Tighzert, L.; Vergnes, B. Importance of Coupling Between Specific Energy and Viscosity in the Modeling of Twin Screw Extrusion of Starchy Products. Polym. Eng. Sci. 2010, 50, 1758–1766. [Google Scholar] [CrossRef]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Ibáñez, R.; Abisset-Chavanne, E.; Ammar, A.; González, D.; Cueto, E.; Huerta, A.; Duval, J.L.; Chinesta, F. A multidimensional data-driven sparse identification technique: The sparse proper generalized decomposition. Complexity 2018, 2018, 5608286. [Google Scholar] [CrossRef]




| Materials | Tmax * | Flow Rate | Screw Rotation Speed |
|---|---|---|---|
| HDPE XRT70 TOTAL, (MFI = 0.7 g/10 min (190 °C, 5 kg)) | 350 °C 390 °C 420 °C | 1 to 6 kg/h | 300 to 1000 rpm |
| UHMWPE GUR 4130, Celanese, (MFI < 0.1 g/10 min (190 °C, 21.6 kg)) | 390 °C 420 °C | 1 and 3 kg/h | 300 to 1000 rpm |
| Symbol | Parameter | Value |
|---|---|---|
| T | Test Temperature | 190 °C |
| α | Relaxation time exponent | 3.6 |
| Plateau modulus | 2.3 × 106 Pa | |
| Ea | Activation Energy | 30 kJ/mol |
| Kλ | Front Factor | 2.5 × 10−21 s·(mol/g)3.6 |
| Me | Entanglement Molecular weight | 1250 g/mol |
| Mr | Reptation Molecular weight | 2500 g/mol |
| Thermal Properties | HDPE XRT70 | UHMWPE GUR 4130 |
|---|---|---|
| Heat Capacity [J kg−1 K−1] | 1550 | 1840 |
| Density [kg m−3] | 947 | 930 |
| Thermal Conductivity [W mK−1] | 0.35 | 0.41 |
| Melting Temperature [°C] | 129 | 135 |
| Melting enthalpy [kJ kg−1] | 190 | 122 |
| Viscosity Law | Carreau-Yasuda: | Power Law: |
| = 2.5 × 106 Pa·s = 0.33 s = 0.25 = 0.058 Tref = 190 °C Ea = 30 kJ·mol−1 | = 0 = 2.86 × 106 Pa·s Tref = 190 °C Ea = 30 kJ·mol−1 |
| R2 Error | Centre Temperature | Exit Temperature | Torque | Engine Power | Die Pressure |
|---|---|---|---|---|---|
| SVR train | 0.93 | 0.93 | 0.91 | 0.93 | 0.92 |
| SVR global | 0.92 | 0.88 | 0.8 | 0.92 | 0.75 |
| sPGD train | 0.99 | 0.91 | 0.82 | 1 | 0.98 |
| sPGD global | 0.99 | 0.88 | 0.71 | 0.99 | 0.84 |
| R2 Error | η0 | Mw | Mn |
|---|---|---|---|
| SVR train | 0.48 | 0.91 | 0.77 |
| SVR global | 0.50 | 0.86 | 0.70 |
| sPGD train | 0.49 | 0.90 | 0.77 |
| sPGD global | 0.50 | 0.82 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castéran, F.; Delage, K.; Hascoët, N.; Ammar, A.; Chinesta, F.; Cassagnau, P. Data-Driven Modelling of Polyethylene Recycling under High-Temperature Extrusion. Polymers 2022, 14, 800. https://doi.org/10.3390/polym14040800
Castéran F, Delage K, Hascoët N, Ammar A, Chinesta F, Cassagnau P. Data-Driven Modelling of Polyethylene Recycling under High-Temperature Extrusion. Polymers. 2022; 14(4):800. https://doi.org/10.3390/polym14040800
Chicago/Turabian StyleCastéran, Fanny, Karim Delage, Nicolas Hascoët, Amine Ammar, Francisco Chinesta, and Philippe Cassagnau. 2022. "Data-Driven Modelling of Polyethylene Recycling under High-Temperature Extrusion" Polymers 14, no. 4: 800. https://doi.org/10.3390/polym14040800
APA StyleCastéran, F., Delage, K., Hascoët, N., Ammar, A., Chinesta, F., & Cassagnau, P. (2022). Data-Driven Modelling of Polyethylene Recycling under High-Temperature Extrusion. Polymers, 14(4), 800. https://doi.org/10.3390/polym14040800









