Effect of 3D-Printed PLA Structure on Sound Reflection Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Characteristics of Samples
2.2. Measurement Methodology
2.2.1. Sound Reflection Coefficient
2.2.2. Sound Reflection Properties
3. Results and Discussion
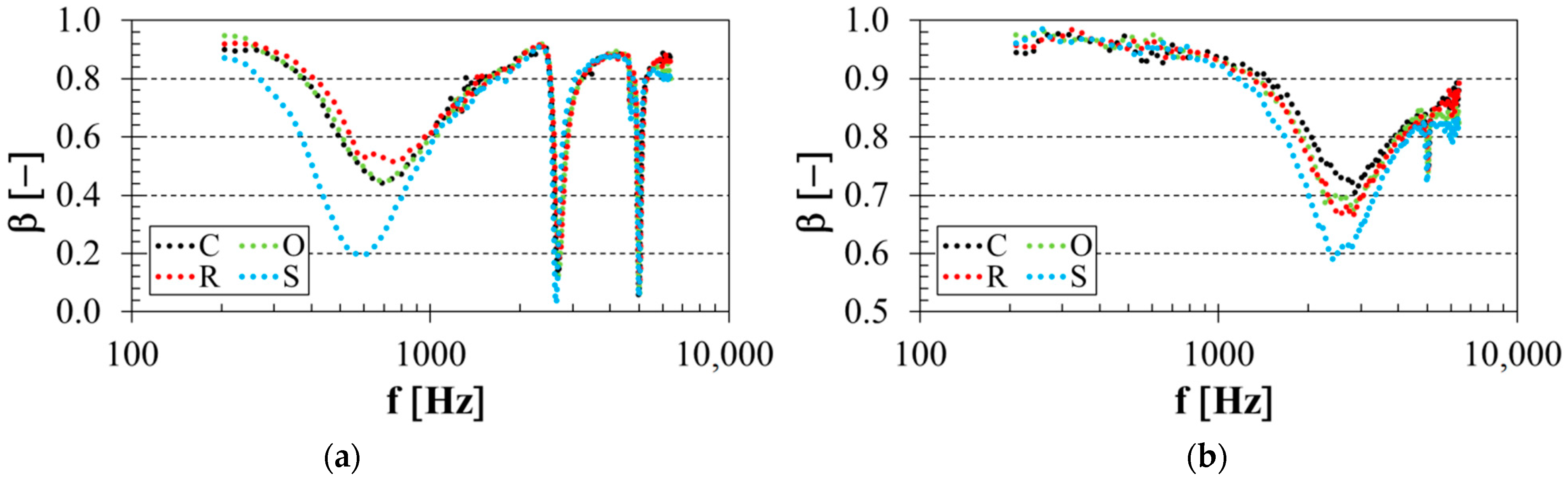
3.1. Influence of Structure Type
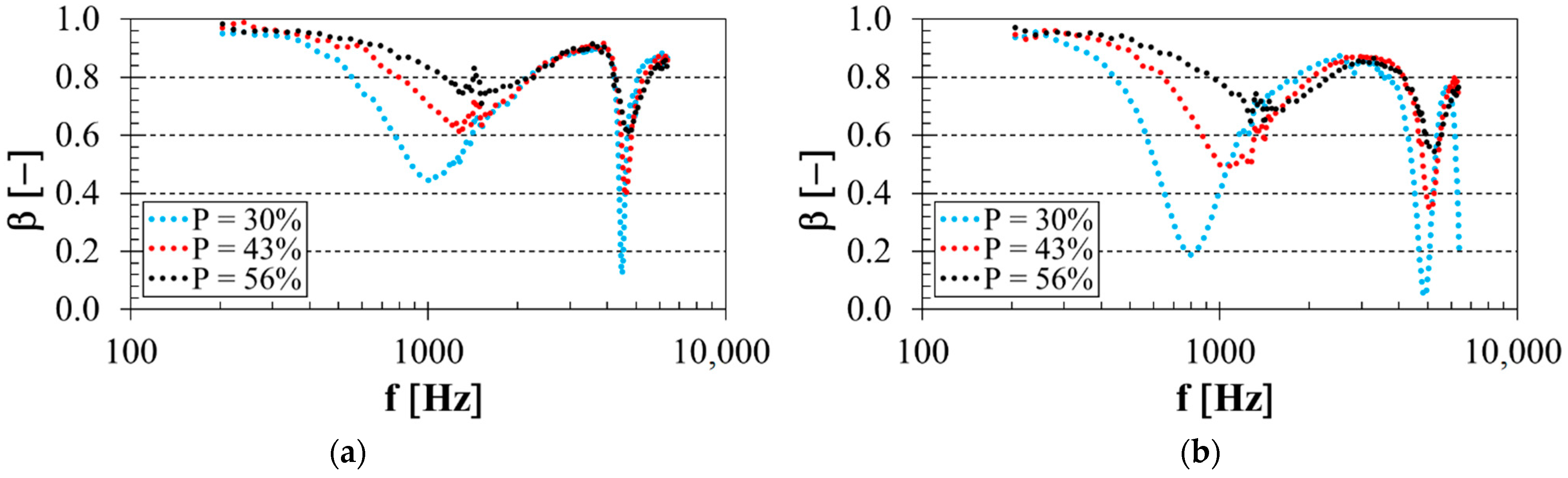
3.2. Influence of Total Volume Porosity
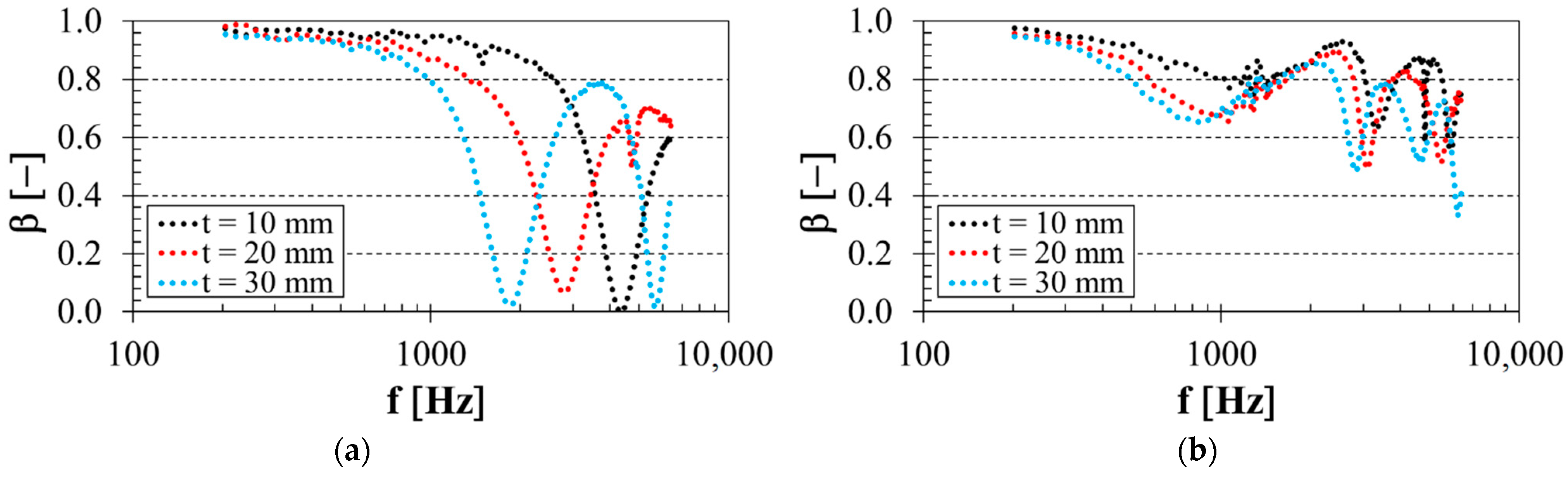
3.3. Influence of Specimen Thickness
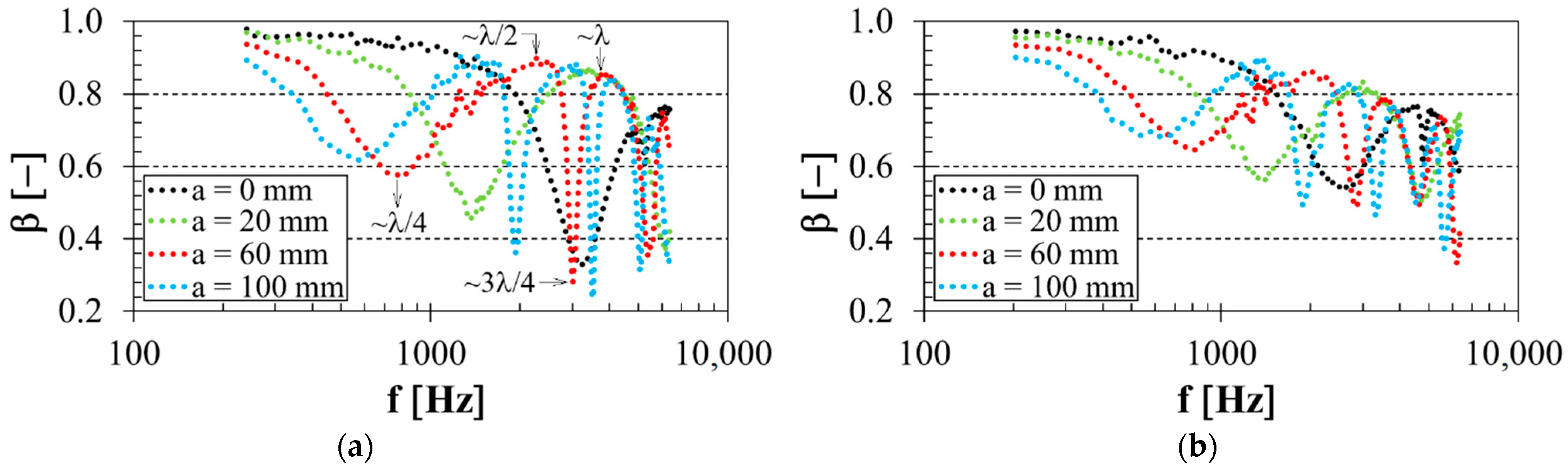
3.4. Influence of Air Gap Size
3.5. Influence of Excitation Frequency
3.6. Comparison of Sound Reflection Properties
4. Summary
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brawata, K.; Kamisinski, T. Effect of Stage Curtain Legs Arrangement on Sound Distribution in Opera Houses. In Proceedings of the 2018 Joint Conference—Acoustics, Ustka, Poland, 11–14 September 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hamdan, N.I.; Zainulabidin, M.H.; Kasron, M.Z.; Kassim, A.S.M. Effect of Perforation Size on Sound Absorption Characteristics of Membrane Absorber. Int. J. Integr. Eng. 2018, 10, 27–34. [Google Scholar] [CrossRef]
- Othman, A.R.; Harith, C.M.; Ibrahim, N.; Ahmad, S.S. The Importance of Acoustic Design in the Mosques towards the Worshipers’ Comfort. Procd. Soc. Behv. 2016, 234, 45–54. [Google Scholar] [CrossRef]
- Rathsam, J.; Wang Lily, M. A review of Diffuse Reflections in Architectural Acoustics. Archit. Eng. 2006, 14, 1–8. [Google Scholar] [CrossRef][Green Version]
- Amares, S.; Sujatmika, E.; Hong, T.W.; Durairaj, D.; Hamid, H.S.H.B. A Review: Characteristics of Noise Absorption Material. J. Phys. Conf. Ser. 2017, 908, 012005. [Google Scholar] [CrossRef]
- Vasina, M.; Bilek, O. Effect of Machined Surface Shape on Sound Reflection. Manuf. Tech. 2016, 16, 830–834. [Google Scholar] [CrossRef]
- Allen, T.; Chally, A.; Moser, B.; Widenhorn, P. Sound Propagation, Reflection, and Its Relevance to Ultrasound Imaging. Phys. Teach. 2019, 57, 134–137. [Google Scholar] [CrossRef]
- Berg, R.E. The Physics of Sound; Department of Physics: Meryland, MD, USA, 2021. [Google Scholar]
- Vercammen, M. Sound Reflections from Concave Spherical Surfaces. Part I: Wave Field Approximation. Acta Acust. Unit. Acust. 2010, 96, 82–91. [Google Scholar] [CrossRef]
- Szelag, A.; Kamisinski, T.M.; Lewinska, M.; Rubacha, J.; Ilch, A. The Characteristic of Sound Reflections from Curved Reflective Panels. Arch. Acoust. 2014, 39, 549–558. [Google Scholar] [CrossRef][Green Version]
- Mosavimehr, E.; Srikantha, P.A. Sound transmission loss characteristics of sandwich panels with a truss lattice core. J. Acoust. Soc. Am. 2017, 141, 2921–2932. [Google Scholar] [CrossRef]
- Domenico, R.; Ruggiero, A. Choice of the optimal acoustic design of a school classroom and experimental verification. Appl. Acoust. 2019, 146, 280–287. [Google Scholar]
- Tsukernikov, I.; Antonov, A.; Ledenev, V.; Shubin, I.; Nevenchannaya, T. Noise Calculation Method for Industrial Premises with Bulky Equipment at Mirror-diffuse Sound Reflection. Proced. Eng. 2017, 176, 218–225. [Google Scholar] [CrossRef]
- Zulkifli, R.; Mohd Nor, M.J.; Mat Tahir, M.F.; Ismail, A.R.; Nuawi, M.Z. Acoustic Properties of Multi-Layer Coir Fibres Sound Absorption Panel. J. Appl. Sci. 2008, 8, 3709–3714. [Google Scholar] [CrossRef]
- Lee, F.C.; Chen, W.H. Acoustic transmission analysis of multi-layer absorbers. J. Sound. Vib. 2001, 248, 621–634. [Google Scholar] [CrossRef]
- Cucharero, J.; Hänninen, T.; Lokki, T. Angle-Dependent Absorption of Sound on Porous Materials. Acoustics 2020, 2, 753–765. [Google Scholar] [CrossRef]
- Gimaltdinov, I.K.; Sitdikova, L.F.; Dmitriev, V.L.; Levina, T.M.; Khabeev, N.S.; Song, W.Q. Reflection of acoustic waves from a porous material at oblique incidence. J. Eng. Phys. Thermophys. 2017, 90, 1043–1052. [Google Scholar] [CrossRef]
- Holmes, N.; Browne, A.; Montague, C. Acoustic properties of concrete panels with crumb rubber as a fine aggregate replacement. Constr. Build. Mater. 2014, 73, 195–204. [Google Scholar] [CrossRef]
- Kuczmarski, M.A.; Johntson, J. Acoustic Absorption in Porous Materials; National Aeronautics and Space Administration: Pasadena, CA, USA, 2011; pp. 1–27. [Google Scholar]
- Fellah, Z.E.A.; Fellah, M.; Depollier, C.; Ogam, E.; Mitri, F.G. Wave Propagation in Porous Materials. In Computational and Experimental Studies of Acoustic Waves; IntechOpen: Rijeka, Croatia, 2017; pp. 99–120. [Google Scholar]
- Sun, X.; Jiang, F.; Wang, J. Acoustic Properties of 316L Stainless Steel Lattice Structures Fabricated via Selective Laser Melting. Metals 2020, 10, 111. [Google Scholar] [CrossRef]
- Dragonetti, R.; Napolitano, M.; Romano, R.A. A study on the energy and the reflection angle of the sound reflected by a porous material. J. Acoust. Soc. Am. 2019, 145, 489–500. [Google Scholar] [CrossRef]
- Otaru, A.J. Review on the Acoustical Properties and Characterization Methods of Sound Absorbing Porous Structures: A Focus on Microcellular Structures Made by a Replication Casting Method. Met. Mater. Int. 2020, 26, 915–932. [Google Scholar] [CrossRef]
- Fan, C.; Tian, Y.; Wang, Z.Q. Structural parameter effect of porous material on sound absorption performance of double-resonance material. IOP Conf. Ser. Mater. Sci. Eng. 2017, 213, 012028. [Google Scholar] [CrossRef]
- Talebitooti, R.; Zarastvand, M.; Darvishgohari, H. Multi-objective optimization approach on diffuse sound transmission through poroelastic composite sandwich structure. J. Sandwich Struct. Mater. 2019, 23, 1221–1252. [Google Scholar] [CrossRef]
- Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Compos. Commun. 2018, 10, 25–35. [Google Scholar] [CrossRef]
- Chen, W.; Chen, T.; Wang, X.; Wu, J.; Li, S. Fractal Model for Acoustic Absorbing of Porous Fibrous Metal Materials. Shock Vib. 2016, 2016, 2890857. [Google Scholar] [CrossRef]
- Guo, Z.K.; Hu, G.B.; Sorokin, V.; Yang, Y.; Tang, L.H. Sound transmission through sandwich plate with hourglass lattice truss core. J. Sandwich Struct. Mater. 2020, 23, 1902–1928. [Google Scholar] [CrossRef]
- Bennett, T.D.; Coudert, F.-X.; James, S.L.; Cooper, A.I. The changing state of porous materials. Nat. Mater. 2021, 20, 1179–1187. [Google Scholar] [CrossRef]
- Voronin, S.V.; Danilushkin, V.S.; Tregub, V.I.; Konovalov, S.V. Computer Simulation of the Process of Crack Propagation in a Brittle Porous Material. J. Surf. Investig. 2021, 15, 1212–1216. [Google Scholar] [CrossRef]
- Chiavi, A.; Miglietta, P.; Guglielmone, C.L. Considerations on the airflow resistivity measurement of porous and fibrous materials as function of temperature. In Proceedings of the 8th European Conference on Noise Control, Euronoise, UK, 26–28 October 2009; pp. 1–11. [Google Scholar]
- Hurrell, A.I.; Horoshenkov, K.V.; Pelegrinis, M.T. The accuracy of some models for the airflow resistivity of nonwoven materials. Appl. Acoust. 2018, 130, 230–237. [Google Scholar] [CrossRef]
- Naghieh, S.; Karamooz Ravari, M.R.; Badrossamay, M.; Foroozmehr, E.; Kadkhodaei, M. Numerical investigation of the mechanical properties of the additive manufactured bone scaffolds fabricated by FDM: The effect of layer penetration and post-heating. J. Mech. Behav. Biomed. Mater. 2016, 59, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Pantazopoulos, G.A. A Short Review on Fracture Mechanisms of Mechanical Components Operated under Industrial Process Conditions: Fractographic Analysis and Selected Prevention Strategies. Metals 2019, 9, 148. [Google Scholar] [CrossRef]
- Seddeq, H.S. Factors influencing acoustic performance of sound absorptive materials. Austral. J. Basic Appl. Sci. 2009, 3, 4610–4617. [Google Scholar]
- Łukaszewski, K.; Buchwald, T.; Wichniarek, R. The FDM Technique in Processes of Prototyping Spare Parts for Servicing and Repairing Agricultural Machines: A General Outline. Int. J. Appl. Mech. Eng. 2021, 26, 145–155. [Google Scholar] [CrossRef]
- Chawla, K.; Singh, R.; Singh, J. On recyclability of thermoplastic ABS polymer as fused filament for FDM technique of additive manufacturing. World J. Eng. 2021. [Google Scholar] [CrossRef]
- Corredor-Bedoya, A.C.; Acuna, B.; Serpa, A.L.; Mesiero, B. Effect of the excitation signal type on the absorption coefficient measurement using the impedance tube. Appl. Acoust. 2021, 171, 107659. [Google Scholar] [CrossRef]
- Fediuk, R.; Amran, M.; Vatin, N.; Vasilev, Y.; Lesovik, V.; Ozbakkaloglu, T. Acoustic Properties of Innovative Concretes: A Review. Materials 2021, 14, 398. [Google Scholar] [CrossRef]
- Zainulabidin, M.; Rani, M.; Nezere, N.; Tobi, A. Optimum sound absorption by materials fraction combination. Int. J. Mech. Mechatron. Eng. 2014, 14, 118–121. [Google Scholar]
- Paul, P.; Mishra, R.; Behera, B.K. Acoustic behaviour of textile structures. Text. Prog. 2021, 53, 1–64. [Google Scholar] [CrossRef]
- Koizumi, T.; Tsujiuchi, N.; Adachi, A. The development of sound absorbing materials using natural bamboo fibers. High Perform. Struct. Mater. 2002, 4, 157–166. [Google Scholar]
- Bujoreanu, C.; Nedeff, F.; Benchea, M.; Agop, M. Experimental and theoretical considerations on sound absorption performance of waste materials including the effect of backing plates. Appl. Acoust. 2017, 119, 88–93. [Google Scholar] [CrossRef]
- Wu, J.J.; Li, C.G.; Wang, D.B.; Gui, M.C. Damping and sound absorption properties of particle reinforced Al matrix composite foams. Compos. Sci. Technol. 2003, 63, 569–574. [Google Scholar] [CrossRef]
- Mendes, C.O.B.; Nunes, M.A.D. Numerical Methodology to Obtain the Sound Absorption of Materials by Inserting the Acoustic Impedance. Arch. Acoust. 2021, 46, 649–656. [Google Scholar] [CrossRef]
- International Organization for Standardization ISO 10534; Acoustics-Determination of Sound Absorption in a Reverberation Room. IOS: Geneva, Switzerland, 2003.
- Scrosati, C.; Martellotta, F.; Pompoli, F.; Schiavi, A.; Prato, A.; D’Orazio, D.; Garai, M.; Granzotto, N.; Di Bella, A.; Scamoni, F. Towards more reliable measurements of sound absorption coefficient in reverberation rooms: An Inter-Laboratory Test. Appl. Acoust. 2020, 165, 107398. [Google Scholar] [CrossRef]
- Shtrepi, L.; Prato, A. Towards a sustainable approach for sound absorption assessment of building materials: Validation of small-scale reverberation room measurements. Appl. Acoust. 2020, 165, 107304. [Google Scholar] [CrossRef]
- Sun, Y.; Hua, B. System error calculation and analysis of underwater sound absorption coefficient measurement experiment. Appl. Acoust. 2022, 186, 108489. [Google Scholar] [CrossRef]
- Amran, M.; Fediuk, R.; Murali, G.; Vatin, N.; Al-Fakih, A. Sound-Absorbing Acoustic Concretes: A Review. Sustainability 2021, 13, 10712. [Google Scholar] [CrossRef]
- International Organization for Standardization ISO 10534-1; Acoustics—Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes—Part 1: Method Using Standing Wave Ratio. IOS: Geneva, Switzerland, 1998.
- International Organization for Standardization ISO 10534-2; Acoustics-Determination of Sound Absorption Coefficient and Impedance in Impedance Tubes-Part 2: Transfer-Function Method; ISO/TC 43/SC2 Building Acoustics. CEN, European Committee for Standardization: Brussels, Belgium, 1998; pp. 10534–10542.
- Doutres, O.; Salissou, Y.; Atalla, N.; Panneton, R. Evaluation of the acoustic and non-acoustic properties of sound absorbing materials using a three-microphone impedance tube. Appl. Acoust. 2010, 71, 506–509. [Google Scholar] [CrossRef]
- Song, W.J.; Cha, D.J. Determination of an acoustic reflection coefficient at the inlet of a model gas turbine combustor for power generation. IOP Conf. Ser. Mater. Sci. Eng. 2017, 164, 012010. [Google Scholar] [CrossRef]
- Taban, E.; Khavanin, A.; Jafari, A.J.; Faridan, M.; Tabrizi, A.K. Experimental and mathematical survey of sound absorption performance of date palm fibers. Heliyon 2019, 5, e01977. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, Z.J.; Zhao, N.Q. Effect of pore size and relative density on the mechanical properties of open cell aluminum foams. Scr. Mater. 2007, 56, 169–172. [Google Scholar] [CrossRef]
- Zhu, W.B.; Chen, S.M.; Wang, Y.B.; Zhu, T.T.; Jiang, Y. Sound Absorption Behavior of Polyurethane Foam Composites with Different Ethylene Propylene Diene Monomer Particles. Arch. Acoust. 2018, 43, 403–411. [Google Scholar] [CrossRef]
- Tiuc, A.E.; Vasile, O.; Usca, A.D.; Gabor, T.; Vermesan, H. The Analysis of Factors That Influence the Sound Absorption Coefficient of Porous Materials. Rom. J. Acoust. Vib. 2014, 11, 105–108. [Google Scholar]
- Everest, F.A. Absorption of sound. In Master Handbook of Acoustics, 4th ed.; McGraw-Hill: New York, NY, USA, 2001; pp. 179–233. ISBN 0-07-139974-7. [Google Scholar]
- Zhu, J.L.; Sun, J.; Tang, J.P.; Wang, J.Z.; Ao, Q.B.; Bao, T.F.; Song, W.D. Gradient-structural optimization of metal fiber porous materials for sound absorption. Powder. Technol. 2016, 301, 1235–1241. [Google Scholar] [CrossRef]
- Liguori, C.; Ruggiero, A.; Russo, D.; Sommella, P. Estimation of the minimum measurement time interval in acoustic noise. Appl. Acoust. 2017, 127, 126–132. [Google Scholar] [CrossRef]
- Liu, X.W.; Yu, C.L.; Xin, F.X. Gradually perforated porous materials backed with Helmholtz resonant cavity for broadband low-frequency sound absorption. Compos. Struct. 2021, 263, 113647. [Google Scholar] [CrossRef]
- Madurelo-Sanz, R.; Acedo-Fuentes, P.; Garcia-Cobos, F.J.; Sánchez-Delgado, F.J.; Mota-López, M.I.; Meneses-Rodríguez, J.M. The recycling of surgical face masks as sound porous absorbers: Preliminary evaluation. Sci. Total Environ. 2021, 786, 147461. [Google Scholar] [CrossRef]
- Guan, Y.-J.; Ge, Y.; Sun, H.-X.; Yuan, S.-Q.; Liu, X.-J. Low-Frequency, Open, Sound-Insulation Barrier by Two Oppositely Oriented Helmholtz Resonators. Micromachines 2021, 12, 1544. [Google Scholar] [CrossRef]



| Structure Type | Label | Volume Porosity (%) | Structure View | Strut Diameter (mm) | Cell Size x/y/z (mm) |
|---|---|---|---|---|---|
| Cartesian | 56 |  | 1 | 5/5/5 | |
| C | 43 | 1.4 | 5/5/5 | ||
| 30 | 1.8 | 5/5/5 | |||
| Octagonal | 56 |  | 1 | 6/7/5 | |
| O | 43 | 1.4 | 6/7/5 | ||
| 30 | 1.7 | 5.5/7/5 | |||
| Rhomboid | 56 |  | 1 | 5.5/7/7 | |
| R | 43 | 1.35 | 5/7/7 | ||
| 30 | 1.7 | 5/7/7 | |||
| Starlit | 56 |  | 1 | 8/9/5 | |
| S | 43 | 1.4 | 7.5/9/5 | ||
| 30 | 1.8 | 8/9/5 |
| Structure Type | a (mm) | fmin1 (Hz) | βmin1 (-) | fmax1 (Hz) | βmax1 (-) |
|---|---|---|---|---|---|
| Cartesian | 25 | 2272 | 0.73 | 5904 | 0.91 |
| 50 | 1392 | 0.75 | 2984 | 0.94 | |
| 70 | 1192 | 0.78 | 2296 | 0.95 | |
| 100 | 784 | 0.81 | 1424 | 0.97 | |
| Octagonal | 25 | 1936 | 0.70 | 5032 | 0.91 |
| 50 | 1336 | 0.74 | 2920 | 0.93 | |
| 70 | 1040 | 0.76 | 2256 | 0.93 | |
| 100 | 728 | 0.81 | 1360 | 0.97 | |
| Rhomboid | 25 | 2024 | 0.71 | 5536 | 0.90 |
| 50 | 1384 | 0.72 | 2960 | 0.91 | |
| 70 | 1080 | 0.77 | 2272 | 0.93 | |
| 100 | 760 | 0.81 | 1392 | 0.98 | |
| Starlit | 25 | 1928 | 0.60 | 5024 | 0.89 |
| 50 | 1320 | 0.64 | 2872 | 0.92 | |
| 70 | 960 | 0.70 | 2224 | 0.92 | |
| 100 | 680 | 0.75 | 1248 | 0.92 |
| Structure Type | a (mm) | fmin1 (Hz) | βmin1 (-) | fmax1 (Hz) | βmax1 (-) |
|---|---|---|---|---|---|
| Cartesian | 0 | 1728 | 0.00 | 3608 | 0.79 |
| 25 | 704 | 0.09 | 2056 | 0.86 | |
| 50 | 488 | 0.14 | 1760 | 0.87 | |
| 100 | 336 | 0.18 | 1288 | 0.91 | |
| Octagonal | 0 | 1776 | 0.01 | 3672 | 0.79 |
| 25 | 712 | 0.10 | 2152 | 0.85 | |
| 50 | 488 | 0.16 | 1808 | 0.86 | |
| 100 | 336 | 0.20 | 1312 | 0.91 | |
| Rhomboid | 0 | 1864 | 0.02 | 3696 | 0.79 |
| 25 | 728 | 0.14 | 2176 | 0.86 | |
| 50 | 512 | 0.19 | 1824 | 0.86 | |
| 100 | 360 | 0.24 | 1344 | 0.88 | |
| Starlit | 0 | 1824 | 0.02 | 3640 | 0.80 |
| 25 | 696 | 0.08 | 2120 | 0.84 | |
| 50 | 504 | 0.13 | 1792 | 0.84 | |
| 100 | 344 | 0.20 | 1296 | 0.86 |
| Structure Type | t (mm) | P (%) | a (mm) | βm (-) |
|---|---|---|---|---|
| Cartesian | 10 | 56 | 0 | 0.857 |
| 20 | 43 | 50 | 0.702 | |
| 30 | 30 | 100 | 0.598 | |
| Octagonal | 10 | 56 | 0 | 0.844 |
| 20 | 43 | 50 | 0.699 | |
| 30 | 30 | 100 | 0.601 | |
| Rhomboid | 10 | 56 | 0 | 0.842 |
| 20 | 43 | 50 | 0.692 | |
| 30 | 30 | 100 | 0.610 | |
| Starlit | 10 | 56 | 0 | 0.820 |
| 20 | 43 | 50 | 0.679 | |
| 30 | 30 | 100 | 0.589 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monkova, K.; Vasina, M.; Monka, P.P.; Vanca, J.; Kozak, D. Effect of 3D-Printed PLA Structure on Sound Reflection Properties. Polymers 2022, 14, 413. https://doi.org/10.3390/polym14030413
Monkova K, Vasina M, Monka PP, Vanca J, Kozak D. Effect of 3D-Printed PLA Structure on Sound Reflection Properties. Polymers. 2022; 14(3):413. https://doi.org/10.3390/polym14030413
Chicago/Turabian StyleMonkova, Katarina, Martin Vasina, Peter Pavol Monka, Jan Vanca, and Dražan Kozak. 2022. "Effect of 3D-Printed PLA Structure on Sound Reflection Properties" Polymers 14, no. 3: 413. https://doi.org/10.3390/polym14030413
APA StyleMonkova, K., Vasina, M., Monka, P. P., Vanca, J., & Kozak, D. (2022). Effect of 3D-Printed PLA Structure on Sound Reflection Properties. Polymers, 14(3), 413. https://doi.org/10.3390/polym14030413











