Prediction of the Viscoelastic Properties of a Cetyl Pyridinium Chloride/Sodium Salicylate Micellar Solution: (II) Prediction of the Step Rate Experiments
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Start-Up Experiment
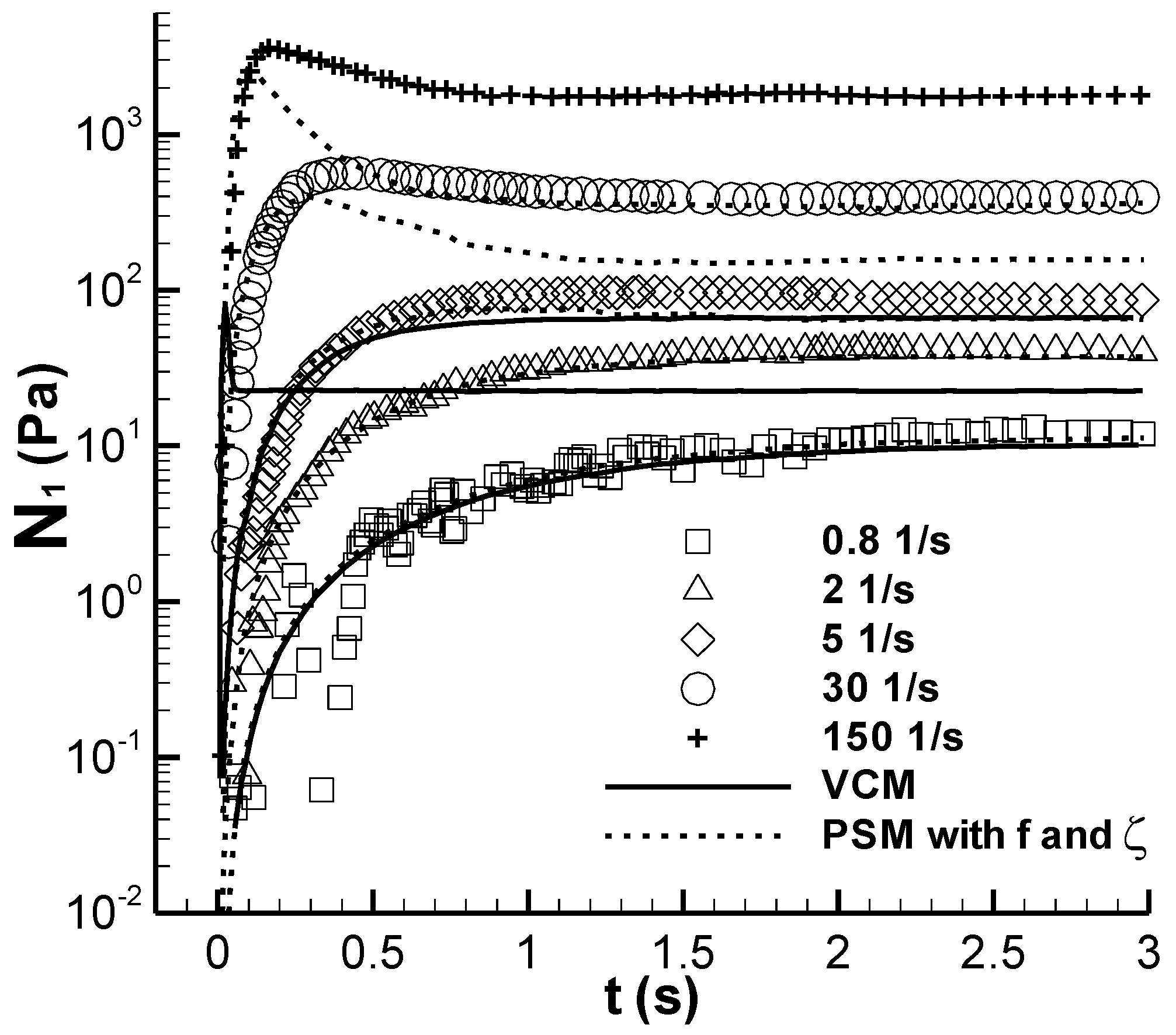
3.1.1. N1
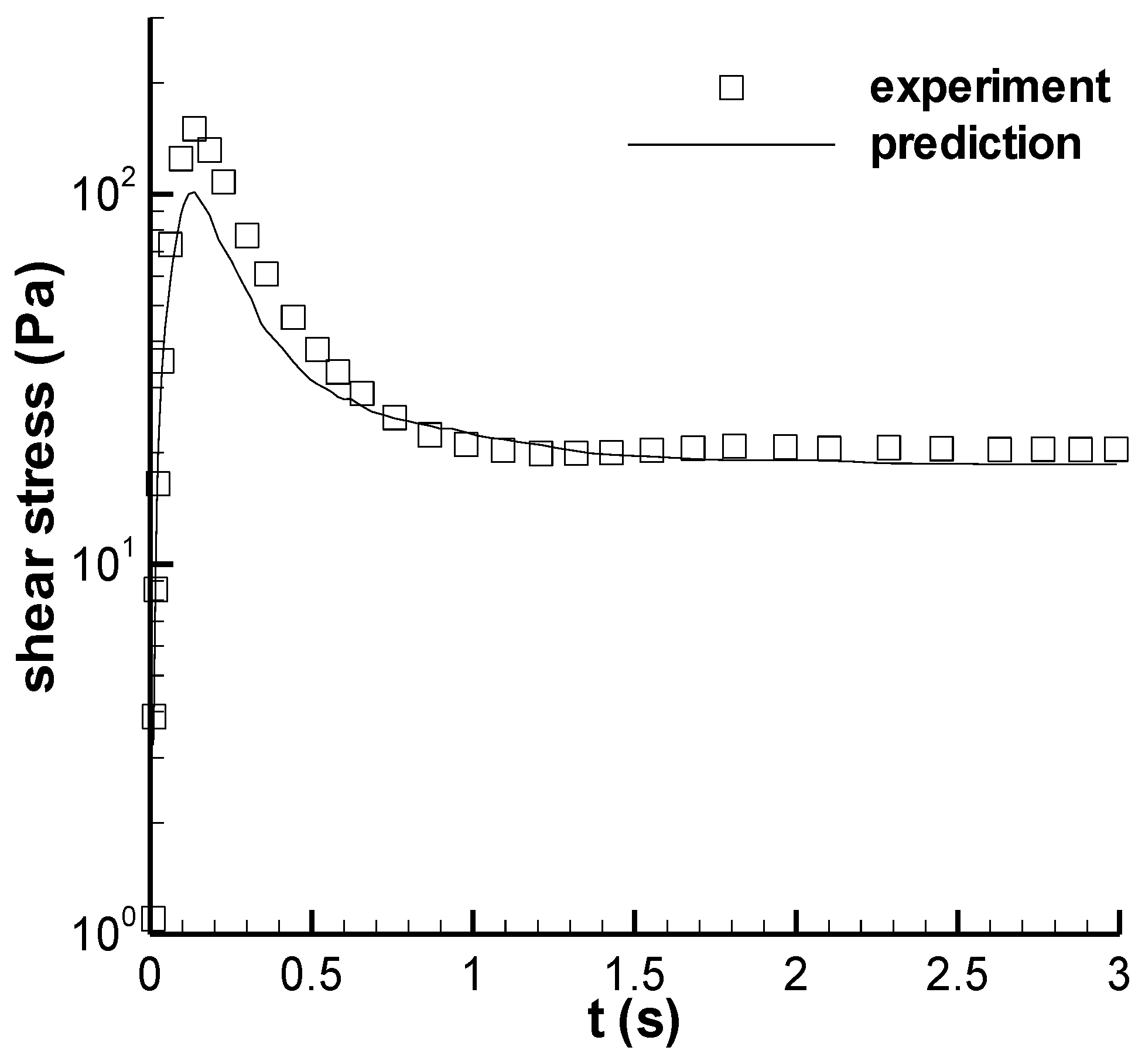
3.1.2. Shear Stress
3.1.3. Long-Term Start-Up Experiment
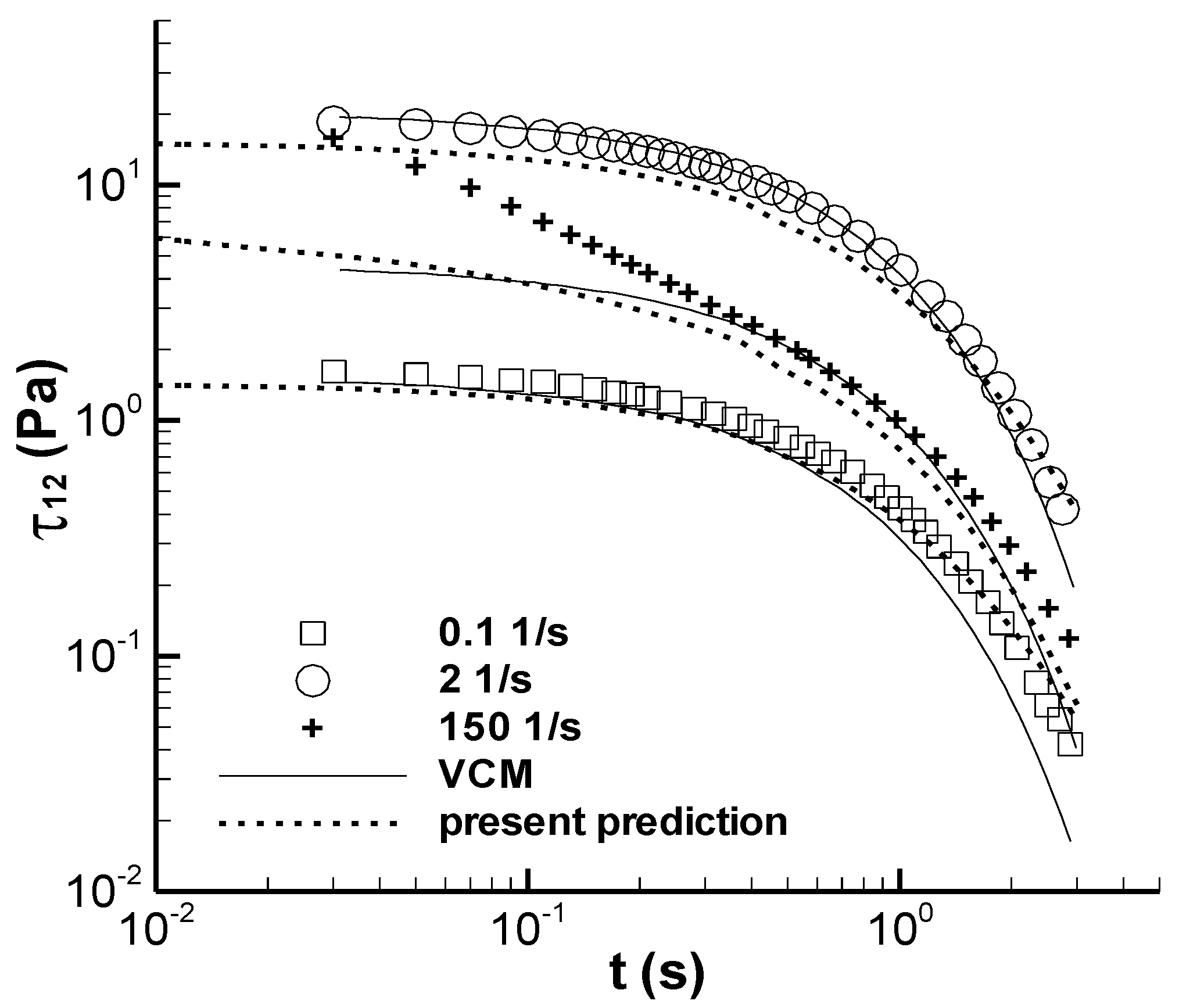
3.2. Stress Relaxation Experiment
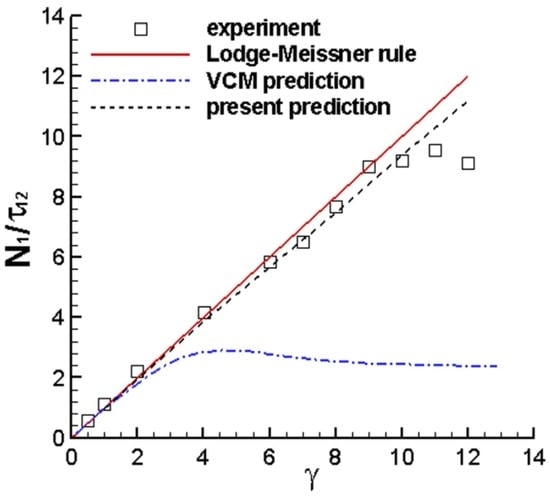
3.3. Step Strain Experiment
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Arjmand, O.; Roostaei, A. Experimental investigation of viscous surfactant based enhanced oil recovery. Pet. Sci. Technol. 2014, 32, 1607–1616. [Google Scholar] [CrossRef]
- Jeirani, Z.; Mohamed Jan, B.; Si Ali, B.; See, C.H.; Saphanuchart, W. Pre-prepared microemulsion flooding in enhanced oil recovery: A review. Pet. Sci. Technol. 2014, 32, 180–193. [Google Scholar] [CrossRef]
- Pipe, C.J.; Kim, N.J.; Vasquez, P.A.; Cook, L.P.; McKinley, G.H. Wormlike micellar solutions. II: Comparison between experimental data and scission model predictions. J. Rheol. 2010, 54, 881–914. [Google Scholar] [CrossRef]
- Zhao, Y.; Haward, S.J.; Shen, A.Q. Rheological characterizations of wormlike micellar solutions containing cationic surfactant and anionic hydrotropic salt. J. Rheol. 2015, 59, 1229–1259. [Google Scholar] [CrossRef]
- Ahmadi, M.A.; Shadizadeh, S.R.; Salari, Z. Dependency of critical micellization concentration of an anionic surfactant on temperature and potassium chloride salt. Pet. Sci. Technol. 2014, 32, 1913–1920. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ahmad, Z.; Phung, L.T.K.; Kashiwao, T.; Bahadori, A. Experimental investigation the effect of nanoparticles on micellization behavior of a surfactant: Application to EOR. Pet. Sci. Technol. 2016, 34, 1055–1061. [Google Scholar] [CrossRef]
- Kumar Sinha, A.; Bera, A.; Raipuria, V.; Kumar, A.; Mandal, A.; Kumar, T. Numerical simulation of enhanced oil recovery by alkali-surfactant-polymer floodings. Pet. Sci. Technol. 2015, 33, 1229–1237. [Google Scholar] [CrossRef]
- Pannu, S.; Phukan, R.; Tiwari, P. Experimental and simulation study of surfactant flooding using a combined surfactant system for enhanced oil recovery. Pet. Sci. Technol. 2022, 40, 2907–2924. [Google Scholar] [CrossRef]
- Huang, S. Prediction of the viscoelastic properties of a cetyl pyridinium chloride/sodium salicylate micellar solution: (I) characterization. Pet. Sci. Technol. 2022. [Google Scholar] [CrossRef]
- Huang, S. Structural viscoelasticity of a water-soluble polysaccharide extract. Int. J. Biol. Macromol. 2018, 120, 1601–1609, Erratum in Int. J. Biol. Macromol. 2021, 193, 2389. [Google Scholar] [CrossRef]
- Huang, S. Viscoelastic characterization and prediction of a wormlike micellar solution. Acta Mech. Sin. 2021, 37, 1648–1658, Erratum in Acta Mech. Sin. 2021, 37, 1714. [Google Scholar] [CrossRef]
- Huang, S. Viscoelastic property of an LDPE melt in triangular- and trapezoidal-loop shear experiment. Polymers 2021, 13, 3997. [Google Scholar] [CrossRef] [PubMed]
- Papanastasiou, A.C.; Scriven, L.E.; Macosko, C.W. An integral constitutive equation for mixed flows: Viscoelastic characterization. J. Rheol. 1983, 27, 387–410. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Fluids, Vol. 1. Fluid Mechanics, 2nd ed.; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Laun, H.M.; Schmidt, G. Rheotens tests and viscoelastic simulations related to high-speed spinning of Polyamide 6. J. Non-Newton. Fluid Mech. 2015, 222, 45–55. [Google Scholar] [CrossRef]
- Gaudino, D.; Costanzo, S.; Ianniruberto, G.; Grizzuti, N.; Pasquino, R. Linear wormlike micelles behave similarly to entangled linear polymers in fast shear flows. J. Rheol. 2020, 64, 879–888. [Google Scholar] [CrossRef]
- Sato, T.; Larson, R.G. Nonlinear rheology of entangled wormlike micellar solutions predicted by a micelle-slip-spring model. J. Rheol. 2022, 66, 639–656. [Google Scholar] [CrossRef]
- Tan, G.; Larson, R.G. Quantitative modeling of threadlike micellar solution rheology. Rheol. Acta 2022, 61, 443–457. [Google Scholar] [CrossRef]
- Hopkins, C.C.; Haward, S.J.; Shen, A.Q. Upstream wall vortices in viscoelastic flow past a cylinder. Soft Matter 2022, 18, 4868–4880. [Google Scholar] [CrossRef]
- Varchanis, S.; Haward, S.J.; Hopkins, C.C.; Tsamopoulos, J.; Shen, A.Q. Evaluation of constitutive models for shear-banding wormlike micellar solutions in simple and complex flows. J. Non-Newton. Fluid Mech. 2022, 307, 104855. [Google Scholar] [CrossRef]
- López-Aguilar, J.E.; Resendiz-Tolentino, O.; Tamaddon-Jahromi, H.R.; Ellero, M.; Manero, O. Flow past a sphere: Numerical predictions of thixo-viscoelastoplastic wormlike micellar solutions. J. Non-Newton. Fluid Mech. 2022, 309, 104902. [Google Scholar] [CrossRef]
- Patel, M.C.; Ayoub, M.A.; Hassan, A.M.; Idress, M.B. A novel ZnO nanoparticles enhanced surfactant based viscoelastic fluid systems for fracturing under high temperature and high shear rate conditions: Synthesis, rheometric analysis, and fluid model derivation. Polymers 2022, 14, 4023. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.L.; Tanner, R.I. Finite element simulation of long and short circular die extrusion experiments using integral models. Int. J. Numer. Meth. Eng. 1988, 25, 9–22. [Google Scholar] [CrossRef]



| γ | Mode 1 | Mode 2 | Mode 3 | |||
|---|---|---|---|---|---|---|
| (s−1) | t0 (s) | (s−1) | t0 (s) | (s−1) | t0 (s) | |
| 1 | 0.006667 | 10 | 16.67 | 0.06 | ||
| 2 | 0.01333 | 20 | 33.33 | 0.06 | ||
| 4 | 0.02667 | 40 | 61.54 | 0.065 | ||
| 6 | 150 | 0.04000 | 60 | 0.1 | 75 | 0.08 |
| 8 | 0.05333 | 80 | 100 | 0.08 | ||
| 10 | 0.06667 | 100 | 125 | 0.08 | ||
| 12 | 0.08000 | 120 | 133.3 | 0.09 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S. Prediction of the Viscoelastic Properties of a Cetyl Pyridinium Chloride/Sodium Salicylate Micellar Solution: (II) Prediction of the Step Rate Experiments. Polymers 2022, 14, 5561. https://doi.org/10.3390/polym14245561
Huang S. Prediction of the Viscoelastic Properties of a Cetyl Pyridinium Chloride/Sodium Salicylate Micellar Solution: (II) Prediction of the Step Rate Experiments. Polymers. 2022; 14(24):5561. https://doi.org/10.3390/polym14245561
Chicago/Turabian StyleHuang, Shuxin. 2022. "Prediction of the Viscoelastic Properties of a Cetyl Pyridinium Chloride/Sodium Salicylate Micellar Solution: (II) Prediction of the Step Rate Experiments" Polymers 14, no. 24: 5561. https://doi.org/10.3390/polym14245561
APA StyleHuang, S. (2022). Prediction of the Viscoelastic Properties of a Cetyl Pyridinium Chloride/Sodium Salicylate Micellar Solution: (II) Prediction of the Step Rate Experiments. Polymers, 14(24), 5561. https://doi.org/10.3390/polym14245561