Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts
Abstract
1. Introduction
2. Materials and Methods
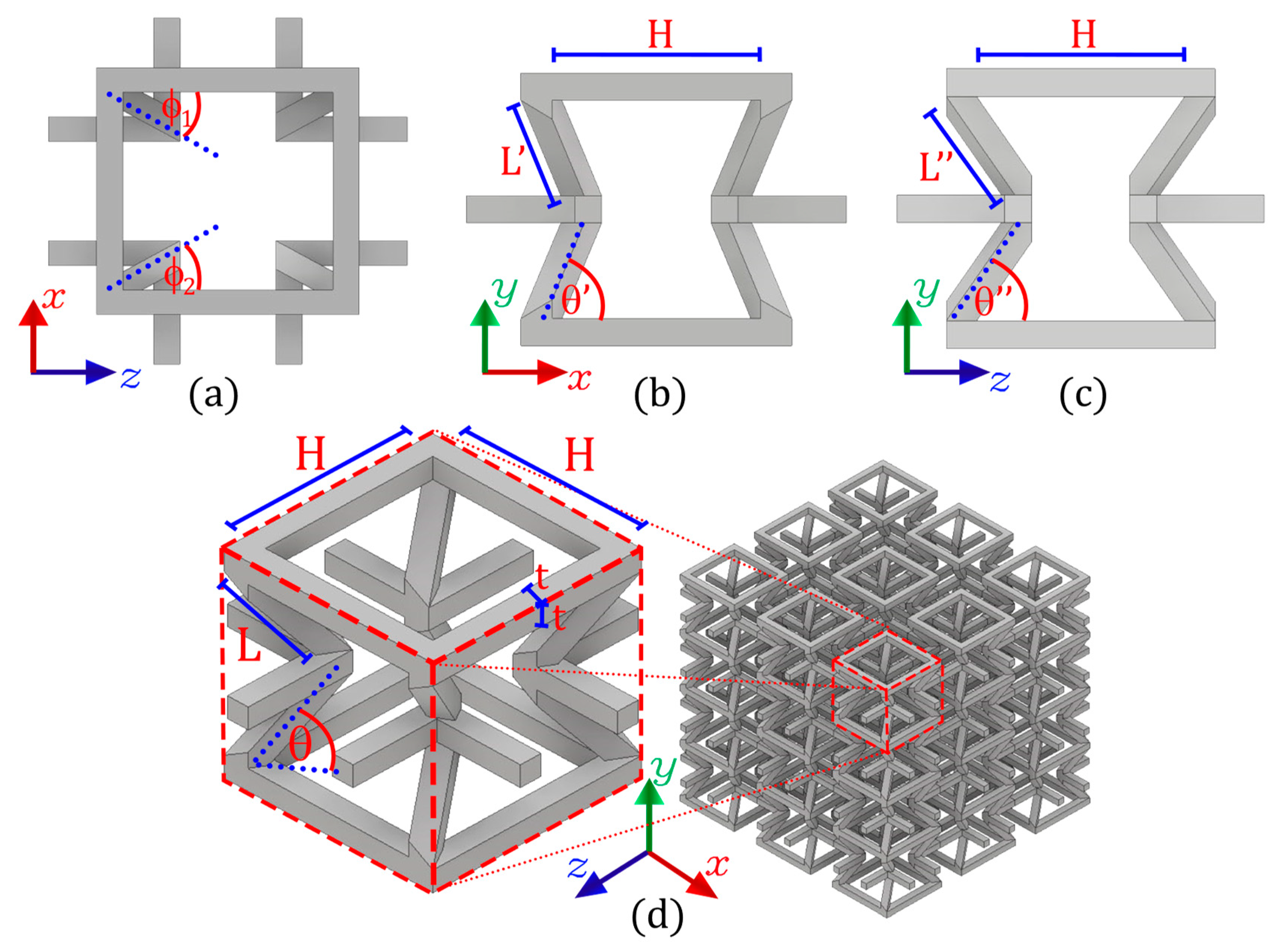
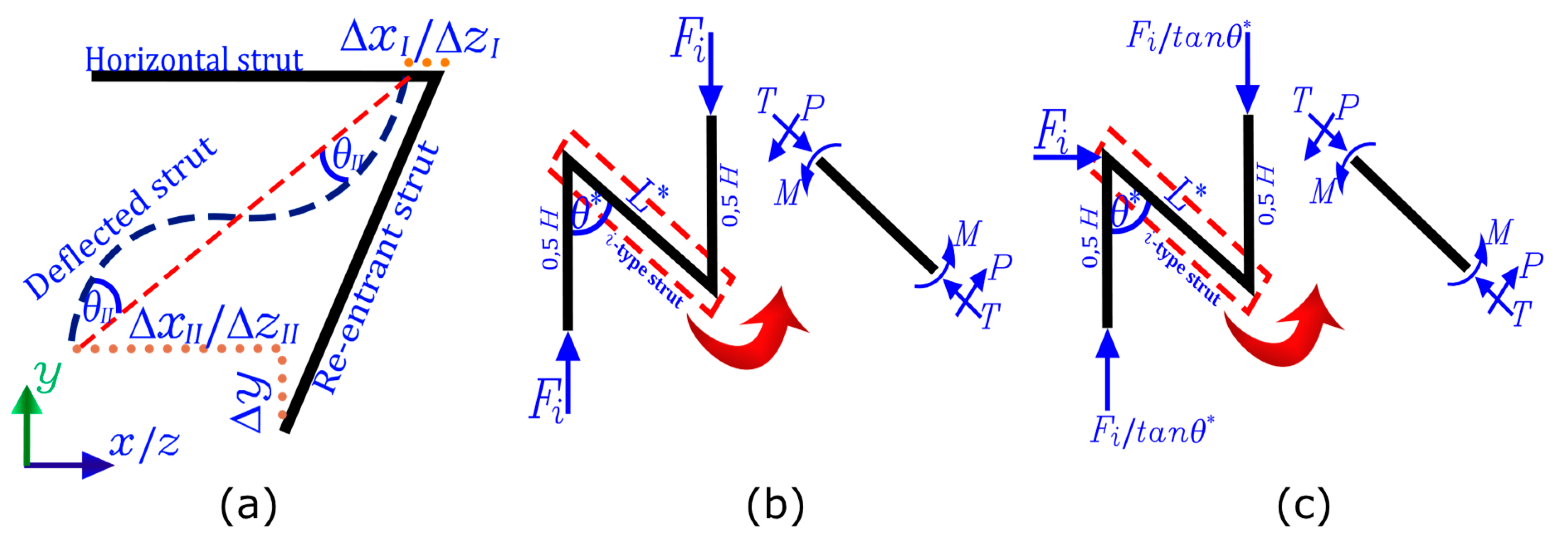
2.1. Orthotropic Mechanical Model of the Cell
2.1.1. Axis Compression
2.1.2. Axis Compression
2.1.3. Axis Compression
2.1.4. Poisson’s Ratio and Young’s Modulus
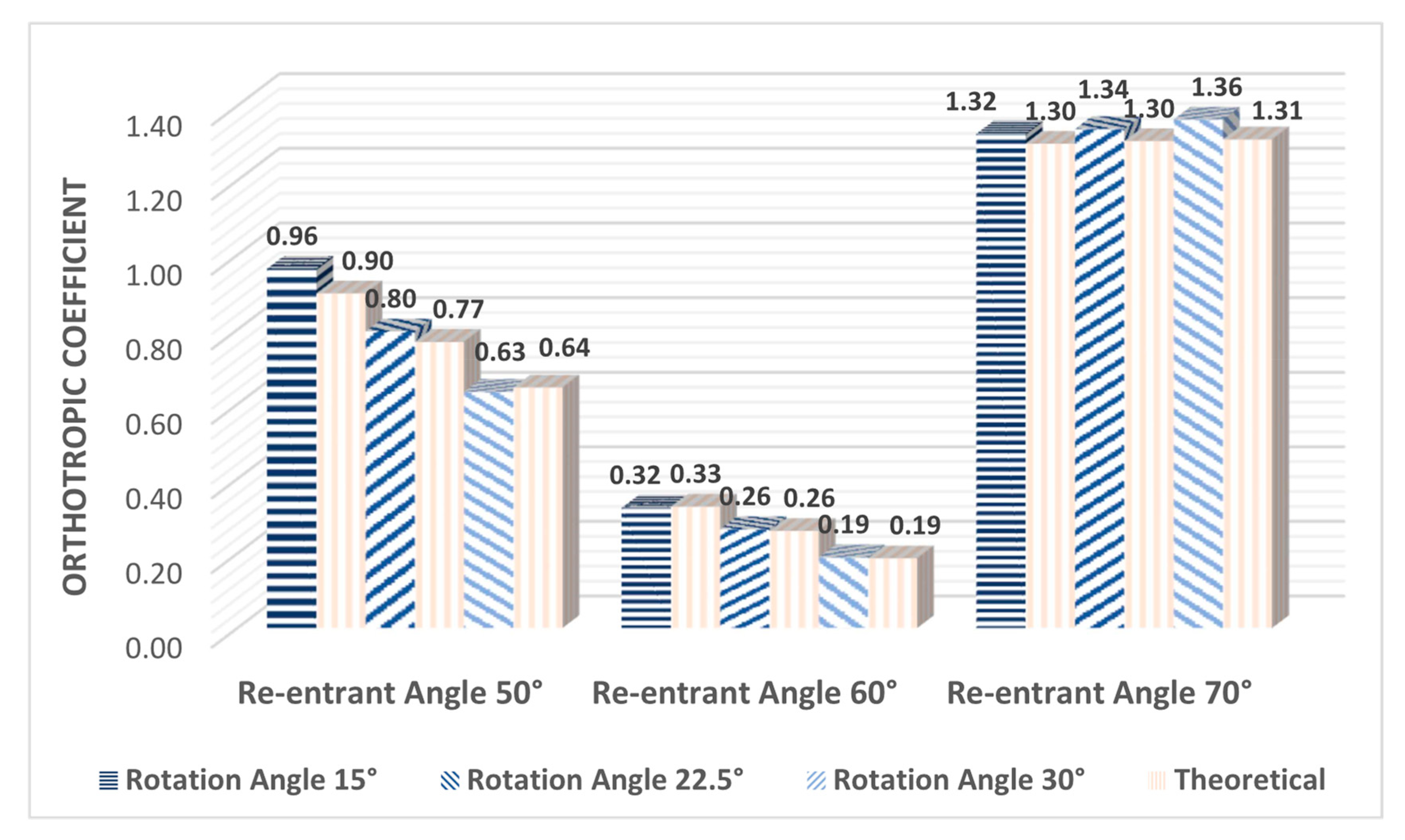
2.1.5. Orthotropy Quantification
2.2. Experimental Procedure
3. Results and Discussion
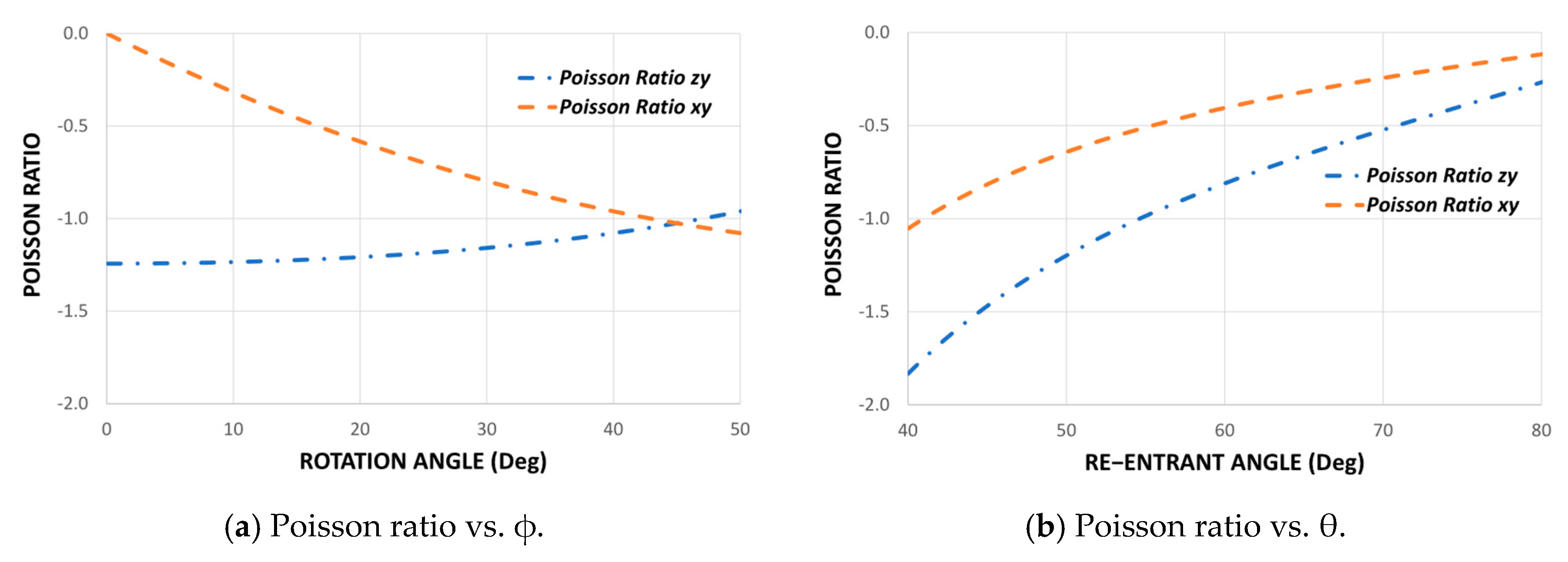
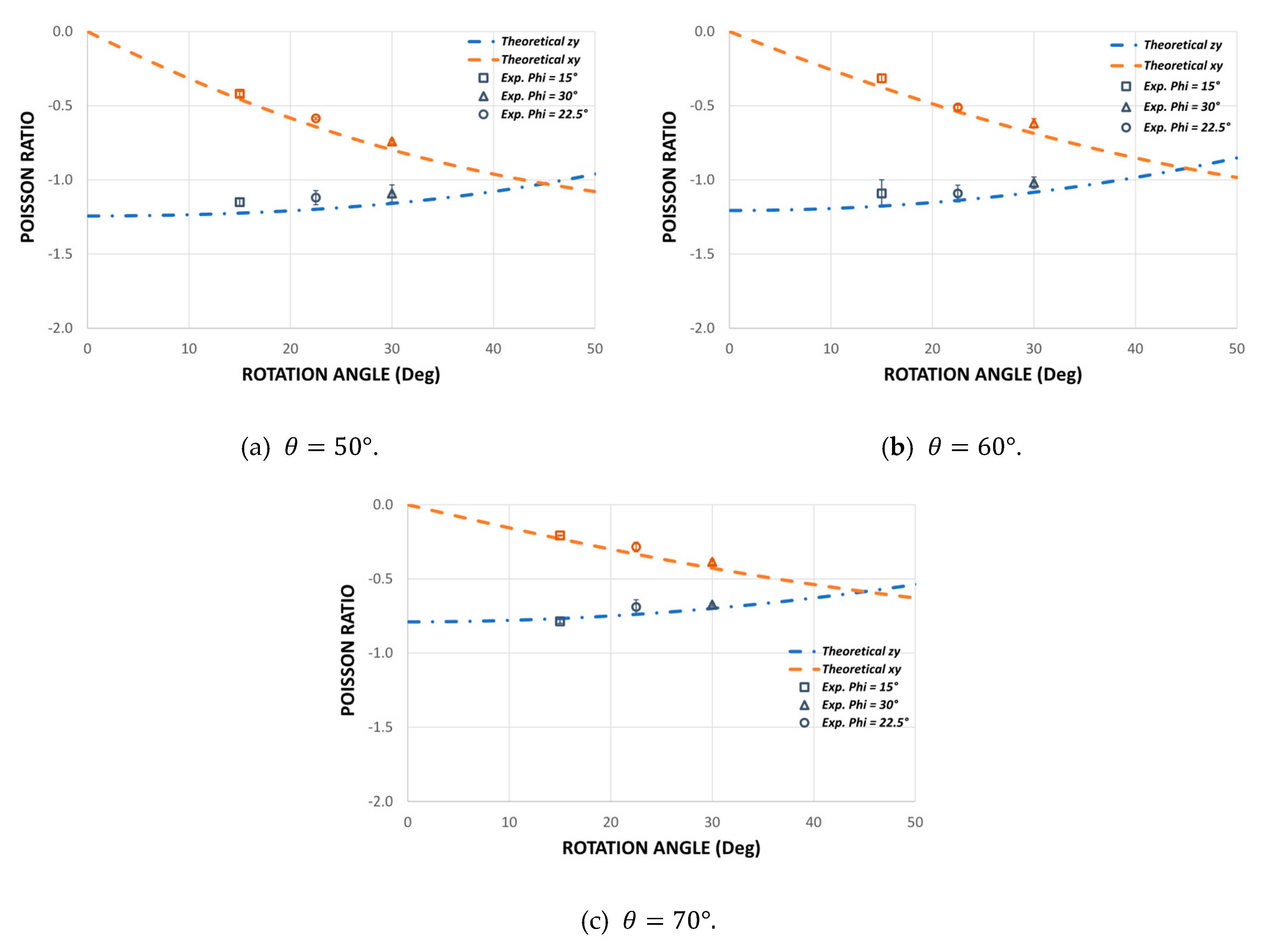
3.1. Poisson’s Ratio
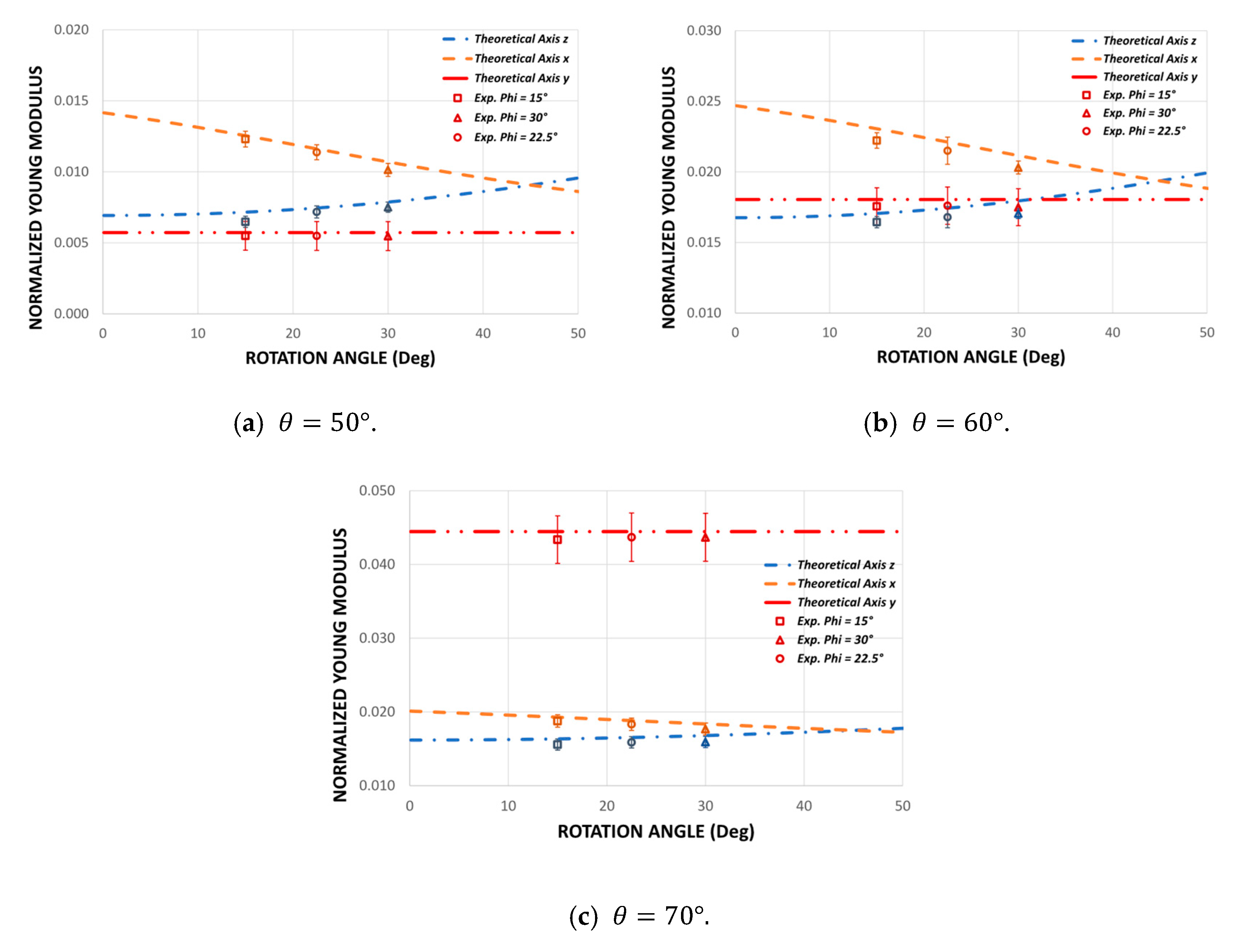
3.2. Young’s Modulus
Orthotropy Quantification
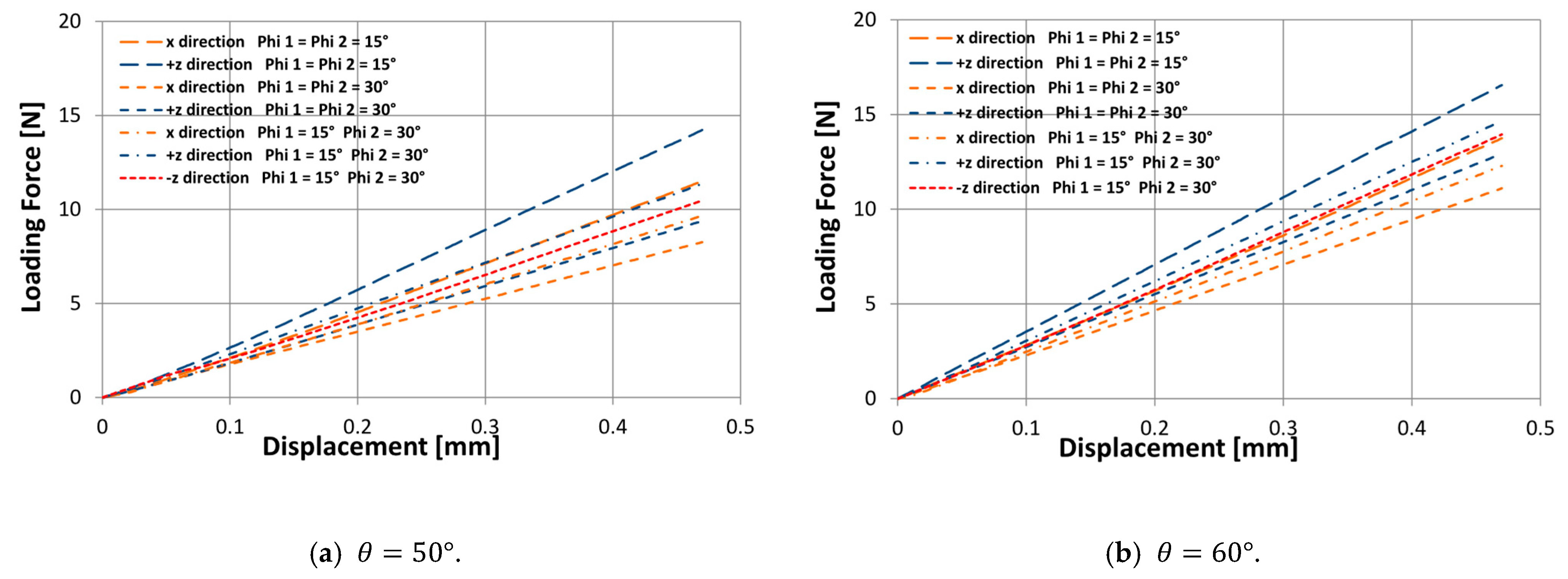
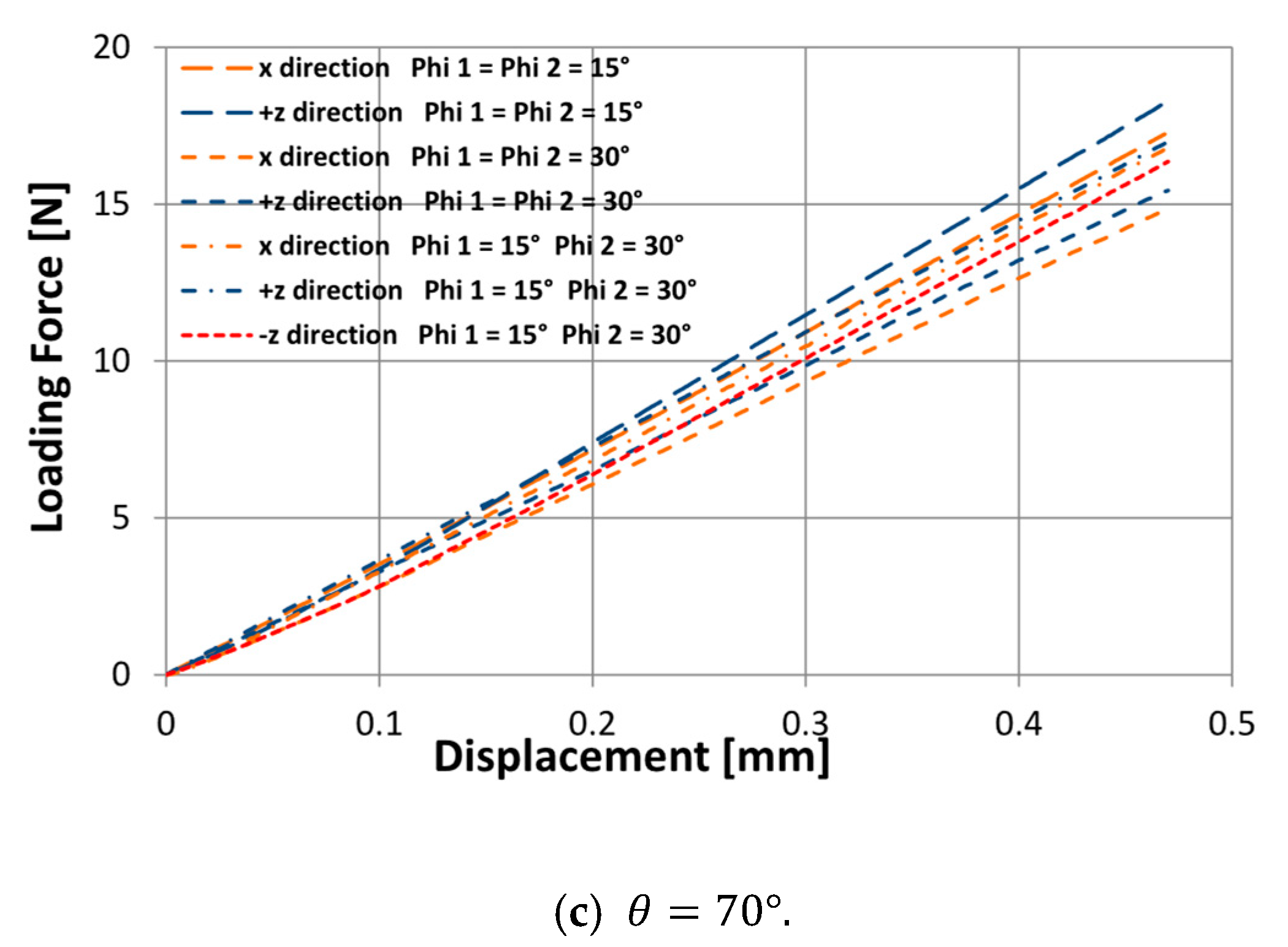
3.3. Flexural Stiffness
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Paolini, A.; Kollmannsberger, S.; Rank, E. Additive manufacturing in construction: A review on processes, applications, and digital planning methods. Addit. Manuf. 2019, 30, 100894. [Google Scholar] [CrossRef]
- Lewandowski, J.J.; Seifi, M. Metal Additive Manufacturing: A Review of Mechanical Properties. Annu. Rev. Mater. Res. 2016, 46, 151–186. [Google Scholar] [CrossRef]
- Neff, C.; Hopkinson, N.; Crane, N.B. Experimental and analytical investigation of mechanical behavior of laser-sintered diamond-lattice structures. Addit. Manuf. 2018, 22, 807–816. [Google Scholar] [CrossRef]
- Garner, E.; Kolken, H.M.A.; Wang, C.C.L.; Zadpoor, A.A.; Wu, J. Compatibility in microstructural optimization for additive manufacturing. Addit. Manuf. 2019, 26, 65–75. [Google Scholar] [CrossRef]
- Li, T.; Chen, Y.; Wang, L. Enhanced fracture toughness in architected interpenetrating phase composites by 3D printing. Compos. Sci. Technol. 2018, 167, 251–259. [Google Scholar] [CrossRef]
- Yang, J.; Gu, D.; Lin, K.; Wu, L.; Zhang, H.; Guo, M.; Yuan, L. Laser additive manufacturing of cellular structure with enhanced compressive performance inspired by Al–Si crystalline microstructure. CIRP J. Manuf. Sci. Technol. 2021, 32, 26–36. [Google Scholar] [CrossRef]
- Liu, J.; Yan, D.; Pang, W.; Zhang, Y. Design, fabrication and applications of soft network materials. Mater. Today 2021, 49, 324–350. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Y.; He, R.; Bai, X.; Zhang, K.; Ai, S.; Yang, Y.; Fang, D. Bending behavior of lightweight C/SiC pyramidal lattice core sandwich panels. Int. J. Mech. Sci. 2020, 171, 105409. [Google Scholar] [CrossRef]
- Ingrole, A.; Aguirre, T.G.; Fuller, L.; Donahue, S.W. Bioinspired energy absorbing material designs using additive manufacturing. J. Mech. Behav. Biomed. Mater. 2021, 119, 104518. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Zou, J.; Li, S.; Jamshidi, P.; Abena, A.; Forsey, A.; Moat, R.J.; Essa, K.; Wang, M.; Zhou, K.; et al. Additive manufacturing of bio-inspired multi-scale hierarchically strengthened lattice structures. Int. J. Mach. Tools Manuf. 2021, 167, 103764. [Google Scholar] [CrossRef]
- Malshe, A.; Bapat, S.; Rajurkar, K.P.; Haitjema, H. Bio-inspired textures for functional applications. CIRP Ann. 2018, 67, 627–650. [Google Scholar] [CrossRef]
- Velasco-Hogan, A.; Xu, J.; Meyers, M.A. Additive Manufacturing as a Method to Design and Optimize Bioinspired Structures. Adv. Mater. 2018, 30, 1800940. [Google Scholar] [CrossRef] [PubMed]
- Ingrole, A.; Hao, A.; Liang, R. Design and modeling of auxetic and hybrid honeycomb structures for in-plane property enhancement. Mater. Des. 2017, 117, 72–83. [Google Scholar] [CrossRef]
- Bai, L.; Gong, C.; Chen, X.; Sun, Y.; Xin, L.; Pu, H.; Peng, Y.; Luo, J. Mechanical properties and energy absorption capabilities of functionally graded lattice structures: Experiments and simulations. Int. J. Mech. Sci. 2020, 182, 105735. [Google Scholar] [CrossRef]
- Chen, X.; Ji, Q.; Wei, J.; Tan, H.; Yu, J.; Zhang, P.; Laude, V.; Kadic, M. Light-weight shell-lattice metamaterials for mechanical shock absorption. Int. J. Mech. Sci. 2020, 169, 105288. [Google Scholar] [CrossRef]
- Rajpal, R.; Lijesh, K.P.; Gangadharan, K.V. Parametric studies on bending stiffness and damping ratio of Sandwich structures. Addit. Manuf. 2018, 22, 583–591. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Mirbolghasemi, A.; Hermenean, K. 3D printed meta-sandwich structures: Failure mechanism, energy absorption and multi-hit capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, K.; Yin, Q.; Zhong, F.; Huang, C. Experimental study on dynamic compressive behaviour of sandwich panel with shear thickening fluid filled pyramidal lattice truss core. Int. J. Mech. Sci. 2018, 138–139, 467–475. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, L.; Bian, W.; Leng, J.; Liu, Y. Compression behavior and energy absorption of 3D printed continuous fiber reinforced composite honeycomb structures with shape memory effects. Addit. Manuf. 2021, 38, 101842. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, M.; Wang, C.H.; Sun, G.; Li, G. Out-of-plane crashworthiness of bio-inspired self-similar regular hierarchical honeycombs. Compos. Struct. 2016, 144, 1–13. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Niknam, H.; Hermenean, K. “3D printed architected polymeric sandwich panels: Energy absorption and structural performance. Compos. Struct. 2018, 200, 886–909. [Google Scholar] [CrossRef]
- Li, T.; Jarrar, F.; Al-Rub, R.A.; Cantwell, W. “Additive manufactured semi-plate lattice materials with high stiffness, strength and toughness. Int. J. Solids Struct. 2021, 230–231, 111153. [Google Scholar] [CrossRef]
- Novak, N.; Biasetto, L.; Rebesan, P.; Zanini, F.; Carmignato, S.; Krstulović-Opara, L.; Vesenjak, M.; Ren, Z. Experimental and computational evaluation of tensile properties of additively manufactured hexa- and tetrachiral auxetic cellular structures. Addit. Manuf. 2021, 45, 102022. [Google Scholar] [CrossRef]
- Babamiri, B.B.; Barnes, B.; Soltani-Tehrani, A.; Shamsaei, N.; Hazeli, K. Designing additively manufactured lattice structures based on deformation mechanisms. Addit. Manuf. 2021, 46, 102143. [Google Scholar] [CrossRef]
- Wang, P.; Yang, F.; Yang, F.; Li, P.; Zheng, B.; Fan, H. Design and additive manufacturing of a modified face-centered cubic lattice with enhanced energy absorption capability. Extrem. Mech. Lett. 2021, 47, 101358. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Jia, Z.; Scarpa, F.; Yao, C.W.; Wang, L. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Mater. Des. 2018, 137, 226–234. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Z.; Lu, Z.; Liao, B.; He, X. Effective elastic properties and initial yield surfaces of two 3D lattice structures. Int. J. Mech. Sci. 2018, 138–139, 146–158. [Google Scholar] [CrossRef]
- Han, S.C.; Kang, D.S.; Kang, K. Two nature-mimicking auxetic materials with potential for high energy absorption. Mater. Today 2019, 26, 30–39. [Google Scholar] [CrossRef]
- Ling, C.A.; Cernicchi, M.D. Gilchrist, and Cardiff, “Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Rawson, S.D.; Puga, H.; Meireles, J.; Withers, J. Additive manufacturing assisted investment casting: A low-cost method to fabricate periodic metallic cellular lattices. Addit. Manuf. 2020, 33, 101085. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Daurel, A.; Jeng, J.Y. Design and additive manufacturing of closed cells from supportless lattice structure. Addit. Manuf. 2020, 33, 101168. [Google Scholar] [CrossRef]
- Drücker, S.; Schulze, M.; Ipsen, H.; Bandegani, L.; Hoch, H.; Kluge, M.; Fiedler, B. Experimental and numerical mechanical characterization of additively manufactured Ti6Al4V lattice structures considering progressive damage. Int. J. Mech. Sci. 2021, 189, 105986. [Google Scholar] [CrossRef]
- Yang, H.; Wang, B.; Ma, L. Designing hierarchical metamaterials by topology analysis with tailored Poisson’s ratio and Young’s modulus. Compos. Struct. 2019, 214, 359–378. [Google Scholar] [CrossRef]
- Johnston, R.; Kazancı, Z. Analysis of additively manufactured (3D printed) dual-material auxetic structures under compression. Addit. Manuf. 2021, 38, 101783. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Liu, M.; Huang, H.; Xu, S.; Xia, Y.; Qian, G.; Wu, W. Mechanical behaviors of SLM additive manufactured octet-truss and truncated-octahedron lattice structures with uniform and taper beams. Int. J. Mech. Sci. 2019, 163, 105091. [Google Scholar] [CrossRef]
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 23001. [Google Scholar] [CrossRef]
- Yang, L.; Cormier, D.; West, H.; Harrysson, O.; Knowlson, K. Non-stochastic Ti-6Al-4V foam structures with negative Poisson’s ratio. Mater. Sci. Eng. A 2012, 558, 579–585. [Google Scholar] [CrossRef]
- Donoghue, J.; Alderson, K.L.; Evans, K.E. The fracture toughness of composite laminates with a negative Poisson’s ratio. Phys. Status Solidi Basic Res. 2009, 246, 2011–2017. [Google Scholar] [CrossRef]
- Elipe, J.C.Á.; Lantada, A.D. Comparative study of auxetic geometries by means of computer-aided design and engineering. Smart Mater. Struct. 2012, 21, 105004. [Google Scholar] [CrossRef]
- Gorodtsov, V.A.; Lisovenko, D.S. Extreme values of Young’s modulus and Poisson’s ratio of hexagonal crystals. Mech. Mater. 2019, 134, 1–8. [Google Scholar] [CrossRef]
- Tretiakov, K.V.; Wojciechowski, K.W. Auxetic, Partially Auxetic, and Nonauxetic Behaviour in 2D Crystals of Hard Cyclic Tetramers. Phys. Status Solidi—Rapid Res. Lett. 2020, 14, 2000198. [Google Scholar] [CrossRef]
- Essassi, K.; Rebiere, J.l.; el Mahi, A.; Souf, M.A.B.; Bouguecha, A.; Haddar, M. Experimental and analytical investigation of the bending behaviour of 3D-printed bio-based sandwich structures composites with auxetic core under cyclic fatigue tests. Compos. Part A Appl. Sci. Manuf. 2020, 131, 105775. [Google Scholar] [CrossRef]
- Almgren, R. An isotropic three-dimensional structure with Poisson’s ratio__1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Lakes, R. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Evans, K.E. Tensile network microstructures exhibiting negative Poisson’s ratio. J. Phys. D. Appl. Phys. 1989, 22, 1870–1876. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Modeling of uniaxial compression in a 3D periodic re-entrant lattice structure. J. Mater. Sci. 2013, 48, 1413–1422. [Google Scholar] [CrossRef]
- Li, Y.; Ola, H.; Denis, C.; Harvey, W.; Haijun, G.; Brent, S. Additive Manufacturing of Metal Cellular Structures: Design and Fabrication. JOM 2015, 67, 608–615. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69–70, 475–490. [Google Scholar] [CrossRef]
- Grima, J.N.; Winczewski, S.; Mizzi, L.; Grech, M.C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W.; Rybicki, J. Tailoring Graphene to Achieve Negative Poisson’s Ratio Properties. Adv. Mater. 2015, 27, 1455–1459. [Google Scholar] [CrossRef] [PubMed]
- Poźniak, A.A.; Wojciechowski, K.W.; Grima, J.N.; Mizzi, L. Planar auxeticity from elliptic inclusions. Compos. Part B Eng. 2016, 94, 379–388. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V.; Smardzewski, J.; Scarpa, F.; Piglowski, P.M.; Kowalik, M.; Imre, A.R.; Bilski, M. Auxetic Properties of a f.c.c. Crystal of Hard Spheres with an Array of [001]-Nanochannels Filled by Hard Spheres of Another Diameter. Phys. Status Solidi 2019, 256, 1800611. [Google Scholar] [CrossRef]
- Raturi, A.; Biswas, K.; Gurao, N. Elastic and plastic anisotropy in a refractory high entropy alloy utilizing combinatorial instrumented indentation and electron backscatter diffraction. J. Alloys Compd. 2022, 896, 162902. [Google Scholar] [CrossRef]
- Tuninetti, V.; Jaramillo, A.F.; Riu, G.; Rojas-Ulloa, C.; Znaidi, A.; Medina, C.; Mateo, A.M.; Roa, J.J. Experimental correlation of mechanical properties of the ti-6al-4v alloy at different length scales. Metals 2021, 11, 104. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Valenzuela, M.; Tuninetti, V.; Habraken, A.M. Identification and validation of an extended Stewart-Cazacu micromechanics damage model applied to Ti–6Al–4V specimens exhibiting positive stress triaxialities. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1248–1261. [Google Scholar] [CrossRef]
- Tuninetti, V.; Gilles, G.; Flores, P.; Pincheira, G.; Duchêne, L.; Habraken, A.M. Impact of distortional hardening and the strength differential effect on the prediction of large deformation behavior of the Ti6Al4V alloy. Meccanica 2019, 54, 1823–1840. [Google Scholar] [CrossRef]
- Rojas-Ulloa, C.; Bouffioux, C.; Jaramillo, A.F.; García-Herrera, C.M.; Hussain, T.; Duchêne, L.; Riu, G.; Roa, J.J.; Flores, P.; Habraken, A.M.; et al. Nanomechanical Characterization of the Deformation Response of Orthotropic Ti–6Al–4V. Adv. Eng. Mater. 2021, 23, 2001341. [Google Scholar] [CrossRef]
- Harbaoui, R.; Daghfas, O.; Znaidi, A.; Tuninetti, V. Mechanical behavior of materials with a compact hexagonal structure obtained by an advanced identification strategy of HCP material, AZ31B-H24. Frat. Integrita Strutt. 2020, 14, 295–305. [Google Scholar] [CrossRef]
- Nguyen, C.H.; Choi, Y. Concurrent density distribution and build orientation optimization of additively manufactured functionally graded lattice structures. CAD Comput. Aided Des. 2020, 127, 102884. [Google Scholar] [CrossRef]
- Harris, J.A.; McShane, G.J. Metallic stacked origami cellular materials: Additive manufacturing, properties, and modelling. Int. J. Solids Struct. 2020, 185–186, 448–466. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, L. Modeling and analysis of material anisotropy-topology effects of 3D cellular structures fabricated by powder bed fusion additive manufacturing. Int. J. Mech. Sci. 2021, 197, 106325. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V.; Fernandez, E.; Uribe-Lam, E. Design and Characterization of Asymmetric Cell Structure of Auxetic Material for Predictable Directional Mechanical Response. Materials 2022, 15, 1841. [Google Scholar] [CrossRef]
- Valle, R.; Pincheira, G.; Tuninetti, V. Design of an auxetic cellular structure with different elastic properties in its three orthogonal directions. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1341–1350. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, L.; Liu, C.; Zhang, Z.; Ma, L.; Chen, C.; Banthia, N.; Zhang, Y. Mechanical anisotropy evolution of 3D-printed alkali-activated materials with different GGBFS/FA combinations. J. Build. Eng. 2022, 50, 104126. [Google Scholar] [CrossRef]
- Tuninetti, V.; Flores, P.; Valenzuela, M.; Pincheira, G.; Medina, C.; Duchêne, L.; Habraken, A.-M. Experimental characterization of the compressive mechanical behaviour of Ti6Al4V alloy at constant strain rates over the full elastoplastic range. Int. J. Mater. Form. 2020, 13, 709–724. [Google Scholar] [CrossRef]
- Tuninetti, V.; Habraken, A.M. Impact of anisotropy and viscosity to model the mechanical behavior of Ti-6Al-4V alloy. Mater. Sci. Eng. A 2014, 605, 39–50. [Google Scholar] [CrossRef]
- Cansizoglu, O.; Harrysson, O.; Cormier, D.; West, H.; Mahale, T. Properties of Ti-6Al-4V non-stochastic lattice structures fabricated via electron beam melting. Mater. Sci. Eng. A 2008, 492, 468–474. [Google Scholar] [CrossRef]
- Joseph, A.; Mahesh, V.; Harursampath, D. On the application of additive manufacturing methods for auxetic structures: A review. Adv. Manuf. 2021, 9, 342–368. [Google Scholar] [CrossRef] [PubMed]
- Jardin, R.T.; Tuninetti, V.; Tchuindjang, J.T.; Hashemi, N.; Carrus, R.; Mertens, A.; Duchêne, L.; Tran, H.S.; Habraken, A.M. Sensitivity analysis in the modeling of a high-speed, steel, thin wall produced by directed energy deposition. Metals 2020, 10, 1554. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valle, R.; Pincheira, G.; Tuninetti, V.; Garrido, C.; Treviño, C.; Morales, J. Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts. Polymers 2022, 14, 4325. https://doi.org/10.3390/polym14204325
Valle R, Pincheira G, Tuninetti V, Garrido C, Treviño C, Morales J. Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts. Polymers. 2022; 14(20):4325. https://doi.org/10.3390/polym14204325
Chicago/Turabian StyleValle, Rodrigo, Gonzalo Pincheira, Víctor Tuninetti, Cesar Garrido, Cecilia Treviño, and Jorge Morales. 2022. "Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts" Polymers 14, no. 20: 4325. https://doi.org/10.3390/polym14204325
APA StyleValle, R., Pincheira, G., Tuninetti, V., Garrido, C., Treviño, C., & Morales, J. (2022). Evaluation of the Orthotropic Behavior in an Auxetic Structure Based on a Novel Design Parameter of a Square Cell with Re-Entrant Struts. Polymers, 14(20), 4325. https://doi.org/10.3390/polym14204325






