Author Contributions
Conceptualization, H.A. and W.R.; methodology, H.A. and W.R.; software, H.A.; validation, H.A.; formal analysis, H.A.; investigation, H.A.; resources, H.A., W.R. and C.F.; data curation, H.A.; writing—original draft preparation, H.A.; writing—review and editing, W.R.; visualization, H.A.; supervision, G.R.B.-W.; project administration, H.A. and W.R.; funding acquisition, W.R. All authors have read and agreed to the published version of the manuscript.
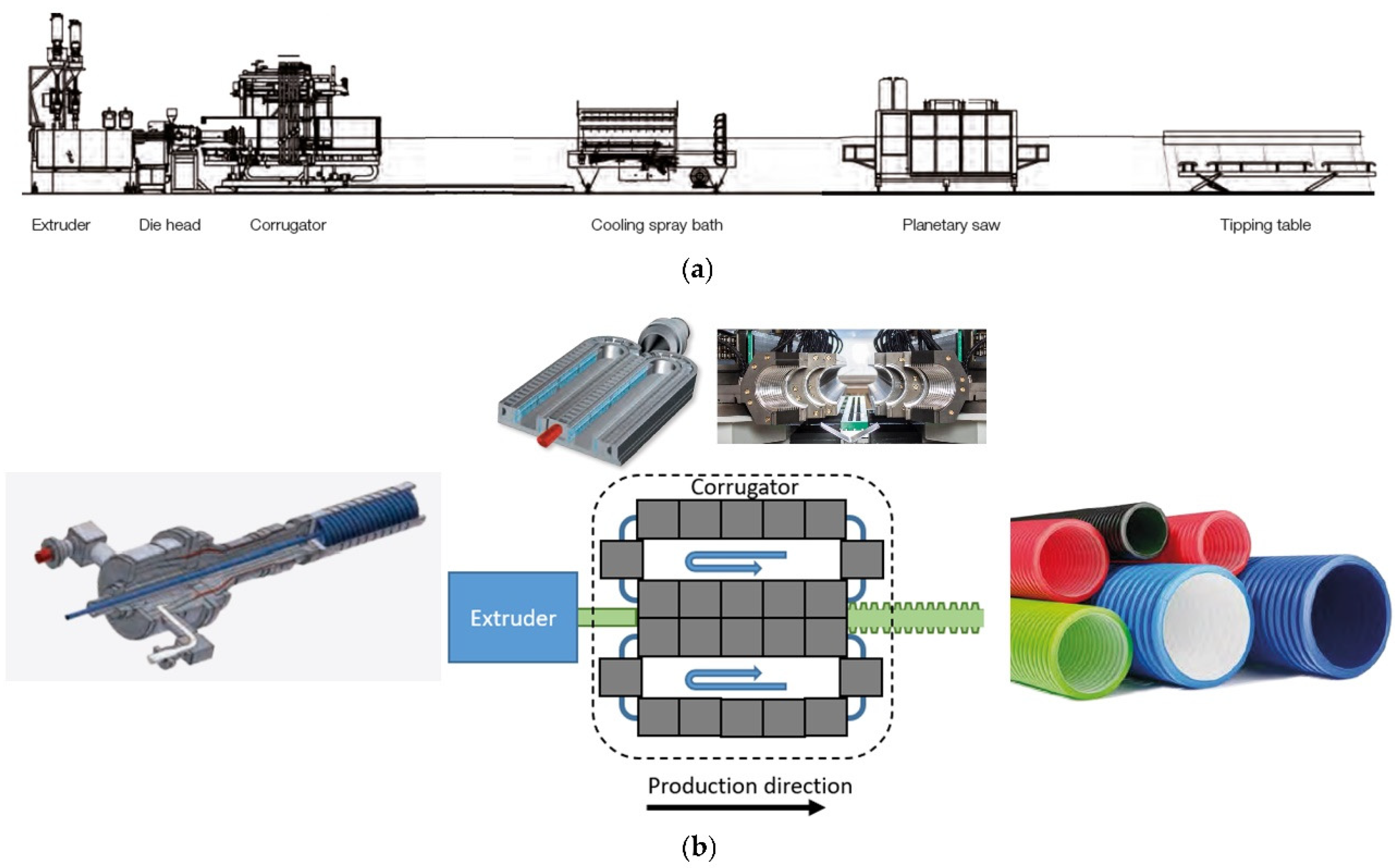
Figure 1.
(a) Schematic of a corrugated pipe production line and of the corrugator with (b) the die head.
Figure 1.
(a) Schematic of a corrugated pipe production line and of the corrugator with (b) the die head.
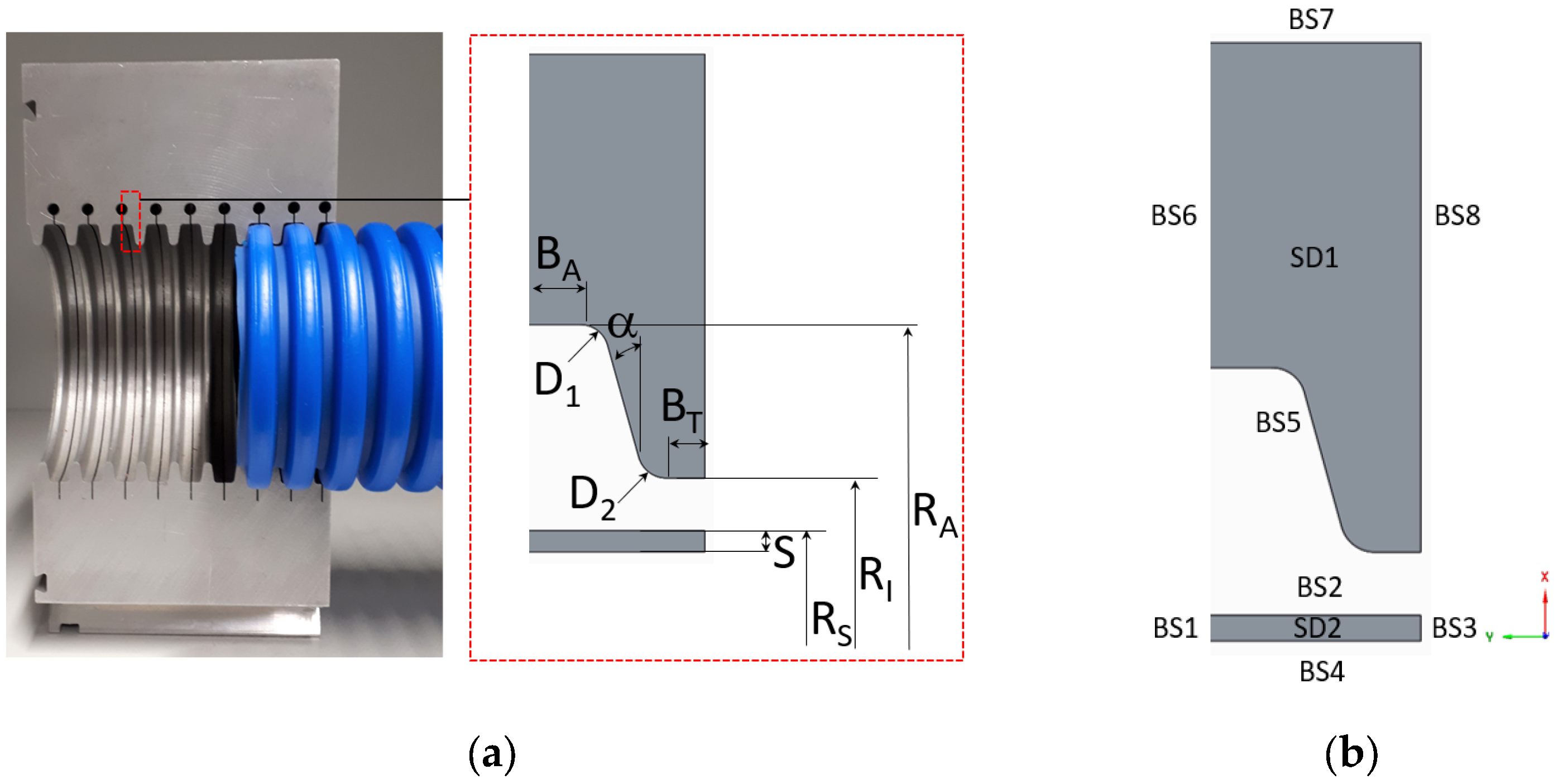
Figure 2.
(a) 3D Mold block geometry on which the 2D axisymmetric model is based; (b) simulation boundary conditions.
Figure 2.
(a) 3D Mold block geometry on which the 2D axisymmetric model is based; (b) simulation boundary conditions.
Figure 3.
Wall thickness evaluation positions: crest, valley, lower and upper flank.
Figure 3.
Wall thickness evaluation positions: crest, valley, lower and upper flank.
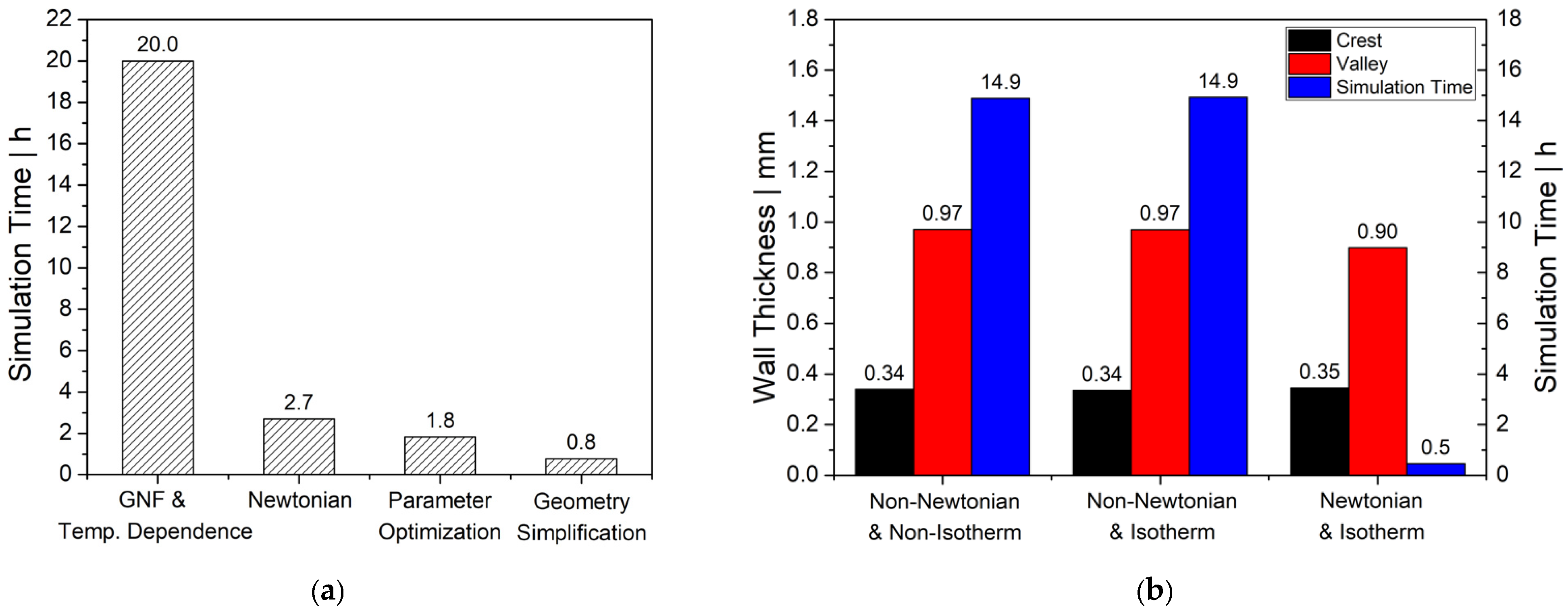
Figure 4.
(a) Optimization of the simulation time, (b) comparison study of wall thickness distribution and simulation time.
Figure 4.
(a) Optimization of the simulation time, (b) comparison study of wall thickness distribution and simulation time.
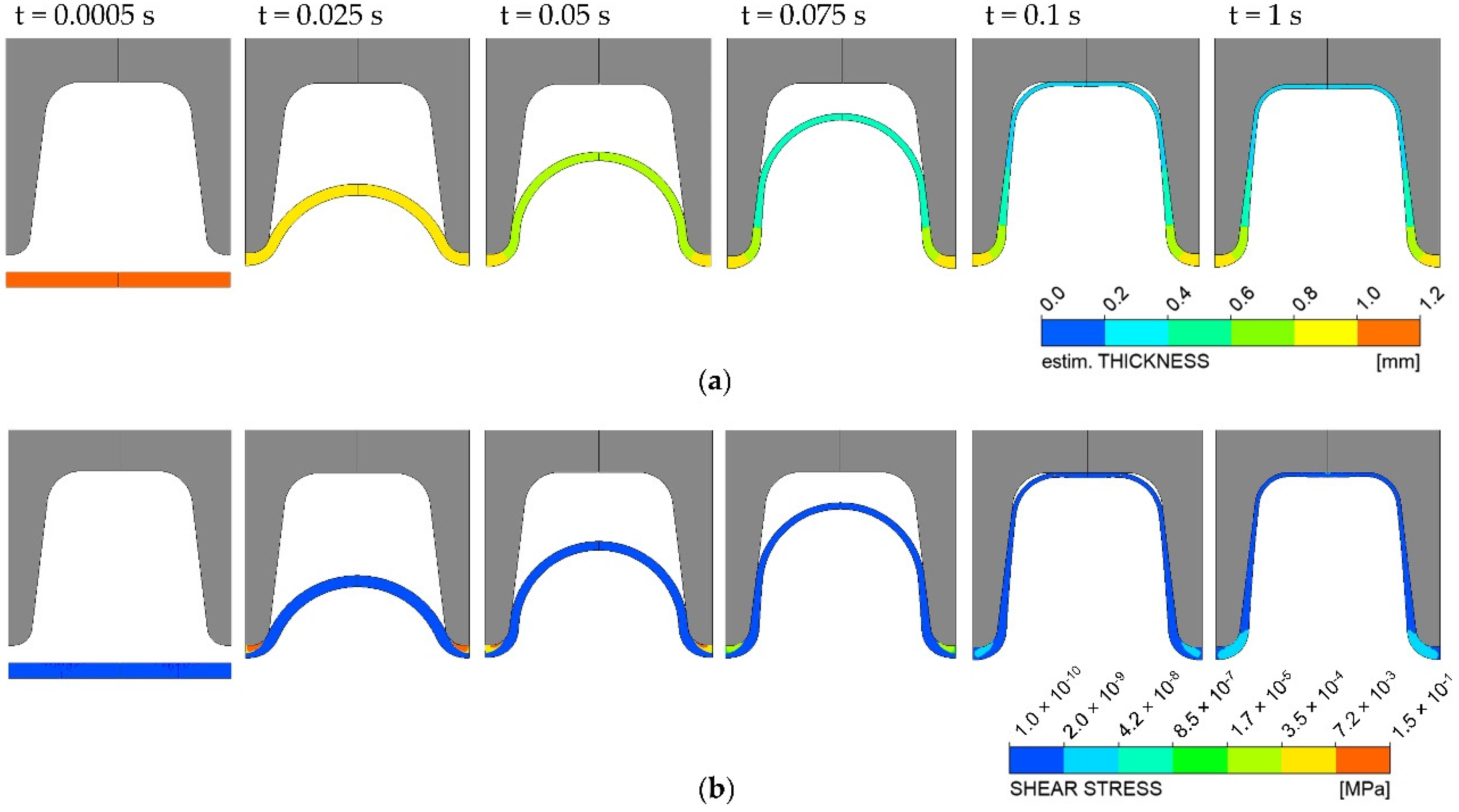
Figure 5.
Simulation results of the blow-molding process showing that the parison is fully inflated after an inflation time of 1 s: (a) wall thickness distribution, (b) shear stress distribution.
Figure 5.
Simulation results of the blow-molding process showing that the parison is fully inflated after an inflation time of 1 s: (a) wall thickness distribution, (b) shear stress distribution.
Figure 6.
Finite element meshes used.
Figure 6.
Finite element meshes used.
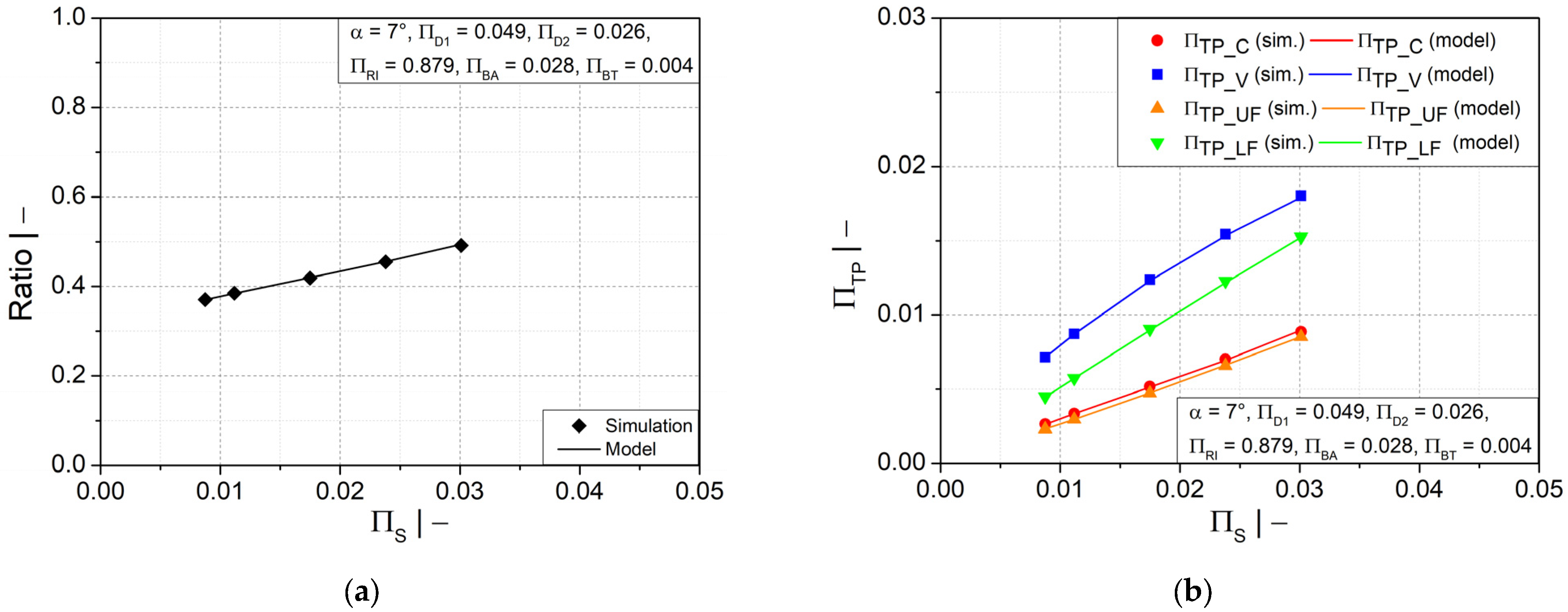
Figure 7.
Ratio of wall thicknesses at crest and valley as a function of dimensionless (a) half profile width at valley and (b) valley diameter .
Figure 7.
Ratio of wall thicknesses at crest and valley as a function of dimensionless (a) half profile width at valley and (b) valley diameter .
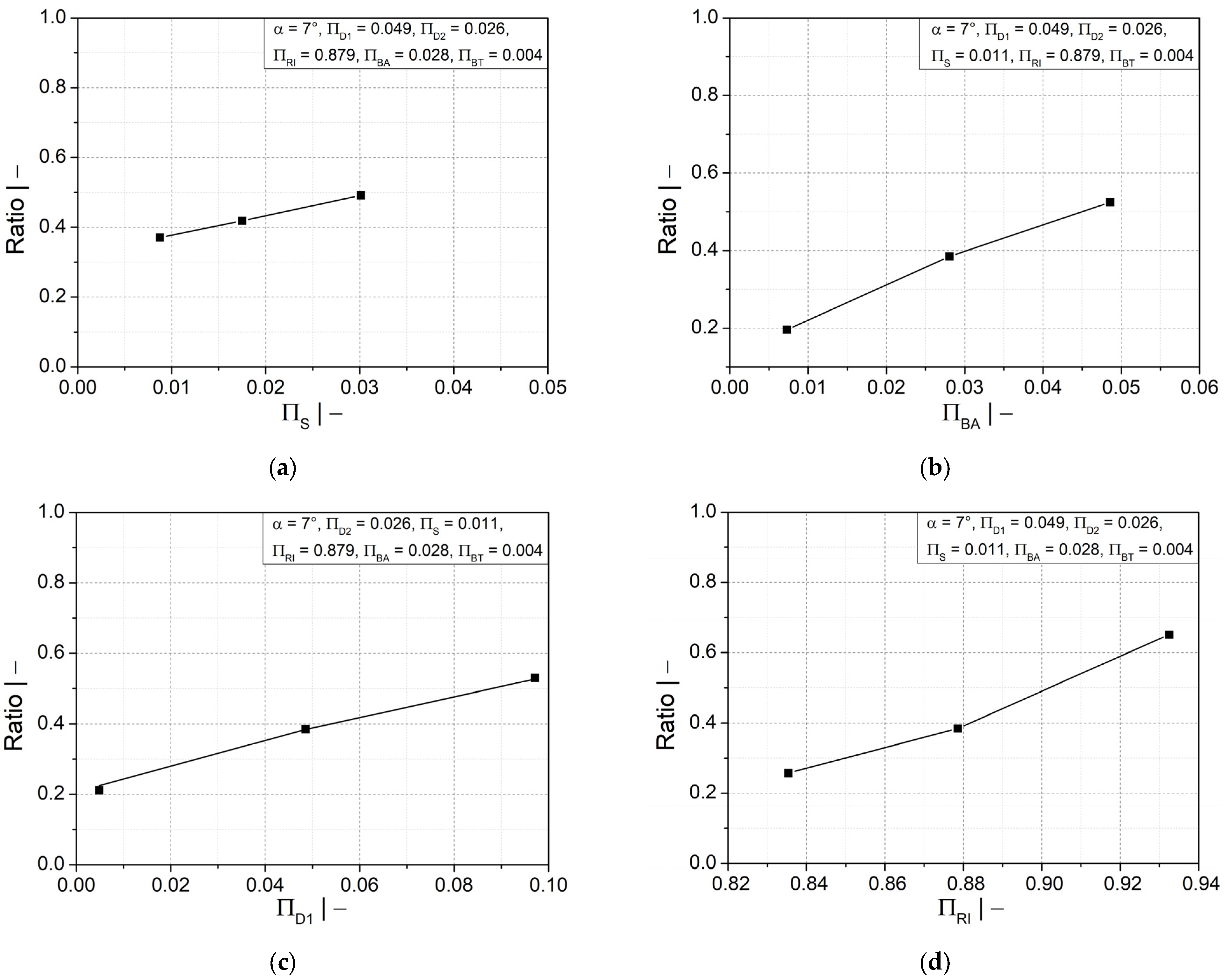
Figure 8.
Ratio of wall thicknesses at crest and valley as a function of dimensionless (a) initial thickness of fluid parison b) half profile width at crest ; (c) crest diameter ; (d) mold block inner radius ; and (e) flank angle .
Figure 8.
Ratio of wall thicknesses at crest and valley as a function of dimensionless (a) initial thickness of fluid parison b) half profile width at crest ; (c) crest diameter ; (d) mold block inner radius ; and (e) flank angle .
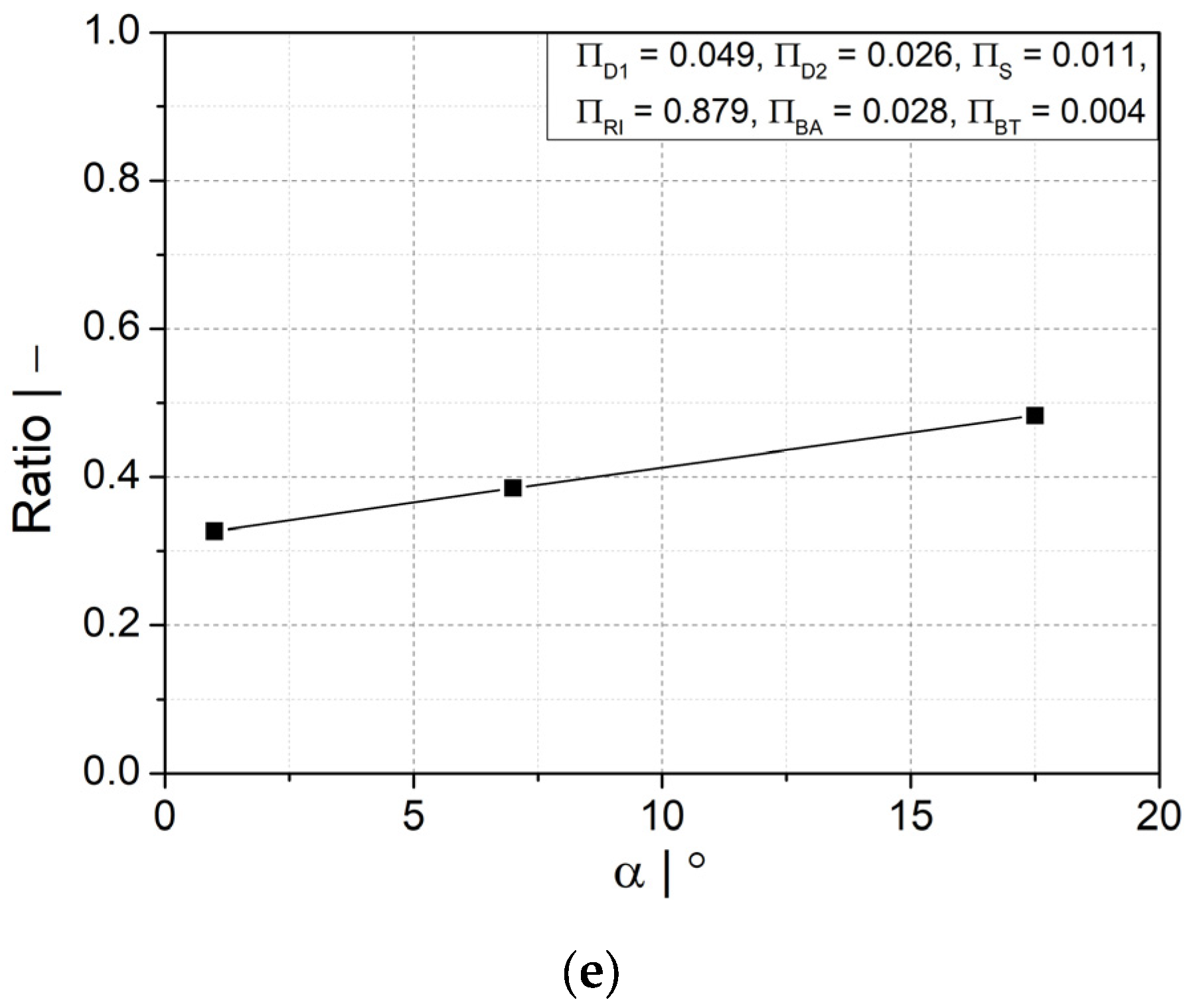
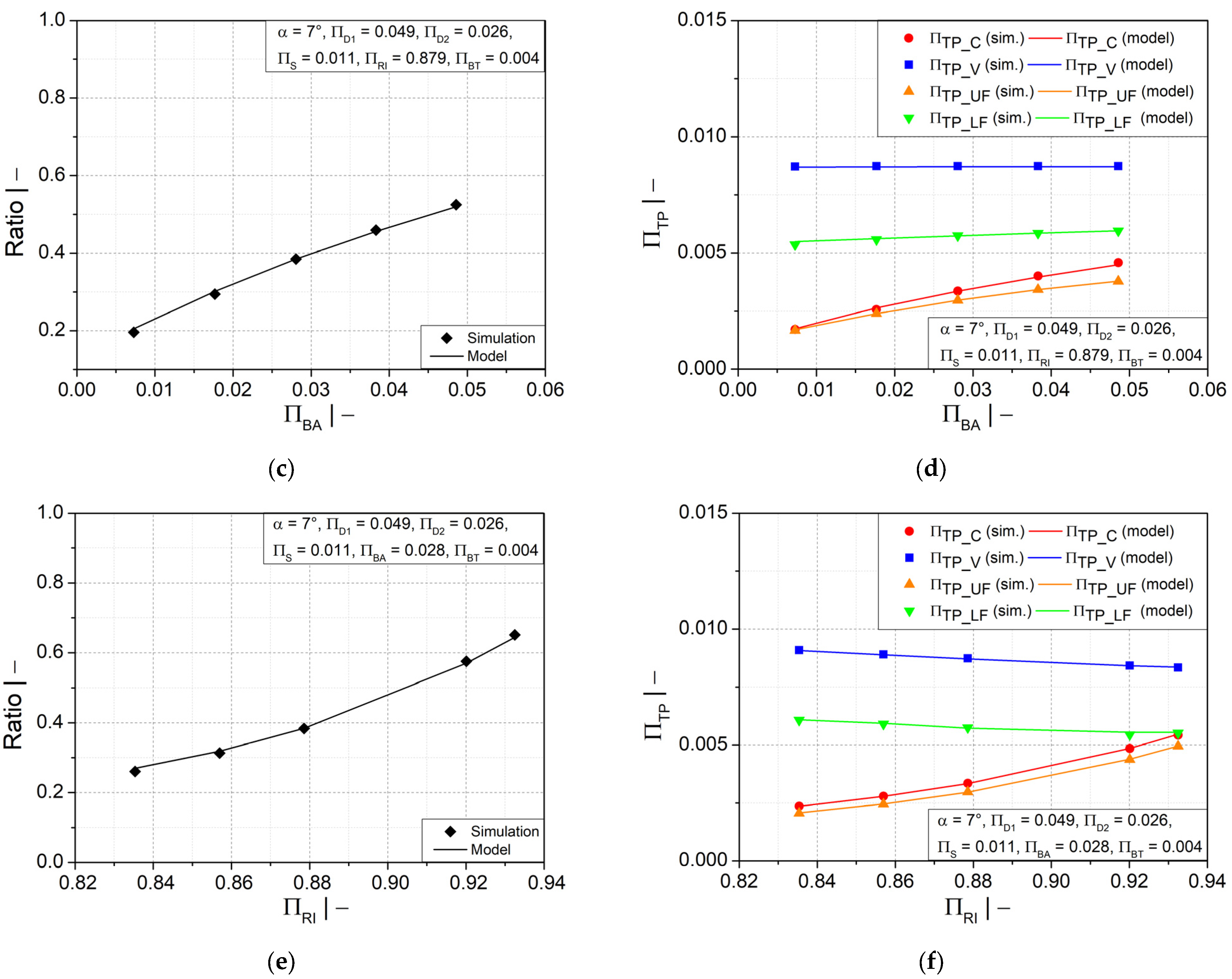
Figure 9.
Ratio of wall thicknesses at crest and valley and dimensionless wall thickness as functions of (a,b) flank angle and (c,d) dimensionless crest diameter .
Figure 9.
Ratio of wall thicknesses at crest and valley and dimensionless wall thickness as functions of (a,b) flank angle and (c,d) dimensionless crest diameter .
Figure 10.
Ratio of wall thicknesses at crest and valley and dimensionless wall thickness as functions of dimensionless (a,b) half profile width at crest and (c,d) initial thickness of fluid parison .
Figure 10.
Ratio of wall thicknesses at crest and valley and dimensionless wall thickness as functions of dimensionless (a,b) half profile width at crest and (c,d) initial thickness of fluid parison .
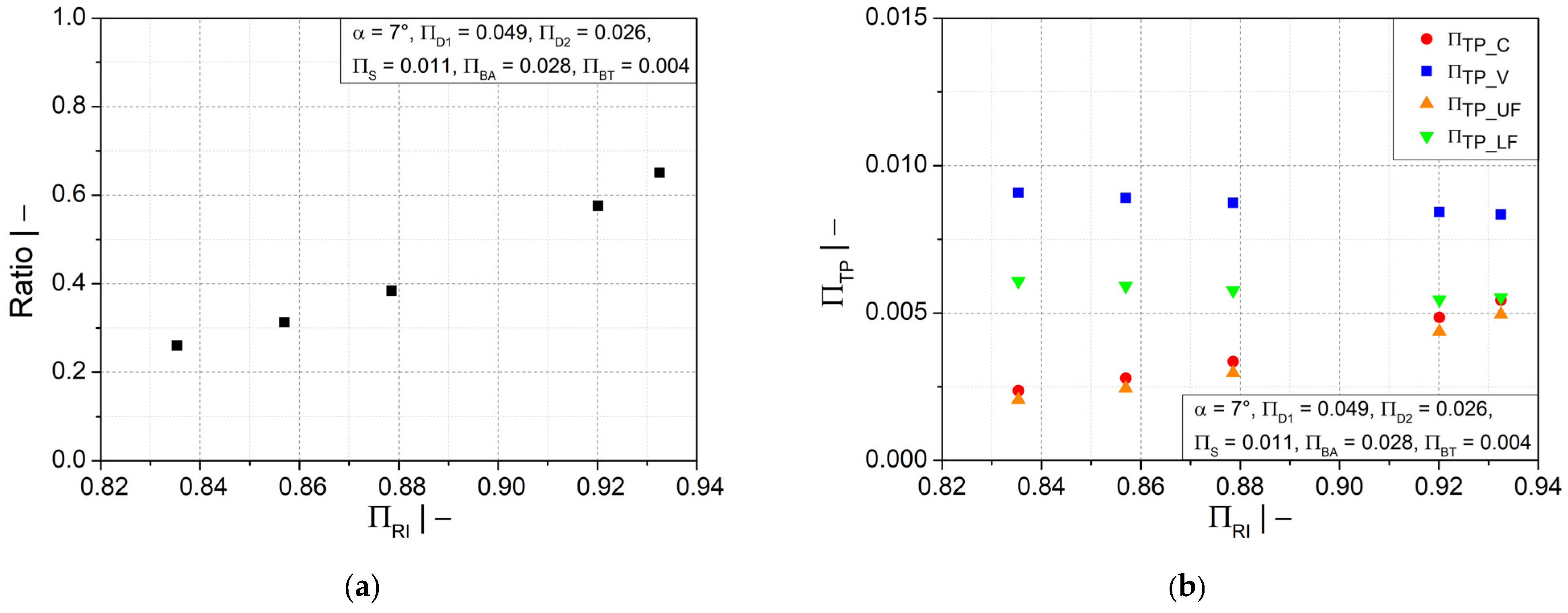
Figure 11.
(a) Ratio of wall thicknesses at crest and valley and (b) dimensionless wall thickness as functions of dimensionless mold block inner radius .
Figure 11.
(a) Ratio of wall thicknesses at crest and valley and (b) dimensionless wall thickness as functions of dimensionless mold block inner radius .
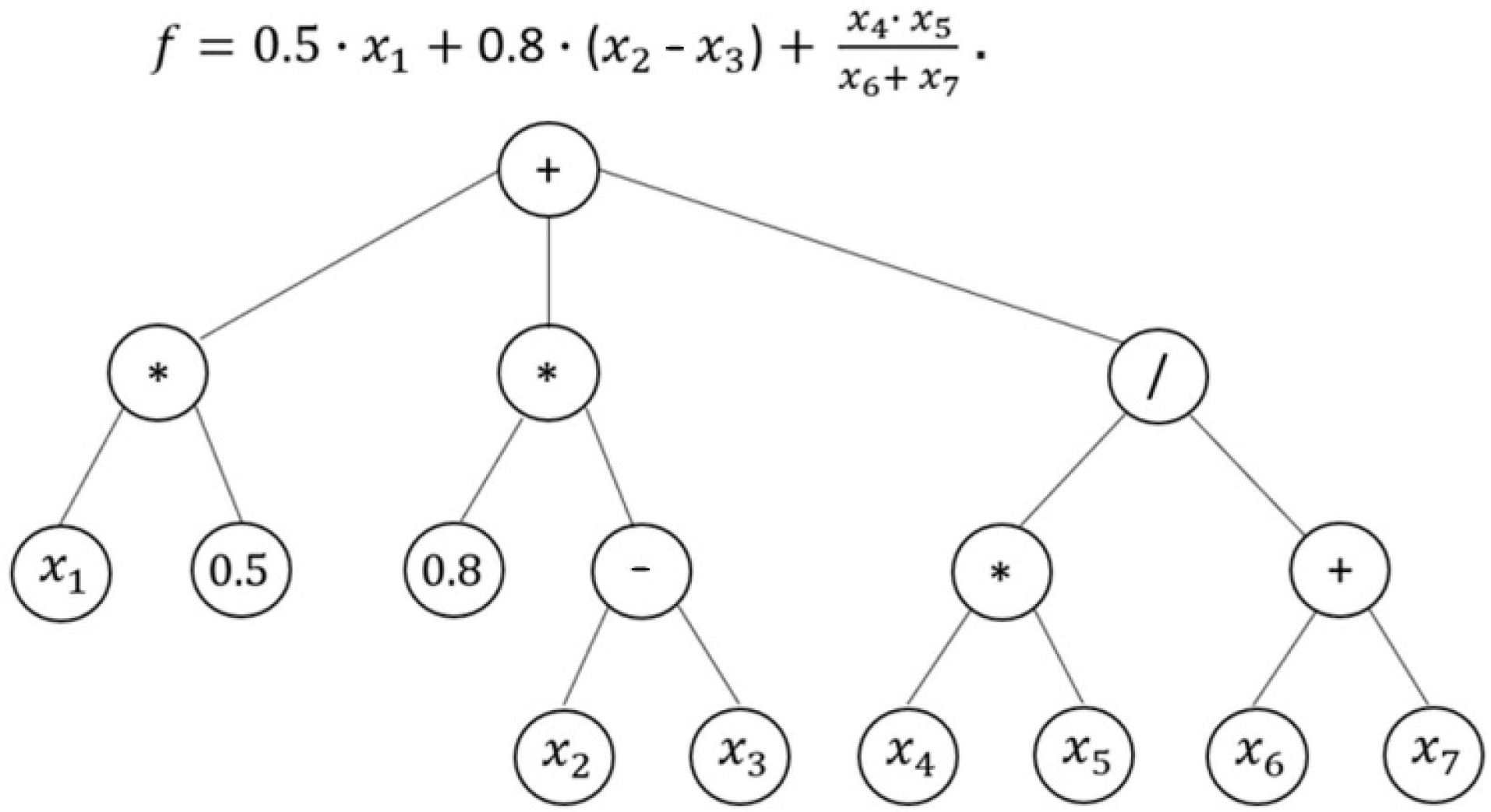
Figure 12.
Symbolic regression model in mathematical notation and in the form of a parse tree.
Figure 12.
Symbolic regression model in mathematical notation and in the form of a parse tree.
Figure 13.
Comparisons of the estimated models for wall thickness distribution ratio and dimensionless wall thickness at several evaluation positions as functions of (a,b) dimensionless crest diameter , (c,d) dimensionless half profile width at crest (e,f) dimensionless mold block inner radius .
Figure 13.
Comparisons of the estimated models for wall thickness distribution ratio and dimensionless wall thickness at several evaluation positions as functions of (a,b) dimensionless crest diameter , (c,d) dimensionless half profile width at crest (e,f) dimensionless mold block inner radius .
Figure 14.
Comparisons of the estimated models for wall thickness distribution ratio and dimensionless wall thickness at several evaluation positions as functions of (a,b) dimensionless initial thickness of fluid parison and (c,d) flank angle .
Figure 14.
Comparisons of the estimated models for wall thickness distribution ratio and dimensionless wall thickness at several evaluation positions as functions of (a,b) dimensionless initial thickness of fluid parison and (c,d) flank angle .
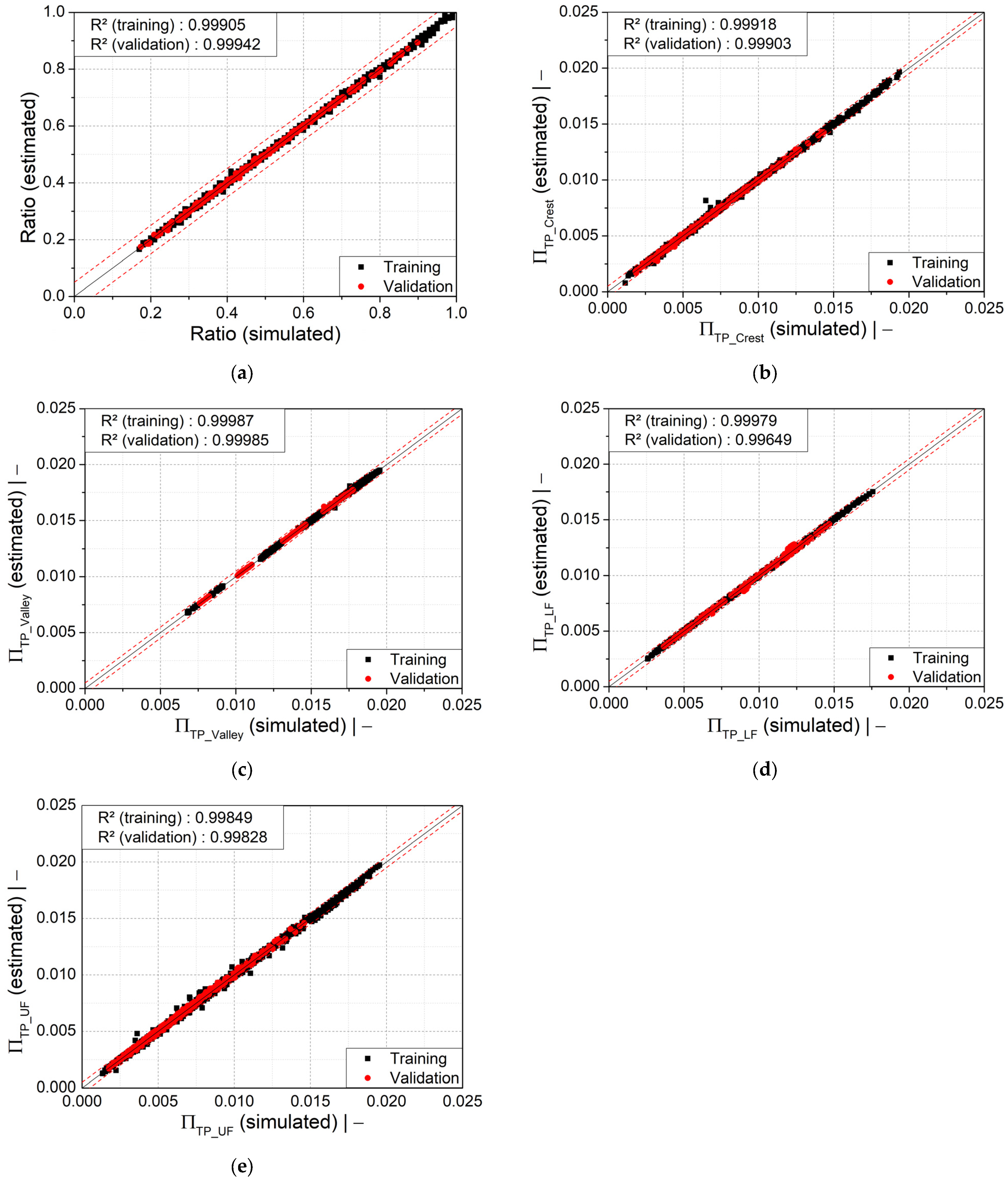
Figure 15.
Scatter plots of (a) wall thickness ratio, (b) dimensionless wall thickness at the crest, (c) dimensionless wall thickness at the valley, (d) dimensionless wall thickness at the lower flank, and (e) dimensionless wall thickness at the upper flank. The dashed red lines indicate a relative error of ±5%.
Figure 15.
Scatter plots of (a) wall thickness ratio, (b) dimensionless wall thickness at the crest, (c) dimensionless wall thickness at the valley, (d) dimensionless wall thickness at the lower flank, and (e) dimensionless wall thickness at the upper flank. The dashed red lines indicate a relative error of ±5%.
Table 1.
Mesh sensitivity analysis.
Table 1.
Mesh sensitivity analysis.
| Parameter | Mesh 1 | Mesh 2 | Mesh 3 | Mesh 4 | Mesh 5 | Mesh 6 |
|---|
| Edge Sizes [mm] | 0.01 | 0.025 | 0.05 | 0.075 | 0.1 | 0.15 |
| CPU Time [s] | 5282 | 2300 | 1358 | 992 | 953 | 519 |
| Wall thickness at crest [mm] | 0.3475 | 0.3470 | 0.3450 | 0.3447 | 0.3435 | 0.3417 |
| Wall thickness at valley [mm] | 0.8997 | 0.8992 | 0.8992 | 0.8987 | 0.8985 | 0.8976 |
Table 2.
Range of geometry parameters in the screening design.
Table 2.
Range of geometry parameters in the screening design.
| Parameter | Unit | Value |
|---|
| - | 0.835 | 0.879 | 0.932 |
| - | 0.005 | 0.049 | 0.097 |
| - | 0.002 | 0.026 | 0.052 |
| - | 0.007 | 0.028 | 0.049 |
| - | 0.001 | 0.004 | 0.015 |
| - | 0.009 | 0.011 | 0.030 |
| | 1 | 7 | 17.5 |
Table 3.
Multiple regression analysis output from the screening design study.
Table 3.
Multiple regression analysis output from the screening design study.
| Term | Estimated Regression Coefficient | p-Value |
|---|
| 0.0401725 | 6.25418 × 10−5 |
| 0.0332355 | 0.000293 |
| −0.013532 | 0.186159 |
| 0.0775136 | 0.000227 |
| −0.040225 | 0.226997 |
| 0.0526789 | 0.020054 |
| 0.0092651 | 0.012899 |
Table 4.
Geometry parameter ranges for the parametric design study.
Table 4.
Geometry parameter ranges for the parametric design study.
| Parameter | Unit | | | Value |
|---|
| - | 0.835 | 0.857 | 0.879 | 0.920 | 0.932 |
| - | 0.005 | 0.024 | 0.049 | 0.073 | 0.097 |
| - | 0.007 | 0.018 | 0.028 | 0.038 | 0.049 |
| - | 0.009 | 0.011 | 0.017 | 0.024 | 0.030 |
| | 1 | 3.5 | 7 | 10.5 | 17.5 |
Table 5.
OSGA parameter configurations.
Table 5.
OSGA parameter configurations.
| Parameter | Value |
|---|
| Population size | 100 |
| Selected parents | 200 |
| Crossover probability | 90% |
| Mutation probability | 25% |
| Maximum tree depth | 30 |
| Maximum tree length | 100 |
| Fitness function | Pearson R2 |
| Maximum generations | 75 |
| Maximum selection pressure | 100 |
| Operators | +, −, ∗, / |
| | Power functions (square) |
Table 6.
Geometry parameter ranges for the validation dataset.
Table 6.
Geometry parameter ranges for the validation dataset.
| Parameter | Unit | | Value |
|---|
| - | 0.846 | 0.868 | 0.899 | 0.926 |
| - | 0.015 | 0.036 | 0.061 | 0.085 |
| - | 0.012 | 0.023 | 0.033 | 0.043 |
| - | 0.010 | 0.014 | 0.021 | 0.027 |
| ° | 2.25 | 5.25 | 8.75 | 14 |
Table 7.
Results of the error analysis of the wall thickness prediction models.
Table 7.
Results of the error analysis of the wall thickness prediction models.
| Model | R2 (−) | MAE (−) | MRE (%) |
|---|
| Ratio | 0.99942 | 3.101 × 10−3 | 0.720 |
| 0.99903 | 6.255 × 10−5 | 1.232 |
| 0.99985 | 2.550 × 10−5 | 0.194 |
| 0.99649 | 1.058 × 10−4 | 1.073 |
| 0.99828 | 9.235 × 10−5 | 1.632 |