1. Introduction
Plastics recycling gained a lot of public, governmental, and scientific interest within the last few years [
1,
2,
3,
4]. According to the EU directive 2018/852, at least 50% and 55% of plastic packaging waste must be recycled annually until the end of 2025 and 2030, respectively [
5]. In addition to the design for recycling approach, which specifies that products must be designed in a way that they can be recycled (e.g., mono-material), there is also the design from recycling approach [
6]. A promising way of design from recycling without sacrificing visual quality and mechanical stability while using the required amount of plastic recyclates is to produce products with a multilayer structure to encapsulate the recyclates. Recyclates, which often have a grayish or greenish appearance and are therefore not as attractive as transparent, clear white, or brightly colored materials, can be wrapped in pigmented top layers [
7]. Furthermore, migration can be weakened by the use of multilayer structures, which could help recyclates to be applicable for food contact products [
8].
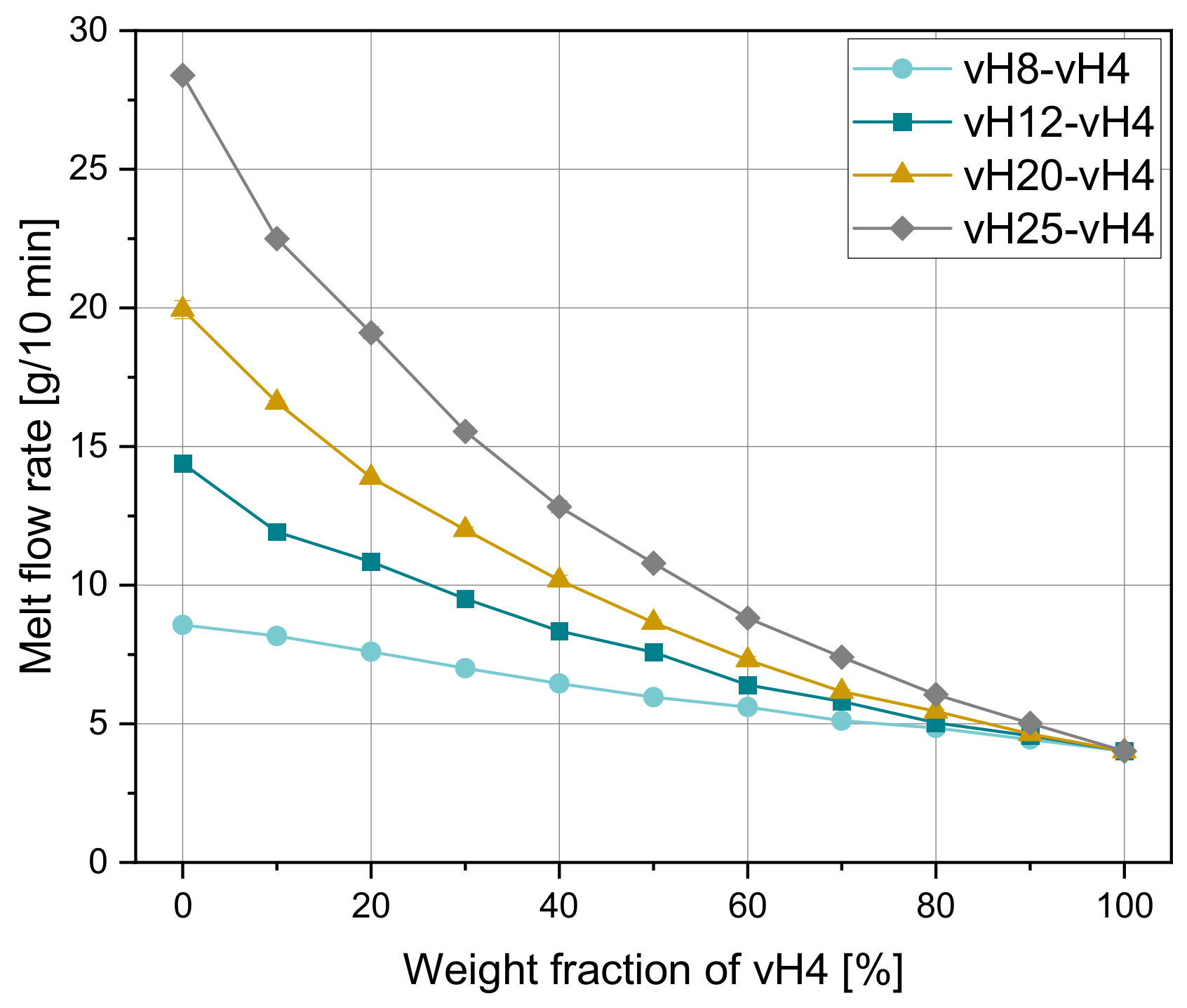
A huge drawback of post-consumer polyolefin recyclates is the strongly fluctuating melt flow properties, which depend on the constantly changing waste input streams caused by different compositions of the waste fractions. Moreover, this is associated with fluctuating property profiles of the recyclates. Varying melt flow rates (MFRs) are often stated as a problem in the recycling of polypropylene (PP), which is widely used in the plastics packaging industry with a share of around 20% [
9]. Due to the MFR variations, recyclate suppliers often only provide a wide range for the MFR in their data sheets [
10]. While, for thermoforming of packaging products, PP needs a rather low MFR of around 4 g/10 min (230 °C/2.16 kg), when processing PP by blow and cast film extrusion, grades with MFR of up to 11 g/10 min are used. Depending on the wall thickness of the product and with focus on energy consumption savings, for injection molded products PP with MFR of 3 to 100 g/10 min is utilized [
11]. Packaging products such as films, trays, cups, bottles, buckets, and containers are produced with a wide range of melt flow properties. If collected in a separate collection, at their end-of-life they are mixed together in the lightweight packaging waste fraction. Even when separated into their plastics recycling codes in the further steps of waste management, a mixture of materials with different MFRs is inevitable. The material mix leads to averaged and rather high MFR values of commercial PP recyclates. Additionally, material degradation within the previous life cycle could also negatively influence the property profile (e.g., increase in MFR) of the PP recyclate. The high MFR values resulting due to material mixtures and material degradation could result in poor performance in extrusion and thermoforming as low MFR values are required.
The MFR in general is an important parameter in polymer processing and due to its simplicity widely used as an input quality assurance parameter in industry. In contrast to the viscosity, which can be evaluated by a number of rheological measurements (e.g., parallel plate rheometer or high-pressure capillary rheometer) and is expressed as multipoint data, the MFR can be expressed as a single point value with a minor dependency on temperature and shear rate given solely by the used testing temperature and weight. The standards ISO 1133 and ASTM D1238 are generally used to evaluate the MFR. It is determined by extruding the molten polymer at a fixed temperature and weight, which represents a certain shear rate, through a standardized die [
12,
13,
14]. The MFR of polymers is basically dependent on their molar mass and its distribution. Additionally, additives can influence the MFR. The higher the molar mass the lower the MFR. Furthermore, branching and the presence of plasticizers affect its magnitude [
15]. Especially in PP, the MFR is strongly affected by material degradation. PP is influenced by thermo-oxidative and UV light-initiated degradation in warm and bright environments leading to chain scission and thus to molar mass reduction and MFR increase [
16]. This effect in combination with the influence of material changes on thermal and mechanical properties is already discussed in the literature by parametrization of different formulations [
17,
18,
19,
20,
21,
22,
23]. Nevertheless, this paper discusses MFR value changes as they are of most importance for machine operators. To overcome the inferior mechanical properties, virgin materials are added in terms of blends but also by using multilayer structures or by changing the product design.
The coextrusion process of multilayer films is rather sensitive to MFR fluctuations. Multilayer films are used, for example, to minimize migration and permeation [
24]. Three- and five-layer films are mostly used for this purpose. To prevent flow instabilities, the middle layer of a multilayer structure is typically supposed to have either the same or a lower MFR compared to its embedding layers. Otherwise, viscous encapsulation effects may occur, where the lower viscous material encapsulates the material with the higher viscosity during the extrusion process [
25]. This effect, which has been widely studied in the literature [
26,
27,
28,
29], typically occurs in stratified flows in rectangular cross sections.
In particular, post-consumer recyclates often exhibit strongly fluctuating MFR values from one lot to another. As a result, recyclate manufacturers usually indicate only rough MFR ranges in their data sheets. Therefore, attention must be paid to the MFR value of the specific lot of the recyclate. In an ideal world, it is stated in the lot certificate of the recyclate, which is required due to recycling material specifications.
Mixing rules can be used to calculate the MFR of binary blends. For a large number of mixing rules, only the MFR values and the weight fractions of the mixing components must be known to evaluate the MFR of the mixture. While these mixing rules have been intensively analyzed for a variety of virgin polymers [
30,
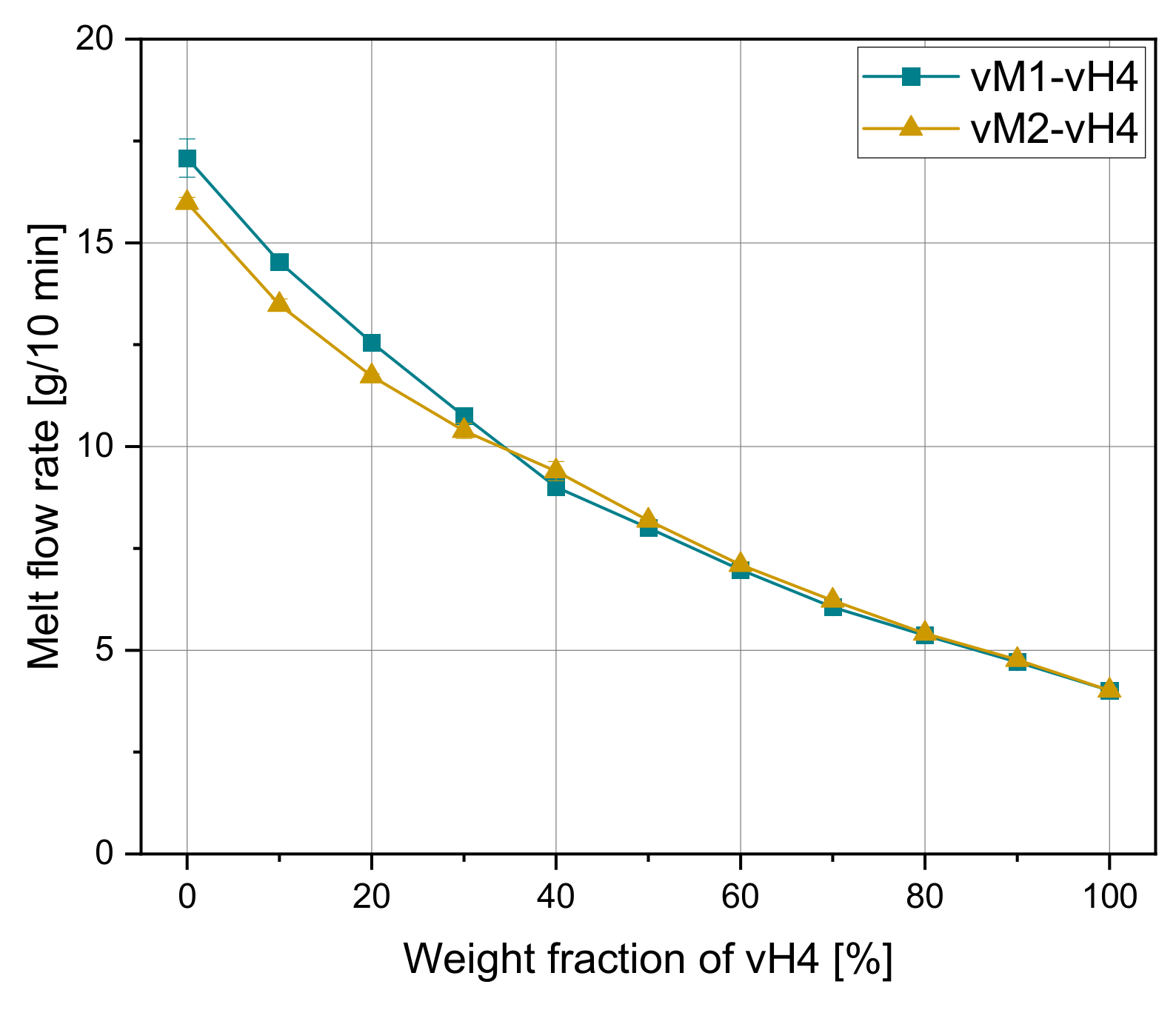
31], recyclates have received less attention. In this work, the accuracy of selected mixing rules in predicting the MFR of binary PP blends was investigated. To this end, samples were produced by compounding at least two different PP types. The melt flow behavior of one component was changed stepwise from 8 to 25 g/10 min, whereas the other component was fixed at an MFR of 4 g/10 min. The contents of the components were varied between 0% and 100% with an increment of 10%. PP homopolymers, PP copolymers, and post-consumer PP recyclates were used to cover a large variety of possible combinations. The overall objective was to assess the accuracy of selected existing mixing rules and to find a relationship, which can be used universally for various PP blends with a particular focus on recyclates. Based on the observed relationships and the measured experimental data, a new mixing rule is presented, using symbolic regression based on genetic programming.
5. Discussion
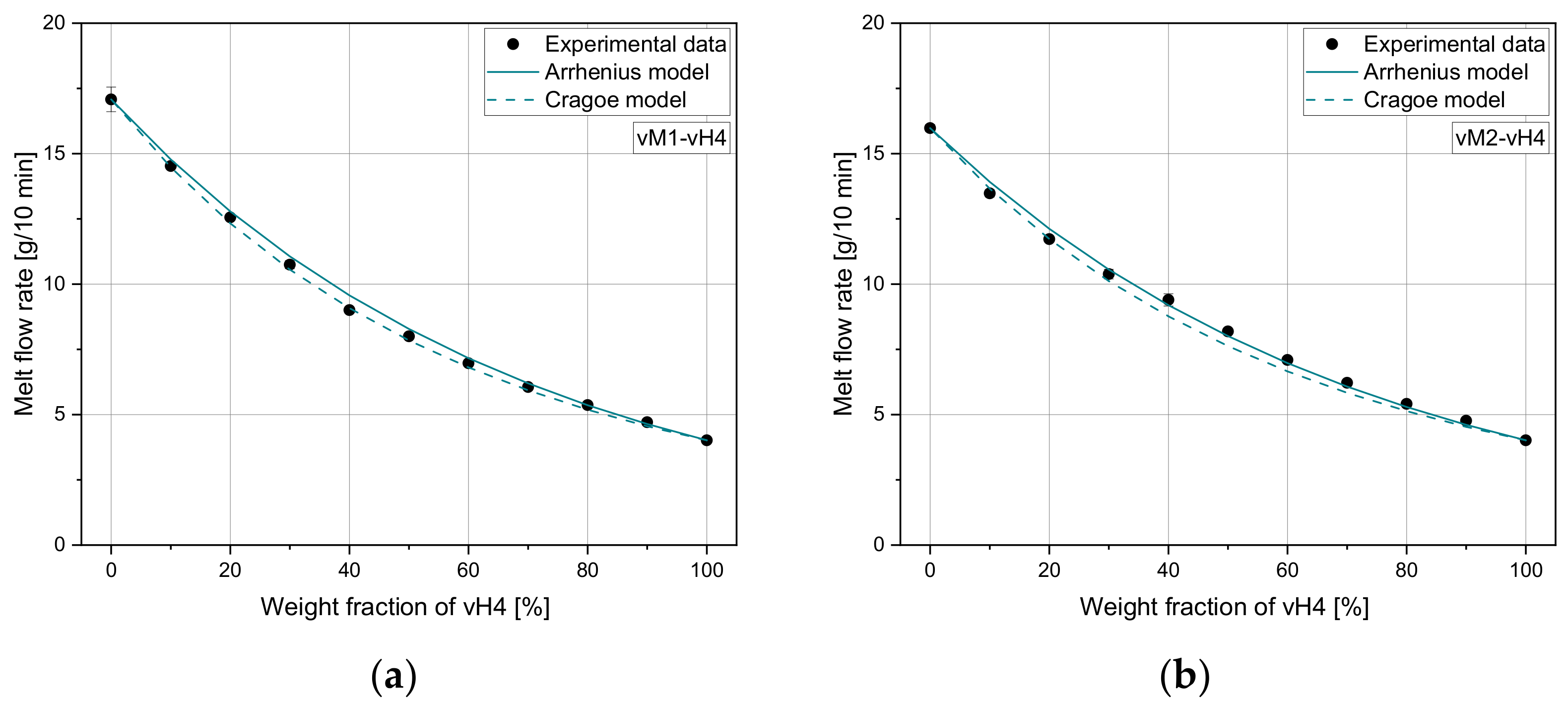
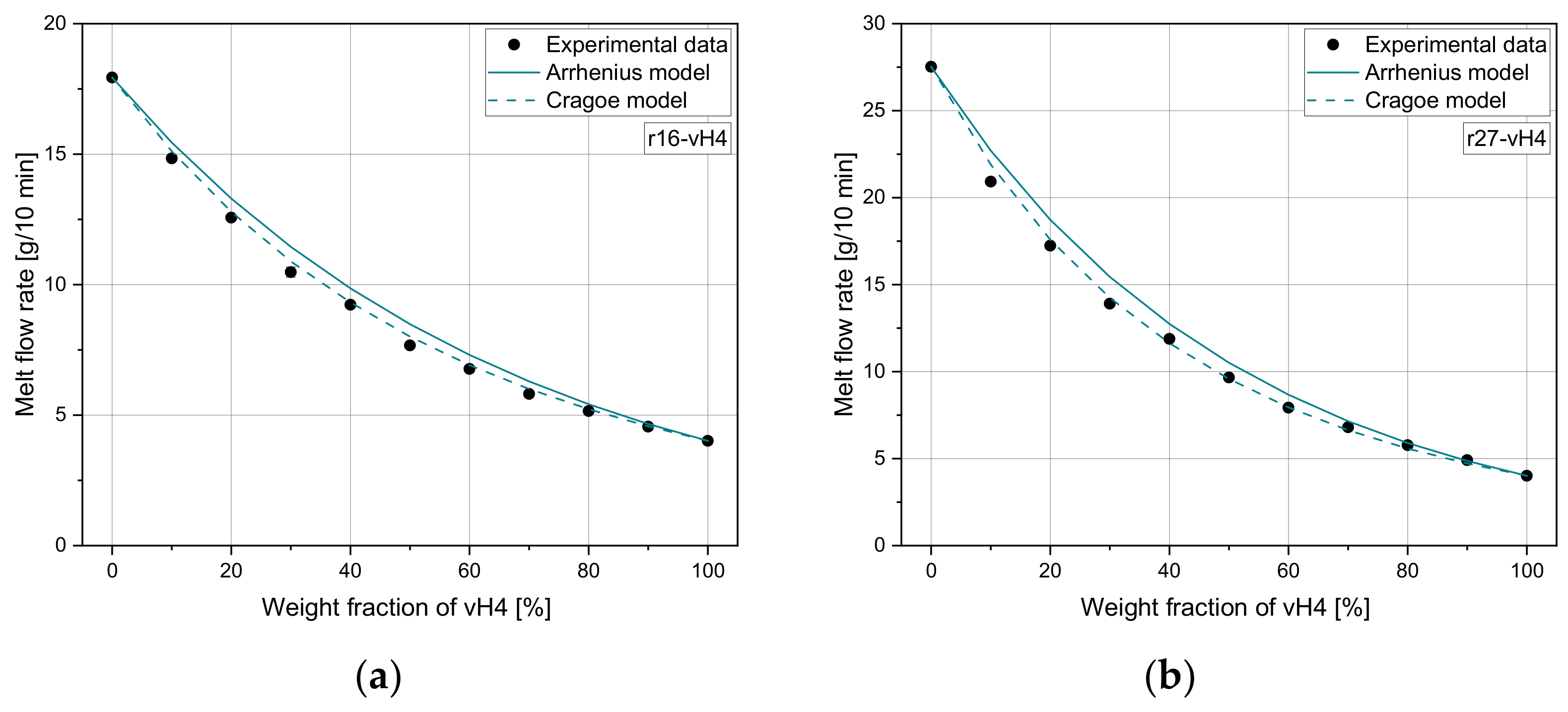
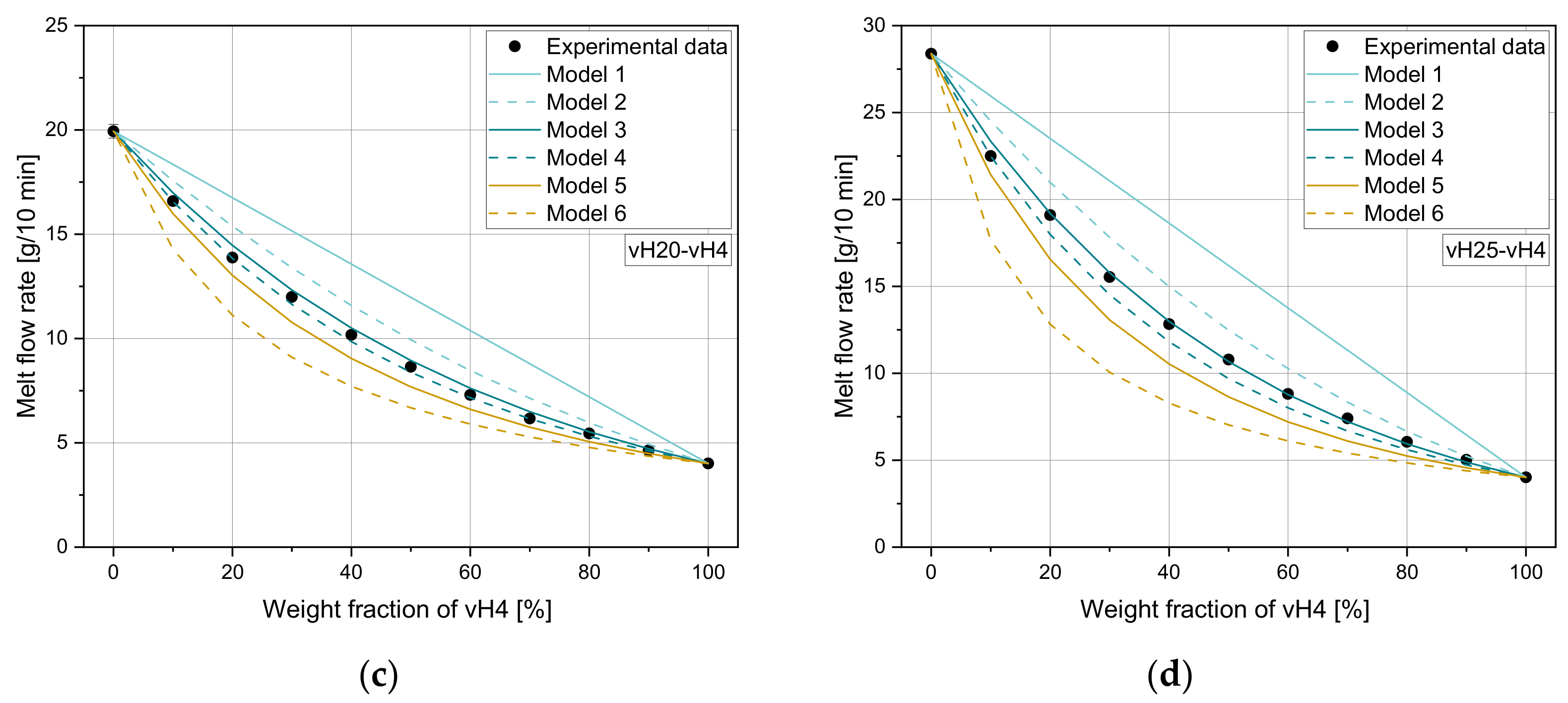
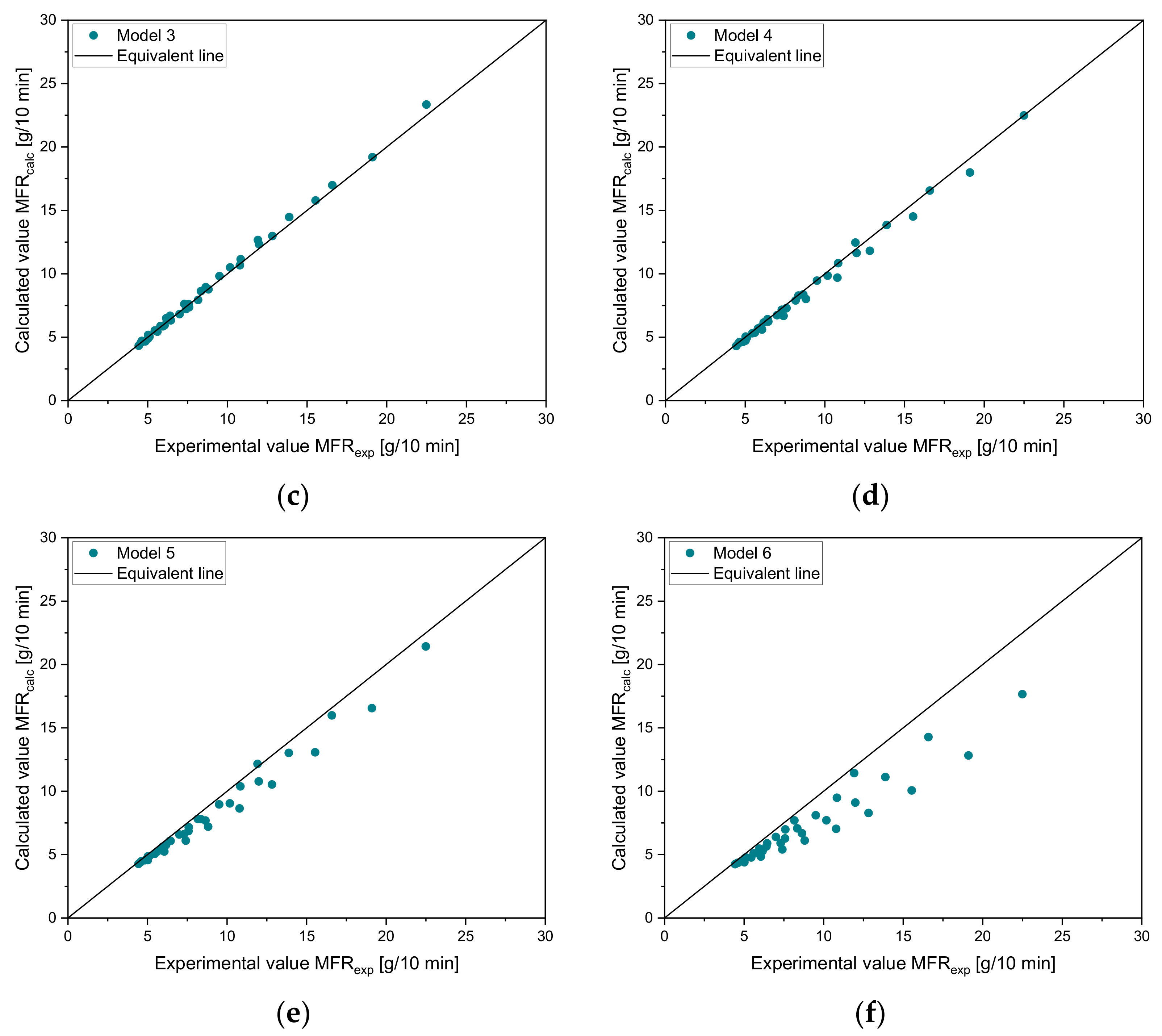
Flowability adjustment by the use of mixing rules is a widely used method when it comes to viscosity adjustment of crude oil [
32,
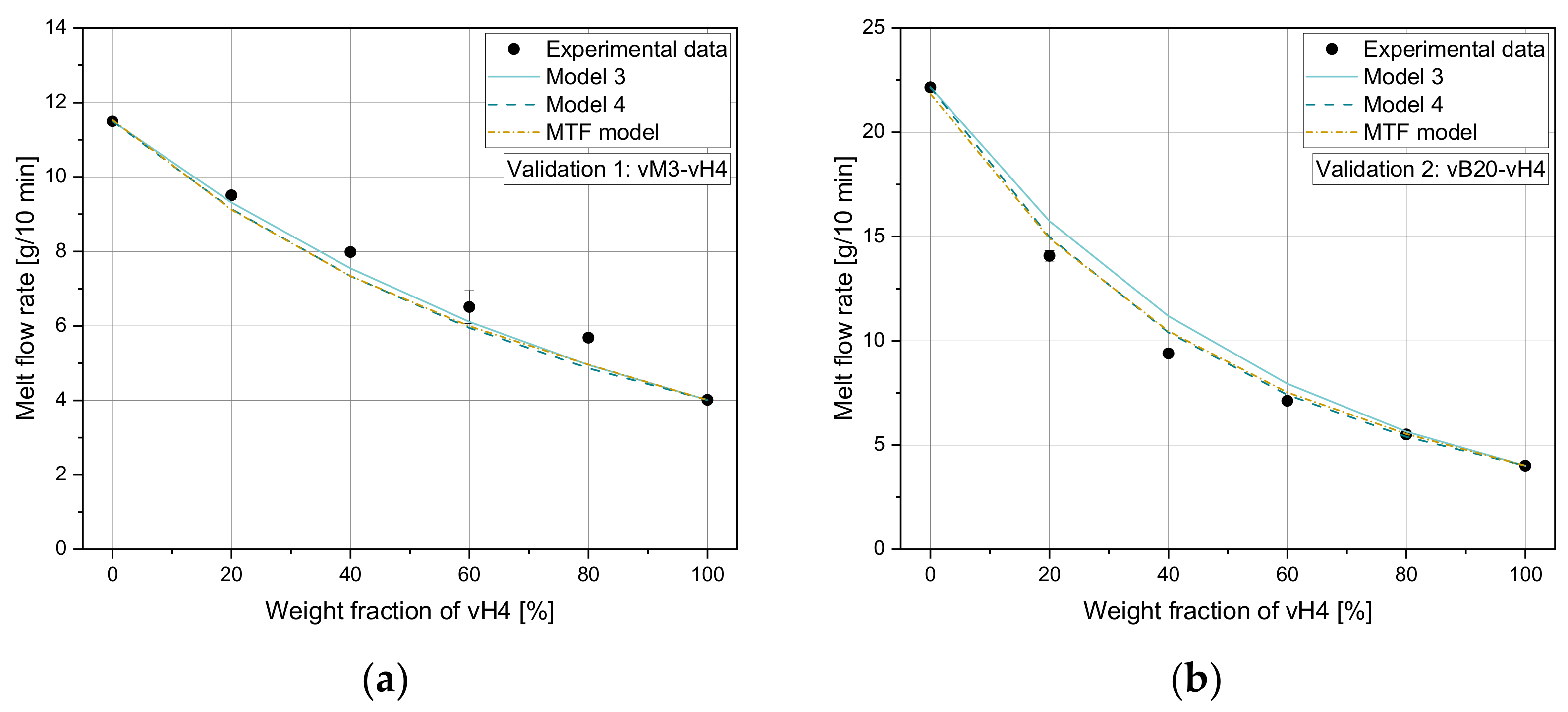
34]. The application of mixing rules for adjusting the MFR of re-granules via compounding with low MFR grades is a practicable method to achieve more uniform recyclate compounds and therefore higher product quality. While conventional mixing rules such as the frequently used Arrhenius mixing rule (model 3) achieve good agreement for blends of virgin polymers, for recyclates Cragoe’s mixing rule (model 4) delivers more accurate results with a maximum relative error of 5.70%, which was shown in the Results. However, both mentioned rules lack an accurate applicability for all polymer types used in this research work. A rule which reaches low error for blends of one virgin partner with a pre-defined MFR with (i) virgin, (ii) artificial recyclate, and (iii) recyclate materials was not found within the selected mixing rules. Therefore, the MTF mixing rule was established. From the overall perspective, with this predictive model a higher accuracy for all tested blends was achieved in the considered data ranges. The maximum relative errors were 3.40% and 5.52% for the training and test set and the validation set, respectively. In contrast, maximum relative errors of 7.51% and 5.84% for the mixing rules of Arrhenius and Cragoe, respectively, were determined in the validation set.
Table 11 shows that the MTF mixing rule outperforms both existing mixing rules according to Arrhenius and Cragoe with an overall lower
and
considering sample sets 1 to 3. Compared to crude oils, recyclates are a complex blend from various waste streams with several contaminations, and it was expected that an existing mixing rule cannot describe all of the data. Hence, a tailored mixing rule was developed.
In terms of continuous polymer processing, well-adjusted MFR values in polyolefin recyclate grades are essential to enable constant processing and good-quality products. When it comes to products of virgin polymer grades, these grades are developed for certain processing methods and for specific applications. Hence, their property profile is well defined and constant, independent of the material batch. However, even high-quality post-consumer recyclate grades are always a blend of plastics waste out of products of various applications and produced by different processing methods. The mixture of the whole plastic waste of one polymer type leads to averaged rheological and mechanical properties. To ensure the production of recyclates that are within a certain specification, it is of utmost importance that at least the MFR is well-adjusted for its respective field of application allowing for constant processing without errors and defects. For this purpose, mixing rules can be used to enable constant melt flow rates even when the recycling streams have fluctuating melt flow properties. Furthermore, mixing rules can be used, if the best fitting recyclate is not available on the market and therefore the MFR values of the available recyclates can be adjusted by mixing with a virgin polymer grades.
6. Conclusions and Outlook
This paper deals with the evaluation of the applicability of mixing rules on polypropylene (PP) mixtures using three datasets of (i) virgin mixtures, (ii) artificial recyclates, and (iii) commercial recyclates. Six selected mixing rules were tested by comparing the calculated values with experimentally determined melt flow rate (MFR) results. The mixing rules of Arrhenius and Cragoe showed the smallest deviations from the measured results, with Cragoe’s mixing rule being more suitable for recyclates. In the next step, a new mixing rule, called the MTF mixing rule, was developed using symbolic regression. Although this mixing rule is more complex than the existing ones, a higher overall agreement with the experimental values was observed for all measured values. Finally, the MTF model was validated by two additional series of measurements in previously uncovered MFR ranges, and the accuracy of this new developed mixing rule was confirmed.
In further research, the applicability of selected mixing rules and the MTF model will be tested on additional PP mixtures to make it generally applicable. The variation in the second component, which was chosen to be constant in this publication, and the determination of the influence of different PP types such as random and block copolymers, additionally to homopolymers, are of particular interest. Furthermore, other polymers apart from PP will be investigated.