Effects of Melt Temperature and Non-Isothermal Flow in Design of Coat Hanger Dies Based on Flow Network of Non-Newtonian Fluids
Abstract
:1. Introduction
2. Model and Methods
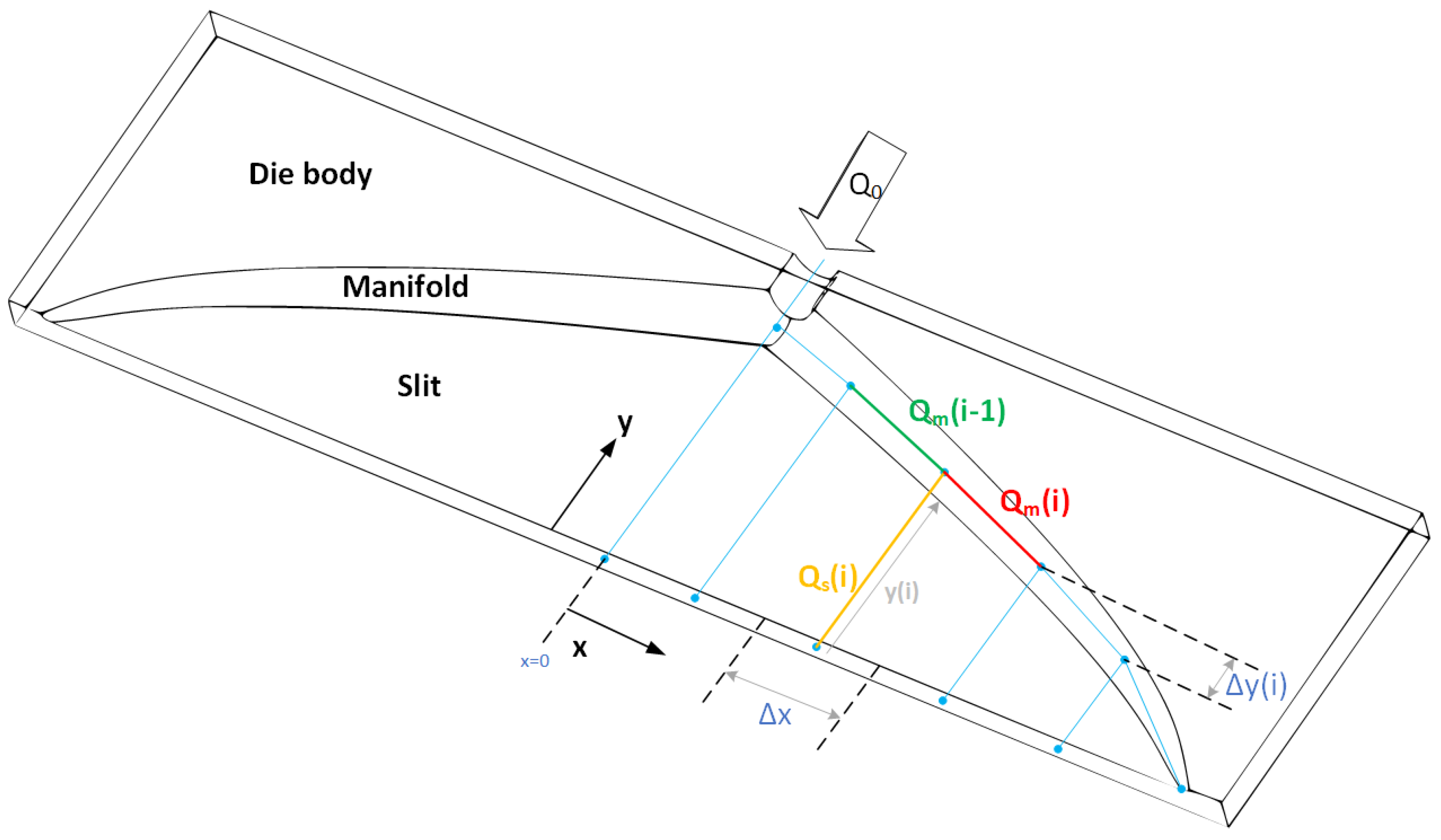
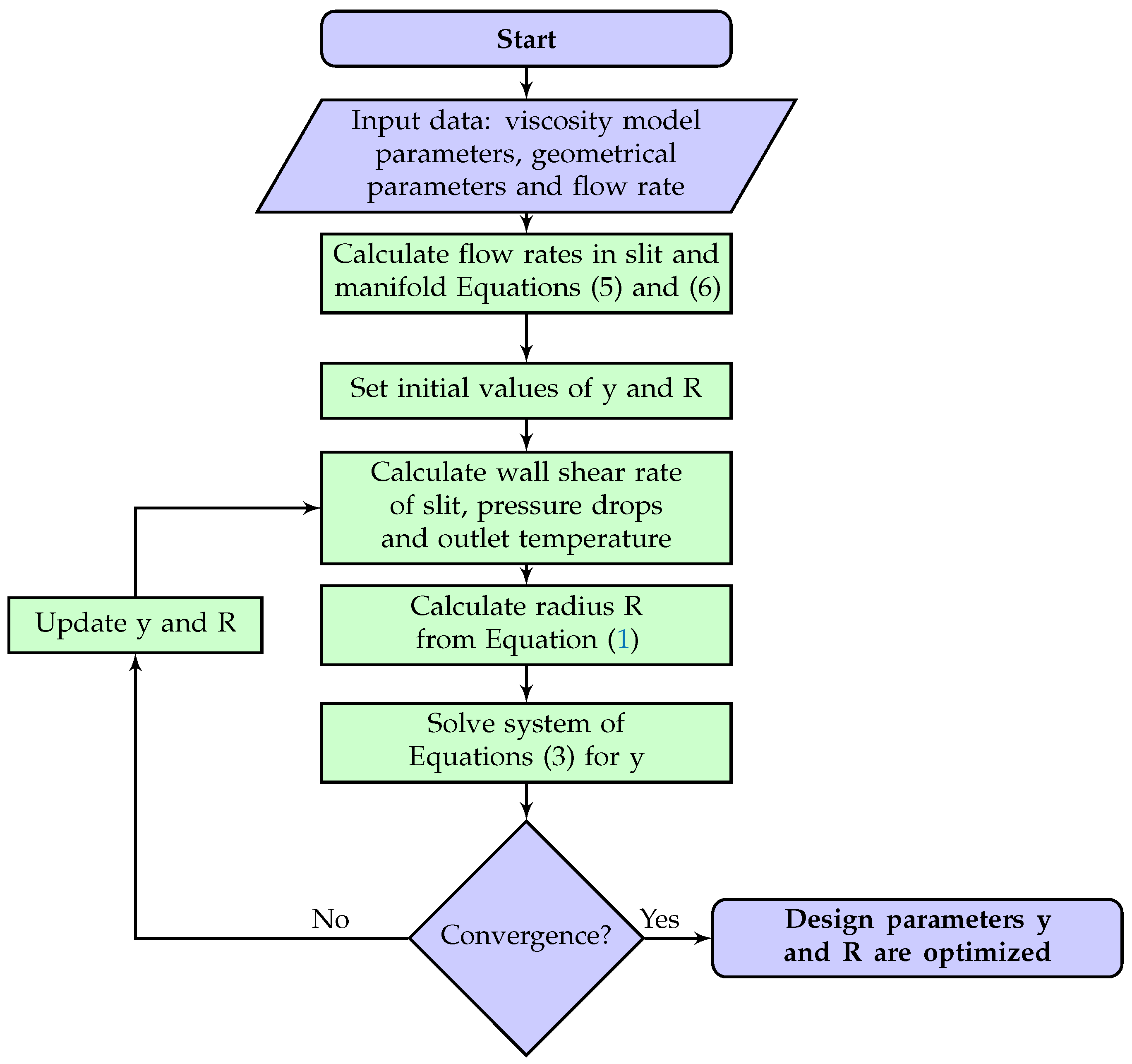
2.1. Flow Network Method for Die Design
- Steady-state, non-isothermal, incompressible flow;
- Streamlined flow;
- Uniform pressure and flow rates at die exit;
- Unidirectional and fully-developed flow in both manifold and slit;
- Constant wall shear rate in the manifold and the slit.
2.2. Non-Newtonian Models
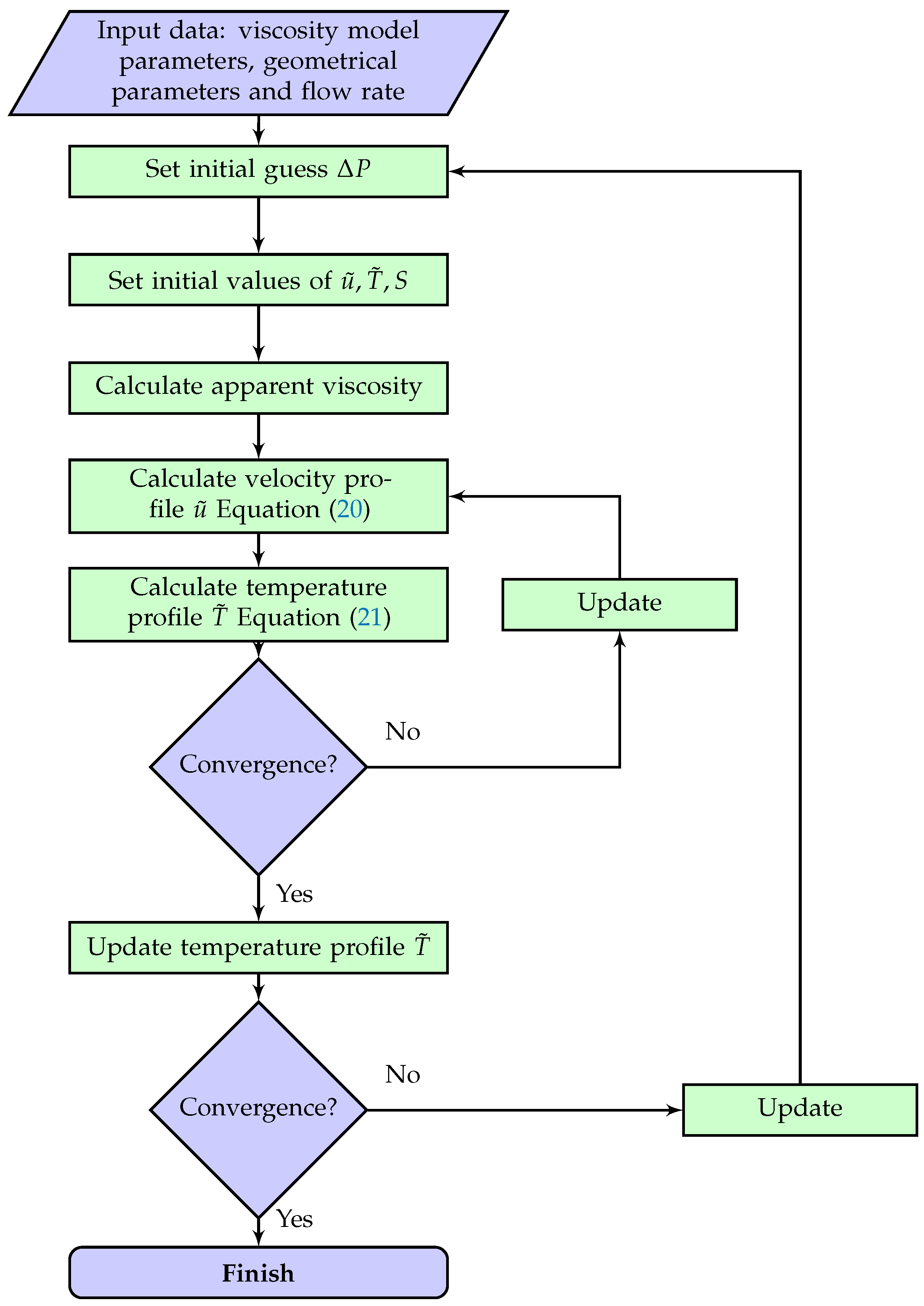
2.3. Pressure Drop Calculation
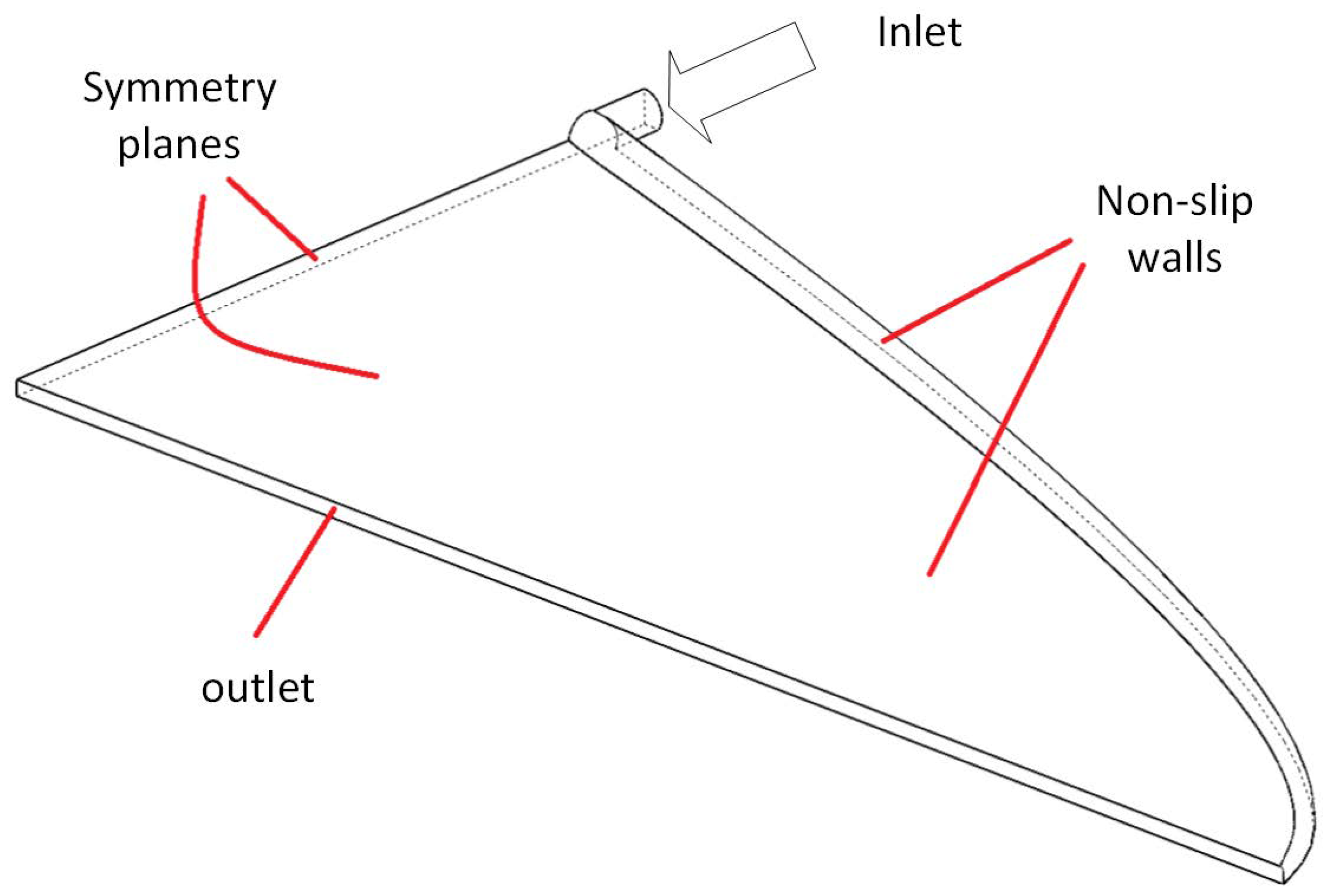
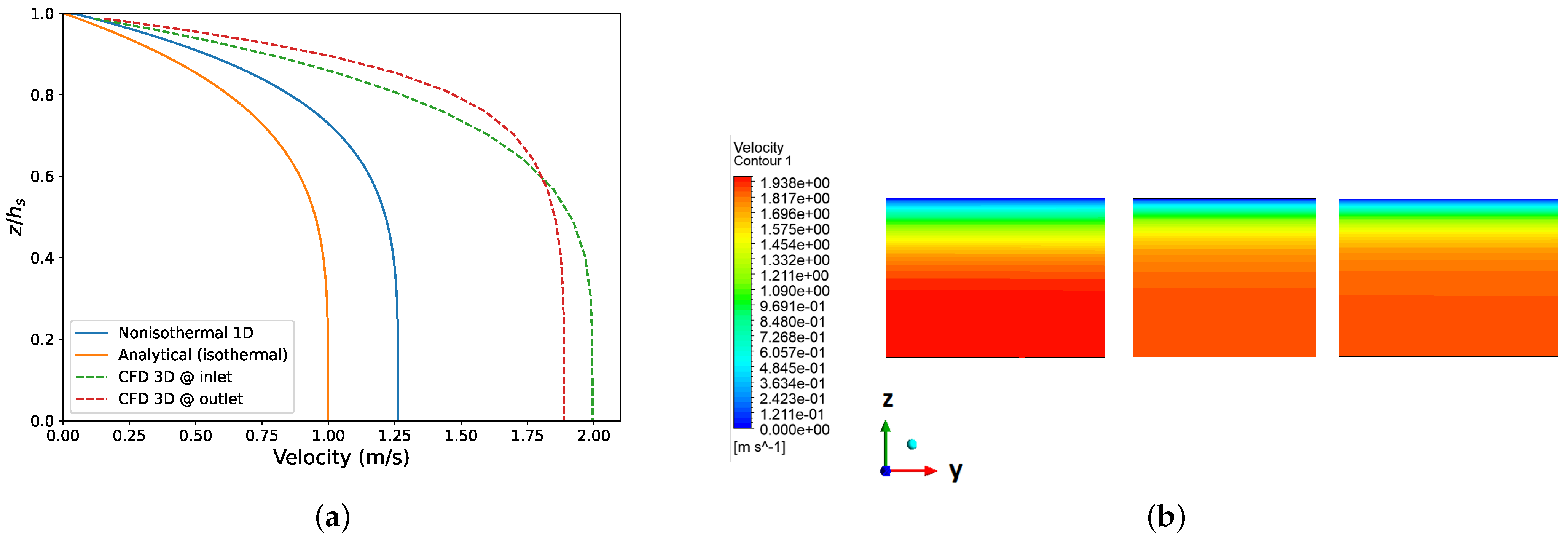
2.4. Verification and Validation by CFD
3. Results and Discussion
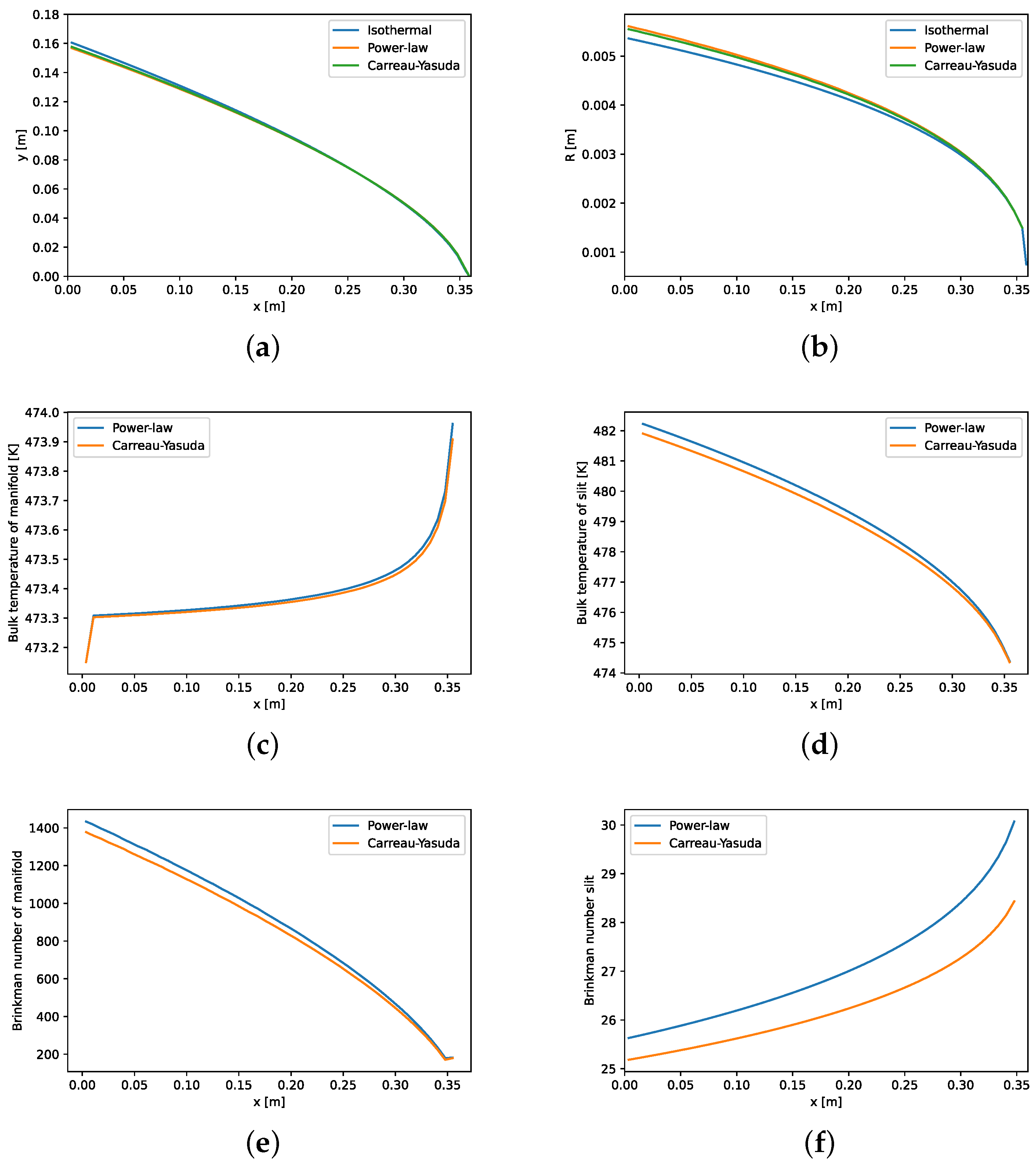
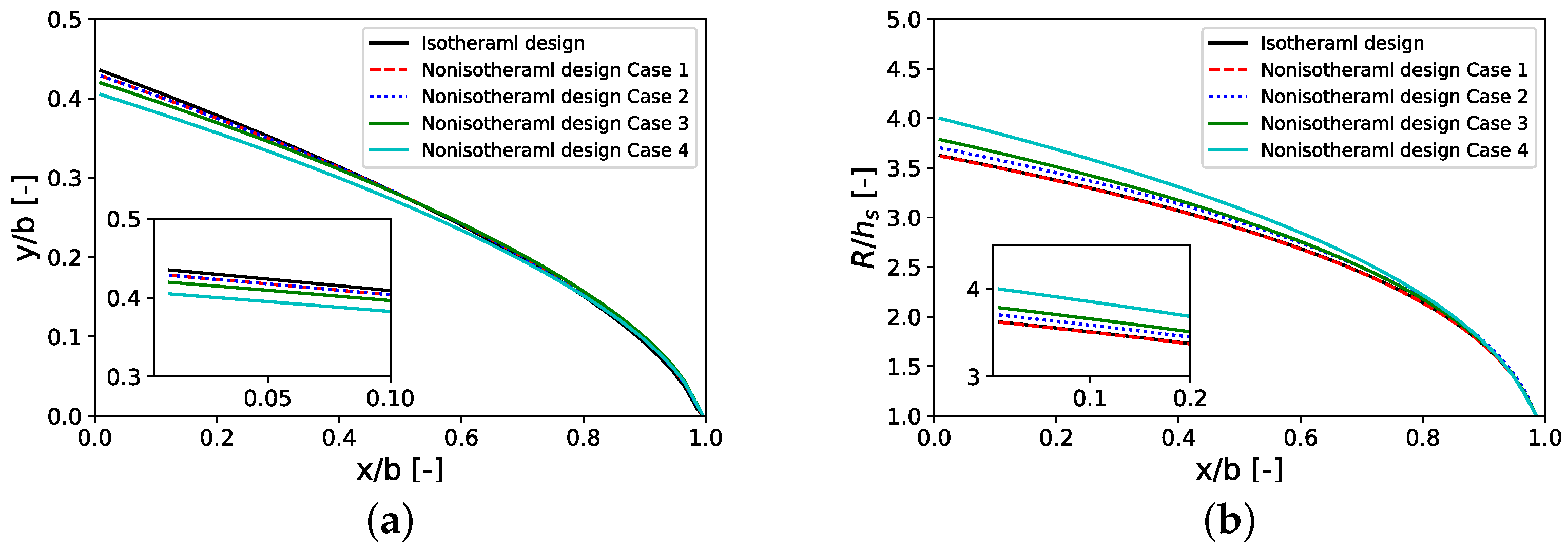
3.1. Design Curves
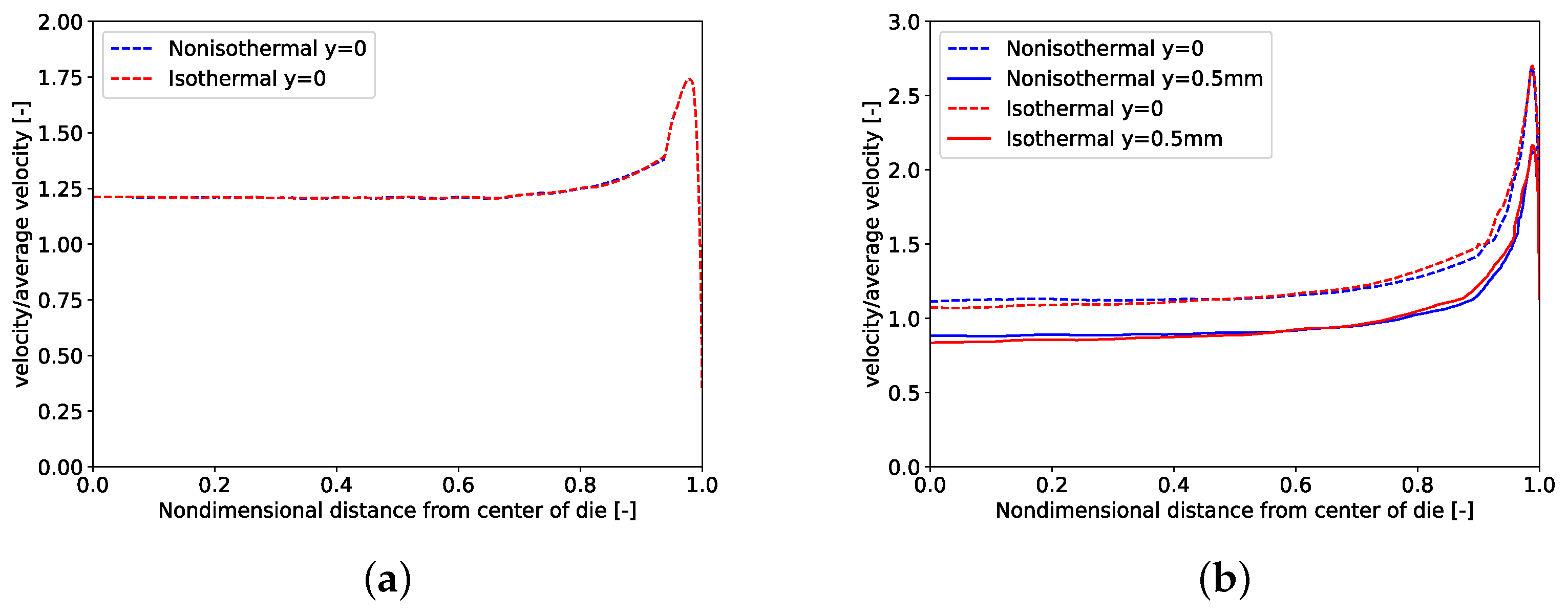
3.2. Effect of Heat Viscous Dissipation
3.3. Effect of Temperature on Pressure Drop vs. Flow Rate Relation
3.4. Effect of Temperature Sensitivity Parameter
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Biot number | |
| Brinkman number | |
| overall Brinkman number | |
| L | length of a segment |
| characteristic length (i.e., radius or height) | |
| N | number of segments |
| Prandtl number | |
| Q | flow rate |
| R | radius of manifold |
| S | non-dimensional shear rate |
| T | temperature |
| temperature at entry | |
| reference temperature in power-law and Carreau–Yasuda models | |
| length of a manifold segment | |
| non-dimensional temperature | |
| non-dimensional velocity | |
| non-dimensional transverse coordinate | |
| non-dimensional axial coordinate | |
| velocity vector | |
| temperature dependence function of viscosity model | |
| b | half width of die |
| heat capacity | |
| h | heat transfer coefficient |
| temperature of heater | |
| land height | |
| thermal conductivity | |
| power-law model consistency parameter | |
| n | power-law index |
| p | pressure |
| u | velocity |
| transverse coordinate | |
| axial coordinate | |
| distance from center of manifold to die exit | |
| Greek letters | |
| thermal diffusivity | |
| Carreau–Yasuda model parameter | |
| power-law or Carreau–Yasuda model parameter | |
| shear rate | |
| convergence criterion | |
| viscosity | |
| Carreau–Yasuda model parameter | |
| Carreau–Yasuda model parameter | |
| non-dimensional viscosity | |
| Carreau–Yasuda model parameter | |
| apparent viscosity | |
| flow uniformity index | |
| density | |
| stress tensor | |
| Subscripts | |
| 0 | at entry |
| ave | average |
| m | manifold |
| s | slit |
| w | evaluated at wall |
References
- Michaeli, W.; Kaul, S.; Wolff, T. Computer-aided optimization of extrusion dies. J. Polym. Eng. 2001, 21, 225–238. [Google Scholar] [CrossRef]
- Michaeli, W.; Hopmann, C. Extrusion Dies for Plastics and Rubber; Hanser Publishers: Munich, Germany, 2016. [Google Scholar]
- Winter, H.; Fritz, H. Design of dies for the extrusion of sheets and annular parisons: The distribution problem. Polym. Eng. Sci. 1986, 26, 543–553. [Google Scholar] [CrossRef]
- Awe, T.J.; Eligindi, M.; Langer, R. Internal Design of Uniform Shear Rate Dies. Morehead Electron. J. Appl. Math. 2005, 1–10. Available online: https://www.google.com.hk/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwijhYzZxaf5AhX-mFYBHRfgBm8QFnoECA0QAQ&url=https%3A%2F%2Fscholarworks.moreheadstate.edu%2Fcgi%2Fviewcontent.cgi%3Farticle%3D1000%26context%3Dmejam_archives&usg=AOvVaw1Q6VmaMtFhflxsayPvSPR7 (accessed on 30 May 2022).
- Igali, D.; Perveen, A.; Zhang, D.; Wei, D. Shear rate coat-hanger die using casson viscosity model. Processes 2020, 8, 1524. [Google Scholar] [CrossRef]
- Razeghiyadaki, A.; Wei, D.; Perveen, A.; Zhang, D. A Multi-Rheology Design Method of Sheeting Polymer Extrusion Dies Based on Flow Network and the Winter–Fritz Design Equation. Polymers 2021, 13, 1924. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, O.; Kirkkopru, K. Inverse Design and Flow Distribution Analysis of Carreau Type Fluid Flow through Coat-Hanger Die. Fibers Polym. 2020, 21, 204–215. [Google Scholar] [CrossRef]
- Raju, G.; Sharma, M.L.; Meena, M.L. Recent methods for optimization of plastic extrusion process: A literature review. Int. J. Adv. Mech. Eng. 2014, 4, 583–588. [Google Scholar]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2012, 12, 515–545. [Google Scholar] [CrossRef]
- Igali, D.; Perveen, A.; Wei, D.; Zhang, D.C.; Mentbayeva, A. 3D FEM Study of the Flow Uniformity of Flat Polypropylene Film/Sheet Extrusion Dies. Key Eng. Mater. Trans. Tech. Publ. 2020, 841, 375–380. [Google Scholar] [CrossRef]
- Lebaal, N.; Puissant, S.; Schmidt, F.; Schläfli, D. An optimization method with experimental validation for the design of extrusion wire coating dies for a range of different materials and operating conditions. Polym. Eng. Sci. 2012, 52, 2675–2687. [Google Scholar] [CrossRef] [Green Version]
- Lebaal, N.; Schmidt, F.; Puissant, S. Design and optimization of three-dimensional extrusion dies, using constraint optimization algorithm. Finite Elem. Anal. Des. 2009, 45, 333–340. [Google Scholar] [CrossRef]
- Wu, P.Y.; Huang, L.M.; Liu, T.J. A simple model for heat transfer inside an extrusion die. Polym. Eng. Sci. 1995, 35, 1713–1724. [Google Scholar] [CrossRef]
- Lebaal, N.; Puissant, S.; Schmidt, F. Application of a response surface method to the optimal design of the wall temperature profiles in extrusion die. Int. J. Mater. Form. 2010, 3, 47–58. [Google Scholar] [CrossRef]
- Lebaal, N. Robust low cost meta-modeling optimization algorithm based on meta-heuristic and knowledge databases approach: Application to polymer extrusion die design. Finite Elem. Anal. Des. 2019, 162, 51–66. [Google Scholar] [CrossRef]
- Amangeldi, M.; Wang, Y.; Perveen, A.; Zhang, D.; Wei, D. An Iterative Approach for the Parameter Estimation of Shear-Rate and Temperature-Dependent Rheological Models for Polymeric Liquids. Polymers 2021, 13, 4185. [Google Scholar] [CrossRef] [PubMed]
- Bergman, T.; Lavine, A.; Incropera, F. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Astarita, G. Rheology: Volume 2: Fluids; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Santos, C.; Quaresma, J.; Lima, J. Convective Heat Transfer in Ducts: The Integral Transform Approach; Editora E-papers: Rio de Janeiro, Brazil, 2001. [Google Scholar]
- Sato, S.; Oka, K.; Murakami, A. Heat transfer behavior of melting polymers in laminar flow field. Polym. Eng. Sci. 2004, 44, 423–432. [Google Scholar] [CrossRef]
- Yang, H. Conjugate thermal simulation for sheet extrusion die. Polym. Eng. Sci. 2014, 54, 682–694. [Google Scholar] [CrossRef]
- Arpin, B.; Lafleur, P.; Sanschagrin, B. A personal computer software program for coathanger die simulation. Polym. Eng. Sci. 1994, 34, 657–664. [Google Scholar] [CrossRef]
- Etemad, S.G.; Majumdar, A.; Huang, B. Viscous dissipation effects in entrance region heat transfer for a power law fluid flowing between parallel plates. Int. J. Heat Fluid Flow 1994, 15, 122–131. [Google Scholar] [CrossRef]


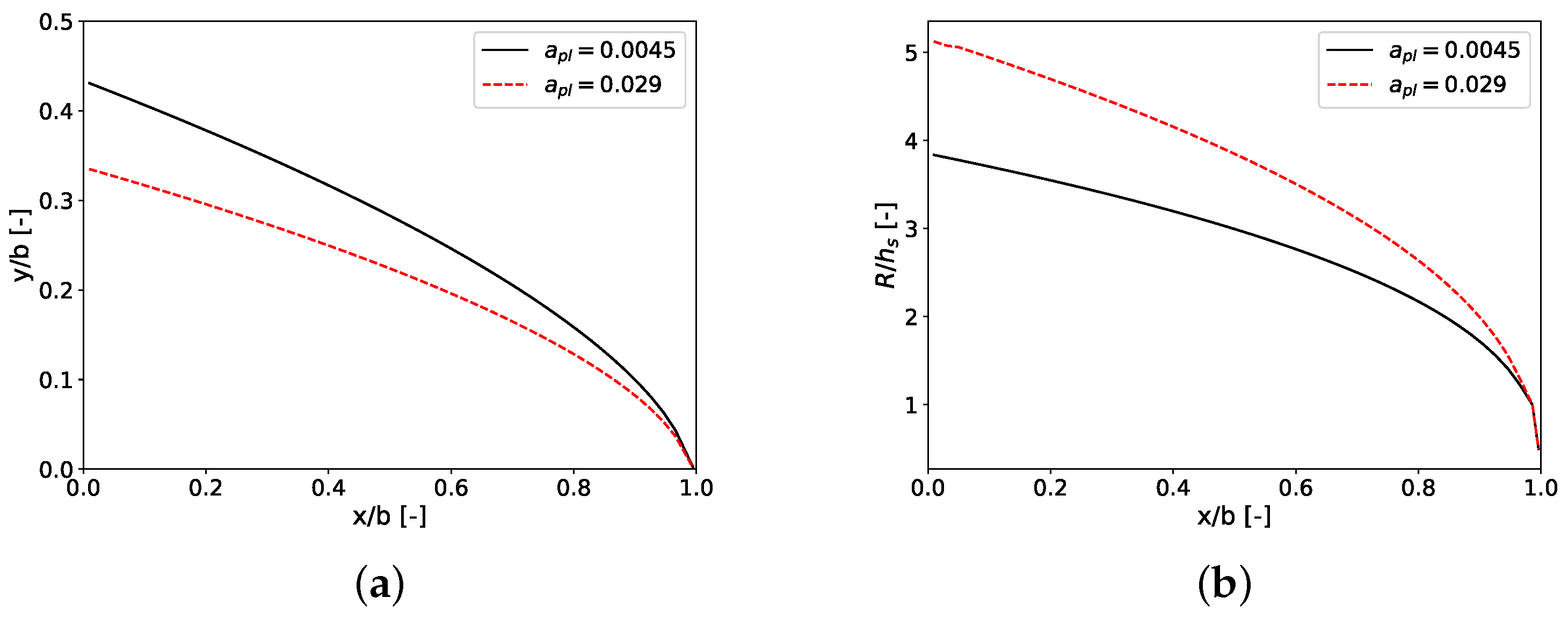
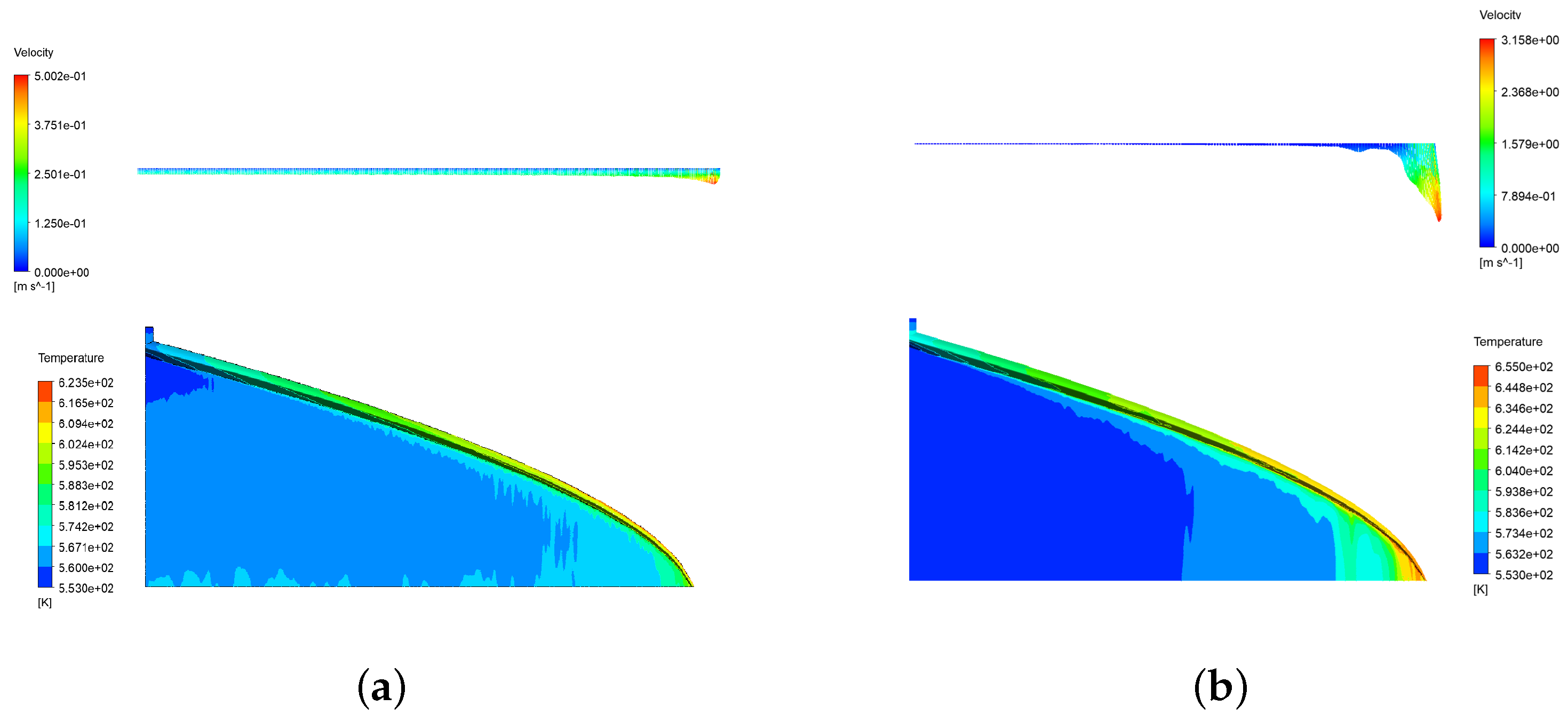
| Parameter | Dimension | Non-Dimensional |
|---|---|---|
| distance | ||
| axial distance | ||
| velocity | u | |
| temperature | T |
| Parameter | Value |
|---|---|
| Flow rate at entry of die, | |
| Land height, | |
| Half width of die, b | |
| Temperature at entry, | |
| Temperature of heater, | |
| Thermal conductivity, | |
| Density, | |
| Specific heat, |
| Values | |
|---|---|
| Power-law model parameter, n | 0.296 |
| Power-law model parameter, | 0.0045 |
| Power-law model parameter, | 503.15 |
| Flow rate () | 1.99 |
| Inlet temperature () | 553.15 |
| Heater temperature () | 543.15 |
| Half die width (b) | 360 |
| Land height | 1.5 |
| Thermal diffusivity () |
| Design | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| [] | 100 | 5000 | 10,000 | 15,000 |
| 2.42 | 122 | 243 | 365 | |
| of Isothermal design | 0.269825 | 0.270569 | 0.285509 | 0.304196 |
| of nonisothermal design (This work) | 0.269825 | 0.278016 | 0.276205 | 0.288235 |
| Values | |
|---|---|
| Power-law model parameter, n | 0.296 |
| Power-law model parameter, | |
| Power-law model parameter, | 0.0045 |
| Power-law model parameter, | 503.15 |
| Pressure drop () | 40 |
| Length of channel (L) | 0.155 |
| Inlet temperature () | 553.15 |
| Heater temperature () | 543.15 |
| Distance between two plates () | 1.5 |
| Thermal diffusivity () | |
| Thermal boundary condition |
| Quantity | Values |
|---|---|
| Power-law model parameter, n | 0.296 |
| Power-law model parameter, | |
| Power-law model parameter, | 503.15 |
| Flow rate () | 1.99 |
| Inlet temperature () | 553.15 |
| Heater temperature () | 543.15 |
| Half die width (b) | 360 |
| Land height | 1.5 |
| Thermal diffusivity () |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razeghiyadaki, A.; Wei, D.; Perveen, A.; Zhang, D.; Wang, Y. Effects of Melt Temperature and Non-Isothermal Flow in Design of Coat Hanger Dies Based on Flow Network of Non-Newtonian Fluids. Polymers 2022, 14, 3161. https://doi.org/10.3390/polym14153161
Razeghiyadaki A, Wei D, Perveen A, Zhang D, Wang Y. Effects of Melt Temperature and Non-Isothermal Flow in Design of Coat Hanger Dies Based on Flow Network of Non-Newtonian Fluids. Polymers. 2022; 14(15):3161. https://doi.org/10.3390/polym14153161
Chicago/Turabian StyleRazeghiyadaki, Amin, Dongming Wei, Asma Perveen, Dichuan Zhang, and Yanwei Wang. 2022. "Effects of Melt Temperature and Non-Isothermal Flow in Design of Coat Hanger Dies Based on Flow Network of Non-Newtonian Fluids" Polymers 14, no. 15: 3161. https://doi.org/10.3390/polym14153161
APA StyleRazeghiyadaki, A., Wei, D., Perveen, A., Zhang, D., & Wang, Y. (2022). Effects of Melt Temperature and Non-Isothermal Flow in Design of Coat Hanger Dies Based on Flow Network of Non-Newtonian Fluids. Polymers, 14(15), 3161. https://doi.org/10.3390/polym14153161








