Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics
Abstract
:1. Introduction
2. Theory and Hypothesis
2.1. Definition of Printing Parameters
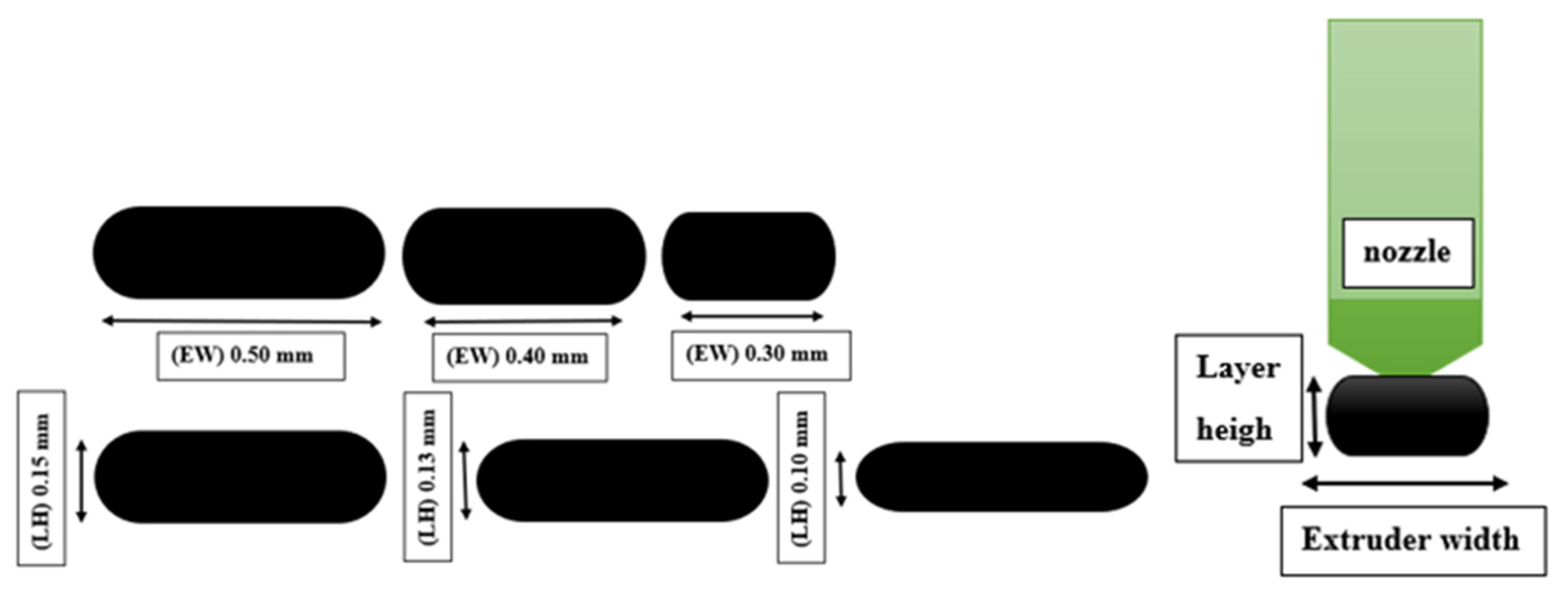
- Layer height (LH) mm: The height of each layer in the printed specimen. It influences the number of layers printed for a given thickness of specimen, as shown in Figure 1.
- A fixed number of layers with different values of layer height will provide different values of fabric thickness.
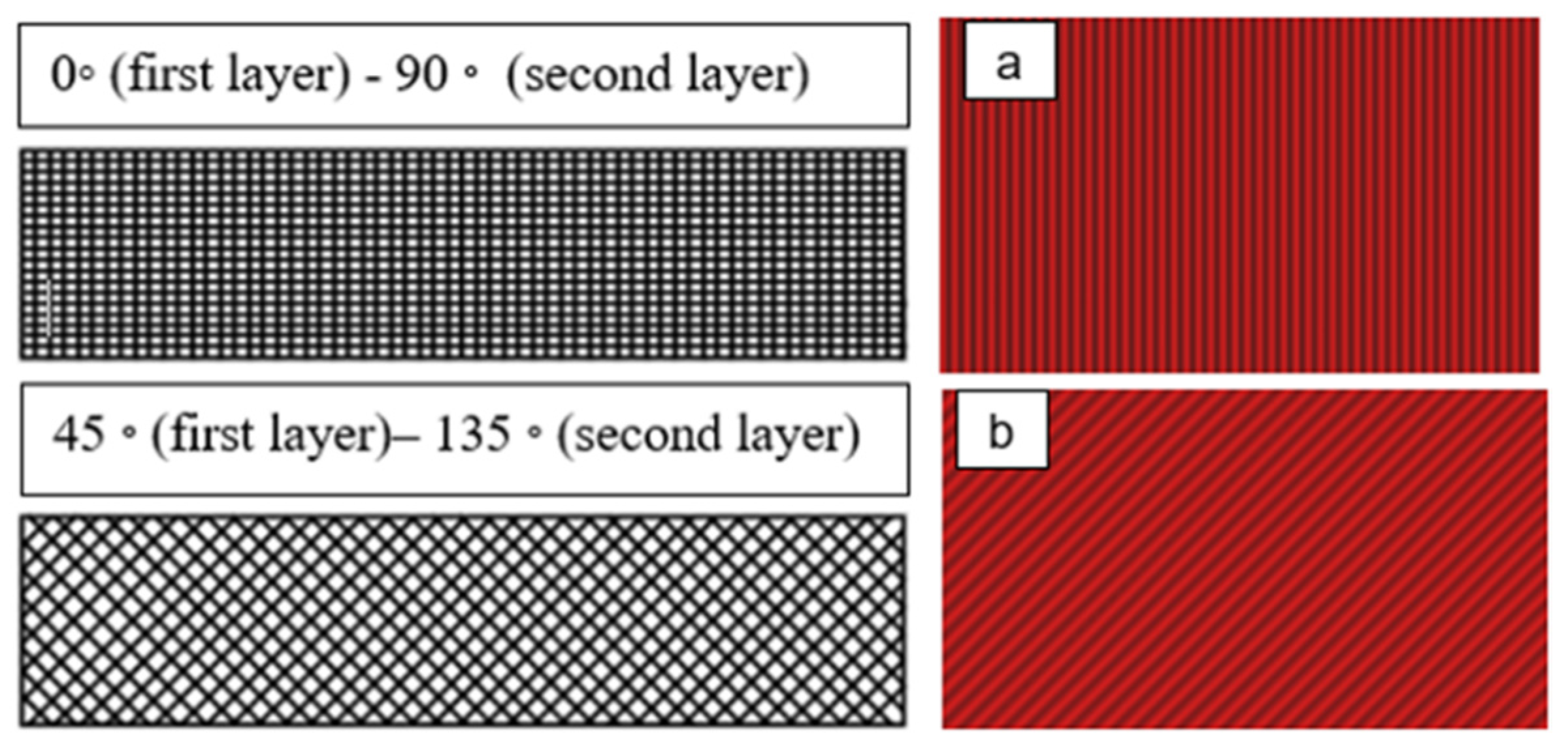
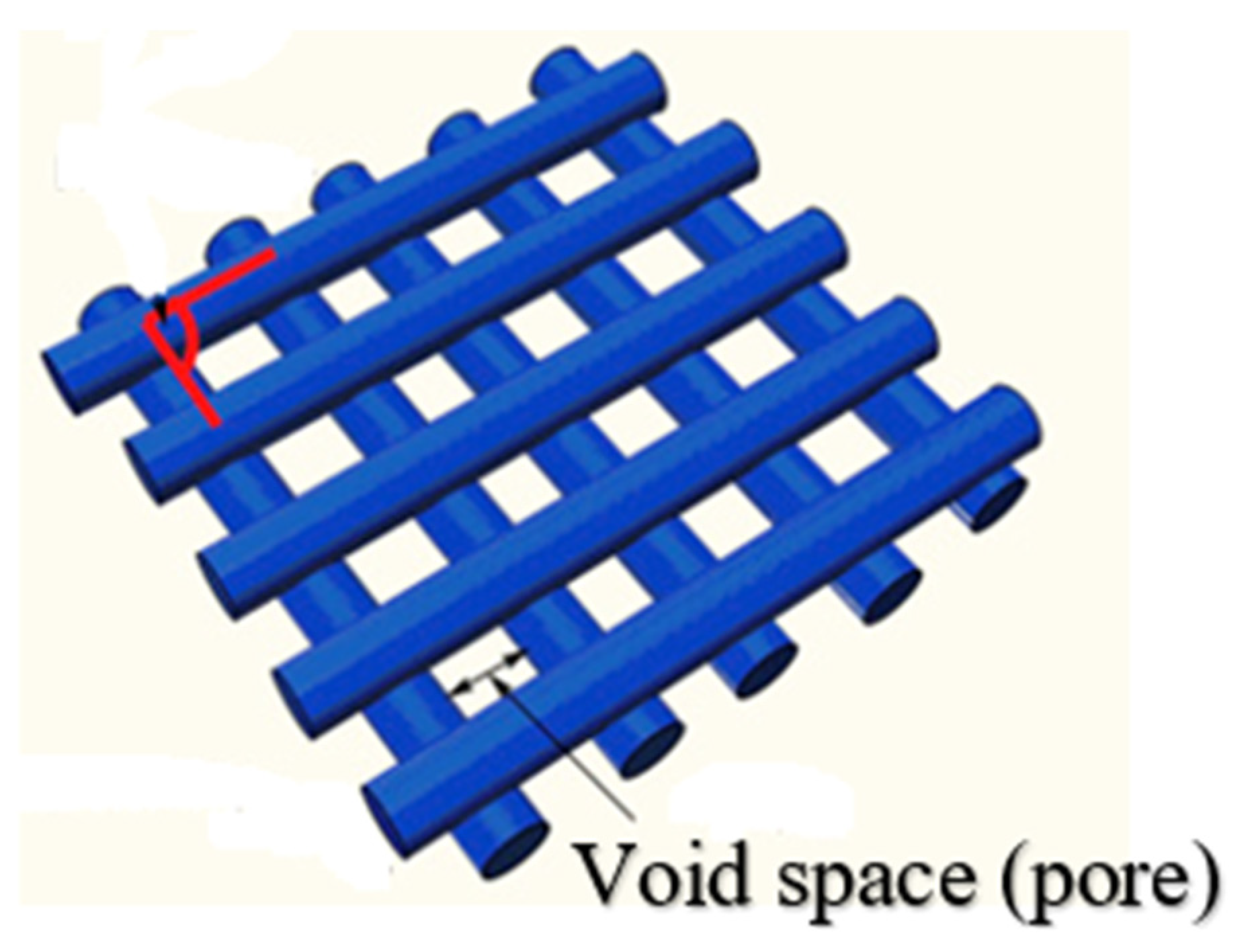
- Orientation angle (O)°: The path on which the nozzle moves on each layer of the (FFF) 3D printer part as in Figure 2.
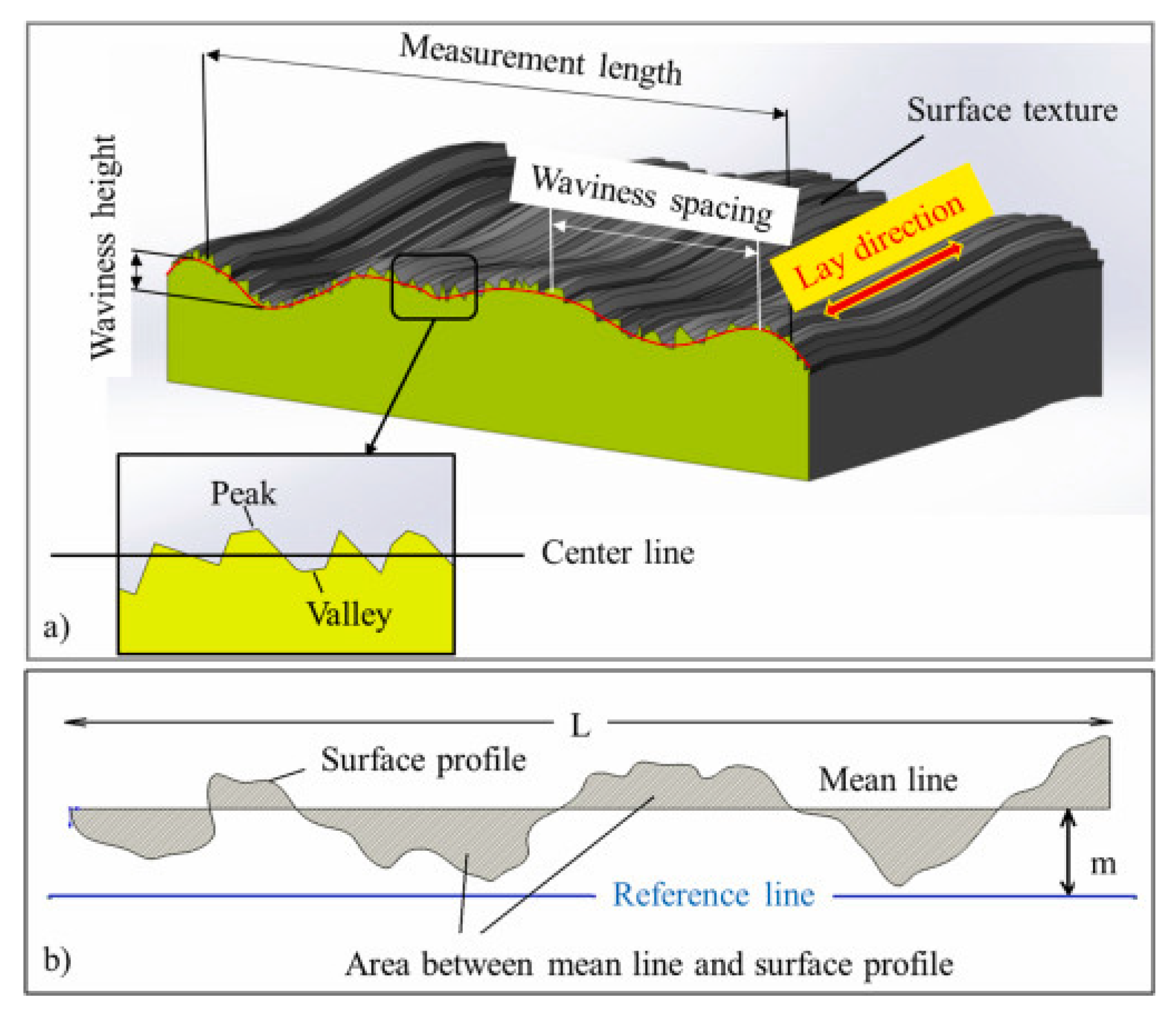
2.2. Definition of Microscopic Features
2.3. Interrelationship of Printing Parameters and Microscopic Features
3. Methodology
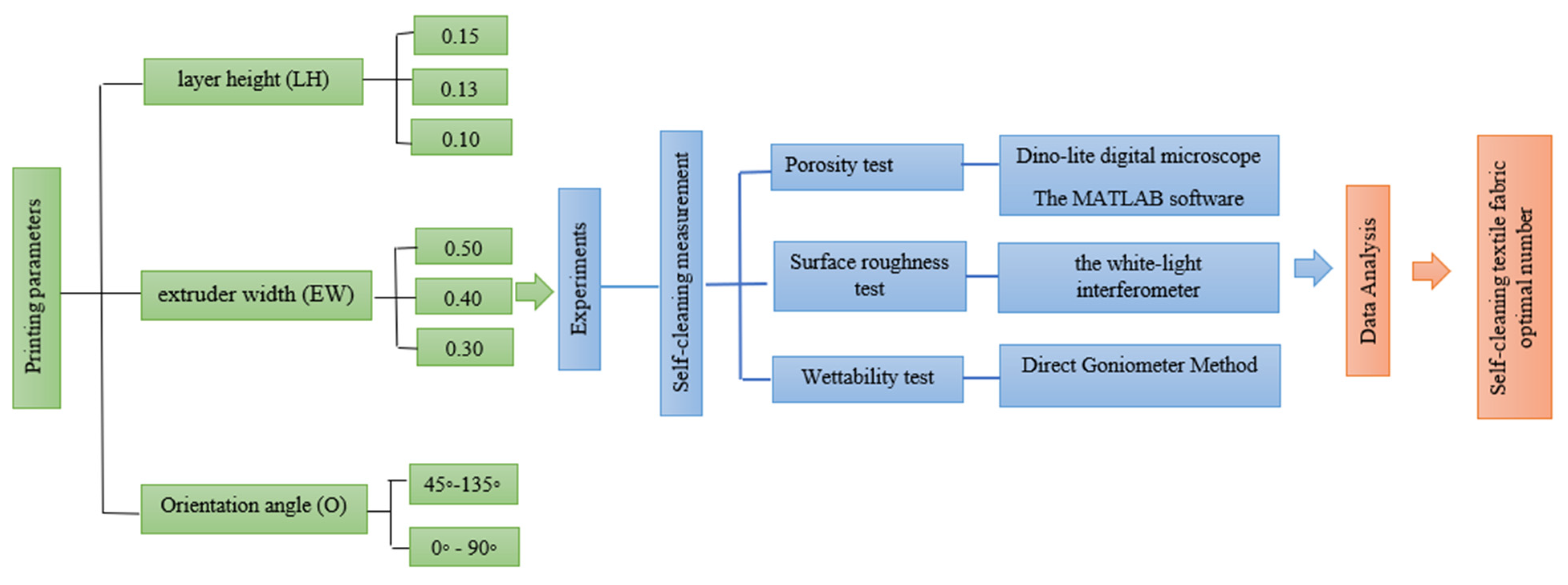
3.1. Design of Experiment
- The specimens were designed and printed with three different parameters and three different materials. The chosen values provided an excellent printing quality and the other parameters remained constant for all the samples. The prepared samples were tested based on an experimental scheme to evaluate the self-cleaning ability.
- The microscopic features (porosity-roughness and wettability), which are mainly responsible for this ability, were measured and recorded to evaluate and compare the best values for self-cleaning between the three chosen materials.
- The data were analyzed to define the optimal self-cleaning number.
3.2. FFF Materials
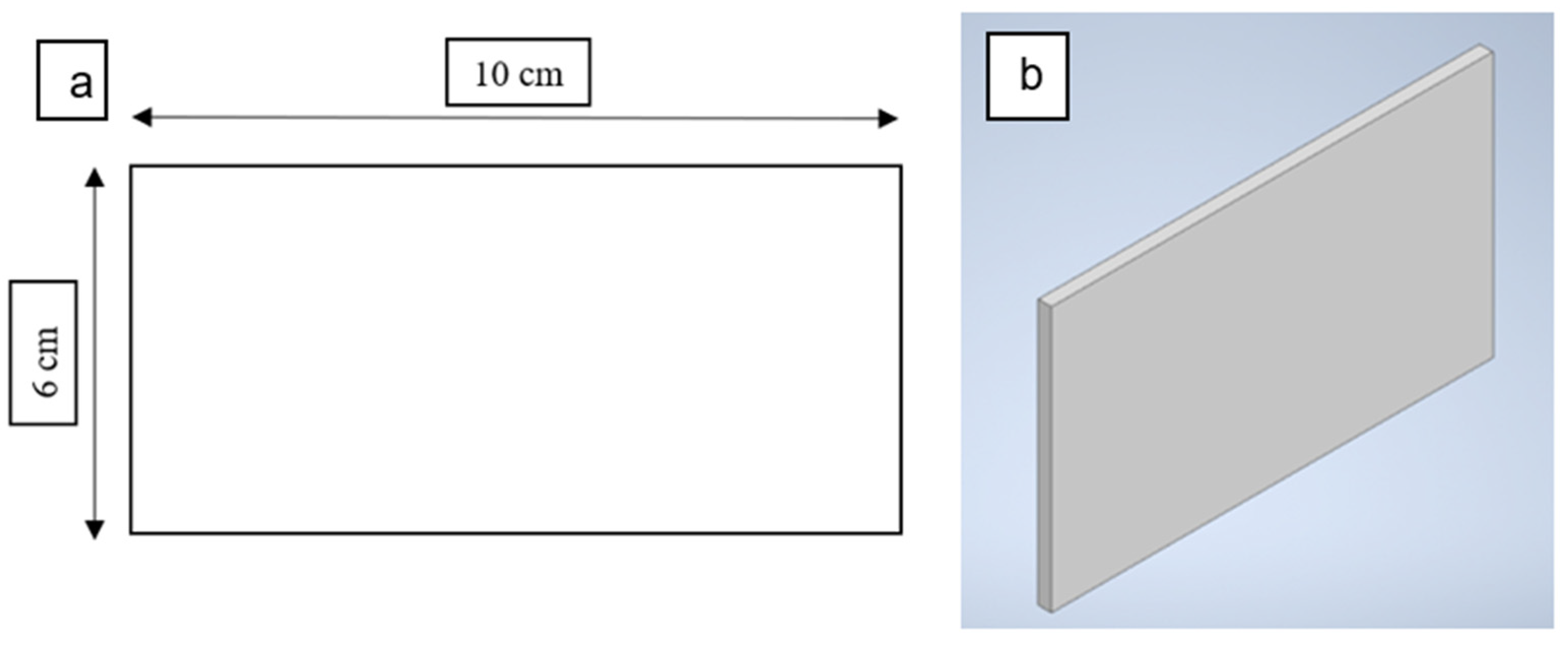
3.3. Samples Preparation
3.4. Experimental Setup and Measurements Procedure
3.4.1. The Measurement Method for Porosity
3.4.2. The Measurement Method of Surface Roughness
3.4.3. The Measurement Method of Wettability
3.4.4. The Unit Cell Measure
3.4.5. Data Process
- The porosity, surface roughness and wettability values were recorded and evaluated for the three different materials. A multiple linear regression (MLR) model was used to show the relationship between the printing parameters changes and the mentioned microscopic features. Therefore, their effect on the self-cleaning ability is shown in the equation.where yˆ is the microscopic feature (porosity, roughness, and wettability), and x1 represents the layer height, x2 represents the extruder width, x3 represents the orientation angle, and b0−3 is the estimated regression coefficient that quantifies the association between the parameters X and the dependent variable yˆ.
- The most basic principle of self-cleaning ability is forming a spherical water droplet that can remove the dirt particles by affecting the surface properties [41]. To explain the optimal self-cleaning number, we applied wettability as the most influential parameter during water droplet impact on a textile fabric. It was used to justify the optimal self-cleaning number. If the contact angle , the solid surface is referred to as a hydrophobic surface: the water rolls off and the surface has the minimum self-cleaning ability; if it is less than , the surface becomes hydrophilic in nature which means the angle is = 0 and the water will be absorbed by the surface. If the contact angle approaches >, the surface is termed a superhydrophobic surface and it has the best self-cleaning ability [42].
4. Result and Discussion
4.1. The Influence of Printing Parameters on the Microscopic Features
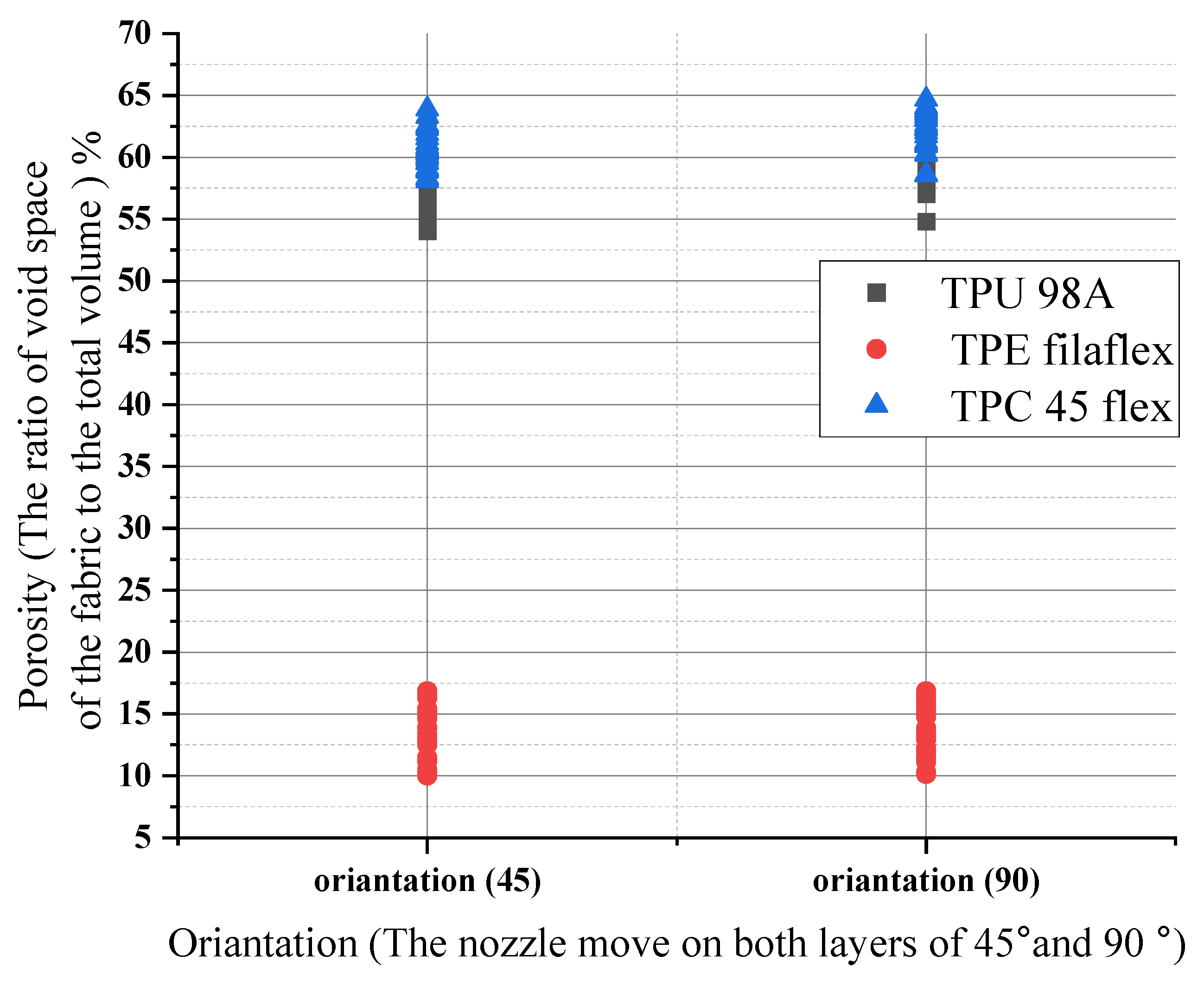
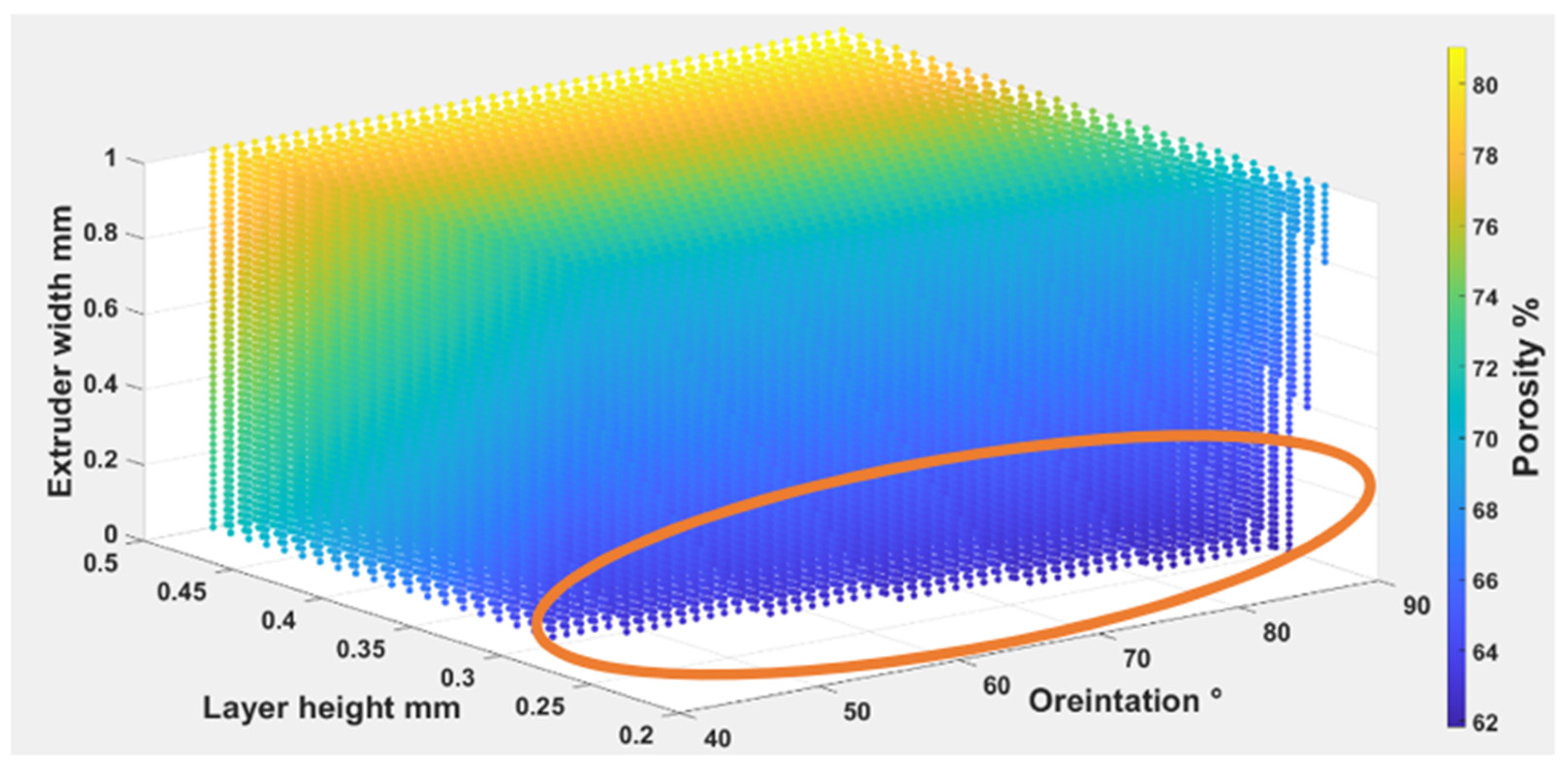
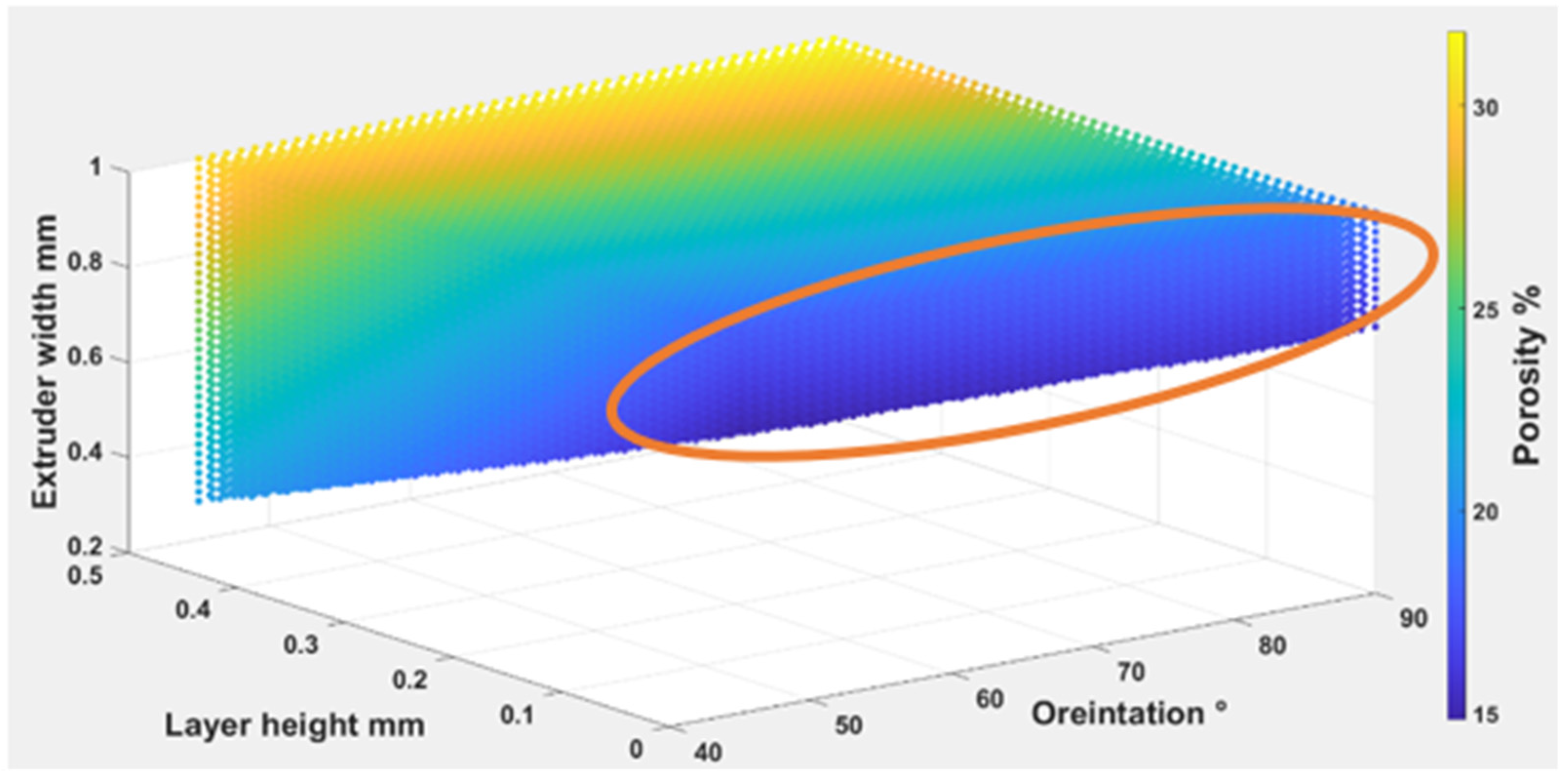
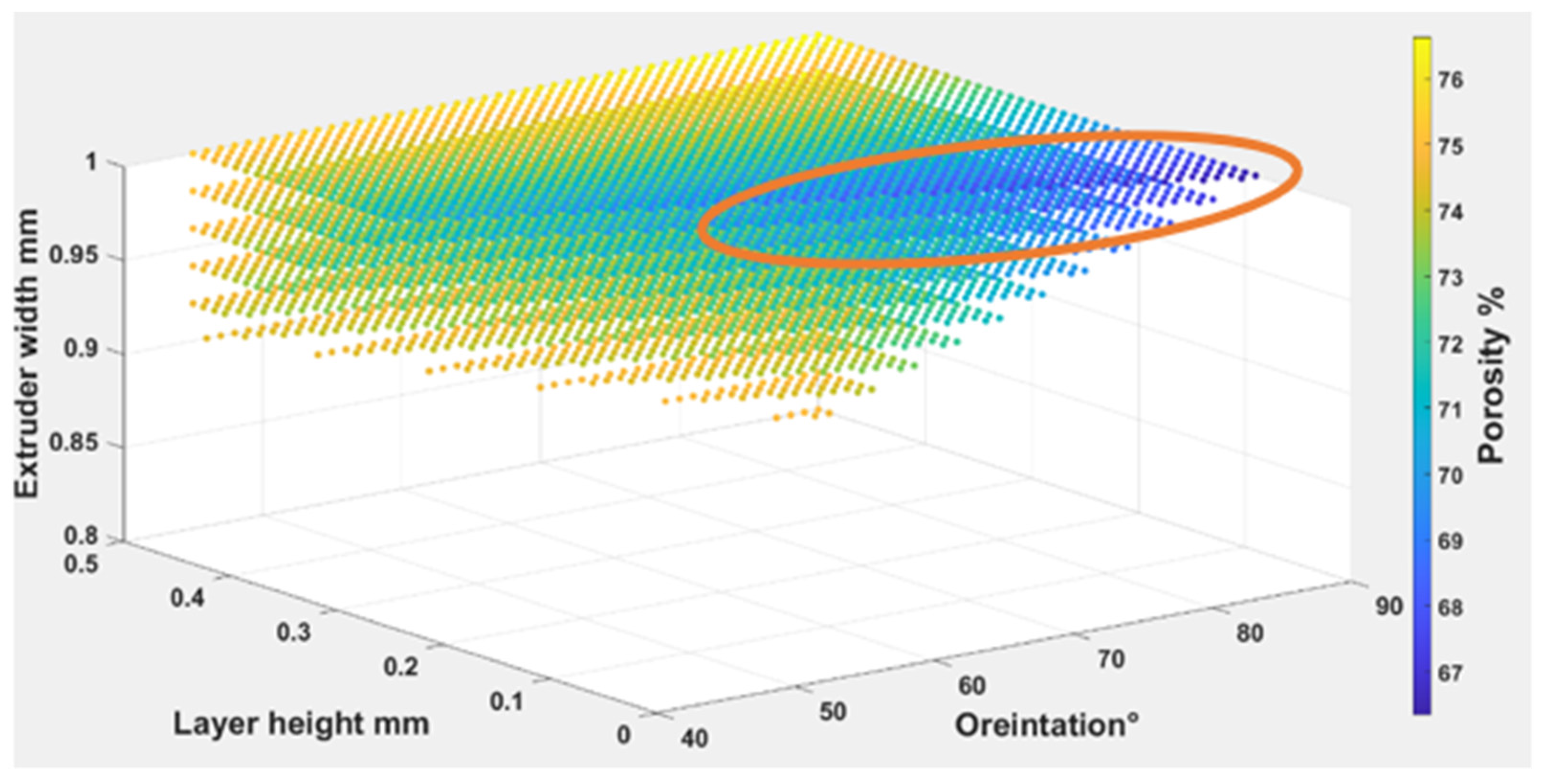
4.1.1. The Influence of Printing Parameters on Porosity
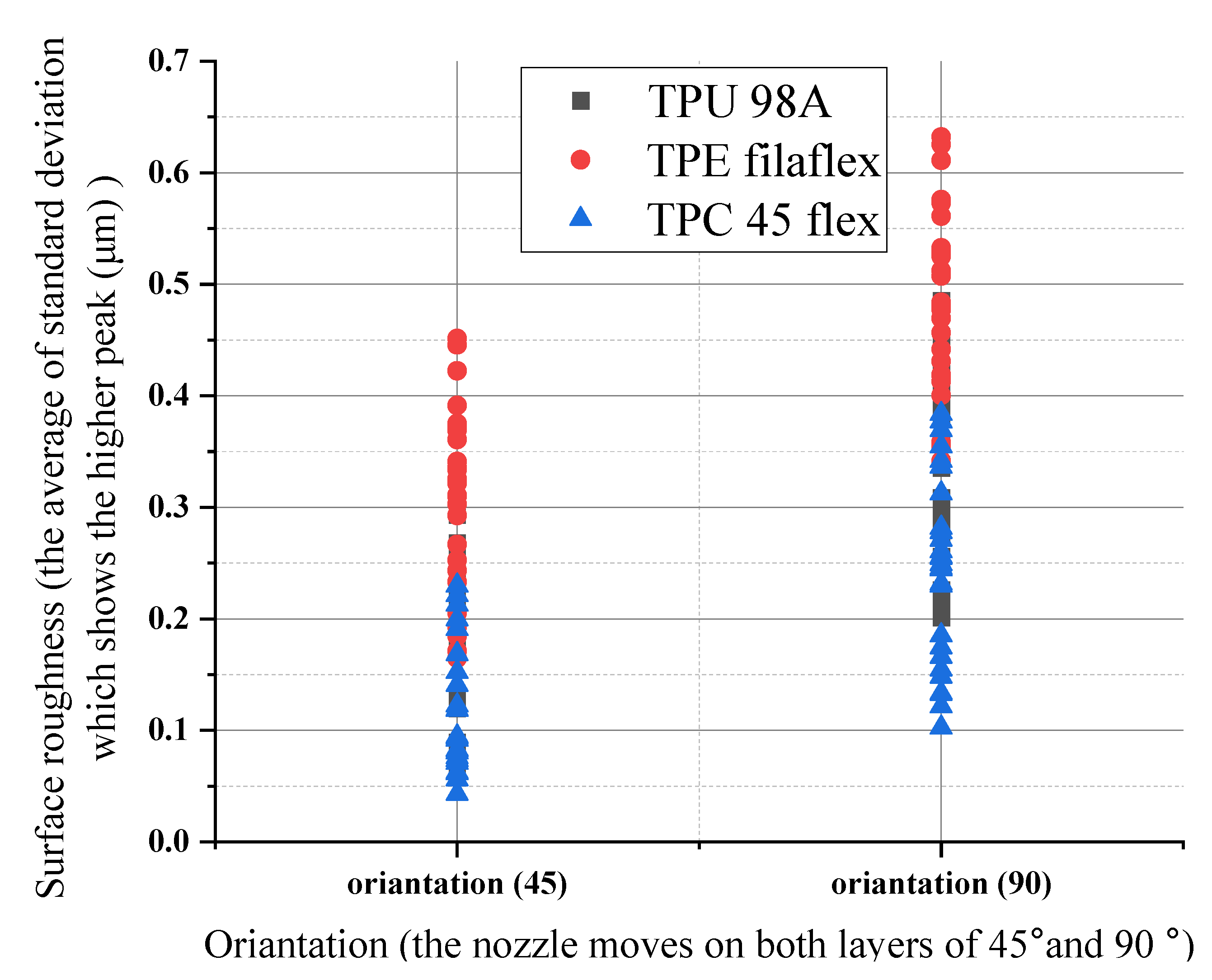
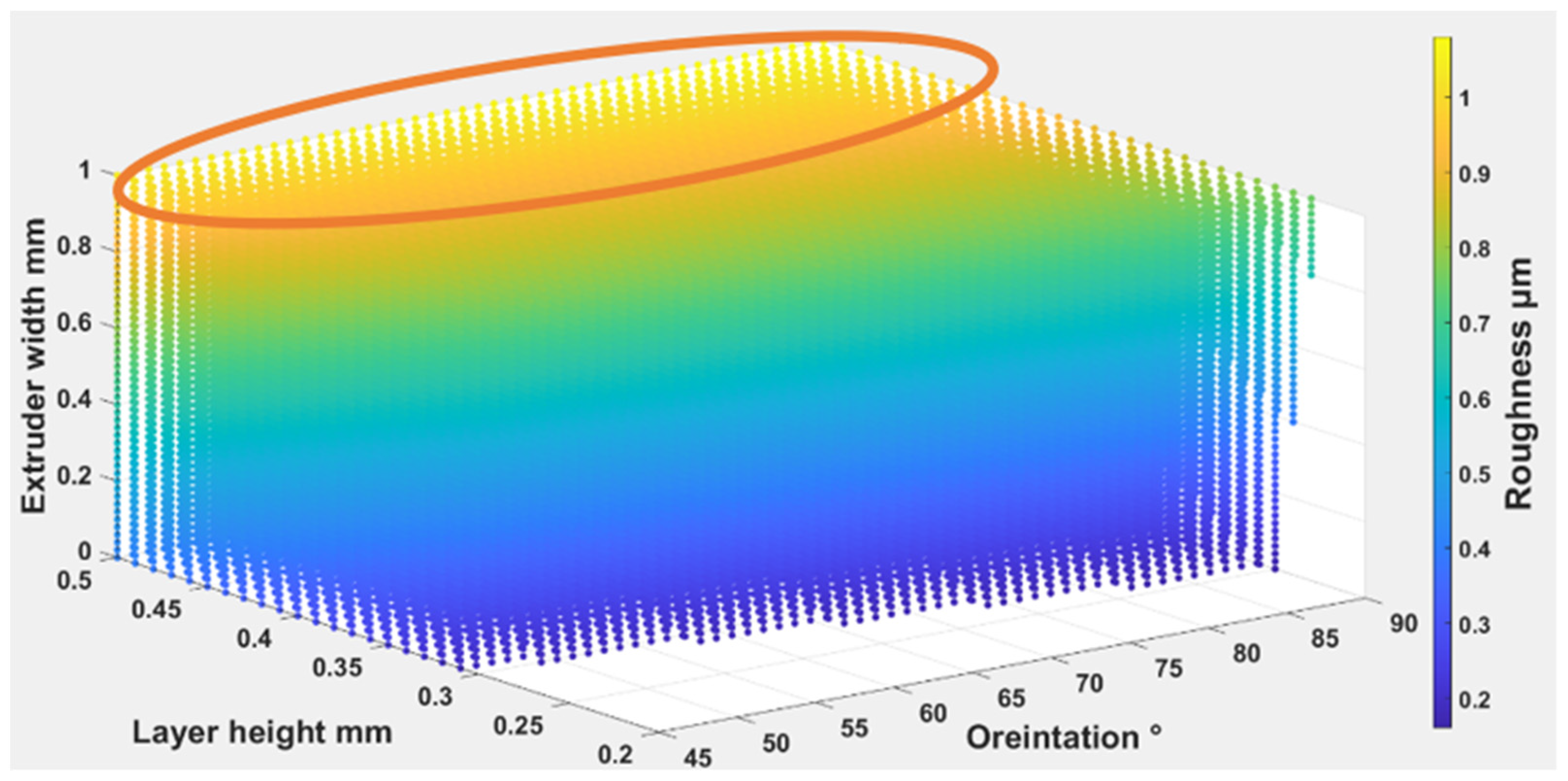
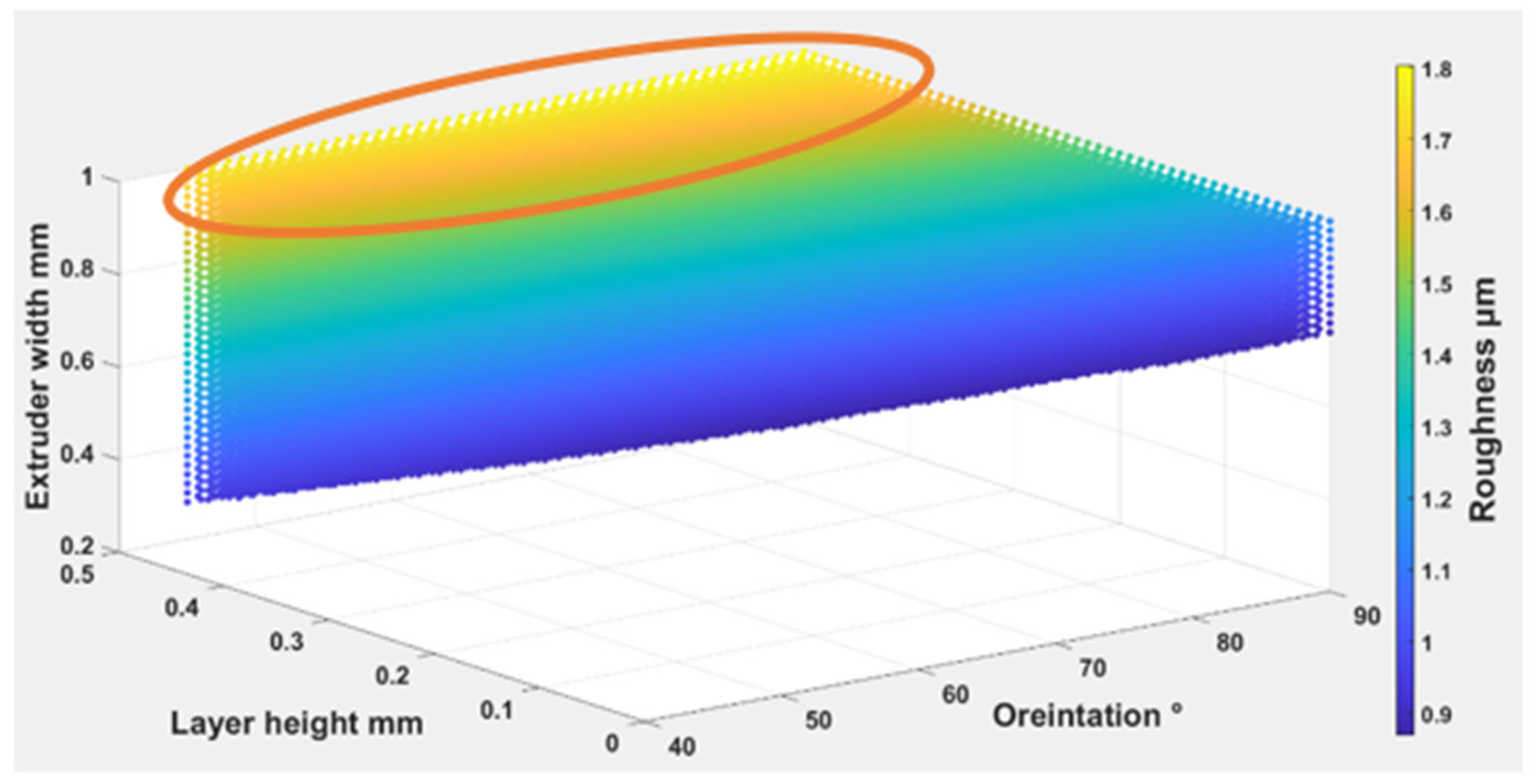
4.1.2. The Parameters’ Influence on Surface Roughness
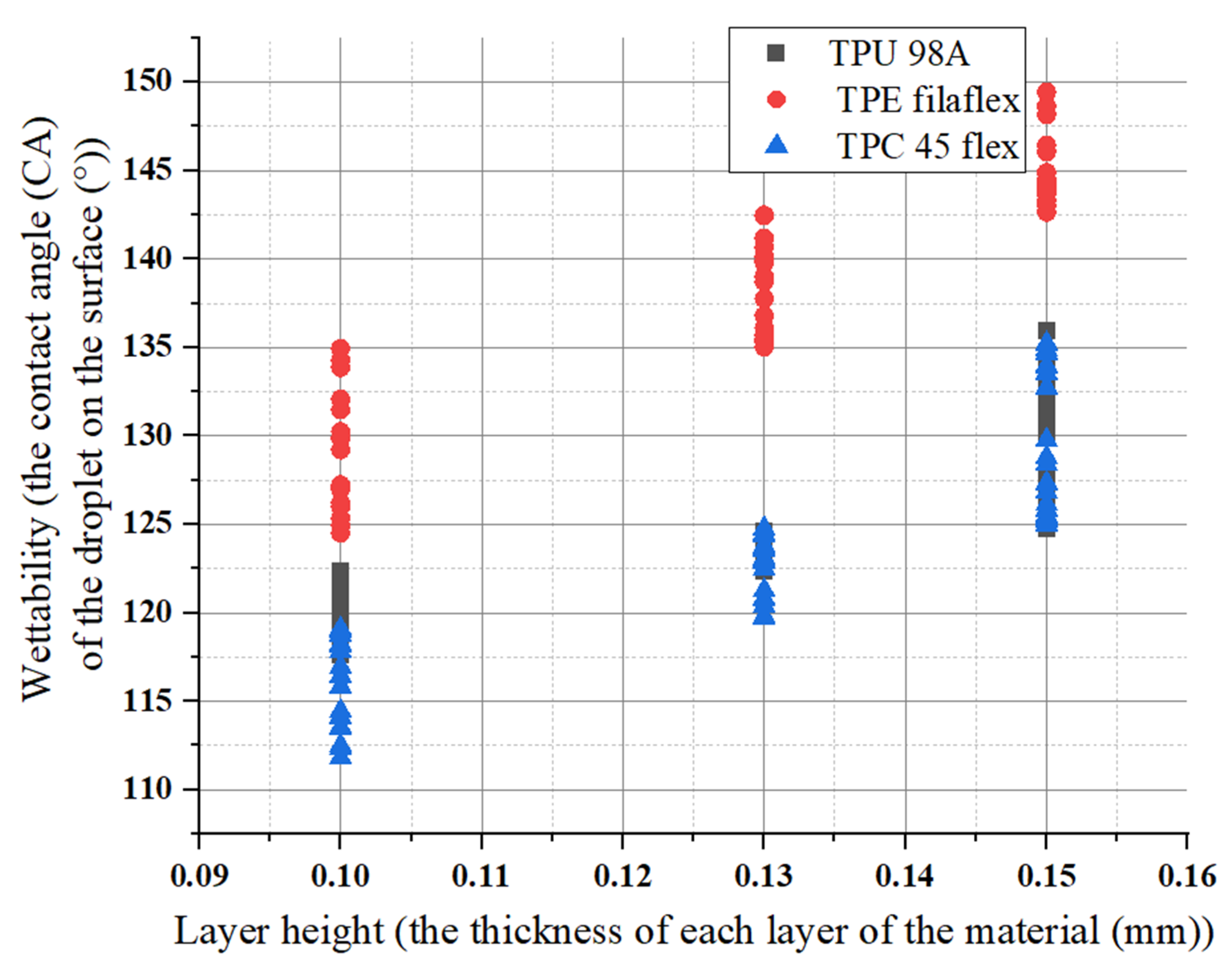
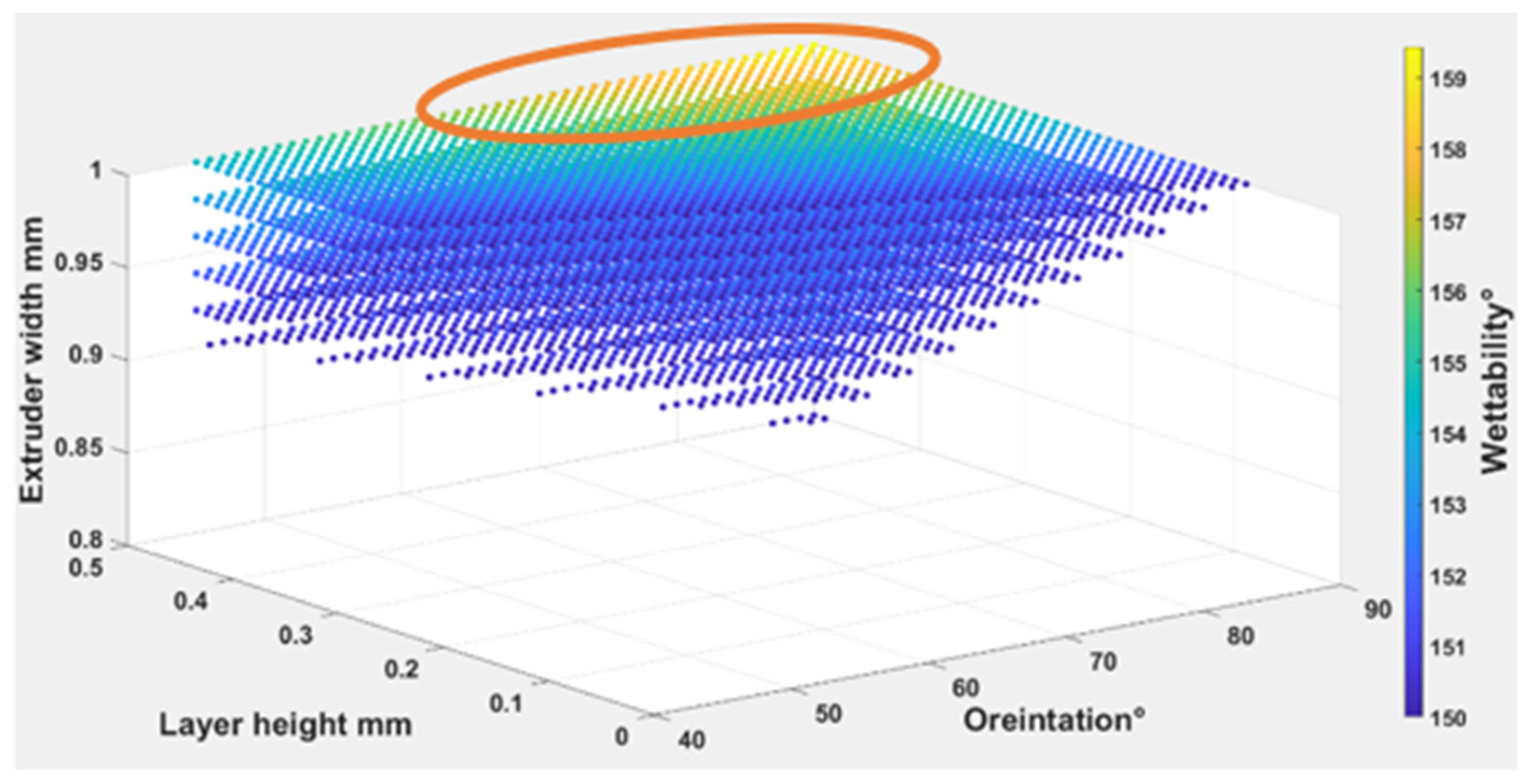
4.1.3. The Parameters’ Influence on Wettability
Water Absorption and Fabric Wettability
- (TPU 98A).
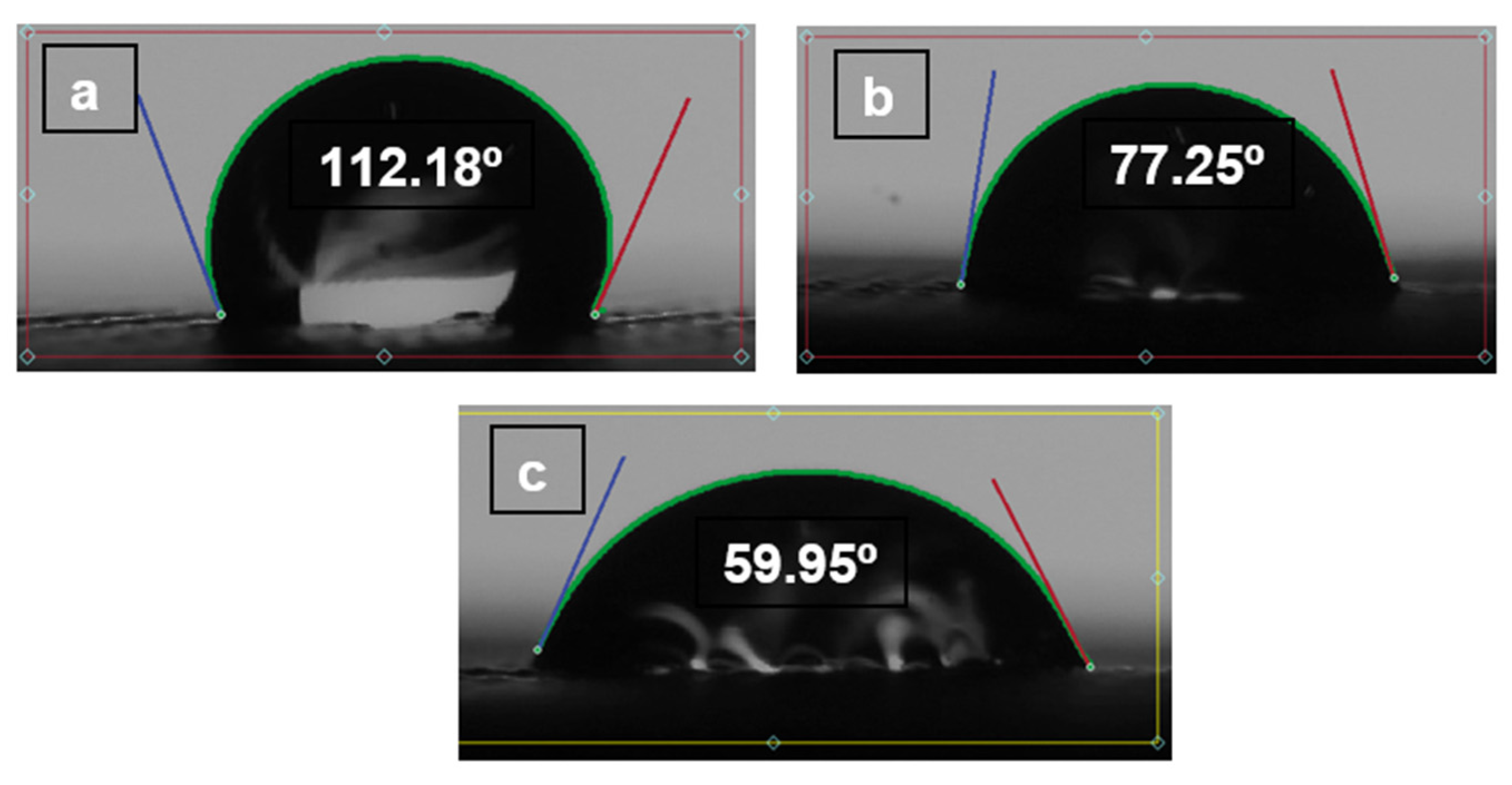
- (TPE filaflex).
- (TPC 45flex).

4.2. The Linear Regression for Different Printing Parameters
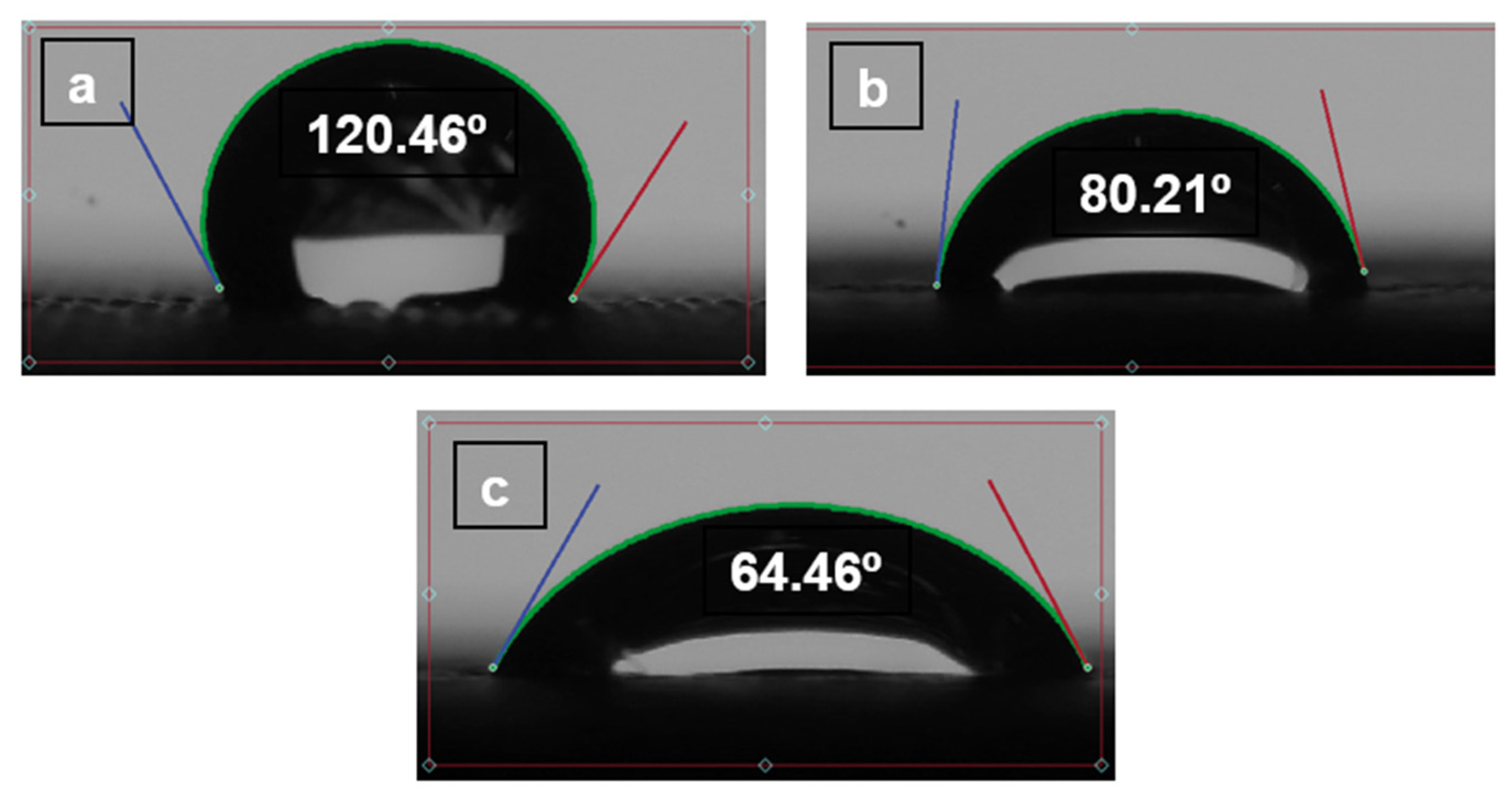
- (TPU 98A).
- (TPE filaflex).
- (TPC 45flex).
4.3. The Self-Cleaning Number
- (TPU 98A) showed that several scale values varied between 44.11, which is the lowest value with wettability of (0.10 mm LH, 0.3 mm EW and 45° O), and 73.49, which is the highest value of (0.15 mm LH, 0.5 mm EW and 90° O) for a self-cleaning number.
- (TPE filaflex) showed that several scale values varied between 55.22, which is the lowest value with wettability of (0.10 mm LH, 0.3 mm EW and 45° O), and 94.90, which is the highest value of (0.15 mm LH, 0.5 mm EW and 90° O) for a self-cleaning number.
- (TPC 45flex) showed that several scale values varied between 34.91, which is the lowest value with wettability of (0.10 mm LH, 0.3 mm EW and 45° O), and 72.33 which is the highest value of (0.15 mm LH, 0.5 mm EW and 90° O) for a self-cleaning number.
4.4. The Optimization of Printing Parameters
- TPU 98A
- TPE filaflex
- TPC 45flex
5. Validation
6. Conclusions
- It was found that the printing parameters have a very significant effect on the self-cleaning properties when optimizing the selection of the process parameter combination of layer height, extruder width, and printing orientation. The results showed that changing layer height and extruder width combined can affect the porosity, surface roughness, and wettability. The highest layer height has a rougher impact on the surface texture.
- The changes in porosity numbers are dependent on the material itself rather than the layer height changes. They show porosity values obtained between 9% and 18% for the chosen layer height. They slightly change by about 2% to 5% at higher and lower layer height, respectively.
- The lowest surface roughness occurs on 0.10 mm of layer height for TPC with (112°) wettability contact angle, whereas the highest occurs on the 0.15 mm of layer height for TPE with (149°) wettability contact angle. Changing the print layer height and extruder width produces samples that span relative roughness ranges between (0.04–0.65 μm).
- The experimental results showed that TPE has a better self-cleaning ability than the other two materials. It showed that several scale values varied between 55.22, which was the lowest value with wettability of (0.10 mm LH, 0.3 mm EW and 45° O), and 94.90, which was the highest value of (0.15 mm LH, 0.5 mm EW and 90° O) for self-cleaning number.
- Printing different layer heights can affect the printing time and divide a 3D model into more layers affecting the quality of the printed fabric. Extruder width was found to be much more critical for surface printed quality, as lowering the width deteriorated the printed surface, causing more threads to be printed to cover the surface. A desirable structural geometry and fiber orientation are achievable with reasonable and accurate control of printing parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hua, X.C.; Wu, Y.; Guo, X.J.; Liu, B.Y.; Wang, H.D.; Jia, S.T. Superhydrophobic, Flame-Retardant and Conductive Cotton Fabrics via Layer-by-Layer Assembly of Carbon Nanotubes for Flexible Sensing Electronics. Cellulose 2020, 27, 3455–3468. [Google Scholar] [CrossRef]
- Roy, S.; Zhai, L.; Kim, J.W.; Kim, H.C.; Kim, J. A Novel Approach of Developing Sustainable Cellulose Coating for Self-Cleaning-Healing Fabric. Prog. Org. Coat. 2020, 140, 105500. [Google Scholar] [CrossRef]
- Saad, S.R.; Mahmed, N.; Abdullah, M.M.A.B.; Sandu, A.V. Self-Cleaning Technology in Fabric: A Review. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Iasi, Romania, 19–20 May 2016; Institute of Physics Publishing: Bristol, UK, 2016; Volume 133. [Google Scholar]
- Sas, I.; Gorga, R.E.; Joines, J.A.; Thoney, K.A. Literature Review on Superhydrophobic Self-Cleaning Surfaces Produced by Electrospinning. J. Polym. Sci. Part B Polym. Phys. 2012, 50, 824–845. [Google Scholar] [CrossRef]
- Ahmad, I.; Kan, C.W. Visible-Light-Driven, Dye-Sensitized TiO 2 Photo-Catalyst for Self-Cleaning Cotton Fabrics. Coatings 2017, 7, 192. [Google Scholar] [CrossRef] [Green Version]
- Latthe, S.S.; Sutar, R.S.; Kodag, V.S.; Bhosale, A.K.; Kumar, A.M.; Kumar Sadasivuni, K.; Xing, R.; Liu, S. Self—Cleaning Superhydrophobic Coatings: Potential Industrial Applications. Prog. Org. Coat. 2019, 128, 52–58. [Google Scholar] [CrossRef]
- Ahmad, I.; Kan, C.W. A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles. Materials 2016, 9, 892. [Google Scholar] [CrossRef]
- Ahmad, I.; Kan, C.W.; Yao, Z. Reactive Blue-25 Dye/TiO2 Coated Cotton Fabrics with Self-Cleaning and UV Blocking Properties. Cellulose 2019, 26, 2821–2832. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, J.; Park, C.H. Fabrication of Self-Cleaning Textiles by TiO2-Carbon Nanotube Treatment. Text. Res. J. 2014, 84, 267–278. [Google Scholar] [CrossRef]
- Yang, H.; Ji, F.; Li, Z.; Tao, S. Preparation of Hydrophobic Surface on PLA and ABS by Fused Deposition Modeling. Polymers 2020, 12, 1539. [Google Scholar] [CrossRef] [PubMed]
- Atwah, A.A.; Khan, M.A. Influence of Microscopic Features on the Self-Cleaning Ability of Textile Fabrics. Text. Res. J. 2021. [Google Scholar] [CrossRef]
- Karaguzel, B. Characterization and Role of Porosity in Knitted Fabrics. Available online: https://repository.lib.ncsu.edu/handle/1840.16/1073 (accessed on 23 June 2022).
- Çay, A.; Vassiliadis, S.; Rangoussi, M.; Tarakçıolu, I. On the Use of Image Processing Techniques for the Estimation of the Porosity of Textile Fabrics. 23 June 1884. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.193.1884 (accessed on 23 June 2022).
- Vassiliadis, S.G.; Provatidis, C.G. Structural Characterization of Textile Fabrics Using Surface Roughness Data. Int. J. Cloth. Sci. Technol. 2004, 16, 445–457. [Google Scholar] [CrossRef]
- Matin, A.; Baig, U.; Akhtar, S.; Merah, N.; Gondal, M.A.; Bake, A.H.; Ibrahim, A. UV-Resistant and Transparent Hydrophobic Surfaces with Different Wetting States by a Facile Dip-Coating Method. Prog. Org. Coat. 2019, 136, 105192. [Google Scholar] [CrossRef]
- Chinchwade, S.S.; Landage, S.M.; Bonsule, S. Super-Hydrophobicity on Textiles—A Review. Int. J. Adv. Res. Eng. Appl. Sci. 2014, 3, 1–9. [Google Scholar]
- Khojasteh, D.; Kazerooni, M.; Salarian, S.; Kamali, R. Droplet Impact on Superhydrophobic Surfaces: A Review of Recent Developments. J. Ind. Eng. Chem. 2016, 42, 1–14. [Google Scholar] [CrossRef]
- Shams, H.; Basit, K.; Khan, M.A.; Saleem, S.; Mansoor, A. Realizing Surface Amphiphobicity Using 3D Printing Techniques: A Critical Move towards Manufacturing Low-Cost Reentrant Geometries. Addit. Manuf. 2021, 38, 101777. [Google Scholar] [CrossRef]
- Shams, H.; Basit, K.; Khan, M.A.; Mansoor, A.; Saleem, S. Scalable Wear Resistant 3D Printed Slippery Liquid Infused Porous Surfaces (SLIPS). Addit. Manuf. 2021, 48, 102379. [Google Scholar] [CrossRef]
- He, F.; Alshammari, Y.L.A.; Khan, M. The Effect of Printing Parameters on Crack Growth Rate of FDM ABS Cantilever Beam under Thermo-Mechanical Loads. Procedia Struct. Integr. 2021, 34, 59–64. [Google Scholar] [CrossRef]
- He, F.; Khan, M. Effects of Printing Parameters on the Fatigue Behaviour of 3d-Printed Abs under Dynamic Thermo-Mechanical Loads. Polymers 2021, 13, 2362. [Google Scholar] [CrossRef]
- He, F.; Khan, M.; Aldosari, S. Interdependencies between Dynamic Response and Crack Growth in a 3D-Printed Acrylonitrile Butadiene Styrene (ABS) Cantilever Beam under Thermo-Mechanical Loads. Polymers 2022, 14, 982. [Google Scholar] [CrossRef] [PubMed]
- Alshammari, Y.L.A.; He, F.; Khan, M.A. Modelling and Investigation of Crack Growth for 3d-Printed Acrylonitrile Butadiene Styrene (Abs) with Various Printing Parameters and Ambient Temperatures. Polymers 2021, 13, 3737. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Thakur, V.K.; Khan, M. Evolution and New Horizons in Modeling Crack Mechanics of 3D Printing Polymeric Structures. Mater. Today Chem. 2021, 20, 100393. [Google Scholar] [CrossRef]
- Almutairi, M.D.; Aria, A.I.; Thakur, V.K.; Khan, M.A. Self-Healing Mechanisms for 3D-Printed Polymeric Structures: From Lab to Reality. Polymers 2020, 12, 1534. [Google Scholar] [CrossRef] [PubMed]
- Baqasah, H.; He, F.; Zai, B.A.; Asif, M.; Khan, K.A.; Thakur, V.K.; Khan, M.A. In-Situ Dynamic Response Measurement for Damage Quantification of 3D Printed ABS Cantilever Beam under Thermomechanical Load. Polymers 2019, 11, 2079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jafari, R.; Cloutier, C.; Allahdini, A.; Momen, G. Recent Progress and Challenges with 3D Printing of Patterned Hydrophobic and Superhydrophobic Surfaces. Int. J. Adv. Manuf. Technol. 2019, 103, 1225–1238. [Google Scholar] [CrossRef]
- Barrios, J.M.; Romero, P.E. Improvement of Surface Roughness and Hydrophobicity in PETG Parts Manufactured via Fused Deposition Modeling (FDM): An Application in 3D Printed Self-Cleaning Parts. Materials 2019, 12, 2499. [Google Scholar] [CrossRef] [Green Version]
- Buj-Corral, I.; Bagheri, A.; Sivatte-Adroer, M. Effect of Printing Parameters on Dimensional Error, Surface Roughness and Porosity of FFF Printed Parts with Grid Structure. Polymers 2021, 13, 1213. [Google Scholar] [CrossRef] [PubMed]
- Hartcher-O’Brien, J.; Evers, J.; Tempelman, E. Surface Roughness of 3D Printed Materials: Comparing Physical Measurements and Human Perception. Mater. Today Commun. 2019, 19, 300–305. [Google Scholar] [CrossRef]
- Hanon, M.M.; Alshammas, Y.; Zsidai, L. Effect of Print Orientation and Bronze Existence on Tribological and Mechanical Properties of 3D-Printed Bronze/PLA Composite. Int. J. Adv. Manuf. Technol. 2020, 108, 553–570. [Google Scholar] [CrossRef]
- Cappetti, N.; Naddeo, A.; Salerno, G. Influence of Control Parameters on Consumer FDM 3D Printing. Adv. Transdiscipl. Eng. 2018, 7, 165–177. [Google Scholar] [CrossRef]
- Myshkin, N.K.; Grigoriev, A.Y.; Chizhik, S.A.; Choi, K.Y.; Petrokovets, M.I. Surface Roughness and Texture Analysis in Microscale. Wear 2003, 254, 1001–1009. [Google Scholar] [CrossRef]
- Alsoufi, M.S.; El-Sayed, A.; Elsayed, A.E. How Surface Roughness Performance of Printed Parts Manufactured by Desktop FDM 3D Printer with PLA+ Is Influenced by Measuring Direction Environmental Sustainability and Energy Conservation during Machining Processes View Project How Surface Roughness Per. Am. J. Mech. Eng. 2017, 5, 211–222. [Google Scholar] [CrossRef]
- Kalami, H.; Urbanic, J. Exploration of Surface Roughness Measurement Solutions for Additive Manufactured Components Built by Multi-Axis Tool Paths. Addit. Manuf. 2021, 38, 101822. [Google Scholar] [CrossRef]
- Chen, Y.; He, B.; Lee, J.; Patankar, N.A. Anisotropy in the Wetting of Rough Surfaces. J. Colloid Interface Sci. 2005, 281, 458–464. [Google Scholar] [CrossRef] [PubMed]
- Erbil, H.Y. The Debate on the Dependence of Apparent Contact Angles on Drop Contact Area or Three-Phase Contact Line: A Review. Surf. Sci. Rep. 2014, 69, 325–365. [Google Scholar] [CrossRef]
- Feng, X.; Jiang, L. Design and Creation of Superwetting/Antiwetting Surfaces. Adv. Mater. 2006, 18, 3063–3078. [Google Scholar] [CrossRef]
- Akgun, M. Effect of Yarn Filament Fineness on the Surface Roughness of Polyester Woven Fabrics. J. Eng. Fibers Fabr. 2015, 10, 121–128. [Google Scholar] [CrossRef]
- Takahashi, H.; Kim, J. 3D Printed Fabric: Techniques for Design and 3D Weaving Programmable Textiles. In Proceedings of the UIST 2019—Proceedings of the 32nd Annual ACM Symposium on User Interface Software and Technology, New Orleans, LA, USA, 20–23 October 2019; Association for Computing Machinery, Inc.: New York, NY, USA, 2019; pp. 43–51. [Google Scholar]
- Dalawai, S.P.; Saad Aly, M.A.; Latthe, S.S.; Xing, R.; Sutar, R.S.; Nagappan, S.; Ha, C.S.; Kumar Sadasivuni, K.; Liu, S. Recent Advances in Durability of Superhydrophobic Self-Cleaning Technology: A Critical Review. Prog. Org. Coat. 2020, 138, 105381. [Google Scholar] [CrossRef]
- Verplanck, N.; Coffinier, Y.; Thomy, V.; Boukherroub, R. Wettability Switching Techniques on Superhydrophobic Surfaces. Nanoscale Res. Lett. 2007, 2, 577–596. [Google Scholar] [CrossRef] [Green Version]
- Korger, M.; Bergschneider, J.; Lutz, M.; Mahltig, B.; Finsterbusch, K.; Rabe, M. Possible Applications of 3D Printing Technology on Textile Substrates. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Moenchengladbach, Germany, 8–11 June 2016; Institute of Physics Publishing: Bristol, UK, 2016; Volume 141. [Google Scholar]



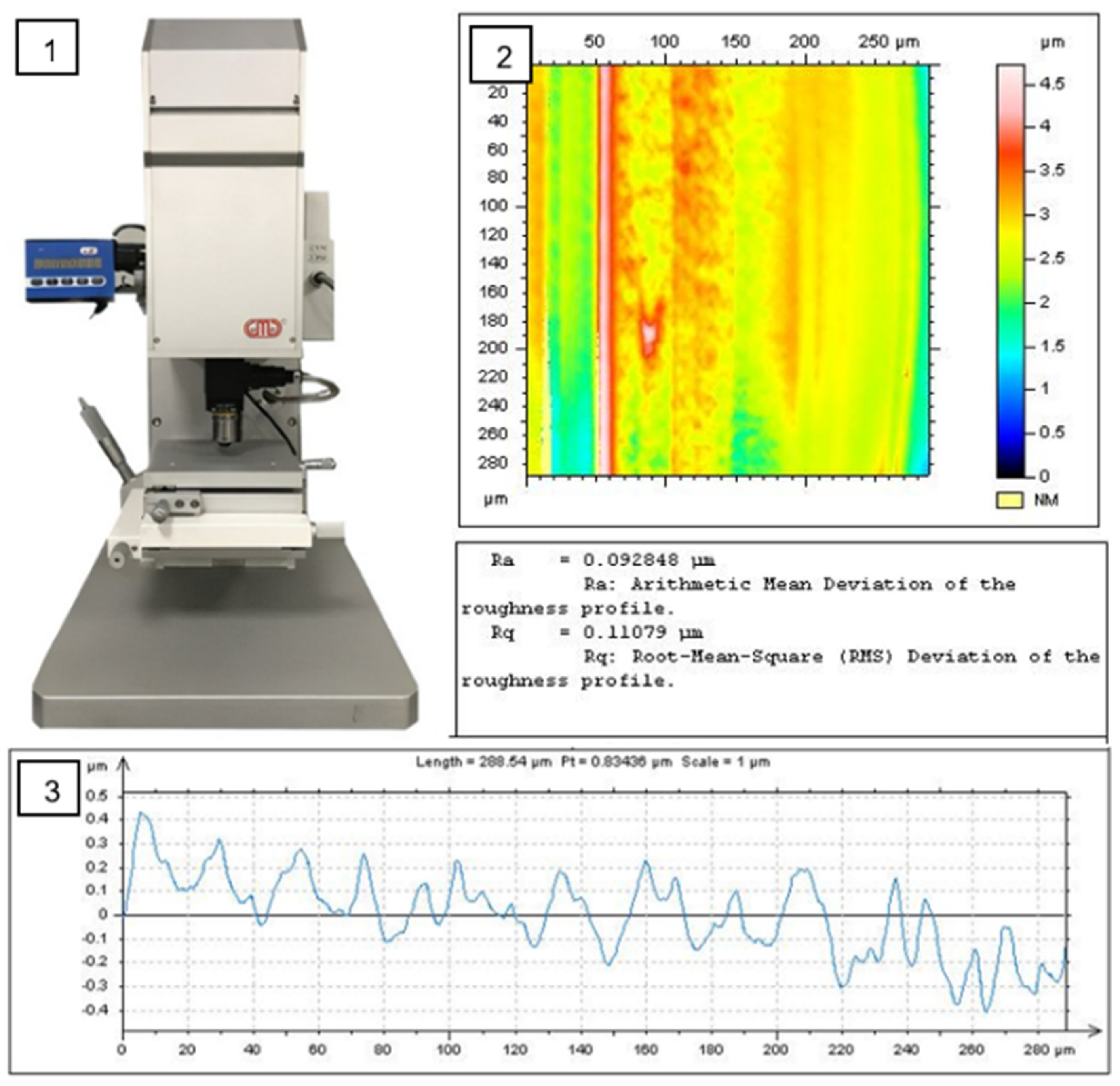

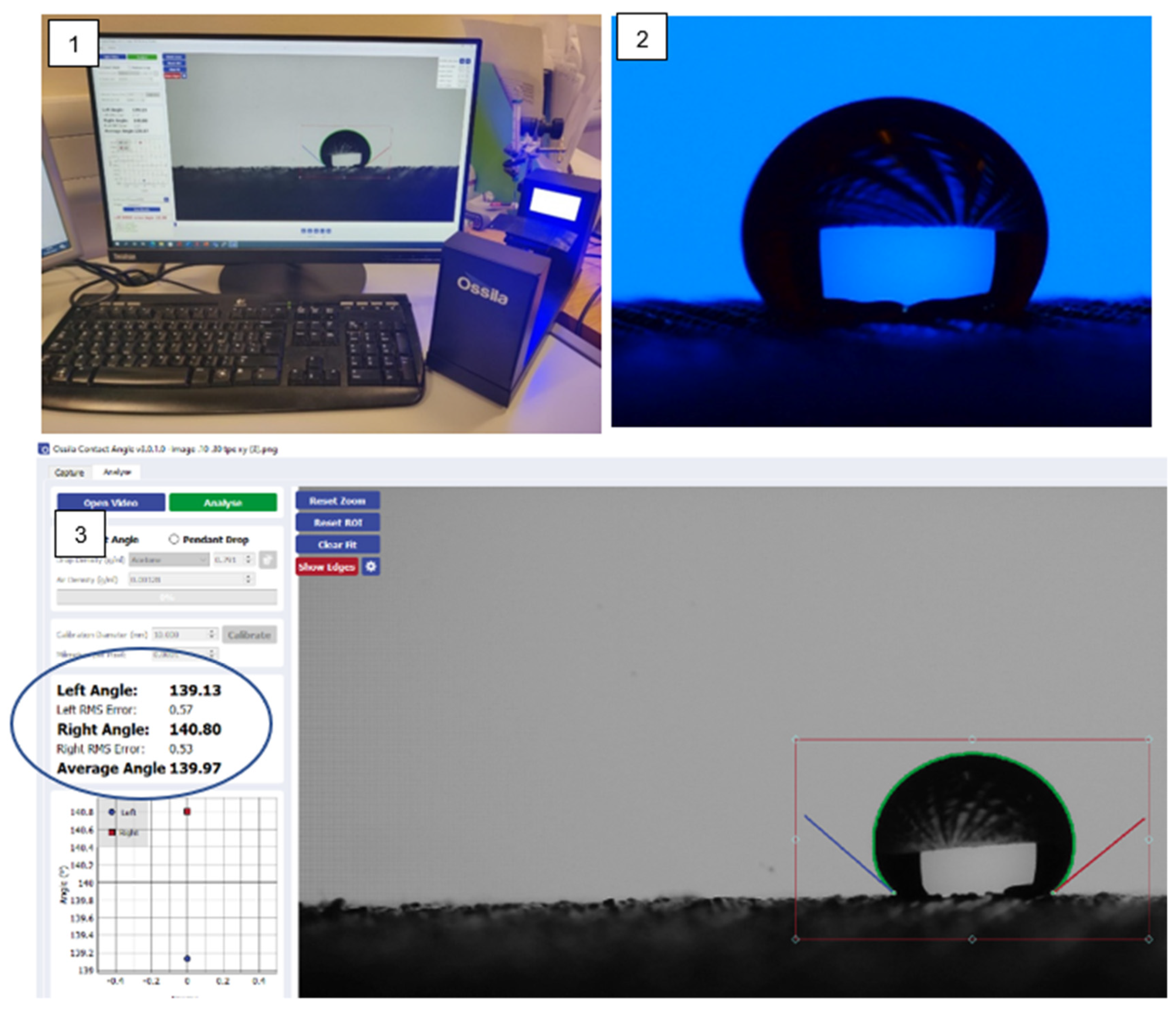










| Layer Height (LH) mm | Extruder Width (EW) mm | Orientation Angle (O) Degree ° |
|---|---|---|
| 0.15 | 0.50 | 0° (first layer)–90° (second layer), 45° (first layer)–135° (second layer) |
| 0.13 | 0.40 | 0–90°, 45–135° |
| 0.10 | 0.30 | 0–90°, 45–135° |
| Properties/Filament | TPU 98A | TPE Fila Flex | TPC Flex 45 |
|---|---|---|---|
| Chemical name/blend | Thermoplastic polyurethane | Thermo Plastic Elastomer | Thermoplastic Co-Polyester |
| Cost per kilo(£/kg) | 22–40 | 20–30 | 30–60 |
| supplier | RS Components | RS Components | RS Components |
| Diameter (mm) | 1.75 | 1.75 | 1.75 |
| Printing temperature (°C) | 205–230 | 210–240 | 210–250 |
| Density (g/m3) | 1.14 | 1.09 | 1.16 |
| Filament | Layer Height (mm) | Number of Layers | Extruder Width (mm) | Orientation Degree (°) | Number of Samples |
|---|---|---|---|---|---|
| TPU 98A | 0.15 | 2 | 0.50 | 45–135° 0–90° | 3 |
| 0.40 | |||||
| 0.30 | |||||
| 0.13 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 | |||||
| 0.10 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 | |||||
| TPE Filaflex | 0.15 | 2 | 0.50 | 45–135° 0–90° | 3 |
| 0.40 | |||||
| 0.30 | |||||
| 0.13 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 | |||||
| 0.10 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 | |||||
| TPC 45 Flex | 0.15 | 2 | 0.50 | 45–135° 0–90° | 3 |
| 0.40 | |||||
| 0.30 | |||||
| 0.13 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 | |||||
| 0.10 | 2 | 0.50 | 45–135° 0–90° | 3 | |
| 0.40 | |||||
| 0.30 |
| Name | TPU 98A | TPE fila flex | TPC 45 flex |
|---|---|---|---|
| Porosity (P1) length (mm) | 0.044 | 0.035 | 0.047 |
| Porosity (P2) width (mm) | 0.044 | 0.035 | 0.047 |
| Water Droplet (WD) | Circumference (mm) | Circumference (mm) | Circumference (mm) |
| 1.867 | 1.928 | 1.932 | |
| Area (mm) | Area (mm) | Area (mm) | |
| 0.277 | 0.296 | 0.297 | |
| Radius (mm) | Radius (mm) | Radius (mm) | |
| 0.297 | 0.307 | 0.307 | |
| Diameter (mm) | Diameter (mm) | Diameter (mm) | |
| 0.594 | 0.614 | 0.615 |
| Layer Height (LH) mm | Extruder Width (EW) mm | Orientation Angle (O)° | Standardized Value |
|---|---|---|---|
| 0.10 | 0.30 | - | −1 |
| 0.13 | 0.40 | 45° | 0 |
| 0.15 | 0.50 | 90° | 1 |
| Layer Height (LH) mm | Extruder Width (EW) mm | Orientation Angle (O) Degree ° |
|---|---|---|
| 0.14 | 0.60 | 70° (first layer)–210° (second layer) |
| (TPU)—Orientation 70° | |||||
| Sample | (LH) mm | (EW) mm | Wettability Experimentally Degree ° | Wettability Based on Equation (6) Degree ° | R-Square (%) |
| 1 | 0.14 | 0.6 | 133.52 | 133.7301 | −0.1573 |
| 2 | 0.14 | 0.6 | 132.34 | 133.7301 | −1.0504 |
| (TPE)—Orientation 70° | |||||
| Sample | (LH) mm | (EW) mm | Wettability Experimentally Degree ° | Wettability Based on Equation (9) Degree ° | R-Square (%) |
| 1 | 0.14 | 0.6 | 146.79 | 147.0002 | −0.1432 |
| 2 | 0.14 | 0.6 | 146.8 | 147.0002 | −0.1364 |
| (TPC)—Orientation 70° | |||||
| Sample | (LH) mm | (EW) mm | Wettability Experimentally Degree ° | Wettability Based on Equation (12) Degree ° | R-Square (%) |
| 1 | 0.14 | 0.6 | 131.52 | 130.8233 | 0.5297 |
| 2 | 0.14 | 0.6 | 130.34 | 130.8233 | −0.3708 |
| Samples | (O) Degree ° | (LH) mm | (EW) mm | Porosity Experiment (%) | Porosity Based on the Equations (%) | R-Square (%) |
|---|---|---|---|---|---|---|
| TPU 1 | 70 | 0.14 | 0.6 | 60.5487 | 61.18675 | −1.0538 |
| TPU 2 | 70 | 0.14 | 0.6 | 61.3495 | 61.18675 | 0.2653 |
| TPE 1 | 70 | 0.14 | 0.6 | 15.9889 | 16.5023 | 0.8902 |
| TPE 2 | 70 | 0.14 | 0.6 | 16.2713 | 16.5023 | 0.9843 |
| TPC 1 | 70 | 0.14 | 0.6 | 62.2025 | 63.46319 | −2.0267 |
| TPC 2 | 70 | 0.14 | 0.6 | 61.1086 | 63.46319 | −3.8531 |
| Samples | (O) Degree ° | (LH) mm | (EW) mm | Surface Roughness Experiment μm | Surface Roughness Based on the Equations μm | R-Square (%) |
|---|---|---|---|---|---|---|
| TPU 1 | 70 | 0.14 | 0.6 | 0.37949 | 0.383772 | −1.1284 |
| TPU 2 | 70 | 0.14 | 0.6 | 0.38049 | 0.383772 | −0.8626 |
| TPE 1 | 70 | 0.14 | 0.6 | 0.63273 | 0.64494 | −1.9297 |
| TPE 2 | 70 | 0.14 | 0.6 | 0.64253 | 0.64494 | −0.3751 |
| TPC 1 | 70 | 0.14 | 0.6 | 0.35156 | 0.357016 | −1.5519 |
| TPC 2 | 70 | 0.14 | 0.6 | 0.34996 | 0.357016 | −2.0162 |
| Samples | (O) Degree ° | (LH) mm | (EW) mm | Wettability Degree ° | Self-Cleaning Number |
|---|---|---|---|---|---|
| TPU 1 | 70 | 0.14 | 0.6 | 133.52 | 69.632 |
| TPU 2 | 70 | 0.14 | 0.6 | 132.34 | 67.744 |
| TPE 1 | 70 | 0.14 | 0.6 | 146.79 | 90.864 |
| TPE 2 | 70 | 0.14 | 0.6 | 146.8 | 90.88 |
| TPC 1 | 70 | 0.14 | 0.6 | 131.52 | 66.432 |
| TPC 2 | 70 | 0.14 | 0.6 | 130.34 | 64.544 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atwah, A.A.; Almutairi, M.D.; He, F.; Khan, M.A. Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics. Polymers 2022, 14, 3128. https://doi.org/10.3390/polym14153128
Atwah AA, Almutairi MD, He F, Khan MA. Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics. Polymers. 2022; 14(15):3128. https://doi.org/10.3390/polym14153128
Chicago/Turabian StyleAtwah, Ayat Adnan, Mohammed Dukhi Almutairi, Feiyang He, and Muhammad A. Khan. 2022. "Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics" Polymers 14, no. 15: 3128. https://doi.org/10.3390/polym14153128
APA StyleAtwah, A. A., Almutairi, M. D., He, F., & Khan, M. A. (2022). Influence of Printing Parameters on Self-Cleaning Properties of 3D Printed Polymeric Fabrics. Polymers, 14(15), 3128. https://doi.org/10.3390/polym14153128






