Investigating the Bond Strength of FRP Rebars in Concrete under High Temperature Using Gene-Expression Programming Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Database
2.2. GEP Model Development
2.3. Evaluation Criteria
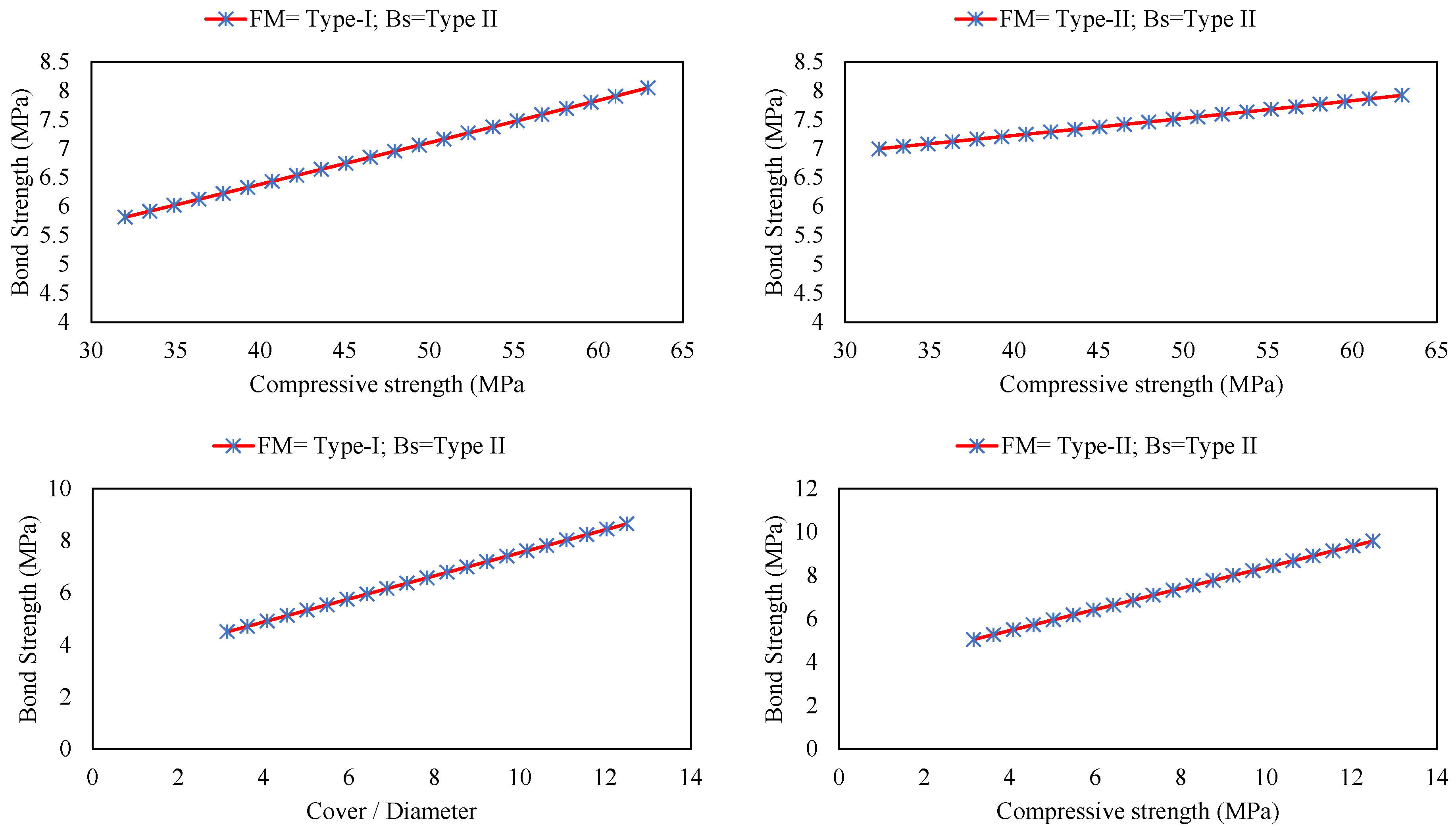
3. Results and Discussion
3.1. Effect of Genetic Variables
3.2. Performance of the Undertaken Trials
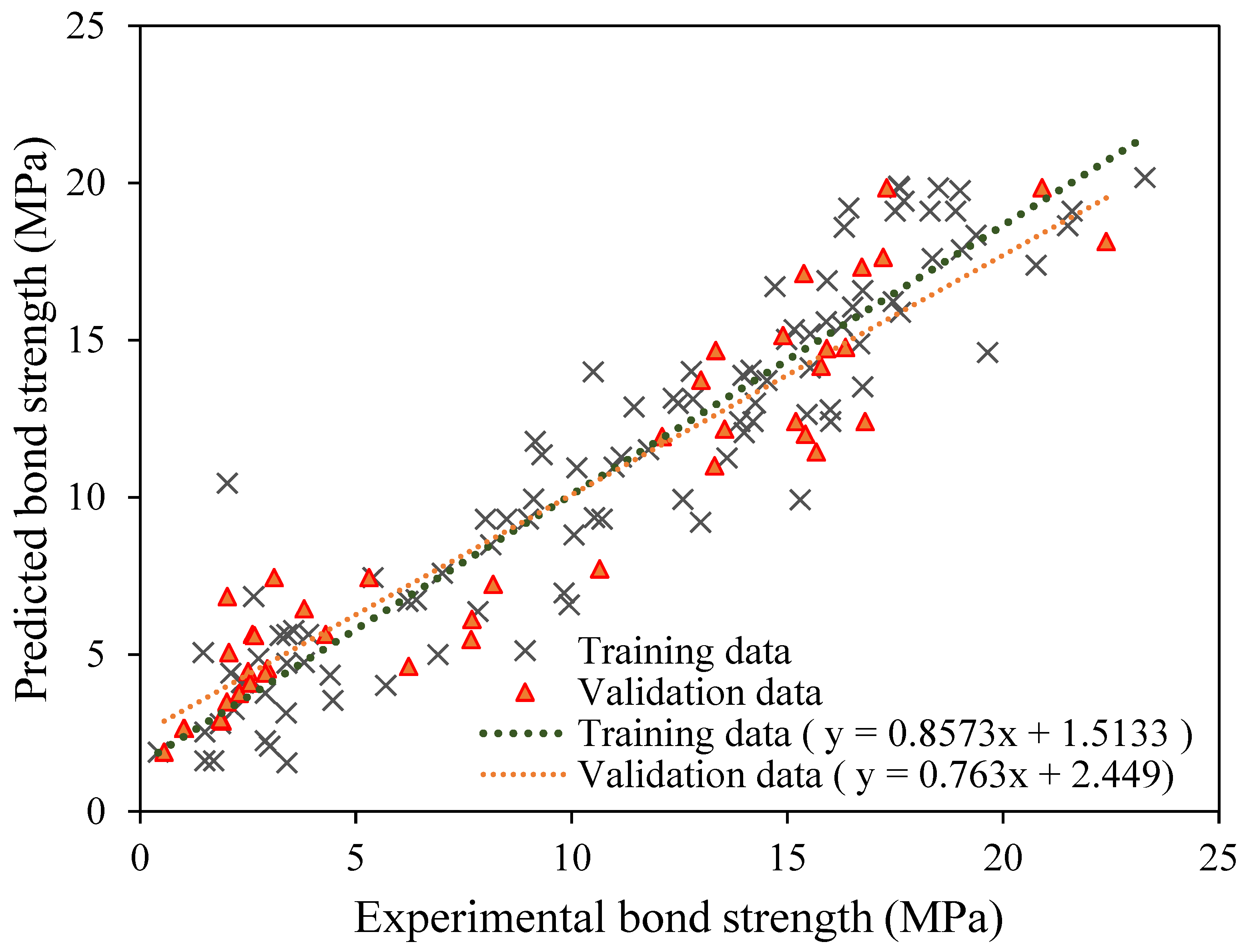
3.2.1. Statistical Indices Analysis
3.2.2. Regression Plot Analysis and Error Analysis
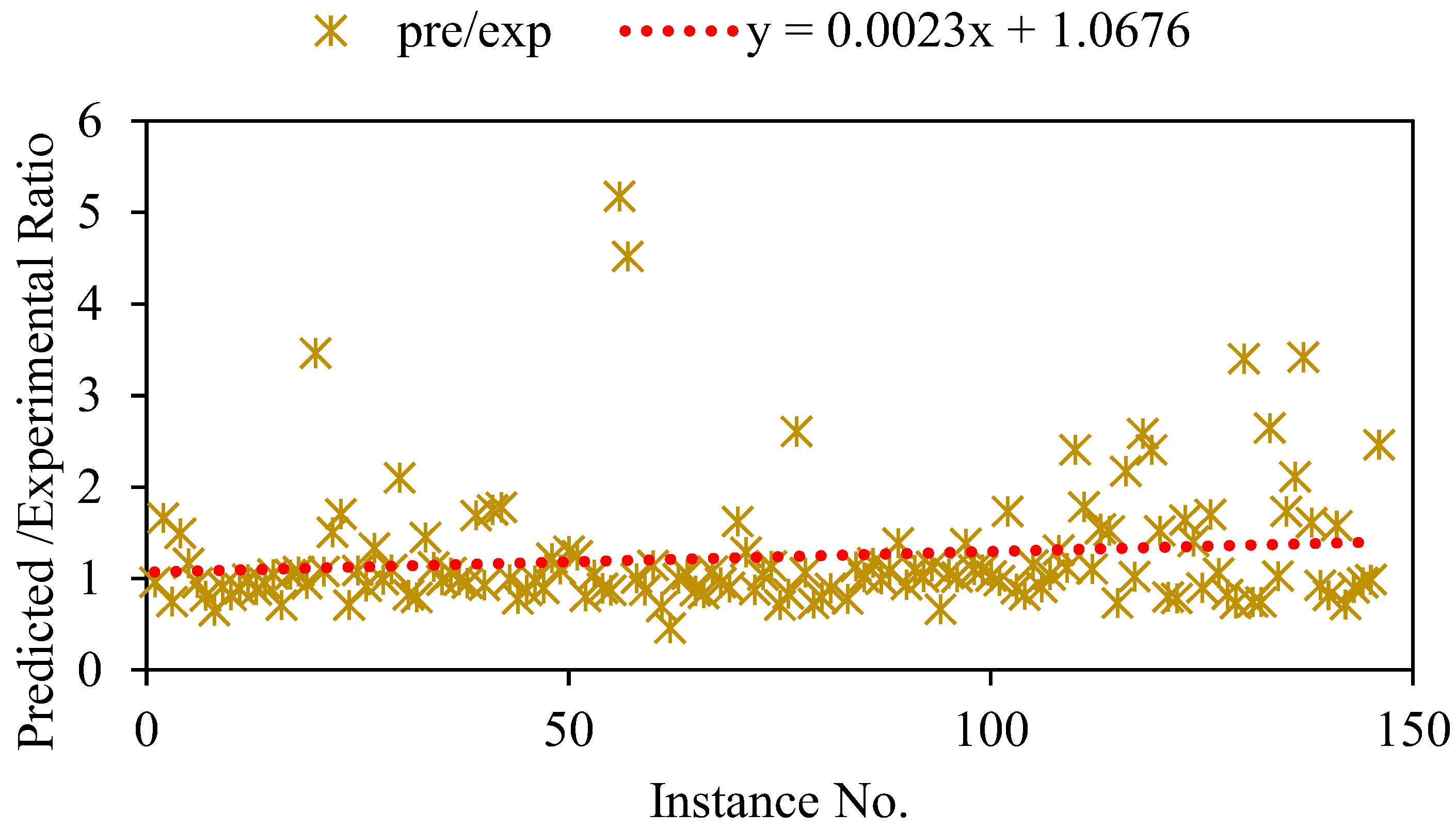
3.2.3. Predicted vs. Experimental Ratio
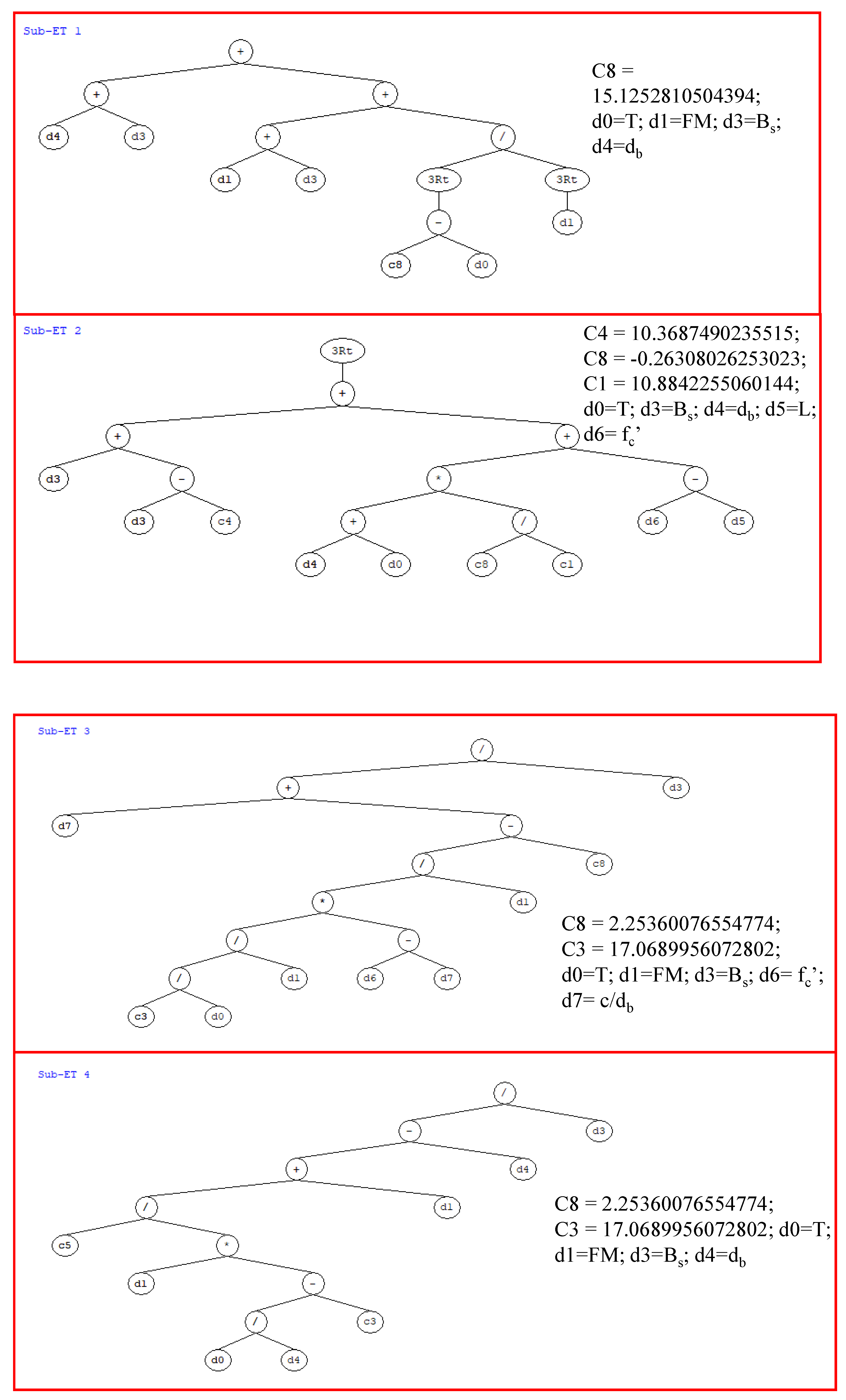
3.3. GEP Formulations
3.4. Parametric Analysis
4. Conclusions
- The proposed GEP model has the potential to be used as a tool for extracting features and making predictions in very intricate nonlinear engineering systems. The GEP architecture needs to be optimised via hit-and-trial method based on the dataset’s size and complexity. Dependence on the amount and quality of the dataset is a key factor in the GEP model’s utility and accuracy.
- Measures of statistical performance including R, RMSE, and MAE were applied to both the training data and the validation data to assess the quality of the models. R = 0.941, MAE = 1.620, and RMSE = 2.087 for training, and 0.935, 2.046, and 2.370 for validation, according to the statistical indices, demonstrates that the established GEP model can accurately estimate bond strength.
- The parametric analysis shows that the developed GEP model can accurately predict the response of different input variables on the strength of FRP bars. Due to the limited data, this analysis is limited to ribbed bars.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Yang, Z.; Zhu, C.; Zhang, C.; Hui, X. Study on Bonding Properties of Reinforced Composite Concrete Structure with Fiber Materials. Tumu Gongcheng Xuebao/China Civ. Eng. J. 2020, 53, 259–264. [Google Scholar]
- Amin, M.N.; Iqbal, M.; Khan, K.; Qadir, M.G.; Shalabi, F.I.; Jamal, A. Ensemble Tree-Based Approach towards Flexural Strength Prediction of FRP Reinforced Concrete Beams. Polymers 2022, 14, 1303. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yin, X.; Liu, Y.; Guo, R.; Xian, G. Long-Term Service Evaluation of a Pultruded Carbon/Glass Hybrid Rod Exposed to Elevated Temperature, Hydraulic Pressure and Fatigue Load Coupling. Int. J. Fatigue 2020, 134, 105480. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, X.L.; Xian, G.; Wu, G.; Raman, R.K.S.; Al-Saadi, S. Effect of Sustained Load and Seawater and Sea Sand Concrete Environment on Durability of Basalt- and Glass-Fibre Reinforced Polymer (B/GFRP) Bars. Corros. Sci. 2018, 138, 200–218. [Google Scholar] [CrossRef]
- Li, C.; Guo, R.; Xian, G.; Li, H. Innovative Compound-Type Anchorage System for a Large-Diameter Pultruded Carbon/Glass Hybrid Rod for Bridge Cable. Mater. Struct. Constr. 2020, 53, 1–15. [Google Scholar] [CrossRef]
- Taerwe, L. Analytical Modelling of Bond between FRP Reinforcing Bars and Concrete. In Non-Metallic Reinforcement for Concrete Structures; CRC Press: Boca Raton, FL, USA, 2020; pp. 182–189. [Google Scholar] [CrossRef]
- Tighiouart, B.; Benmokrane, B.; Gao, D. Investigation of Bond in Concrete Member with Fibre Reinforced Polymer (FRP) Bars. Constr. Build. Mater. 1998, 12, 453–462. [Google Scholar] [CrossRef]
- Malvar, L.J. Tensile and Bond Properties of GFRP Reinforcing Bars. ACI Mater. J. 1995, 92, 276–285. [Google Scholar] [CrossRef]
- Guo, R.; Xian, G.; Li, F.; Li, C.; Hong, B. Hygrothermal Resistance of Pultruded Carbon, Glass and Carbon/Glass Hybrid Fiber Reinforced Epoxy Composites. Constr. Build. Mater. 2022, 315, 125710. [Google Scholar] [CrossRef]
- Kumahara, S.; Masuda, Y.; Tanano, H.; Shimizu, A. Tensile strength of continuous fiber bar under high temperature. Special Publication. ACI Symp. Pap. 1993, 138, 731–742. [Google Scholar]
- Ahmet, B.; Rüstem, G.Ü.L. Donatı-beton aderansı, yüksek sıcaklıkların beton dayanımına ve aderansa etkileri konusunda bir derleme. Tübav Bilim Dergisi 2009, 2, 211–230. [Google Scholar]
- Khoury, G.A. Performance of Heated Concrete-Mechanical Properties; Contract NUC/56/3604A with Nuclear Installations Inspectorate; Imperial College: London, UK, 1996. [Google Scholar]
- Katz, A.; Berman, N. Modeling the effect of high temperature on the bond of FRP reinforcing bars to concrete. Cem. Concr. Compos. 2000, 22, 433–443. [Google Scholar] [CrossRef]
- Spagnuolo, S.; Meda, A.; Rinaldi, Z.; Nanni, A. Residual Behaviour of Glass FRP Bars Subjected to High Temperatures. Compos. Struct. 2018, 203, 886–893. [Google Scholar] [CrossRef]
- Naser, M.Z.; Uppala, V.A. Properties and Material Models for Construction Materials Post Exposure to Elevated Temperatures. Mech. Mater. 2020, 142, 103293. [Google Scholar] [CrossRef]
- Robert, M.; Benmokrane, B. Behavior of GFRP Reinforcing Bars Subjected to Extreme Temperatures. J. Compos. Constr. 2010, 14, 353–360. [Google Scholar] [CrossRef]
- Hamad, R.J.A.; Megat Johari, M.A.; Haddad, R.H. Mechanical properties and bond characteristics of different fiber reinforced polymer rebars at elevated temperatures. Constr. Build. Mater. 2017, 142, 521–535. [Google Scholar] [CrossRef]
- Özkal, F.M.; Polat, M.; Yağan, M.; Öztürk, M.O. Mechanical properties and bond strength degradation of GFRP and steel rebars at elevated temperatures. Constr. Build. Mater. 2018, 184, 45–57. [Google Scholar] [CrossRef]
- El-Gamal, S. Bond strength of glass fiber-reinforced polymer bars in concrete after exposure to elevated temperatures. J Reinf. Plast. Compos. 2014, 33, 2151–2163. [Google Scholar] [CrossRef]
- Wang, Y.L. Experimental Study on Tensile Property of FRP Bars and Bond Behavior between FRP Bars and Concrete after High Temperature; Zhengzhou University: Zhengzhou, China, 2013. [Google Scholar]
- Lu, X.L.; Zhou, C.D.; Jin, Y. Test study on bond behavior between GFRP bar andconcrete in high temperature. J. Build. Struct. 2007, 28, 32–39. [Google Scholar]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the Compaction Characteristics of Expansive Soils Using Two Genetic Programming-Based Algorithms. Transp. Geotech. 2021, 30, 100608. [Google Scholar] [CrossRef]
- Trong, D.K.; Pham, B.T.; Jalal, F.E.; Iqbal, M.; Roussis, P.C.; Mamou, A.; Ferentinou, M.; Vu, D.Q.; Dam, N.D.; Tran, Q.A.; et al. On Random Subspace Optimization-Based Hybrid Computing Models Predicting the California Bearing Ratio of Soils. Materials 2021, 14, 6516. [Google Scholar] [CrossRef]
- Khan, K.; Jalal, F.E.; Iqbal, M.; Khan, M.I.; Amin, M.N.; Al-Faiad, M.A. Predictive Modeling of Compression Strength of Waste PET/SCM Blended Cementitious Grout Using Gene Expression Programming. Materials 2022, 15, 3077. [Google Scholar] [CrossRef] [PubMed]
- Bardhan, A.; Samui, P.; Ghosh, K.; Gandomi, A.H.; Bhattacharyya, S. ELM-Based Adaptive Neuro Swarm Intelligence Techniques for Predicting the California Bearing Ratio of Soils in Soaked Conditions. Appl. Soft Comput. 2021, 110, 107595. [Google Scholar] [CrossRef]
- Huang, L.; Chen, J.; Tan, X. BP-ANN based bond strength prediction for FRP reinforced concrete at high temperature. Eng. Struct. 2022, 257, 114026. [Google Scholar] [CrossRef]
- Tran, T.H.; Dam, N.D.; Jalal, F.E.; Al-Ansari, N.; Ho, L.S.; Van Phong, T.; Iqbal, M.; Van Le, H.; Nguyen, H.B.T.; Prakash, I.; et al. GIS-Based Soft Computing Models for Landslide Susceptibility Mapping: A Case Study of Pithoragarh District, Uttarakhand State, India. Math. Probl. Eng. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C. Prediction of shear strength of FRP-reinforced concrete flexural members without stirrups using artificial neural networks. Eng. Struct. 2014, 61, 99–112. [Google Scholar] [CrossRef]
- Congro, M.; Monteiro, V.M.D.A.; Brandão, A.L.T.; dos Santos, B.F.; Roehl, D.; Silva, F.D.A. Prediction of the Residual Flexural Strength of Fiber Reinforced Concrete Using Artificial Neural Networks. Constr. Build. Mater. 2021, 303, 124502. [Google Scholar] [CrossRef]
- Alam, M.S.; Sultana, N.; Hossain, S.Z. Bayesian optimization algorithm based support vector regression analysis for estimation of shear capacity of FRP reinforced concrete members. Appl. Soft Comput. 2021, 105, 107281. [Google Scholar] [CrossRef]
- Köroglu, M.A. Artificial Neural Network for Predicting the Flexural Bond Strength of FRP Bars in Concrete. Sci. Eng. Compos. Mater. 2019, 26, 12–29. [Google Scholar] [CrossRef]
- Lee, S.; Moy, S. A Method for Predicting the Flexural Strength of RC Beams Strengthened with Carbon Fiber Reinforced Polymer. J. Reinf. Plast. Compos. 2007, 26, 1383–1401. [Google Scholar] [CrossRef]
- Pham, H.; Al-Mahaidi, R. Assessment of Available Prediction Models for the Strength of FRP Retrofitted RC Beams. Compos. Struct. 2004, 66, 601–610. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Shukla, S.K. Multivariate Adaptive Regression Splines Model for Reinforced Soil Foundations. Geosynth. Int. 2021, 28, 368–390. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Shukla, S.K. An Extreme Learning Machine Model for Geosynthetic-Reinforced Sandy Soil Foundations. Proc. Inst. Civ. Eng.-Geotech. Eng. 2020, 1–42. [Google Scholar] [CrossRef]
- Kardani, N.; Bardhan, A.; Gupta, S.; Samui, P.; Nazem, M.; Zhang, Y.; Zhou, A. Predicting Permeability of Tight Carbonates Using a Hybrid Machine Learning Approach of Modified Equilibrium Optimizer and Extreme Learning Machine. Acta Geotech. 2021, 17, 1239–1255. [Google Scholar] [CrossRef]
- Kardani, N.; Bardhan, A.; Samui, P.; Nazem, M.; Zhou, A.; Armaghani, D.J. A Novel Technique Based on the Improved Firefly Algorithm Coupled with Extreme Learning Machine (ELM-IFF) for Predicting the Thermal Conductivity of Soil. Eng. Comput. 2021, 1–20. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. Interpretable Machine Learning Algorithms to Predict the Axial Capacity of FRP-Reinforced Concrete Columns. Materials 2022, 15, 2742. [Google Scholar] [CrossRef] [PubMed]
- Kaveh, A.; Javadi, S.M.; Moghanni, R.M. Shear Strength Prediction of FRP-Reinforced Concrete Beams Using an Extreme Gradient Boosting Framework. Period. Polytech. Civ. Eng. 2022, 66, 18–29. [Google Scholar] [CrossRef]
- Abbasloo, A.A.; Shayanfar, M.A.; Pahlavan, H.; Barkhordari, M.A.; Hamze-Ziabari, S.M. Prediction of Shear Strength of FRP-Reinforced Concrete Members Using a Rule-Based Method. Mag. Concr. Res. 2019, 71, 271–286. [Google Scholar] [CrossRef]
- Deifalla, A.; Salem, N.M. A Machine Learning Model for Torsion Strength of Externally Bonded FRP-Reinforced Concrete Beams. Polymers 2022, 14, 1824. [Google Scholar] [CrossRef]
- Chen, S.Z.; Zhang, S.Y.; Han, W.S.; Wu, G. Ensemble Learning Based Approach for FRP-Concrete Bond Strength Prediction. Constr. Build. Mater. 2021, 302, 124230. [Google Scholar] [CrossRef]
- Shahri, S.F.; Mousavi, S.R. Bond Strength Prediction of Spliced GFRP Bars in Concrete Beams Using Soft Computing Methods. Comput. Concr. 2021, 24, 305–317. [Google Scholar] [CrossRef]
- Concha, N.C. Neural Network Model for Bond Strength of FRP Bars in Concrete. Structures 2022, 41, 306–317. [Google Scholar] [CrossRef]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive Modeling of Swell-Strength of Expansive Soils Using Artificial Intelligence Approaches: ANN, ANFIS and GEP. J. Environ. Manag. 2021, 289, 112420. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.; Zhang, D.; Jalal, F.E.; Faisal Javed, M. Computational AI Prediction Models for Residual Tensile Strength of GFRP Bars Aged in the Alkaline Concrete Environment. Ocean Eng. 2021, 232, 109134. [Google Scholar] [CrossRef]
- Murad, Y.; Tarawneh, A.; Arar, F.; Al-Zu’bi, A.; Al-Ghwairi, A.; Al-Jaafreh, A.; Tarawneh, M. Flexural Strength Prediction for Concrete Beams Reinforced with FRP Bars Using Gene Expression Programming. Structures 2021, 33, 3163–3172. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Samui, P.; Iqbal, M.; Hu, J.W. Soft Computing Approaches towards Tensile Strength Estimation of GFRP Rebars Subjected to Alkaline-Concrete Environment. Case Stud. Constr. Mater. 2022, 16, e00955. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: A New Adaptive Algorithm for Solving Problems. arXiv 2001, arXiv:cs/0102027. [Google Scholar]
- Cevik, A. A New Formulation for Longitudinally Stiffened Webs Subjected to Patch Loading. J. Constr. Steel Res. 2007, 63, 1328–1340. [Google Scholar] [CrossRef]
- Kayadelen, C. Soil Liquefaction Modeling by Genetic Expression Programming and Neuro-Fuzzy. Expert Syst. Appl. 2011, 38, 4080–4087. [Google Scholar] [CrossRef]
- Teodorescu, L.; Sherwood, D. High Energy Physics Event Selection with Gene Expression Programming. Comput. Phys. Commun. 2008, 178, 409–419. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Shukla, S.K.; Khan, M.U.A. An Intelligent Approach for Predicting the Strength of Geosynthetic-Reinforced Subgrade Soil. Int. J. Pavement Eng. 2021, 1–7. [Google Scholar] [CrossRef]
- Khan, M.U.A.; Shukla, S.K.; Raja, M.N.A. Load-Settlement Response of a Footing over Buried Conduit in a Sloping Terrain: A Numerical Experiment-Based Artificial Intelligent Approach. Soft Comput. 2022, 26, 6839–6856. [Google Scholar] [CrossRef]
- Khan, M.U.A.; Shukla, S.K.; Raja, M.N.A. Soil–Conduit Interaction: An Artificial Intelligence Application for Reinforced Concrete and Corrugated Steel Conduits. Neural Comput. Appl. 2021, 33, 14861–14885. [Google Scholar] [CrossRef]
- Bardhan, A.; Kardani, N.; Alzo’ubi, A.K.; Samui, P.; Gandomi, A.H.; Gokceoglu, C. A Comparative Analysis of Hybrid Computational Models Constructed with Swarm Intelligence Algorithms for Estimating Soil Compression Index. Arch. Comput. Methods Eng. 2022, 1–39. [Google Scholar] [CrossRef]
- Topal, U.; Goodarzimehr, V.; Bardhan, A.; Vo-Duy, T.; Shojaee, S. Maximization of the Fundamental Frequency of the FG-CNTRC Quadrilateral Plates Using a New Hybrid PSOG Algorithm. Compos. Struct. 2022, 295, 115823. [Google Scholar] [CrossRef]
- Kingston, G.B.; Maier, H.R.; Lambert, M.F. Calibration and Validation of Neural Networks to Ensure Physically Plausible Hydrological Modeling. J. Hydrol. 2005, 314, 158–176. [Google Scholar] [CrossRef]
- Aamir, M.; Tolouei-Rad, M.; Vafadar, A.; Raja, M.N.A.; Giasin, K. Performance Analysis of Multi-Spindle Drilling of Al2024 with TiN and TiCN Coated Drills Using Experimental and Artificial Neural Networks Technique. Appl. Sci. 2020, 10, 8633. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q. feng Prediction Model for Compressive Arch Action Capacity of RC Frame Structures under Column Removal Scenario Using Gene Expression Programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Abunama, T. Proposed Formulation of Surface Water Quality and Modelling Using Gene Expression, Machine Learning, and Regression Techniques. Environ. Sci. Pollut. Res. 2021, 28, 13202–13220. [Google Scholar] [CrossRef]
- Raja, M.N.A.; Shukla, S.K. Predicting the Settlement of Geosynthetic-Reinforced Soil Foundations Using Evolutionary Artificial Intelligence Technique. Geotext. Geomembr. 2021, 49, 1280–1293. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Liu, Q.F.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of Mechanical Properties of Green Concrete Incorporating Waste Foundry Sand Based on Gene Expression Programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef]
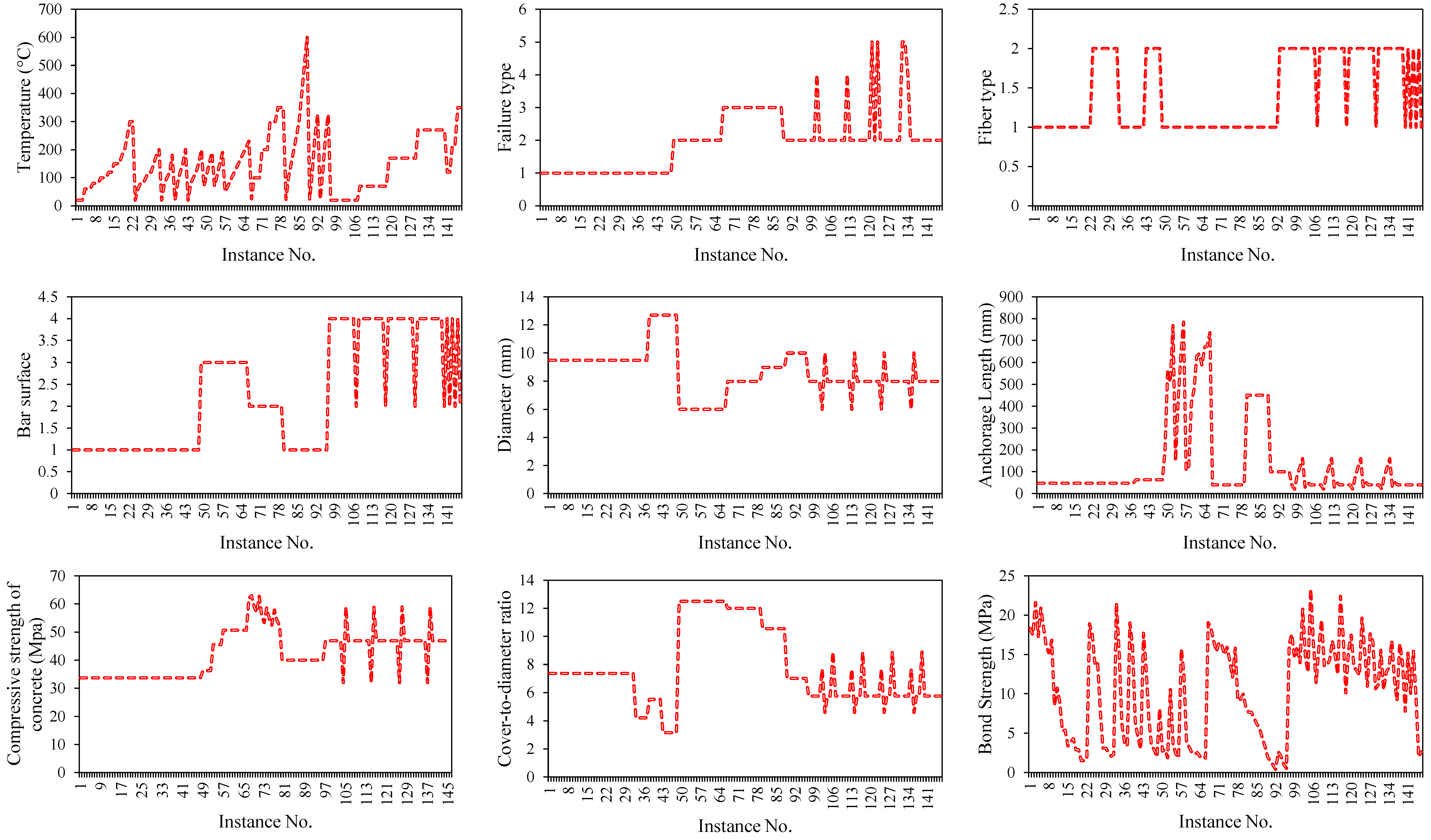





| Variable | Input Variables | Target | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Temperature | Failure Mode | Fibre Type | Bar Surface | Diameter | Anchorage Length | Compressive Strength | Cover-to-Diameter Ratio | Bond Strength | |
| Identification | T | FM | FT | Bs | db | L | c/db | BS | |
| Descriptive statistics | °C | - | - | - | mm | mm | MPa | - | MPa |
| Mean | 150.99 | 1.95 | 1.43 | 2.27 | 8.66 | 135.61 | 42.52 | 7.80 | 10.32 |
| Standard Error | 8.74 | 0.07 | 0.04 | 0.11 | 0.14 | 15.46 | 0.69 | 0.23 | 0.53 |
| Median | 125.00 | 2.00 | 1.00 | 2.00 | 8.00 | 47.50 | 42.76 | 7.37 | 10.84 |
| Mode | 20.00 | 2.00 | 1.00 | 1.00 | 8.00 | 40.00 | 33.70 | 5.75 | 3.40 |
| Standard Deviation | 105.59 | 0.90 | 0.50 | 1.30 | 1.68 | 186.75 | 8.30 | 2.79 | 6.35 |
| Sample Variance | 11,149.45 | 0.81 | 0.25 | 1.69 | 2.81 | 34,875.73 | 68.89 | 7.81 | 40.34 |
| Kurtosis | 1.70 | 2.05 | −1.95 | −1.65 | 0.66 | 3.04 | −0.75 | −0.91 | −1.36 |
| Skewness | 1.06 | 1.20 | 0.28 | 0.31 | 0.52 | 2.07 | 0.45 | 0.54 | −0.01 |
| Range | 580.00 | 4.00 | 1.00 | 3.00 | 6.70 | 764.00 | 30.93 | 9.35 | 22.87 |
| Minimum | 20.00 | 1.00 | 1.00 | 1.00 | 6.00 | 20.00 | 32.00 | 3.15 | 0.42 |
| Maximum | 600.00 | 5.00 | 2.00 | 4.00 | 12.70 | 784.00 | 62.93 | 12.50 | 23.29 |
| Count | 146.00 | 146.00 | 146.00 | 146.00 | 146.00 | 146.00 | 146.00 | 146.00 | 146.00 |
| Confidence Level (95.0%) | 17.27 | 0.15 | 0.08 | 0.21 | 0.27 | 30.55 | 1.36 | 0.46 | 1.04 |
| Categorical Input Variable | Property | Code |
|---|---|---|
| Bar Surface (Bs) | Sand-coated (SC) | 1 |
| Ribbed (RB) | 2 | |
| Fibre-wounded (SW) | ||
| SC + SW | 3 | |
| SC + RB | 4 | |
| Failure mode (FM) | Debonding (D) | 1 |
| Pull-out (P) | 2 | |
| Shear failure of concrete (SF) | 3 | |
| FRP rupture (R) | 4 | |
| Splitting of concrete (S) | 5 | |
| Type of FRP | GFRP | 1 |
| BFRP | 2 |
| Trial No. | Used Variables | No. of Chromosomes | Head Size | Number of Genes | Constants per Gene | No. of Literals | Program Size | Training Dataset | Validation Dataset | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Best Fitness | RMSE | MAE | R2 | R | Best Fitness | RMSE | MAE | R2 | R | ||||||||
| 1 | 8 | 30 | 8 | 3 | 10 | 17 | 41 | 249.7 | 3.004 | 2.326 | 0.764 | 0.874 | 198.550 | 4.036 | 3.197 | 0.626 | 0.791 |
| 2 | 8 | 50 | 8 | 3 | 10 | 15 | 42 | 245.3 | 3.076 | 2.442 | 0.749 | 0.865 | 229.980 | 3.348 | 2.750 | 0.754 | 0.868 |
| 3 | 8 | 100 | 8 | 3 | 10 | 15 | 35 | 241.9 | 3.133 | 2.430 | 0.741 | 0.861 | 204.770 | 3.883 | 3.136 | 0.653 | 0.808 |
| 4 | 7 | 150 | 8 | 3 | 10 | 13 | 41 | 307.9 | 2.248 | 1.580 | 0.866 | 0.931 | 265.820 | 2.762 | 1.876 | 0.823 | 0.907 |
| 5 | 8 | 200 | 8 | 3 | 10 | 16 | 37 | 236.8 | 3.223 | 2.649 | 0.725 | 0.851 | 205.790 | 3.859 | 3.152 | 0.693 | 0.832 |
| 6 | 8 | 150 | 9 | 3 | 10 | 20 | 47 | 261.5 | 2.820 | 2.188 | 0.790 | 0.889 | 207.110 | 3.820 | 3.040 | 0.767 | 0.876 |
| 7 | 8 | 150 | 10 | 3 | 10 | 19 | 45 | 226.4 | 3.417 | 2.617 | 0.691 | 0.831 | 177.080 | 4.647 | 3.647 | 0.521 | 0.722 |
| 8 | 8 | 150 | 11 | 3 | 10 | 16 | 45 | 270.8 | 2.692 | 2.071 | 0.807 | 0.898 | 203.860 | 3.905 | 3.186 | 0.647 | 0.804 |
| 9 | 8 | 150 | 12 | 3 | 10 | 16 | 55 | 330.2 | 2.028 | 1.567 | 0.892 | 0.944 | 286.760 | 2.487 | 2.148 | 0.862 | 0.928 |
| 10 | 7 | 150 | 8 | 4 | 10 | 25 | 65 | 323.9 | 2.087 | 1.620 | 0.885 | 0.941 | 296.750 | 2.370 | 2.046 | 0.875 | 0.935 |
| 11 | 7 | 150 | 8 | 5 | 10 | 20 | 83 | 261.0 | 2.830 | 2.314 | 0.787 | 0.887 | 230.950 | 3.329 | 2.750 | 0.763 | 0.873 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, M.N.; Iqbal, M.; Althoey, F.; Khan, K.; Faraz, M.I.; Qadir, M.G.; Alabdullah, A.A.; Ajwad, A. Investigating the Bond Strength of FRP Rebars in Concrete under High Temperature Using Gene-Expression Programming Model. Polymers 2022, 14, 2992. https://doi.org/10.3390/polym14152992
Amin MN, Iqbal M, Althoey F, Khan K, Faraz MI, Qadir MG, Alabdullah AA, Ajwad A. Investigating the Bond Strength of FRP Rebars in Concrete under High Temperature Using Gene-Expression Programming Model. Polymers. 2022; 14(15):2992. https://doi.org/10.3390/polym14152992
Chicago/Turabian StyleAmin, Muhammad Nasir, Mudassir Iqbal, Fadi Althoey, Kaffayatullah Khan, Muhammad Iftikhar Faraz, Muhammad Ghulam Qadir, Anas Abdulalim Alabdullah, and Ali Ajwad. 2022. "Investigating the Bond Strength of FRP Rebars in Concrete under High Temperature Using Gene-Expression Programming Model" Polymers 14, no. 15: 2992. https://doi.org/10.3390/polym14152992
APA StyleAmin, M. N., Iqbal, M., Althoey, F., Khan, K., Faraz, M. I., Qadir, M. G., Alabdullah, A. A., & Ajwad, A. (2022). Investigating the Bond Strength of FRP Rebars in Concrete under High Temperature Using Gene-Expression Programming Model. Polymers, 14(15), 2992. https://doi.org/10.3390/polym14152992







