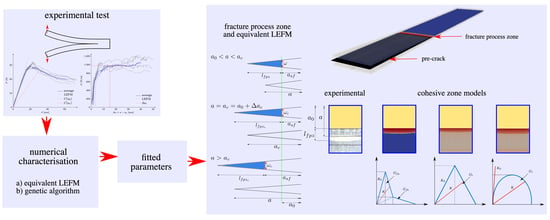
Simulation of Mode I Interlaminar Damage of a GFRP Composite Using Cohesive Laws in the Framework of the Equivalent LEFM R-Curve and an Optimised Algorithm
Abstract
1. Introduction
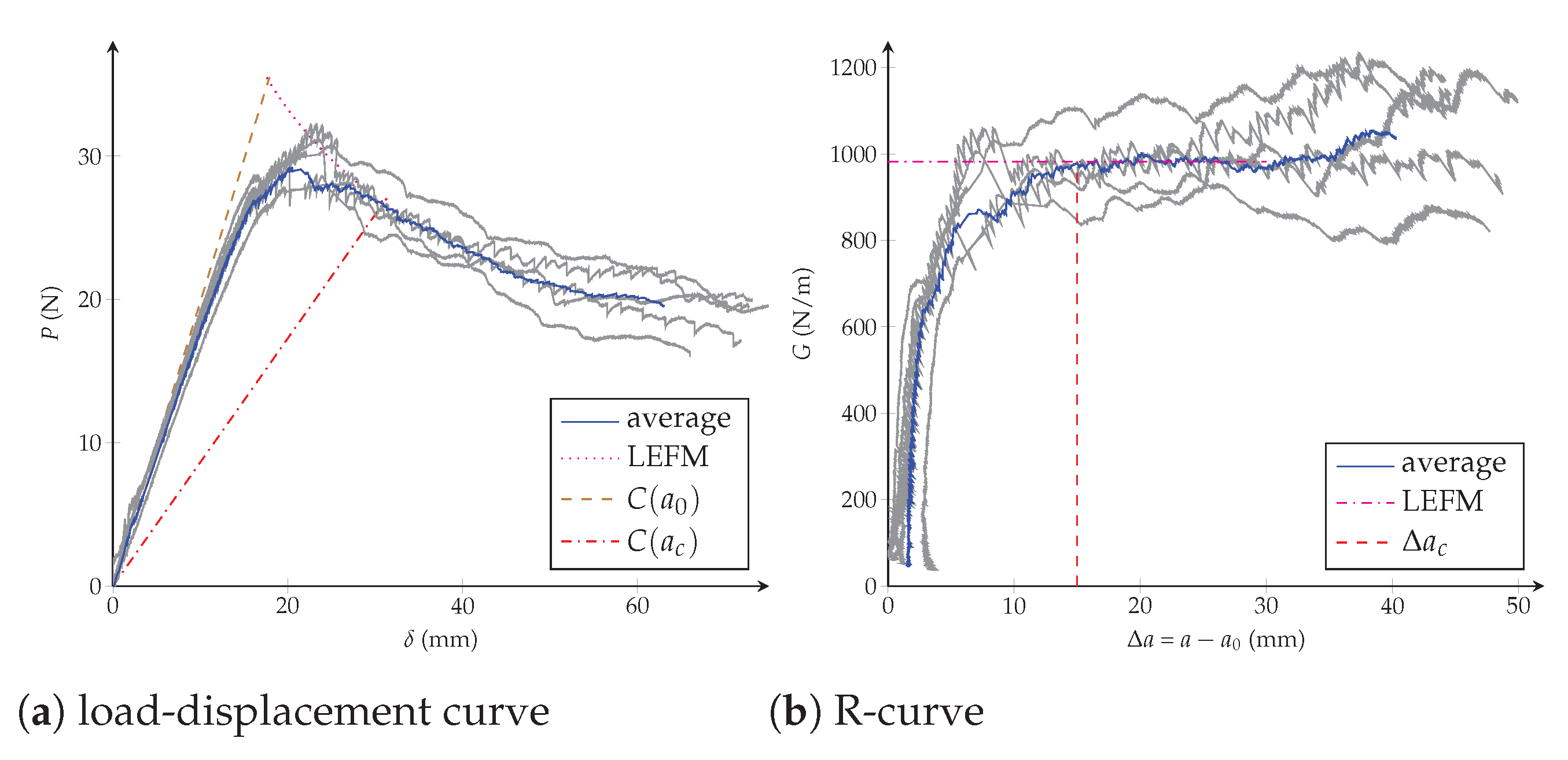
2. Experimental Test
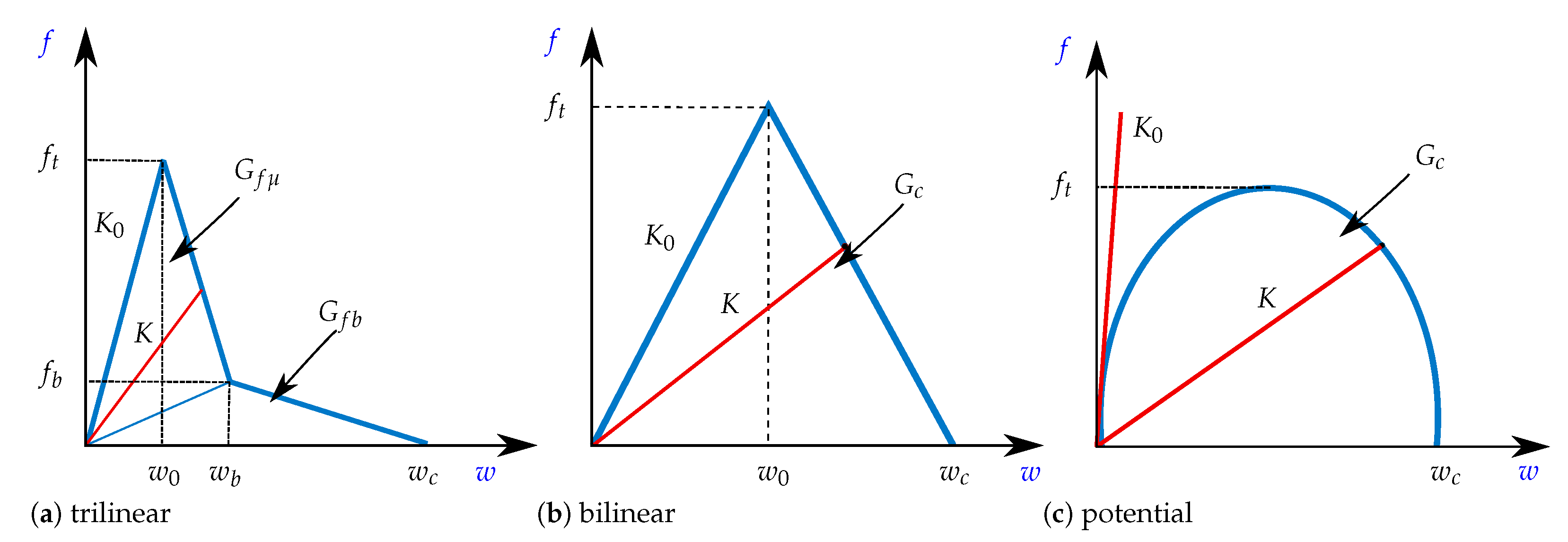
3. Cohesive Zone Models
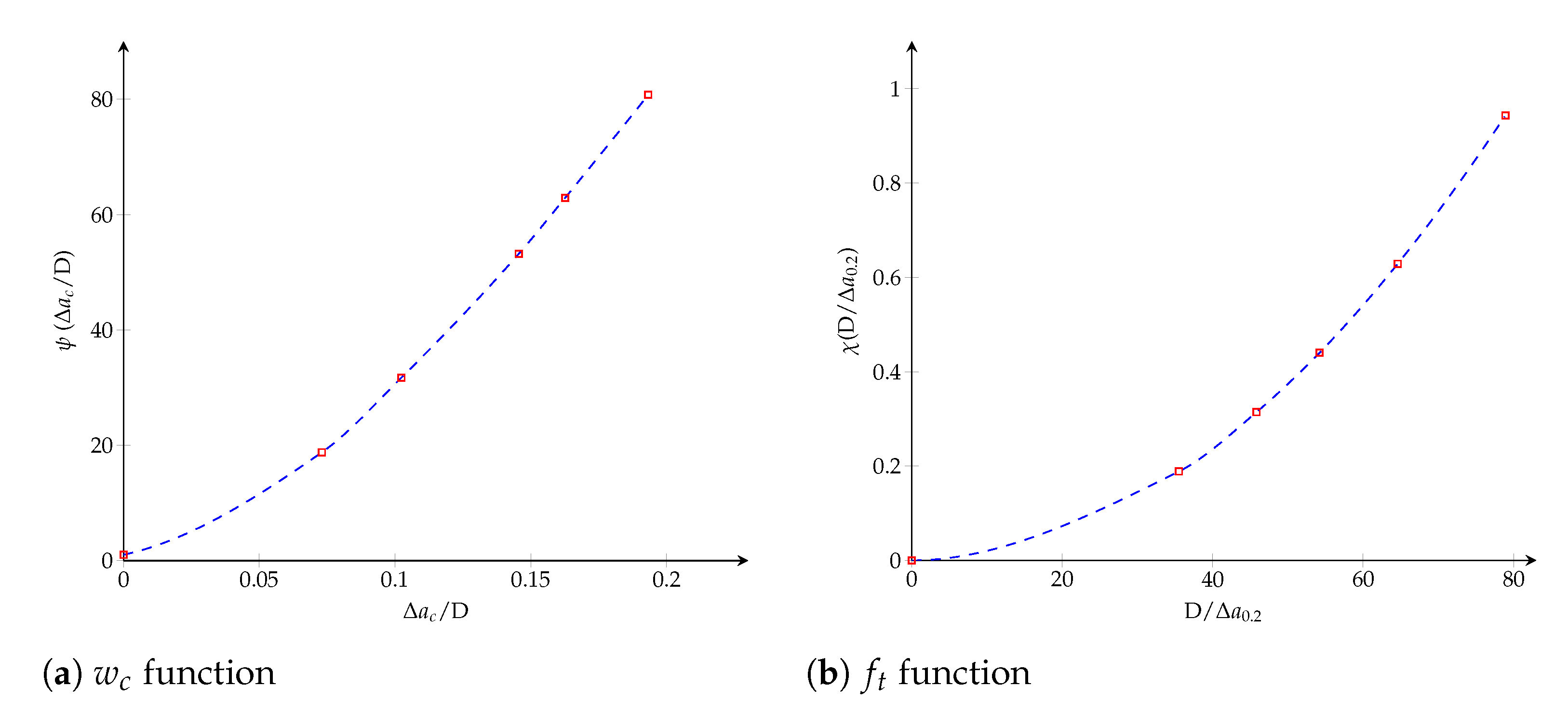
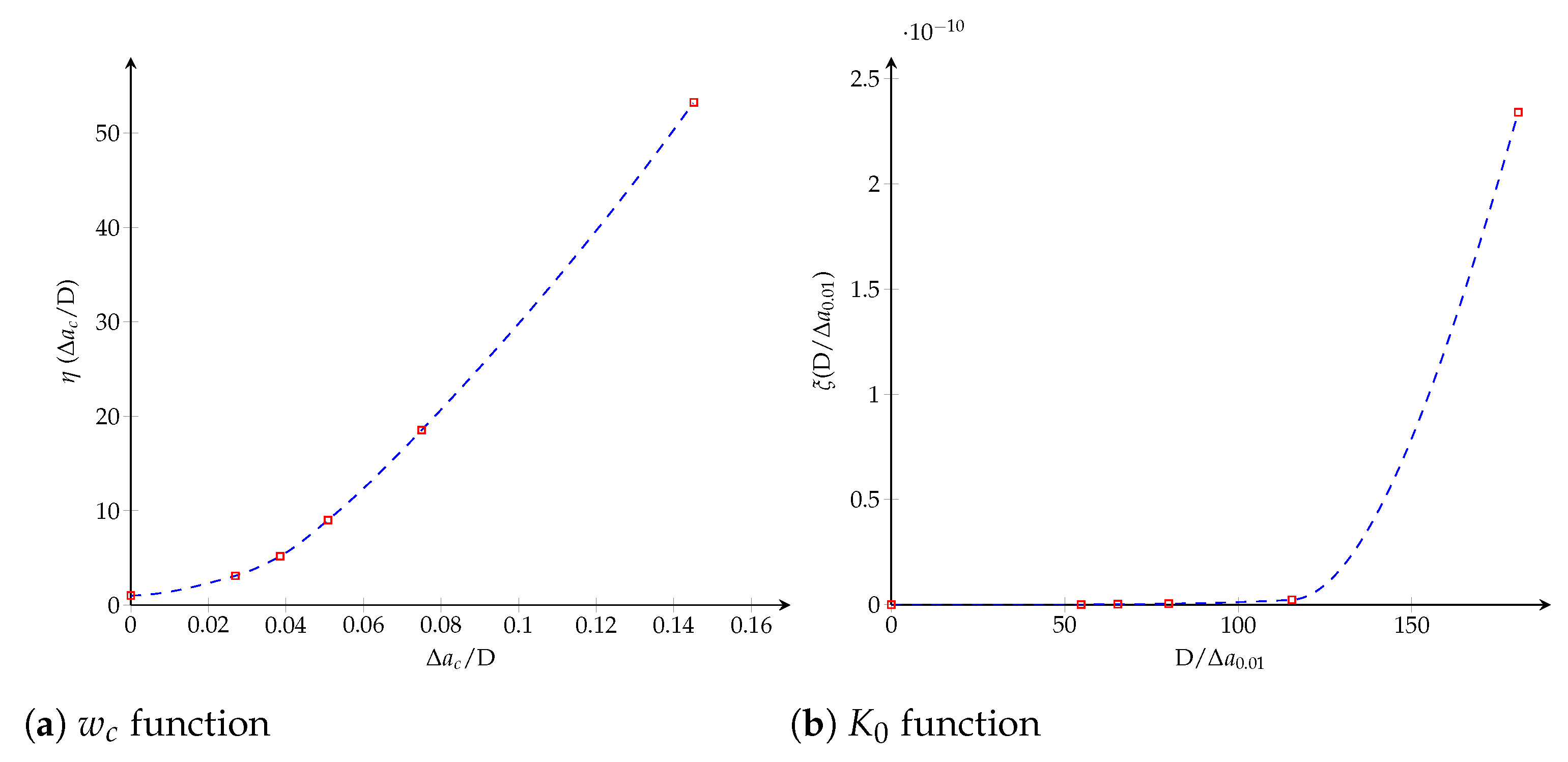
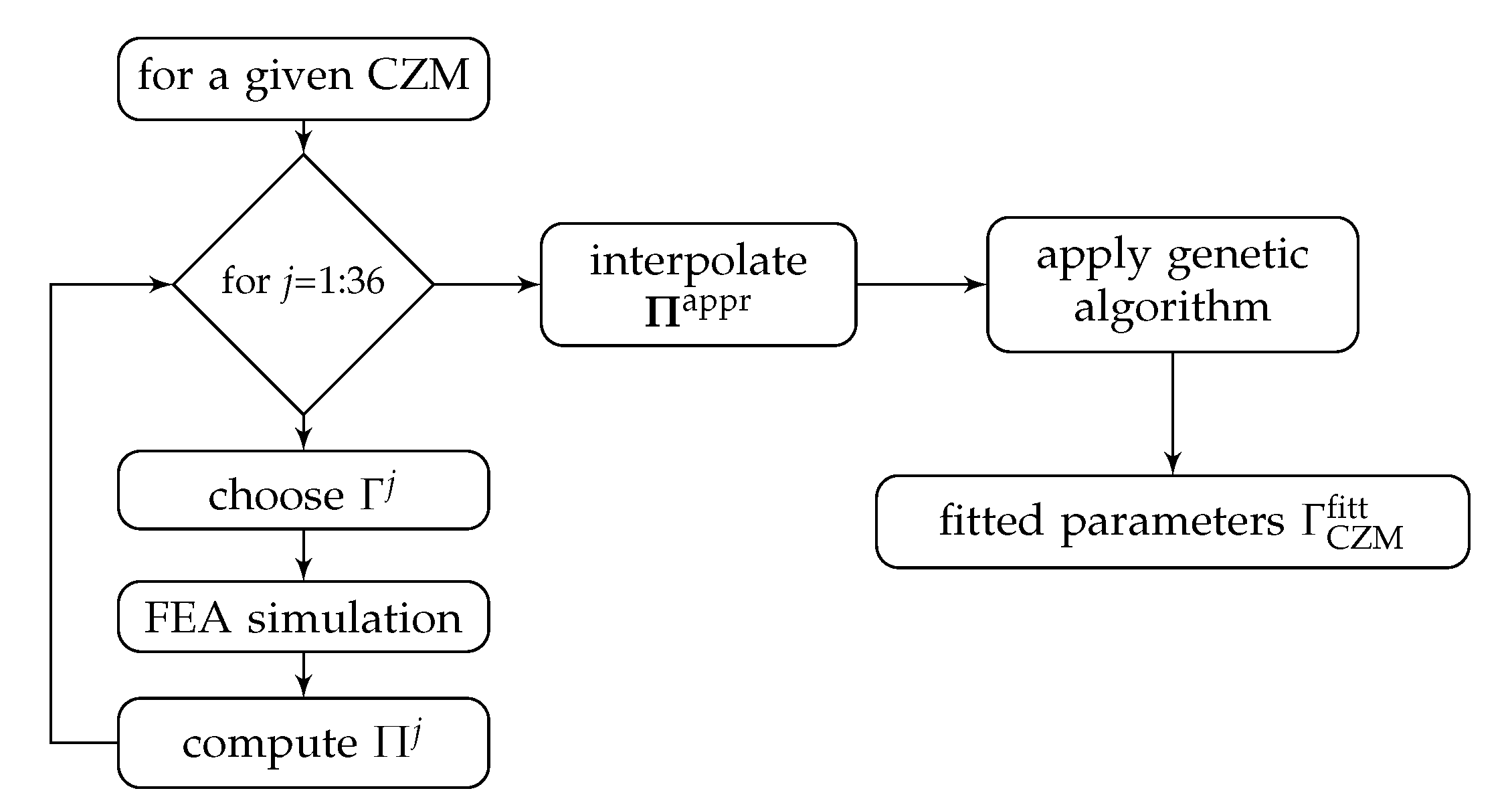
4. CZM Characterization Using the Equivalent LEFM R-Curve
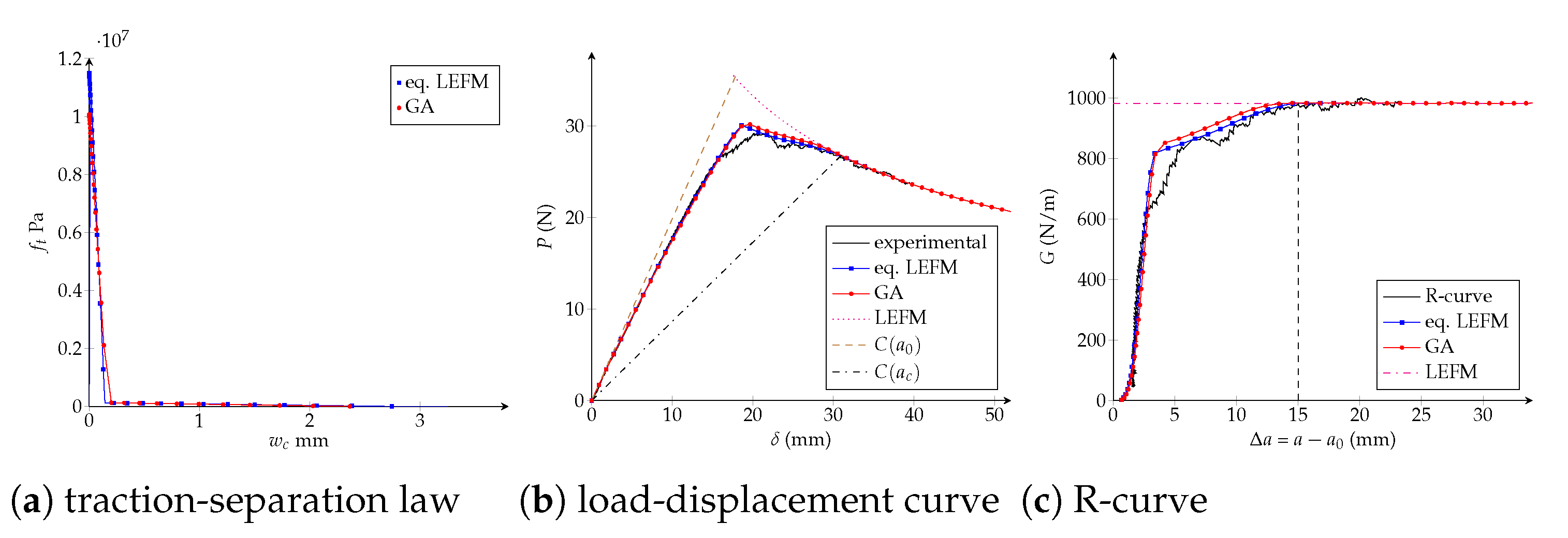
4.1. Trilinear CZM
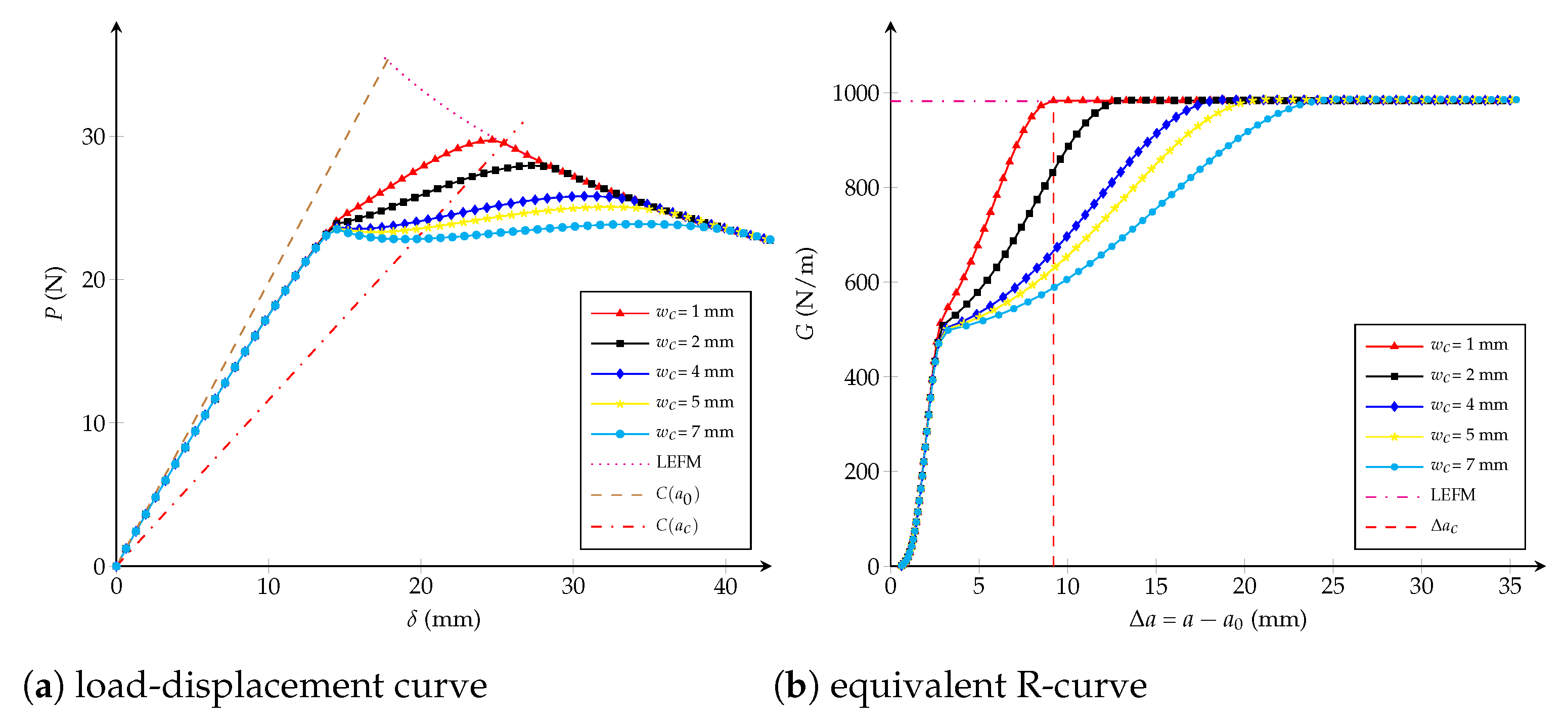
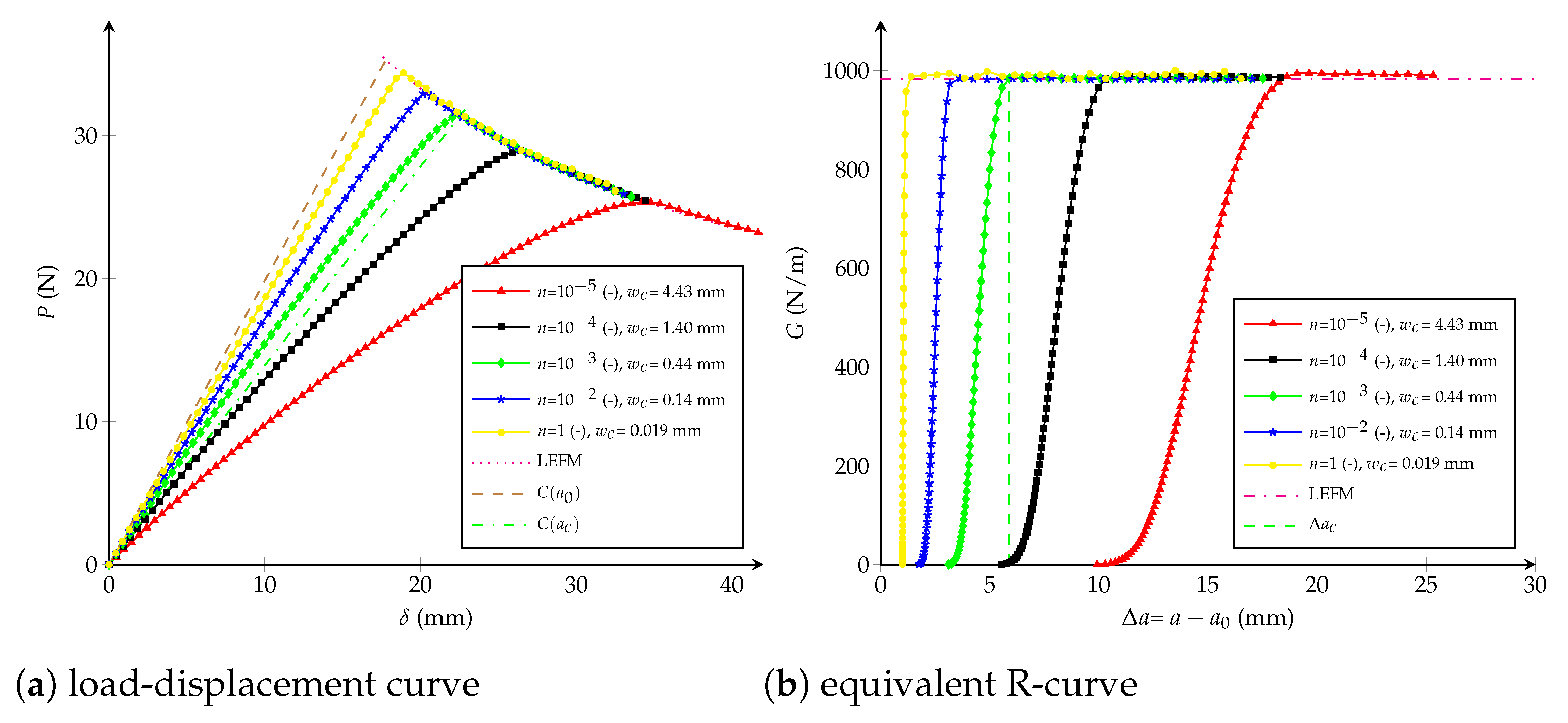
- Influence of the critical opening: numerical simulations are carried out affecting the critical opening mm but fixing the values (-) and Pa. From Figure 6, it is observed that does not have an influence before reaching the 50% of . After that, the critical crack extension and the critical displacement jump have a positive correlation, which means that the length of the fracture process zone increases when increases.
- Influence of the fracture energy distribution: keeping constant Pa and mm, Figure 7 shows that at varying the critical energy release rate (-), the load-displacement plot and the equivalent LEFM R-curve are invariable if the dissipated energies are lower than , respectively. If the ratio tends to one, the R-curve look like a one of a brittle material and the maximal load on the load-displacement curve increases. The critical crack extension always remains the same.
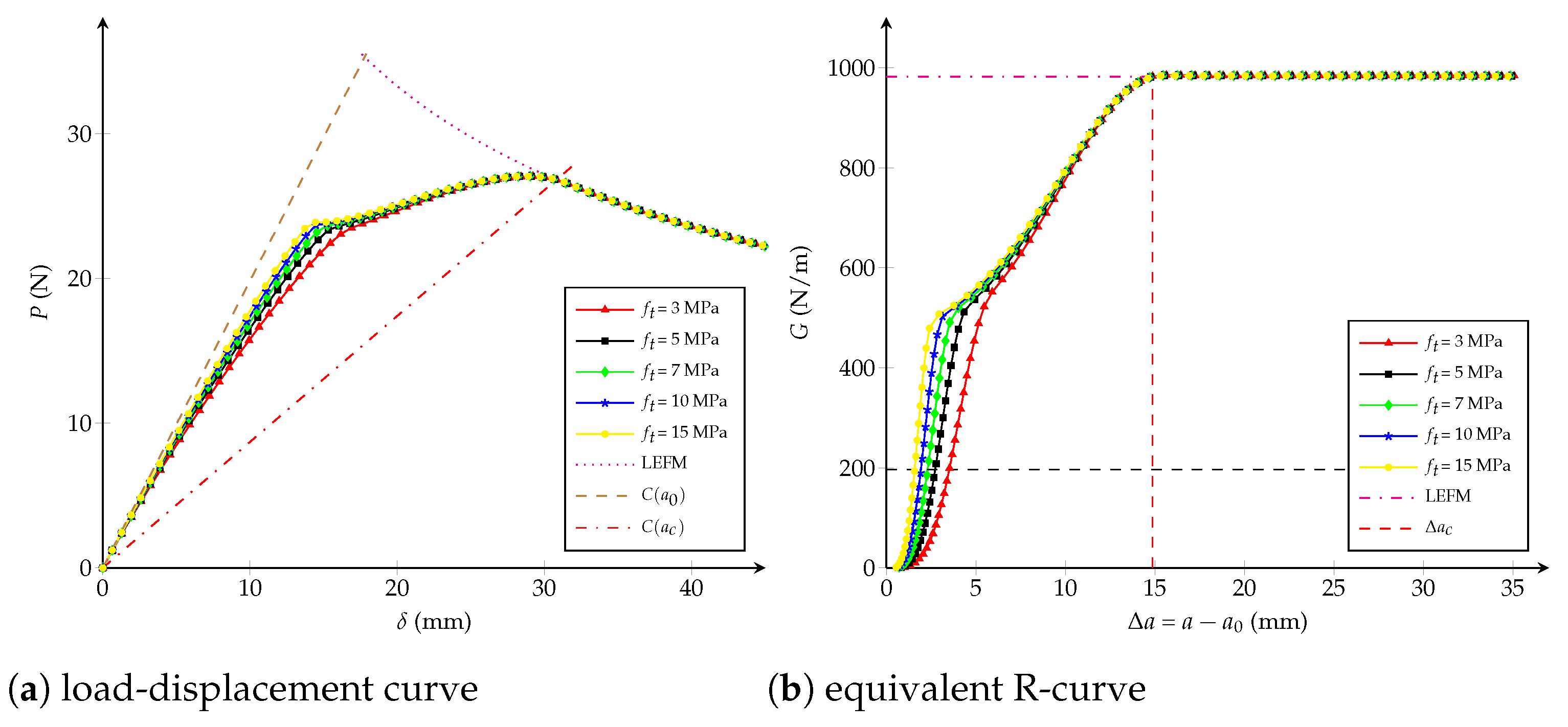
- Influence of the tensile strength: Figure 8 shows the impact at varying [ Pa] whereas (-) and mm are unchanged. It can be concluded that the tensile strength impacts the response at the beginning of both curves: if increases, the behaviour becomes a brittle one. When the dissipated energy reaches the value , the fracture response starts to be the same for any value of and the critical crack extension becomes identical.

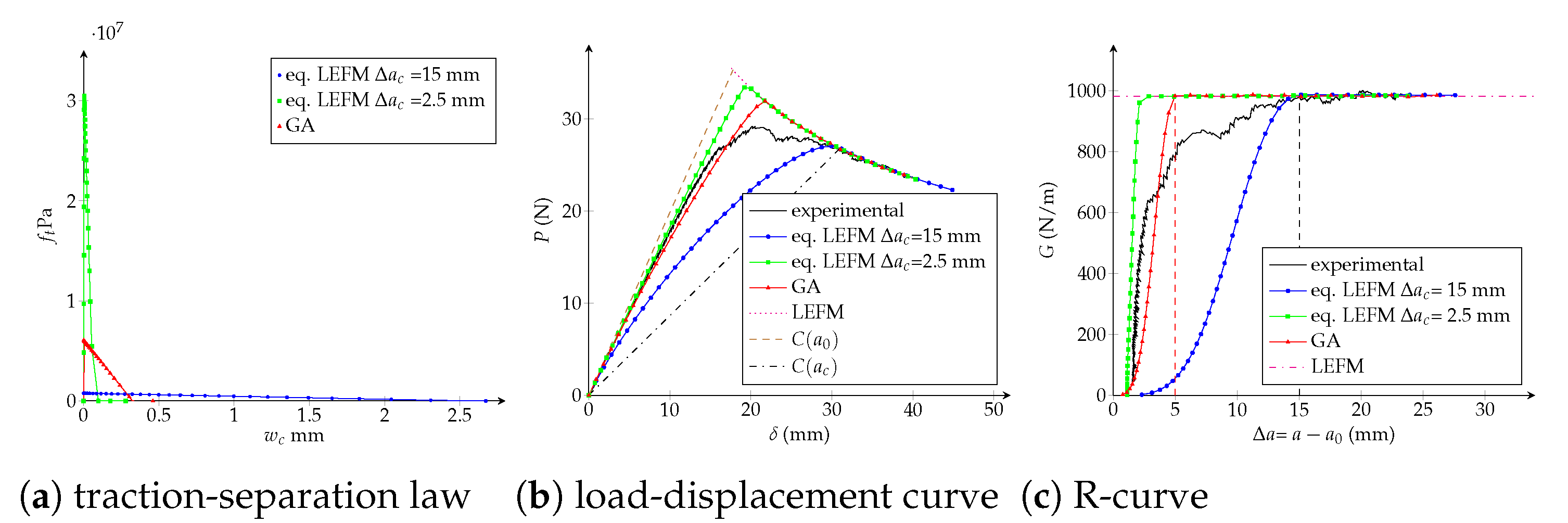
4.2. Bilinear CZM
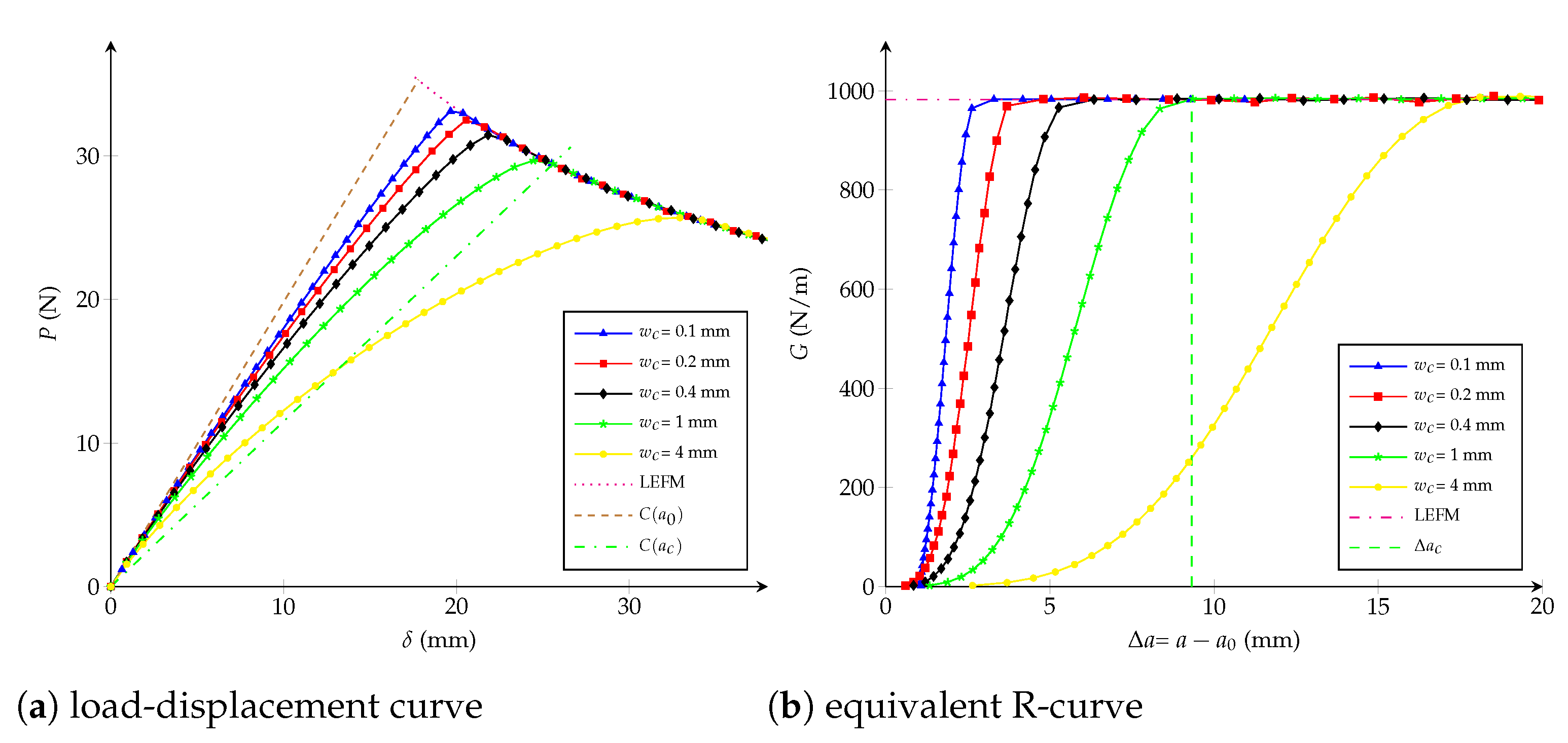
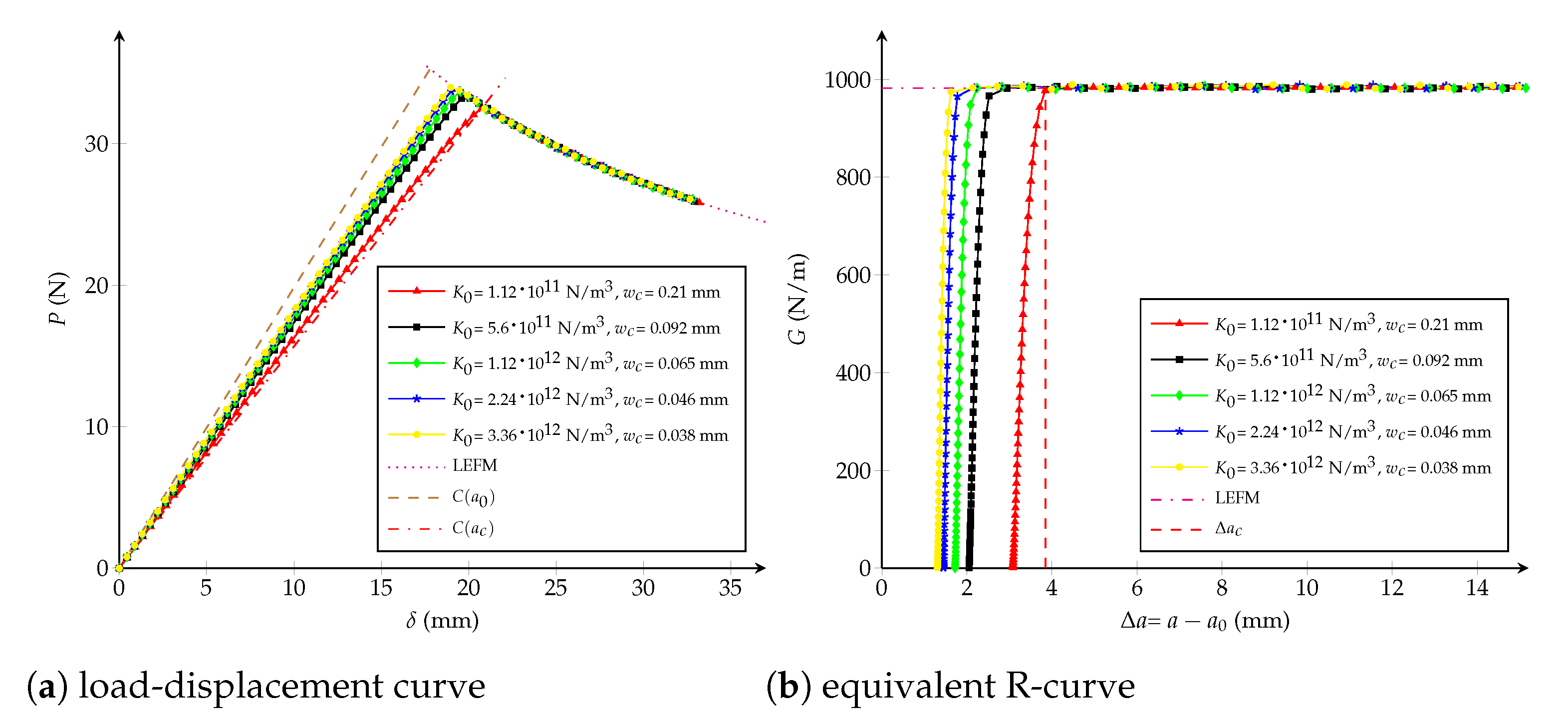
- Influence of the critical opening: has an inverse correlation with the maximal applied load P when considering mm and keeping unchanged N/m, as observed in Figure 10a. Moreover, Figure 10b shows that the critical crack extension is inversely proportional to the tensile strength , i.e., the interface becomes more brittle for higher values of .
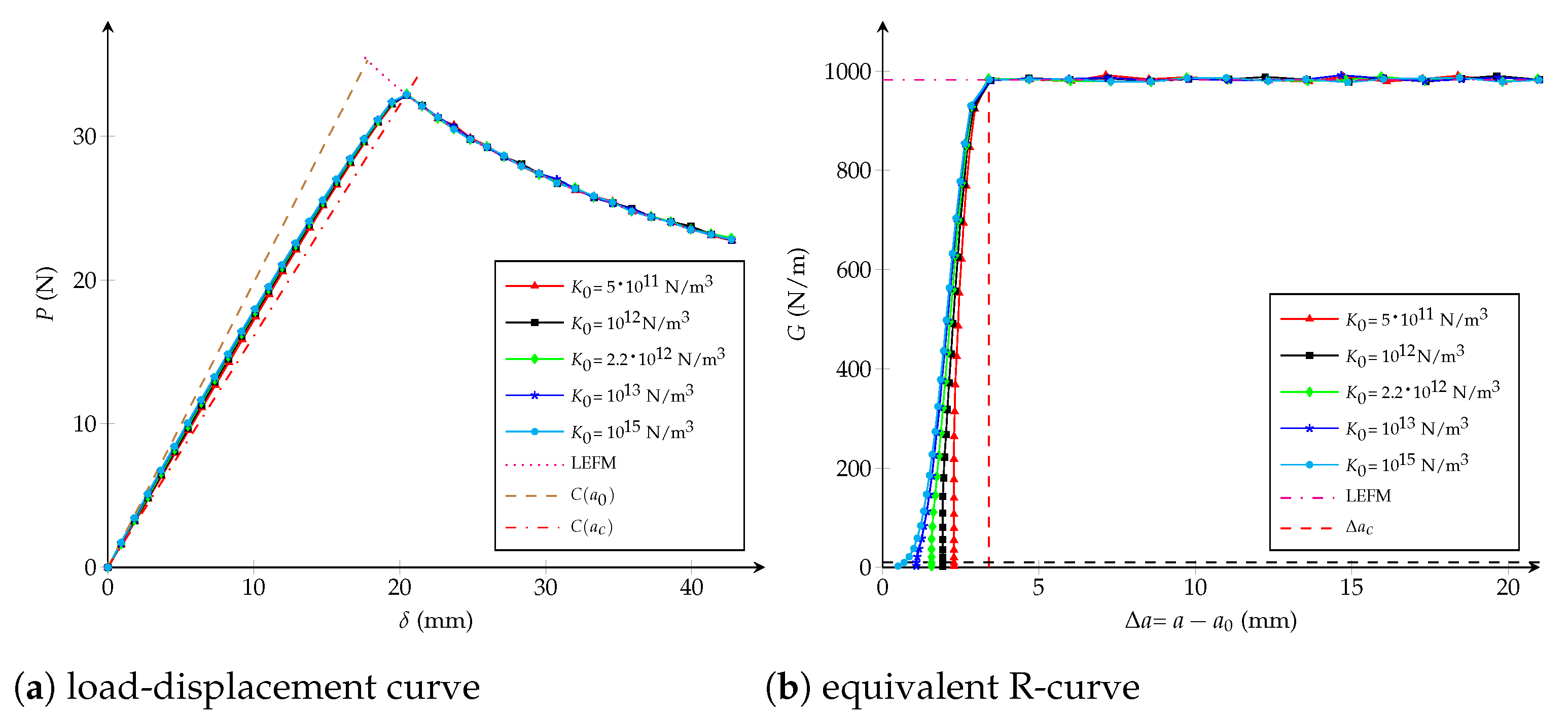
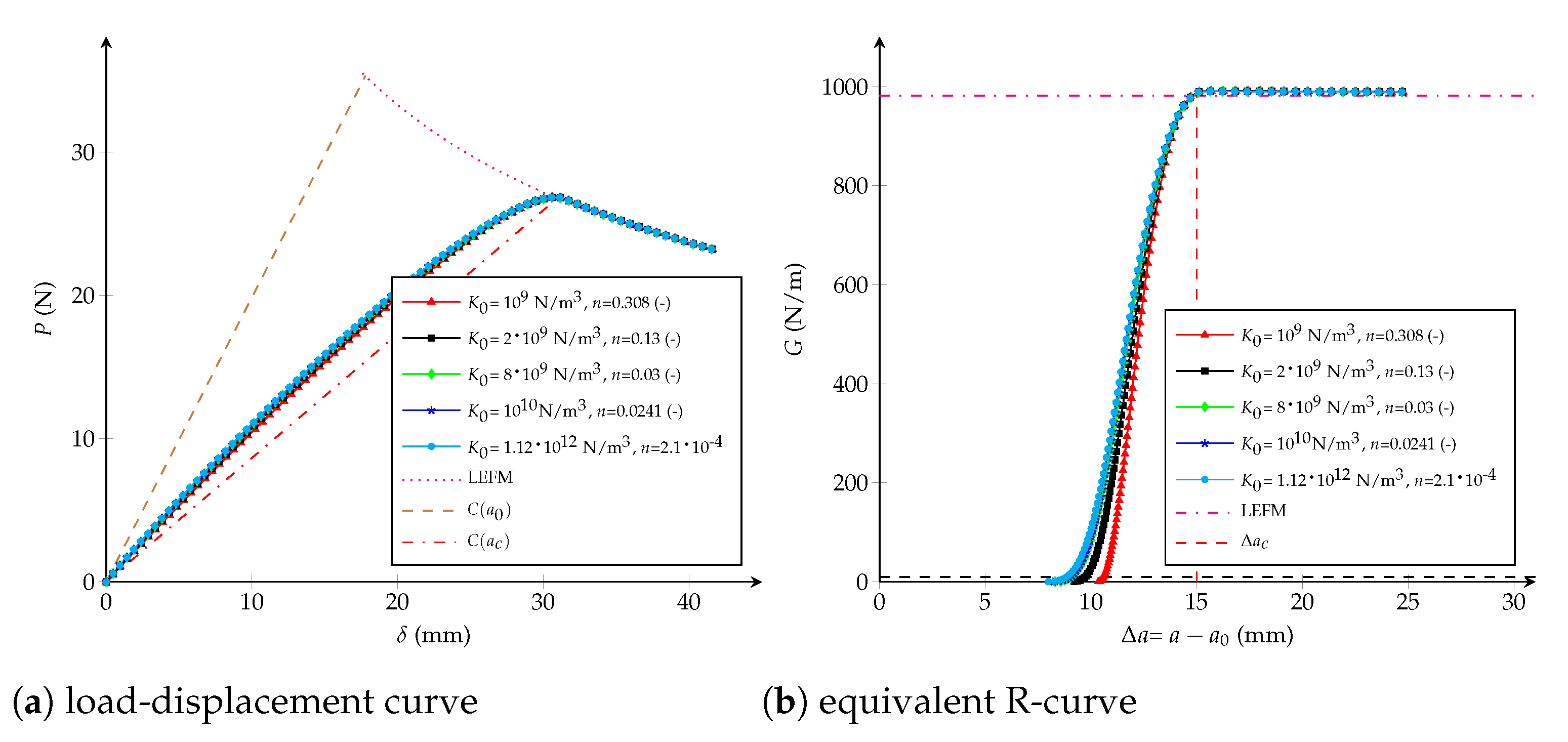
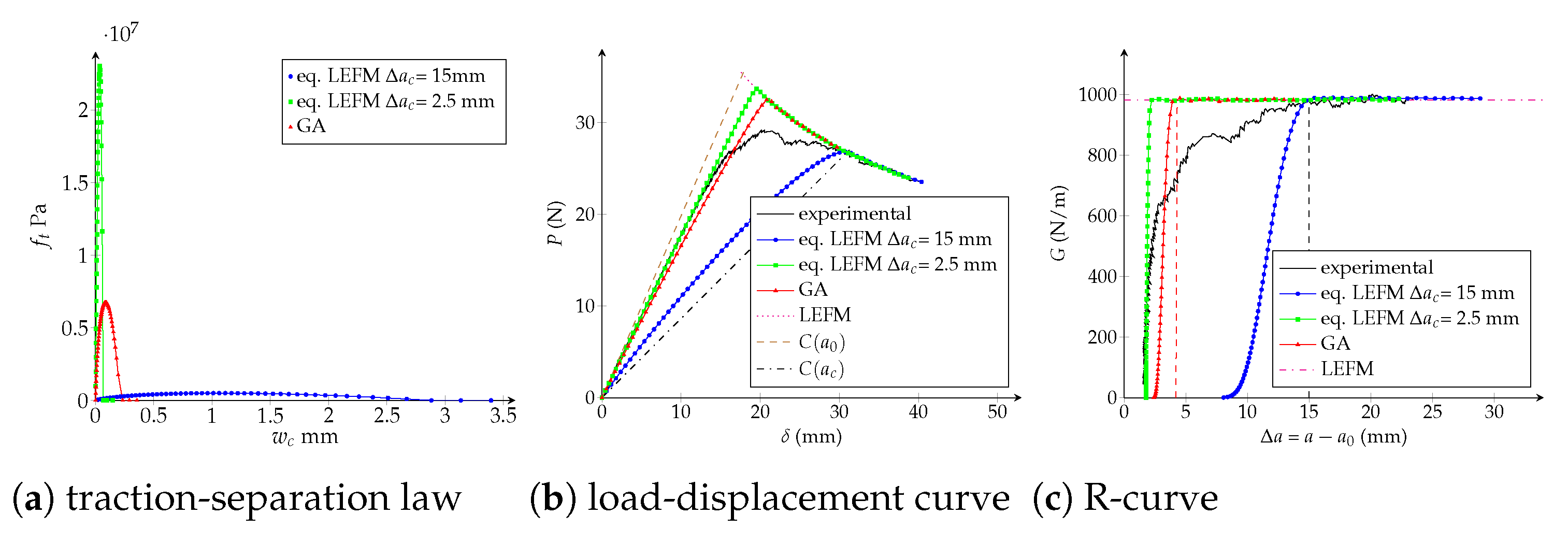
4.3. Potential CZM
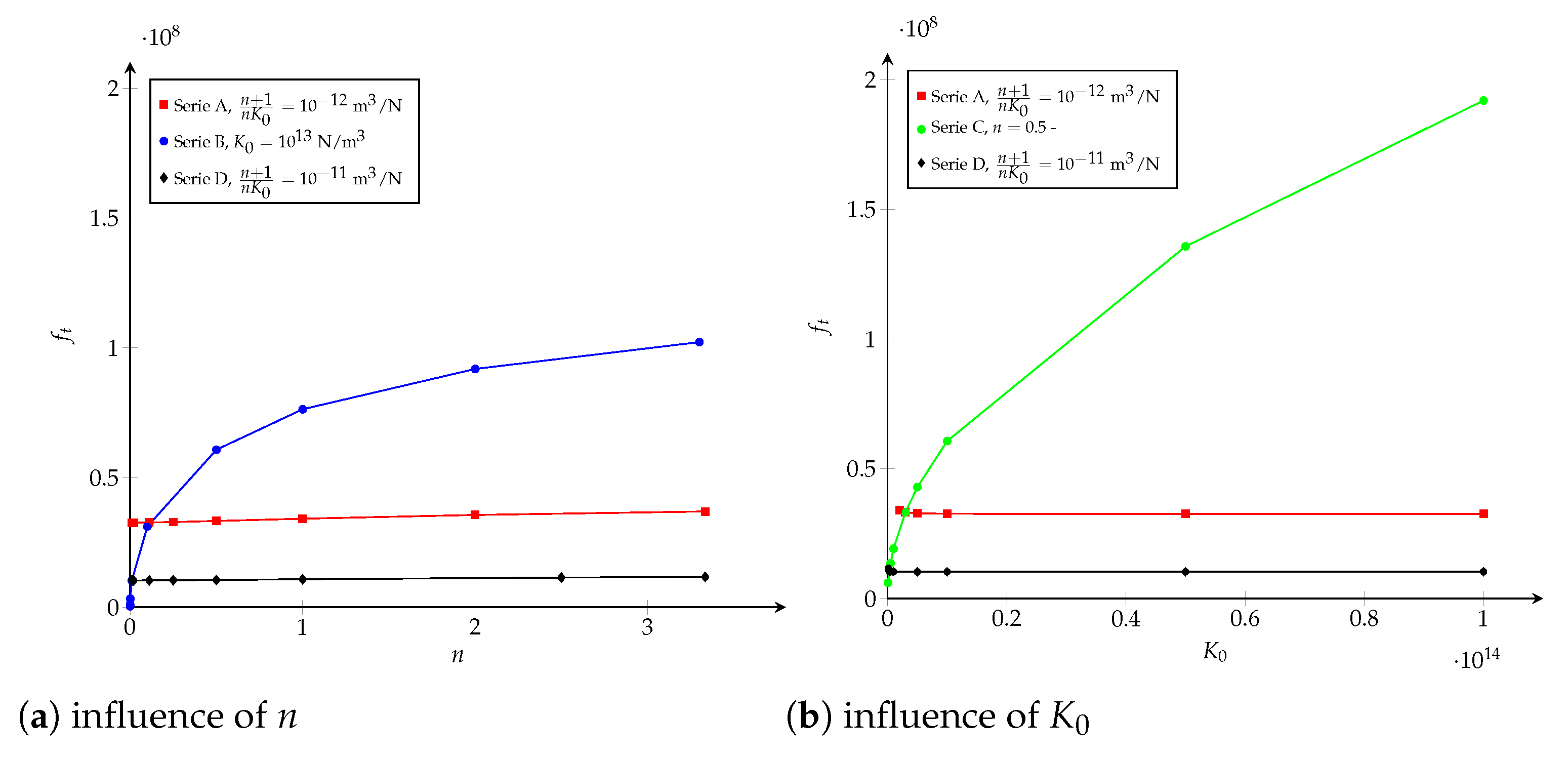
- Influence of and n: when the critical opening is kept constant and equals to mm (or m/N), but modifying N/m and (-), the critical extension crack remains unchanged, as shown in Figure 16b. n and only have an influence in the beginning of the R-curve, while the load-displacement plot is almost the same.
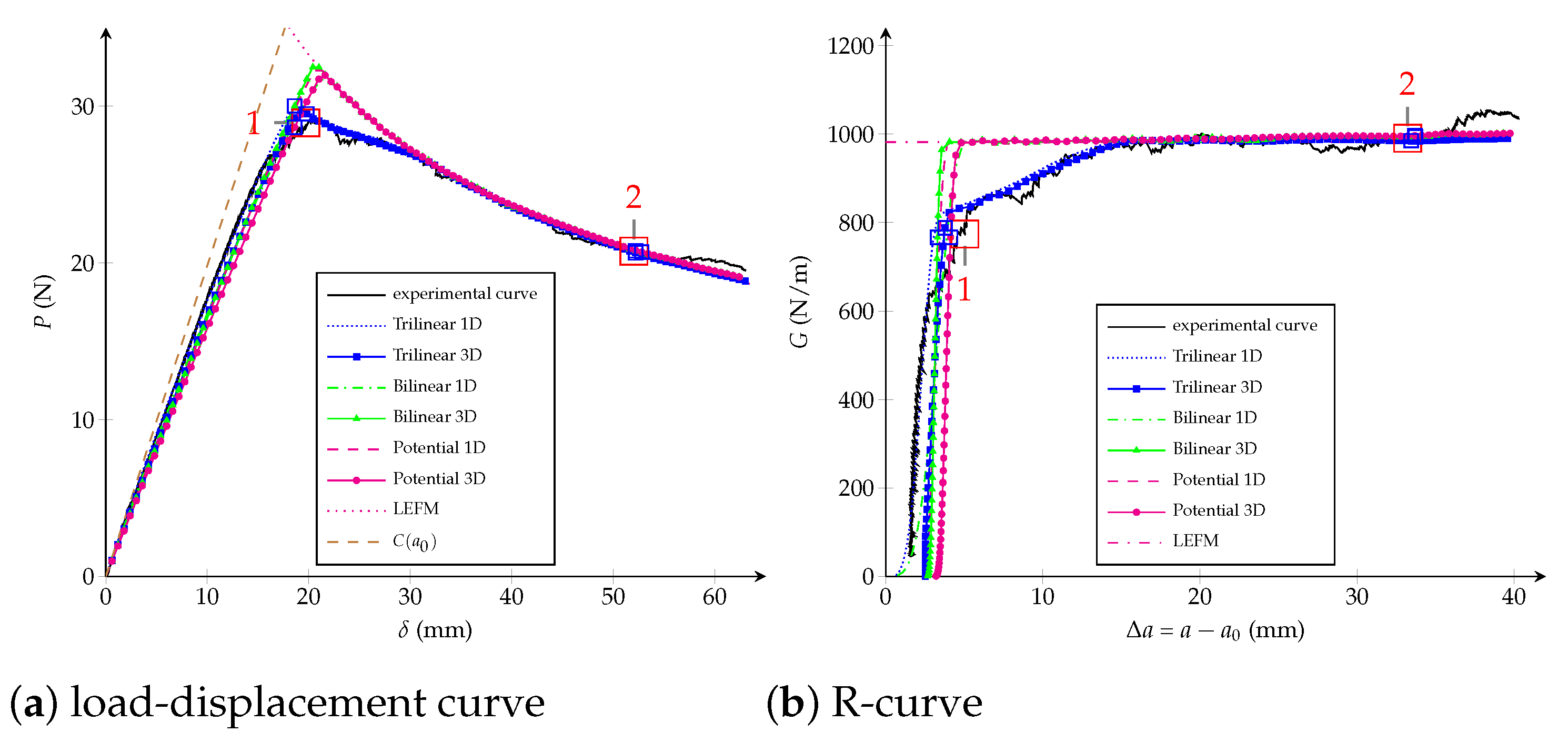
5. Comparison of the CZM Characterization
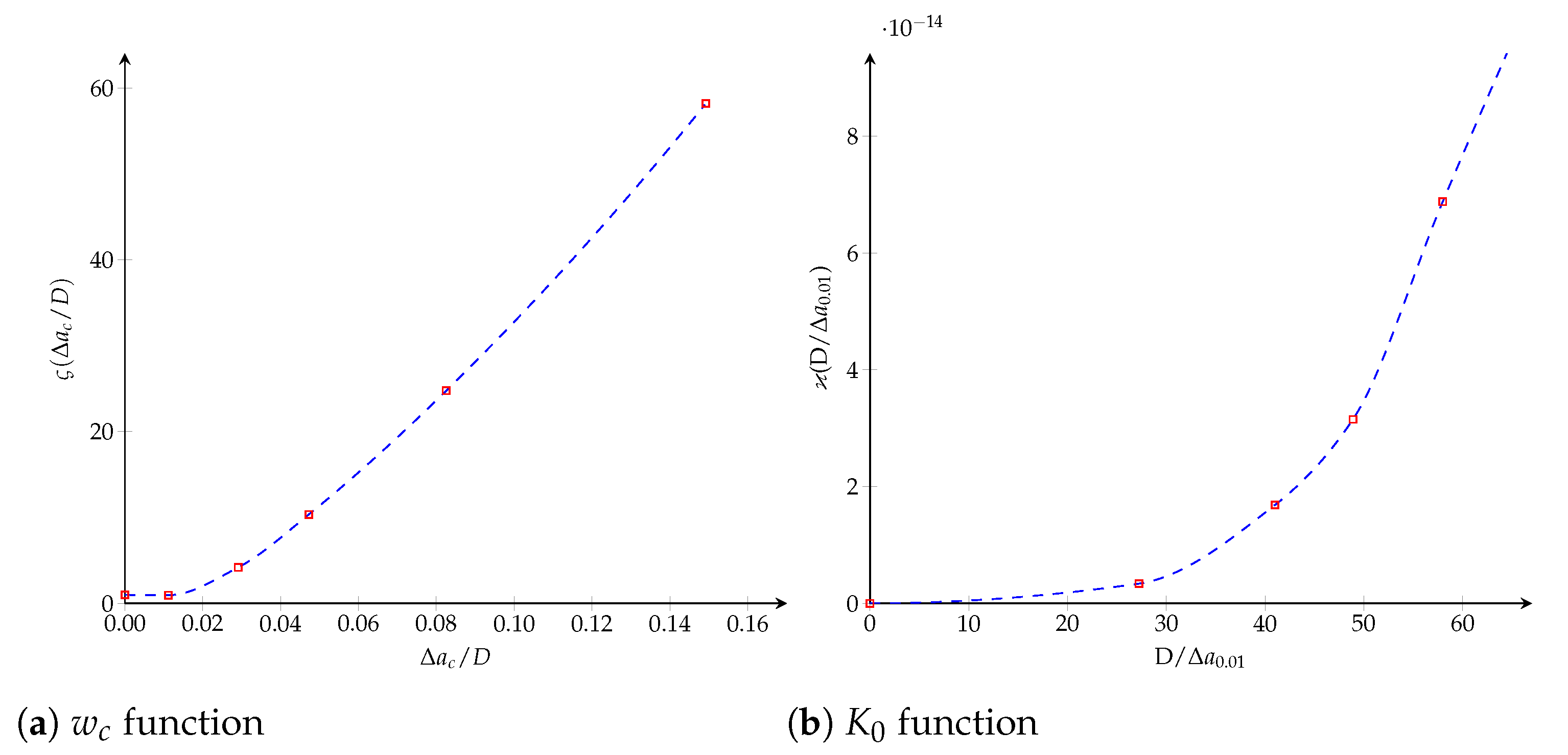
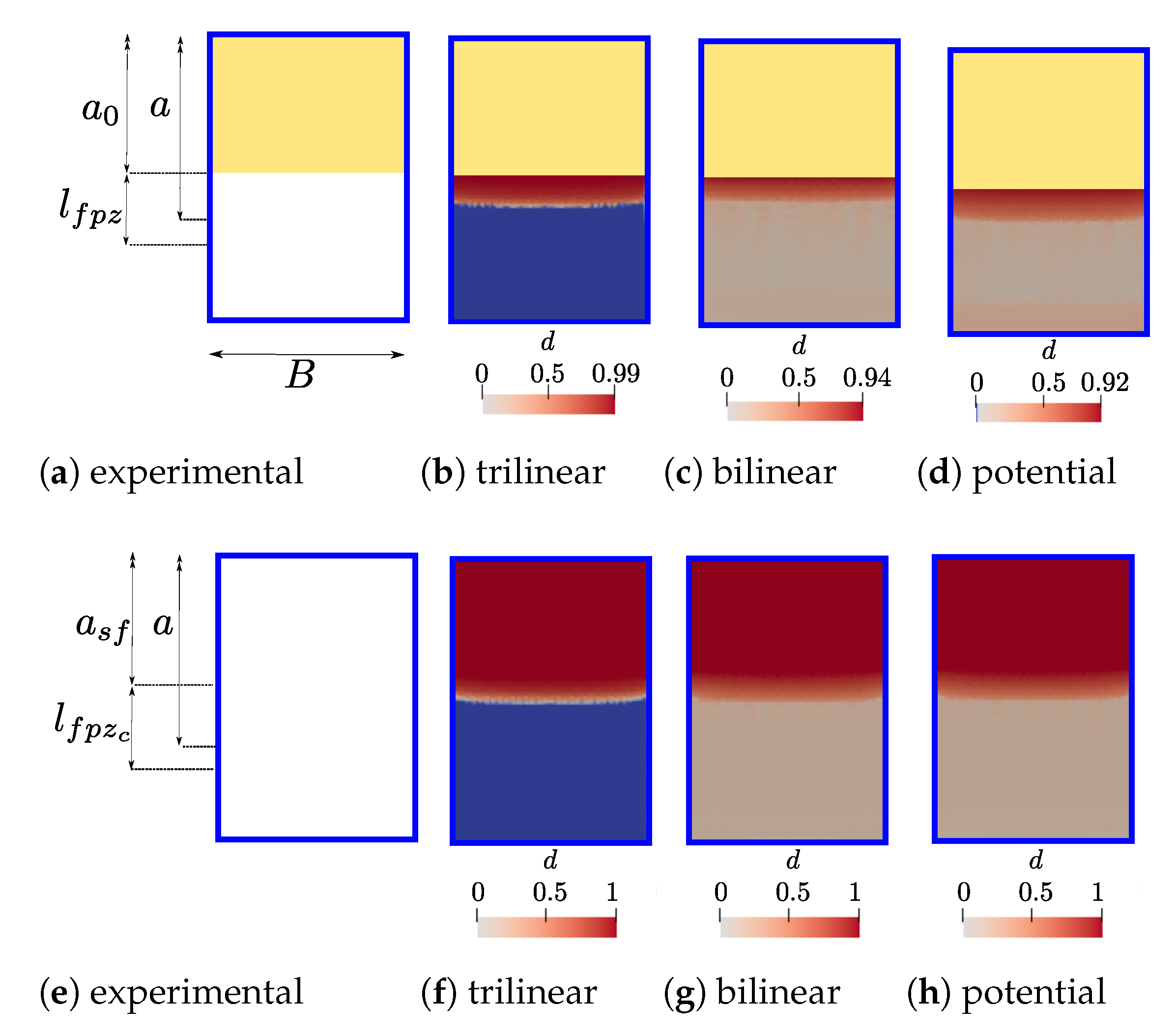
6. 3D Fracture Process Zone (FPZ)
7. Conclusions
- it is possible to characterise a bilinear and a potential CZM using a framework based on the equivalent LEFM R-curve;
- for the linear, bilinear and potential CZM, the parameters’ identification based on the equivalent LEFM R-curve enables the same accuracy but reduces 72% the numerical efforts respect to a “blind fitting” which minimise the residual between experimental and numerical load-displacement curves;
- when applying the equivalent LEFM R-curve framework for characterising a quasibrittle GFRP, the trilinear law achieves the best adjustment which is also proven comparing 3D simulations of the fracture process zones. However, it is expected that a trilinear CZM fits materials with large FPZ better than bilinear and potential models. Latter will be fully exploited when characterising more brittle materials;
- finally, even if optimisation techniques become popular at present due to their easy numerical implementation, strategies founded on physical models are still better solutions especially when evaluating the objective function is expensive as in mechanical problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| (N/m) | n (-) | (m/N) | (m) | (Pa) | |
|---|---|---|---|---|---|
| 1 | 0.01 | 1 | 4.43 | 3.26 | |
| 5 | 0.02 | 1 | 4.43 | 3.26 | |
| 1 | 0.11 | 1 | 4.43 | 3.27 | |
| serie A | 5 | 0.25 | 1 | 4.43 | 3.28 |
| 3 | 0.5 | 1 | 4.43 | 3.32 | |
| 2 | 1 | 1 | 4.43 | 3.41 | |
| 1.5 | 2 | 1 | 4.43 | 3.56 | |
| 1.3 | 3.3 | 1 | 4.43 | 3.69 | |
| 1 | 2 | 1.5 | 1.72 | 9.18 | |
| 1 | 1 | 2 | 1.98 | 7.63 | |
| 1 | 0.5 | 3 | 2.43 | 6.07 | |
| serie B | 1 | 0.1 | 1.1 | 4.65 | 3.11 |
| 1 | 0.01 | 1 | 1.41 | 1.03 | |
| 1 | 0.001 | 1 | 4.43 | 3.26 | |
| 1 | 0.0001 | 1 | 1.4 | 1.03 | |
| 1 | 0.00001 | 1 | 4.43 | 3.26 | |
| 1 | 0.5 | 3 | 7.68 | 1.92 | |
| 5 | 0.5 | 6 | 1.09 | 1.36 | |
| 1 | 0.5 | 3 | 2.43 | 6.07 | |
| serie C | 5 | 0.5 | 6 | 3.43 | 4.29 |
| 3 | 0.5 | 1 | 4.43 | 3.32 | |
| 1 | 0.5 | 3 | 7.68 | 1.92 | |
| 5 | 0.5 | 6 | 1.09 | 1.36 | |
| 1 | 0.5 | 3 | 2.43 | 6.07 | |
| 1 | 0.001 | 1 | 1.40 | 1.03 | |
| 5 | 0.002 | 1 | 1.40 | 1.03 | |
| 1 | 0.0101 | 1 | 1.40 | 1.03 | |
| serie D | 5 | 0.0204 | 1 | 1.40 | 1.03 |
| 1 | 0.111 | 1 | 1.40 | 1.03 | |
| 5 | 0.25 | 1 | 1.40 | 1.04 | |
| 3 | 0.5 | 1 | 1.40 | 1.05 | |
| 2 | 1 | 1 | 1.40 | 1.08 |
References
- González, C.; Vilatela, J.; Molina-Aldareguía, J.; Lopes, C.; LLorca, J. Structural composites for multifunctional applications: Current challenges and future trends. Prog. Mater. Sci. 2017, 89, 194–251. [Google Scholar] [CrossRef]
- Tabiei, A.; Zhang, W. Composite Laminate Delamination Simulation and Experiment: A Review of Recent. Appl. Mech. Rev. 2018, 70, 030801. [Google Scholar] [CrossRef]
- Fish, J.E. Multiscale Methods: Bridging the Scales in Science and Engineering; OUP Oxford: Oxford, UK, 2009. [Google Scholar]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- LLorca, J.; González, C.; Molina-Aldareguía, J.M.; Lópes, C.S. Multiscale Modeling of Composites: Toward Virtual Testing … and Beyond. JOM 2013, 65, 215–225. [Google Scholar] [CrossRef]
- Okereke, M.; Akpoyomare, A.; Bingley, M. Virtual testing of advanced composites, cellular materials and biomaterials: A review. Compos. Part B Eng. 2014, 60, 637–662. [Google Scholar] [CrossRef]
- Bouvet, C.; Castanié, B.; Bizeul, M.; Barrau, J. Low velocity impact modelling in laminate composite panels with discrete interface elements. Int. J. Solids Struct. 2009, 46, 2809–2821. [Google Scholar] [CrossRef]
- Pakdel, H.; Mohammadi, B. Stiffness degradation of composite laminates due to matrix cracking and induced delamination during tension-tension fatigue. Eng. Fract. Mech. 2019, 216, 106489. [Google Scholar] [CrossRef]
- Green, B.; Wisnom, M.; Hallett, S. An experimental investigation into the tensile strength scaling of notched composites. Compos. Part A Appl. Sci. Manuf. 2007, 38, 867–878. [Google Scholar] [CrossRef]
- Sridharan, S. (Ed.) Delamination Behaviour of Composites; Series in Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2008. [Google Scholar]
- Wisnom, M.R. The role of delamination in failure of fibre-reinforced composites. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 1850–1870. [Google Scholar] [CrossRef] [PubMed]
- Jäger, S.; Pickett, A.; Middendorf, P. A Discrete Model for Simulation of Composites Plate Impact Including Coupled Intra- and Inter-ply Failure. Appl. Compos. Mater. 2016, 23, 179–195. [Google Scholar] [CrossRef]
- Saavedra, K.; Allix, O.; Gosselet, P.; Hinojosa, J.; Viard, A. An enhanced nonlinear multi-scale strategy for the simulation of buckling and delamination on 3D composite plates. Comput. Methods Appl. Mech. Eng. 2017, 317, 952–969. [Google Scholar] [CrossRef]
- ASTM-D5528-94a. Standard Test Method for Mode I Inter-laminar Fracture Toughness of Unidirectional Continuous Fiber Rein- forced Polymer Matrix Composites; ASTM: Philadelphia, PA, USA, 1994. [Google Scholar]
- ASTM-D6671. Standard Test Method for Mixed Mode I–Mode II Interlaminar Fracture Toughness of Unidirectional Fiber Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM-D9705-14. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; Protocols for Interlaminar Fracture Testing of Composites; European Structural Integrity Society (ESIS): Delft, The Netherlands, 1993. [Google Scholar]
- ISO-15024. Fiber-reinforced Plastic Composites—Determination of Mode I Interlaminar Fracture Toughness, GIc, for Unidirectionally Reinforced Materials; International Organization for Standardization: Geneva Switzerland, 2001. [Google Scholar]
- Irwin, G.R.; Kies, J.A. Critical Energy Rate Analysis of Fracture Strength. Weld. J. Res. Suppl. 1954, 33, 193–198. [Google Scholar]
- Kanninen, M.F. An augmented double cantilever beam model for studying crack propagation and arrest. Int. J. Fract. 1973, 9, 83–92. [Google Scholar]
- Allix, O.; Ladevéze, P.; Corigliano, A. Damage analysis of interlaminar fracture specimens. Compos. Struct. 1995, 31, 61–74. [Google Scholar] [CrossRef]
- Suo, Z.; Bao, G.; Fan, B. Delamination R-curve phenomena due to damage. J. Mech. Phys. Solids 1992, 40, 1–16. [Google Scholar] [CrossRef]
- Frossard, G.; Cugnoni, J.; Gmür, T.; Botsis, J. Mode I interlaminar fracture of carbon epoxy laminates: Effects of ply thickness. Compos. Part A Appl. Sci. Manuf. 2016, 91, 1–8. [Google Scholar] [CrossRef]
- Canal, L.P.; Alfano, M.; Botsis, J. A multi-scale based cohesive zone model for the analysis of thickness scaling effect in fiber bridging. Compos. Sci. Technol. 2017, 139, 90–98. [Google Scholar] [CrossRef]
- Cameselle-Molares, A.; Vassilopoulos, A.P.; Renart, J.; Turon, A.; Keller, T. Numerical simulation of two-dimensional in-plane crack propagation in FRP laminates. Compos. Struct. 2018, 200, 396–407. [Google Scholar] [CrossRef]
- Bazǎnt, Z. Concrete fracture models: Testing and practice. Eng. Fract. Mech. 2002, 69, 165–205. [Google Scholar] [CrossRef]
- Morel, S.; Lespine, C.; Coureau, J.L.; Planas, J.; Dourado, N. Bilinear softening parameters and equivalent LEFM R-curve in quasibrittle failure. Int. J. Solids Struct. 2010, 47, 837–850. [Google Scholar] [CrossRef]
- Rybicki, E.F.; Kanninen, M.F. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Krueger, R. The Virtual Crack Closure Technique for modeling interlaminar failure and delamination in advanced composite materials. In Numerical Modelling of Failure in Advanced Composite Materials; Camanho, P.P., Hallett, S.R., Eds.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2015; pp. 3–53. [Google Scholar]
- Marjanović, M.; Meschke, G.; Vuksanović, D. A finite element model for propagating delamination in laminated composite plates based on the Virtual Crack Closure method. Compos. Struct. 2016, 150, 8–19. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Sosa, J.C.; Karapurath, N. Delamination modelling of GLARE using the extended finite element method. Compos. Sci. Technol. 2012, 72, 788–791. [Google Scholar] [CrossRef]
- Yazdani, S.; Rust, W.J.; Wriggers, P. An XFEM approach for modelling delamination in composite laminates. Compos. Struct. 2016, 135, 353–364. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Barenblatt, G. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1962; Volume 7, pp. 55–129. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103. [Google Scholar] [CrossRef]
- Petersson, P. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials. Ph.D. Thesis, Lund University, Lund, Sweden, 1981. [Google Scholar]
- Mai, Y.; Lawn, B. Crack-Interface Grain Bridging as a Fracture Resistance Mechanism in Ceramics: II, Theoretical Fracture Mechanics Model. J. Am. Ceram. Soc. 1984, 70, 289–294. [Google Scholar] [CrossRef]
- Allix, O.; Lévêque, D.; Perret, L. Identification and forecast of delamination in composite laminates by an interlaminar interface model. Compos. Sci. Technol. 1998, 58, 671–678. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J. Effect of T-Stress on mode I crack growth resistance in a ductile solid. Int. J. Solids Struct. 1994, 31, 823–833. [Google Scholar] [CrossRef]
- Rakin, M.; Medjo, B.; Gubeljak, N.; Sedmak, A. Micromechanical assessment of mismatch effects on fracture of high-strength low alloyed steel welded joints. Eng. Fract. Mech. 2013, 109, 221–235. [Google Scholar] [CrossRef]
- Tijssens, M.; van der Giessen, E.; Sluys, L. Modeling of crazing using a cohesive surface methodology. Mech. Mater. 2000, 32, 19–35. [Google Scholar] [CrossRef]
- Dourado, N.; Morel, S.; de Moura, M.; Valentin, G.; Morais, J. Comparison of fracture properties of two wood species through cohesive crack simulations. Compos. Part A Appl. Sci. Manuf. 2008, 39, 415–427. [Google Scholar] [CrossRef]
- de Morais, A.; Pereira, A. Application of the effective crack method to mode I and mode II interlaminar fracture of carbon/epoxy unidirectional laminates. Compos. Part A Appl. Sci. Manuf. 2007, 38, 785–794. [Google Scholar] [CrossRef]
- Su, Z.; Tay, T.; Ridha, M.; Chen, B. Progressive damage modeling of open-hole composite laminates under compression. Compos. Struct. 2015, 122, 507–517. [Google Scholar] [CrossRef]
- Flores, E.S.; Saavedra, K.; Hinojosa, J.; Chandra, Y.; Das, R. Multi-scale modelling of rolling shear failure in cross-laminated timber structures by homogenisation and cohesive zone models. Int. J. Solids Struct. 2016, 81, 219–232. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wang, Y.Q.; Gao, H.; Li, R.; Bao, Y. A progressive damage model for predicting damage evolution of laminated composites subjected to three-point bending. Compos. Sci. Technol. 2017, 151, 85–93. [Google Scholar] [CrossRef]
- Koloor, S.R.; Ayatollahi, M.; Tamin, M. Elastic-damage deformation response of fiber-reinforced polymer composite laminates with lamina interfaces. J. Reinf. Plast. Compos. 2017, 36, 832–849. [Google Scholar] [CrossRef]
- Koloor, S.R.; Tamin, M. Mode-II interlaminar fracture and crack-jump phenomenon in CFRP composite laminate materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Confalonieri, F.; Perego, U. A new framework for the formulation and validation of cohesive mixed-mode delamination models. Int. J. Solids Struct. 2019, 164, 168–190. [Google Scholar] [CrossRef]
- Park, K.; Paulino, G.H. Cohesive Zone Models: A Critical Review of Traction-Separation Relationships Across Fracture Surfaces. Appl. Mech. Rev. 2013, 64, 060802. [Google Scholar] [CrossRef]
- Sorensen, L.; Botsis, J.; Gmür, T.; Humbert, L. Bridging tractions in mode I delamination: Measurements and simulations. Compos. Sci. Technol. 2008, 68, 2350–2358. [Google Scholar] [CrossRef]
- Stutz, S.; Cugnoni, J.; Botsis, J. Crack–fiber sensor interaction and characterization of the bridging tractions in mode I delamination. Eng. Fract. Mech. 2011, 78, 890–900. [Google Scholar] [CrossRef]
- Pappas, G.; Canal, L.; Botsis, J. Characterization of intralaminar mode I fracture of AS4/PPS composite using inverse identification and micromechanics. Compos. Part A Appl. Sci. Manuf. 2016, 91, 117–126. [Google Scholar] [CrossRef]
- Alfano, M.; Lubineau, G.; Paulino, G.H. Global sensitivity analysis in the identification of cohesive models using full-field kinematic data. Int. J. Solids Struct. 2015, 55, 66–78. [Google Scholar] [CrossRef]
- Ostapska, K.; Malo, K.A. Crack path tracking using DIC and XFEM modelling of mixed-mode fracture in wood. Theor. Appl. Fract. Mech. 2021, 112, 102896. [Google Scholar] [CrossRef]
- Sorensen, B.F.; Jacobsen, T.K. Determination of cohesive laws by the J integral approach. Eng. Fract. Mech. 2003, 70, 1841–1858. [Google Scholar] [CrossRef]
- Frossard, G.; Cugnoni, J.; Gmür, T.; Botsis, J. An efficient method for fiber bridging traction identification based on the R-curve: Formulation and experimental validation. Compos. Struct. 2017, 175, 135–144. [Google Scholar] [CrossRef]
- Kharratzadeh, M.; Shokrieh, M.; Salamat-talab, M. Effect of interface fiber angle on the mode I delamination growth of plain woven glass fiber-reinforced composites. Theor. Appl. Fract. Mech. 2018, 98, 1–12. [Google Scholar] [CrossRef]
- Gheibi, M.R.; Shojaeefard, M.H.; Googarchin, H.S. Direct determination of a new mode-dependent cohesive zone model to simulate metal-to-metal adhesive joints. J. Adhes. 2019, 95, 943–970. [Google Scholar] [CrossRef]
- Montenegro, D.; Pappas, G.; Botsis, J.; Zogg, M.; Wegener, K. A comparative study of mode I delamination behavior of unidirectional glass fiber-reinforced polymers with epoxy and polyurethane matrices using two methods. Eng. Fract. Mech. 2019, 206, 485–500. [Google Scholar] [CrossRef]
- Kottner, R.; Hynek, R.; Kroupa, T. Identification of parameters of cohesive elements for modeling of adhesively bonded joints of epoxy composites. Appl. Comput. Mech. 2013, 7, 137–144. [Google Scholar]
- Xu, Y.; Li, X.; Wang, X.; Liang, L. Inverse parameter identification of cohesive zone model for simulating mixed-mode crack propagation. Int. J. Solids Struct. 2014, 51, 2400–2410. [Google Scholar] [CrossRef]
- de Morais, A.; Pereira, A.; de Moura, M.; Silva, F.; Dourado, N. Bilinear approximations to the mixed-mode I–II delamination cohesive law using an inverse method. Compos. Struct. 2015, 122, 361–366. [Google Scholar] [CrossRef]
- Pincheira, G.; Ferrada, N.; Hinojosa, J.; Montecino, G.; Torres, L.; Saavedra, K. A study of interlaminar properties for a unidirectional glass fiber reinforced epoxy composite. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2019, 233, 348–357. [Google Scholar] [CrossRef]
- Joki, R.; Grytten, F.; Hayman, B.; Sørensen, B. Determination of a cohesive law for delamination modelling – Accounting for variation in crack opening and stress state across the test specimen width. Compos. Sci. Technol. 2016, 128, 49–57. [Google Scholar] [CrossRef]
- Abdel Monsef, S.; Ortega, A.; Turon, A.; Maimí, P.; Renart, J. An efficient method to extract a mode I cohesive law for bonded joints using the double cantilever beam test. Compos. Part B Eng. 2019, 178, 107424. [Google Scholar] [CrossRef]
- Skec, L. Identification of parameters of a bi-linear cohesive-zone model using analytical solutions for mode-I delamination. Eng. Fract. Mech. 2019, 214, 558–577. [Google Scholar] [CrossRef]
- Avalos, F.; Pincheira, G.; Inostroza, J.; Flores, P. Material parameter identification for vacuum infusion manufactured components. Int. J. Mater. Form. 2010, 3, 579–582. [Google Scholar] [CrossRef]
- Camacho, G.; Ortiz, M. Computational modelling of impact damage in brittle materials. Int. J. Solids Struct. 1996, 33, 2899–2938. [Google Scholar] [CrossRef]
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Stanzl-Tschegg, S.; Tan, D.M.; Tschegg, E. New splitting method for wood fracture characterization. Wood Sci. Technol. 1995, 29, 31–50. [Google Scholar] [CrossRef]
- Elices, M.; Planas, J. The equivalent elastic crack: 1. Load-Y equivalences. Int. J. Fract. 1993, 61, 159–172. [Google Scholar] [CrossRef]
- Allix, O.; Gosselet, P.; Kerfriden, P.; Saavedra, K. Virtual delamination testing through non-linear multi-scale computational methods: Some recent progress. Comput. Mater. Contin. 2012, 32, 107–132. [Google Scholar]
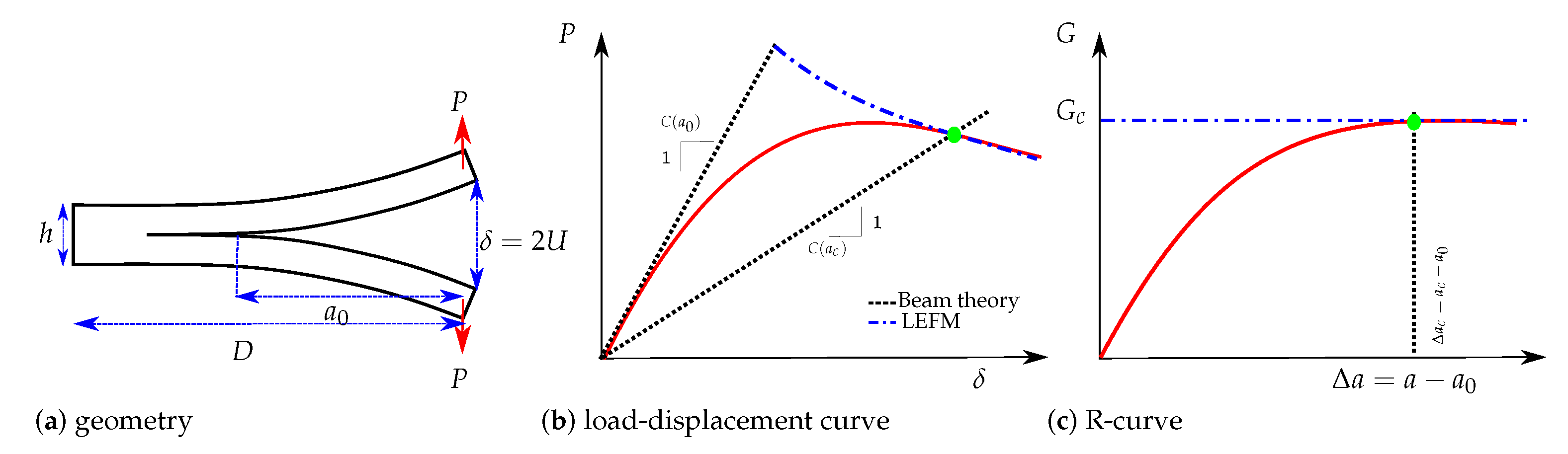
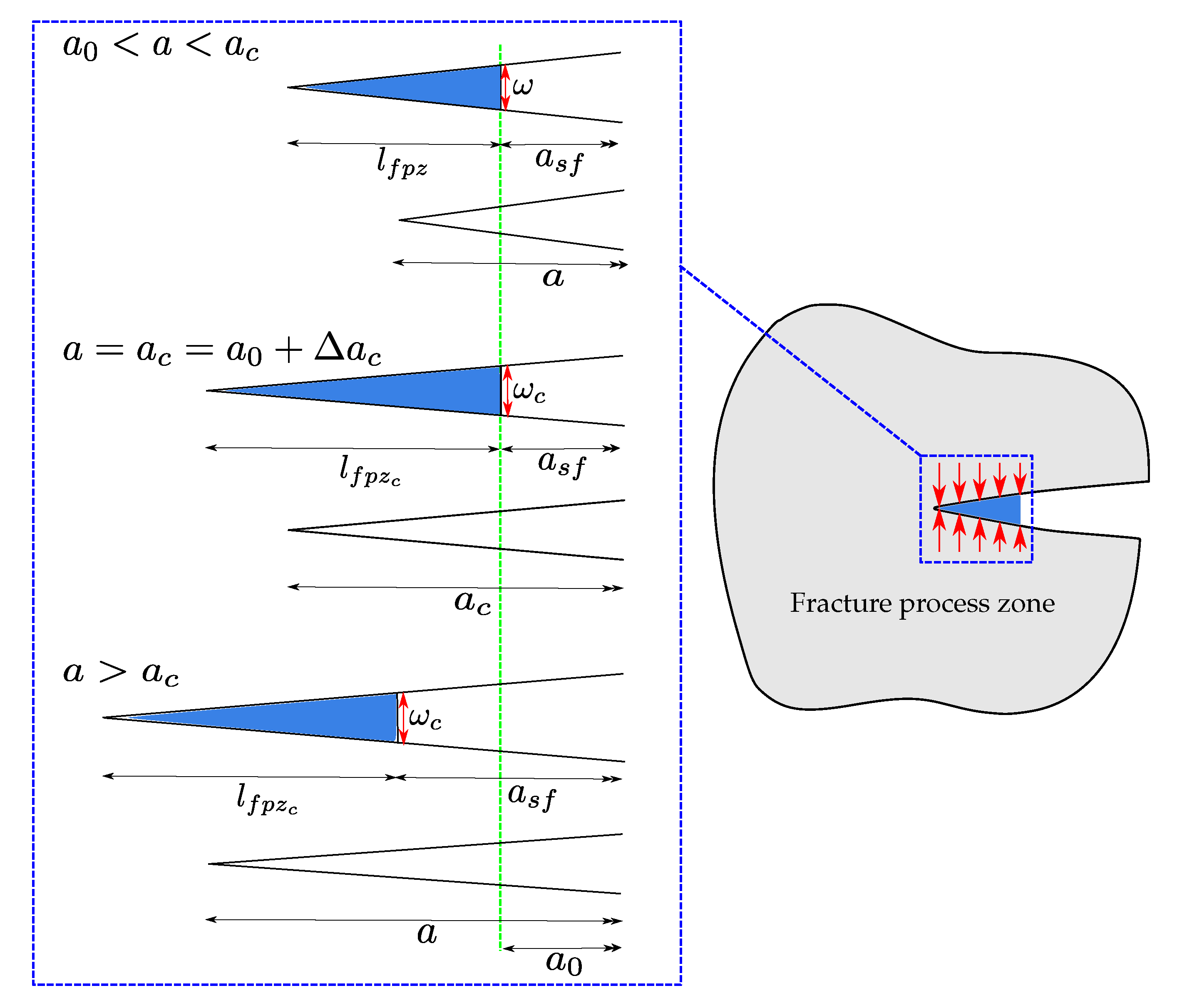

| Thickness h (mm) | Width B (mm) | Length D (mm) | Pre-Crack (mm) |
|---|---|---|---|
| 2.72 ± 0.07 | 20.4 ± 0.08 | 124.68 ± 0.52 | 47 |
| Specimen | (N/m) | (N) |
|---|---|---|
| 1 | 981.65 | 31.08 |
| 2 | 926.60 | 32.16 |
| 3 | 1062.80 | 29.72 |
| 4 | 964.90 | 27.98 |
| 5 | 974.8 | 30.70 |
| average value | 982.15 | 30.33 |
| standard deviation | 49.85 | 1.58 |
| CZM | Trilinear [26] | Bilinear [72] | Potential [40] |
|---|---|---|---|
| , | , | ||
| , | where | ||
| damage law | , | ||
| where | where | ||
| parametersto be identified | , , | , | , n |
| poblation size | 5000 |
| crossover probability | 0.7 |
| mutation probability | 0.1 |
| number of generation | 300 |
| number of couples | 500 |
| pressure | 0.05 |
| CZM | Characterization | Number of DCB Virtual Tests | (mm) | Fitted Parameters | |
|---|---|---|---|---|---|
| trilinear | eq. LEFM R-curve | 10 | 0.33 | 15.0 | MPa |
| mm | |||||
| (-) | |||||
| genetic algorithm | 36 | 0.46 | 14.5 | MPa | |
| mm | |||||
| (-) | |||||
| bilinear | eq. LEFM R-curve | 10 | 16.2 | 15.0 | mm |
| N/m | |||||
| eq. LEFM R-curve | 10 | 3.21 | 2.5 | mm | |
| N/m | |||||
| genetic algorithm | 36 | 1.67 | 4.96 | mm | |
| N/m | |||||
| potential | eq. LEFM R-curve | 10 | 32.2 | 15.0 | (-) |
| N/m | |||||
| eq. LEFM R-curve | 10 | 2.98 | 2.5 | (-) | |
| N/m | |||||
| genetic algorithm | 36 | 2.22 | 4.3 | (-) | |
| N/m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, L.; Saavedra, K.; Pincheira, G.; Pina, J.C. Simulation of Mode I Interlaminar Damage of a GFRP Composite Using Cohesive Laws in the Framework of the Equivalent LEFM R-Curve and an Optimised Algorithm. Polymers 2021, 13, 1482. https://doi.org/10.3390/polym13091482
Torres L, Saavedra K, Pincheira G, Pina JC. Simulation of Mode I Interlaminar Damage of a GFRP Composite Using Cohesive Laws in the Framework of the Equivalent LEFM R-Curve and an Optimised Algorithm. Polymers. 2021; 13(9):1482. https://doi.org/10.3390/polym13091482
Chicago/Turabian StyleTorres, Luis, Karin Saavedra, Gonzalo Pincheira, and Juan Carlos Pina. 2021. "Simulation of Mode I Interlaminar Damage of a GFRP Composite Using Cohesive Laws in the Framework of the Equivalent LEFM R-Curve and an Optimised Algorithm" Polymers 13, no. 9: 1482. https://doi.org/10.3390/polym13091482
APA StyleTorres, L., Saavedra, K., Pincheira, G., & Pina, J. C. (2021). Simulation of Mode I Interlaminar Damage of a GFRP Composite Using Cohesive Laws in the Framework of the Equivalent LEFM R-Curve and an Optimised Algorithm. Polymers, 13(9), 1482. https://doi.org/10.3390/polym13091482