Engineering Toolbox for Systematic Design of PolyHIPE Architecture
Abstract
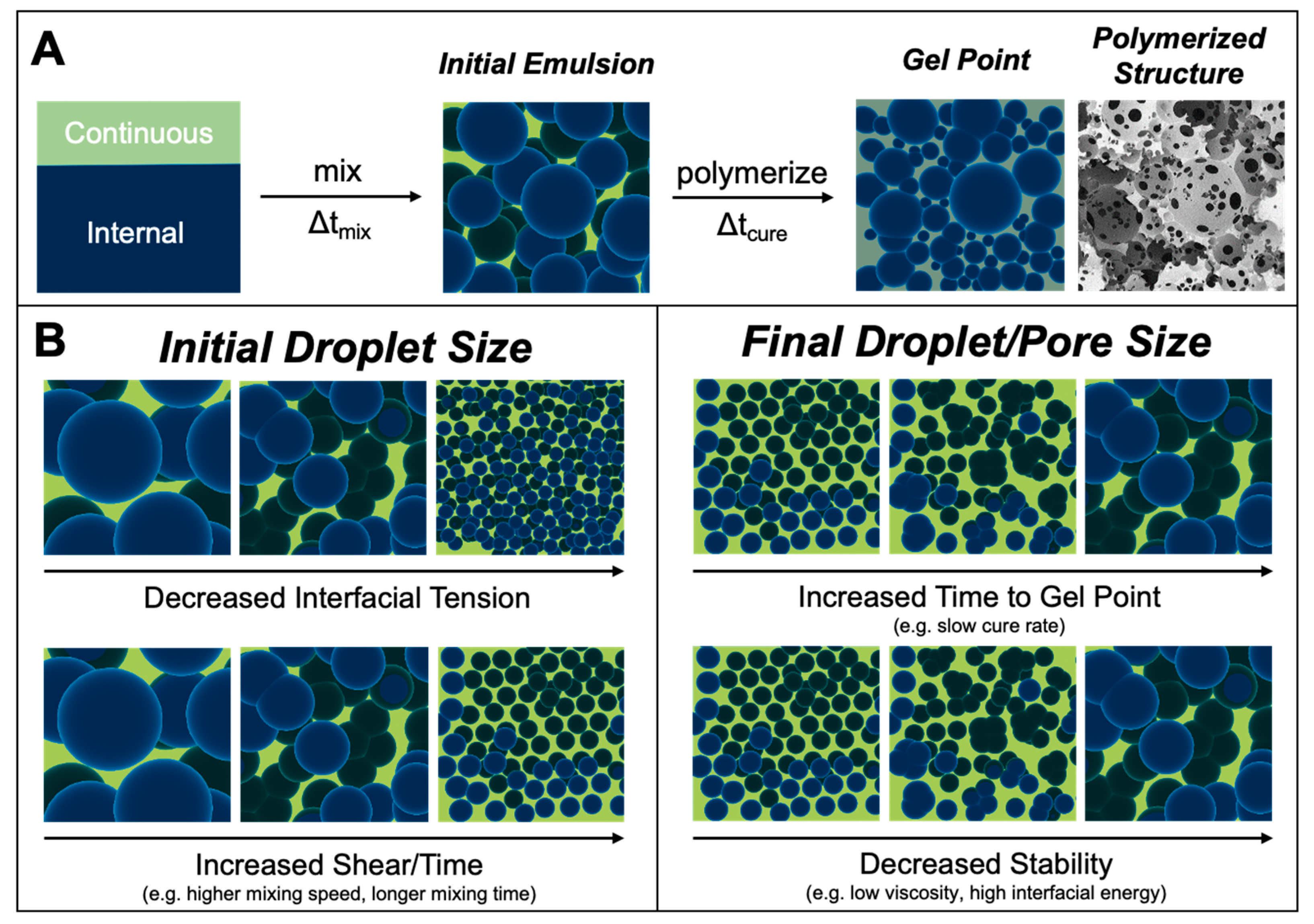
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Molecular Hydrophobicity Estimates
2.3. PFDMA Synthesis
2.4. Viscosity Measurements
2.5. PolyHIPE Fabrication
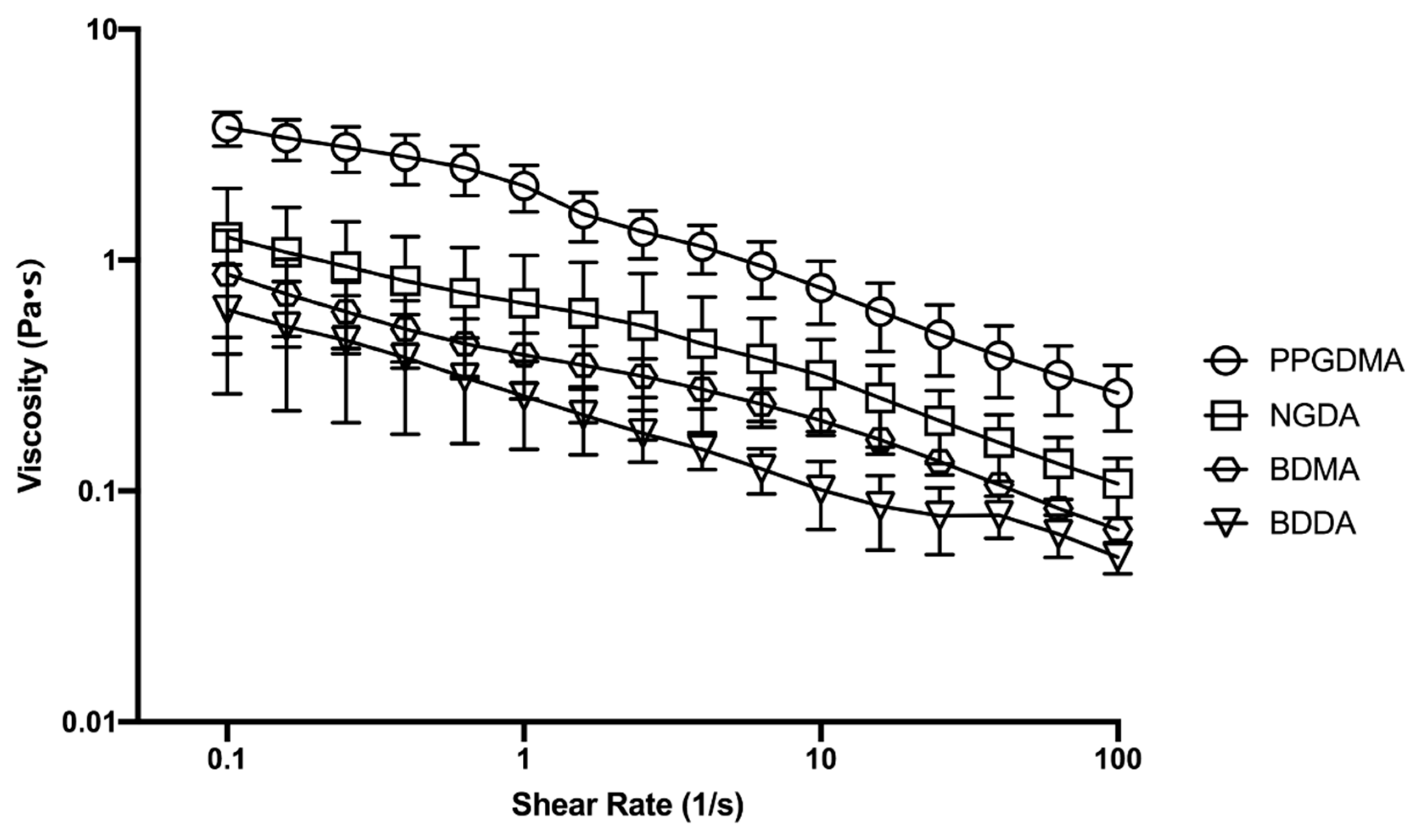
2.6. Emulsion Rheology
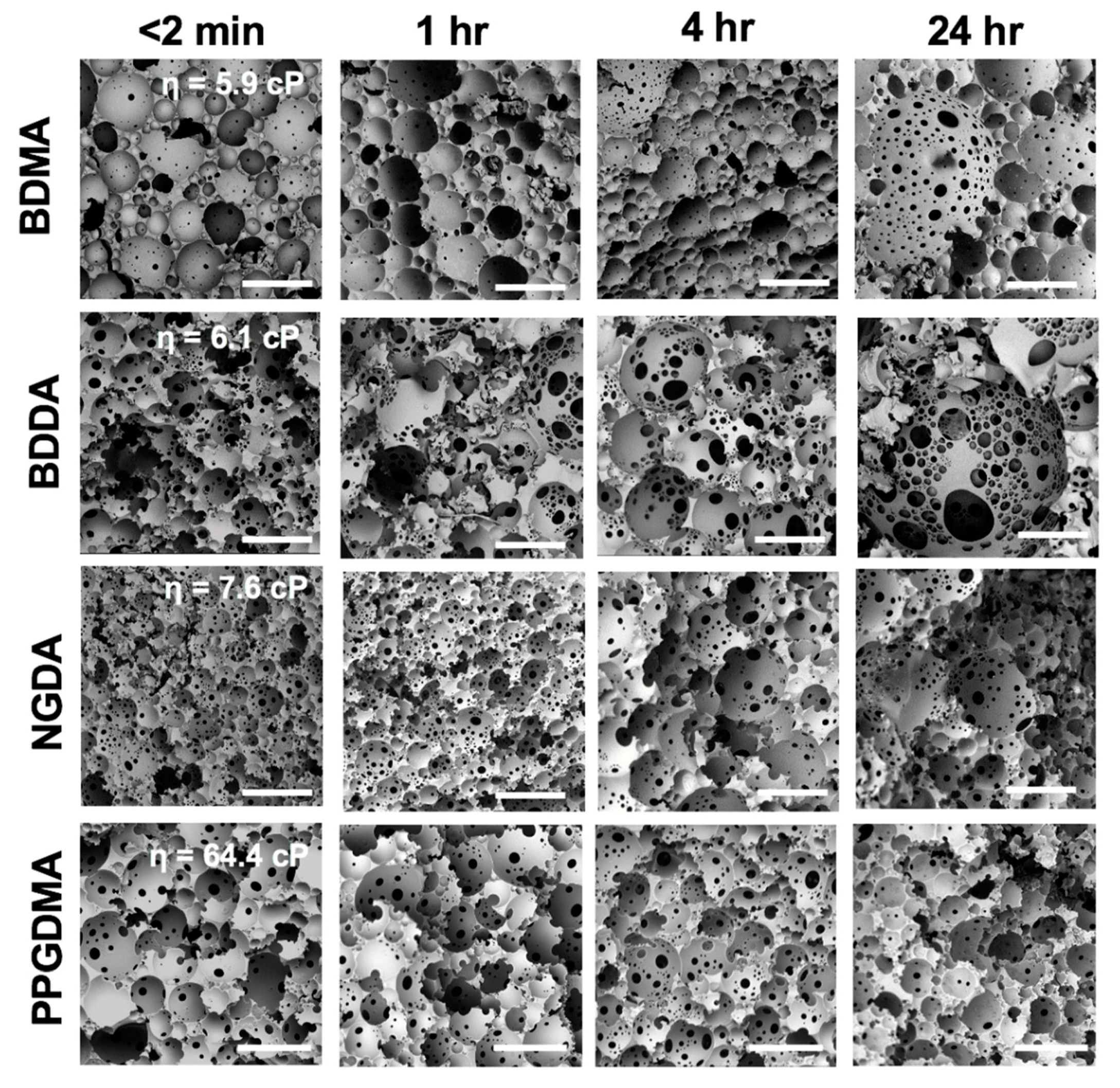
2.7. Stability Studies
2.8. Cure Time and Gel Fraction
2.9. Effect of Cure Time
2.10. PolyHIPE Architecture
2.11. Statistical Analysis
3. Results and Discussion
3.1. Effect of Surfactant Concentration
3.2. Effect of Mixing Speed
3.3. Effect of Macromer Chemistry
3.4. Effect of Emulsion Viscosity on Initial and Final Droplet Size
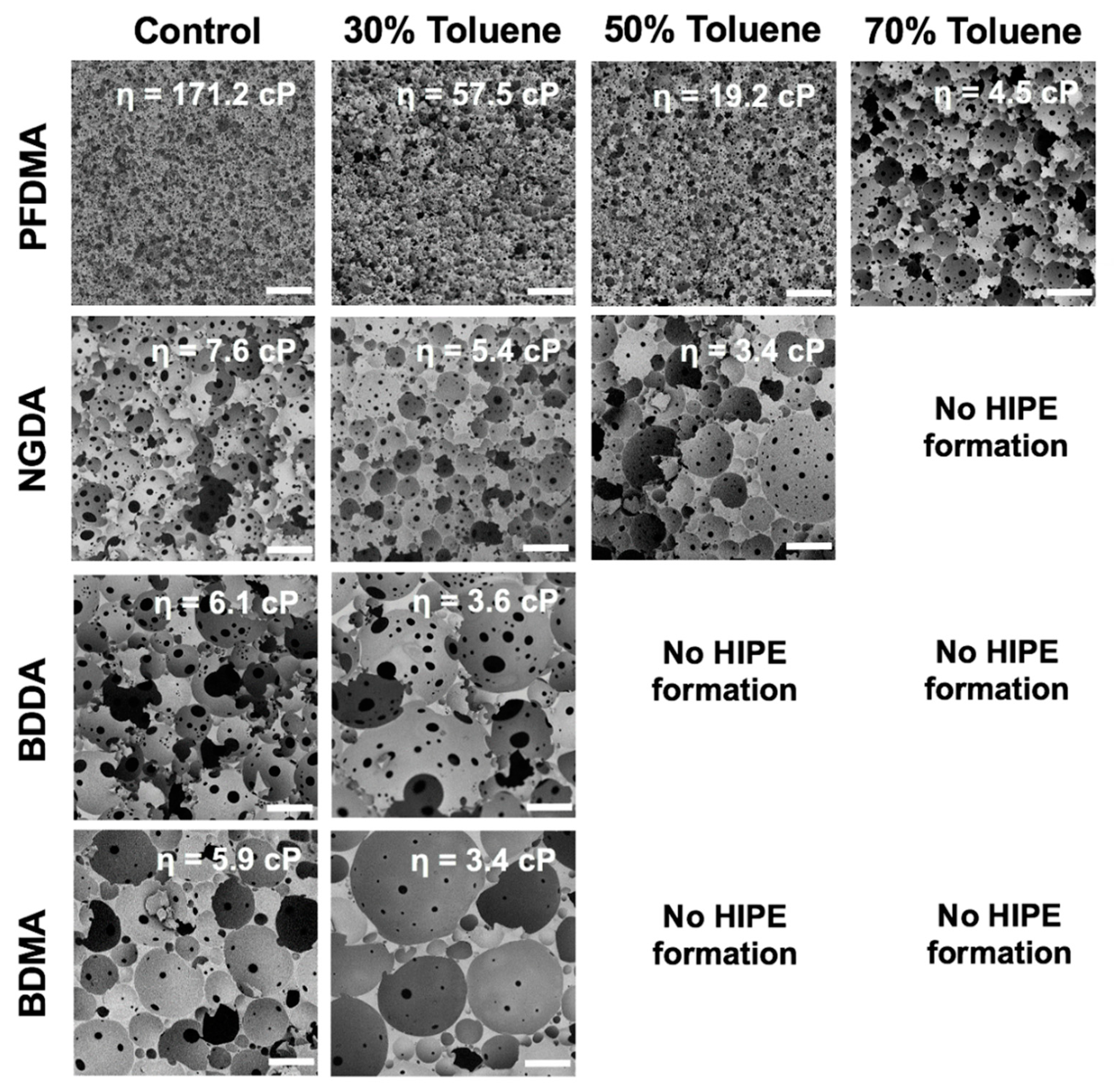
3.5. Diluent Effects on PolyHIPE Architecture
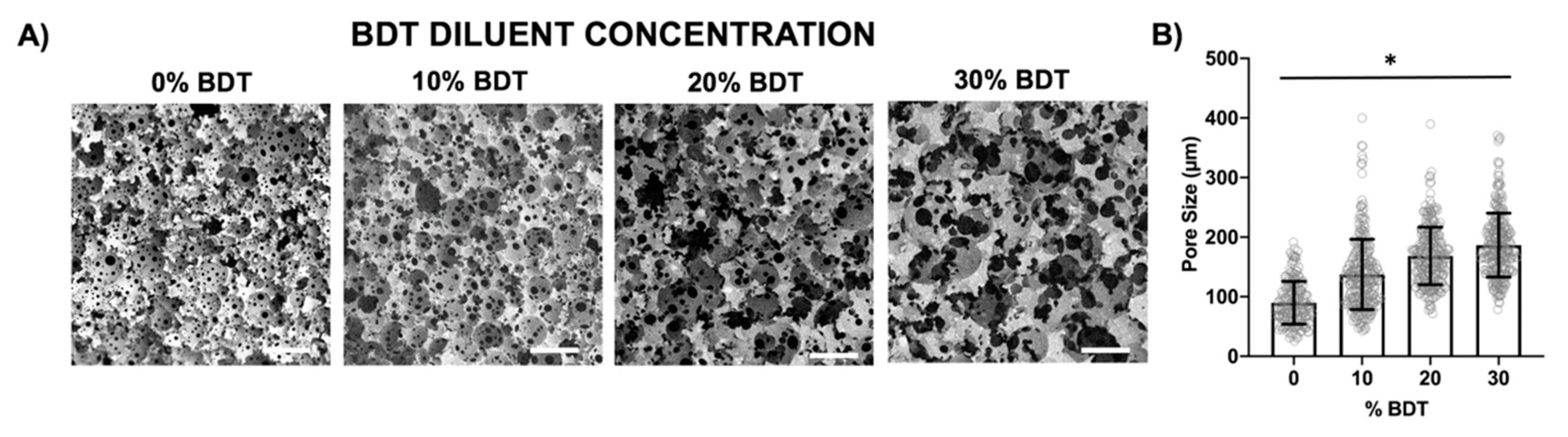
3.6. Increasing Pore Size with a Reactive Diluent
3.7. Perspectives on the Rational Design of PolyHIPE Architecture
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Jiang, C.; Yan, J.; Shen, Y.; Chen, Y.; Xu, L.; Zhu, H. Structuring the reduced graphene oxide/polyHIPE foam for piezoresistive sensing via emulsion-templated polymerization. Compos. Part A Appl. Sci. Manuf. 2020, 134, 105898. [Google Scholar] [CrossRef]
- Vásquez, L.; Davis, A.; Gatto, F.; An, M.N.; Drago, F.; Pompa, P.P.; Athanassiou, A.; Fragouli, D. Multifunctional PDMS polyHIPE filters for oil-water separation and antibacterial activity. Sep. Purif. Technol. 2021, 255, 117748. [Google Scholar] [CrossRef]
- Whitely, M.E.; Robinson, J.L.; Stuebben, M.C.; Pearce, H.A.; McEnery, M.A.; Cosgriff-Hernandez, E. Prevention of Oxygen Inhibition of PolyHIPE Radical Polymerization Using a Thiol-Based Cross-Linker. ACS Biomater. Sci. Eng. 2017, 3, 409–419. [Google Scholar] [CrossRef]
- Cameron, N.; Sherrington, D. High internal phase emulsions (HIPEs)—Structure, properties and use in polymer prepa-ration. In Biopolymers Liquid Crystalline Polymers Phase Emulsion; Springer: Berlin/Heidelberg, Germany, 1996; pp. 163–214. [Google Scholar]
- Even, W.R.; Gregory, D.P. Emulsion-Derived Foams Preparation, Properties, and Application. MRS Bull. 1994, 19, 29–33. [Google Scholar] [CrossRef]
- Buchmeiser, M.R. Polymeric monolithic materials: Syntheses, properties, functionalization and applications. Polymer 2007, 48, 2187–2198. [Google Scholar] [CrossRef]
- Grace, H.P. Dispersion Phenomena in High Viscosity Immiscible Fluid Systems And Application Of Static Mixers As Dispersion Devices In Such Systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- Bazhlekov, I.B.; Anderson, P.D.; Meijer, H.E. Numerical investigation of the effect of insoluble surfactants on drop deformation and breakup in simple shear flow. J. Colloid Interface Sci. 2006, 298, 369–394. [Google Scholar] [CrossRef] [PubMed]
- Stang, M.; Schuchmann, H.; Schubert, H. Emulsification in high-pressure homogenizers. Eng. Life Sci. 2001, 1, 151–157. [Google Scholar] [CrossRef]
- Quell, A.; Elsing, J.; Drenckhan, W.; Stubenrauch, C. Monodisperse Polystyrene Foams via Microfluidics—A Novel Templating Route. Adv. Eng. Mater. 2015, 17, 604–609. [Google Scholar] [CrossRef]
- Foudazi, R.; Zhao, B.; Gokun, P.; Manas-Zloczower, I.; Rowan, S.J.; Feke, D.L. The Effect of Shear on the Evolution of Morphology in High Internal Phase Emulsions Used as Templates for Structural and Functional Polymer Foams. ACS Appl. Polym. Mater. 2020, 2, 1579–1586. [Google Scholar] [CrossRef]
- Carnachan, R.J.; Bokhari, M.; Przyborski, S.A.; Cameron, N.R. Tailoring the morphology of emulsion-templated porous polymers. Soft Matter 2006, 2, 608–616. [Google Scholar] [CrossRef]
- Foudazi, R. HIPEs to PolyHIPEs. React. Funct. Polym. 2021, 104917. [Google Scholar] [CrossRef]
- Masalova, I.; Kharatyan, E.; Tshilumbu, N. Effect of the type of the oil phase on stability of highly concentrated wa-ter-in-oil emulsions. Colloid J. 2013, 75, 579–585. [Google Scholar] [CrossRef]
- Huš, S.; Kolar, M.; Krajnc, P. Tailoring morphological features of cross-linked emulsion-templated poly(glycidyl meth-acrylate). Des. Monomers Polym. 2015, 18, 698–703. [Google Scholar] [CrossRef]
- Moglia, R.S.; Holm, J.L.; Sears, N.A.; Wilson, C.J.; Harrison, D.M.; Cosgriff-Hernandez, E. Injectable PolyHIPEs as High-Porosity Bone Grafts. Biomacromolecules 2011, 12, 3621–3628. [Google Scholar] [CrossRef]
- Christenson, E.M.; Soofi, W.; Holm, J.L.; Cameron, N.R.; Mikos, A.G. Biodegradable Fumarate-Based PolyHIPEs as Tissue Engineering Scaffolds. Biomacromolecules 2007, 8, 3806–3814. [Google Scholar] [CrossRef]
- Rohm, K.; Manas-Zloczower, I.; Feke, D. Poly(HIPE) morphology, crosslink density, and mechanical properties influenced by surfactant concentration and composition. Colloids Surfaces A Physicochem. Eng. Asp. 2019, 583, 123913. [Google Scholar] [CrossRef]
- Molinspiration. Available online: https://www.molinspiration.com (accessed on 12 July 2020).
- Malakian, A.; Zhou, M.; Zowada, R.T.; Foudazi, R. Synthesis and in situ functionalization of microfiltration membranes via high internal phase emulsion templating. Polym. Int. 2019, 68, 1378–1386. [Google Scholar] [CrossRef]
- Williams, M.J.; Gray, A.J.; Wilkerson, M.H. Emulsion stability and rigid foams from styrene or divinylbenzene wa-ter-in-oil emulsions. Langmuir 1990, 6, 437–444. [Google Scholar] [CrossRef]
- Abbasian, Z.; Moghbeli, M.R. Open porous emulsion-templated monoliths: Effect of the emulsion preparation conditions on the foam microstructure and properties. J. Appl. Polym. Sci. 2009, 116, 986–994. [Google Scholar] [CrossRef]
- Gurevitch, I.; Silverstein, M.S. Polymerized pickering HIPEs: Effects of synthesis parameters on porous structure. J. Polym. Sci. Part A: Polym. Chem. 2010, 48, 1516–1525. [Google Scholar] [CrossRef]
- Politova, N.; Tcholakova, S.; Denkov, N. Factors affecting the stability of water-oil-water emulsion films. Colloids Surfaces A Physicochem. Eng. Asp. 2017, 522, 608–620. [Google Scholar] [CrossRef]
- Wooster, T.J.; Golding, M.; Sanguansri, P. Impact of Oil Type on Nanoemulsion Formation and Ostwald Ripening Stability. Langmuir 2008, 24, 12758–12765. [Google Scholar] [CrossRef]
- Ushikubo, F.; Cunha, R. Stability mechanisms of liquid water-in-oil emulsions. Food Hydrocoll. 2014, 34, 145–153. [Google Scholar] [CrossRef]
- Cottrell, T.; Van Peij, J. Sorbitan Esters and Polysorbates. Emulsifiers Food Technol. 2007, 162–185. [Google Scholar] [CrossRef]
- Weyland, M.; Hartel, R.W. Emulsifiers in confectionery. In Food Emulsifiers and Their Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 285–305. [Google Scholar]
- Berry, J.D.; Neeson, M.J.; Dagastine, R.R.; Chan, D.Y.; Tabor, R.F. Measurement of surface and interfacial tension using pendant drop tensiometry. J. Colloid Interface Sci. 2015, 454, 226–237. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Blair, L. The effect of coalescence on drop size distribution in an agitated liquid-liquid dispersion. Chem. Eng. Sci. 1975, 30, 1057–1064. [Google Scholar] [CrossRef]
- Leiva, J.M.; Geffroy, E. Evolution of the Size Distribution of an Emulsion under a Simple Shear Flow. Fluids 2018, 3, 46. [Google Scholar] [CrossRef]
- Pandolfe, W.D. Effect of dispersed and continuous phase viscosity on droplet size of emulsions generated by homogeniza-tion. J. Dispers. Sci. Technol. 1981, 2, 459–474. [Google Scholar] [CrossRef]
- Jansen, K.M.B.; Agterof, W.G.M.; Mellema, J. Droplet breakup in concentrated emulsions. J. Rheol. 2001, 45, 227–236. [Google Scholar] [CrossRef]
- Wieringa, J.A.; Vandieren, F.; Janssen, J.J.; Agterof, W.G. Droplet breakup mechanisms during emulsification in colloid mills at high dispersed phase volume fraction. Chem. Eng. Res. Des. 1996, 74, 554–562. [Google Scholar]
- Moglia, R.S.; Whitely, M.; Dhavalikar, P.; Robinson, J.; Pearce, H.; Brooks, M.; Stuebben, M.; Cordner, N.; Cosgriff-Hernandez, E. Injectable Polymerized High Internal Phase Emulsions with Rapid in Situ Curing. Biomacromolecules 2014, 15, 2870–2878. [Google Scholar] [CrossRef]
- Fairbanks, B.D.; Scott, T.F.; Kloxin, C.J.; Anseth, K.S.; Bowman, C.N. Thiol−Yne Photopolymerizations: Novel Mechanism, Kinetics, and Step-Growth Formation of Highly Cross-Linked Networks. Macromolecules 2009, 42, 211–217. [Google Scholar] [CrossRef]
- Nair, D.P.; Podgórski, M.; Chatani, S.; Gong, T.; Xi, W.; Fenoli, C.R.; Bowman, C.N. The Thiol-Michael Addition Click Reaction: A Powerful and Widely Used Tool in Materials Chemistry. Chem. Mater. 2014, 26, 724–744. [Google Scholar] [CrossRef]
- Chen, C.-M.; Chou, H.-C.; Lin, W.; Tseng, C. Surfactant effects on the viability and function of human mesenchymal stem cells: In vitro and in vivo assessment. Stem Cell Res. Ther. 2017, 8, 1–10. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pawar, A.B.; Caggioni, M.; Ergun, R.; Hartel, R.W.; Spicer, P.T. Arrested coalescence in Pickering emulsions. Soft Matter 2011, 7, 7710–7716. [Google Scholar] [CrossRef]
- Destribats, M.; Faure, B.; Birot, M.; Babot, O.; Schmitt, V.; Backov, R. Tailored Silica Macrocellular Foams: Combining Limited Coalescence-Based Pickering Emulsion and Sol-Gel Process. Adv. Funct. Mater. 2012, 22, 2642–2654. [Google Scholar] [CrossRef]
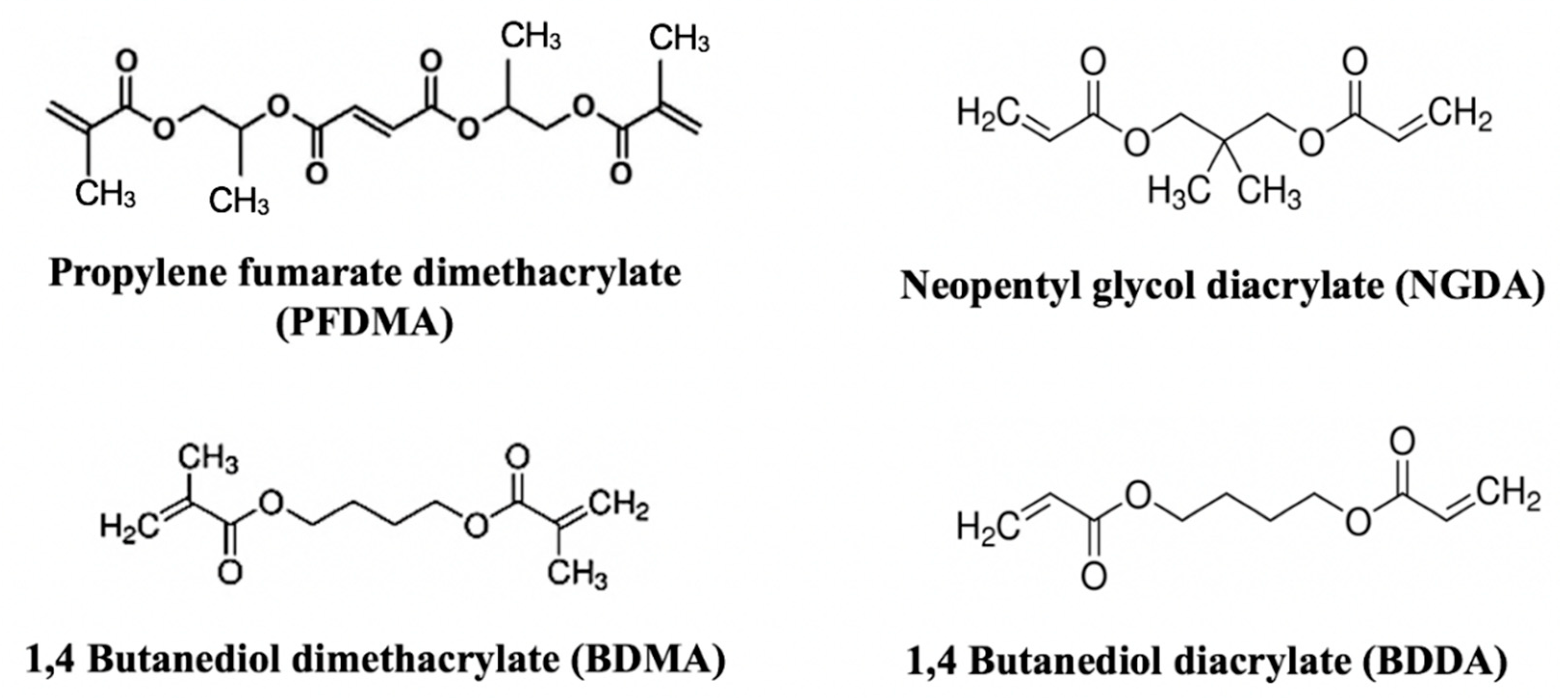
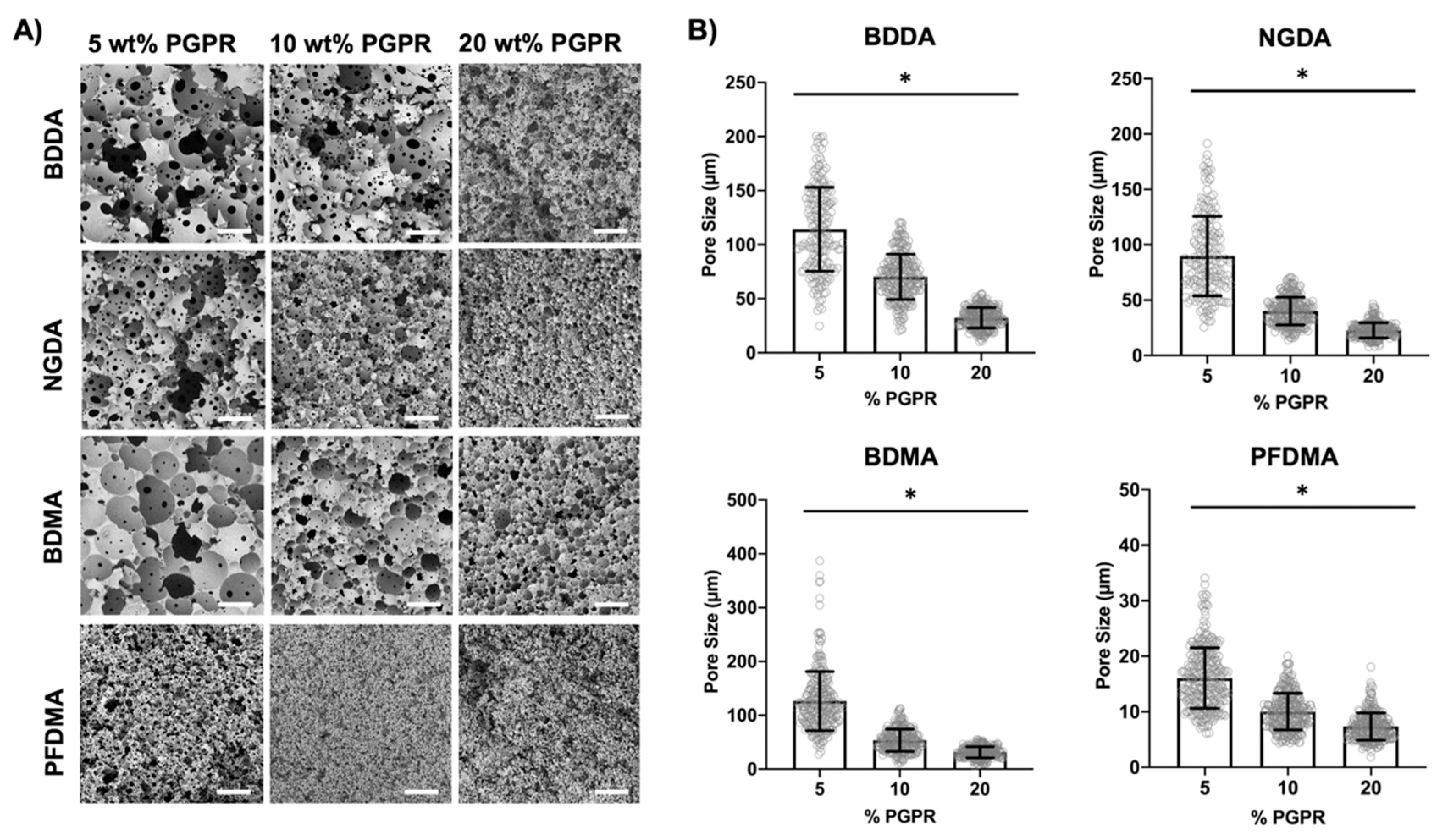

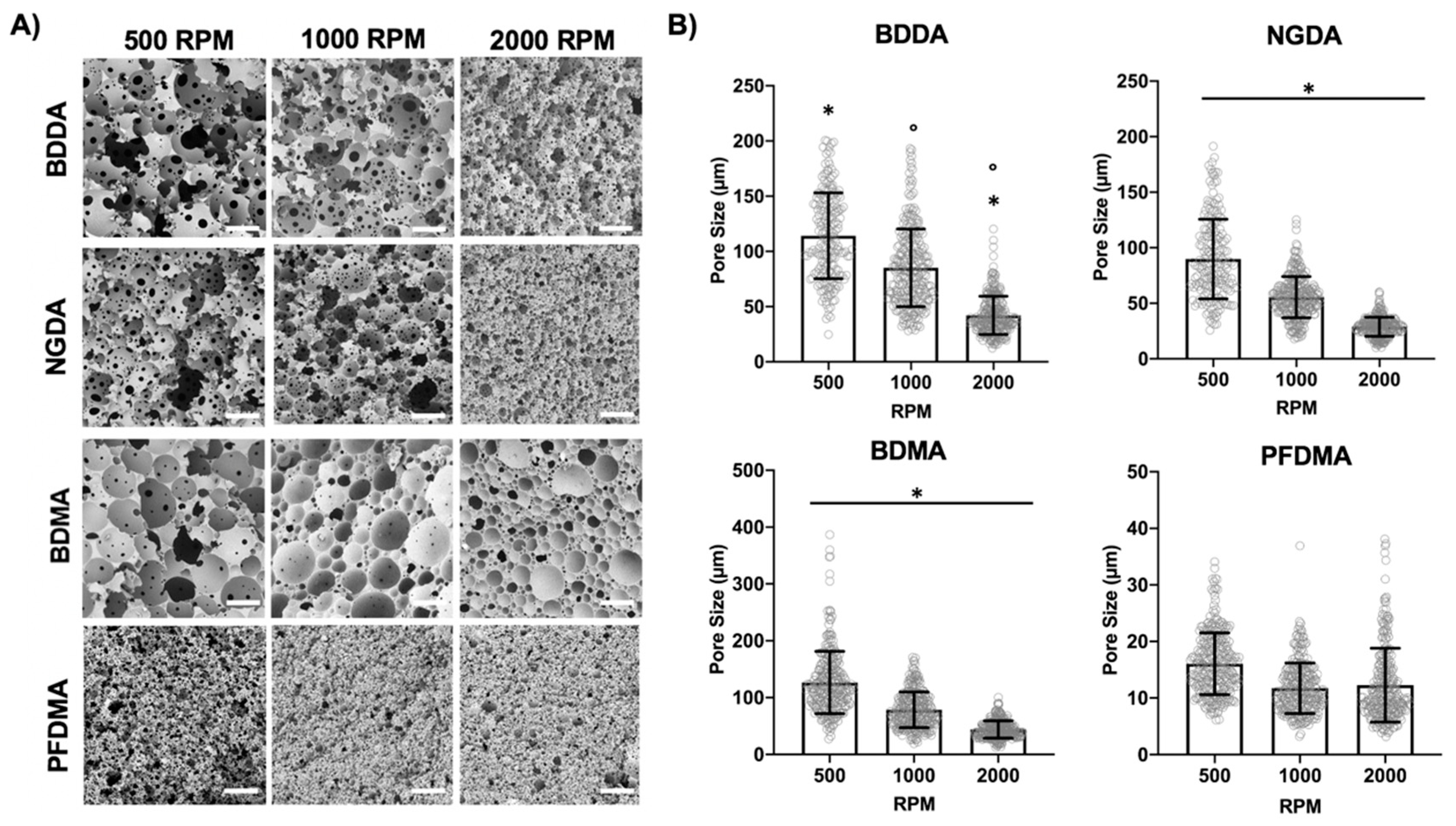
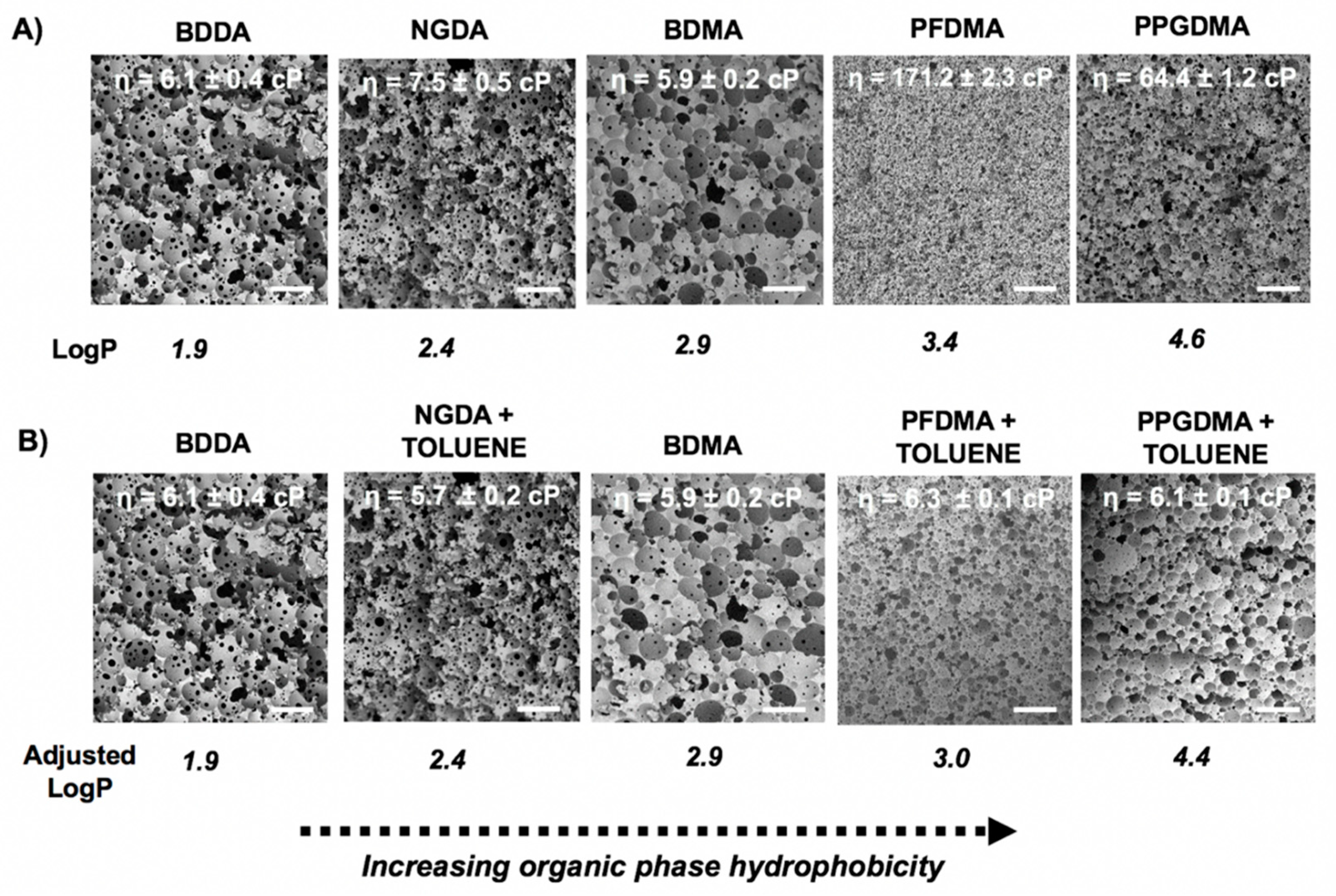
| Macromer | LogP | Viscosity (cP) | Density (g/mL) | Molecular Weight (g/mol) |
|---|---|---|---|---|
| PFDMA | 3.4 | 171.2 ± 2.3 | 1.00 | 362 |
| NGDA | 2.5 | 7.6 ± 0.5 | 1.03 | 212 |
| BDMA | 2.9 | 5.9 ± 0.2 | 1.02 | 226 |
| BDDA | 1.9 | 6.1 ± 0.4 | 1.05 | 196 |
| Macromer | LogP * | [Toluene] (wt%) | Adjusted LogP ** | Viscosity (cP) | Average Pore Diameter (μm) |
|---|---|---|---|---|---|
| PFDMA | 3.4 | 0 | 3.4 | 171.2 ± 2.3 | 14 ± 5 |
| 30 | 3.1 | 57.5 ± 1.3 | 18 ± 8 | ||
| 50 | 2.9 | 19.2 ± 2.8 | 26 ± 8 | ||
| 70 | 2.7 | 4.5 ± 0.1 | 50 ± 30 | ||
| NGDA | 2.5 | 0 | 2.5 | 7.6 ± 0.5 | 58 ± 18 |
| 30 | 2.4 | 5.4 ± 0.1 | 78 ± 15 | ||
| 50 | 2.4 | 3.4 ± 0.1 | 101 ± 76 | ||
| 70 | 2.3 | n.d. | n.d. | ||
| BDDA | 1.9 | 0 | 1.9 | 6.1 ± 0.4 | 106 ± 36 |
| 30 | 2 | 3.6 ± 0.2 | 142 ± 67 | ||
| 50 | 2.1 | n.d. | n.d. | ||
| 70 | 2.2 | n.d. | n.d. | ||
| BDMA | 2.9 | 0 | 2.9 | 5.9 ± 0.2 | 102 ± 37 |
| 30 | 2.7 | 3.4 ± 0.1 | 141 ± 66 | ||
| 50 | 2.6 | n.d. | n.d. | ||
| 70 | 2.5 | n.d. | n.d. |
| Macromer | LogP * | [BDT] (mol%) | Adjusted LogP ** | Viscosity (cP) |
|---|---|---|---|---|
| PFDMA | 3.4 | 0 | 3.4 | 171.0 ± 0.1 |
| 10 | 3.2 | 168.3 ± 0.5 | ||
| 20 | 3.0 | 149.5 ± 1.4 | ||
| 30 | 2.8 | 130 ± 0.4 | ||
| NGDA | 2.5 | 0 | 2.5 | 7.6 ± 0.5 |
| 10 | 2.4 | 6.9 ± 0.1 | ||
| 20 | 2.3 | 6.4 ± 0.1 | ||
| 30 | 2.2 | n.d. | ||
| BDDA | 1.9 | 0 | 1.9 | 6.1 ± 0.4 |
| 10 | 1.8 | 4.9 ± 0.2 | ||
| 20 | 1.8 | 4.4 ± 0.1 | ||
| 30 | 1.8 | n.d. | ||
| BDMA | 2.9 | 0 | 2.9 | 5.9 ± 0.2 |
| 10 | 2.8 | 5.3 ± 0.1 | ||
| 20 | 2.5 | 4.3 ± 0.1 | ||
| 30 | 2.5 | n.d. |
| Parameter | Range for Parameter | Range of PolyHIPE Pore Size | Fold Change (Pore Size) |
|---|---|---|---|
| Mixing speed | 500–1000 RPM | 30–120 μm | 4× |
| Surfactant concentration | 5–20% (wt%) | 20–120 μm | 6× |
| Viscosity | 6–170 cP | 20–80 μm, 50–200 μm | 3–4× |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhavalikar, P.; Shenoi, J.; Salhadar, K.; Chwatko, M.; Rodriguez-Rivera, G.; Cheshire, J.; Foudazi, R.; Cosgriff-Hernandez, E. Engineering Toolbox for Systematic Design of PolyHIPE Architecture. Polymers 2021, 13, 1479. https://doi.org/10.3390/polym13091479
Dhavalikar P, Shenoi J, Salhadar K, Chwatko M, Rodriguez-Rivera G, Cheshire J, Foudazi R, Cosgriff-Hernandez E. Engineering Toolbox for Systematic Design of PolyHIPE Architecture. Polymers. 2021; 13(9):1479. https://doi.org/10.3390/polym13091479
Chicago/Turabian StyleDhavalikar, Prachi, Jason Shenoi, Karim Salhadar, Malgorzata Chwatko, Gabriel Rodriguez-Rivera, Joy Cheshire, Reza Foudazi, and Elizabeth Cosgriff-Hernandez. 2021. "Engineering Toolbox for Systematic Design of PolyHIPE Architecture" Polymers 13, no. 9: 1479. https://doi.org/10.3390/polym13091479
APA StyleDhavalikar, P., Shenoi, J., Salhadar, K., Chwatko, M., Rodriguez-Rivera, G., Cheshire, J., Foudazi, R., & Cosgriff-Hernandez, E. (2021). Engineering Toolbox for Systematic Design of PolyHIPE Architecture. Polymers, 13(9), 1479. https://doi.org/10.3390/polym13091479




_Chwatko.png)


