Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement
Abstract
1. Introduction
2. Molecular Model, Simulation Method, and Systems Studied
3. Analysis of the Local Structure
4. Results
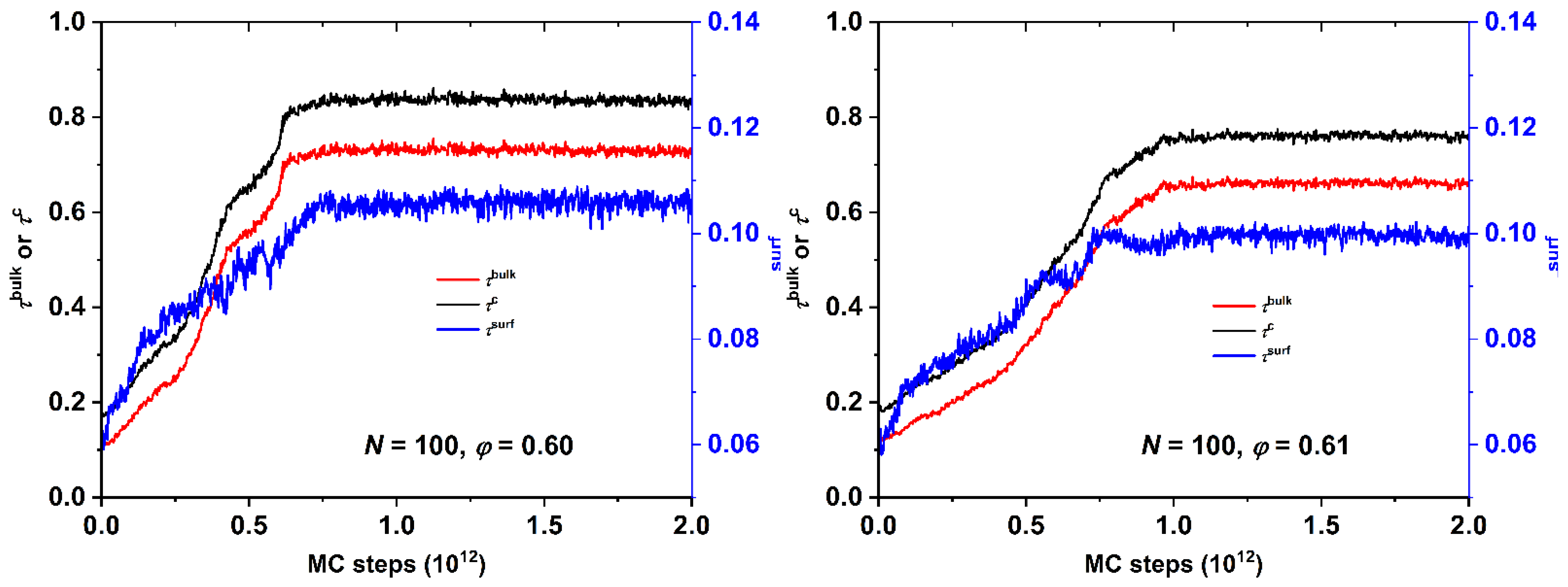
4.1. Total Crystallinity
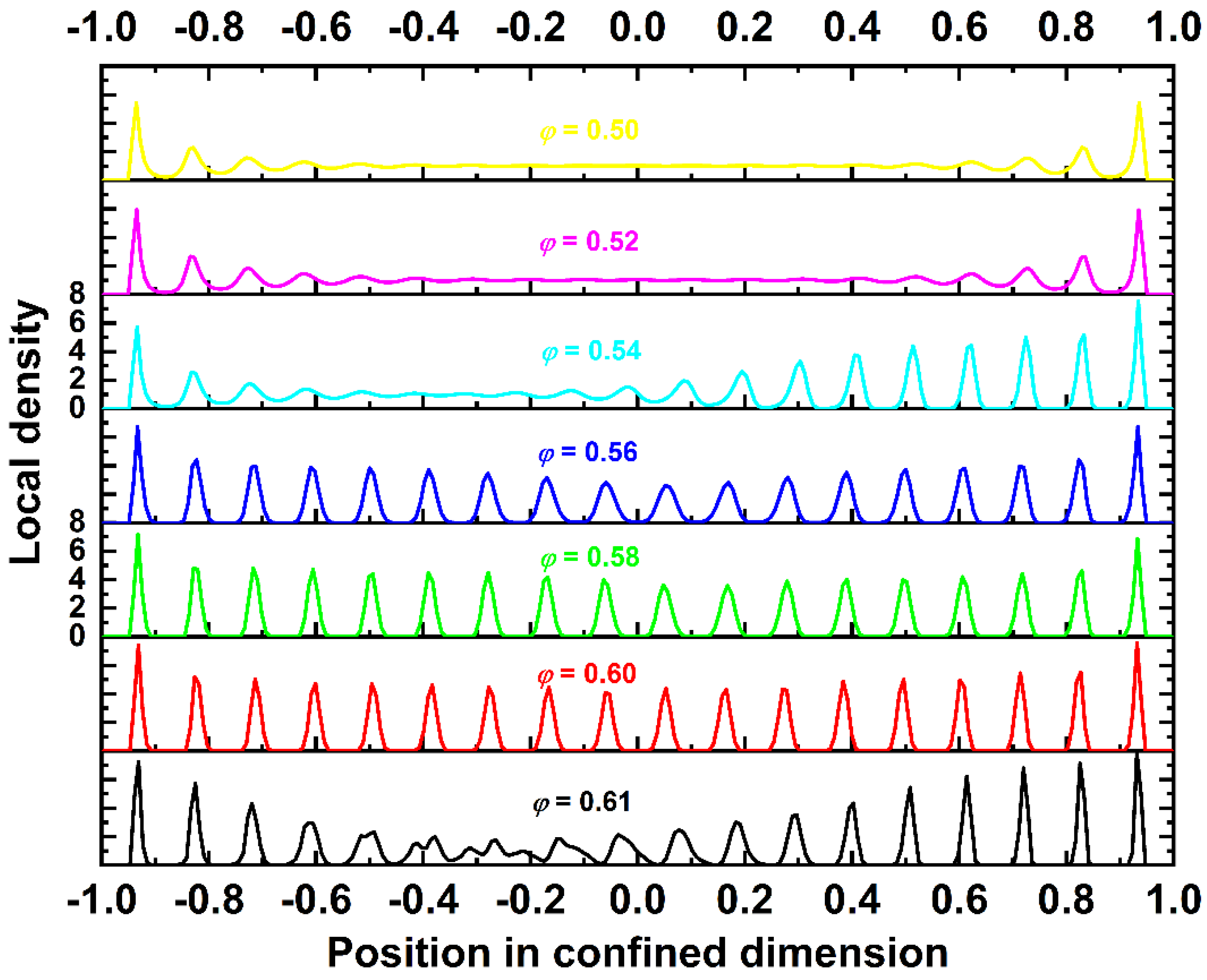
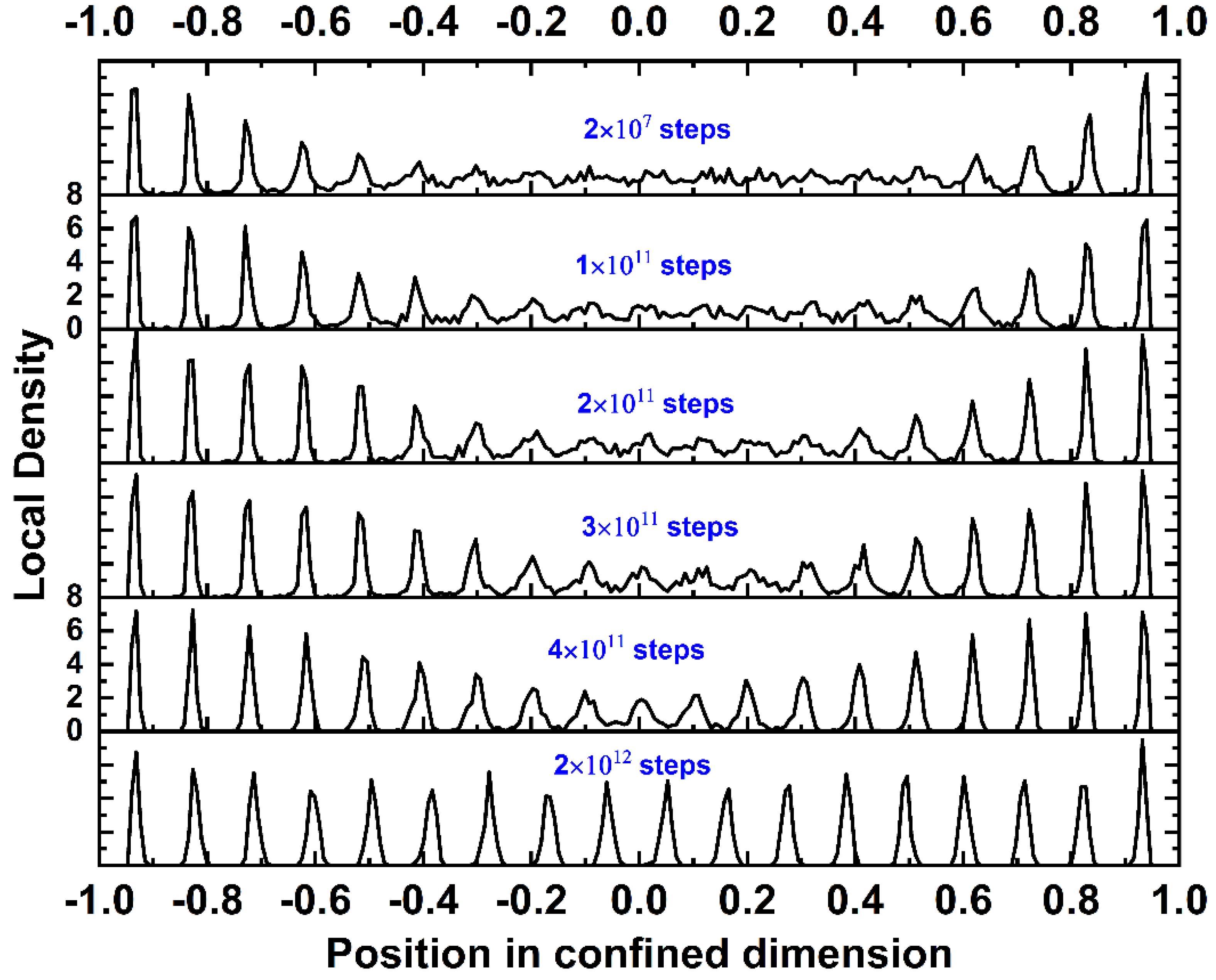
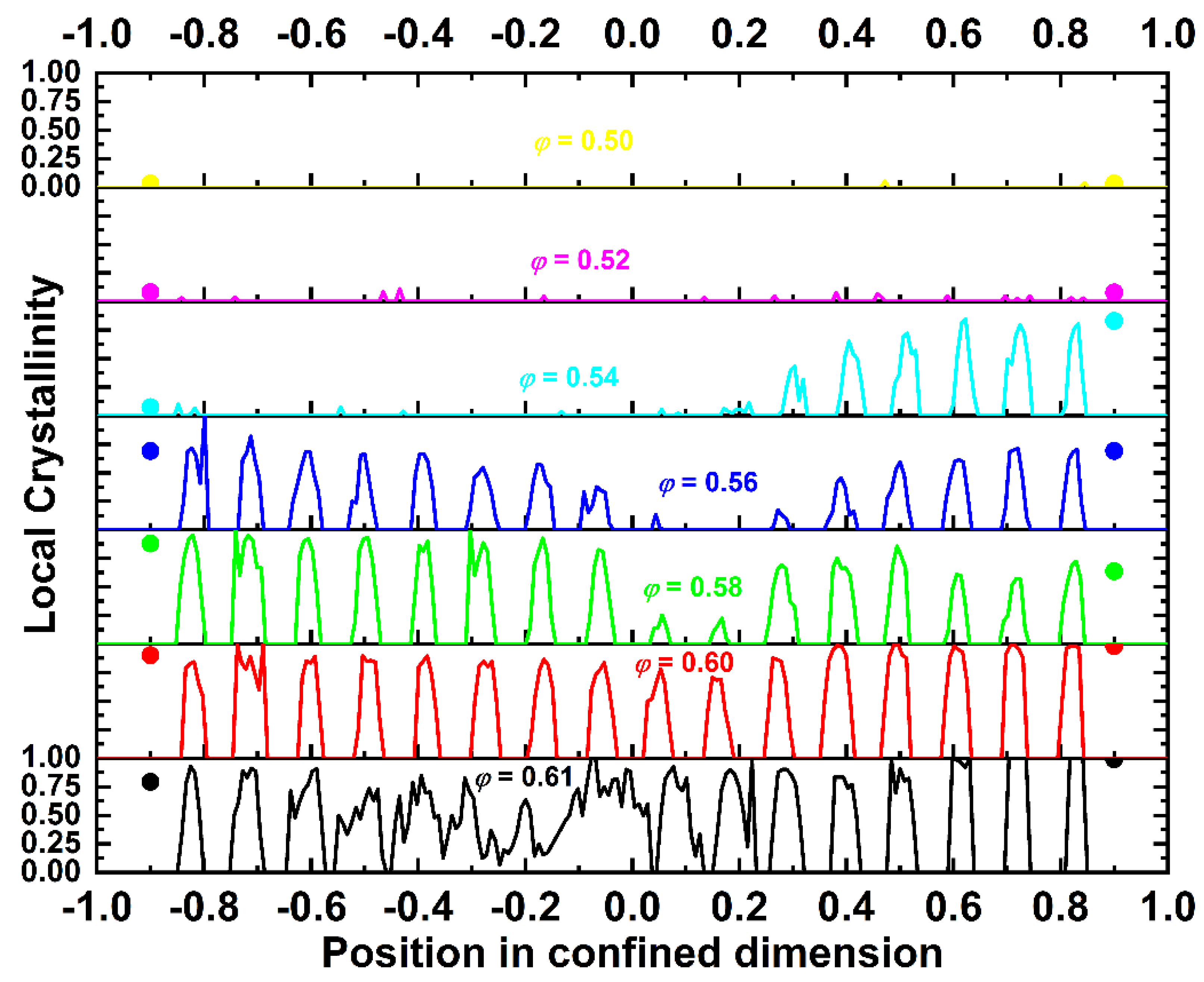
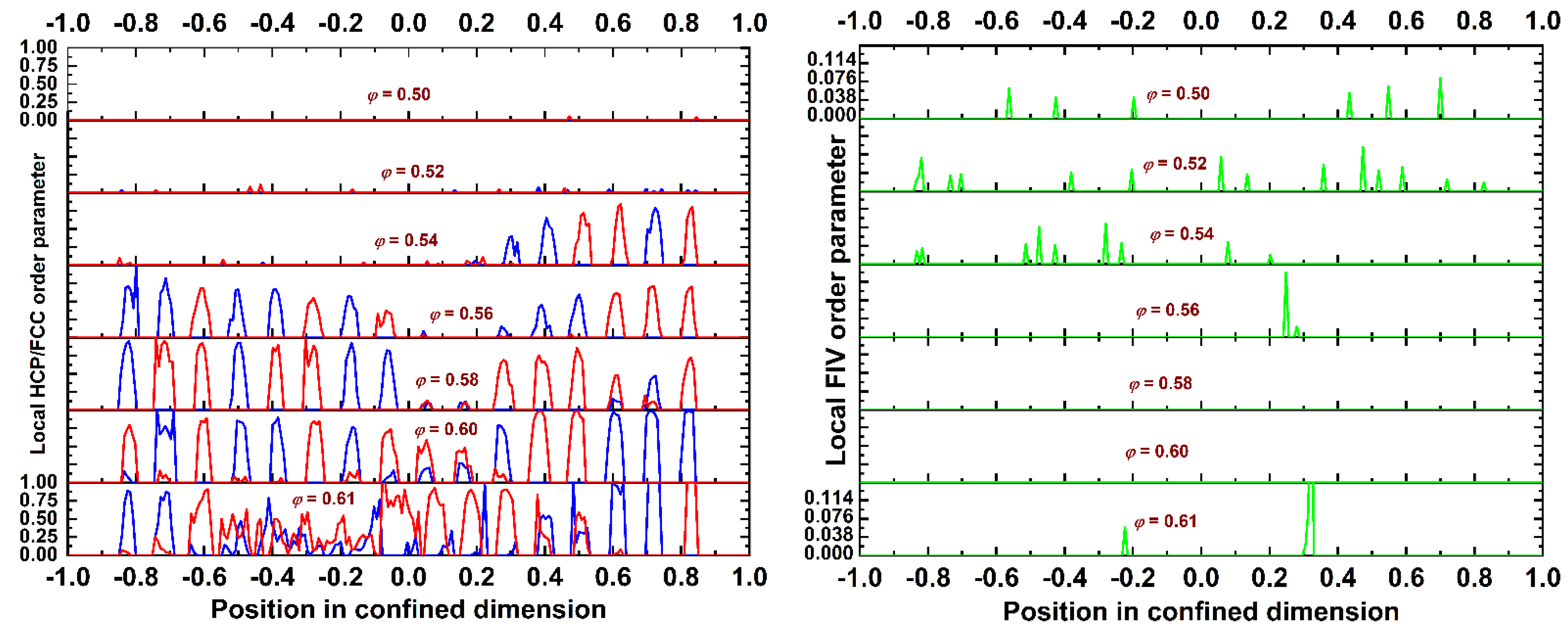
4.2. Local Density and Crystallinity
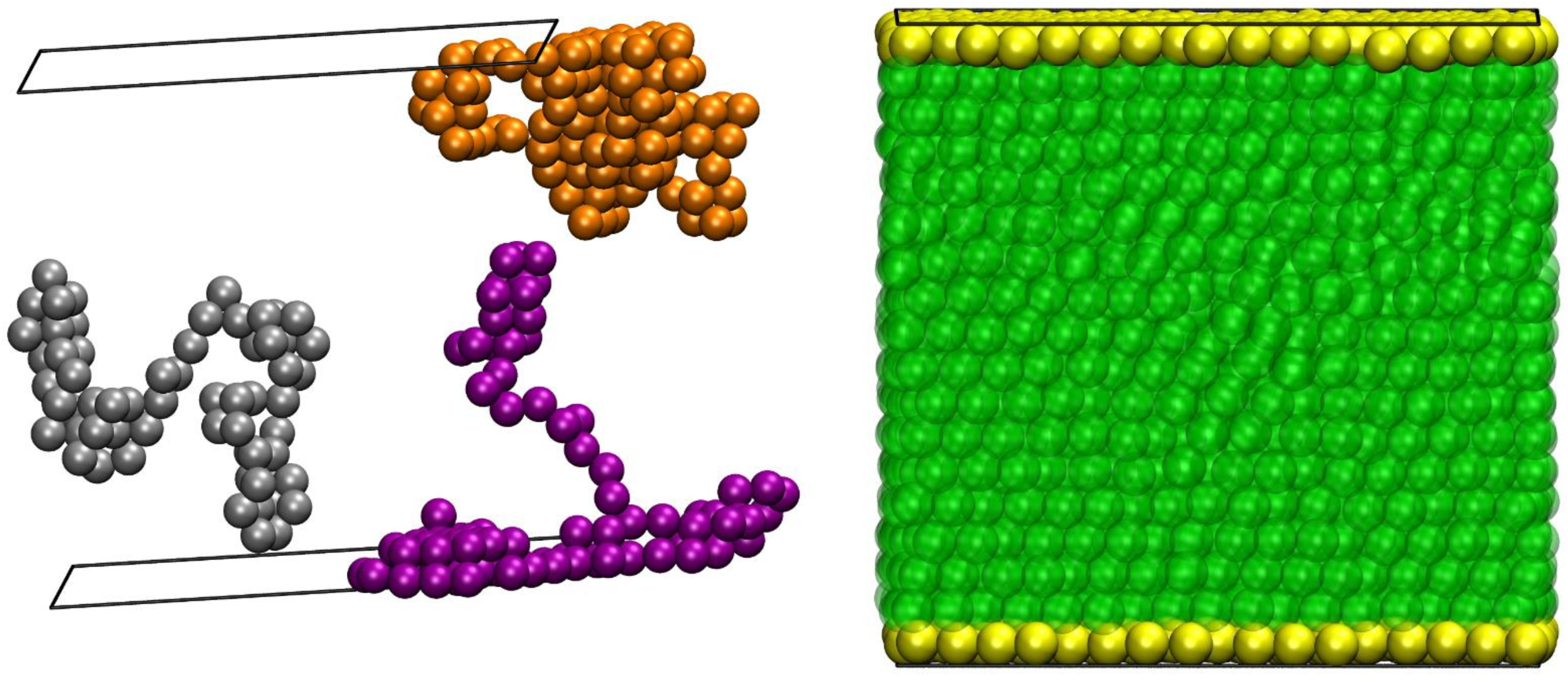
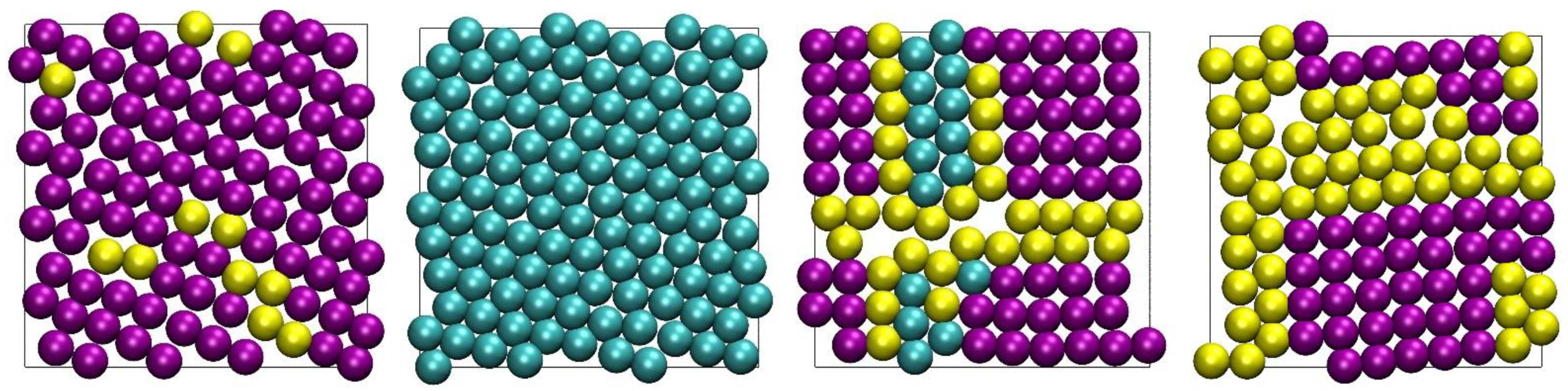
4.3. Snapshots of Computer-Generated Configurations
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AMO | Amorphous |
| BCC | Body-centered Cubic |
| CCE | Characteristic Crystallographic Element (norm) |
| FCC | Face-centered Cubic |
| FIV | Fivefold |
| HCP | Hexagonal close-packed |
| HEX | Hexagonal |
| HON | Honeycomb |
| HS | Hard Sphere |
| MC | Monte Carlo |
| PBC | Periodic Boundary Condition |
| PEN | Pentagonal |
| SQU | Square |
| TRI | Triangular |
References
- Chen, Y.S.; Yao, Z.W.; Tang, S.X.; Tong, H.; Yanagishima, T.; Tanaka, H.; Tan, P. Morphology selection kinetics of crystallization in a sphere. Nat. Phys. 2021, 17, 121–127. [Google Scholar] [CrossRef]
- Arai, S.; Tanaka, H. Surface-assisted single-crystal formation of charged colloids. Nat. Phys. 2017, 13, 503–509. [Google Scholar] [CrossRef]
- De Nijs, B.; Dussi, S.; Smallenburg, F.; Meeldijk, J.D.; Groenendijk, D.J.; Filion, L.; Imhof, A.; van Blaaderen, A.; Dijkstra, M. Entropy-driven formation of large icosahedral colloidal clusters by spherical confinement. Nat. Mater. 2015, 14, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.M.; Vitelli, V.; Chaikin, P.M. Pleats in crystals on curved surfaces. Nature 2010, 468, 947–951. [Google Scholar] [CrossRef]
- Tang, X.L.; Chen, W.; Li, L.B. The tough journey of polymer crystallization: Battling with chain flexibility and connectivity. Macromolecules 2019, 52, 3575–3591. [Google Scholar] [CrossRef]
- Agbolaghi, S.; Abbaspoor, S.; Abbasi, F. A comprehensive review on polymer single crystals-from fundamental concepts to applications. Prog. Polym. Sci. 2018, 81, 22–79. [Google Scholar] [CrossRef]
- Cheng, S.Z.D.; Lotz, B. Enthalpic and entropic origins of nucleation barriers during polymer crystallization: The hoffman-lauritzen theory and beyond. Polymer 2005, 46, 8662–8681. [Google Scholar] [CrossRef]
- Strobl, G. Crystallization and melting of bulk polymers: New observations, conclusions and a thermodynamic scheme. Prog. Polym. Sci. 2006, 31, 398–442. [Google Scholar] [CrossRef]
- Luo, C.F.; Sommer, J.U. Frozen topology: Entanglements control nucleation and crystallization in polymers. Phys. Rev. Lett. 2014, 112. [Google Scholar] [CrossRef]
- Luo, C.F.; Sommertt, J.U. Role of thermal history and entanglement related thickness selection in polymer crystallization. ACS Macro Lett. 2016, 5, 35–39. [Google Scholar] [CrossRef]
- Li, C.Y. The rise of semicrystalline polymers and why are they still interesting. Polymer 2020, 211. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Rintoul, M.D.; Torquato, S. Metastability and crystallization in hard-sphere systems. Phys. Rev. Lett. 1996, 77, 4198–4201. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-driven crystallization in dense systems of athermal chain molecules. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Twinning of polymer crystals suppressed by entropy. Symmetry 2014, 6, 758–780. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter. 2015, 11, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- Ni, R.; Dijkstra, M. Effect of bond length fluctuations on crystal nucleation of hard bead chains. Soft Matter. 2013, 9, 365–369. [Google Scholar] [CrossRef]
- Shakirov, T. Crystallisation in melts of short, semi-flexible hard-sphere polymer chains: The role of the non-bonded interaction range. Entropy 2019, 21, 856. [Google Scholar] [CrossRef]
- Shakirov, T.; Paul, W. Crystallization in melts of short, semiflexible hard polymer chains: An interplay of entropies and dimensions. Phys. Rev. E 2018, 97. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter. 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous crystallization in athermal polymer packings. Int. J. Mol. Sci. 2013, 14, 332–358. [Google Scholar] [CrossRef]
- Dietz, J.D.; Hoy, R.S. Two-stage athermal solidification of semiflexible polymers and fibers. Soft Matter. 2020, 16, 6206–6217. [Google Scholar] [CrossRef]
- Schilling, T.; Schope, H.J.; Oettel, M.; Opletal, G.; Snook, I. Precursor-mediated crystallization process in suspensions of hard spheres. Phys. Rev. Lett. 2010, 105. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, T.; Tanaka, H. Formation of a crystal nucleus from liquid. Proc. Natl. Acad. Sci. USA 2010, 107, 14036–14041. [Google Scholar] [CrossRef] [PubMed]
- Zaccarelli, E.; Valeriani, C.; Sanz, E.; Poon, W.C.K.; Cates, M.E.; Pusey, P.N. Crystallization of hard-sphere glasses. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef]
- Williams, S.R.; Royall, C.P.; Bryant, G. Crystallization of dense binary hard-sphere mixtures with marginal size ratio. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
- O’Malley, B.; Snook, I. Structure of hard-sphere fluid and precursor structures to crystallization. J. Chem. Phys. 2005, 123. [Google Scholar] [CrossRef]
- O’Malley, B.; Snook, I. Crystal nucleation in the hard sphere system. Phys. Rev. Lett. 2003, 90. [Google Scholar] [CrossRef]
- Isobe, M.; Krauth, W. Hard-sphere melting and crystallization with event-chain monte carlo. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Auer, S.; Frenkel, D. Line tension controls wall-induced crystal nucleation in hard-sphere colloids. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Van Blaaderen, A.; Ruel, R.; Wiltzius, P. Template-directed colloidal crystallization. Nature 1997, 385, 321–324. [Google Scholar] [CrossRef]
- Chen, D.; Torquato, S. Confined disordered strictly jammed binary sphere packings. Phys. Rev. E 2015, 92. [Google Scholar] [CrossRef] [PubMed]
- Fortini, A.; Dijkstra, M. Phase behaviour of hard spheres confined between parallel hard plates: Manipulation of colloidal crystal structures by confinement. J. Phys. Condens. Matter. 2006, 18, L371–L378. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; van Roij, R.; Roth, R.; Fortini, A. Effect of many-body interactions on the bulk and interfacial phase behavior of a model colloid-polymer mixture. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef] [PubMed]
- Fortini, A.; Schmidt, M.; Dijkstra, M. Phase behavior and structure of model colloid-polymer mixtures confined between two parallel planar walls. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef]
- Benito, J.; Karayiannis, N.C.; Laso, M. Confined polymers as self-avoiding random walks on restricted lattices. Polymers 2018, 10, 1394. [Google Scholar] [CrossRef]
- Sandomirski, K.; Walta, S.; Dubbert, J.; Allahyarov, E.; Schofield, A.B.; Lowen, H.; Richtering, W.; Egelhaaf, S.U. Heterogeneous crystallization of hard and soft spheres near flat and curved walls. Eur. Phys. J. Spec. Top. 2014, 223, 439–454. [Google Scholar] [CrossRef]
- Luo, C.F.; Kroger, M.; Sommer, J.U. Molecular dynamics simulations of polymer crystallization under confinement: Entanglement effect. Polymer 2017, 109, 71–84. [Google Scholar] [CrossRef]
- Zhang, W.; Zou, L. Molecular dynamics simulations of crystal nucleation near interfaces in incompatible polymer blends. Polymers 2021, 13, 347. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Vega, C.; Valeriani, C.; Frenkel, D.; Sanz, E. Heterogeneous versus homogeneous crystal nucleation of hard spheres. Soft Matter. 2019, 15, 9625–9631. [Google Scholar] [CrossRef]
- Curk, T.; de Hoogh, A.; Martinez-Veracoechea, F.J.; Eiser, E.; Frenkel, D.; Dobnikar, J.; Leunissen, M.E. Layering, freezing, and re-entrant melting of hard spheres in soft confinement. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef] [PubMed]
- Soik, S.M.; Sharp, T.A. Effects of spherical confinement and backbone stiffness on flexible polymer jamming. Phys. Rev. E 2019, 99. [Google Scholar] [CrossRef] [PubMed]
- Meldrum, F.C.; O’Shaughnessy, C. Crystallization in confinement. Adv. Mater. 2020, 32. [Google Scholar] [CrossRef] [PubMed]
- Bechinger, C. Colloidal suspensions in confined geometries. Curr. Opin. Colloid Interface Sci. 2002, 7, 204–209. [Google Scholar] [CrossRef]
- Pusey, P.N.; Vanmegen, W. Phase-behavior of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Neser, S.; Bechinger, C.; Leiderer, P.; Palberg, T. Finite-size effects on the closest packing of hard spheres. Phys. Rev. Lett. 1997, 79, 2348–2351. [Google Scholar] [CrossRef]
- Pieranski, P.; Strzelecki, L.; Pansu, B. Thin colloidal crystals. Phys. Rev. Lett. 1983, 50, 900–903. [Google Scholar] [CrossRef]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Monte carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of local structure in 2-d and 3-d atomic systems through crystallographic analysis. Crystals 2020, 10, 1008. [Google Scholar] [CrossRef]
- Herranz, M.; Santiago, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Crystal, fivefold and glass formation in clusters of polymers interacting with the square well potential. Polymers 2020, 12, 1111. [Google Scholar] [CrossRef]
- Pant, P.V.K.; Theodorou, D.N. Variable connectivity method for the atomistic monte-carlo simulation of polydisperse polymer melts. Macromolecules 1995, 28, 7224–7234. [Google Scholar] [CrossRef]
- Mavrantzas, V.G.; Boone, T.D.; Zervopoulou, E.; Theodorou, D.N. End-bridging Monte Carlo: A fast algorithm for atomistic simulation of condensed phases of long polymer chains. Macromolecules 1999, 32, 5072–5096. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter. 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. Vmd: Visual molecular dynamics. J. Mol. Graphics Modell. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Hoy, R.S.; Karayiannis, N.C. Simple model for chain packing and crystallization of soft colloidal polymers. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef]
- Kumar, S.K.; Vacatello, M.; Yoon, D.Y. Off-lattice monte-carlo simulations of polymer melts confined between 2 plates. 2. Effects of chain-length and plate separation. Macromolecules 1990, 23, 2189–2197. [Google Scholar] [CrossRef]
- Kumar, S.K.; Vacatello, M.; Yoon, D.Y. Off-lattice monte-carlo simulations of polymer melts confined between 2 plates. J. Chem. Phys. 1988, 89, 5206–5215. [Google Scholar] [CrossRef]







| φ | 0.50 | 0.52 | 0.54 | 0.56 | 0.58 | 0.60 | 0.61 |
|---|---|---|---|---|---|---|---|
| dwall (n = 1200) | 10.79 | 10.65 | 10.52 | 10.39 | 10.27 | 10.16 | 10.10 |
| dwall (n = 4800) | 17.13 | 16.91 | 16.70 | 16.50 | 16.30 | 16.12 | 16.03 |
| φwall (n = 1200) | 0.551 | 0.574 | 0.596 | 0.620 | 0.643 | 0.665 | 0.677 |
| φwall (n = 4800) | 0.531 | 0.552 | 0.574 | 0.596 | 0.618 | 0.640 | 0.651 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers 2021, 13, 1352. https://doi.org/10.3390/polym13091352
Ramos PM, Herranz M, Foteinopoulou K, Karayiannis NC, Laso M. Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers. 2021; 13(9):1352. https://doi.org/10.3390/polym13091352
Chicago/Turabian StyleRamos, Pablo Miguel, Miguel Herranz, Katerina Foteinopoulou, Nikos Ch. Karayiannis, and Manuel Laso. 2021. "Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement" Polymers 13, no. 9: 1352. https://doi.org/10.3390/polym13091352
APA StyleRamos, P. M., Herranz, M., Foteinopoulou, K., Karayiannis, N. C., & Laso, M. (2021). Entropy-Driven Heterogeneous Crystallization of Hard-Sphere Chains under Unidimensional Confinement. Polymers, 13(9), 1352. https://doi.org/10.3390/polym13091352








