Characteristics of Poly(vinyl Alcohol) (PVA) Based Composites Integrated with Green Synthesized Al3+-Metal Complex: Structural, Optical, and Localized Density of State Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
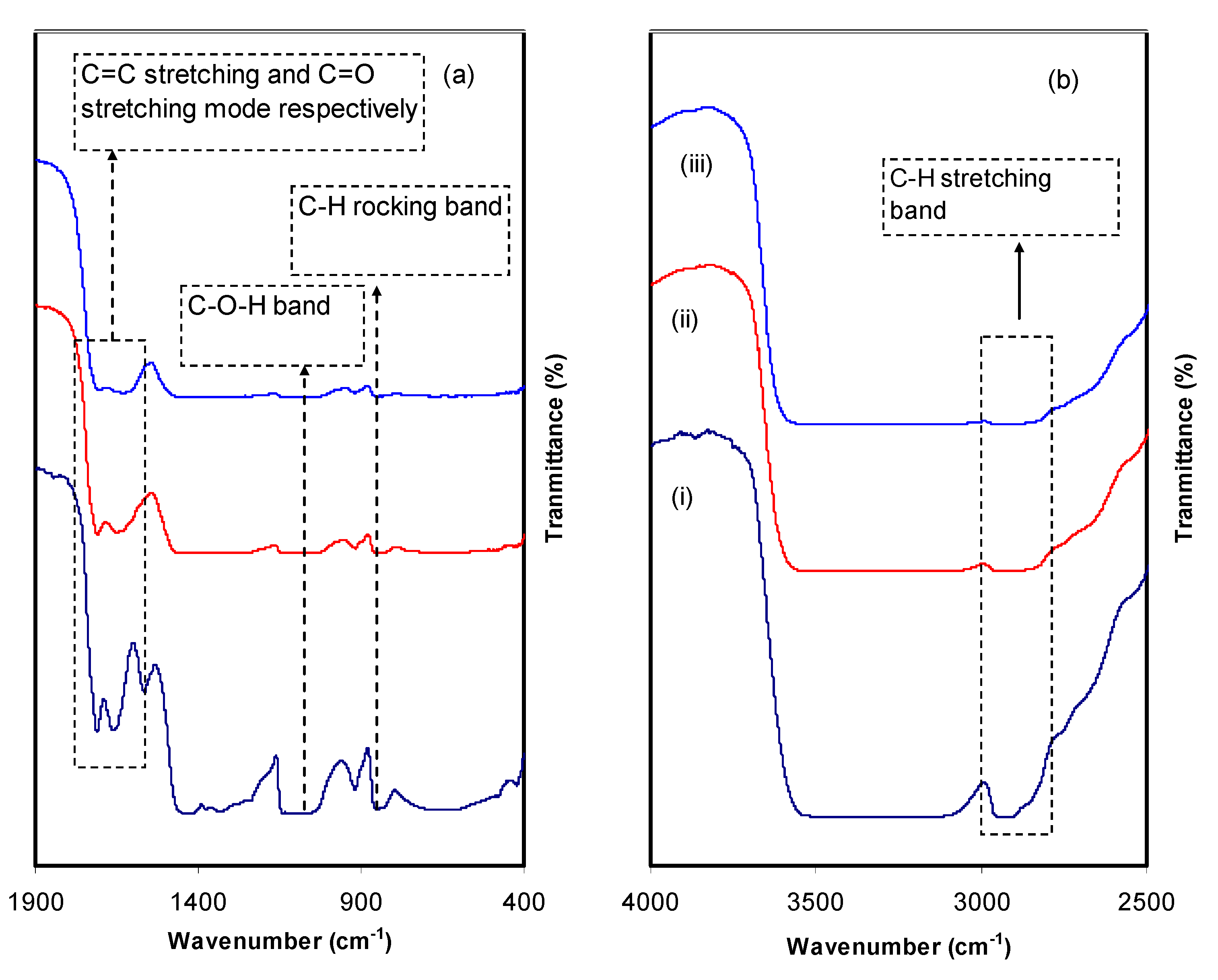
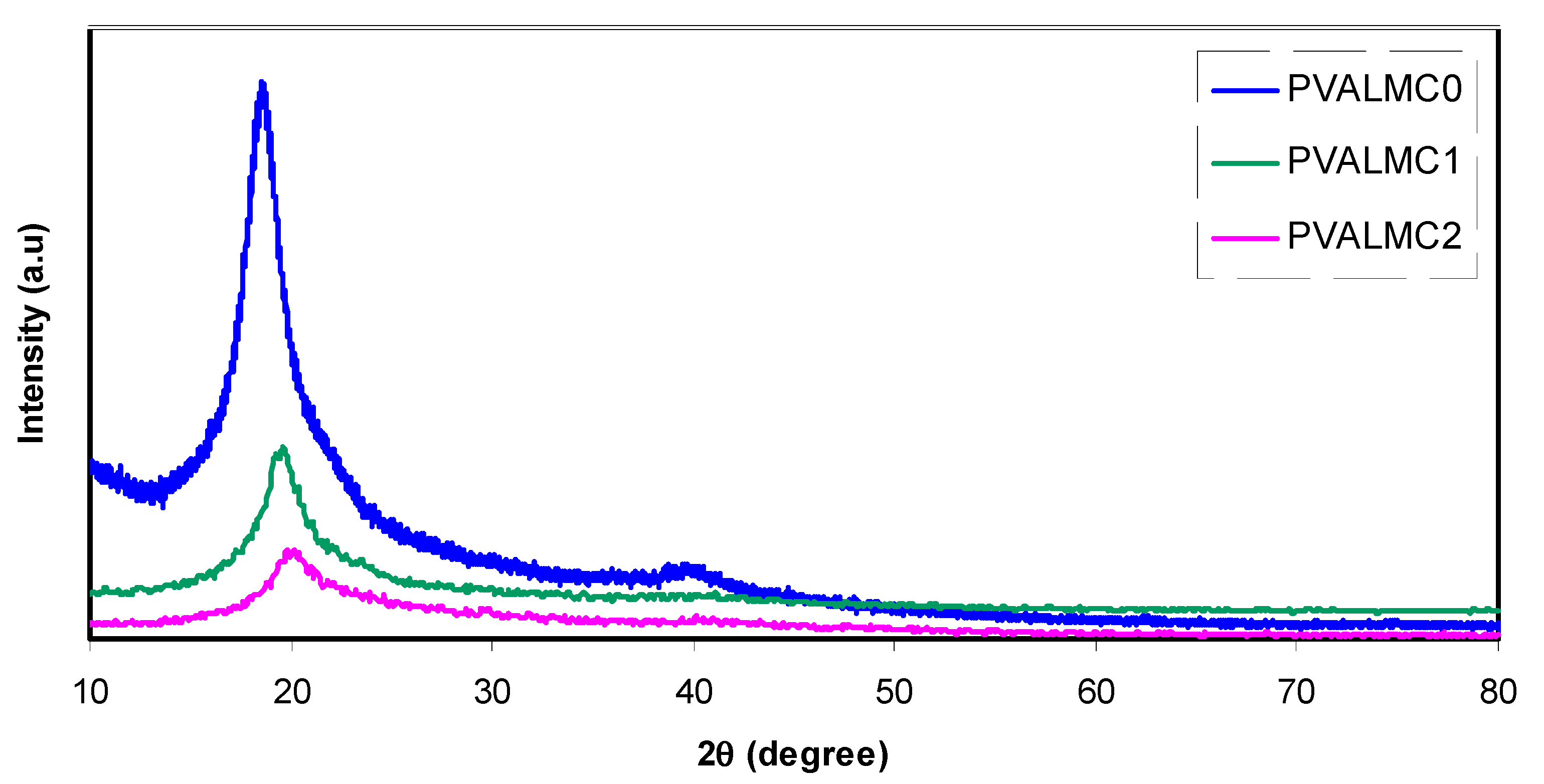
2.3. X-ray Diffraction and FTIR Measurements
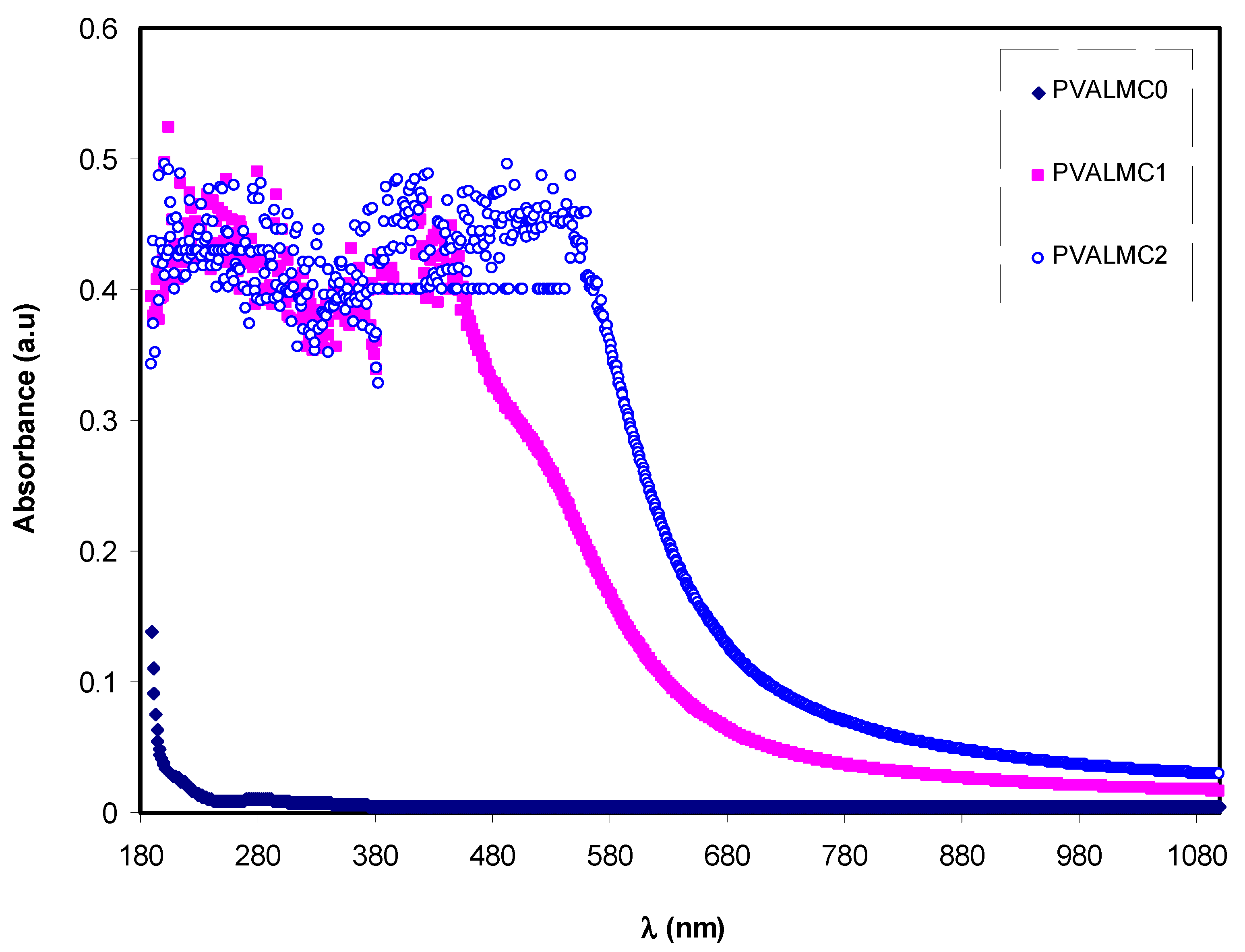
2.4. UV-Vis Spectroscopy
3. Results and Discussion
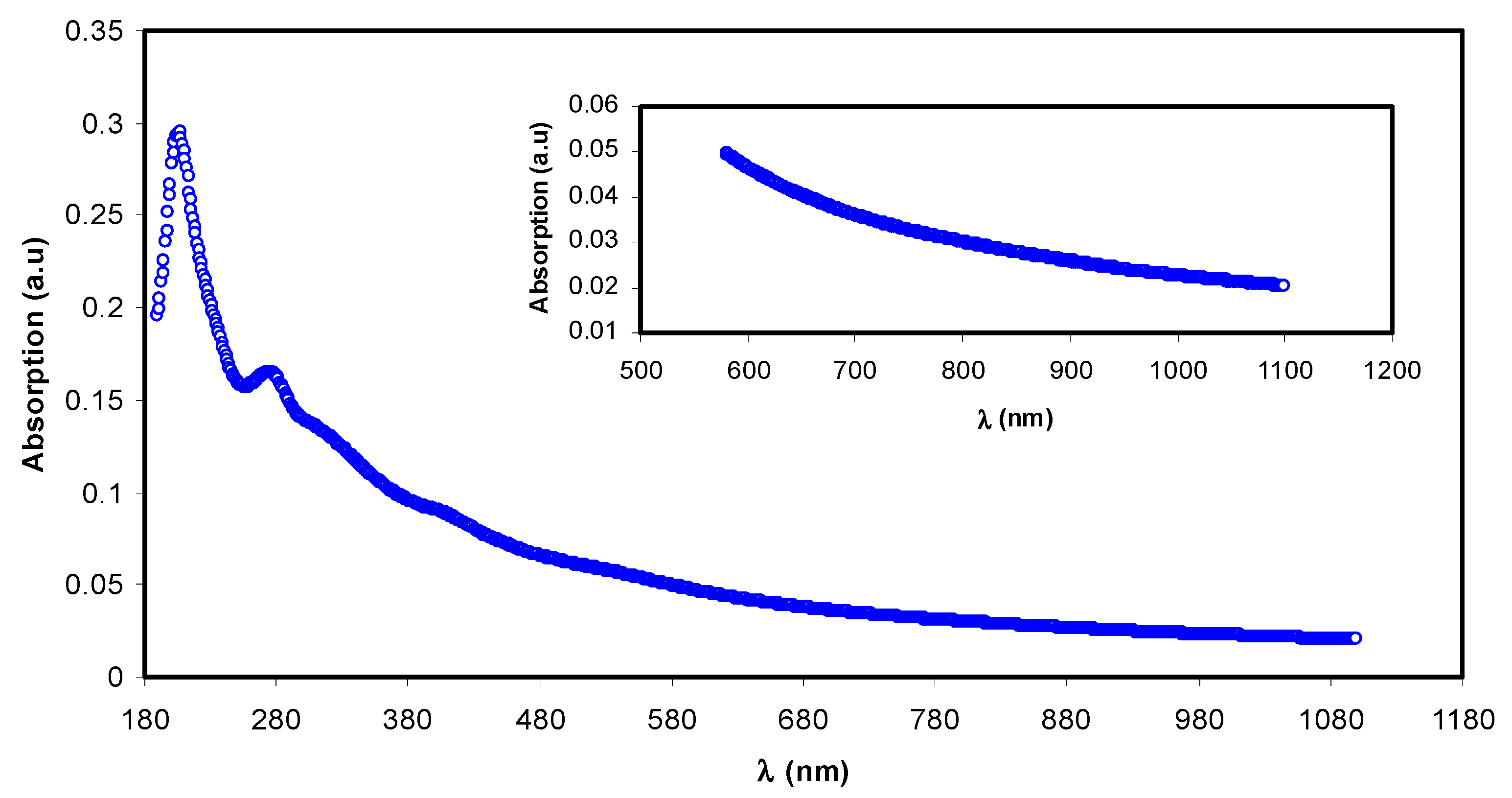
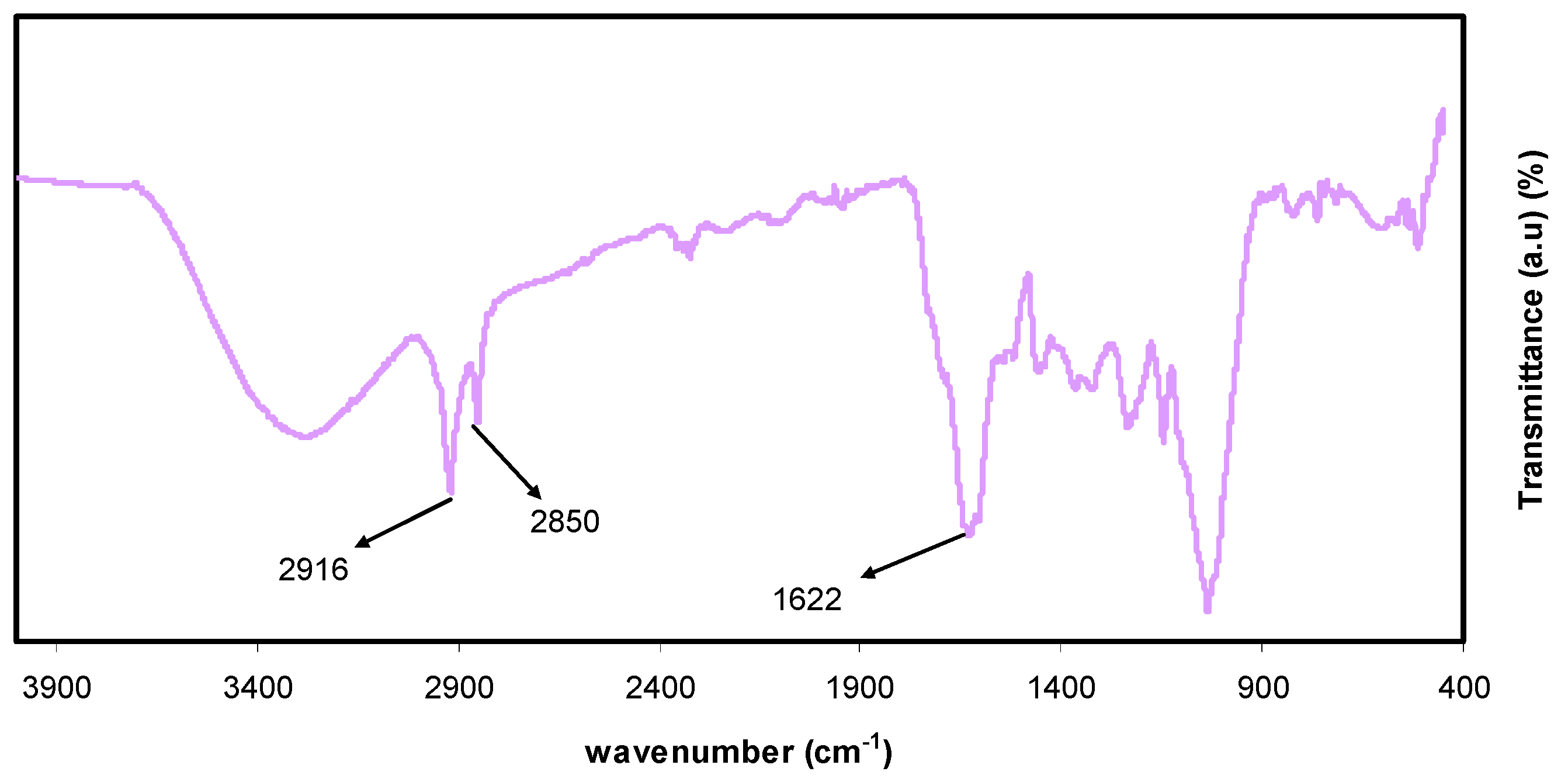
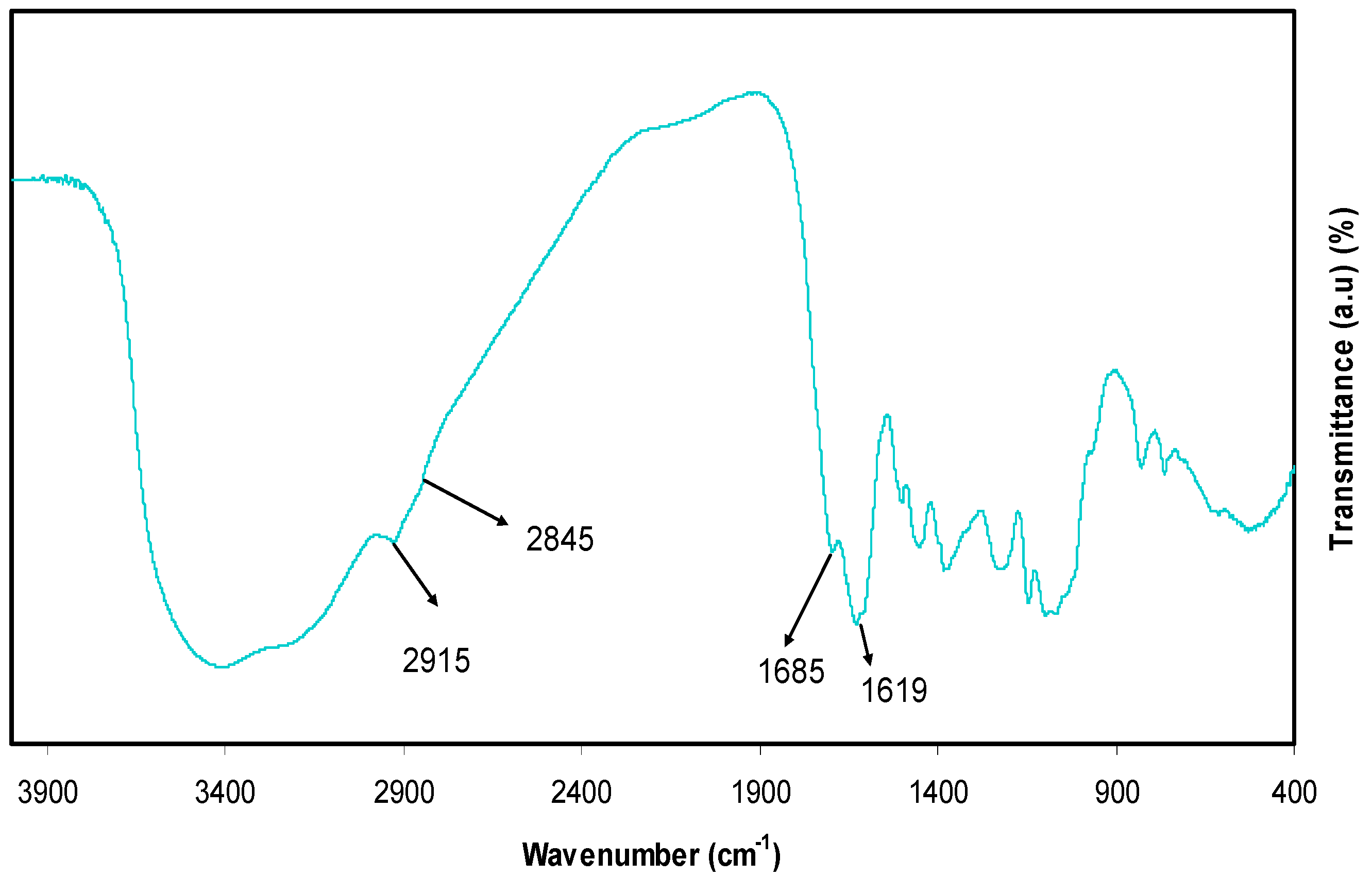
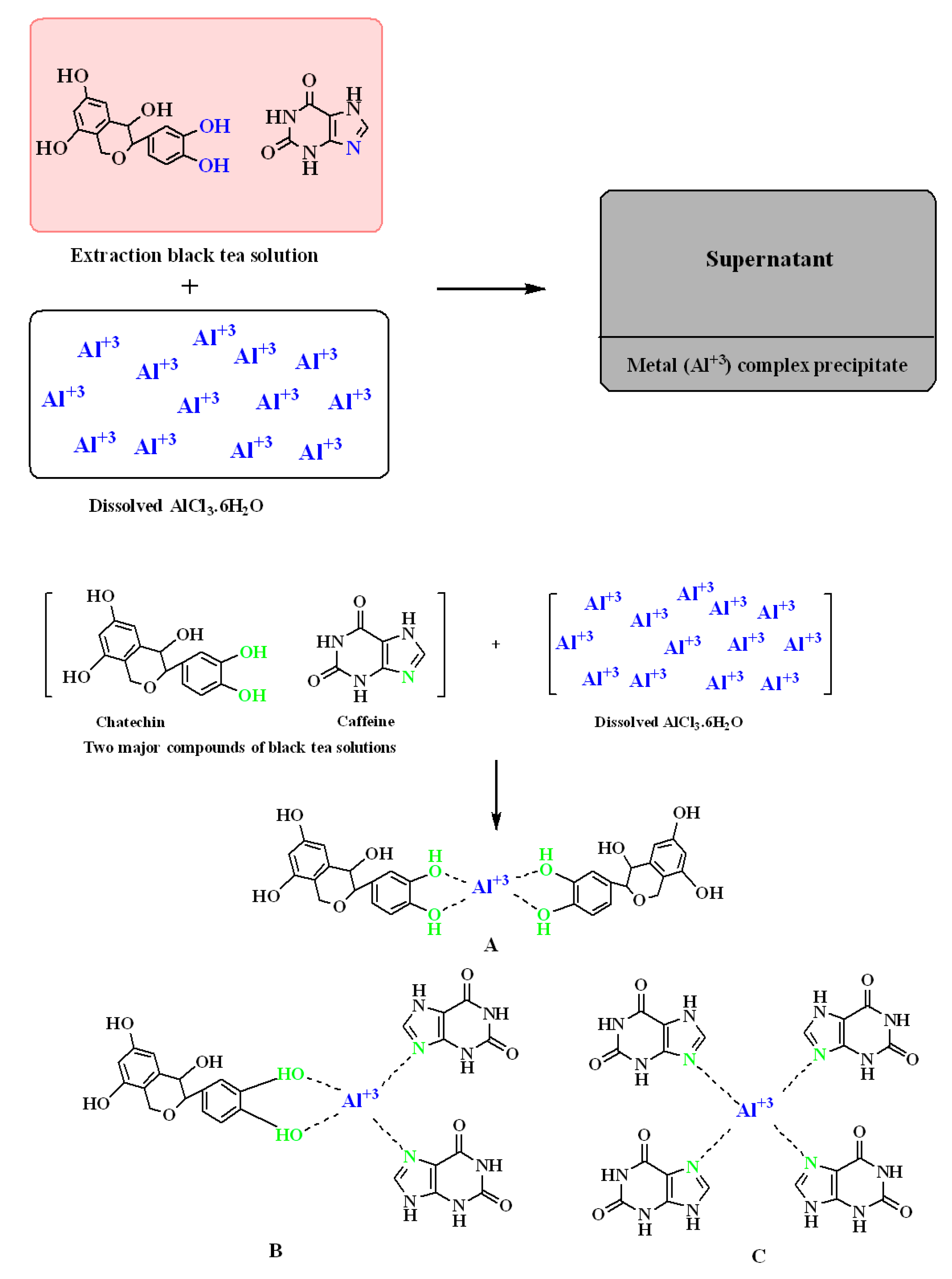
3.1. UV-Vis and FTIR Study of Al3+-Metal Complex
3.2. FTIR Analysis for PVA/Al+3-Complex Hybrids
3.3. XRD Study of PVA/Al+3-Complex Hybrids
3.4. Optical Properties
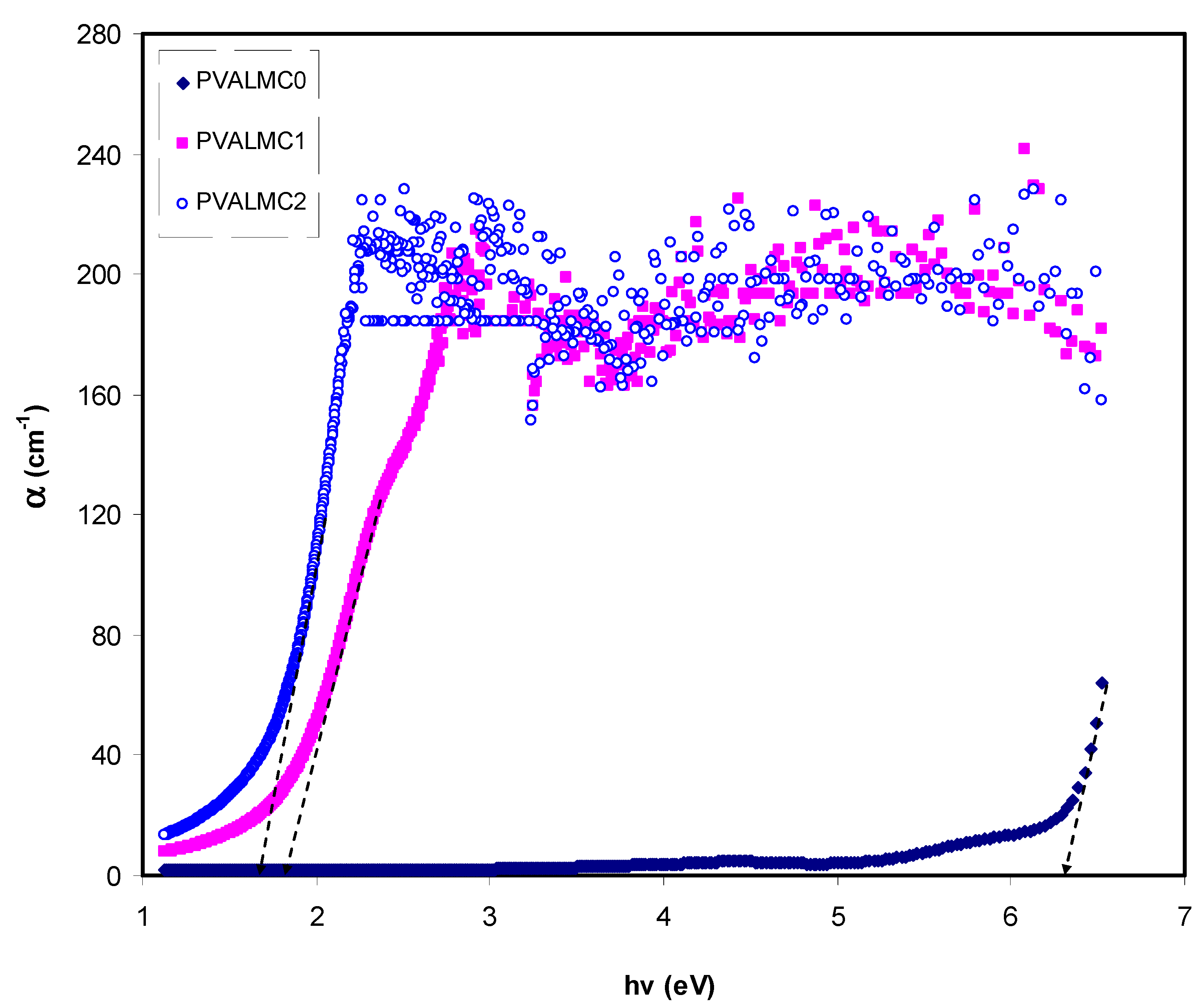
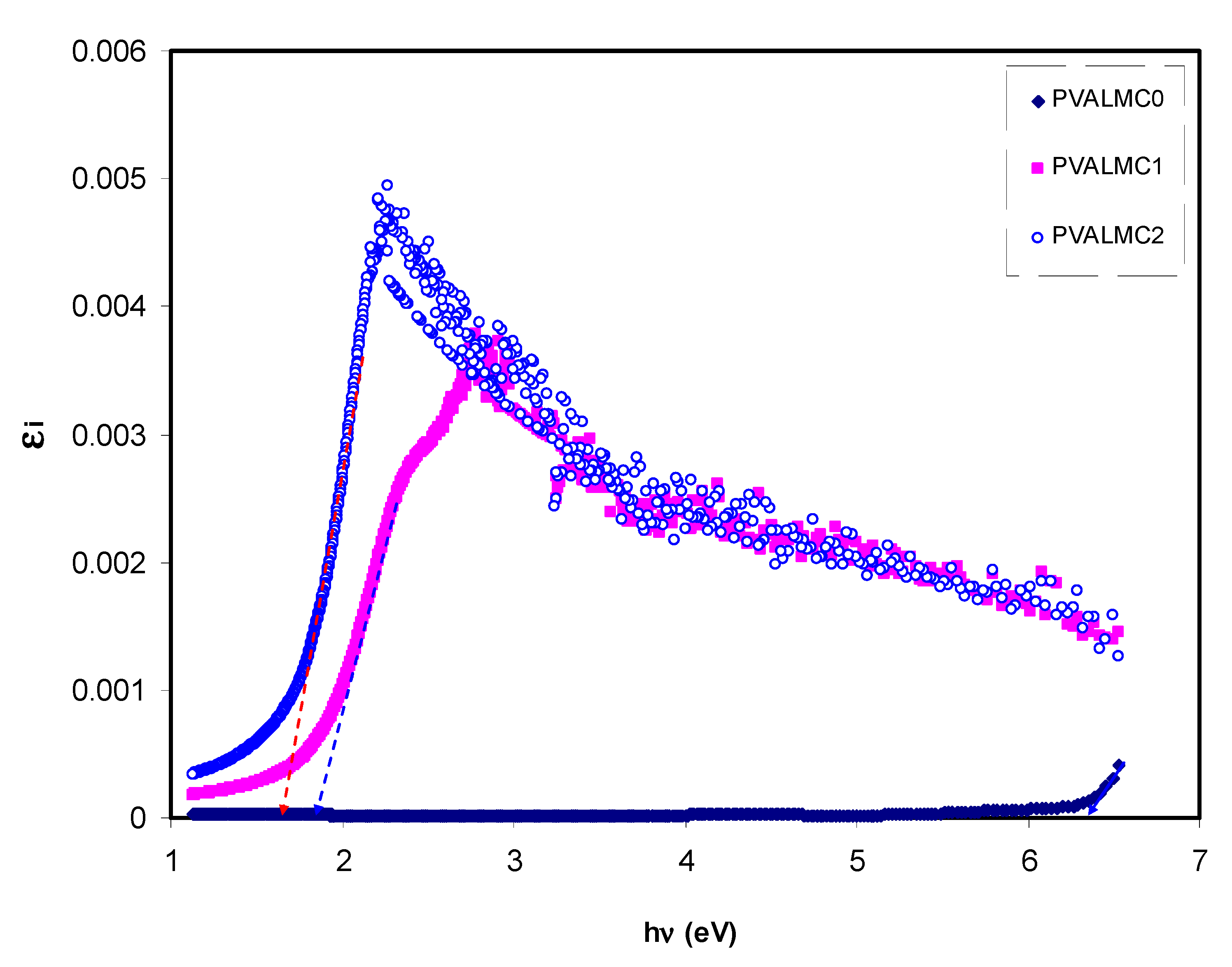
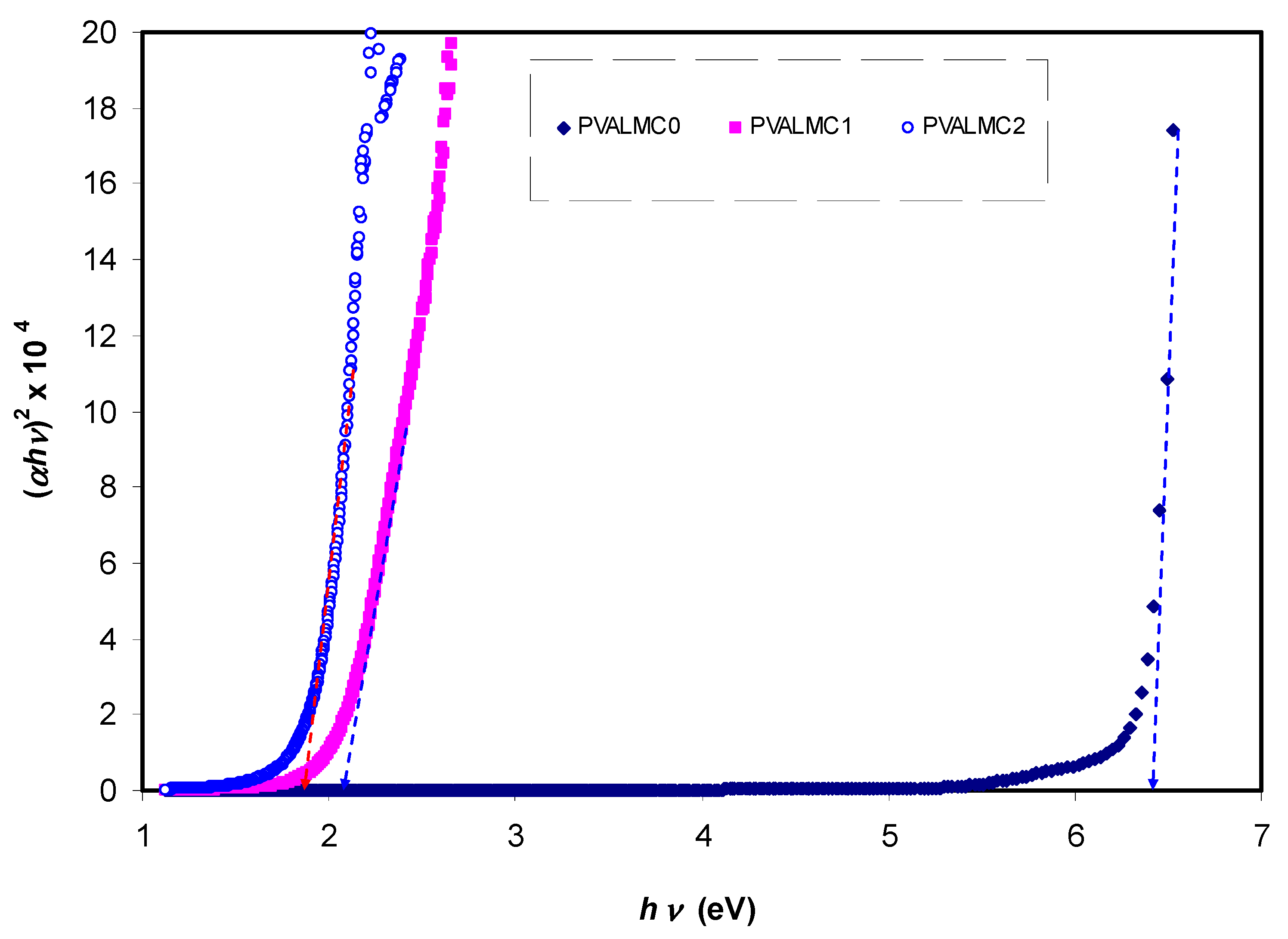
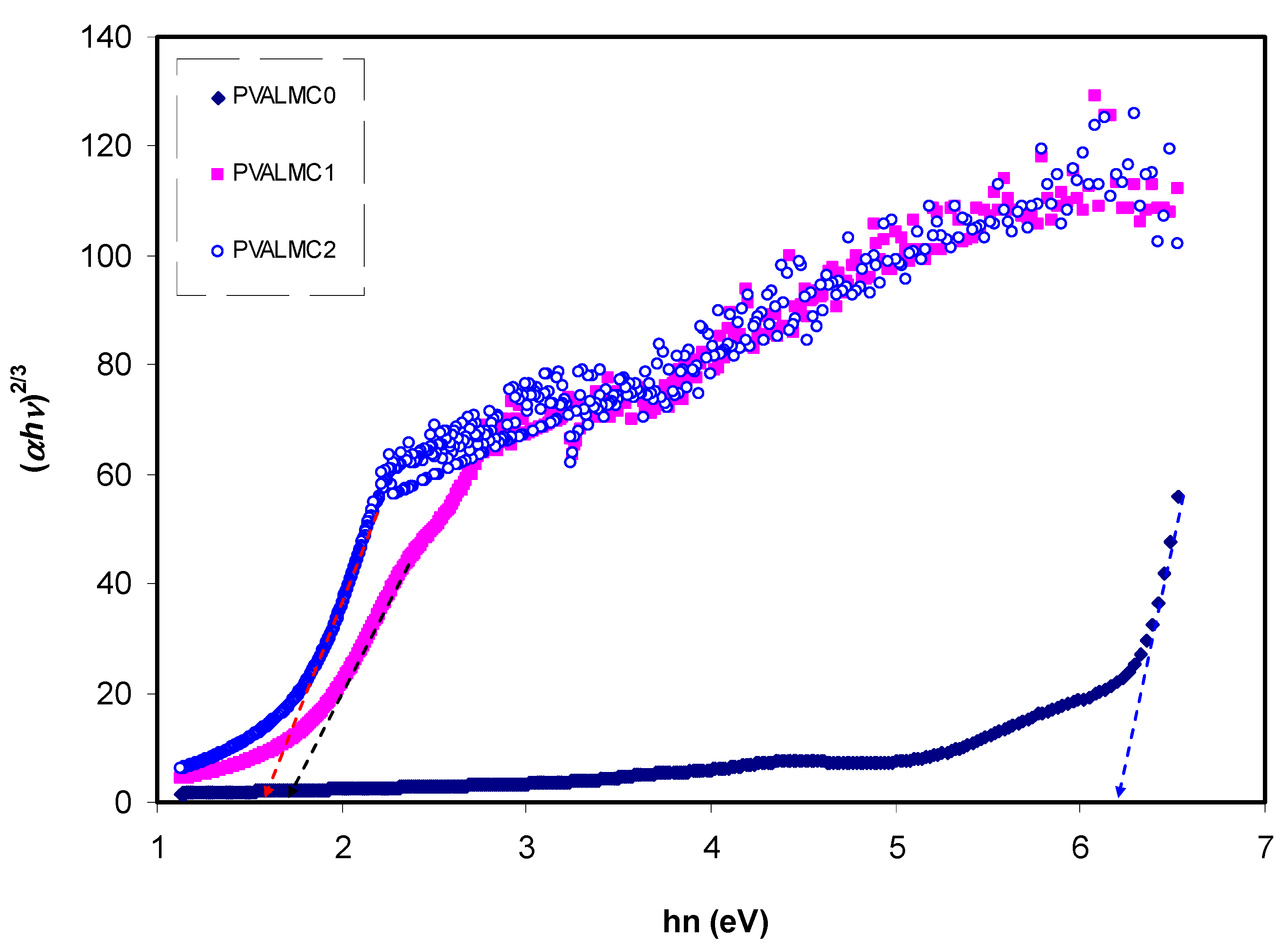
3.4.1. Absorbance and Absorption Edge Study
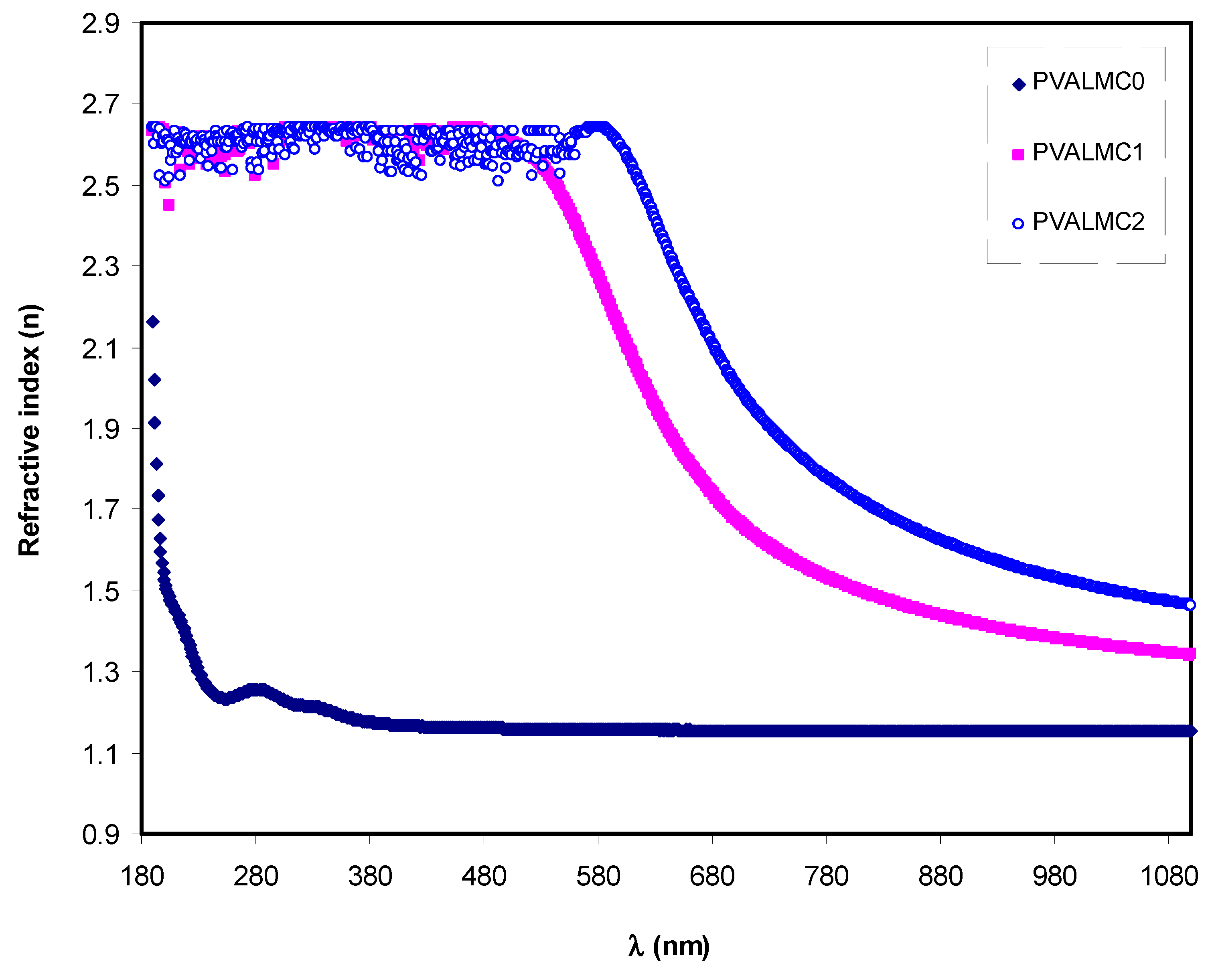
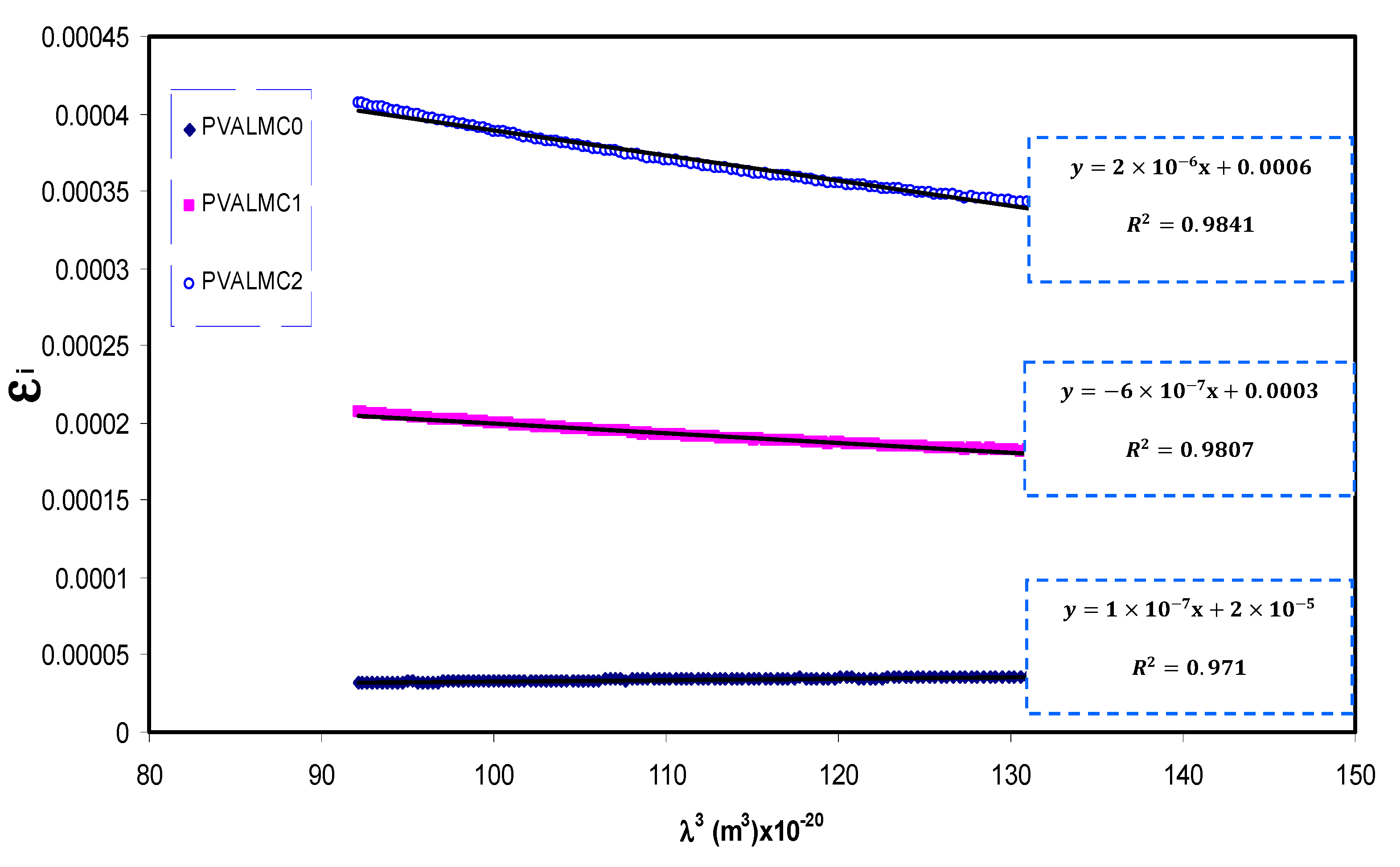
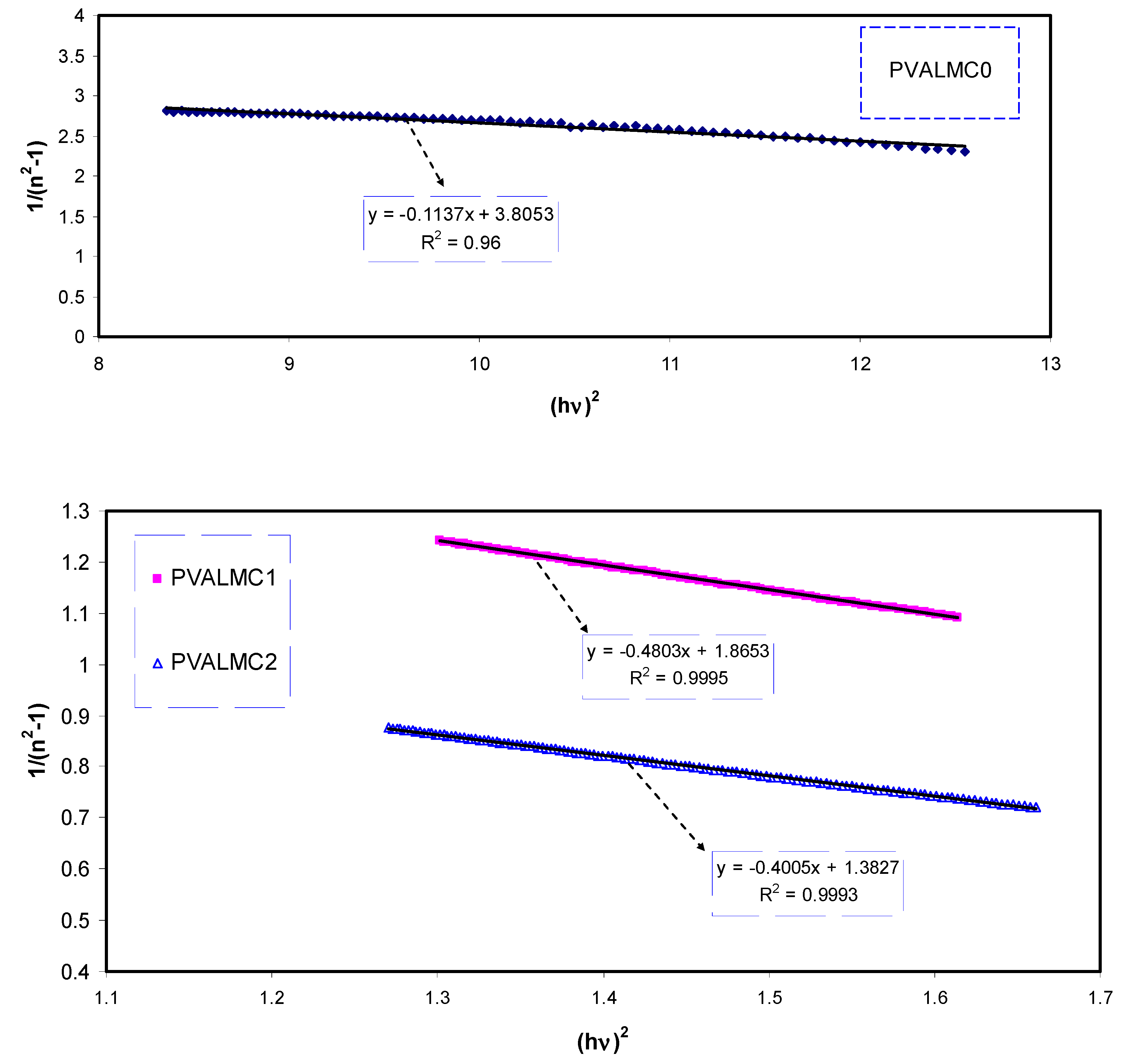
3.4.2. Refractive Index and Localized Density of State (N/m*) Study
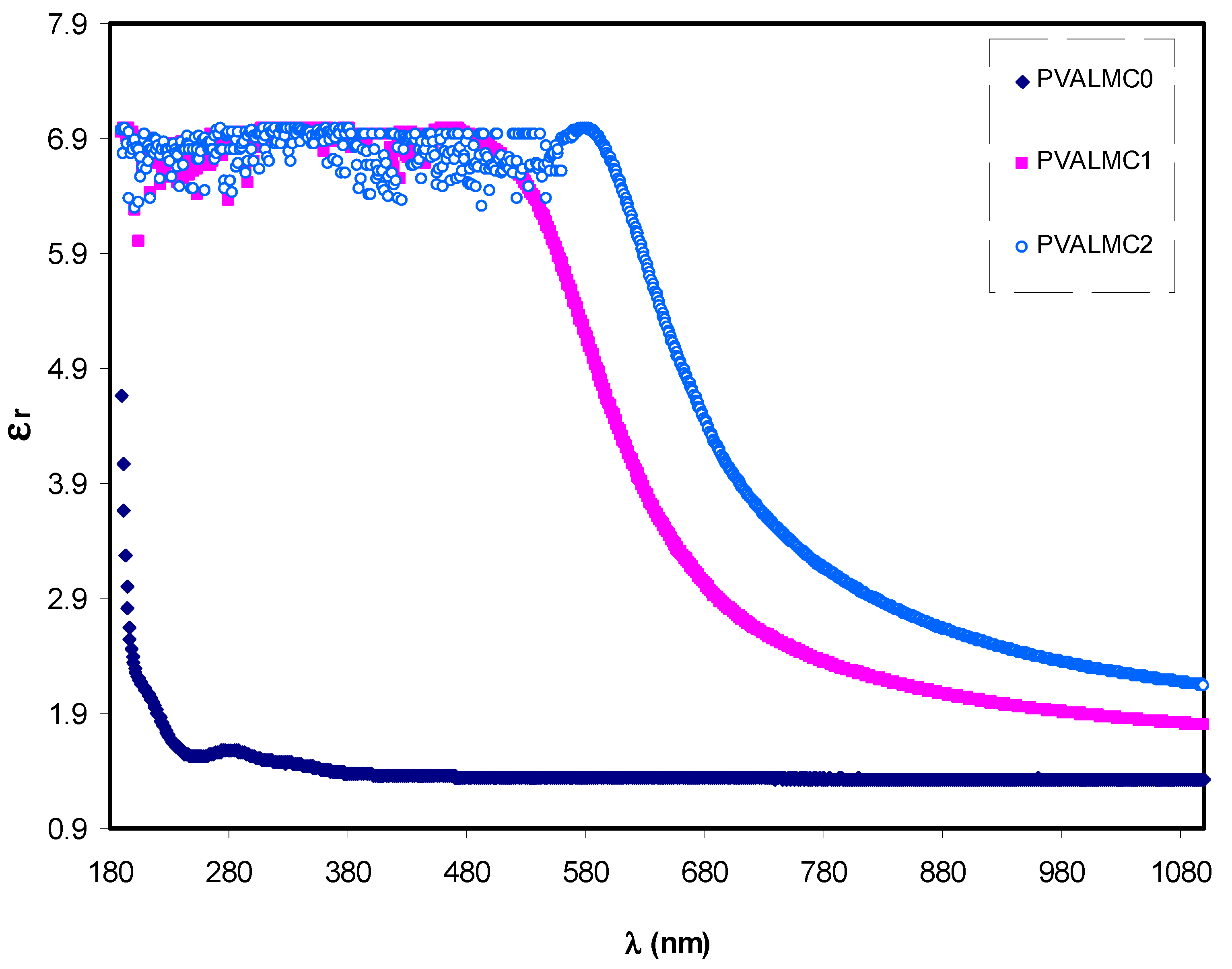
3.4.3. Optical Dielectric Losses and Tauc’s Model
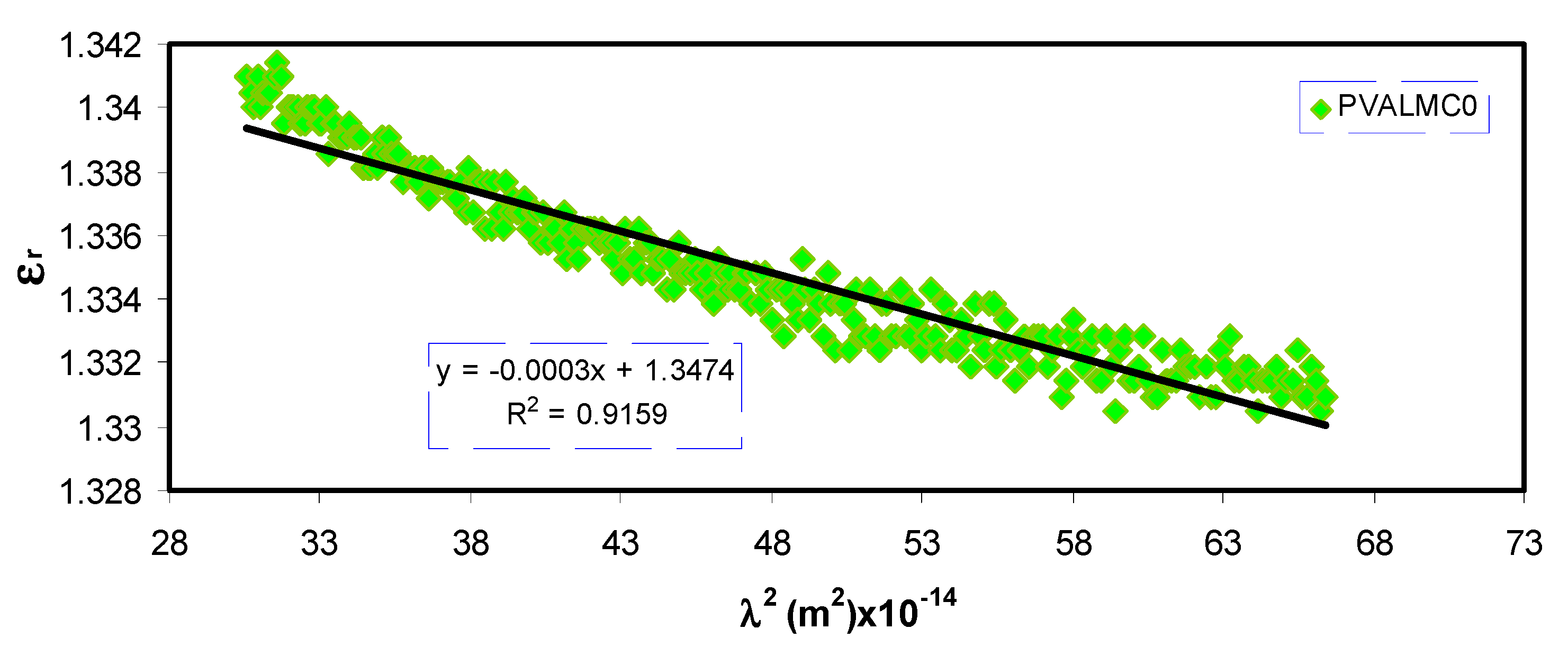
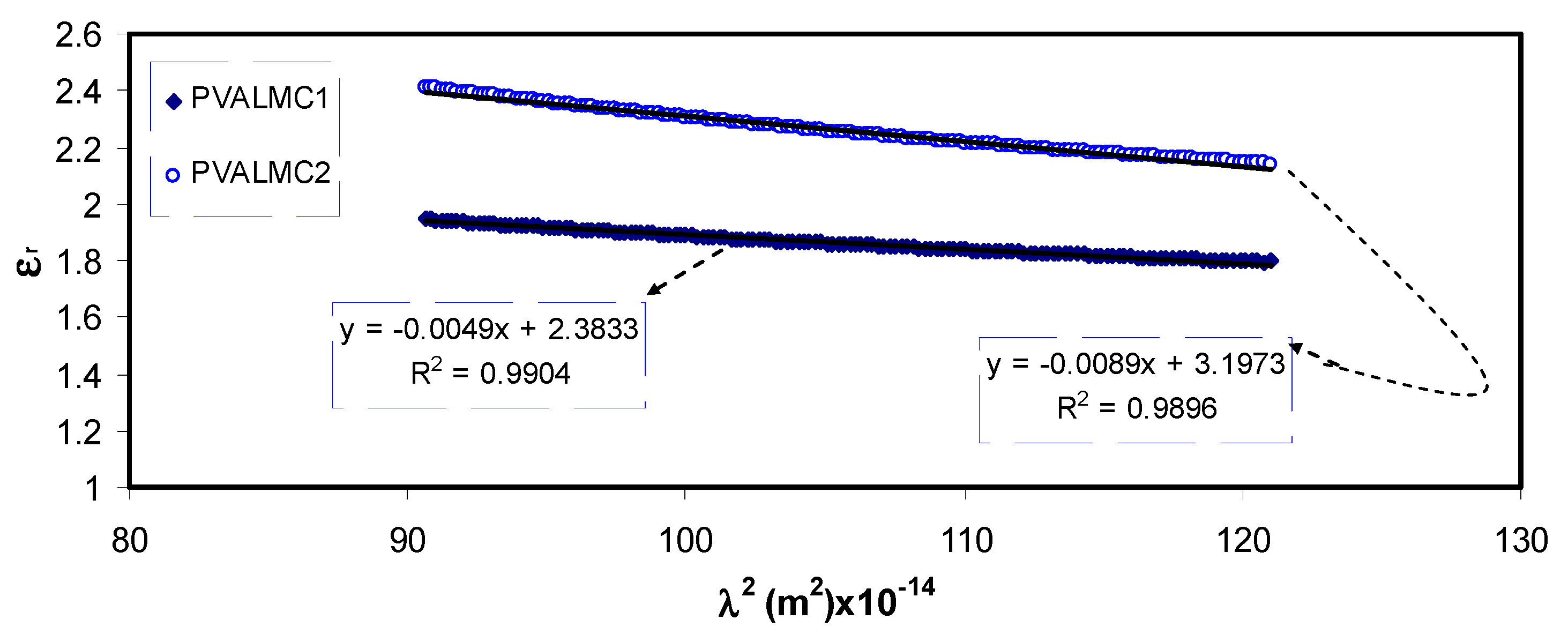
3.4.4. Wemple-DiDomenico (WD) Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, Y.Y.; Chien, W.C.; Chen, S.Y. Preparation and optical properties of organic/inorganic nanocomposite materials by UV curing process. Mater. Des. 2010, 31, 2061–2070. [Google Scholar] [CrossRef]
- Hegde, S.S.; Kunjomana, A.G.; Chandrasekharan, K.A.; Ramesh, K.; Prashantha, M. Optical and electrical properties of SnS semiconductor crystals grown by physical vapor deposition technique. Phys. B Condens. Matter 2011, 406, 1143–1148. [Google Scholar] [CrossRef]
- Aguilera, I.; Palacios, P.; Wahnón, P. Optical properties of chalcopyrite-type intermediate transition metal band materials from first principles. Thin Solid Film 2008, 516, 7055–7059. [Google Scholar] [CrossRef]
- Paquin, F.; Rivnay, J.; Salleo, A.; Stingelin, N.; Silva, C. Multi-phase semicrystalline microstructures drive exciton dissociation in neat plastic semiconductors. J. Mater. Chem. C 2015, 3, 10715–10722. [Google Scholar] [CrossRef]
- Macek, T.; Mackova, M. Potential of Biosorption Technology. In Microbial Biosorption of Metals; Springer: Dordrecht, The Netherlands, 2011; pp. 7–17. [Google Scholar] [CrossRef]
- Karman, S.B.; Diah, S.Z.M.; Gebeshuber, I.C. Raw Materials Synthesis from Heavy Metal Industry Effluents with Bioremediation and Phytomining: A Biomimetic Resource Management Approach. Adv. Mater. Sci. Eng. 2015, 2015, 1–21. [Google Scholar] [CrossRef]
- Baysal, A.; Ozbek, N.; Akman, S. Determination of Trace Metals in Waste Water and Their Removal Processes. In Waste Water—Treatment Technologies and Recent Analytical Developments; García Einschlag, F.S., Carlos, L., Eds.; IntechOpen: London, UK, 2013. [Google Scholar]
- Iravani, S. Green synthesis of metal nanoparticles using plants. Green Chem. 2011, 13, 2638–2650. [Google Scholar] [CrossRef]
- Balentine, D.A.; Wiseman, S.A.; Bouwens, L.C. The chemistry of tea flavonoids. Crit. Rev. Food Sci. Nutr. 1997, 37, 693–704. [Google Scholar] [CrossRef] [PubMed]
- Aziz, S.B.; Hussein, G.; Brza, M.A.; Mohammed, S.J.; Abdulwahid, R.T.; Saeed, R.S.; Hassanzadeh, A. Fabrication of Interconnected Plasmonic Spherical Silver Nanoparticles with Enhanced Localized Surface Plasmon Resonance (LSPR) Peaks Using Quince Leaf Extract Solution. Nanomaterials 2019, 9, 1557. [Google Scholar] [CrossRef]
- Atkins, P.W. Physical Chemistry, 6th ed.; W.H. Freeman and Company: New York, NY, USA, 1997; ISBN 9780716734659. [Google Scholar]
- Wang, Z. Iron complex nanoparticles synthesized by eucalyptus leaves. ACS Sustain. Chem. Eng. 2013, 1, 1551–1554. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, C.; Mallavarapu, M. Characterization of iron-polyphenol complex nanoparticles synthesized by Sage (Salvia officinalis) leaves. Environ. Technol. Innov. 2015, 4, 92–97. [Google Scholar] [CrossRef]
- Acácio, A.F.Z.; Charles, W.I.H.; Aline, A.; Alessandro, N.; Ivo, M.D.; Daniel, G. A comparative study of the phenolic compounds and the in vitro antioxidant activity of different Brazilian teas using multivariatestatistical techniques. Food Res. Int. 2014, 60, 246–254. [Google Scholar]
- James, E. House, Inorganic Chemistry; Elsevier: Amsterdam, The Netherlands, 2008; 577p. [Google Scholar]
- Brza, M.A.; Aziz, S.B.; Anuar, H.; Al Hazza, M.H.F. From green remediation to polymer hybrid fabrication with improved optical band gaps. Int. J. Mol. Sci. 2019, 20, 3910. [Google Scholar] [CrossRef]
- Xu, H.; Chen, R.; Sun, Q.; Lai, W.; Su, Q.; Huang, W.; Liu, X. Recent progress in metal–organic complexes for optoelectronic applications. Chem. Soc. Rev. 2014, 43, 3259–3302. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, C.; Megharaj, M. Characterization of Iron–Polyphenol Nanoparticles Synthesized by Three Plant Extracts and Their Fenton Oxidation of Azo Dye. ACS Sustain. Chem. Eng. 2014, 2, 1022–1025. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Fan, W.; Lu, H. Identification of green tea varieties and fast quantification of total polyphenols by near-infrared spectroscopy and ultraviolet-visible spectroscopy with chemometric algorithms. Anal. Methods 2015, 7, 787–792. [Google Scholar] [CrossRef]
- López-Martínez, L.; López-de-Alba, P.L.; García-Campos, R.; De León-Rodríguez, L.M. Simultaneous determination of methylxanthines in coffees and teas by UV-Vis spectrophotometry and partial least squares. Anal. Chim. Acta 2003, 493, 83–94. [Google Scholar] [CrossRef]
- Hoag, G.; Collings, J.; Holcomb, J.; Hoag, J.; Nadagoud, M.; Varma, R. Degradation of bromothymol blue by ‘greener’ nano-scalezero-valent iron synthesized using tea polyphenols. J. Mater. Chem. 2009, 19, 8671–8677. [Google Scholar] [CrossRef]
- Jain, P.K.; Xiao, Y.; Walsworth, R.; Cohen, A.E. Surface plasmon resonance enhanced magneto-optics (SuPREMO): Faraday rotation enhancement in gold-coated iron oxide nanocrystals. Nano Lett. 2009, 9, 1644–1650. [Google Scholar] [CrossRef]
- Aziz, S.B. Morphological and Optical Characteristics of Chitosan(1−x):Cuox (4 ≤ x ≤ 12) Based Polymer Nano-Composites: Optical Dielectric Loss as an Alternative Method for Tauc’s Model. Nanomaterials 2017, 7, 444. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; He, Y. Rapid detection of talcum powder in tea using FT-IR spectroscopy coupled with chemometrics. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Loo, Y.Y.; Chieng, B.W.; Nishibuchi, M.; Radu, S. Synthesis of silver nanoparticles by using tea leaf extract from Camellia Sinensis. Int. J. Nanomed. 2012, 7, 4263–4267. [Google Scholar] [CrossRef]
- Senthilkumar, S.R.; Sivakumar, T. Green tea (Camellia sinensis) mediated synthesis of zinc oxide (ZnO) nanoparticles and studies on their antimicrobial activities. Int. J. Pharm. Pharm. Sci. 2014, 6, 461–465. [Google Scholar]
- Madeja, A.S.; Welna, M.; Zyrnicki, W. Multi-element analysis, bioavailability and fractionation of herbal tea products. J. Braz. Chem. Soc. 2013, 24, 777–787. [Google Scholar]
- Dubey, S.P.; Sillanpaa, M.; Varma, R.S. Reduction of Hexavalent Chromium Using Sorbariasorbifolia Aqueous Leaf Extract. Appl. Sci. 2017, 7, 715. [Google Scholar] [CrossRef]
- Lee, Y.H.; Hwang, E.K.; Kim, H.D. Colorimetric Assay and Antibacterial Activity of Cotton, Silk, and Wool Fabrics Dyed with Peony, Pomegranate, Clove, Coptischinenis and Gallnut Extracts. Materials 2009, 2, 10–21. [Google Scholar] [CrossRef]
- Hwang, E.K.; Lee, Y.H.; Kim, H.D. Dyeing, Fastness, and Deodorizing Properties of Cotton, Silk, and Wool Fabrics Dyed with Gardenia, Coffee Sludge, Cassia tora. L., and Pomegranate Extracts. Fibers Polym. 2008, 9, 334–340. [Google Scholar] [CrossRef]
- Goodman, B.A.; Severino, J.F.; Pirker, K.F. Reactions of green and black teas with Cu(II). Food Funct. 2012, 3, 399–409. [Google Scholar] [CrossRef] [PubMed]
- Kolaylı, S.; Ocak, M.; Kucuk, M.; Abbasoglu, R. Does caffeine bind to metal ions? Food Chem. 2004, 84, 383–388. [Google Scholar] [CrossRef]
- Li, S.; Lo, C.-Y.; Pan, M.-H.; Lai, C.-S.; Ho, C.-T. Black tea: Chemical analysis and stability. Food Funct. 2013, 4, 10–18. [Google Scholar] [CrossRef]
- Hemaa, M.; Selvasekerapandian, S.; Sakunthala, A.; Arunkumar, D.; Nithya, H. Structural, vibrational and electrical characterization of PVA–NH4Br polymer electrolyte system. Phys. B 2008, 403, 2740–2747. [Google Scholar] [CrossRef]
- Malathi, J.; Kumaravadivel, M.; Brahmanandhan, G.M.; Hema, M.; Baskaran, R.; Selvasekarapandian, S. Structural, thermal and electrical properties of PVA–LiCF3SO3 polymer electrolyte. J. Non-Cryst. Solids 2010, 356, 2277–2281. [Google Scholar] [CrossRef]
- Makled, M.H.; Sheha, E.; Shanap, T.S.; El-Mansy, M.K. Electrical conduction and dielectric relaxation in p-type PVA/CuI polymer composite. J. Adv. Res. 2013, 4, 531–538. [Google Scholar] [CrossRef] [PubMed]
- Hadi, J.M.; Aziz, S.B.; Saeed, S.R.; Brza, M.A.; Abdulwahid, R.T.; Hamsan, M.H.; Abdullah, R.M.; Kadir, M.F.Z.; Muzakir, S.K. Investigation of ion transport parameters and electrochemical performance of plasticized biocompatible chitosan-based proton conducting polymer composite electrolytes. Membranes 2020, 10, 363. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Yang, T.; Peng, L.; Dan, Y. Acrylamide modified poly(vinyl alcohol): Crystalline and enhanced water solubility. RSC Adv. 2015, 5, 86598–86605. [Google Scholar] [CrossRef]
- Aziz, S.B.; Rasheed, M.A.; Hussein, A.M.; Ahmed, H.M. Fabrication of polymer blend composites based on [PVA-PVP](1 − x):(Ag2S) x (0.01 ≤ x ≤ 0.03) with small optical band gaps: Structural and optical properties. Mater. Sci. Semicond. Process. 2017, 71, 197–203. [Google Scholar] [CrossRef]
- Aziz, S.B.; Hadi, J.M.; Elham, E.M.; Abdulwahid, R.T.; Saeed, S.R.; Marf, A.S.; Karim, W.O.; Kadir, M.F.Z. The study of plasticized amorphous biopolymer blend electrolytes based on polyvinyl alcohol (PVA): Chitosan with high ion conductivity for energy storage electrical double-layer capacitors (EDLC) device application. Polymers 2020, 12, 1938. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abidin, Z.H.Z. Ion-transport study in nanocomposite solid polymer electrolytes based on chitosan: Electrical and dielectric analysis. J. Appl. Polym. Sci. 2015, 132, 1–10. [Google Scholar] [CrossRef]
- Nofal, M.M.; Aziz, S.B.; Hadi, J.M.; Abdulwahid, R.T.; Dannoun, E.M.A.; Marif, A.S.; Al-Zangana, S.; Zafar, Q.; Brza, M.A.; Kadir, M.F.Z. Synthesis of porous proton ion conducting solid polymer blend electrolytes based on PVA: CS polymers: Structural, morphological and electrochemical properties. Materials 2020, 13, 4890. [Google Scholar] [CrossRef]
- Hamsan, M.H.; Aziz, S.; Nofal, M.M.; Brza, M.A.; Abdulwahid, R.T.; Hadi, J.M.; Karim, W.O.; Kadir, M.F.Z. Characteristics of EDLC device fabricated from plasticized chitosan:MgCl2 based polymer electrolyte. J. Mater. Res. Technol. 2020, 9, 10635–10646. [Google Scholar] [CrossRef]
- Aziz, S.B. Modifying Poly (Vinyl Alcohol) (PVA) from Insulator to Small- Band gap Polymer: A Novel Approach for Organic Solar Cells and Optoelectronic Devices. J. Electron. Mater. 2015, 45, 736–745. [Google Scholar] [CrossRef]
- Asnawi, A.S.F.M.; Aziz, S.B.; Nofal, M.M.; Yusof, Y.M.; Brevik, I.; Hamsan, M.H.; Brza, M.A.; Abdulwahid, R.T.; Kadir, M.F.Z. Metal Complex as a Novel Approach to Enhance the Amorphous Phase and Improve the EDLC Performance of Plasticized Proton Conducting Chitosan-Based Polymer Electrolyte. Membranes 2020, 10, 132. [Google Scholar] [CrossRef] [PubMed]
- Yakuphanoglu, F.; Kandaz, M.; Yaras, M.N.; Senkal, F.B. Electrical transport and optical properties of an organic semiconductor based on phthalocyanine. Phys. B 2007, 393, 235–238. [Google Scholar] [CrossRef]
- Sánchez Vergara, M.E.; Ortiz Rebollo, A.; Alvarez, J.R.; Rivera, M. Molecular materials derived from MPc (M=Fe, Pb, Co) and 1,8-dihydroxiantraquinone thin films: Formation, electrical and optical properties. J. Phys. Chem. Solids 2008, 69, 1–7. [Google Scholar] [CrossRef]
- Ahlawat, N.; Sanghi, S.; Agarwal, A.; Rani, S. Effect of Li2O on structure and optical properties of lithium bismosilicate glasses. J. Alloys Compd. 2009, 480, 516–520. [Google Scholar] [CrossRef]
- Ennis, C.P.; Kaiser, R.I. Mechanistical studies on the electron-induced degradation of polymers: Polyethylene, polytetrafluoroethylene, and polystyrene. Phys. Chem. Chem. Phys. 2010, 12, 14884–14901. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Sekerci, M.; Ozturk, O.F. The determination of the optical constants of cu(ii) compound having 1-chloro-2,3-o-cyclohexylidinepropane thin film. Opt. Commun. 2004, 239, 275–280. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Cukurovali, A.; Yilmaz, I. Refractive index and optical absorption properties of the complexes of a cyclobutane containing thiazolyl hydrazone ligand. Opt. Mater. 2005, 27, 1363–1368. [Google Scholar] [CrossRef]
- French, R.H.; Rodríguez-Parada, J.M.; Yang, M.K.; Derryberry, R.A.; Pfeiffenberger, N.T. Optical properties of polymeric materials for concentrator photovoltaic systems. Sol. Energy Mater. Sol. Cells 2011, 95, 2077–2086. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Sekerci, M.; Balaban, A. The effect of film thickness on the optical absorption edge and optical constants of the Cr(III) organic thin films. Opt. Mater. 2005, 27, 1369–1372. [Google Scholar] [CrossRef]
- Yakuphanoglu, F.; Barım, G.; Erol, I. The effect of FeCl3 on the optical constants and optical band gap of MBZMA-co-MMA polymer thin films. Phys. B 2007, 391, 136–140. [Google Scholar] [CrossRef]
- Wildner, W.; Drummer, D. Nanofiller materials for transparent polymer composites: Influences on the properties and on the transparency—A review. J. Thermoplast. Compos. Mater. 2019, 32, 1547–1565. [Google Scholar] [CrossRef]
- Somesh, T.E.; Al-Gunaid, M.Q.A.; Madhukar, B.S. Siddaramaiah Photosensitization of optical band gap modified polyvinyl alcohol films with hybrid AgAlO2 nanoparticles. J. Mater. Sci. Mater. Electron. 2019, 30, 37–49. [Google Scholar] [CrossRef]
- Ali, F.M.; Kershi, R.M.; Sayed, M.A.; AbouDeif, Y.M. Evaluation of structural and optical properties of Ce3+ ions doped (PVA/PVP) composite films for new organic semiconductors. Phys. B Condens. Matter 2018, 538, 160–166. [Google Scholar] [CrossRef]
- Spitzer, W.G.; Fan, H.Y. Determination of optical constants and carrier effective mass of semiconductors. Phys. Rev. 1957, 106, 882–890. [Google Scholar] [CrossRef]
- Kiselev, A.I.; Akashev, L.A.; Kononenko, V.I. Effective Electron Mass in Melts of Aluminum, Cerium, and Al–3 at.% Ce Binary System. Tech. Phys. 2004, 49, 302–305. [Google Scholar] [CrossRef]
- Alsaad, A.M.; Al-Bataineh, Q.M.; Ahmad, A.A.; Albataineh, Z.; Telfah, A. Optical band gap and refractive index dispersion parameters of boron-doped ZnO thin films: A novel derived mathematical model from the experimental transmission spectra. Optik 2020, 211, 164641. [Google Scholar] [CrossRef]
- Benchaabane, A.; Hajlaoui, M.E.; Hnainia, N.; Al-Tabbakh, A.; Zeinert, A.; Bouchrih, H. Optical properties enhancement of hybrid nanocomposites thin films based on P3HT matrix and ZnO@SiO2 core-shell nanoparticles. Opt. Mater. 2020, 102, 109829. [Google Scholar] [CrossRef]
- Rocquefelte, X.; Jobic, S.; Whangbo, M.-H. Concept of optical channel as a guide for tuning the optical properties of insulating materials. Solid State Sci. 2007, 9, 600–603. [Google Scholar] [CrossRef]
- Rodríguez, A.; Sánchez Vergara, M.E.; García Montalvo, V.; Ortiz, A.; Alvarez, J.R. Thin films of molecular materials synthesized from C 32 H 20 N 10 M (M = Co, Pb, Fe): Film formation, electrical and optical properties. Appl. Surf. Sci. 2010, 256, 3374–3379. [Google Scholar] [CrossRef]
- Hossain, F.M.; Sheppard, L.; Nowotny, J.; Murch, G.E. Optical properties of anatase and rutile titanium dioxide: Ab initio calculations for pure and anion-doped material. J. Phys. Chem. Solids 2008, 69, 1820–1828. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B.; Chen, J.C.; Zhou, C.T.; Du, Y.P.; Zhou, R. Optical properties of new photovoltaic materials: AgCuO2 and Ag2Cu2O3. Solid State Commun. 2009, 149, 1569–1573. [Google Scholar] [CrossRef]
- Ahmed, N.M.; Sauli, Z.; Hashim, U.; Al-douri, Y. Investigation of the absorption coefficient, refractive index, energy GaN by optical transmission method. J. Nanoelectron. Mater. 2009, 2, 189–195. [Google Scholar]
- Hussein, A.M.; Dannoun, E.M.A.; Aziz, S.B.; Brza, M.A.; Abdulwahid, R.T.; Hussen, S.A.; Rostam, S.; Mustafa, D.M.T.; Muhammad, D.S. Steps toward the band gap identification in polystyrene based solid polymer nanocomposites integrated with tin titanate nanoparticles. Polymers 2020, 12, 2320. [Google Scholar] [CrossRef] [PubMed]
- Rodel, T.C.R.; Vivek, M.; Fortuna, F.; F’evre, P.L.; Bertran, F. Two-dimensional electron systems in ATiO3 perovskites (A= Ca, Ba, Sr): Control of orbital hybridization and order. Phys. Rev. B 2017, 96, 041121. [Google Scholar] [CrossRef]
- Aziz, S.B.; Abdulwahid, R.T.; Rsaul, H.A.; Ahmed, H.M. In situ synthesis of CuS nanoparticle with a distinguishable SPR peak in NIR region. J. Mater. Sci. Mater. Electron. 2016, 27, 4163–4171. [Google Scholar] [CrossRef]
- El-Nahass, M.M.; Farid, A.M.; Atta, A.A. Structural and optical properties of Tris(8-hydroxyquinoline) aluminum (III) (Alq3) thermal evaporated thin films. J. Alloy. Compd. 2010, 507, 112–119. [Google Scholar] [CrossRef]
- Logothetidis, S. Optical and electronic properties of amorphous carbon materials. Diam. Relat. Mater. 2003, 12, 141–150. [Google Scholar] [CrossRef]
- Soliman, T.S.; Vshivkov, S.A. Effect of Fe nanoparticles on the structure and optical properties of polyvinyl alcohol nanocomposite films. J. Non-Cryst. Solids 2019, 519, 119452. [Google Scholar] [CrossRef]
- Aziz, S.B.; Ahmed, H.M.; Hussein, A.M.; Fathulla, A.B.; Wsw, R.M.; Hussein, R.T. Tuning the absorption of ultraviolet spectra and optical parameters of aluminum doped PVA based solid polymer composites. J. Mater. Sci. Mater. Electron. 2015, 26, 8022–8028. [Google Scholar] [CrossRef]
- Ghanipour, M.; Dorranian, D. Effect of Ag-Nanoparticles Doped in Polyvinyl Alcohol on the Structural and Optical Properties of PVA Films. J. Nanomater. 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Rashad, M. Tuning optical properties of polyvinyl alcohol doped with different metal oxide nanoparticles. Opt. Mater. 2020, 105, 109857. [Google Scholar] [CrossRef]
- Soliman, T.S.; Zaki, M.F.; Hessien, M.M.; Elkalashy, S.I. The structure and optical properties of PVA-BaTiO3 nanocomposite films. Opt. Mater. 2021, 111, 110648. [Google Scholar] [CrossRef]
- Soliman, T.S.; Vshivkov, S.A.; Elkalashy, S.I. Structural, thermal, and linear optical properties of SiO2 nanoparticles dispersed in polyvinyl alcohol nanocomposite films. Polym. Compos 2020, 41, 3340–3350. [Google Scholar] [CrossRef]
- Banerjee, M.; Jain, A.; Mukherjee, G.S. Microstructural and optical properties of polyvinyl alcohol/manganese chloride composite film. Polym. Compos. 2019, 40, E765–E775. [Google Scholar] [CrossRef]
- Soliman, T.S.; Rashad, A.M.; Ali, I.A.; Khater, S.I.; Elkalashy, S.I. Investigation of Linear Optical Parameters and Dielectric Properties of Polyvinyl Alcohol/ZnO Nanocomposite Films. Phys. Status Solidi Appl. Mater. Sci. 2020, 217, 1–8. [Google Scholar] [CrossRef]
- Abdulwahid, R.T.; Abdullah, O.G.; Aziz, S.B.; Hussein, S.A.; Muhammad, F.F.; Yahya, M.Y. The study of structural and optical properties of PVA:PbO2 based solid polymer nanocomposites. J. Mater. Sci. Mater. Electron. 2016, 27, 12112–12118. [Google Scholar] [CrossRef]
- Saini, I.; Rozra, J.; Chandak, N.; Aggarwal, S.; Sharma, P.K.; Sharma, A. Tailoring of electrical, optical and structural properties of PVA by addition of Ag nanoparticles. Mater. Chem. Phys. 2013, 139, 802–810. [Google Scholar] [CrossRef]
- Wemple, S.H.; DiDomenico, M. Behavior of the electronic dielectric constant in covalent and ionic materials. Phys. Rev. B 1971, 3, 1338–1351. [Google Scholar] [CrossRef]
- Ammar, A.H. Studies on some structural and optical properties of ZnxCd1-xTe thin films. Appl. Surf. Sci. 2002, 201, 9–19. [Google Scholar] [CrossRef]
- Benchaabane, A.; Ben Hamed, Z.; Kouki, F.; Abderrahmane Sanhoury, M.; Zellama, K.; Zeinert, A.; Bouchriha, H. Performances of effective medium model in interpreting optical properties of polyvinylcarbazole:ZnSe nanocomposites. J. Appl. Phys. 2014, 115, 134313. [Google Scholar] [CrossRef]
| Physical Parameters | Values |
|---|---|
| mass of an electron (me) | 9.109 × 10−31 Kg |
| charge of an electron (e) | 1.602 × 10−19 coulombs |
| dielectric constant of free space (ԑo) | 8.85 × 10−12 F/m |
| π | 3.14 |
| speed of light (c) | 2.99 × 108 m/s |
| effective mass (m*) | 10.566 × 10−31 Kg |
| Film Code | N/m* × 1055 (m3/kg) | ε∞ |
|---|---|---|
| PVALMC0 | 3.68 | 1.4 |
| PVALMC1 | 60.1 | 2.6 |
| PVALMC2 | 109 | 3.6 |
| Film Code | τ (fs) | μ (opt) × 10−2 | (Nc) × 1025 | ρ (opt) | ωp × 1015 |
|---|---|---|---|---|---|
| PVALMC0 | 1.59 | 161 | 3.89 | 1.00 × 10−7 | 0.32631 |
| PVALMC1 | 4.33 | 9.44 | 63.5 | 1.04 × 10−7 | 1.3188 |
| PVALMC2 | 2.36 | 6.02 | 115 | 9.03 × 10−8 | 1.77736 |
| Sample Code | Direct Bandgap (eV) | Indirect Bandgap (eV) | Energy gap (Eg) from εi Spectra (eV) |
|---|---|---|---|
| PVALMC0 | 6.4 | 6.2 | 6.39 |
| PVALMC1 | 2.1 | 1.74 | 1.79 |
| PVALMC2 | 1.81 | 1.62 | 1.68 |
| PVA Composite | Direct Bandgap (eV) | Indirect Bandgap (eV) | References |
|---|---|---|---|
| PVA:Fe | 2.8 | - | [72] |
| PVA:Al | 5.2 | - | [73] |
| PVA:Ag | - | 4.78 | [74] |
| PVA:Fe2O3 | - | 4.8 | [75] |
| PVA:BaTiO3 | 5.4 | 4.2 | [76] |
| PVA:SiO2 | 5.2 | 4.35 | [77] |
| PVA:MnCl2 | 4.99 | 4.93 | [78] |
| PVA:ZnO | 5.15 | - | [79] |
| PVA:PbO | 4.33 | - | [80] |
| PVA:Al3+-complex | 1.81 | 1.62 | Present work |
| Sample Code | Dispersion Energy (Ed) | Oscillator Energy (Eo) | Refractive Index (no) |
|---|---|---|---|
| PVALMC0 | 1.620084 | 6.17252 | 1.123596 |
| PVALMC1 | 1.058334 | 1.968502 | 1.240014 |
| PVALMC2 | 1.341104 | 1.864135+ | 1.311268 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, S.B.; Nofal, M.M.; Ghareeb, H.O.; Dannoun, E.M.A.; Hussen, S.A.; Hadi, J.M.; Ahmed, K.K.; Hussein, A.M. Characteristics of Poly(vinyl Alcohol) (PVA) Based Composites Integrated with Green Synthesized Al3+-Metal Complex: Structural, Optical, and Localized Density of State Analysis. Polymers 2021, 13, 1316. https://doi.org/10.3390/polym13081316
Aziz SB, Nofal MM, Ghareeb HO, Dannoun EMA, Hussen SA, Hadi JM, Ahmed KK, Hussein AM. Characteristics of Poly(vinyl Alcohol) (PVA) Based Composites Integrated with Green Synthesized Al3+-Metal Complex: Structural, Optical, and Localized Density of State Analysis. Polymers. 2021; 13(8):1316. https://doi.org/10.3390/polym13081316
Chicago/Turabian StyleAziz, Shujahadeen B., Muaffaq M. Nofal, Hewa O. Ghareeb, Elham M. A. Dannoun, Sarkawt A. Hussen, Jihad M. Hadi, Khayal K. Ahmed, and Ahang M. Hussein. 2021. "Characteristics of Poly(vinyl Alcohol) (PVA) Based Composites Integrated with Green Synthesized Al3+-Metal Complex: Structural, Optical, and Localized Density of State Analysis" Polymers 13, no. 8: 1316. https://doi.org/10.3390/polym13081316
APA StyleAziz, S. B., Nofal, M. M., Ghareeb, H. O., Dannoun, E. M. A., Hussen, S. A., Hadi, J. M., Ahmed, K. K., & Hussein, A. M. (2021). Characteristics of Poly(vinyl Alcohol) (PVA) Based Composites Integrated with Green Synthesized Al3+-Metal Complex: Structural, Optical, and Localized Density of State Analysis. Polymers, 13(8), 1316. https://doi.org/10.3390/polym13081316









