An Effective Interface Tracking Method for Simulating the Extrudate Swell Phenomenon
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Governing Equations
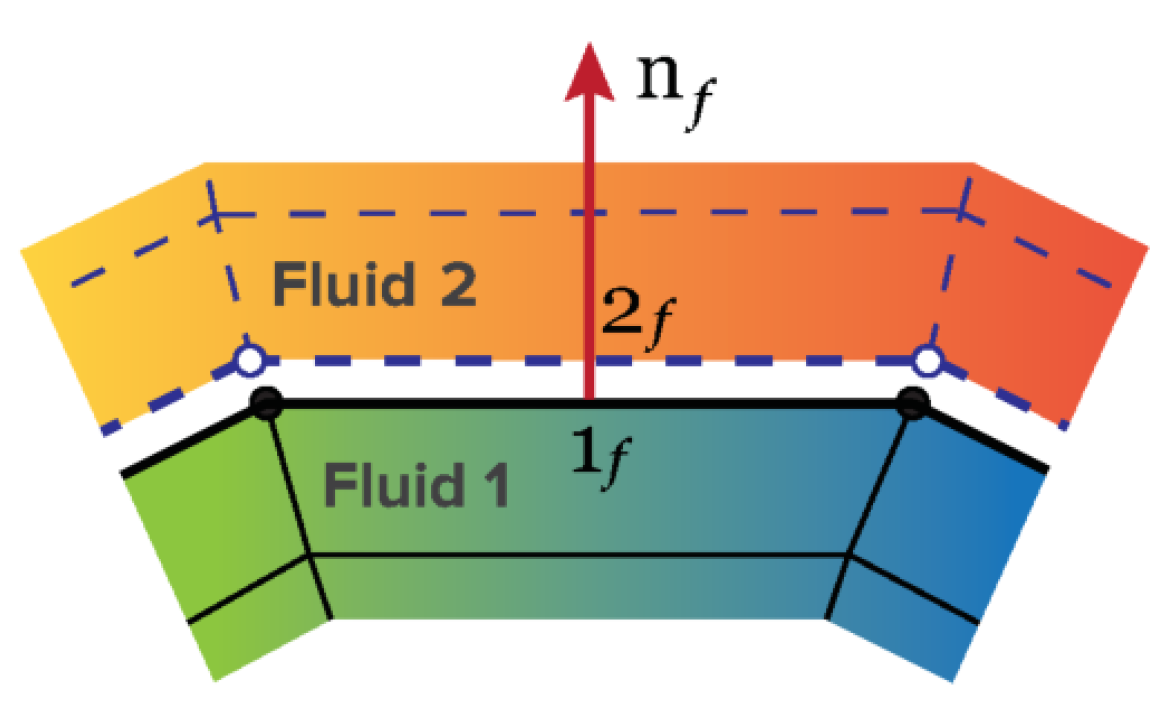
2.1.1. Kinematic Condition
2.1.2. Dynamic Condition
2.2. Numerical Method
2.2.1. Consistent Non-Iterative PISO Algorithm
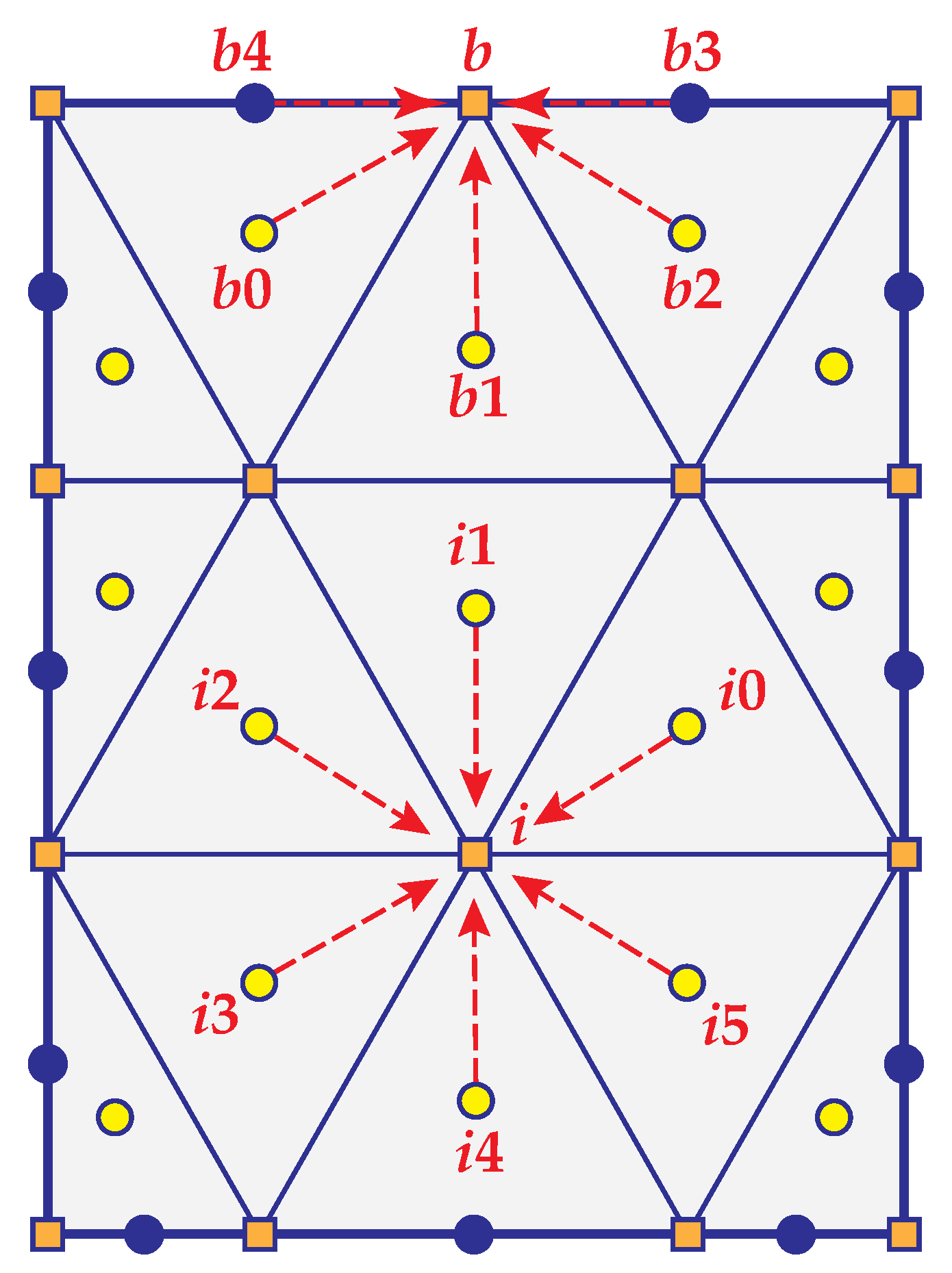
2.2.2. Least-Squares Volume-to-Point Interpolation
3. Results and Discussion
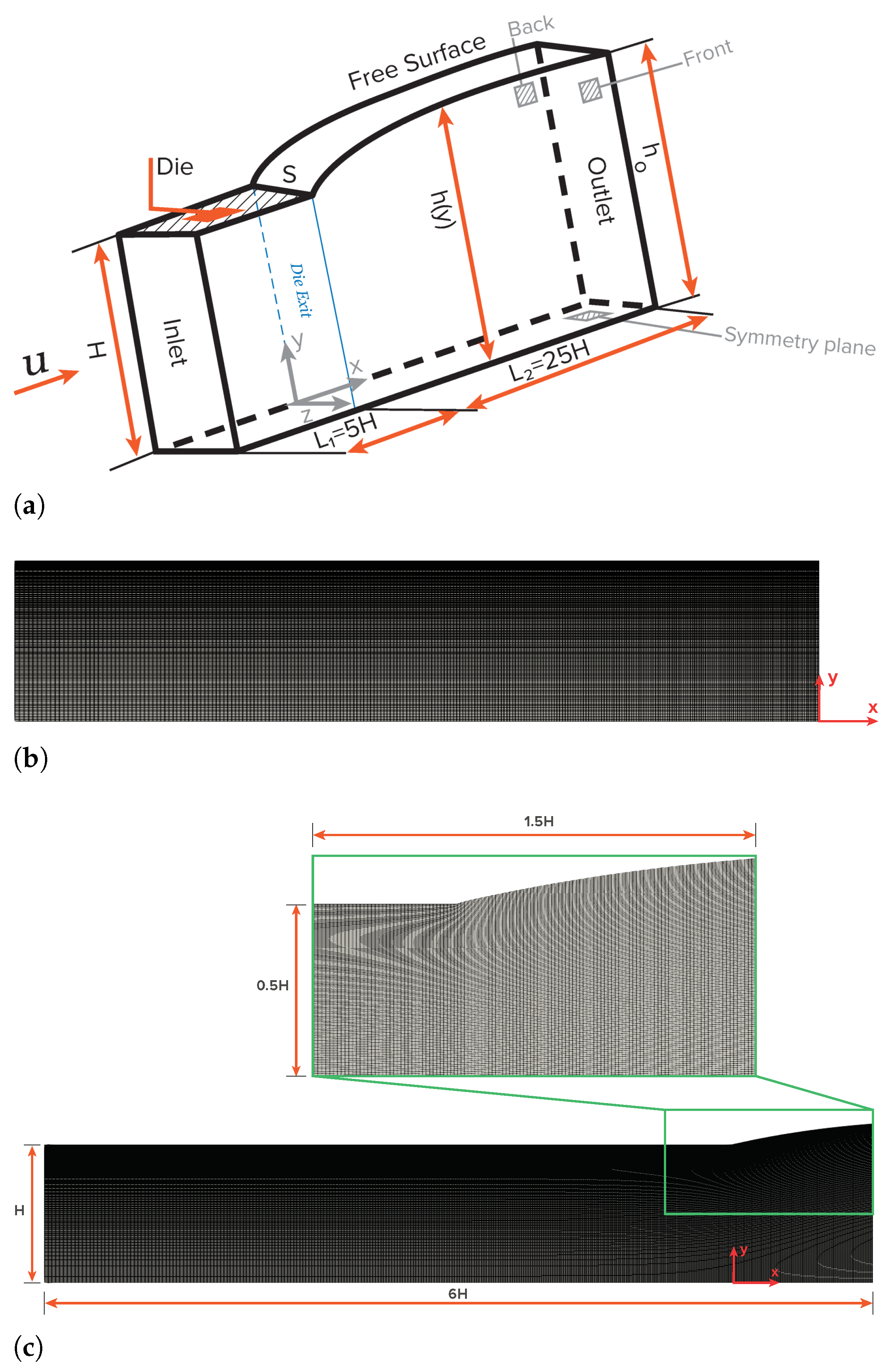
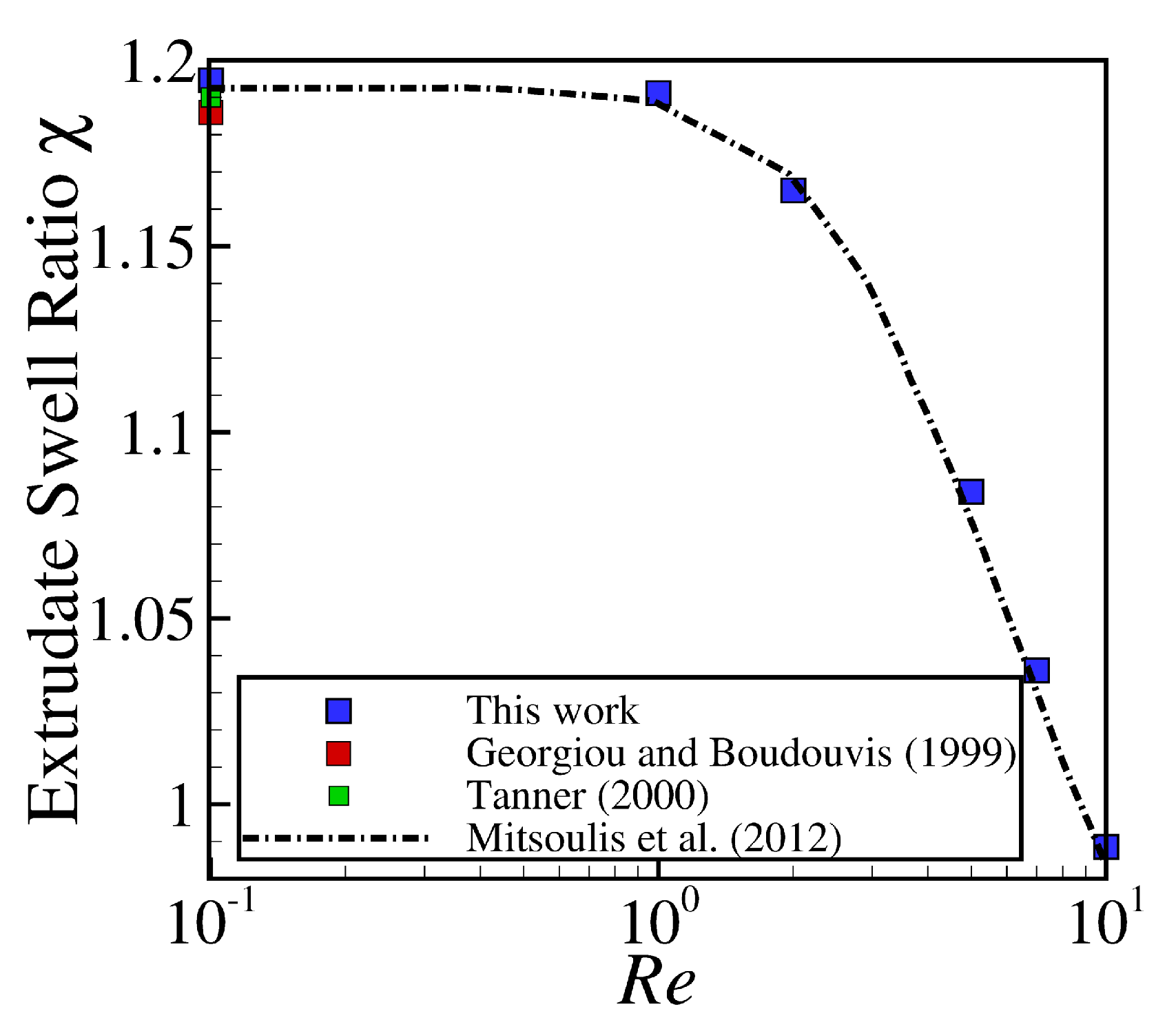
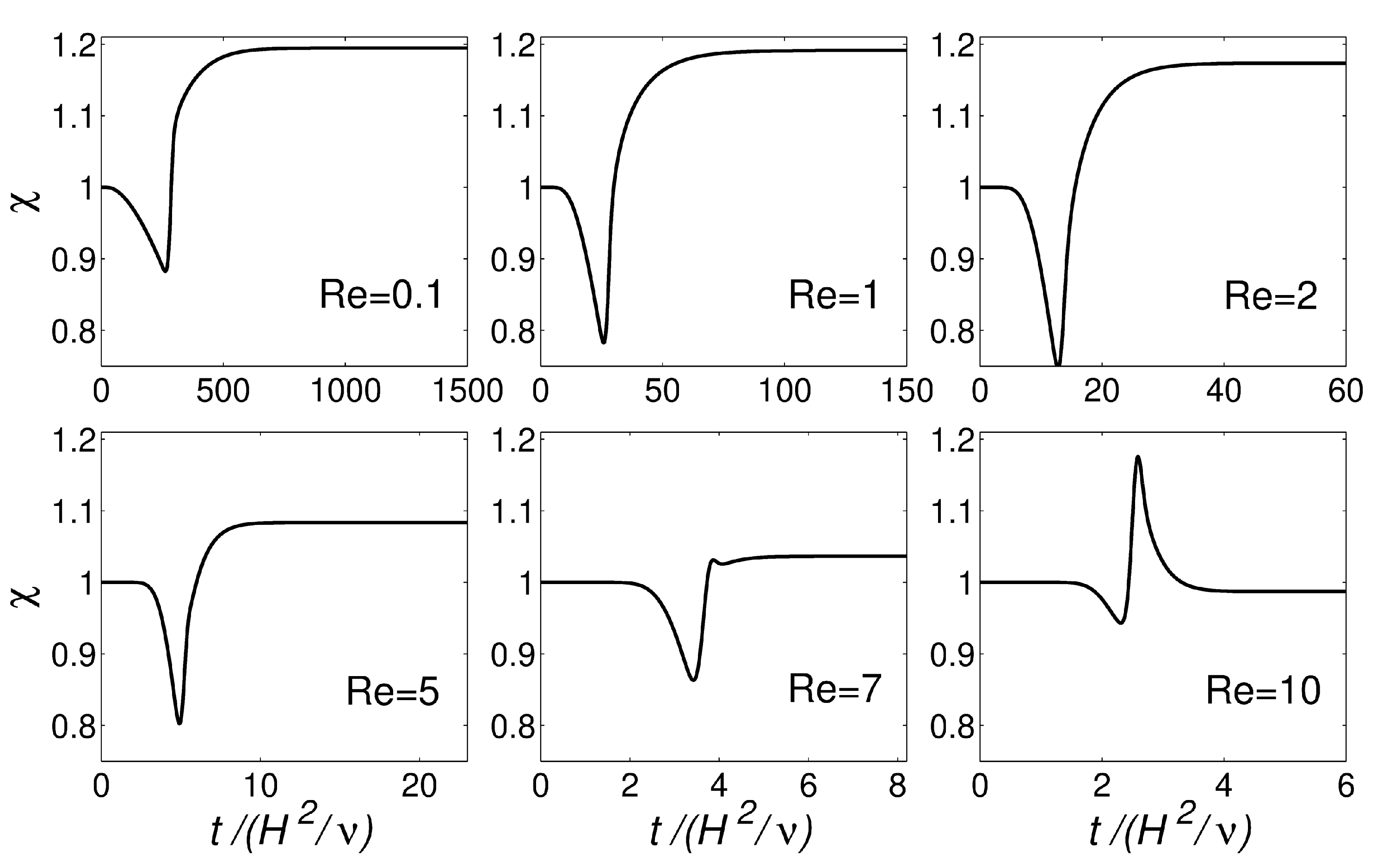
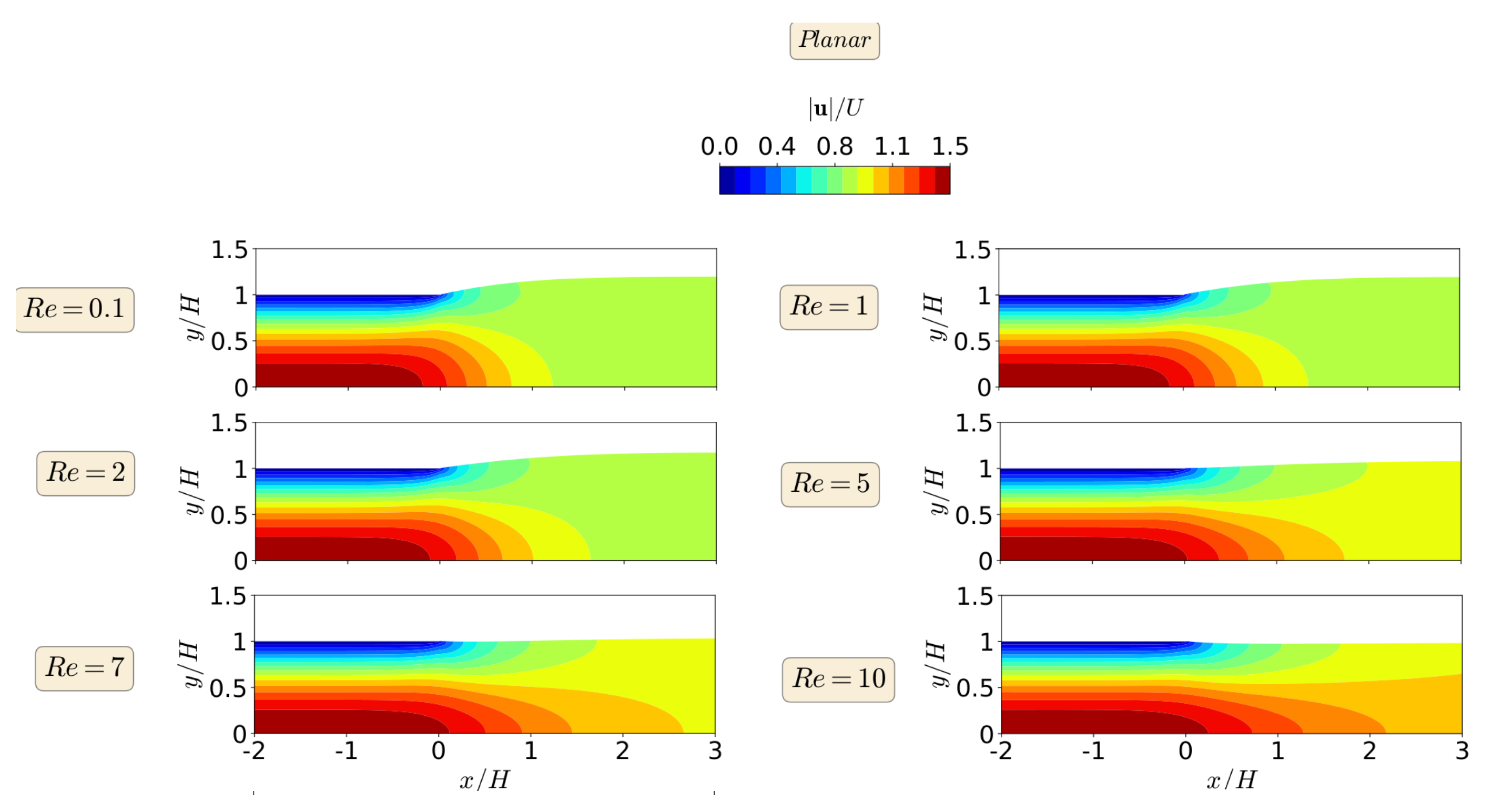
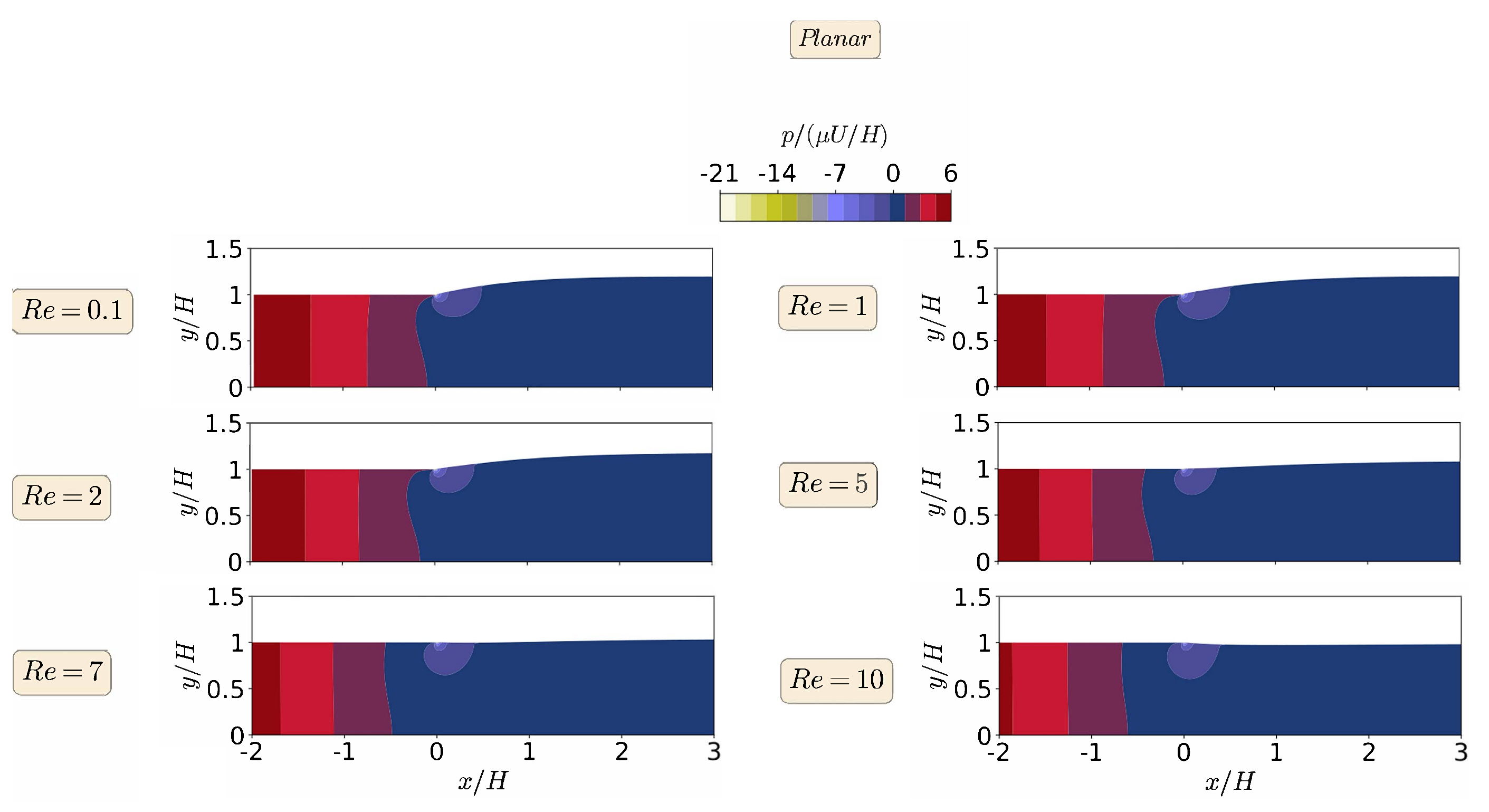
3.1. Planar Extrudate Swell of Newtonian Fluids
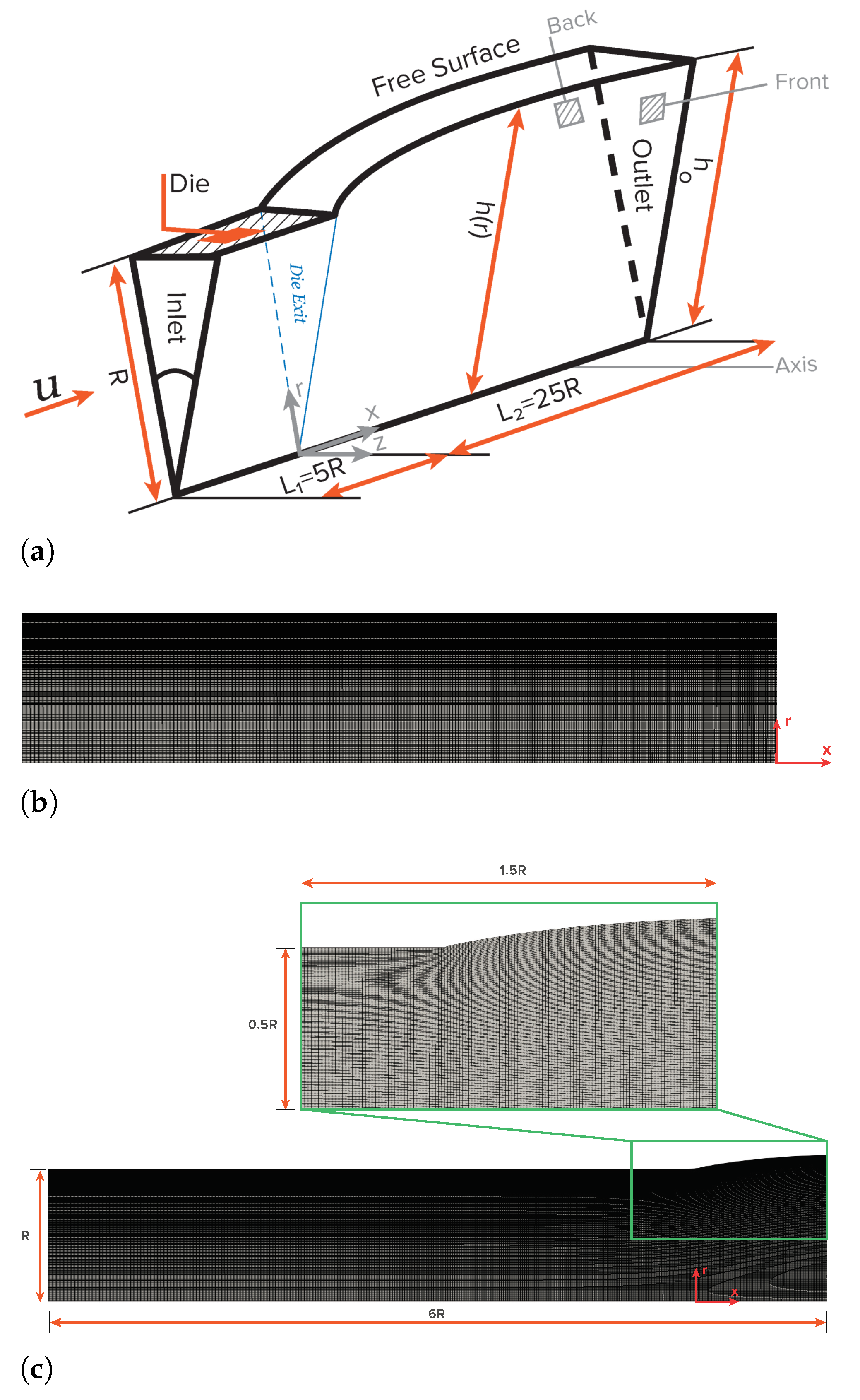
3.2. Axisymmetric Extrudate Swell of Newtonian Fluids
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tanner, R.I. Engineering Rheology, 2nd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, SPE Monograph Series; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Mirjalili, S.; Jain, S.S.; Dodd, M. Interface-capturing methods for two-phase flows: An overview and recent developments. Cent. Turbul. Res. Annu. Res. Briefs 2017, 2017, 117–135. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Multiphase Flow; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Harlaw, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free-surface. Phys. Fluids 1965, 8, 2182. [Google Scholar] [CrossRef]
- McKee, S.; Tomé, M.F.; Cuminato, J.A.; Castelo, A.; Ferreira, V.G. Recent Advances in the Marker and Cell Method. Arch. Comput. Meth. Eng. 2004, 11, 107–142. [Google Scholar] [CrossRef]
- McKee, S.; Tomé, M.F.; Ferreira, V.G.; Cuminato, J.A.; Castelo, A.; Sousa, F.S.; Mangiavacchi, N. The MAC method. Comput. Fluids 2008, 37, 907–930. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P. Axisymmetric free boundary problems. J. Fluid Mech. 1997, 341, 269–294. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Sussman, M.; Fatemi, E. An efficient interface-preserving level set redistancing algorithm and its application to interfacial incompressible fluid flow. J. Sci. Comput. 1999, 20, 1165–1191. [Google Scholar] [CrossRef]
- Sussman, M.; Puckett, E.G. A coupled level set and volume-Of-fluid method for Computing 3D and axisymmetric incompressible Two-Phase Flows. J. Comput. Phys. 2000, 162, 301–337. [Google Scholar] [CrossRef]
- Gueyffier, D.; Li, J.; Scardovelli, R.; Zaleski, S. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows. J. Comput. Phys. 1999, 152, 423–456. [Google Scholar] [CrossRef]
- Queutey, P.; Visonneau, M. An interface capturing method for free-surface hydrodynamic flows. Comput. Fluids 2007, 36, 1481–1510. [Google Scholar] [CrossRef]
- Roenby, J.; Bredmose, H.; Jasak, H. A computational method for sharp interface advection. R. Soc. Open Sci. 1988, 3, 160405. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Losasso, F.; Fedkiw, R.; Osher, S. Spatially adaptive techniques for level set methods and incompressible flow. Comput. Fluids 2006, 35, 995–1010. [Google Scholar] [CrossRef]
- Sethian, J.A. Level Set Methods and Fast Marching Methods Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Tryggvason, G.; Unverdi, S.O. Computations of three-dimensional Rayleigh-Taylor instability. Phys. Fluids 1990, 2, 656–659. [Google Scholar] [CrossRef]
- Unverdi, S.O.; Tryggvason, G. A front-tracking method for viscous incompressible, multi-fluids flows. J. Comput. Phys. 1992, 100, 25–37. [Google Scholar] [CrossRef]
- Crochet, M.J.; Keunings, R. On numerical die swell calculation. J. Non-Newton. Fluid Mech. 1982, 10, 85–94. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Vlachopoulos, J.; Mirza, F.A. Simulation of extrudate swell from long slit and capillary dies. Polym. Process. Eng. 1984, 2, 153–177. [Google Scholar]
- Karagiannis, A.; Hrymak, A.N.; Vlachopoulos, J. Three-dimensional extrudate swell of creeping Newtonian jets. AIChE J. 1988, 34, 2088–2094. [Google Scholar] [CrossRef]
- Wambersie, O.; Crochet, M.J. Transient finite element method for calculating steady state three-dimensional free surfaces. Int. J. Numer. Methods Fluids 1992, 14, 343–360. [Google Scholar] [CrossRef]
- Legat, V.; Marchal, J.-M. Prediction of three-dimensional general shape extrudates by an implicit iterative scheme. Int. J. Numer. Methods Fluids 1992, 14, 609–625. [Google Scholar] [CrossRef]
- Legat, V.; Marchal, J.-M. Die design: An implicit formulation for the inverse problem. Int. J. Numer. Methods Fluids 1993, 16, 29–42. [Google Scholar] [CrossRef]
- Georgiou, G.C.; Boudouvis, A.G. Converged solutions of the Newtonian extrudate-swell problem. Int. J. Numer. Methods Fluids 1999, 29, 363–371. [Google Scholar] [CrossRef]
- Mitsoulis, E.; Georgiou, G.C.; Kountouriotis, Z. A study of various factors affecting Newtonian extrudate swell. Comput. Fluids 2012, 57, 195–207. [Google Scholar] [CrossRef]
- Spanjaards, M.M.A.; Hulsen, M.A.; Anderson, P.D. Transient 3D finite element method for predicting extrudate swell of domain containing sharp edges. J. Non-Newton. Fluid Mech. 2019, 270, 79–95. [Google Scholar] [CrossRef]
- Spanjaards, M.M.A.; Hulsen, M.A.; Anderson, P.D. Computational analysis of the extrudate shape of three-dimensional viscoelastic, non-isothermal extrusion flows. J. Non-Newton. Fluid Mech. 2020, 282, 104310. [Google Scholar] [CrossRef]
- Vlachopoulos, J. Extrudate Swell in Polymer Rheology. Rev. Def. Beh. Mat. 1981, 3, 219–248. [Google Scholar]
- Vlachopoulos, J.; Polychronopoulos, N. Basic Concepts in Polymer Melt Rheology and Their Importance in Processing. In Applied Polymer Rheology: Polymeric Fluids with Industrial Applications; Kontopoulou, M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Hamielec, L.A.; Vlachopoulos, J. Influence of Long Chain Branching on Extrudate Swell of Low-Density Polyethylenes. J. Appl. Polym. Sci. 1983, 28, 2389–2392. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Horie, M.; Lidorikis, S. An Evaluation of Expressions Predicting Die Swell. J. Rheol. 1972, 16, 669. [Google Scholar] [CrossRef]
- Tanner, R.I. A Theory of Die-Swell. J. Polym. Sci. Part A-2 Polym. Phys. 1970, 8, 2067. [Google Scholar] [CrossRef]
- Tanner, R.I. A Theory of Die-Swell Revisited. J. Non-Newt. Fluid Mech. 2005, 129, 85–87. [Google Scholar] [CrossRef]
- OpenCFD. OpenFOAM—The Open Source CFD Toolbox—User’s Guide; OpenCFD Ltd.: London, UK, 2007. [Google Scholar]
- Tuković, Ž.; Jasak, H. A moving mesh finite volume interface tracking method for surface tension dominated interfacial fluid flow. Comput. Fluids 2012, 55, 70–84. [Google Scholar] [CrossRef]
- Van Doormaal, J.P.; Raithby, G.D. Enhancement of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1984, 7, 147–163. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Tuković, Ž.; Perić, M.; Jasak, H. Consistent second-order time-accurate non-iterative PISO-algorithm. Comput. Fluids 2018, 166, 78–85. [Google Scholar] [CrossRef]
- Demirdžić, I.; Perić, M. Space conservation law in finite volume calculations of fluid flow. Int. J. Numer. Methods Fluids 1988, 8, 1037–1050. [Google Scholar] [CrossRef]
- Tuković, Z.; Jasak, H. Simulation of free-rising bubble with soluble surfactant using moving mesh finite volume/area method. In Proceedings of the 6th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, Trondheim, Norway, 10–12 June 2008. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of turbulent flow past an isolated airfol with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Jasak, H.; Tuković, Ž. Automatic mesh motion for the unstructured finite volume method. Trans. FAMENA 2006, 30, 1–20. [Google Scholar]
- Tuković, Ž.; Karač, A.; Cardiff, P.; Jasak, H. OpenFOAM Finite Volume Solver for Fluid-Solid Interaction. Trans. FAMENA 2018, 42, 1–31. [Google Scholar] [CrossRef]
- Celik, I.; Ghia, U.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 1–4. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids; Wiley-Interscience 2nd Ed.; Wiley: New York, NY, USA, 1987; Volume 1. [Google Scholar]
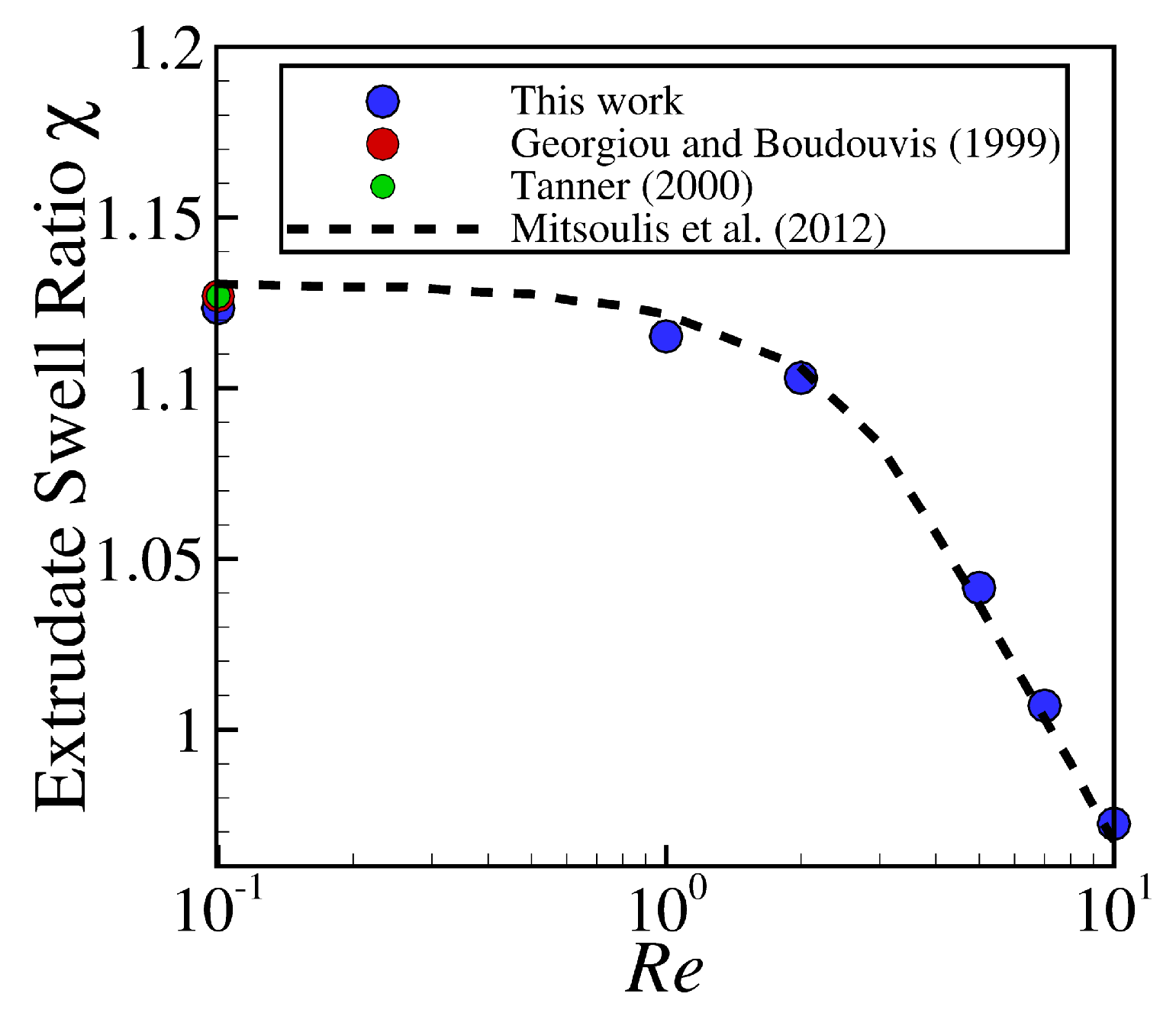
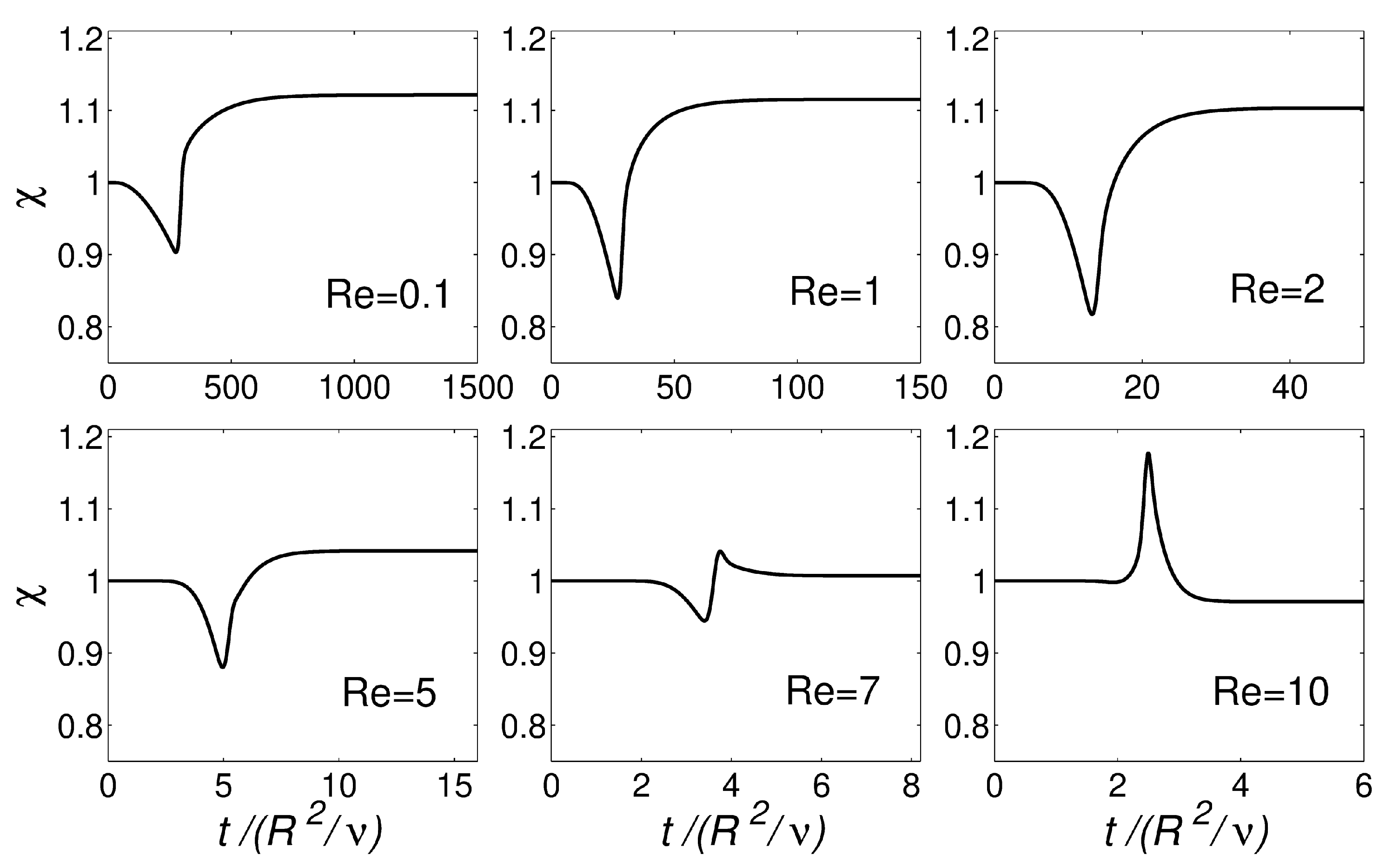
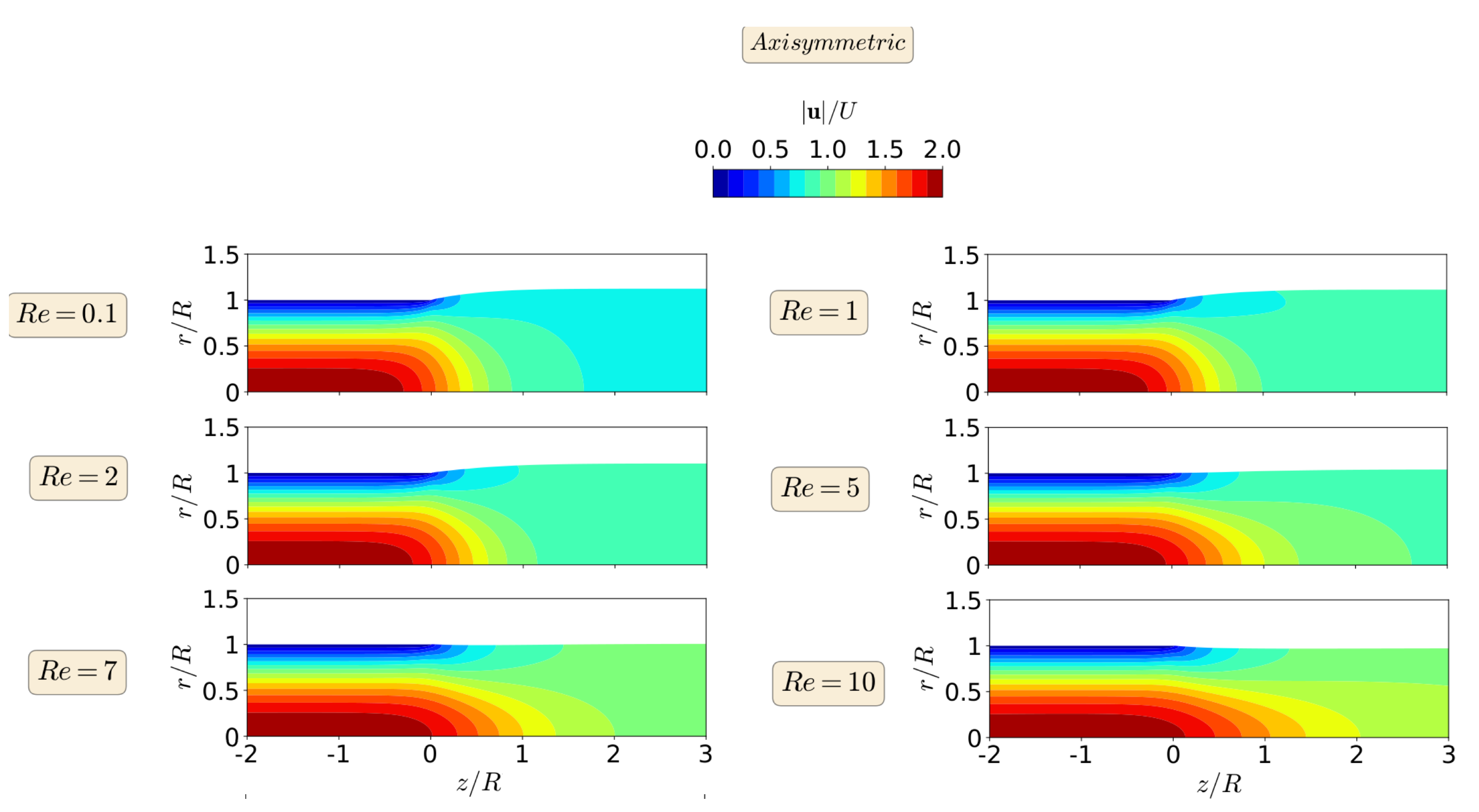
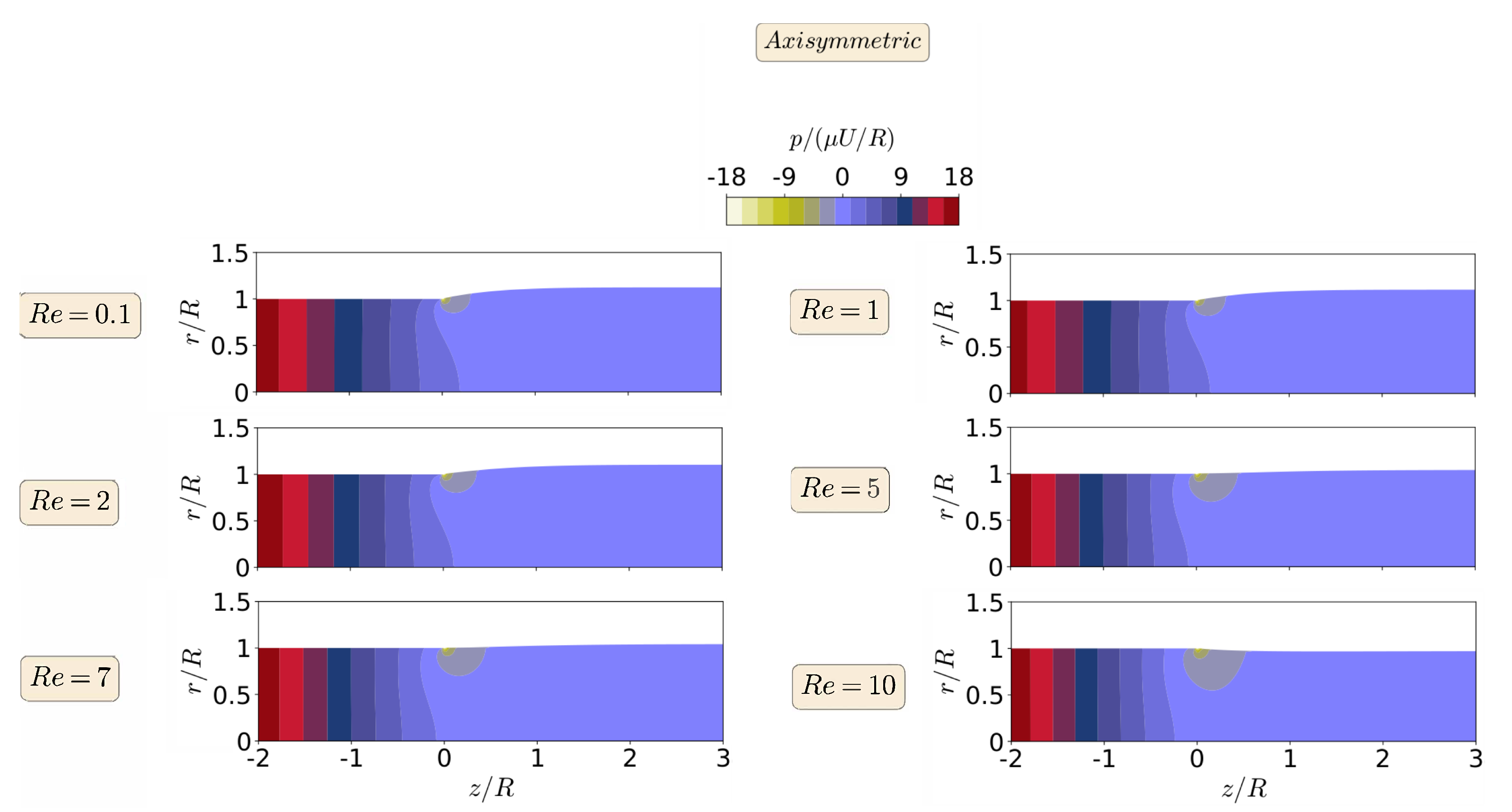
| Mesh | No. of Elements | No. of Dof | Error (%) | ||
|---|---|---|---|---|---|
| M1 | 11,840 | 59,200 | 1.214 | 2.3 | |
| M2 | 26,880 | 134,400 | 1.207 | 1.7 | |
| M3 | 60,480 | 302,400 | 1.201 | 1.2 | |
| M4 | 136,080 | 680,400 | 1.198 | 0.9 | |
| M5 | 306,180 | 1,530,900 | 1.195 | 0.7 | |
| Extrapolated | - | - | - | 1.187 | |
| Mitsoulis et al. [28] | - | - | - | 1.186 | |
| Tanner [1] | - | - | - | 1.190 ± 0.002 | |
| Georgiou and Boudouvis [27] | - | - | - | 1.186 |
| CPU Wall Time (s) Per Time-Step | |||||||
|---|---|---|---|---|---|---|---|
| C-PISO | PISO | C-PISO/PISO | C-PISO | PISO | C-PISO/PISO | Total calculation time [h] | |
| 0.1 | 0.0685 | 0.0032 | 21.4 | 8 | 15 | 0.53 | 24.3 |
| 1 | 0.0069 | 0.0014 | 4.9 | 8 | 11 | 0.72 | 32.2 |
| 10 | 0.0007 | 0.0001 | 7.0 | 7 | 11 | 0.63 | 13.9 |
| CPU Wall Time (s) Per Time-Step | |||||||
|---|---|---|---|---|---|---|---|
| C-PISO | PISO | C-PISO/PISO | C-PISO | PISO | C-PISO/PISO | Total calculation time [h] | |
| 0.1 | 0.0652 | 0.0031 | 21.0 | 7 | 12 | 0.58 | 22.4 |
| 1 | 0.0064 | 0.0013 | 4.9 | 7 | 9 | 0.78 | 30.4 |
| 10 | 0.0006 | 0.0001 | 6 | 5 | 9 | 0.56 | 11.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fakhari, A.; Tukovic, Ž.; Carneiro, O.S.; Fernandes, C. An Effective Interface Tracking Method for Simulating the Extrudate Swell Phenomenon. Polymers 2021, 13, 1305. https://doi.org/10.3390/polym13081305
Fakhari A, Tukovic Ž, Carneiro OS, Fernandes C. An Effective Interface Tracking Method for Simulating the Extrudate Swell Phenomenon. Polymers. 2021; 13(8):1305. https://doi.org/10.3390/polym13081305
Chicago/Turabian StyleFakhari, Ahmad, Željko Tukovic, Olga Sousa Carneiro, and Célio Fernandes. 2021. "An Effective Interface Tracking Method for Simulating the Extrudate Swell Phenomenon" Polymers 13, no. 8: 1305. https://doi.org/10.3390/polym13081305
APA StyleFakhari, A., Tukovic, Ž., Carneiro, O. S., & Fernandes, C. (2021). An Effective Interface Tracking Method for Simulating the Extrudate Swell Phenomenon. Polymers, 13(8), 1305. https://doi.org/10.3390/polym13081305









