Towards a Kinetic Modeling of the Changes in the Electrical Properties of Cable Insulation during Radio-Thermal Ageing in Nuclear Power Plants. Application to Silane-Crosslinked Polyethylene
Abstract
:1. Introduction
- According to Lorentz [37] and Lorenz [38], would be related to the molar polarization P of a given dielectric material as follows:i.e.,where V is the molar volume. In addition, according to van Krevelen [20], P and V would obey molar additive rules, i.e., they could be calculated by summing the molar contributions of the different chemical groups composing the monomer unit or any other constitutive repeating unit (CRU):As an example, Table 1 summarizes the values of and proposed by Goedhart [39] and Fedors [40] for methylene, but also for the various types of oxidation products generally detected during the radio-thermal ageing of PE. It should be noted that few of them were checked by van Krevelen in his handbook [20]. Thus, high uncertainties remain for many data (written in italics), in particular for ketones, carboxylic acids, hydroxyls and hydroperoxides.
- According to Darby [41], as electrical forces caused by polarizability and polar moment also determine the cohesive energy, a relationship should be expected between the dielectric constant and the solubility parameter . Based on a literature compilation of the and values reported for common polymers, Darby proposed the following empirical proportionality:i.e.,It should be recalled that is related to the molar attraction constant F as follows:where, according to van Krevelen [20], F and V are molar additive functions:
2. Materials and Methods
2.1. Materials
2.2. Radio-Thermal Ageing Conditions
2.3. Experimental Characterizations
2.3.1. Physico-Chemical Analyses
2.3.2. Electrical Measurements
3. Foundations of the Kinetic Model
- Initiation:
- (1R) PH + hν → P• + ½H2 ()
- (1T) 2POOH → P• + PO2• (k1)
- Propagation:
- (2) P• + O2 → PO2• (k2)
- (3) PO2• + PH → POOH + P• (k3)
- Termination:
- (4) P• + P• → Inactive products (k4)
- (5) P• + PO2• → Inactive products (k5)
- (6) PO2• + PO2• → Inactive products + O2 (k6)
- 1
- Oxidation is mainly initiated by the polymer radiolysis that occurs throughout the exposure (i.e., ), with the thermal decomposition of POOH being an additional (but secondary) source of radicals for the long term;
- 2
- The radical species reach a steady-state regime from the early periods of the radio-thermal exposure (i.e., ).
- The concentration of POOH:
- The concentration of carbonyls:where and are the respective formation yields of carbonyls in thermal initiation (1T) and termination (6).
- The oxygen consumption:
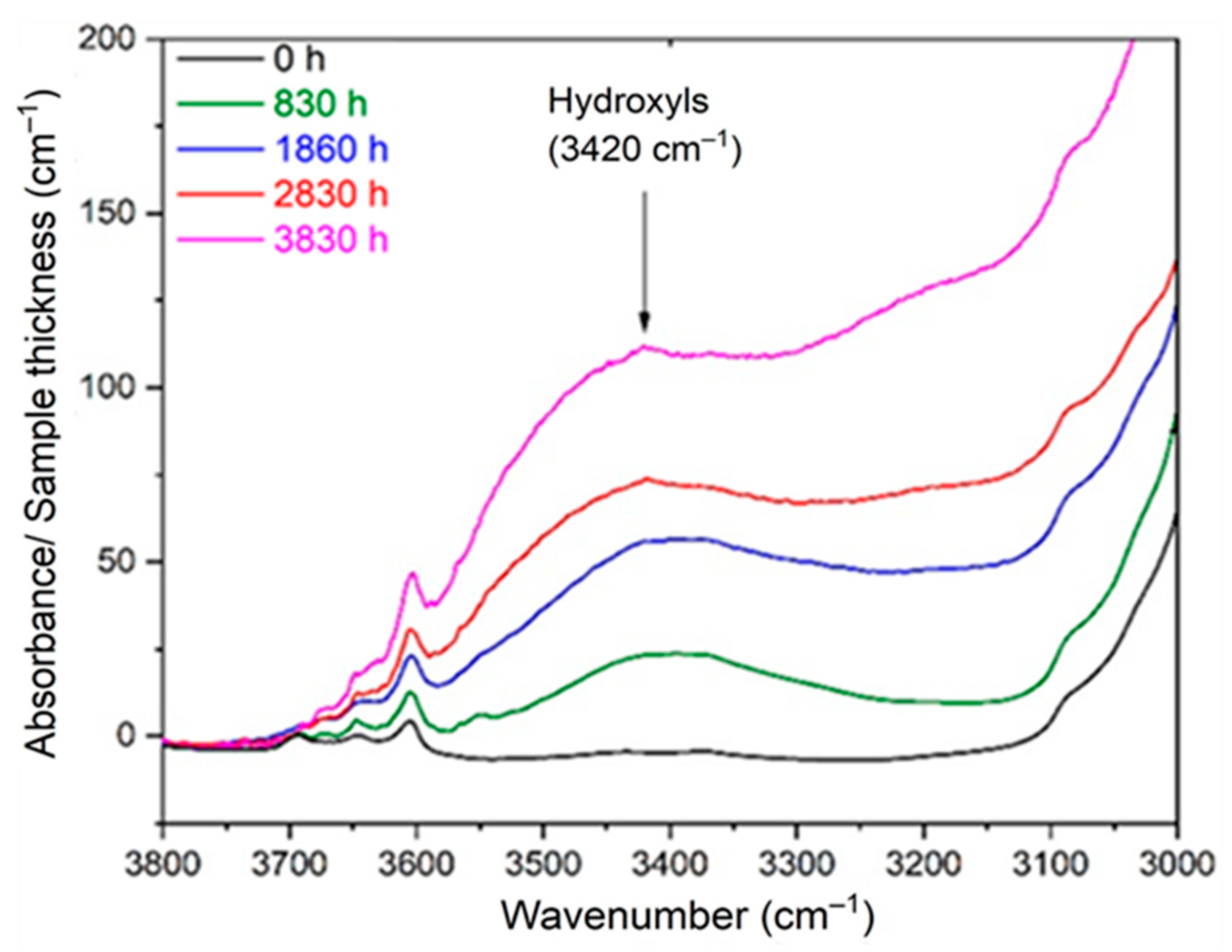
4. Main Oxidation Products
5. Calculation of the Changes in Density
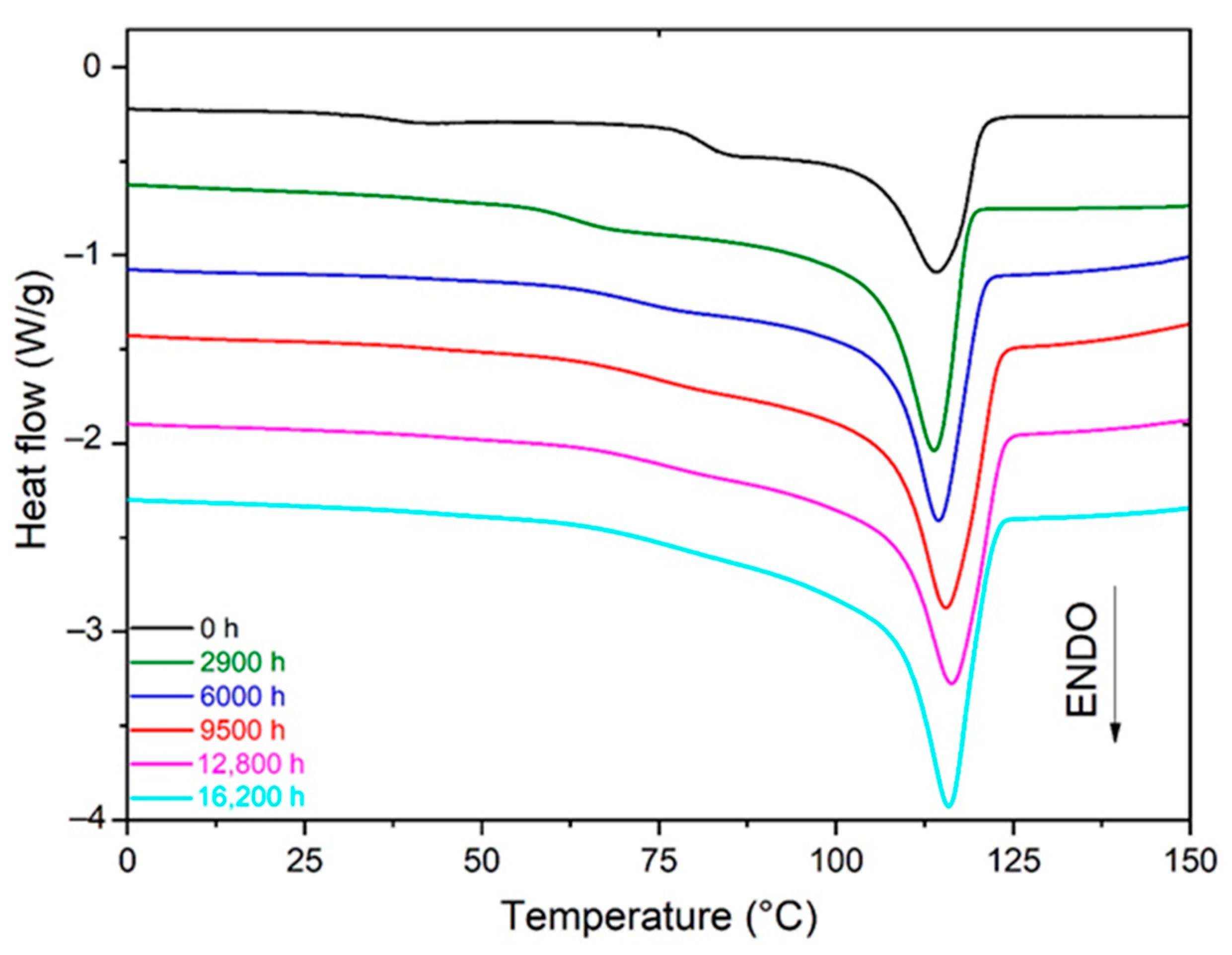
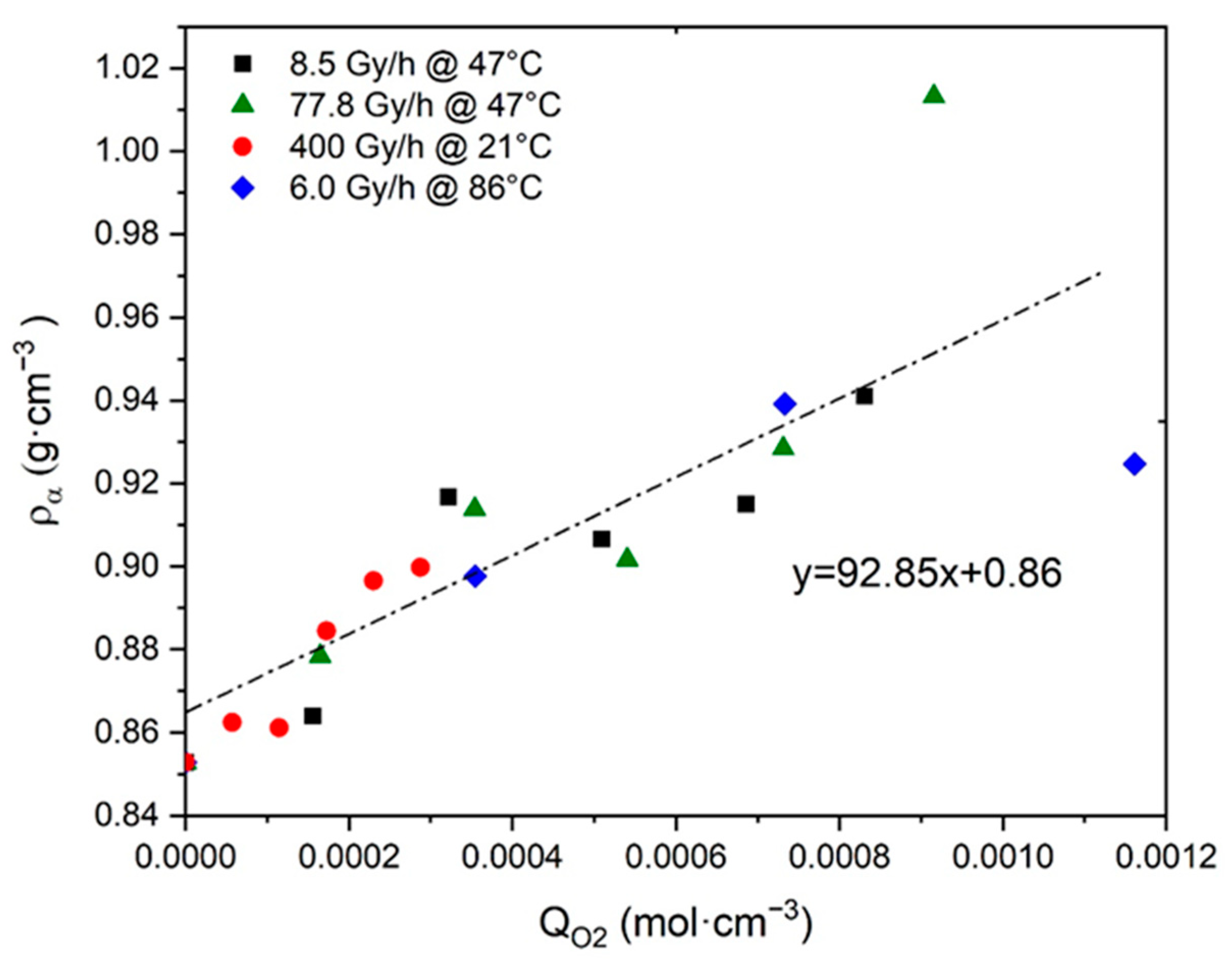
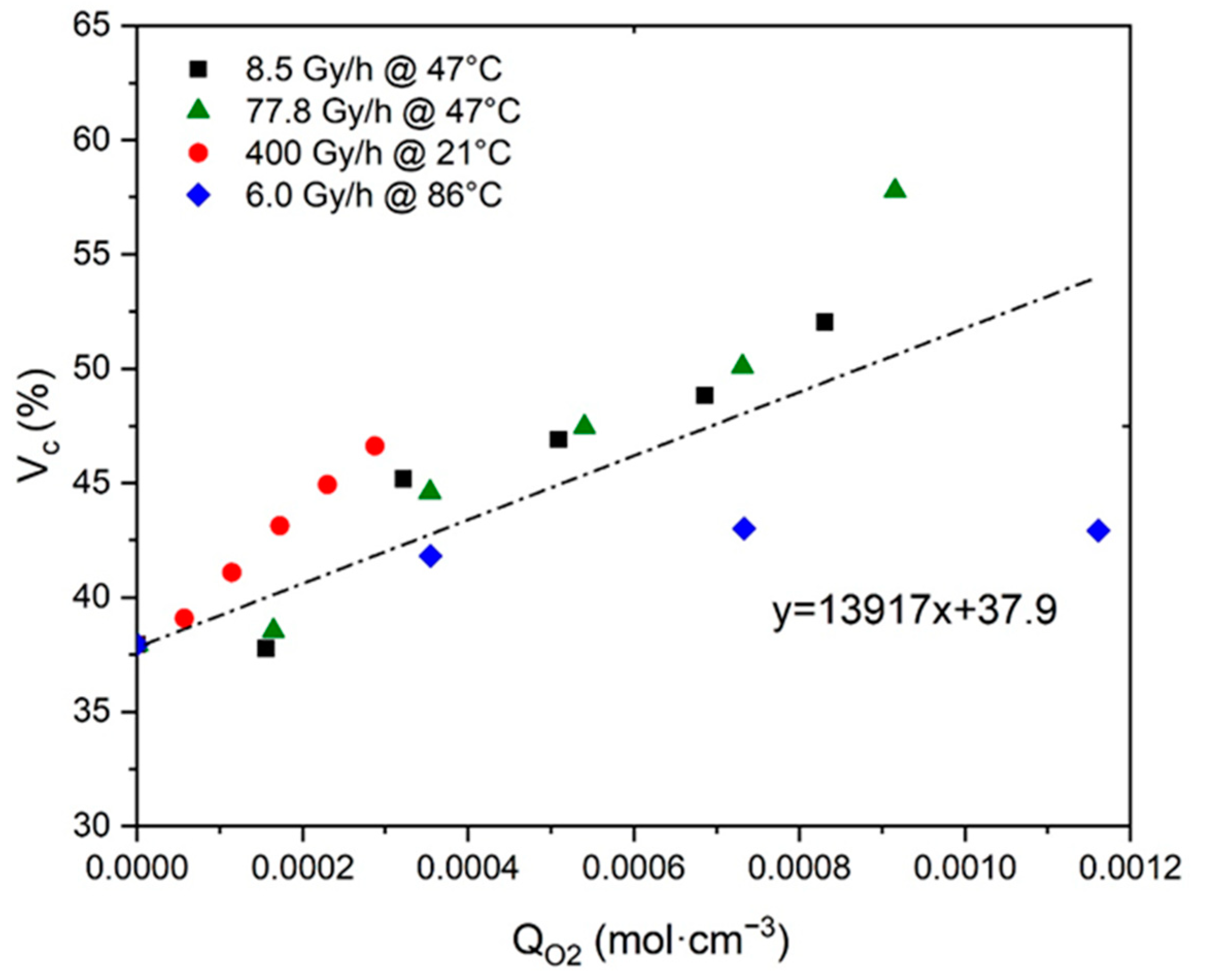
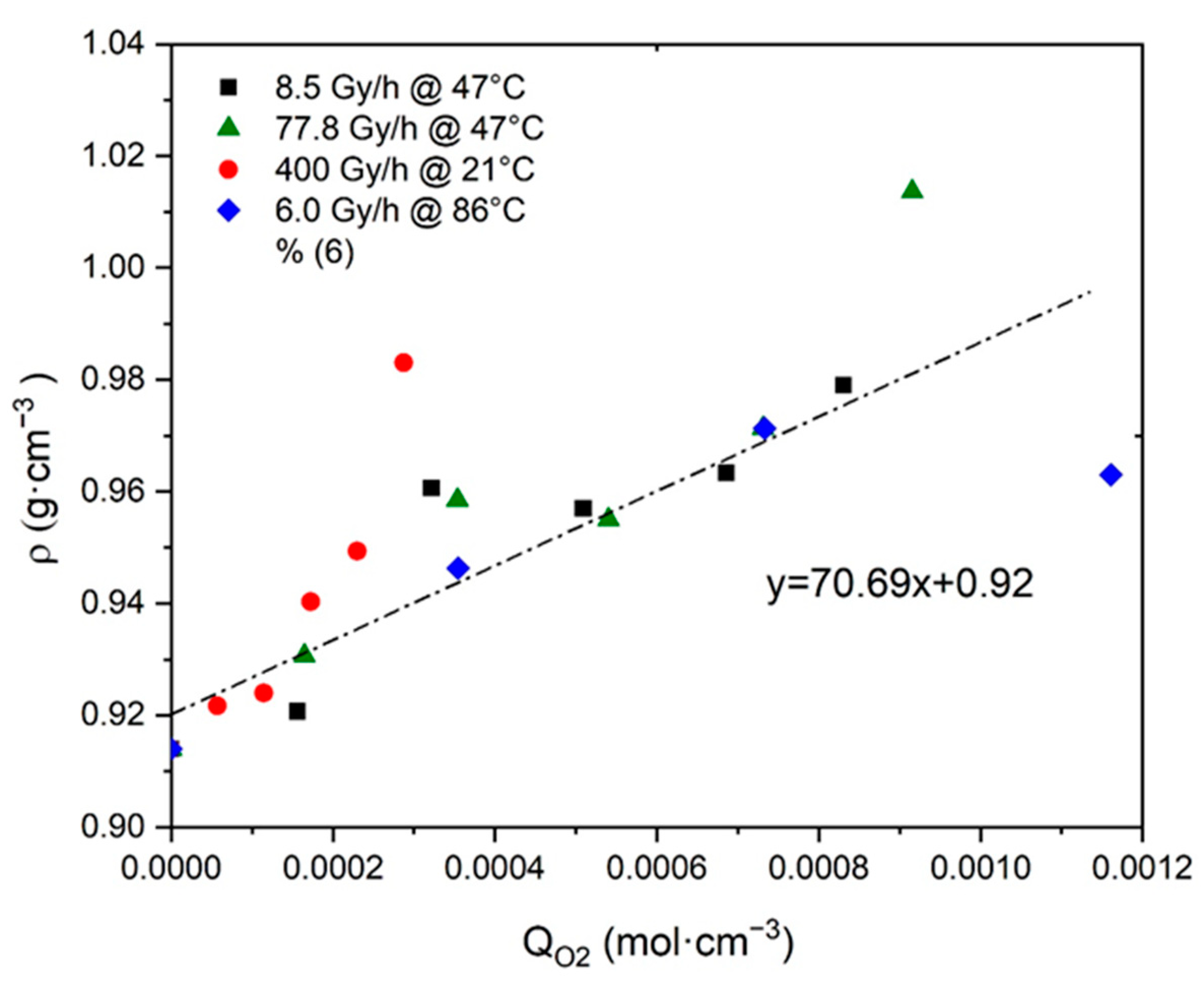
- As recalled in Section 2.3, the incorporation of “heavy” atoms, such as oxygen, into a polymer structure initially containing many “light” atoms (i.e., carbon and hydrogen) induces an increase in its density [32,54,55,56,57,58]. Since crystals are impermeable to oxygen, oxidation only occurs in the amorphous phase where it thus induces an increase in .
- In Si-XLPE, oxidation leads to a predominance of chain scissions over crosslinking [8]. Chain scissions progressively destroy the macromolecular network from which short linear fragments are extracted, which can easily migrate towards crystalline lamellae when the amorphous phase is in a rubbery state. The integration of these short fragments with crystalline lamellae induces a chemi-crystallization, i.e., a thickening of crystalline lamellae and an increase in the crystallinity ratios (i.e., and ).
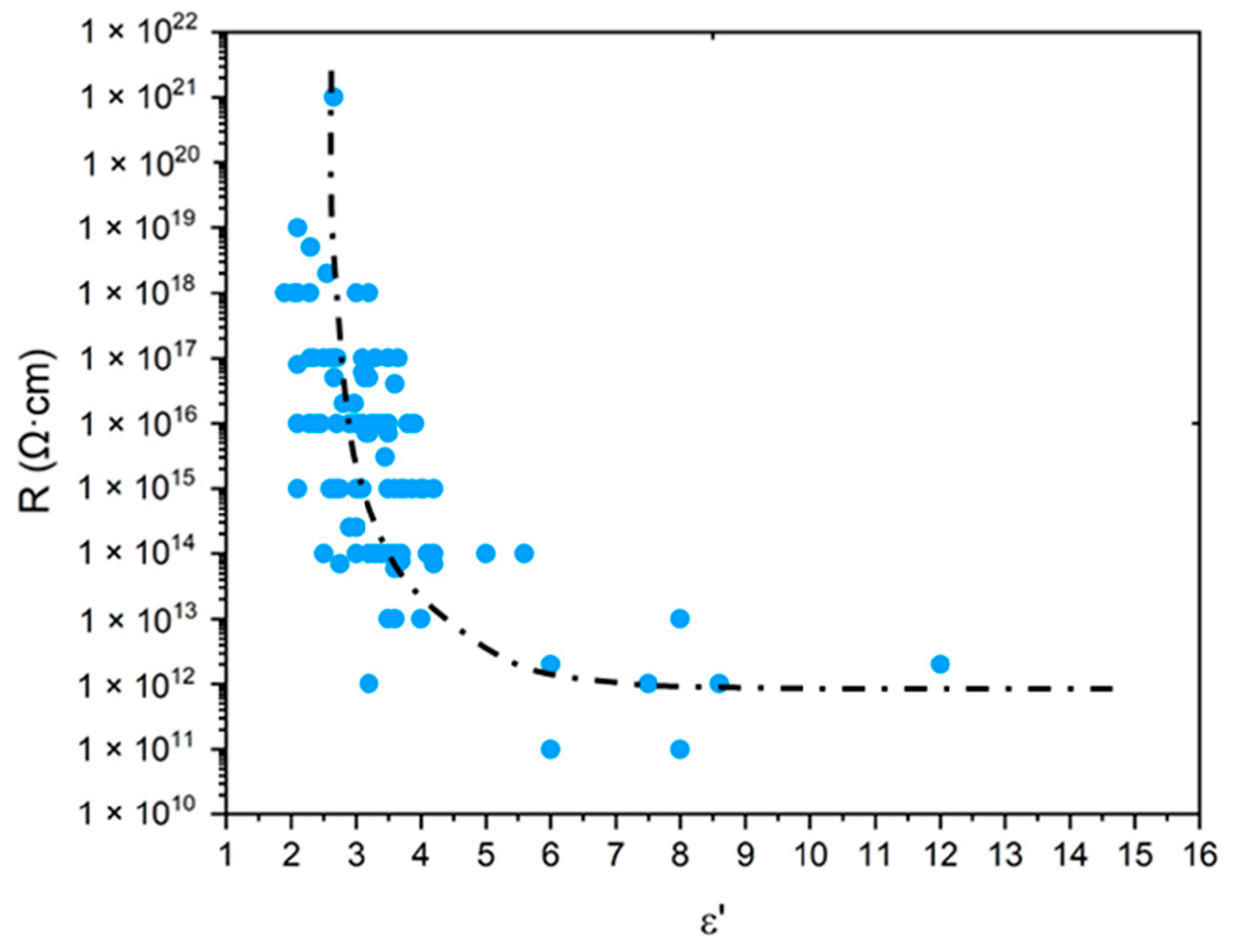
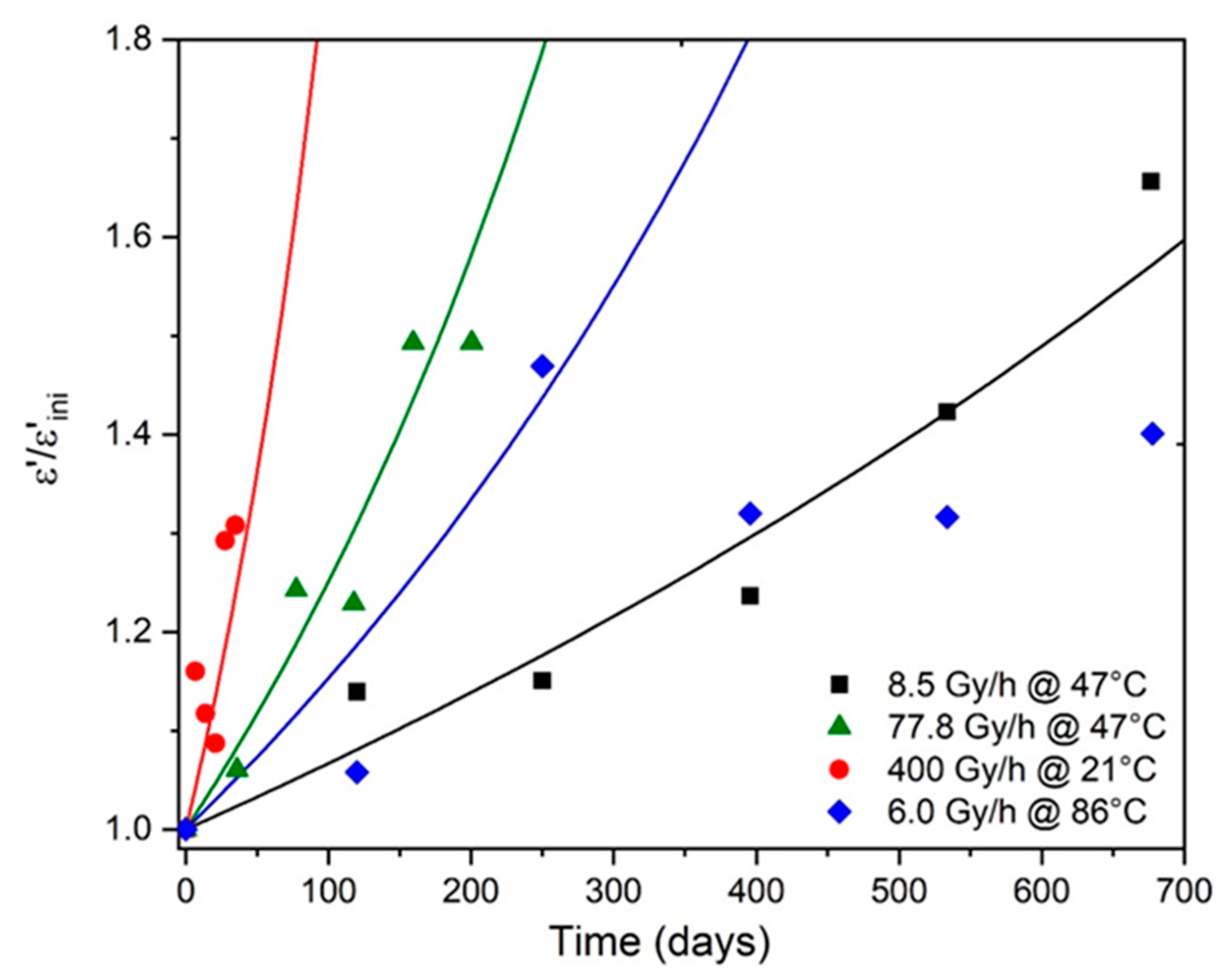
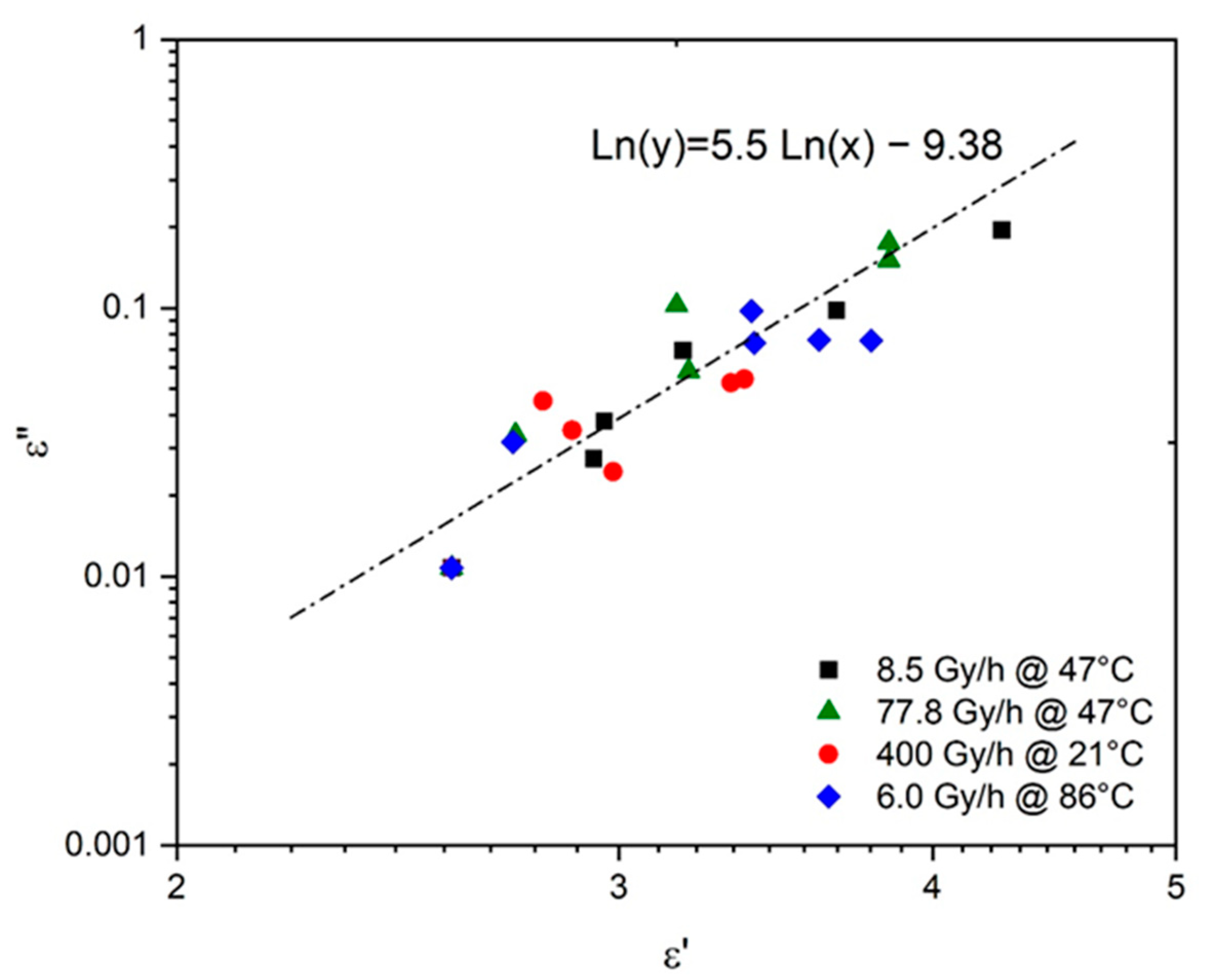
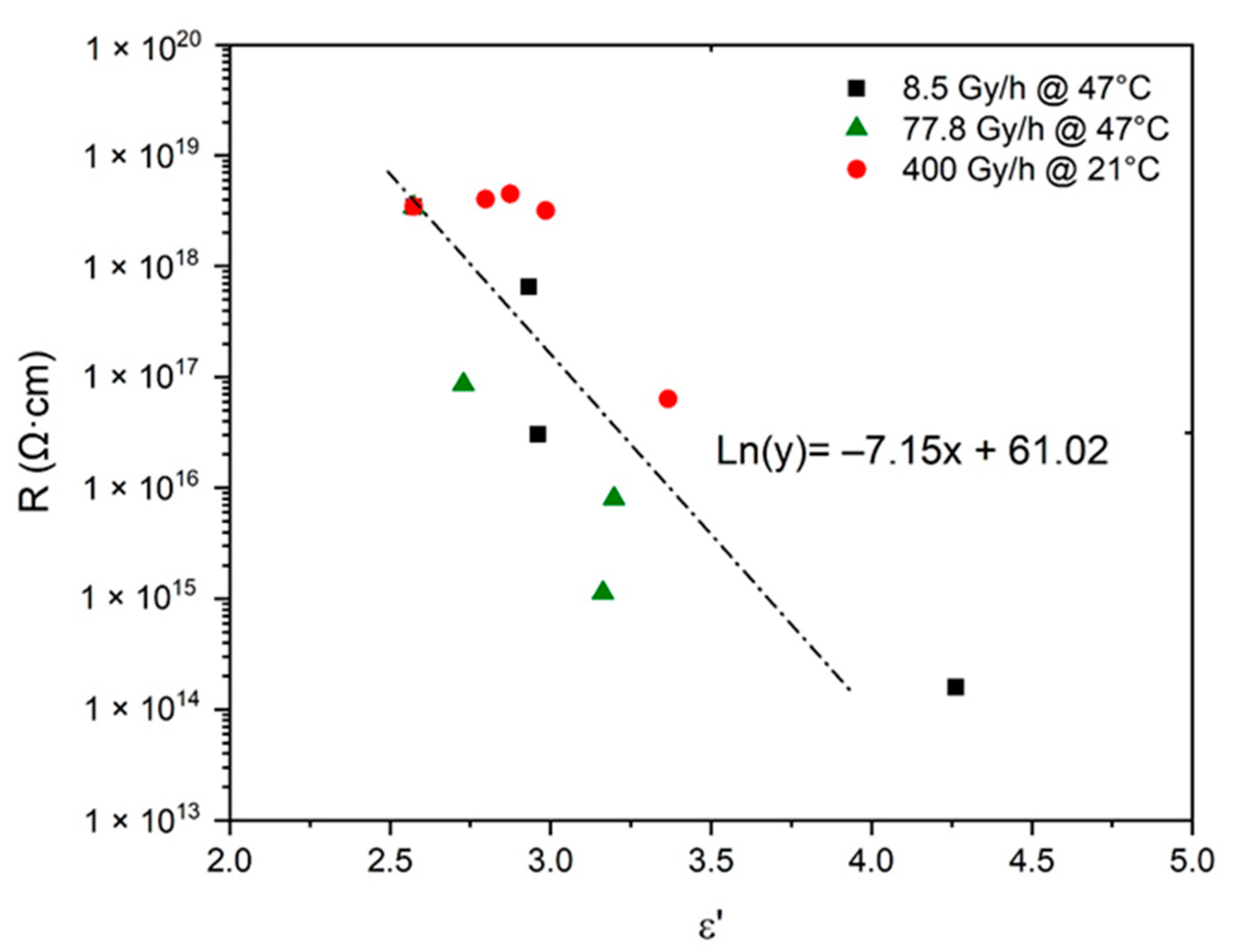
6. Prediction of Electrical Properties
7. Proposal of an End-of-Life Criterion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Evaluation of the Effect of Oxygen Consumption on the PE Density When Hydroperoxides Are the Main Oxidation Products
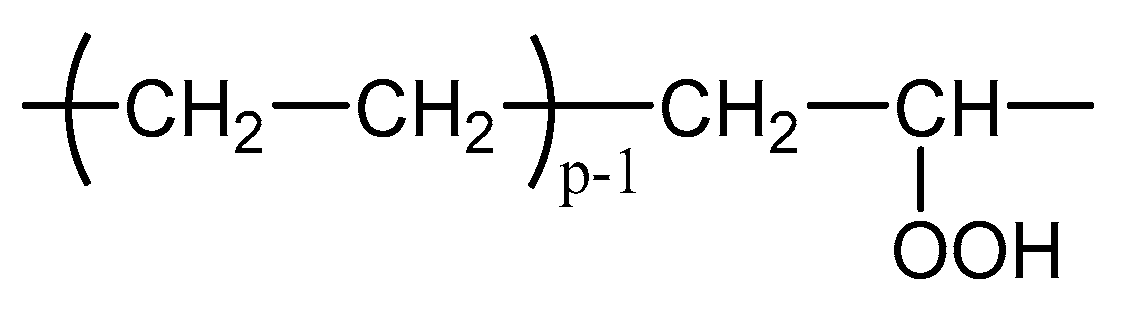
References
- IAEA-TECDOC-1402. Management of Life Cycle and Ageing at Nuclear Power Plants: Improved I&C Maintenance; IAEA Nuclear Energy Series; International Atomic Energy Agency (IAEA): Vienna, Austria, 2004. [Google Scholar]
- TeaM Cables Project Website. Available online: https://www.team-cables.eu/about-the-team-cables-project/ (accessed on 15 December 2021).
- Doduik, H.; Goodman, S.H. Handbook of Thermoset Plastics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Pritchard, G. Plastics Additives: An A-Z Reference; Springer Science & Business Media: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Pastorek, M. Crosslinking and Ageing of Ethylene-Vinyl Silane Copolymers. Ph.D. Dissertation, Tomas Bata University, Zlin, Czech Republic, 2014. [Google Scholar]
- Khelidj, N.; Colin, X.; Audouin, L.; Verdu, J. A simplified approach for the lifetime prediction of PE in nuclear environments. Nucl. Instrum. Methods Phys. Res. 2005, B236, 88–94. [Google Scholar] [CrossRef]
- Colin, X.; Monchy-Leroy, C.; Audouin, L.; Verdu, J. Lifetime prediction of polyethylene in nuclear plants. Nucl. Instrum. Methods Phys. Res. 2007, B265, 251–255. [Google Scholar] [CrossRef]
- Hettal, S.; Roland, S.; Sipila, K.; Joki, H.; Colin, X. A new analytical model for predicting the radio-thermal oxidation and the lifetime of electrical cable insulation in nuclear power plants. Application to silane crosslinked polyethylene. Polym. Degrad. Stab. 2021, 185, 109492. [Google Scholar] [CrossRef]
- Gillen, K.T.; Clough, R.L. A kinetic model for predicting oxidative degradation rates in combined radiation-thermal environments. J. Polym. Sci.: Polym. Chem. Ed. 1985, 23, 2683–2707. [Google Scholar] [CrossRef]
- NP-T-3. 6. Assessing and Managing Cable Ageing in Nuclear Power Plants; IAEA Nuclear Energy Series; International Nuclear Energy Agency (IAEA): Vienna, Austria, 2012. [Google Scholar]
- Verardi, L. Aging of Nuclear Power Plant Cables: In Search of Non-Destructive Diagnostic Quantities. Ph.D. Dissertation, University of Bologna, Bologna, Italy, 2014. [Google Scholar]
- Linde, E.; Verardi, L.; Pourmand, P.; Fabiani, D.; Gedde, U. Non-destructive condition monitoring of aged ethylene-propylene copolymer cable insulation samples using dielectric spectroscopy and NMR spectroscopy. Polym. Test. 2015, 46, 72–78. [Google Scholar] [CrossRef]
- Salivon, T.; Colin, X.; Comte, R. Degradation of XLPE and PVC cable insulators. In Proceedings of the 2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015; pp. 656–659. [Google Scholar]
- Suraci, S.V.; Fabiani, D.; Joki, H.; Sipila, K. Filler impact analysis on aging of cross-linked polyethylene for nuclear applications through dielectric spectroscopy. In Proceedings of the 2019 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Richland, WA, USA, 20–23 October 2019; pp. 166–169. [Google Scholar]
- Boubakeur, A.; Mecheri, Y.; Boumerzoug, M. Comportement électrique et mécanique du polyethylene réticulé chimiquement soumis à un vieillissement thermique continu. Ann. Chim. Sci. Mat. 2000, 25, 457–470. [Google Scholar] [CrossRef]
- Pelzer, Q. Etude du Vieillissement des Isolants Synthétiques des Câbles Moyenne Tension «HTA». Ph.D. Dissertation, Université Grenoble Alpes, Le Bourget-du-Lac, France, 2019. [Google Scholar]
- Simmons, K.L.; Fifield, L.S.; Westman, M.P.; Tedeschi, J.R.; Jones, A.M.; Prowant, M.; Pardini, A.F.; Ramuhalli, P. Determining Remaining Useful Life of Aging Cables in Nuclear Power Plants—Interim Study FY13; Report no. PNNL-22812; Pacific Northwest National Laboratory: Richland, DC, USA, 2013. [Google Scholar]
- Liu, S.; Fifield, L.S.; Bowler, N. Aging mechanisms of filled cross-linked polyethylene (XLPE) cable insulation material exposed to simultaneous thermal and gamma radiation. Radiat. Phys. Chem. 2021, 184, 109486. [Google Scholar] [CrossRef]
- Fabiani, D.; Suraci, S.V. Broadband dielectric spectroscopy: A viable technique for aging assessment of low-voltage cable insulation used in nuclear power plants. Polymers 2021, 13, 494. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Electrical properties. In Properties of polymers: Their Correlation with Chemical Structure. Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 11; pp. 319–354. [Google Scholar]
- Cotts, D.B.; Reyes, Z. Electrically Conductive Organic Polymers for Advanced Applications; William Andrew Publishing, Noyes Data Corporation: Park Ridge, NJ, USA, 1986. [Google Scholar]
- Tan, Q.; Irwin, P.; Cao, Y. Advanced dielectrics for capacitors. IEEJ Trans. Fundam. Mater. 2006, 126, 1153–1159. [Google Scholar] [CrossRef] [Green Version]
- Trotignon, J.-P.; Verdu, J.; Dobraczynski, A.; Piperaud, M. Précis de Matières Plastiques: Structures-Propriétés, Mise en Œuvre, Normalisation; Nathan: Paris, France, 1996. [Google Scholar]
- Dubois, J.-C. Propriétés Diélectriques des Plastiques; Reference AM3140; Techniques de l’Ingénieur: Saint-Denis, France, 2001. [Google Scholar]
- Vassilikou-Dova, A.; Kalogeras, I.M. Dielectric analysis. In Thermal Analysis of Polymers: Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2009; Chapter 6; pp. 497–613. [Google Scholar]
- Suraci, S.V.; Fabiani, D.; Mazzocchetti, L.; Maceratesi, V.; Merighi, S. Investigation on thermal degradation phenomena on low density polyethylene (LDPE) through dielectric spectroscopy. In Proceedings of the 2018 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018; pp. 434–437. [Google Scholar]
- Fabiani, D.; Suraci, S.V.; Bulzaga, S. Aging investigation of low-voltage cable insulation used in nuclear power plants. In Proceedings of the 2018 IEEE Electrical Insulation Conference (EIC), San Antonio, TX, USA, 17–20 June 2018; pp. 516–519. [Google Scholar]
- Kemari, Y.; Mekhaldi, A.; Teisseydre, G.; Teguar, M. Correlations between structural changes and dielectric behavior of thermally aged XLPE. IEEE Trans. Dielect. Electr. Insul. 2019, 26, 1859–1866. [Google Scholar] [CrossRef]
- Suraci, S.V.; Fabiani, D.; Xu, A.; Roland, S.; Colin, X. Ageing assessment of XLPE LV cables for nuclear applications through physico-chemical and electrical measurements. IEEE Access 2020, 8, 27086–27096. [Google Scholar] [CrossRef]
- Suraci, S.V.; Fabiani, D.; Mazzocchetti, L.; Giorgini, L. Degradation assessment of polyethylene-based material through electrical and chemical-physical analyses. Energies 2020, 13, 650. [Google Scholar] [CrossRef] [Green Version]
- Nedjar, M. Effect of thermal ageing on the electrical properties of cross-linked polyethylene. J. Appl. Polym. Sci. 2009, 111, 1985–1990. [Google Scholar] [CrossRef]
- Motori, A.; Sandrolini, F.; Montanari, G.C. Chemical, physical and microstructural properties of thermally aged XLPE cable models. In Proceedings of the Second International Conference on Properties and Applications of Dielectric Materials, Beijing, China, 12–16 September 1988; pp. 764–768. [Google Scholar]
- Motori, A.; Sandrolini, F.; Montanari, G.C. Degradation and electrical behavior of aged XLPE cable models. In Proceedings of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 3–6 July 1989; pp. 352–358. [Google Scholar]
- Mecheri, Y.; Boukezzi, L.; Boubakeur, A.; Lallouani, M. Dielectric and mechanical behavior of cross-linked polethylene under thermal ageing. In Proceedings of the 2000 Annual Report Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Victoria, BC, Canada, 15–18 October 2000; pp. 560–563. [Google Scholar]
- Boukezzi, L.; Boubakeur, A. Prediction of mechanical properties of XLPE cable insulation under thermal ageing: Neural network approach. IEEE Trans. Dielect. Electr. Insul. 2013, 20, 2125–2134. [Google Scholar] [CrossRef]
- Mecheri, Y.; Bouazabia, S.; Boubakeur, A.; Lallouani, M. Effect of thermal ageing on the properties of XLPE as an insulating material for HV cables. In Proceedings of the International Electrical Insulation Conference, IET Centre, Birmingham, UK, 29–31 May 2013; pp. 191–194. [Google Scholar]
- Lorentz, H.A. Ueber die beziehung zwischen der fortpflanzungsgeschwindigkeit des lichtes und der körperdichte. Wied. Ann. Phys. 1880, 9, 641–665. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, L.V. Ueber die refraktion konstante. Wied. Ann. Phys. 1880, 11, 70–75. [Google Scholar]
- Goedhart, D.J. Specific refractive index of segmented polyurethanes. In Proceedings of the International GPC Seminar, Monaco, 12–15 October1969. [Google Scholar]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Darby, J.R.; Touchette, N.W.; Sears, J.K. Dielectric constants of plasticizers as predictors of compatibility with polyvinyl chloride. Polym. Eng. Sci. 1967, 7, 295–309. [Google Scholar] [CrossRef]
- Small, P.A. Some factors affecting the solubility of polymers. J. Appl. Chem. 1953, 3, 71–80. [Google Scholar] [CrossRef]
- Van Krevelen, D.W. Chemical structure and properties of coal. −XXVIII. Coal constitution and solvent extraction. Fuel 1965, 44, 229–242. [Google Scholar]
- Hoy, K.L. New values of the solubility parameters from vapor pressure data. J. Paint Technol. 1970, 42, 76–118. [Google Scholar]
- Zak, P.; Placek, V. Deliverable D2.2: Specifications of Tests—Accelerated Ageing Protocol, Test Strategy. TeaM Cables Report; UJV Rez: Husinec, Czech Republic, 2018. [Google Scholar]
- Geuskens, G.; Kabamba, M.S. Photo-oxidation of polymers –Part V: A new chain scission mechanism in polyolefins. Polym. Degrad. Stab. 1982, 4, 69–76. [Google Scholar] [CrossRef]
- Domke, W.D.; Steinke, H. Oxidative structures in polyolefins: FTIR method of quantitative determination. J. Polym. Sci. Polym. Chem. 1986, 24, 2701–2705. [Google Scholar] [CrossRef]
- Lacoste, J.; Carlsson, D.J. Gamma-, photo-, and thermally-initiated oxidation of linear low density polyethylene: A quantitative comparison of oxidation products. J. Polym. Sci. Polym. Chem. 1992, 30, 493–500. [Google Scholar] [CrossRef]
- Rapp, G.; Tireau, J.; Bussière, P.-O.; Chenal, J.-M.; Rousset, F.; Chazeau, L.; Gardette, J.-L.; Therias, S. Influence of the physical state of a polymer blend on thermal ageing. Polym. Degrad. Stab. 2019, 163, 161–173. [Google Scholar] [CrossRef]
- Blivet, C.; Larché, J.-F.; Israeli, Y.; Bussière, P.-O.; Gardette, J.-L. Thermal oxidation of cross-linked PE and EPR used as insulation materials: Multi-scale correlation over a wide range of temperature. Polym. Test. 2021, 93, 106913. [Google Scholar] [CrossRef]
- Da Cruz, M.; Van Schoors, L.; Benzarti, K.; Colin, X. Thermo-oxidative degradation of additive free polyethylene—Part I: Analysis of chemical modifications at molecular and macromolecular scales. J. Appl. Polym. Sci. 2016, 133, 43287. [Google Scholar] [CrossRef]
- Gulmine, J.V.; Akcelrud, L. FTIR characterization of aged XLPE. Polym. Test. 2006, 25, 932–942. [Google Scholar] [CrossRef]
- Serror-Mimoun, M. Etude du Vieillissement Thermique d’un Jonc Pultrude en Matréiau Composite. Ph.D. Dissertation, ENSAM, Paris, France, 2013. [Google Scholar]
- Motori, A.; Sandrolini, F.; Montanari, G.C. A contribution to the study of aging of XLPE insulated cables. IEEE Trans. Power Delivery 1991, 6, 34–42. [Google Scholar] [CrossRef]
- Langlois, V.; Meyer, M.; Audouin, L.; Verdu, J. Physical aspects of the thermal oxidation of crosslinked polyethylene. Polym. Degrad. Stab. 1992, 36, 207–216. [Google Scholar] [CrossRef]
- Gueguen, V.; Audouin, L.; Pinel, B.; Verdu, J. Thermal oxidation of EPDM terpolymer and vulcanisate. Polym. Degrad. Stab. 1994, 43, 217–223. [Google Scholar] [CrossRef]
- Decelle, J.; Huet, N.; Bellenger, V. Oxidation induced shrinkage for thermally aged epoxy networks. Polym. Degrad. Stab. 2003, 81, 239–248. [Google Scholar] [CrossRef]
- Colin, X.; Verdu, J. Strategy for studying thermal oxidation of organic matrix composites. Compos. Sci. Technol. 2005, 65, 411–419. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Te Nijenhuis, K. Physical constants of the most important solvents. In Properties of Polymers: Their Correlation with Chemical Structure. Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; Tab. IV; pp. 904–919. [Google Scholar]
- Colin, X.; Monchy-Leroy, C.; Verdu, J. Effect of gamma irradiation on tensile properties of low molecular weight polyethylene samples. Radiat. Phys. Chem. 2011, 80, 895–901. [Google Scholar] [CrossRef] [Green Version]
- Walter, E.R.; Reding, P.F. Variations in unit cell dimensions in polyethylene. J. Polym. Sci. 1956, 21, 561–562. [Google Scholar] [CrossRef]
- ASTM D257-14. Test Methods for DC Resistance or Conductance of Insulating Materials; American Society for Testing and Materials (ASTM International): West Conshohocken, PA, USA, 2014. [Google Scholar]
- Huang, J.; Minne, W.; Drozdzak, R.; Recher, G.; Le Gac, P.Y.; Richaud, E. Thermal oxidation of poly(dicyclopentadiene). Decomposition of hydroperoxides. Polym. Degrad. Stab. 2020, 174, 109102. [Google Scholar] [CrossRef]
- Seguchi, T.; Yamamoto, Y. Diffusion and Solubility of Oxygen in γ-Irradiated Polymer Insulation Materials; Japan Atomic Energy Research Institute Report; JAERI 1299: Takasaki, Japan, 1986. [Google Scholar]
- Tidjani, A.; Wanatabe, Y. Gamma-oxidation of linear low-density polyethylene: The dose-rate effect of irradiation on chemical and physical modifications. J. Polym. Sci. Polym. Chem. 1995, 33, 1455–1460. [Google Scholar] [CrossRef]
- Salvalaggio, M.; Bagatin, R.; Fornaroli, M.; Fanutti, S.; Palmery, S.; Battistel, E. Multi-component analysis of linear low density polyethylene oxidative degradation. Polym. Degrad. Stab. 2006, 91, 2775–2785. [Google Scholar] [CrossRef]
- Tireau, J. Propriétés à Long Terme des Gaines de Polyéthylène Haute Densité Utilisées sur les Ponts à Haubans. Ph.D. Dissertation, Arts et Métiers ParisTech, Paris, France, 2011. [Google Scholar]
- Gardette, M.; Perthue, A.; Gardette, J.-L.; Janecska, T.; Foldes, E.; Pukanszky, B.; Thérias, S. Photo- and thermal oxidation of polyethylene: Comparison of mechanisms and influence of unsaturation content. Polym. Degrad. Stab. 2013, 98, 2383–2390. [Google Scholar] [CrossRef] [Green Version]
- Van Krevelen, D.W.; Te Nijenhuis, K. Volumetric properties. In Properties of Polymers: Their Correlation with Chemical Structure. Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 4; pp. 71–108. [Google Scholar]
- Pascault, J.-P.; Sautereau, H.; Verdu, J.; Williams, R.J.J. Thermosetting Polymers; Marcel Dekker, Inc.: New York, NY, USA, 2002; Chapter 10; pp. 282–322. [Google Scholar]
- Muller, R.S.; Kasmins, T.I. Device Electronics for Integrated Circuits, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Gauthier, M. Engineering Materials Handbook; ASM International: Materials Park, OH, USA, 1995; pp. 1113–1230. [Google Scholar]


| Group | Pi (cm3·mol−1) | Fi (J1/2·cm3/2·mol−1) | Vi (cm3·mol−1) |
|---|---|---|---|
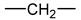 | 4.7 | 275 | 16.1 |
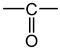 | 10 | 560 | 10.8 |
 | 15 | 590 | 18 |
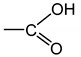 | 15.8 | 825 | 28.5 |
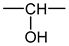 | 9.6 | 725 | 9 |
 | 14.8 | 925 | 12.8 |
| Ageing No. | Dose Rate (Gy·h−1) | Dose Rate (Gy·s−1) | Temperature (°C) | Maximum Duration (h) | Maximum Dose (kGy) |
|---|---|---|---|---|---|
| 1 | 8.5 | 2.36 × 10−3 | 47 | 12,800 | 109 |
| 2 | 6.0 | 1.67 × 10−3 | 86 | 16,267 | 98 |
| 3 | 77.8 | 2.16 × 10−2 | 47 | 3830 | 298 |
| 4 | 400 | 1.11 × 10−1 | 21 | 668 | 269 |
| Oxidation Products | ν (cm−1) | ε (L·mol−1·cm−1) | Reference for ε |
|---|---|---|---|
| Hydroxyls | 3420 | 70 | [51] |
| Anhydrides | 1778 | 730 | [53] |
| γ-Lactones | 1773 | 720 | [52] |
| Esters | 1740 | 590 | [51] |
| Aldehydes | 1736 | 270 | [51] |
| Ketones | 1720 | 300 | [51] |
| T (°C) | 21 | 47 | 47 | 86 |
| I (Gy·h−1) | 400 | 77.8 | 8.5 | 6.0 |
| Gi | 8 | 8 | 8 | 8 |
| k1b (L·mol−1·s−1) | 5.0 × 10−9 | 2.5 × 10−7 | 2.4 × 10−7 | 1.0 × 10−5 |
| k2 (L·mol−1·s−1) | 108 | 108 | 108 | 108 |
| k3 (L·mol−1·s−1) | 1.6 × 10−3 | 1.9 × 10−2 | 1.9 × 10−2 | 3.6 × 10−1 |
| k4 (L·mol−1·s−1) | 8.0 × 1011 | 8.0 × 1011 | 8.0 × 1011 | 8.0 × 1011 |
| k5 (L·mol−1·s−1) | 1.2 × 1010 | 7.0 × 1010 | 9.0 × 1010 | 2.4 × 1011 |
| k6 (L·mol−1·s−1) | 5.0 × 104 | 1.0 × 106 | 2.0 × 106 | 6.0 × 107 |
| γ1CO (%) | 90 | 70 | 75 | 100 |
| γ6CO (%) | 90 | 70 | 75 | 100 |
| T (°C) | 21 | 47 | 47 | 86 |
| I (Gy·h−1) | 400 | 77.8 | 8.5 | 6.0 |
| [POOH] (mol%) | 16.2 | 19.9 | 15.9 | – |
| [Alcohols] (mol%) | 7.3 | 4.0 | 6.6 | 2.7 |
| [Anhydrides] (mol%) | 1.5 | 1.9 | 0.9 | 3.7 |
| [γ-Lactones] (mol%) | 1.0 | 1.5 | 2.1 | 3.0 |
| [Linear esters] (mol%) | 4.5 | 3.7 | 3.1 | 16.7 |
| [Aldehydes] (mol%) | 11.5 | 14.4 | 15.4 | 25.1 |
| [Ketones] (mol%) | 35.3 | 30.2 | 37.6 | 31.0 |
| [Carboxylic acids] (mol%) | 22.7 | 24.3 | 18.4 | 17.8 |
| CRU | ||||||
|---|---|---|---|---|---|---|
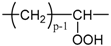 | 14p + 32 | 3p + 2 | 1/p | 7.56 | 124.44 | 37.33 |
 | 14p + 16 | 3p + 1 | 1/2p | 7.56 | 124.44 | 37.33 |
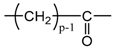 | 14p + 14 | 3p − 1 | 1/2p | 12.44 | 234.24 | 70.27 |
 | 14p + 15 | 3p | 1/2p | 10.00 | 175.69 | 52.71 |
 | 14p + 31 | 3p + 1 | 1/p | 8.78 | 149.23 | 44.77 |
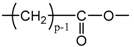 | 14p + 30 | 3p | 1/p | 10.00 | 175.69 | 52.71 |
| I (Gy·h−1) | 400 | 77.8 | 8.5 | 6.0 |
| T (°C) | 21 | 47 | 47 | 86 |
| (days) | 67 | 184 | 629 | 289 |
| (days) | 32 | 43 | 246 | - |
| 2.1 | 4.3 | 2.6 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hettal, S.; Suraci, S.V.; Roland, S.; Fabiani, D.; Colin, X. Towards a Kinetic Modeling of the Changes in the Electrical Properties of Cable Insulation during Radio-Thermal Ageing in Nuclear Power Plants. Application to Silane-Crosslinked Polyethylene. Polymers 2021, 13, 4427. https://doi.org/10.3390/polym13244427
Hettal S, Suraci SV, Roland S, Fabiani D, Colin X. Towards a Kinetic Modeling of the Changes in the Electrical Properties of Cable Insulation during Radio-Thermal Ageing in Nuclear Power Plants. Application to Silane-Crosslinked Polyethylene. Polymers. 2021; 13(24):4427. https://doi.org/10.3390/polym13244427
Chicago/Turabian StyleHettal, Sarah, Simone Vincenzo Suraci, Sébastien Roland, Davide Fabiani, and Xavier Colin. 2021. "Towards a Kinetic Modeling of the Changes in the Electrical Properties of Cable Insulation during Radio-Thermal Ageing in Nuclear Power Plants. Application to Silane-Crosslinked Polyethylene" Polymers 13, no. 24: 4427. https://doi.org/10.3390/polym13244427