Water-Activated Semiquinone Formation and Carboxylic Acid Dissociation in Melanin Revealed by Infrared Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Melanin Synthesis
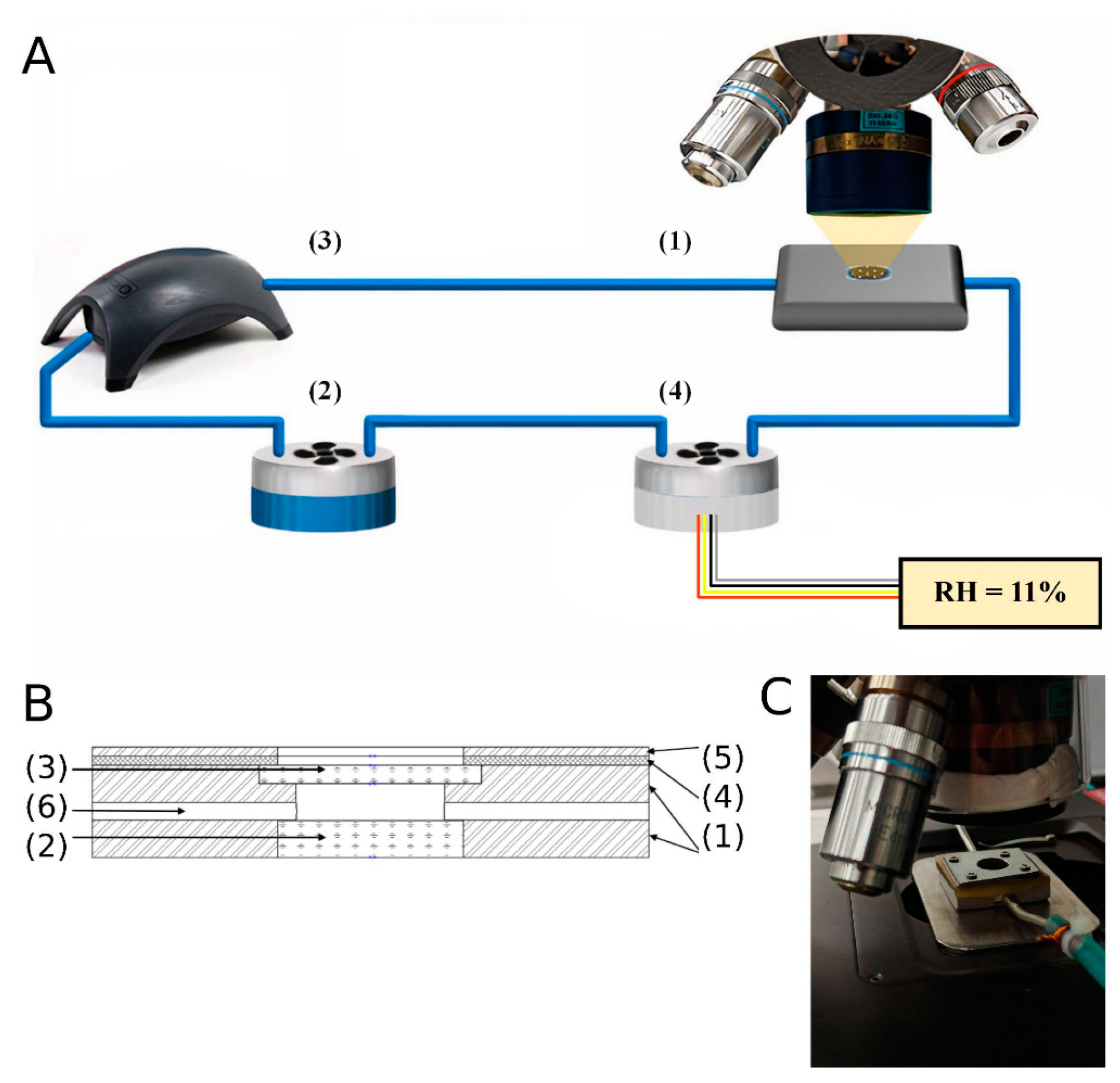
2.2. IR-Measurements
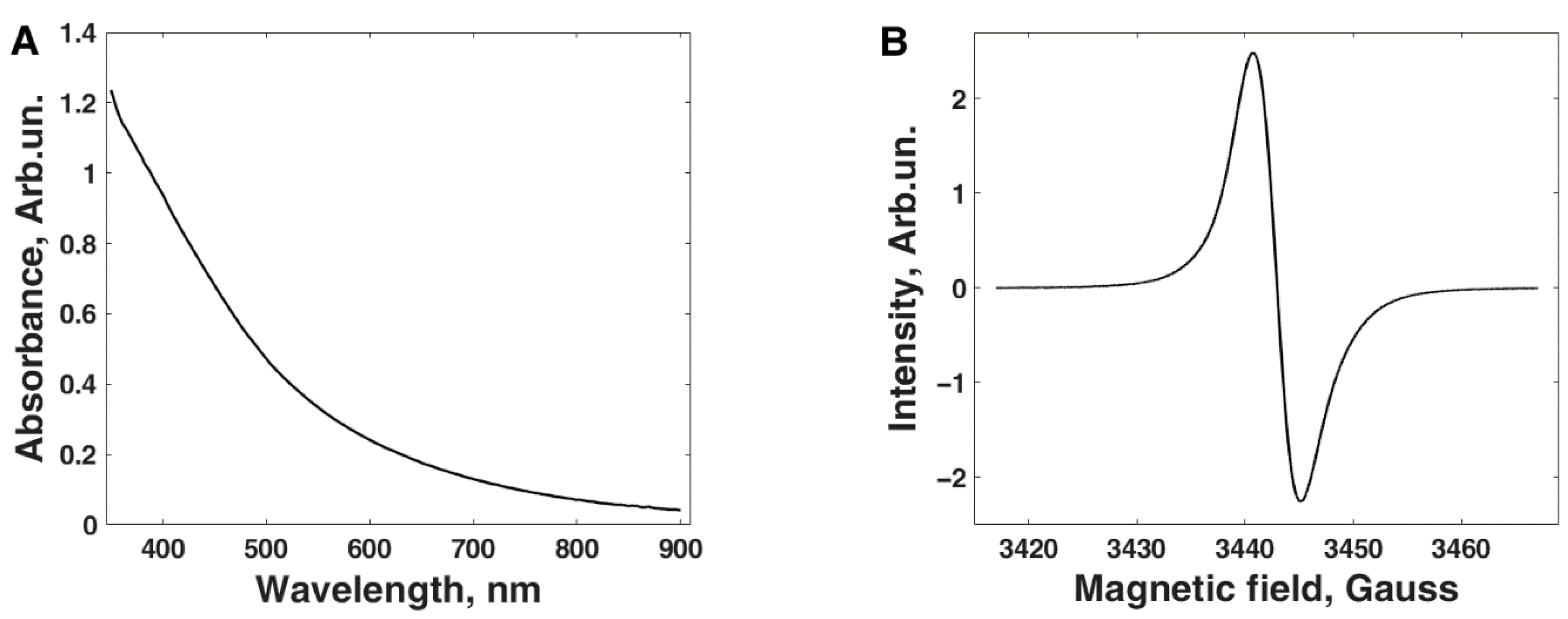
2.3. Melanin Characterization
2.4. Data Processing
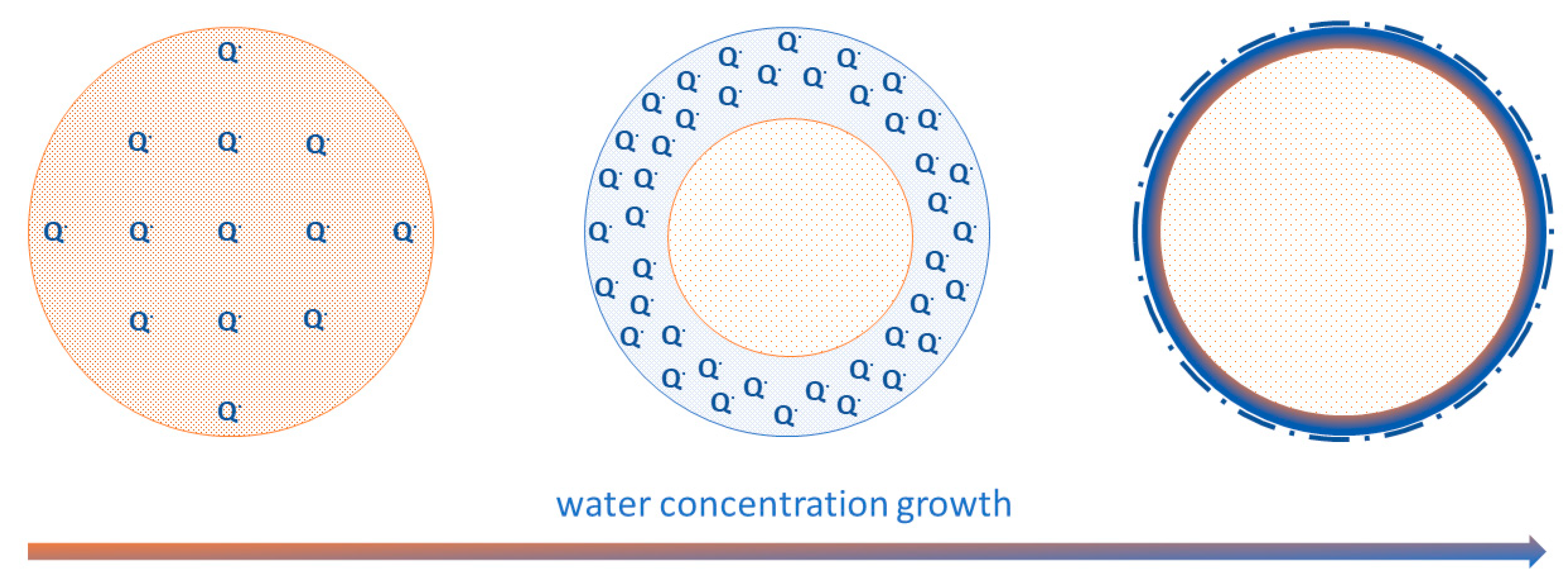
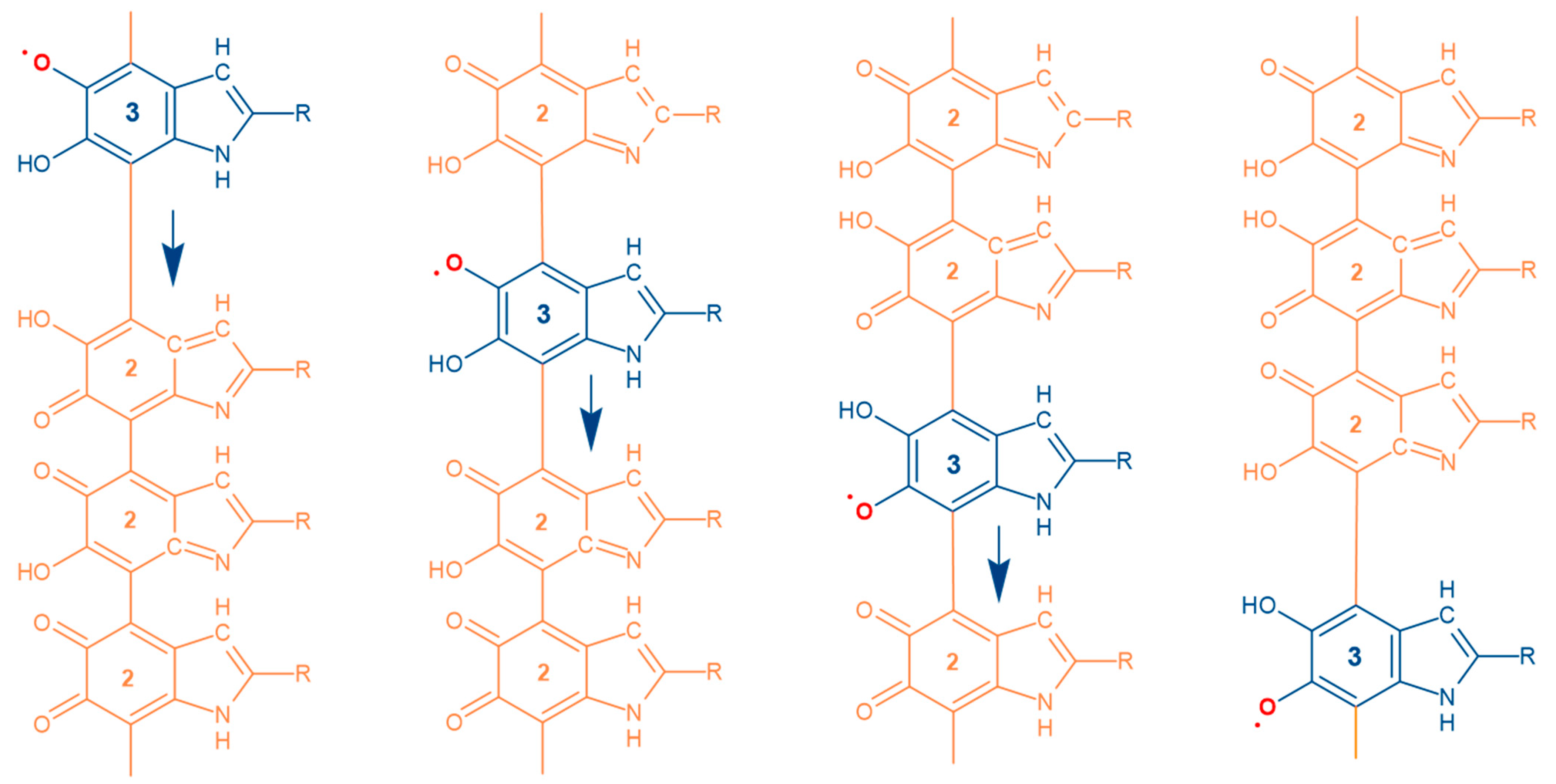
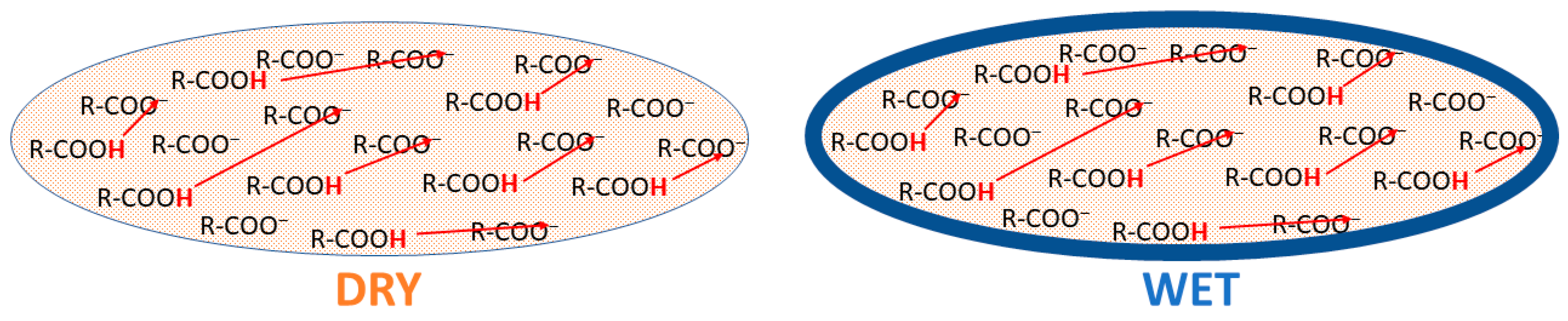
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- D’Alba, L.; Shawkey, M.D. Melanosomes: Biogenesis, Properties, and Evolution of an Ancient Organelle. Physiol. Rev. 2018, 99, 1–19. [Google Scholar] [CrossRef]
- Borovanský, J. History of Melanosome Research. In Melanins and Melanosomes; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; pp. 1–19. [Google Scholar] [CrossRef]
- Prota, G. Melanins and Melanogenesis; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Capozzi, V.; Perna, G.; Gallone, A.; Biagi, P.; Carmone, P.; Fratello, A.; Guida, G.; Zanna, P.; Cicero, R. Raman and optical spectroscopy of eumelanin films. J. Mol. Struct. 2005, 744–747, 717–721. [Google Scholar] [CrossRef]
- Geremia, E.; Corsaro, C.; Bonomo, R.; Giardinelli, R.; Pappalardo, P.; Vanella, A.; Sichel, G. Eumelanins as free radicals trap and superoxide dismutase activities in Amphibia. Comp. Biochem. Physiol. Part B Comp. Biochem. 1984, 79, 67–69. [Google Scholar] [CrossRef]
- Sarna, T.; Pilas, B.; Land, E.J.; Truscott, T.G. Interaction of radicals from water radiolysis with melanin. Biochim. Biophys. Acta BBA—Gen. Subj. 1986, 883, 62–167. [Google Scholar] [CrossRef]
- Wielgus, A.R.; Sarna, T. Melanin in human irides of different color and age of donors. Pigment Cell Res. 2005, 18, 454–464. [Google Scholar] [CrossRef] [PubMed]
- Wolff, D. Melanin in the Inner Ear. Arch. Otolaryngol. 1931, 14, 195–211. [Google Scholar] [CrossRef]
- Pan, T.; Li, X.; Jankovic, J. The association between Parkinson’s disease and melanoma. Int. J. Cancer 2011, 128, 2251–2260. [Google Scholar] [CrossRef]
- Lin, J.Y.; Fisher, D.E. Melanocyte biology and skin pigmentation. Nature 2007, 445, 7130. [Google Scholar] [CrossRef]
- Meredith, P.; Sarna, T. The physical and chemical properties of eumelanin. Pigment Cell Res. 2006, 19, 572–594. [Google Scholar] [CrossRef]
- Bush, W.D.; Garguilo, J.; Zucca, F.A.; Albertini, A.; Zecca, L.; Edwards, G.S.; Nemanich, R.J.; Simon, J.D. The surface oxidation potential of human neuromelanin reveals a spherical architecture with a pheomelanin core and a eumelanin surface. Proc. Natl. Acad. Sci. USA 2006, 103, 14785–14789. [Google Scholar] [CrossRef]
- Meredith, P.; Riesz, J. Radiative Relaxation Quantum Yields for Synthetic Eumelanin. Photochem. Photobiol. 2004, 79, 211–216. [Google Scholar] [CrossRef]
- Wolbarsht, M.L.; Walsh, A.W.; George, G. Melanin, a unique biological absorber. Appl. Opt. 1981, 20, 2184–2186. [Google Scholar] [CrossRef]
- Gonçalves, P.J.; Filho, O.B.; Graeff, C.F.O. Effects of hydrogen on the electronic properties of synthetic melanin. J. Appl. Phys. 2006, 99, 104701. [Google Scholar] [CrossRef]
- Chio, S.-S.; Hyde, J.S.; Sealy, R.C. Temperature-dependent paramagnetism in melanin polymers. Arch. Biochem. Biophys. 1980, 199, 133–139. [Google Scholar] [CrossRef]
- Blois, M.; Zahlan, A.; Maling, J. Electron Spin Resonance Studies on Melanin. Biophys. J. 1964, 4, 471–490. [Google Scholar] [CrossRef]
- Dadachova, E.; Bryan, R.A.; Huang, X.; Moadel, T.; Schweitzer, A.; Aisen, P.; Nosanchuk, J.D.; Casadevall, A. Ionizing Radiation Changes the Electronic Properties of Melanin and Enhances the Growth of Melanized Fungi. PLoS ONE 2007, 2, e457. [Google Scholar] [CrossRef] [PubMed]
- Felix, C.C.; Hyde, J.S.; Sarna, T.; Sealy, R.C. Interactions of melanin with metal ions. Electron spin resonance evidence for chelate complexes of metal ions with free radicals. J. Am. Chem. Soc. 1978, 100, 3922–3926. [Google Scholar] [CrossRef]
- Hong, L.; Simon, J.D. Current Understanding of the Binding Sites, Capacity, Affinity, and Biological Significance of Metals in Melanin. J. Phys. Chem. B 2007, 111, 7938–7947. [Google Scholar] [CrossRef]
- Mostert, A.; Powell, B.; Pratt, F.; Hanson, G.R.; Sarna, T.; Gentle, I.; Meredith, P. Role of semiconductivity and ion transport in the electrical conduction of melanin. Proc. Natl. Acad. Sci. USA 2012, 109, 8943–8947. [Google Scholar] [CrossRef]
- Jastrzebska, M.M.; Isotalo, H.; Paloheimo, J.; Stubb, H. Electrical conductivity of synthetic DOPA-melanin polymer for different hydration states and temperatures. J. Biomater. Sci. Polym. Ed. 1996, 7, 577–586. [Google Scholar] [CrossRef]
- Mostert, A.B.; Powell, B.J.; Gentle, I.; Meredith, P. On the origin of electrical conductivity in the bio-electronic material melanin. Appl. Phys. Lett. 2012, 100, 093701. [Google Scholar] [CrossRef]
- Motovilov, K.A.; Grinenko, V.; Savinov, M.; Gagkaeva, Z.V.; Kadyrov, L.S.; Pronin, A.A.; Bedran, Z.V.; Zhukova, E.S.; Mostert, A.B.; Gorshunov, B.P. Redox chemistry in the pigment eumelanin as a function of temperature using broadband dielectric spectroscopy. RSC Adv. 2019, 9, 3857–3867. [Google Scholar] [CrossRef]
- Crippa, P.R.; Cristofoletti, V.; Romeo, N. A band model for melanin deduced from optical absorption and photoconductivity experiments. Biochim. Biophys. Acta BBA—Gen. Subj. 1978, 538, 164–170. [Google Scholar] [CrossRef]
- Jastrzebska, M.; Kocot, A.; Tajber, L. Photoconductivity of synthetic dopa–melanin polymer. J. Photochem. Photobiol. B 2002, 66, 201–206. [Google Scholar] [CrossRef]
- Reali, M.; Gouda, A.; Bellemare, J.; Ménard, D.; Nunzi, J.-M.; Soavi, F.; Santato, C. Electronic Transport in the Biopigment Sepia Melanin. ACS Appl. Bio Mater. 2020, 3, 5244–5252. [Google Scholar] [CrossRef]
- Di Mauro, E.; Carpentier, O.; Sánchez, S.I.Y.; Ignoumba, N.I.; Lalancette-Jean, M.; Lefebvre, J.; Zhang, S.; Graeff, C.F.O.; Cicoira, F.; Santato, C. Resistive switching controlled by the hydration level in thin films of the biopigment eumelanin. J. Mater. Chem. C 2016, 4, 9544–9553. [Google Scholar] [CrossRef]
- McGinness, J.; Corry, P.; Proctor, P. Amorphous Semiconductor Switching in Melanins. Science 1974, 183, 853–855. [Google Scholar] [CrossRef]
- Sheliakina, M.; Mostert, A.B.; Meredith, P. An all-solid-state biocompatible ion-to-electron transducer for bioelectronics. Mater. Horiz. 2018, 5, 256–263. [Google Scholar] [CrossRef]
- Mostert, A.B.; Rienecker, S.B.; Sheliakina, M.; Zierep, P.; Hanson, G.R.; Harmer, J.R.; Schenk, G.; Meredith, P. Engineering proton conductivity in melanin using metal doping. J. Mater. Chem. B 2020, 8, 8050–8060. [Google Scholar] [CrossRef]
- Vahidzadeh, E.; Kalra, A.; Shankar, K. Melanin-based electronics: From proton conductors to photovoltaics and beyond. Biosens. Bioelectron. 2018, 122, 127–139. [Google Scholar] [CrossRef]
- Pezzella, A.; Wünsche, J. Eumelanin: An Old Natural Pigment and a New Material for Organic Electronics—Chemical, Physical, and Structural Properties in Relation to Potential Applications. In Organic Electronics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 113–137. [Google Scholar] [CrossRef]
- Kumar, P.; Di Mauro, E.; Zhang, S.; Pezzella, A.; Soavi, F.; Santato, C.; Cicoira, F. Melanin-based flexible supercapacitors. J. Mater. Chem. C 2016, 4, 9516–9525. [Google Scholar] [CrossRef]
- Bettinger, C.J.; Whitacre, J. Water-Activated, Ingestible Battery. U.S. Patent US9985320B2, 29 May 2018. [Google Scholar]
- Liu, H.; Yang, Y.; Liu, Y.; Pan, J.; Wang, J.; Man, F.; Zhang, W.; Liu, G. Melanin-Like Nanomaterials for Advanced Biomedical Applications: A Versatile Platform with Extraordinary Promise. Adv. Sci. 2020, 7, 1903129. [Google Scholar] [CrossRef] [PubMed]
- Caldas, M.; Santos, A.C.; Veiga, F.; Rebelo, R.; Reis, R.L.; Correlo, V.M. Melanin nanoparticles as a promising tool for biomedical applications—A review. Acta Biomater. 2020, 105, 26–43. [Google Scholar] [CrossRef] [PubMed]
- Xie, W.; Pakdel, E.; Liang, Y.; Kim, Y.J.; Liu, D.; Sun, L.; Wang, X. Natural eumelanin and its derivatives as multifunctional materials for bioinspired applications: A review. Biomacromolecules 2019, 20, 4312–4331. [Google Scholar] [CrossRef]
- Gouda, A.; Bobbara, S.R.; Reali, M.; Santato, C. Light-assisted melanin-based electrochemical energy storage: Physicochemical aspects. J. Phys. Appl. Phys. 2019, 53, 043003. [Google Scholar] [CrossRef]
- Clark, M.B.; Gardella, J.A.; Schultz, T.M.; Patil, D.G.; Salvati, L. Solid-state analysis of eumelanin biopolymers by electron spectroscopy for chemical analysis. Anal. Chem. 1990, 62, 949–956. [Google Scholar] [CrossRef]
- Wünsche, J.; Deng, Y.; Kumar, P.; Di Mauro, E.; Josberger, E.; Sayago, J.; Pezzella, A.; Soavi, F.; Cicoira, F.; Rolandi, M.; et al. Protonic and Electronic Transport in Hydrated Thin Films of the Pigment Eumelanin. Chem. Mater. 2015, 27, 436–442. [Google Scholar] [CrossRef]
- Sheliakina, M.; Mostert, A.B.; Meredith, P. Decoupling Ionic and Electronic Currents in Melanin. Adv. Funct. Mater. 2018, 28, 1805514. [Google Scholar] [CrossRef]
- Paulin, J.V.; Batagin-Neto, A.; Meredith, P.; Graeff, C.F.O.; Mostert, A.B. Shedding Light on the Free Radical Nature of Sulfonated Melanins. J. Phys. Chem. B 2020, 124, 10365–10373. [Google Scholar] [CrossRef] [PubMed]
- Bridelli, M.G.; Crippa, P.R. Optical properties of melanin; a comment. Appl. Opt. 1982, 21, 2669–2670. [Google Scholar] [CrossRef]
- Bilińska, B. Progress of infrared investigations of melanin structures. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1996, 52, 1157–1162. [Google Scholar] [CrossRef]
- Bridelli, M.; Tampellini, D.; Zecca, L. The structure of neuromelanin and its iron binding site studied by infrared spectroscopy. FEBS Lett. 1999, 457, 18–22. [Google Scholar] [CrossRef]
- Huang, Z.; Lui, H.; Chen, X.K.; Alajlan, A.; McLean, D.I.; Zeng, H. Raman spectroscopy of in vivo cutaneous melanin. J. Biomed. Opt. 2004, 9, 1198–1205. [Google Scholar] [CrossRef] [PubMed]
- Centeno, S.A.; Shamir, J. Surface enhanced Raman scattering (SERS) and FTIR characterization of the sepia melanin pigment used in works of art. J. Mol. Struct. 2008, 873, 149–159. [Google Scholar] [CrossRef]
- Sangaletti, L.; Borghetti, P.; Ghosh, P.; Pagliara, S.; Vilmercati, P.; Castellarin-Cudia, C.; Floreano, L.; Cossaro, A.; Verdini, A.; Gebauer, R.; et al. Polymerization effects and localized electronic states in condensed-phase eumelanin. Phys. Rev. B 2009, 80, 174203. [Google Scholar] [CrossRef]
- Bridelli, M.G.; Crippa, P.R. Infrared and Water Sorption Studies of the Hydration Structure and Mechanism in Natural and Synthetic Melanin. J. Phys. Chem. B 2010, 114, 9381–9390. [Google Scholar] [CrossRef]
- Abbas, M.; Ali, M.; Shah, S.K.; D’Amico, F.; Postorino, P.; Mangialardo, S.; Guidi, M.C.; Cricenti, A.; Gunnella, R. Control of Structural, Electronic, and Optical Properties of Eumelanin Films by Electrospray Deposition. J. Phys. Chem. B 2011, 115, 11199–11207. [Google Scholar] [CrossRef]
- Hyogo, R.; Nakamura, A.; Okuda, H.; Wakamatsu, K.; Ito, S.; Sota, T. Mid-infrared vibrational spectroscopic characterization of 5,6-dihydroxyindole and eumelanin derived from it. Chem. Phys. Lett. 2011, 517, 211–216. [Google Scholar] [CrossRef]
- Bronze-Uhle, E.S.; Batagin-Neto, A.; Xavier, P.H.; Fernandes, N.I.; de Azevedo, E.R.; Graeff, C.F. Synthesis and characterization of melanin in DMSO. J. Mol. Struct. 2013, 1047, 102–108. [Google Scholar] [CrossRef]
- Perna, G.; Lasalvia, M.; Gallo, C.; Quartucci, G.; Capozzi, V. Vibrational Characterization of Synthetic Eumelanin by Means of Raman and Surface Enhanced Raman Scattering. Open Surf. Sci. J. 2013, 5, 1–8. Available online: https://benthamopen.com/ABSTRACT/TOSURSJ-5-1 (accessed on 9 February 2021). [CrossRef]
- Zangmeister, R.A.; Morris, T.A.; Tarlov, M.J. Characterization of Polydopamine Thin Films Deposited at Short Times by Autoxidation of Dopamine. Langmuir 2013, 29, 8619–8628. [Google Scholar] [CrossRef]
- Roldán, M.L.; Centeno, S.A.; Rizzo, A. An improved methodology for the characterization and identification of sepia in works of art by normal Raman and SERS, complemented by FTIR, Py-GC/MS, and XRF. J. Raman Spectrosc. 2014, 45, 1160–1171. [Google Scholar] [CrossRef]
- Perna, G.; Lasalvia, M.; Capozzi, V. Vibrational spectroscopy of synthetic and natural eumelanin. Polym. Int. 2016, 65, 1323–1330. [Google Scholar] [CrossRef]
- Kim, Y.J.; Khetan, A.; Wu, W.; Chun, S.-E.; Viswanathan, V.; Whitacre, J.F.; Bettinger, C.J. Evidence of Porphyrin-Like Structures in Natural Melanin Pigments Using Electrochemical Fingerprinting. Adv. Mater. 2016, 28, 3173–3180. [Google Scholar] [CrossRef] [PubMed]
- Okuda, H.; Nakamura, A.; Wakamatsu, K.; Ito, S.; Sota, T. Mid-infrared absorption spectrum of 5,6-dihydroxyindole-2-carboxylic acid. Chem. Phys. Lett. 2007, 433, 355–359. [Google Scholar] [CrossRef]
- Nighswander-Rempel, S.P.; Olsen, S.; Mahadevan, I.B.; Netchev, G.; Wilson, B.C.; Smith, S.C.; Rubinsztein-Dunlop, H.; Meredith, P. Effect of Dimerization on Vibrational Spectra of Eumelanin Precursors. Photochem. Photobiol. 2008, 84, 613–619. [Google Scholar] [CrossRef] [PubMed]
- Bridelli, M.; Capelletti, R.; Crippa, P. Infrared-Spectroscopy of Eye and Synthetic Melanins at Various Values of pH and Hydration. Physiol. Chem. Phys. 1980, 12, 233–240. [Google Scholar]
- Martinez-Gonzalez, J.A.; Cavaye, H.; McGettrick, J.D.; Meredith, P.; Motovilov, K.A.; Mostert, A.B. Interfacial water morphology in hydrated melanin. Soft Matter 2021, 17, 7940–7952. [Google Scholar] [CrossRef]
- Rienecker, S.B.; Mostert, A.B.; Schenk, G.; Hanson, G.R.; Meredith, P. Heavy Water as a Probe of the Free Radical Nature and Electrical Conductivity of Melanin. J. Phys. Chem. B 2015, 119, 14994–15000. [Google Scholar] [CrossRef]
- Mostert, A.; Hanson, G.R.; Sarna, T.; Gentle, I.; Powell, B.; Meredith, P. Hydration-Controlled X-Band EPR Spectroscopy: A Tool for Unravelling the Complexities of the Solid-State Free Radical in Eumelanin. J. Phys. Chem. B 2013, 117, 4965–4972. [Google Scholar] [CrossRef]
- Mostert, A.B.; Rienecker, S.B.; Noble, C.; Hanson, G.R.; Meredith, P. The photoreactive free radical in eumelanin. Sci. Adv. 2018, 4, eaaq1293. [Google Scholar] [CrossRef] [PubMed]
- D’Ischia, M.; Wakamatsu, K.; Napolitano, A.; Briganti, S.; Garcia-Borron, J.C.; Kovacs, D.; Meredith, P.; Pezzella, A.; Picardo, M.; Sarna, T.; et al. Melanins and melanogenesis: Methods, standards, protocols. Pigment. Cell Melanoma Res. 2013, 26, 616–633. [Google Scholar] [CrossRef] [PubMed]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Load HITRAN 2004+ Data. Available online: https://www.mathworks.com/matlabcentral/fileexchange/45819-load-hitran-2004-data (accessed on 24 March 2021).
- Meredith, P.; Powell, B.J.; Riesz, J.; Nighswander-Rempel, S.P.; Pederson, M.R.; Moore, E.G. Towards structure–property–function relationships for eumelanin. Soft Matter 2005, 2, 37–44. [Google Scholar] [CrossRef]
- Baer, D.R.; Artyushkova, K.; Cohen, H.; Easton, C.D.; Engelhard, M.; Gengenbach, T.R.; Greczynski, G.; Mack, P.; Morgan, D.J.; Roberts, A. XPS guide: Charge neutralization and binding energy referencing for insulating samples. J. Vac. Sci. Technol. A 2020, 38, 031204. [Google Scholar] [CrossRef]
- Chartrand, R. Numerical Differentiation of Noisy, Nonsmooth Data. ISRN Appl. Math. 2011, 2011, e164564. [Google Scholar] [CrossRef]
- D’Ischia, M.; Wakamatsu, K.; Cicoira, F.; Di Mauro, E.; Garcia-Borron, J.C.; Commo, S.; Galván, I.; Ghanem, G.; Kenzo, K.; Meredith, P.; et al. Melanins and melanogenesis: From pigment cells to human health and technological applications. Pigment. Cell Melanoma Res. 2015, 28, 520–544. [Google Scholar] [CrossRef]
- Mostert, A.B. Melanin, the What, the Why and the How: An Introductory Review for Materials Scientists Interested in Flexible and Versatile Polymers. Polymers 2021, 13, 1670. [Google Scholar] [CrossRef]
- Napolitano, A.; Pezzella, A.; Vincensi, M.R.; Prota, G. Oxidative degradation of melanins to pyrrole acids: A model study. Tetrahedron 1995, 51, 5913–5920. [Google Scholar] [CrossRef]
- Paulin, J.; McGettrick, J.; Graeff, C.; Mostert, A. Melanin system composition analyzed by XPS depth profiling. Surfaces Interfaces 2021, 24, 101053. [Google Scholar] [CrossRef]
- Costa, T.G.; Szpoganicz, B.; Caramori, G.; De Almeida, V.R.; Mangrich, A.S.; Mangoni, A.P. Spectroscopy and theoretical studies of natural melanin (eumelanin) and its complexation by iron(III). J. Co-Ord. Chem. 2014, 67, 986–1001. [Google Scholar] [CrossRef]
- Müller, M.; Keßler, B. Deposition from Dopamine Solutions at Ge Substrates: An in Situ ATR-FTIR Study. Langmuir 2011, 27, 12499–12505. [Google Scholar] [CrossRef] [PubMed]
- Pretsch, E.; Bühlmann, P.; Affolter, C. Structure Determination of Organic Compounds: Tables of Spectral Data, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Brown, D.G.; Johnson, W.L. Preparation and Properties of Two Tris o-Semiquinone Complexes. Z. Für Nat. B 1979, 34, 712–715. [Google Scholar] [CrossRef][Green Version]
- Lynch, M.W.; Valentine, M.; Hendrickson, D.N. Mixed-valence semiquinone-catecholate-iron complexes. J. Am. Chem. Soc. 1982, 104, 6982–6989. [Google Scholar] [CrossRef]
- Shaikh, N.; Goswami, S.; Panja, A.; Sun, H.-L.; Pan, F.; Gao, S.; Banerjee, P. Syntheses, Crystal Structures, and Spectroscopic and Magnetic Properties of [Mn2III(H2L1)(Cl4Cat)4·2H2O]∞ and [Mn2III(H2L2)(Cl4Cat)4·2CH3CN·2H2O]∞: Temperature-Dependent Valence Tautomerism in Solution. Inorg. Chem. 2005, 44, 9714–9722. [Google Scholar] [CrossRef] [PubMed]
- Grieco, C.; Hanes, A.T.; Blancafort, L.; Kohler, B. Effects of Intra- and Intermolecular Hydrogen Bonding on O–H Bond Photodissociation Pathways of a Catechol Derivative. J. Phys. Chem. A 2019, 123, 5356–5366. [Google Scholar] [CrossRef]
- Wright, J.S.; Johnson, E.R.; DiLabio, G.A. Predicting the Activity of Phenolic Antioxidants: Theoretical Method, Analysis of Substituent Effects, and Application to Major Families of Antioxidants. J. Am. Chem. Soc. 2001, 123, 1173–1183. [Google Scholar] [CrossRef] [PubMed]
- Paulin, J.V.; Batagin-Neto, A.; Naydenov, B.; Lips, K.; Graeff, C.F.O. High-field/high-frequency EPR spectroscopy on synthetic melanin: On the origin of carbon-centered radicals. Mater. Adv. 2021, 2, 6297–6305. [Google Scholar] [CrossRef]
- Paulin, J.V.; Coleone, A.P.; Batagin-Neto, A.; Burwell, G.; Meredith, P.; Graeff, C.F.O.; Mostert, A.B. Melanin thin-films: A perspective on optical and electrical properties. J. Mater. Chem. C 2021, 9, 8345–8358. [Google Scholar] [CrossRef]
- Mostert, A.B. On the free radical redox chemistry of 5,6-dihydroxyindole. Chem. Phys. 2021, 546, 111158. [Google Scholar] [CrossRef]
- Savéant, J.-M. Concerted Proton-Electron Transfers: Fundamentals and Recent Developments. Annu. Rev. Anal. Chem. 2014, 7, 537–560. [Google Scholar] [CrossRef] [PubMed]
- Kolokolov, D.I.; Kazantsev, M.S.; Luzgin, M.V.; Jobic, H.; Stepanov, A.G. Characterization and Dynamics of the Different Protonic Species in Hydrated 12-Tungstophosphoric Acid Studied by 2H NMR. J. Phys. Chem. C 2014, 118, 30023–30033. [Google Scholar] [CrossRef]
- Uchida, S.; Inumaru, A.K.; Misono, M. States and Dynamic Behavior of Protons and Water Molecules in H3PW12O40 Pseudoliquid Phase Analyzed by Solid-State MAS NMR. J. Phys. Chem. B 2000, 104, 8108–8115. [Google Scholar] [CrossRef]
- Uchida, S.; Inumaru, K.; Dereppe, J.M.; Misono, M. The First Direct Detection of Rapid Migration of Acidic Protons between Heteropolyanions in H3PW12O40·nH2O (n < 6) by31P NMR. Chem. Lett. 1998, 27, 643–644. [Google Scholar] [CrossRef]
- Yukhnevich, G.V.; Tarakanova, E.G.; Maiorov, V.D.; Librovich, N.B. The structure and vibrational spectra of proton solvates in solution. Russ. Chem. Rev. 1995, 64, 901–911. [Google Scholar] [CrossRef]
- Alves, G.G.; Lavarda, F.C.; Graeff, C.F.; Batagin-Neto, A. Reactivity of eumelanin building blocks: A DFT study of monomers and dimers. J. Mol. Graph. Model. 2020, 98, 107609. [Google Scholar] [CrossRef]
- Sapunkov, O.; Khetan, A.; Pande, V.; Viswanathan, V. Theoretical characterization of structural disorder in the tetramer model structure of eumelanin. Phys. Rev. Mater. 2019, 3, 105403. [Google Scholar] [CrossRef]
- Chen, C.-T.; Martin-Martinez, F.J.; Jung, G.S.; Buehler, M.J. Polydopamine and eumelanin molecular structures investigated with ab initio calculations. Chem. Sci. 2017, 8, 1631–1641. [Google Scholar] [CrossRef]
- Powell, B.J.; Baruah, T.; Bernstein, N.; Brake, K.; McKenzie, R.; Meredith, P.; Pederson, M.R. A first-principles density-functional calculation of the electronic and vibrational structure of the key melanin monomers. J. Chem. Phys. 2004, 120, 8608–8615. [Google Scholar] [CrossRef]
- Koch, W.; Holthausen, M.C. Molecular Structures and Vibrational Frequencies. In A Chemist’s Guide to Density Functional Theory; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001; pp. 119–136. [Google Scholar] [CrossRef]

| Salt | LiCl | MgCl2 | K2CO3 | Na2Cr2O7 | NaCl | KCl |
|---|---|---|---|---|---|---|
| RH at 25 °C, % | 11 | 33 | 43 | 54 | 75 | 84 |
| Sample | C (at%) | O (at%) | N (at%) | C/N | O/N | C/O |
|---|---|---|---|---|---|---|
| DHI—Expected | 72.7 | 18.2 | 9.1 | 8 | 2 | 4 |
| DHICA—Expected | 64.3 | 29.6 | 7.1 | 9 | 4 | 2.2 |
| Sample | 69.5 ± 0.3 | 21.2 ± 0.4 | 9.2 ± 0.2 | 7.6 | 2.3 | 3.3 |
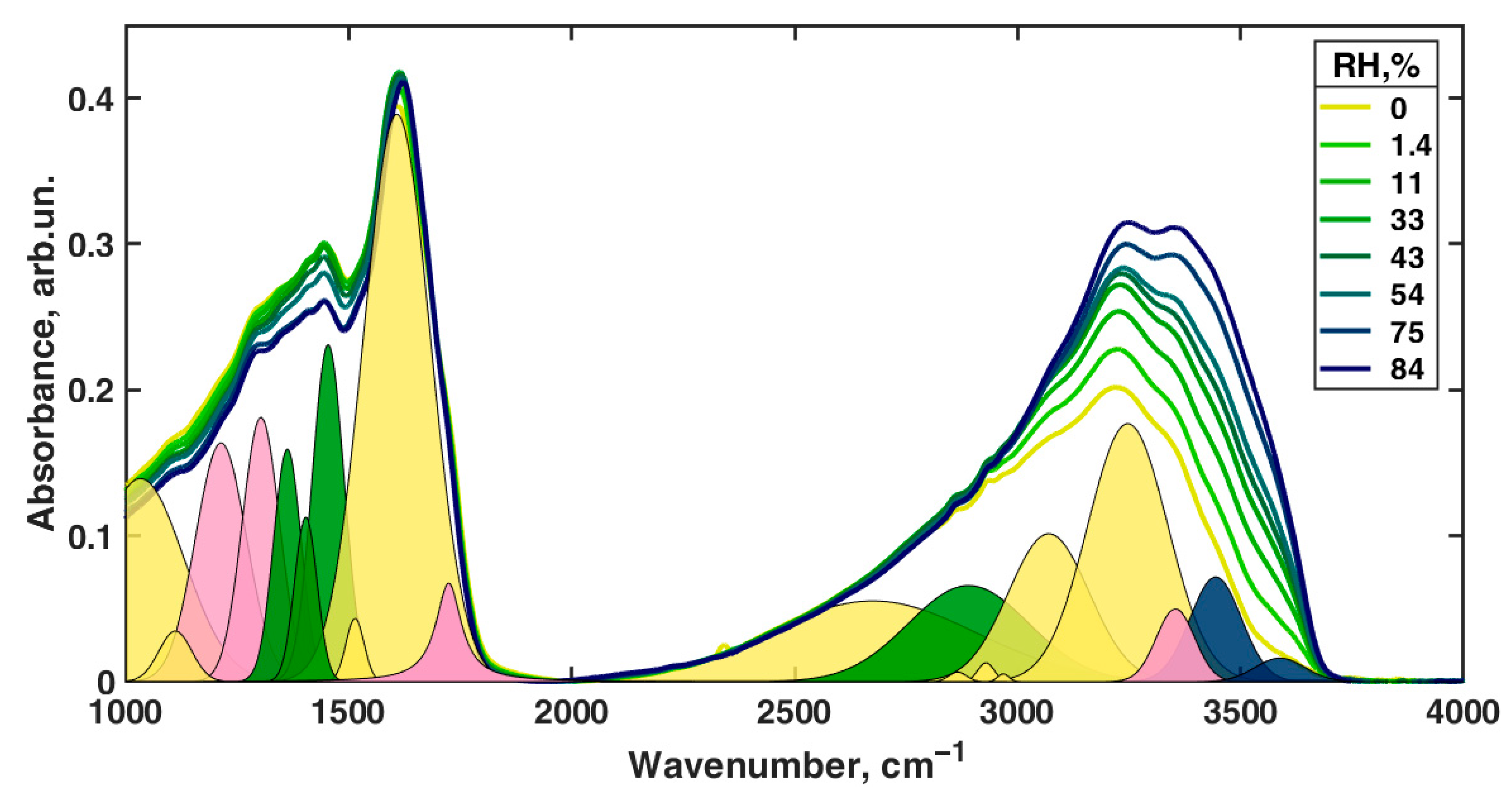
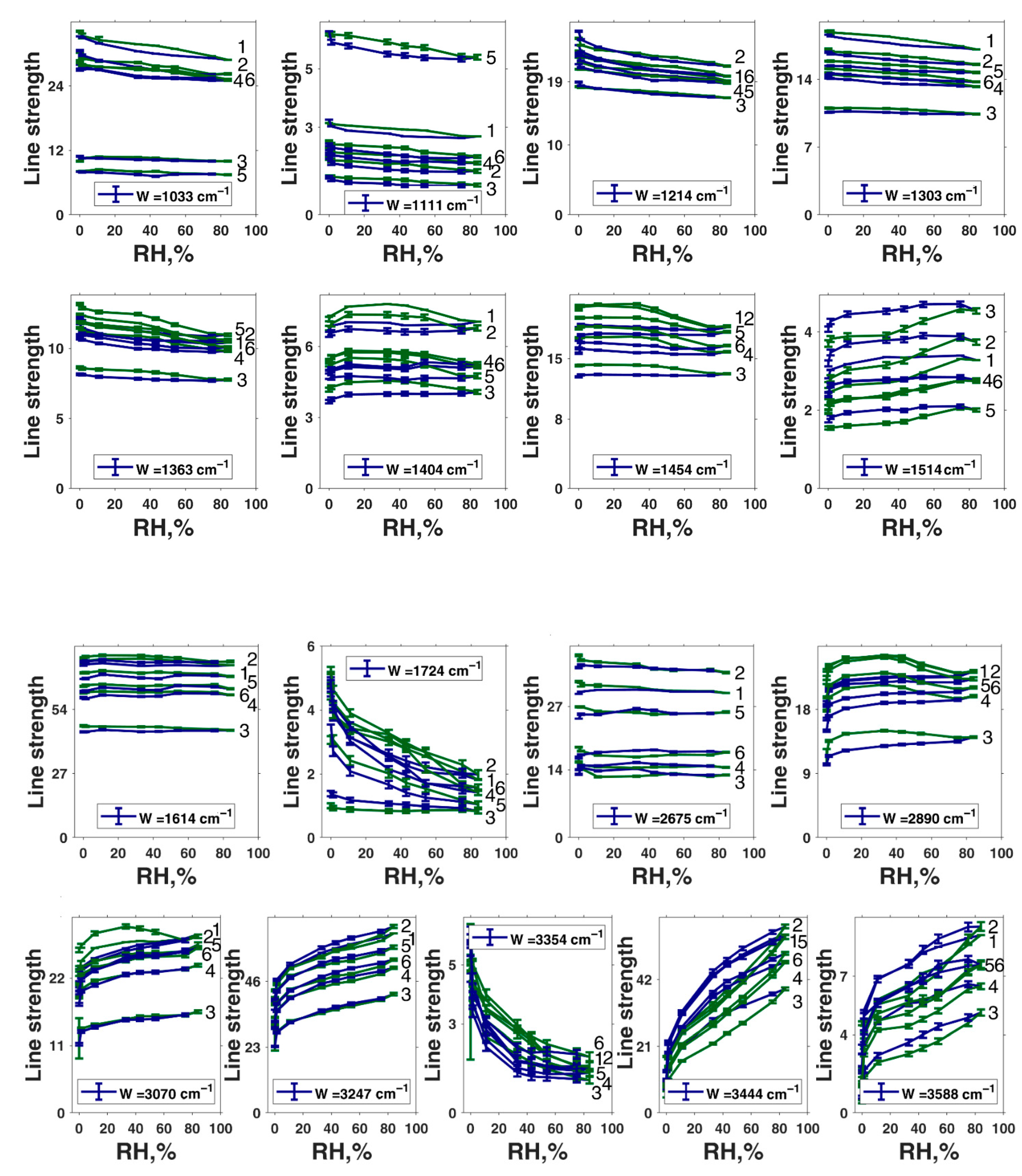
| Peak Position in Fit, cm−1 | Second-Derivative Peak Position, cm−1 | αmax | αmin | Assignment of Roldán et al. [56] | Assignment of Centeno and Shamir [48] | Assignment of Bridelli et al. [61] | Assignment of Perna et al. [57] | Other Assignments | Assignment in the Current Work |
|---|---|---|---|---|---|---|---|---|---|
| 1033 | 1031 | 151.6 | 2.7 | δ(CH) + δ(NH) + ν(CO) | CH in-plane/CH out-of-plane deformation | Aromatic C–H bending | CH in-plane deformation | C–O in catechol, quinone-imine, and carboxylate [76] | δ(CH) + δ(NH) + ν(C–O) |
| 1111 | 1102 | 272.5 | 2 | CH in-plane deformation | Aromatic C–H bending | O–H, C–H, N–H deformation | δ(CH) + δ(NH) + ν(C–O) | ||
| --- | 1165 | 110.8 | 0.2 | δ(OH) + δ(CH) + δ(NH) | Pyrrole NH in-plane deformation/ring breathing | Aromatic C–H bending | C–H in-plane deformation | δ(OH) + δ(CH) + δ(NH) | |
| 1214 | 1215 | 99.1 | 0.1 | δ(OH) + δ(CH) | CO stretching/OH in-plane deformation in COOH | Carboxylic C–O stretching or OH bending | C–H in-plane deformation | C- stretching and C–O–H asymmetrical of COOH [15] | δ(OH) + δ(CH) + ν(C(O)–OH in carboxyls) + ν(C–OH in conjugated cycles) |
| 1303 | 1267 | 0.5 | 0.1 | ν(CO) + δ(CH) + δ(ring) | CH in-plane deformation | Carboxylic C–O stretching or OH bending | C–C and C–N stretching in pyrrole, C–OH stretching in phenolic group, amide III | Phenolic moieties [77] | ν(CO) + δ(CH) + δring |
| 1289 | 400 | 0.1 | ν(CO) + δ(NH) + δ(CH) | Carboxylic C–O stretching or OH bending | Carboxylic C–O stretching or OH bending | ||||
| 1318 | 0.3 | 0.1 | Amide III proteins | Carboxylic C–O stretching or OH bending | 1310–C–OH stretching in COOH, C–N stretching in pyrrole, C–OH stretching, and O–H deformation combination in phenolic groups | Carboxylic C–O stretching or OH bending | |||
| 1363 | 1345 | 10.1 | 0.1 | ν(CN) + δ(OH) + ν(ring) | Indole ring vibration/CN stretching | ν(CN) + δ(OH) + ν(ring) | |||
| 1380 | 16 | 0.1 | δ(CH2), ν(CC) polysaccharides, ν(CO), δ(CH), δ(CN), δ(NH) proteins | Pyrrole ring stretching | C–N stretching, indole ring vibration | Cyclic semiquinone C𝌁O stretching or C–N stretching, indole ring vibration | |||
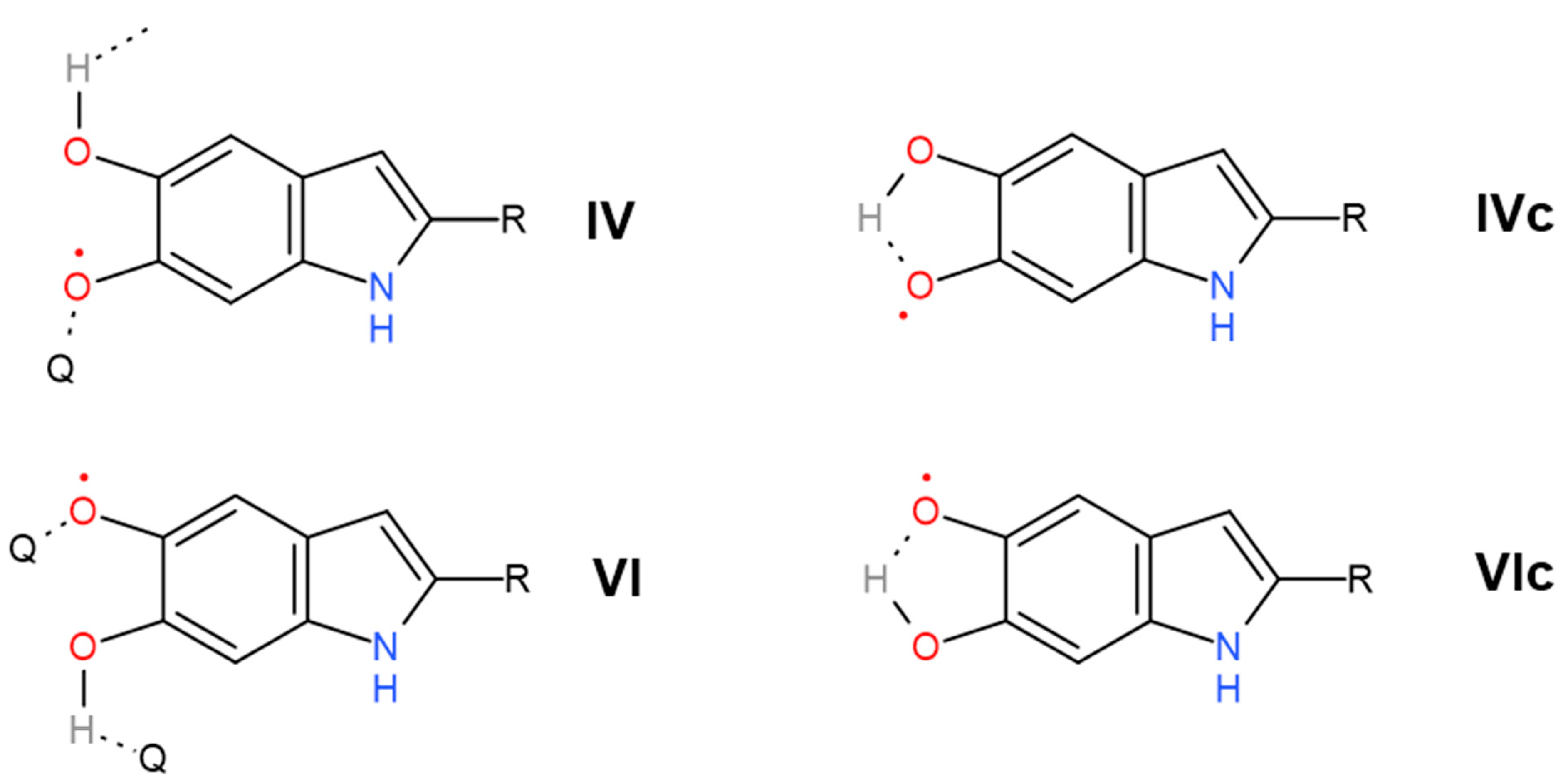
| 1404 | 1406 | 1.5 | 0.1 | δ(OH) + ν(ring) [56] | Pyrrole ring stretching | Carboxylate ion symmetrical stretching | C–O symmetric stretching in COOH | phenolic C–O–H bending [15] | Cyclic semiquinone C𝌁O stretching |
| 1454 | 1443 | 167 | 0.1 | ν(ring) + δ(CN) + δ(OH) | C=C aromatic ring vibration | Semiquinone C𝌁O stretching | |||
| 1468 | 83.7 | 0.1 | ν(ring) + δ(CN) + δ(OH) | Pyrrole ring stretching vibration | Indole ring vibration, C–C in-plane vibration in pyrrole | lower wavenumber C–C of aromatic C–C moieties [77] | Semiquinone C𝌁O stretching | ||
| 1514 | 1518 | 22.5 | 0.2 | ν(ring) + δ(NH) + δ(CH) | C–H deformation mixed modes, amide II | ν(ring) + δ(NH) + δ(CH) OR semiquinone anion C𝌁O stretching | |||
| 1614 | 1592 | 4.3 | 0.1 | ν(ring) + ν(C=O) | C=C aromatic/pyrrole ring stretching | Indole ring vibration | ionized carboxylic acid (COO–) [53]; aromatic C=C stretching and COO– asymmetrical stretching [15] | ν(ring) + ν(C=O); | |
| 1629 | 400 | 0 | ν(ring) + δ(CH) | OH bending (H2O) | Indole ring vibration | C=C and C=N bending modes and C=O stretching mode from noncarboxylic acid moieties [53]; C=O in catechol, quinone-imine, and carboxylate [76] | ν(ring) + ν(C=O) + OH bending (H2O) | ||
| 1653 | 0.3 | 0.1 | ν(C=O) | C=O stretching in quinone | ν(C=C) + ν(C=O) | ||||
| 1671 | 1.6 | 0.1 | C=O stretching in quinone | ν(C=C) + ν(C=O) | |||||
| 1684 | 0.1 | 0.1 | C=O COOH stretching | C=O stretching mode in –COOH [53] | ν(C=C) + ν(C=O) | ||||
| 1700 | 0.1 | 0.1 | C=O COOH stretching | C=O of COOH stretching [15] | ν(C=O) | ||||
| 1724 | 1717 | 16.9 | 0.1 | C–O asymmetric stretching in COOH | C=O COOH stretching | ||||
| 1730 | 87.5 | 0.1 | ν(C=O) lipids, polysaccharides | C=O COOH stretching | C=O COOH stretching | C=O COOH stretching | |||
| 1745 | 0.1 | 0.1 | C=O COOH stretching | C=O COOH stretching | |||||
| 1771 | 0.4 | 0.1 | C=O COOH stretching | C=O COOH stretching | |||||
| 1882 | 400 | 25 | sample preparation residuals | ||||||
| --- | 2092 | 333.3 | 12.6 | sample preparation residuals | |||||
| --- | 2224 | 233.3 | 0.6 | sample preparation residuals | |||||
| --- | 2474 | 275 | 38.7 | –OH and –NH stretching modes of the carboxylic acid (C–O and –COOH); phenolic (C–O/carboxyl OH) and aromatic amino functions in the indolic and pyrrolic systems present in DHI and DHICA- derivatives [53] | |||||
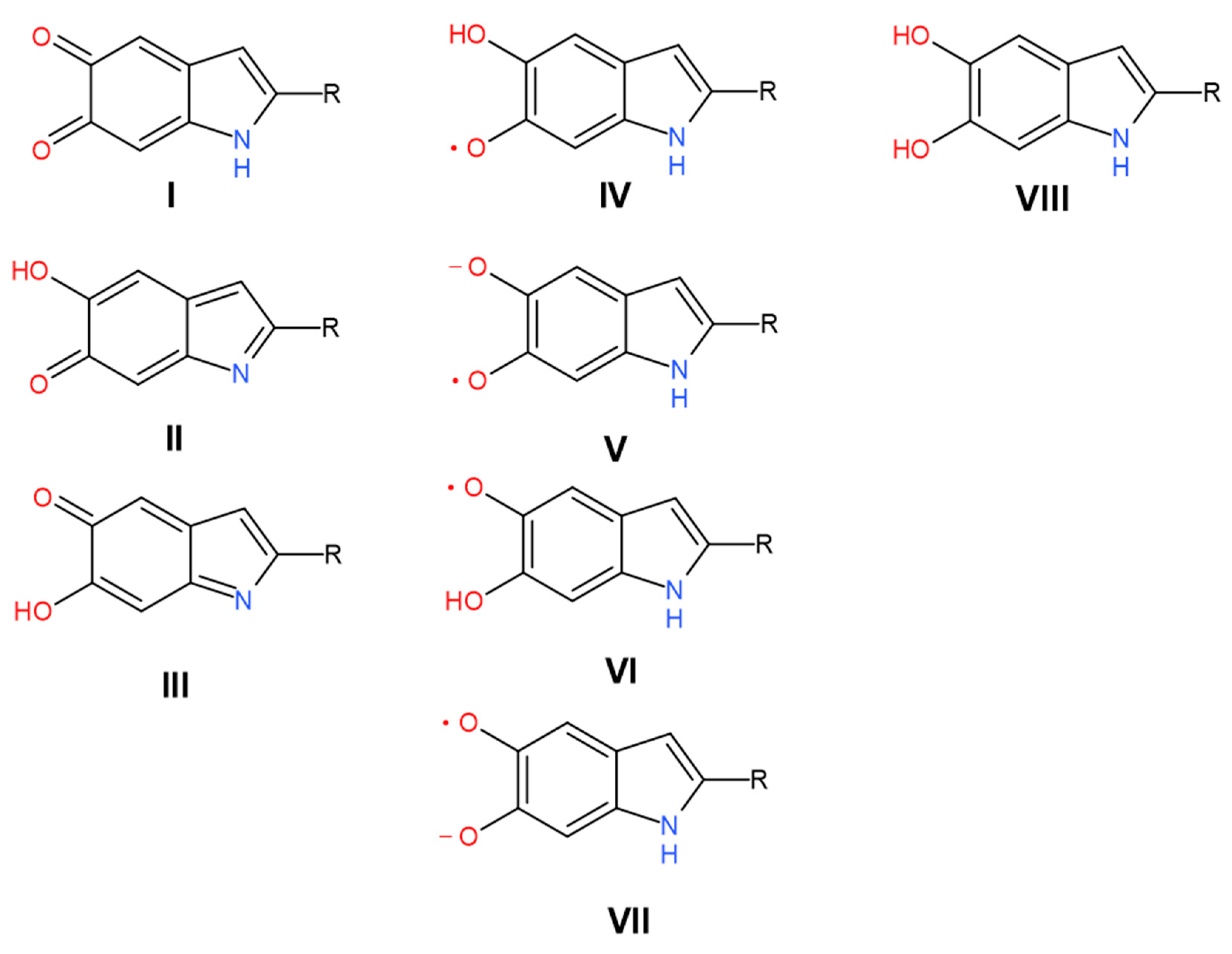
| 2675 | 2598 | 266.6 | 11 | Carboxylic H-bonded OH stretching | Carboxylic H-bonded OH stretching [15] | Enol H-bonded OH stretching (oxidized monomers II, III on Figure 1) | |||
| --- | 2756 | 366.6 | 8.3 | Carboxylic H-bonded OH stretching | Carboxylic H-bonded OH stretching | ||||
| 2866 | 2858 | 116.6 | 0.1 | Aliphatic C–H stretching | Aliphatic C–H stretching | ||||
| 2890 | 2878 | 0.1 | 0.1 | νsym(CH3) lipids | ν(CH) | Cyclic semiquinone O–H stretching (intramolecular H-bond) | |||
| 2902 | 0.9 | 0.1 | ν(CH) | ν(CH) | |||||
| 2929 | 2930 | 400 | 0.1 | νassym(CH2) lipids | ν(CH) | Aliphatic C–H stretching | Aliphatic C–H stretching | ||
| 2968 | 2965 | 4.3 | 0.1 | νassym(CH3) lipids, cholesterol, proteins | Aliphatic C–H stretching | ||||
| 3018 | 1 | 0.3 | Aliphatic C–H stretching | ||||||
| 3070 | 3069 | 400 | 0.1 | ν(=CH) | ν(CH) | Aromatic C–H stretching | |||
| 3247 | 3214 | 400 | 0.1 | N–H–NH3+ stretching | Water-connected ν(OH) [50] | ν(NH) in aromatic system | |||
| 3354 | 3361 | 400 | 0.1 | ν(NH) | ν(NH) | N–H stretching and OH–H-bonded stretching [15] | ν(C(O)O–H) hydrogen bonded | ||
| 3444 | 3462 | 400 | 0.1 | N–H–NH2 symmetrical and asymmetrical stretching OR OH–H-bonded stretching | Water-connected ν(OH) [50] | OH H-bonded stretching in water | |||
| 3588 | 3610 | 400 | 0.1 | –OH and –NH stretching modes of the carboxylic acid (C–O and –COOH); phenolic (C–O/carboxyl OH) and aromatic amino functions in the indolic and pyrrolic systems present in DHI and DHIC derivatives [53]; water-connected ν(OH) [50] | OH stretching in water |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedran, Z.V.; Zhukov, S.S.; Abramov, P.A.; Tyurenkov, I.O.; Gorshunov, B.P.; Mostert, A.B.; Motovilov, K.A. Water-Activated Semiquinone Formation and Carboxylic Acid Dissociation in Melanin Revealed by Infrared Spectroscopy. Polymers 2021, 13, 4403. https://doi.org/10.3390/polym13244403
Bedran ZV, Zhukov SS, Abramov PA, Tyurenkov IO, Gorshunov BP, Mostert AB, Motovilov KA. Water-Activated Semiquinone Formation and Carboxylic Acid Dissociation in Melanin Revealed by Infrared Spectroscopy. Polymers. 2021; 13(24):4403. https://doi.org/10.3390/polym13244403
Chicago/Turabian StyleBedran, Zakhar V., Sergey S. Zhukov, Pavel A. Abramov, Ilya O. Tyurenkov, Boris P. Gorshunov, A. Bernardus Mostert, and Konstantin A. Motovilov. 2021. "Water-Activated Semiquinone Formation and Carboxylic Acid Dissociation in Melanin Revealed by Infrared Spectroscopy" Polymers 13, no. 24: 4403. https://doi.org/10.3390/polym13244403
APA StyleBedran, Z. V., Zhukov, S. S., Abramov, P. A., Tyurenkov, I. O., Gorshunov, B. P., Mostert, A. B., & Motovilov, K. A. (2021). Water-Activated Semiquinone Formation and Carboxylic Acid Dissociation in Melanin Revealed by Infrared Spectroscopy. Polymers, 13(24), 4403. https://doi.org/10.3390/polym13244403







