Reinforcement Mechanism of Carbon Black-Filled Rubber Nanocomposite as Revealed by Atomic Force Microscopy Nanomechanics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Sample Preparation
2.2. AFM Measurements
2.3. Macroscopic Tensile Measurements
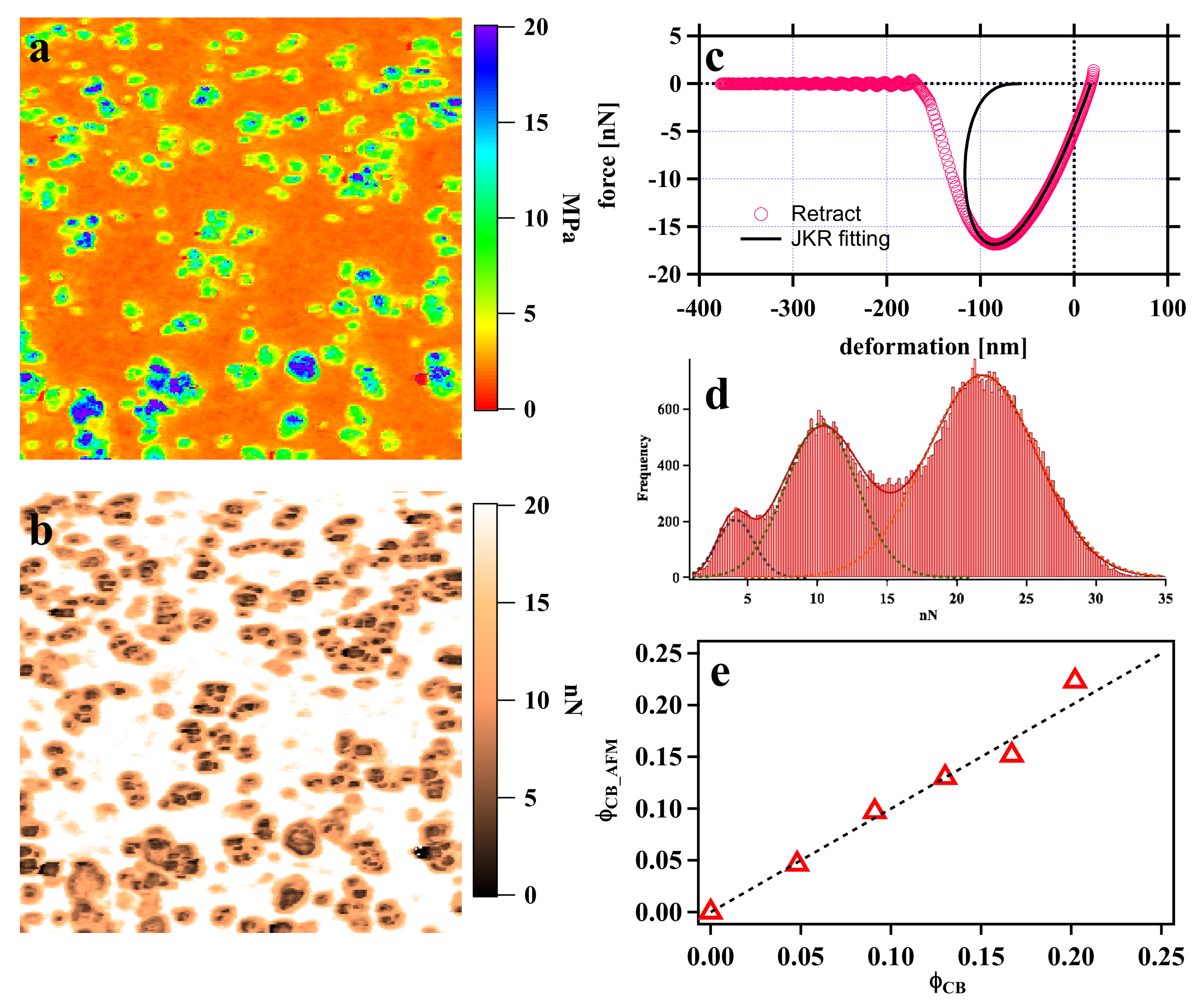
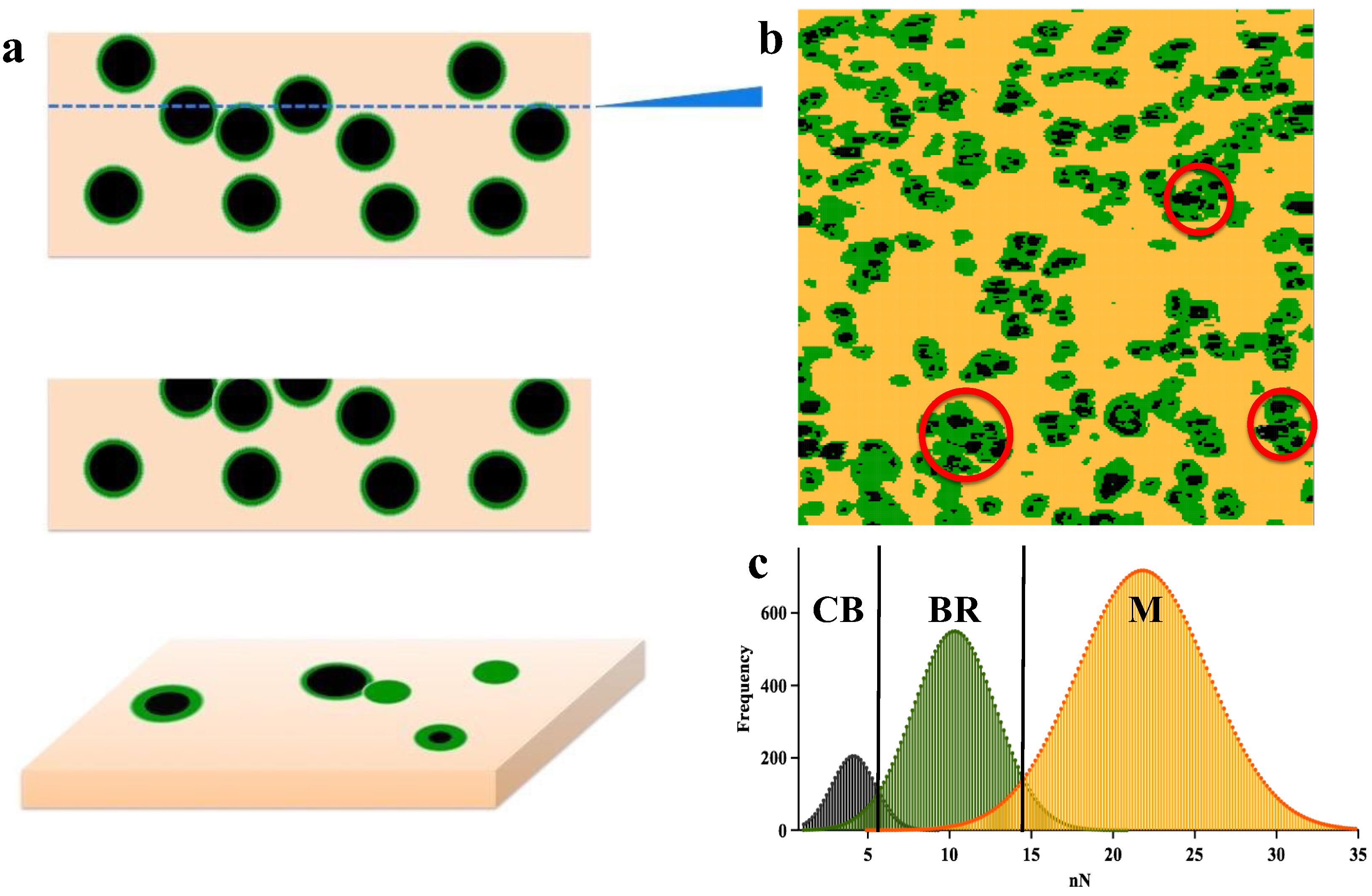
2.4. Analysis of Nanoscale Stress Distribution
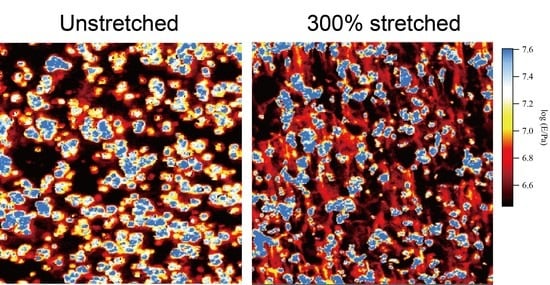
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Oommen, Z.; Nair, M.R.G.; Thomas, S. Compatibilizing effect of natural rubber-g-poly (methyl methacrylate) in heterogeneous natural rubber/poly (methyl methacrylate) blends. Polym. Eng. Sci. 1996, 36, 151–160. [Google Scholar] [CrossRef]
- Perrin-Sarazin, F.; Ton-That, M.T.; Bureau, M.N.; Denault, J. Micro-and nano-structure in polypropylene/clay nanocomposites. Polymer 2005, 46, 11624–11634. [Google Scholar] [CrossRef] [Green Version]
- Sternstein, S.S.; Zhu, A.J. Reinforcement mechanism of nanofilled polymer melts as elucidated by nonlinear viscoelastic behavior. Macromolecules 2002, 35, 7262–7273. [Google Scholar] [CrossRef]
- Fong, H.; Liu, W.; Wang, C.S.; Vaia, R.A. Generation of electrospun fibers of nylon 6 and nylon 6-montmorillonite nanocomposite. Polymer 2002, 43, 775–780. [Google Scholar] [CrossRef]
- Paul, D.R.; Robeson, L.M. Polymer nanotechnology: Nanocomposites. Polymer 2008, 49, 3187–3204. [Google Scholar] [CrossRef] [Green Version]
- Zhang, A.; Wang, L.; Lin, Y.; Mi, X. Carbon black filled powdered natural rubber: Preparation, particle size distribution, mechanical properties, and structures. J. Appl. Polym. Sci. 2006, 101, 1763–1774. [Google Scholar] [CrossRef]
- Bokobza, L.; Rahmani, M.; Belin, C.; Bruneel, J.L.; El Bounia, N.E. Blends of carbon blacks and multiwall carbon nanotubes as reinforcing fillers for hydrocarbon rubbers. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 1939–1951. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Ikeda, Y.; Kohjiya, S. In situ formed silica particles in rubber vulcanizate by the sol-gel method. Polymer 1997, 38, 4417–4423. [Google Scholar] [CrossRef]
- Varghese, S.; Kocsis, J.K. Natural rubber-based nanocomposites by latex compounding with layered silicates. Polymer 2003, 44, 4921–4927. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Y.; Mao, K.; Xue, G.; Chen, T.; Zhu, J.; Li, B.; Sun, P.; Jin, Q.; Ding, D. Unusual Rheological Behavior of Liquid Polybutadiene Rubber/Clay Nanocomposite Gels: The Role of Polymer–Clay Interaction, Clay Exfoliation, and Clay Orientation and Disorientation. Macromolecules 2006, 39, 6653–6660. [Google Scholar] [CrossRef]
- Stickney, P.B.; Falb, R.D. Carbon black-rubber interactions and bound rubbera. Rubber Chem. Technol. 1964, 37, 1299–1340. [Google Scholar] [CrossRef]
- Donnet, J.B.; Voet, A. Carbon Black Physics, Chemistry and Elastomer Reinforcement; Marcel Dekker: New York, NY, USA, 1976. [Google Scholar]
- Nishi, T. Effect of solvent and carbon black species on the rubber–carbon black interactions studied by pulsed NMR. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 685–693. [Google Scholar] [CrossRef]
- Litvinov, V.M.; Steeman, P.A. EPDM–Carbon Black Interactions and the Reinforcement Mechanisms, As Studied by Low-Resolution 1H NMR. Macromolecules 1999, 32, 8476–8490. [Google Scholar] [CrossRef]
- Barrantes, I.M.; Ibarra, L.; Rodriguez, A.; Gonzalez, L.; Valentin, J.L. Elastomer composites based on improved fumed silica and carbon black. Advantages of mixed reinforcing systems. J. Mater. Chem. 2011, 21, 17526–17533. [Google Scholar] [CrossRef]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1951, 16, 21–22. [Google Scholar]
- Guth, E.; Gold, O. On the hydrodynamical theory of the viscosity of suspensions. Phys. Rev. 1938, 53, 322. [Google Scholar]
- Einstein, A. Investigation on Theory of Brownian Motion; Dover Publications: New York, NY, USA, 1956. [Google Scholar]
- Merabia, S.; Sotta, P.; Long, D.R. A microscopic model for the reinforcement and the nonlinear behavior of filled elastomers and thermoplastic elastomers (Payne and Mullins effects). Macromolecules 2008, 41, 8252–8266. [Google Scholar] [CrossRef]
- Kohjiya, S.; Katoh, A.; Suda, T.; Shimanuki, J.; Ikeda, Y. Visualisation of carbon black networks in rubbery matrix by skeletonisation of 3D-TEM image. Polymer 2006, 47, 3298–3301. [Google Scholar] [CrossRef]
- Jouault, N.; Dalmas, F.; Boué, F.; Jestin, J. Nanoparticles reorganizations in polymer nanocomposites under large deformation. Polymer 2014, 55, 2523–2534. [Google Scholar] [CrossRef]
- Zhang, H.; Scholz, A.K.; Merckel, Y.; Brieu, M.; Berghezan, D.; Kramer, E.J.; Creton, C. Strain induced nanocavitation and crystallization in natural rubber probed by real time small and wide angle X-ray scatteringa. Polym. Phys. 2013, 51, 1125–1138. [Google Scholar] [CrossRef]
- Karino, T.; Ikeda, Y.; Yasuda, Y.; Kohjiya, S.; Shibayama, M. Nonuniformity in natural rubber as revealed by small-angle neutron scattering, small-angle X-ray scattering, and atomic force microscopy. Biomacromolecules 2007, 8, 693–699. [Google Scholar] [CrossRef]
- Candau, N.; Laghmach, R.; Chazeau, L.; Chenal, J.M.; Gauthier, C.; Biben, T.; Munch, E. Strain-induced crystallization of natural rubber and cross-link densities heterogeneities. Macromolecules 2014, 47, 5815–5824. [Google Scholar] [CrossRef]
- Kato, A.; Ikeda, Y.; Tsushi, R.; Kokubo, Y.; Kojima, N. A new approach to visualizing the carbon black/natural rubber interaction layer in carbon black-filled natural rubber vulcanizates and to elucidating the dependence of mechanical properties on quantitative parameters. Colloid Polym. Sci. 2013, 291, 2101–2110. [Google Scholar] [CrossRef]
- Sarkawi, S.S.; Dierkes, W.K.; Noordermeer, J.W.M. Elucidation of filler-to-filler and filler-to-rubber interactions in silica-reinforced natural rubber by TEM Network Visualization. Eur. Polym. J. 2014, 54, 118–127. [Google Scholar] [CrossRef]
- Qu, M.; Deng, F.; Kalkhoran, S.M.; Gouldstone, A.; Robisson, A.; Van Vliet, K.J. Nanoscale visualization and multiscale mechanical implications of bound rubber interphases in rubber–carbon black nanocomposites. Soft Matter 2011, 7, 1066–1077. [Google Scholar] [CrossRef]
- Lapra, A.; Clement, F.; Bokobza, L.; Monnerie, L. Straining effects in silica-filled elastomers investigated by atomic force microscopy: From macroscopic stretching to nanoscale strainfield. Rubber Chem. Technol. 2003, 76, 60–81. [Google Scholar] [CrossRef]
- Le Diagon, Y.; Mallarino, S.; Fretigny, C. Particle structuring under the effect of an uniaxial deformation in soft/hard nanocomposites. Eur. Phys. J. E 2007, 22, 77–83. [Google Scholar] [CrossRef]
- Díez-Pascual, A.; Gómez-Fatou, M.; Ania, F.; Flores, A. Nanoindentation Assessment of the Interphase in Carbon Nanotube-Based Hierarchical Composites. J. Phys. Chem. C 2012, 116, 24193–24200. [Google Scholar] [CrossRef]
- Díez-Pascual, A.; Gómez-Fatou, M.; Ania, F.; Flores, A. Nanoindentation in polymer nanocomposites. Prog. Mater. Sci. 2015, 67, 1–94. [Google Scholar] [CrossRef] [Green Version]
- Yatsuyanagi, F.; Suzuki, N.; Ito, M.; Kaidou, H. Effects of secondary structure of fillers on the mechanical properties of silica filled rubber systems. Polymer 2001, 42, 9523–9529. [Google Scholar] [CrossRef]
- Watanabe, D.; Miyata, T.; Nagao, T.; Kumagai, A.; Jinnai, H. Nanoscale Stress Distribution in Silica-Nanoparticle-Filled Rubber as Observed by Transmission Electron Microscopy: Implications for Tire Application. J. Polym. Sci. 2021, 4, 4452–4461. [Google Scholar]
- Wang, D.; Liang, X.; Russell, T.P.; Nakajima, K. Visualization and quantification of the chemical and physical properties at a diffusion-induced interface using AFM nanomechanical mapping. Macromolecules 2014, 47, 3761–3765. [Google Scholar] [CrossRef]
- Nakajima, K.; Ito, M.; Wang, D.; Liu, H.; Nguyen, H.K.; Liang, X.; Kumagai, A.; Fujinami, S. Nano-palpation AFM and its quantitative mechanical property mapping. Microscopy 2014, 63, 193–208. [Google Scholar] [CrossRef]
- Dokukin, M.E.; Sokolov, I. Quantitative mapping of the elastic modulus of soft materials with HarmoniX and PeakForce QNM AFM modes. Langmuir 2012, 28, 16060–16071. [Google Scholar] [CrossRef] [PubMed]
- Adamcik, J.; Lara, C.; Usov, I.; Jeong, J.S.; Ruggeri, F.S.; Dietler, G.; Lashuel, H.A.; Hamley, I.W.; Mezzenga, R. Measurement of intrinsic properties of amyloid fibrils by the peak force QNM method. Nanoscale 2012, 4, 4426–4429. [Google Scholar] [CrossRef] [Green Version]
- Nakajima, K.; Ito, M.; Nguyen, H.; Liang, X. Nanomechanics of the rubber–filler interface. Rubber Chem. Technol. 2017, 90, 272–284. [Google Scholar] [CrossRef]
- Nakajima, K.; Nishi, T. Chapter 21 Recent developments in rubber research using atomic force microscopy. In Current Topics in Elastomers Research; Bhomik, A.K., Ed.; CRC Press: Boca Raton, FL, USA, 2008; pp. 579–604. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. Ser. A 1971, 324, 301–320. [Google Scholar]
- Sun, Y.; Walker, G.C. Using the adhesive interaction between atomic force microscopy tips and polymer surfaces to measure the elastic modulus of compliant samples. Langmuir 2004, 20, 5837–5845. [Google Scholar] [CrossRef]
- Omnès, B.; Thuillier, S.; Pilvin, P.; Grohens, Y.; Gillet, S. Effective properties of carbon black filled natural rubber: Experiments and modeling. Compsites Part A Appl. Sci. Manuf. 2008, 39, 1141–1149. [Google Scholar] [CrossRef]
- Wang, D.; Fujinami, S.; Nakajima, K.; Inukai, S.; Ueki, H.; Magario, A.; Noguchi, T.; Endo, M.; Nishi, T. Visualization of nanomechanical mapping on polymer nanocomposites by AFM force measurement. Polymer 2010, 51, 2455–2459. [Google Scholar] [CrossRef]
- Broutman, L.J.; Krock, R.H. Modern Composite Materials; Addison Wesley: Reading, MA, USA, 1967. [Google Scholar]
- Hansen, T.C. Influence of aggregate and voids on modulus of elasticity of concrete, cement mortar, and cement paste. J. Proc. 1965, 62, 193–216. [Google Scholar]
- Kaplan, M.F. Flexural and Compressive Strength of Concrete as Affected by the Properties of Coarse Aggregates. Rilem Bull. 1959, 1, 58–73. [Google Scholar]
- Chow, T.S. Effect of particle shape at finite concentration on the elastic moduli of filled polymers. J. Polym. Sci. Polym. Phys. 1978, 16, 959. [Google Scholar] [CrossRef]
- Takayanagi, M.; Uemura, S.; Minami, S. Application of equivalent model method to dynamic rheooptical properties of crystalline polymer. J. Polym. Sci. Part C 1964, 5, 113–122. [Google Scholar]



| Component | Composition (phr) |
|---|---|
| isoprene rubber, IR | 100 |
| Sulfur | 2 |
| Stearic acid | 1 |
| Zinc oxide | 5 |
| N-cyclohexylbenzothiazole-2-sulfenamide, CBS | 1 |
| Carbon black, CB | 0, 10, 20, 30, 40, 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, X.; Ito, M.; Nakajima, K. Reinforcement Mechanism of Carbon Black-Filled Rubber Nanocomposite as Revealed by Atomic Force Microscopy Nanomechanics. Polymers 2021, 13, 3922. https://doi.org/10.3390/polym13223922
Liang X, Ito M, Nakajima K. Reinforcement Mechanism of Carbon Black-Filled Rubber Nanocomposite as Revealed by Atomic Force Microscopy Nanomechanics. Polymers. 2021; 13(22):3922. https://doi.org/10.3390/polym13223922
Chicago/Turabian StyleLiang, Xiaobin, Makiko Ito, and Ken Nakajima. 2021. "Reinforcement Mechanism of Carbon Black-Filled Rubber Nanocomposite as Revealed by Atomic Force Microscopy Nanomechanics" Polymers 13, no. 22: 3922. https://doi.org/10.3390/polym13223922
APA StyleLiang, X., Ito, M., & Nakajima, K. (2021). Reinforcement Mechanism of Carbon Black-Filled Rubber Nanocomposite as Revealed by Atomic Force Microscopy Nanomechanics. Polymers, 13(22), 3922. https://doi.org/10.3390/polym13223922