Graphene and Polyethylene: A Strong Combination Towards Multifunctional Nanocomposites
Abstract
1. Introduction
2. Experimental
2.1. Materials
2.2. Modification of Graphene
2.3. Preparation of Nanocomposites
2.4. Characterization
3. Results and Discussion
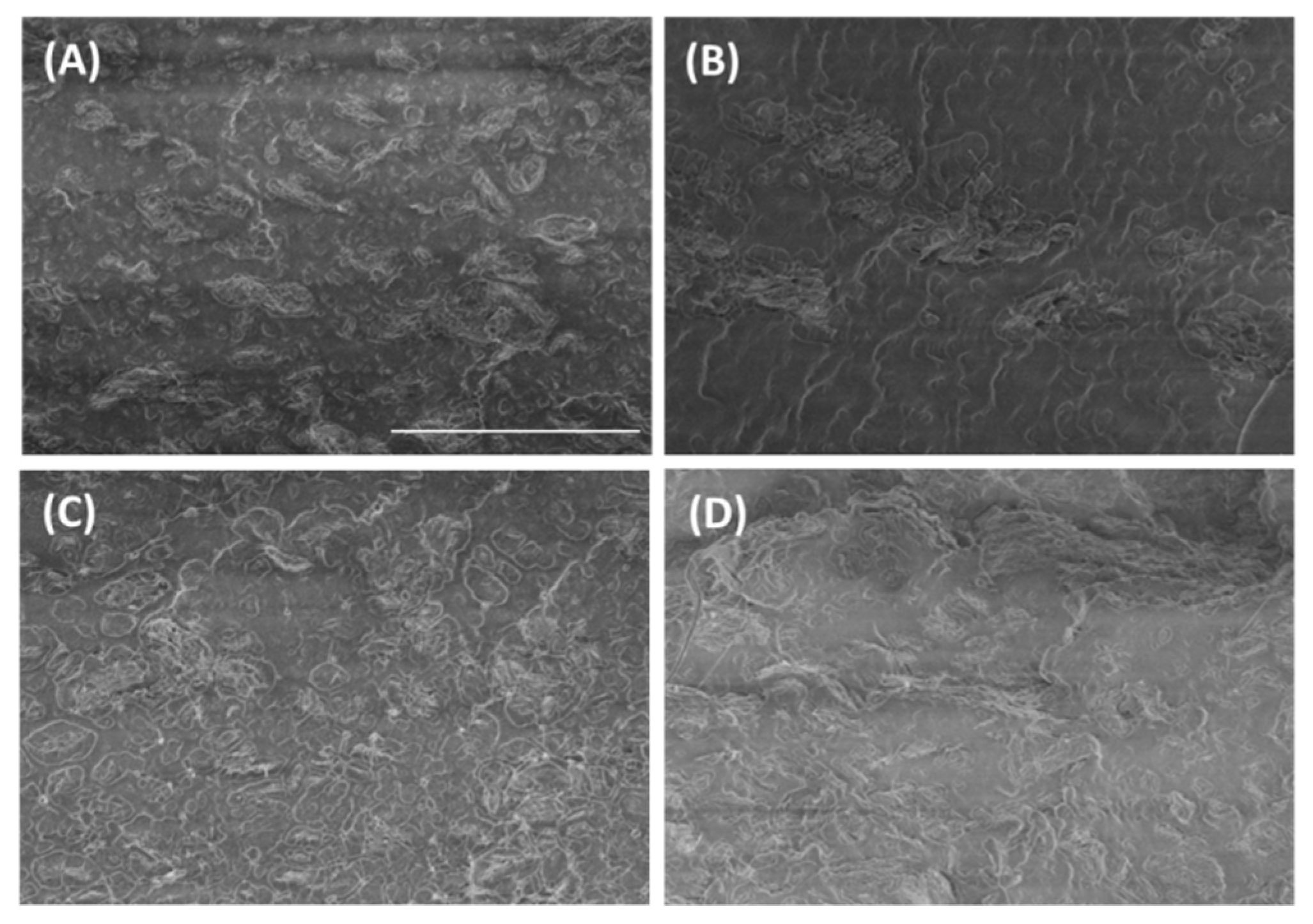
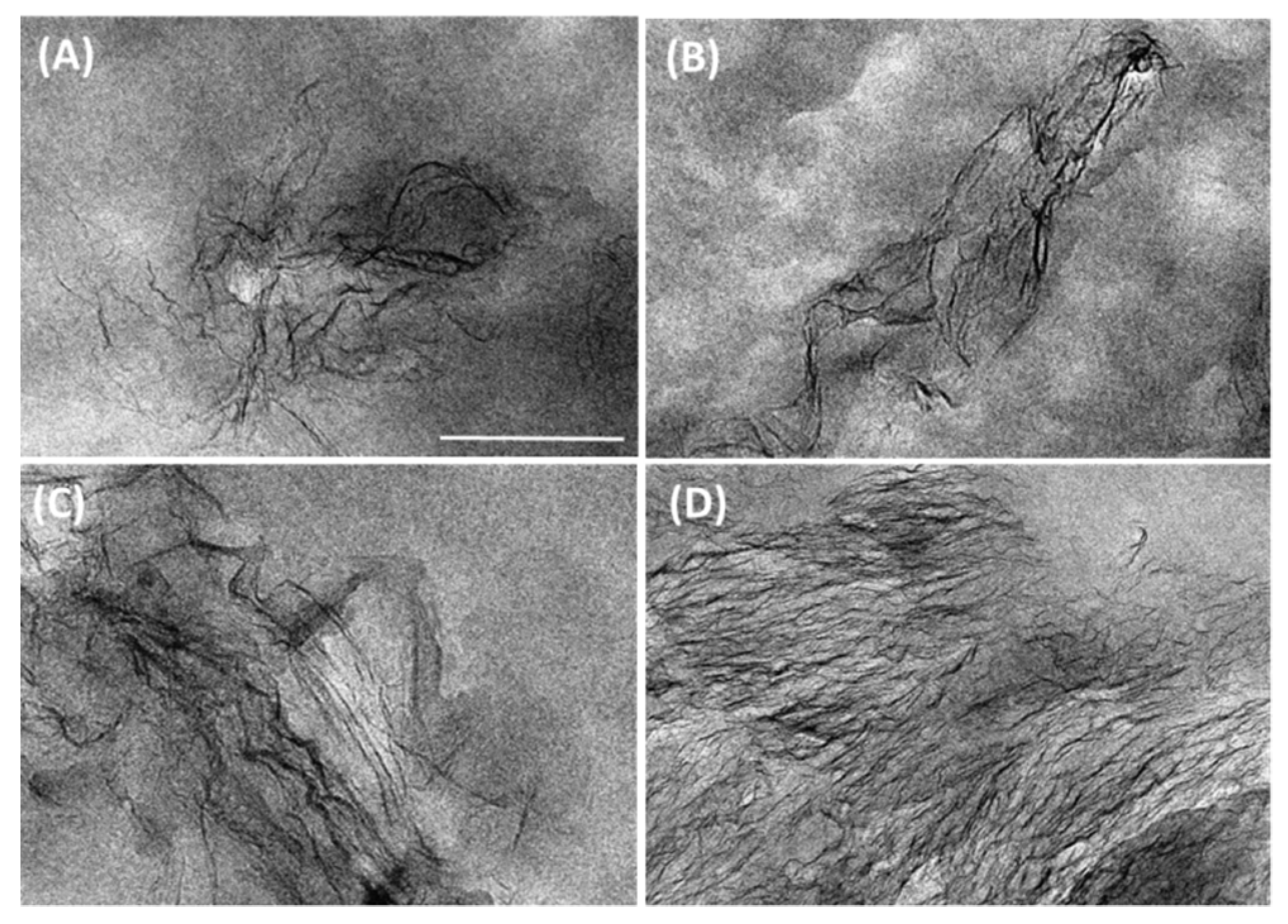
3.1. Graphene Dispersion
3.2. Thermal Behavior
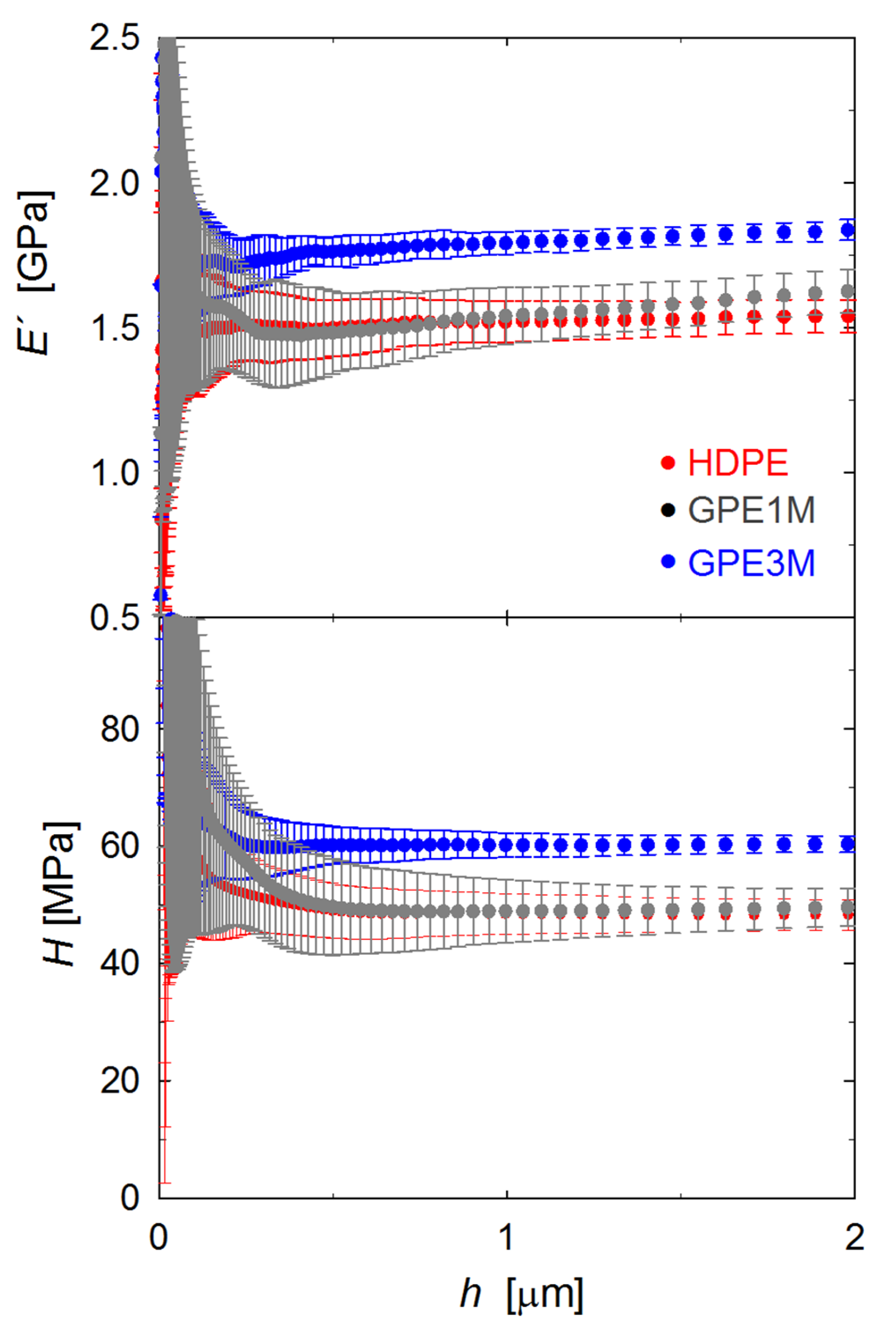
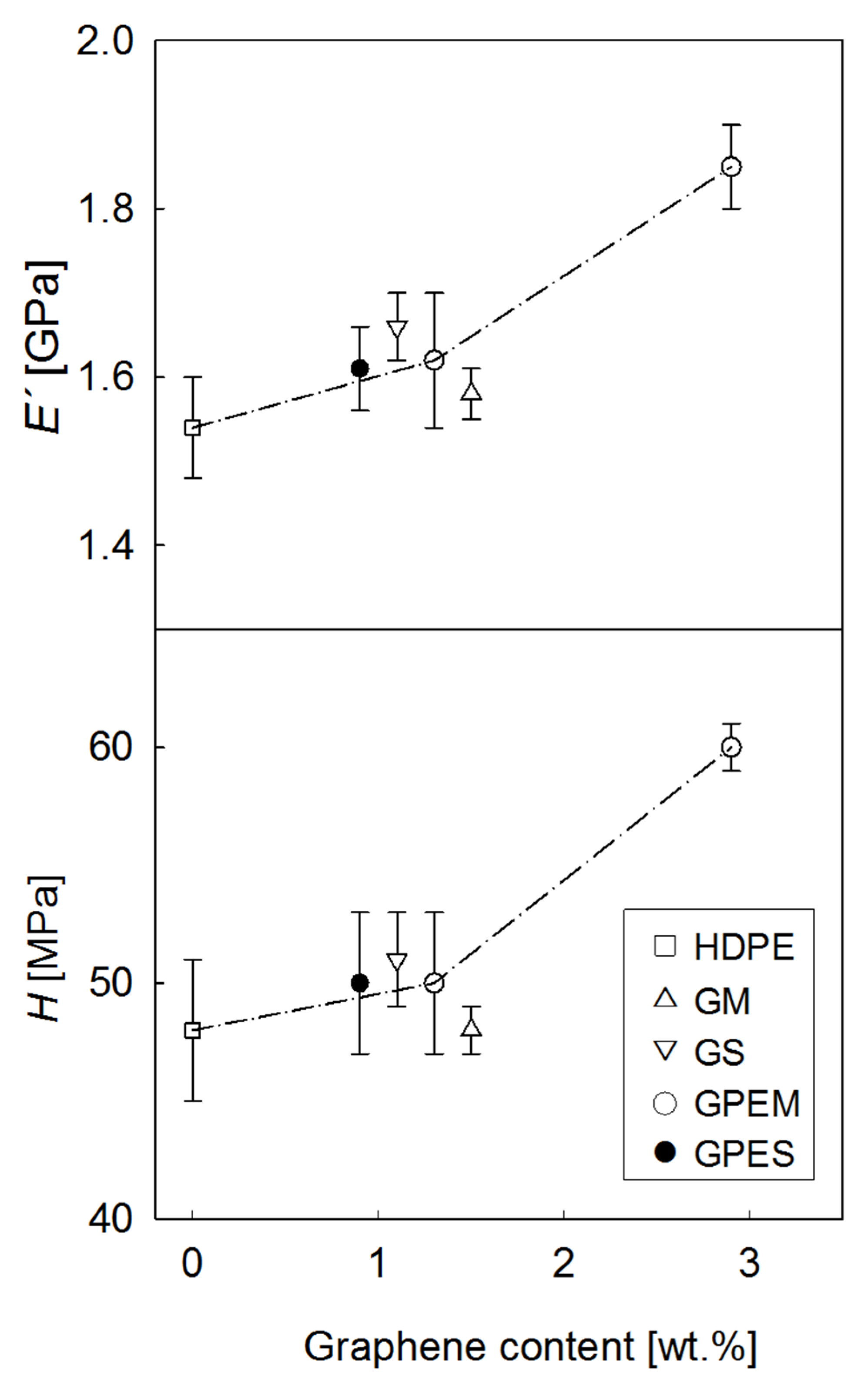
3.3. Mechanical Properties
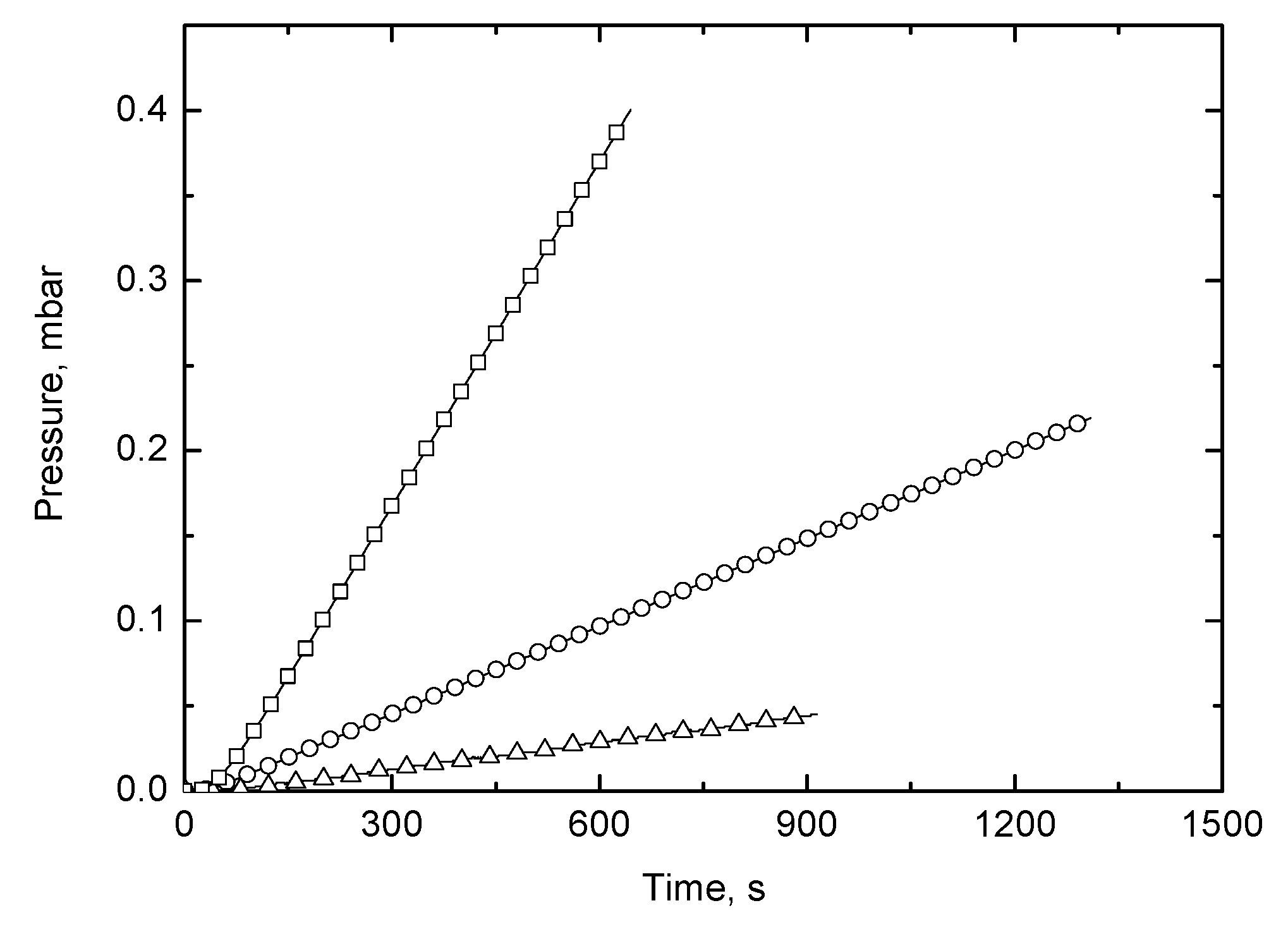
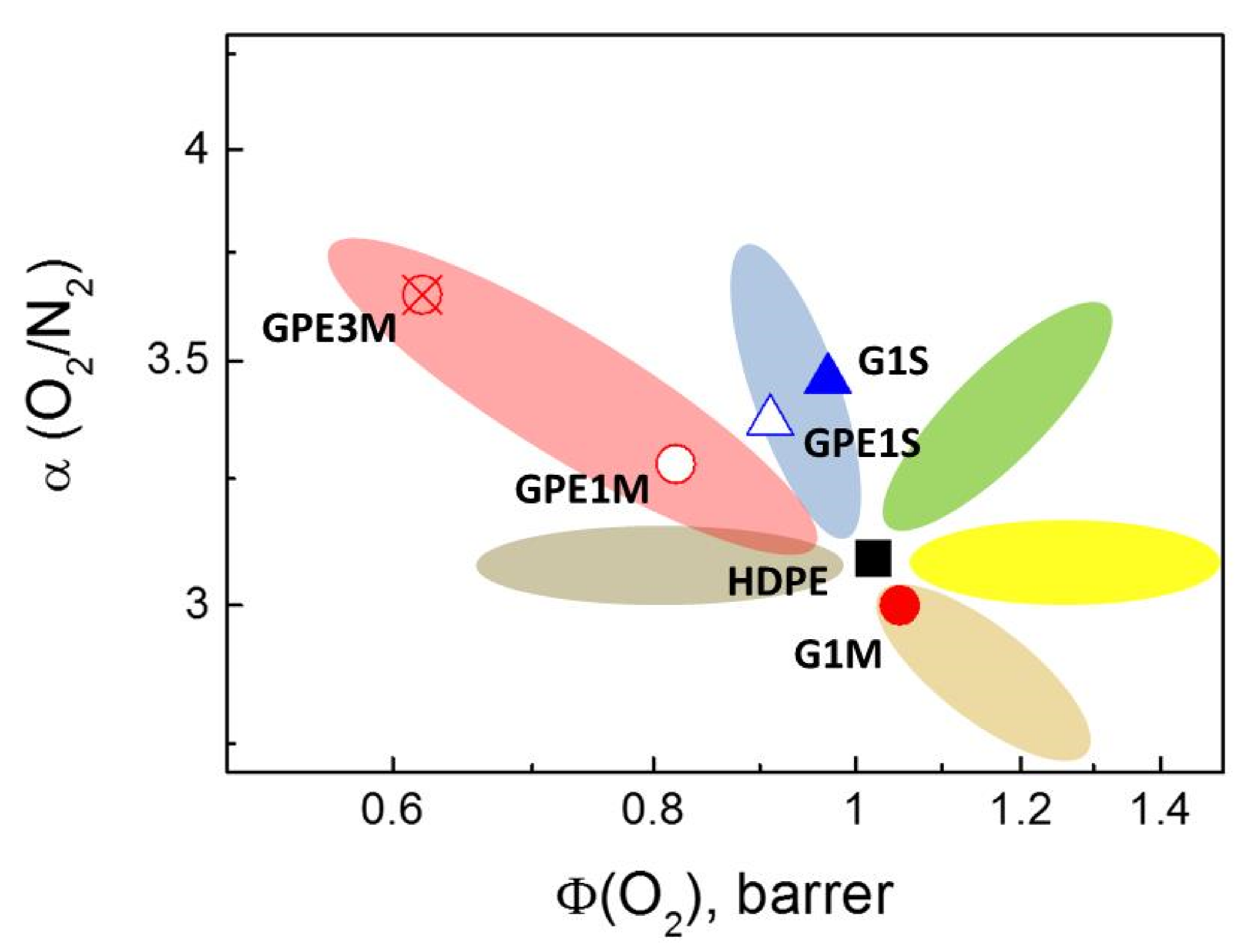
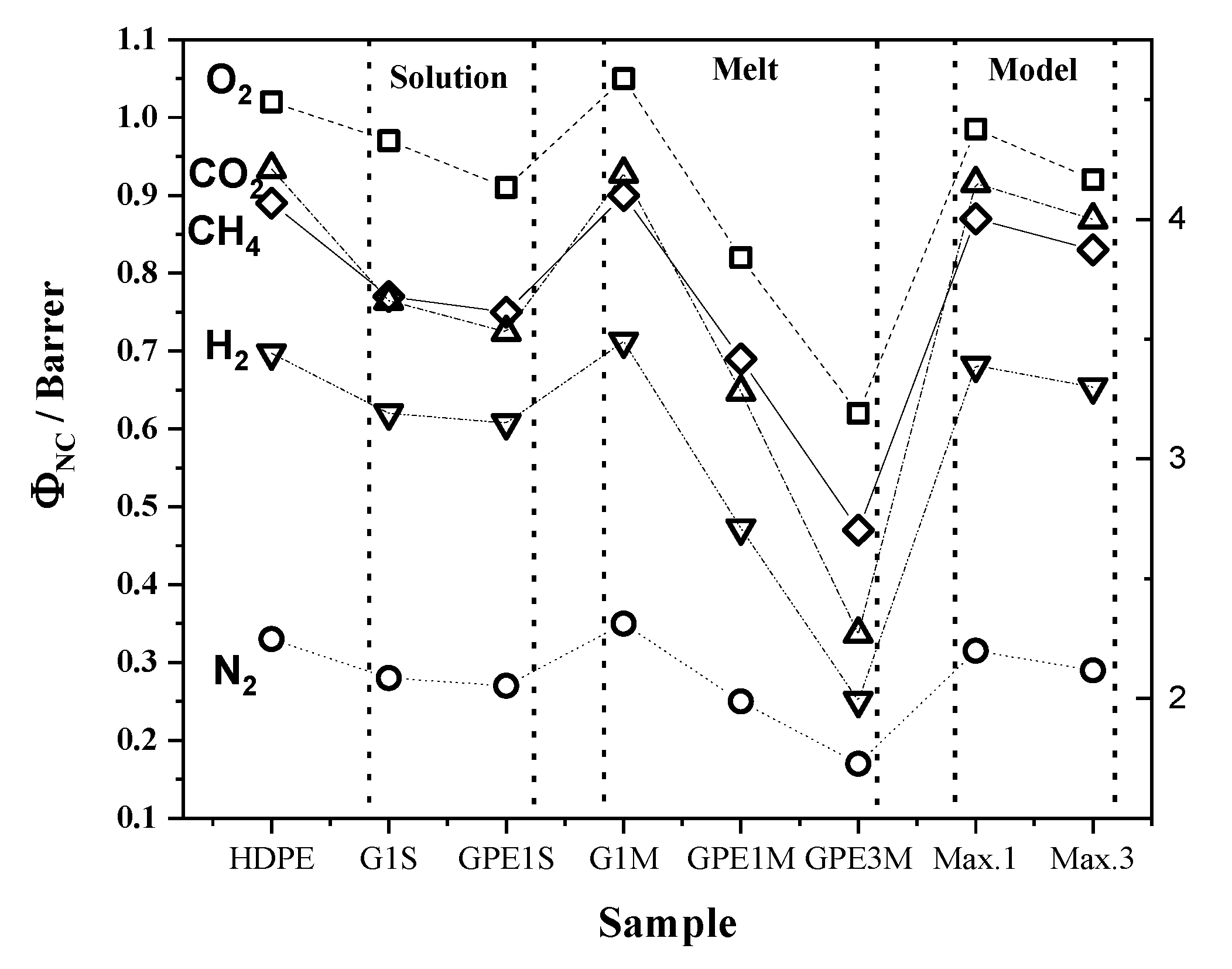
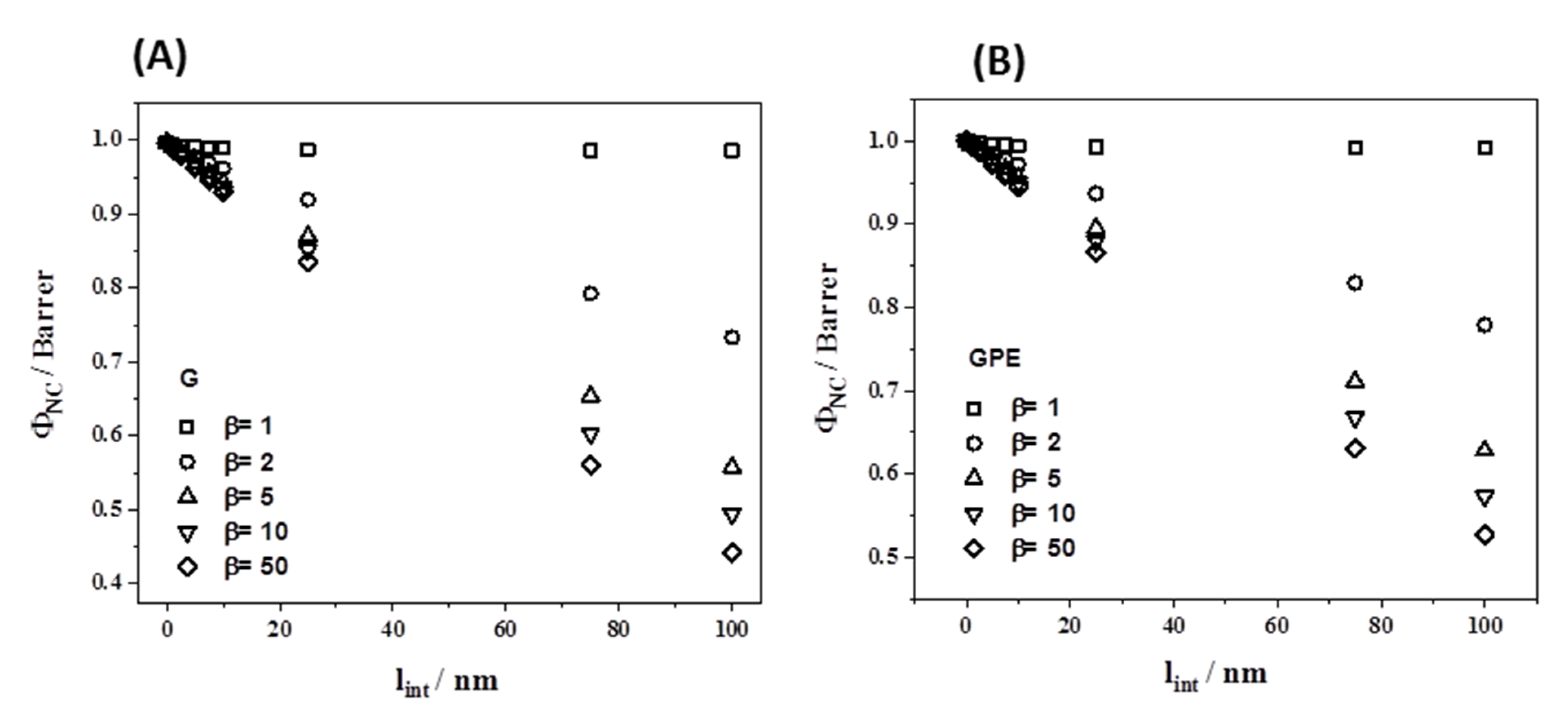
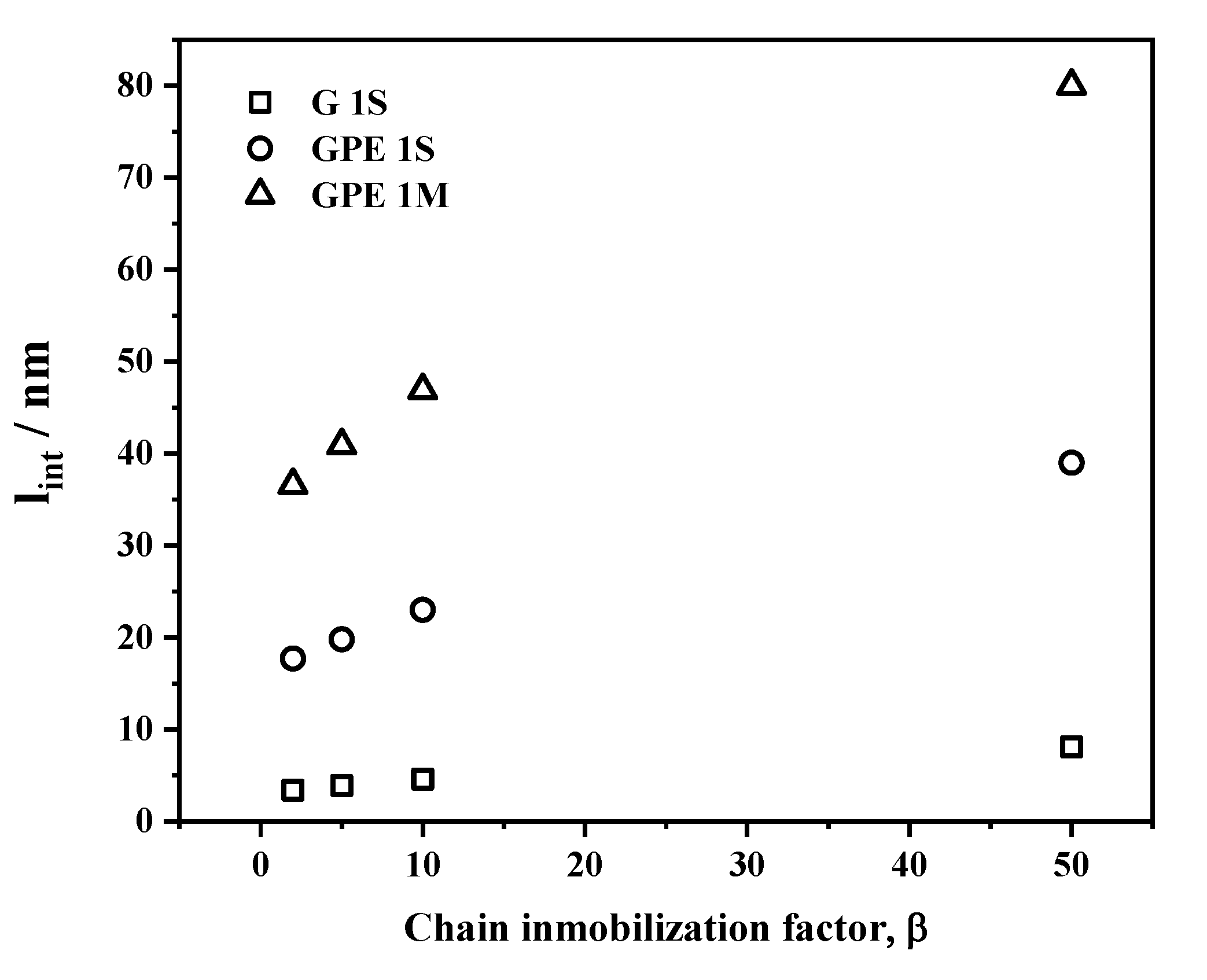
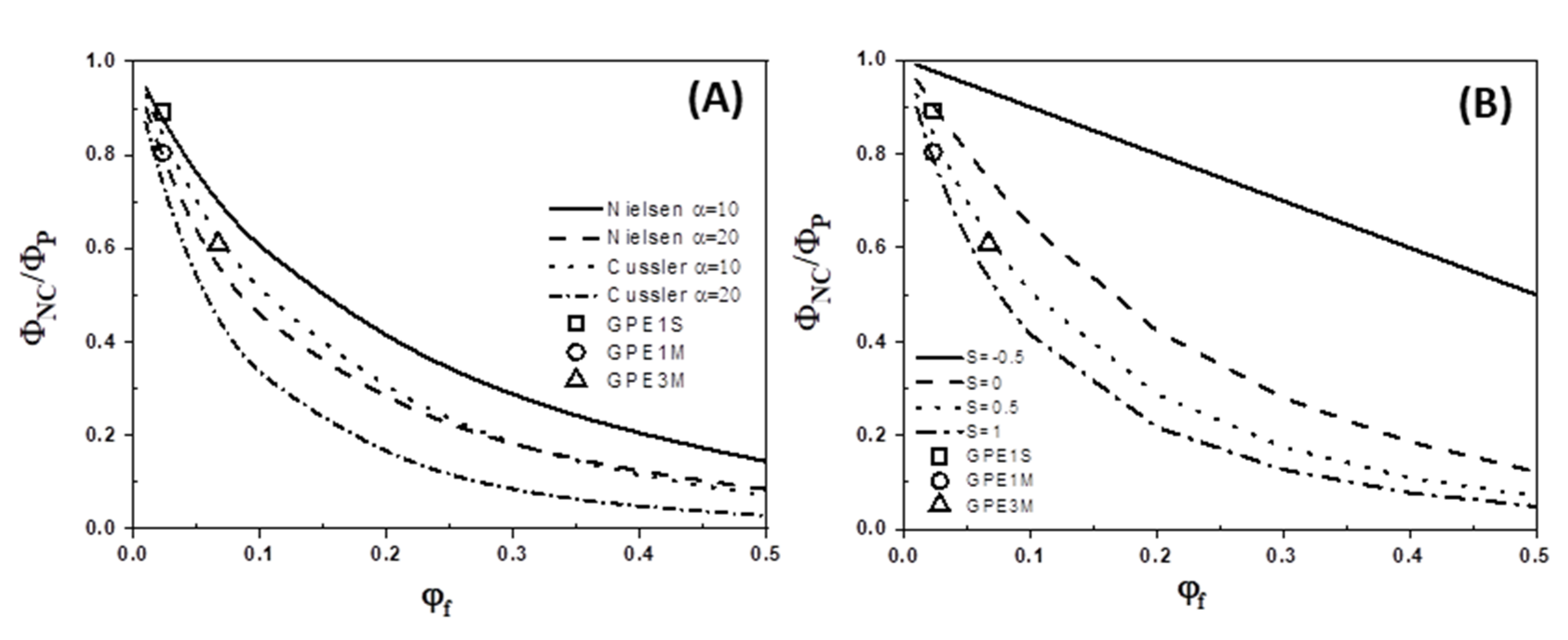
3.4. Gas Permeability
3.5. Electrical Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Geyer, R.; Jambeck, J.R.; Law, K.L. Production, use, and fate of all plastics ever made. Sci. Adv. 2017, 3, e1700782. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Du, X.; Skachko, I.; Barker, A.; Andrei, E.Y. Approaching ballistic transport in suspended graphene. Nat. Nanotechnol. 2008, 3, 491–495. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Tripathi, S.N.; Rao, G.S.S.; Mathur, A.B.; Jasra, R. Polyolefin/graphene nanocomposites: A review. RSC Adv. 2017, 7, 23615–23632. [Google Scholar] [CrossRef]
- Salavagione, H.J. Covalent Graphene-Polymer Nanocomposites. In Graphene Materials. Fundamentals and Emerging Applications, 1st ed.; Tiwari, A., Syväjärvi, M., Eds.; Scrivener Publishing: Beverly, MA, USA, 2015; pp. 101–149. [Google Scholar]
- Toh, G.Y.; Ong, H.L.; Bindumadhavan, K.; Doong, R.-A. Physicochemical properties of reduced graphite oxide conglomerated polyethylene nanocomposites. Polym. Int. 2018, 67, 1638–1647. [Google Scholar] [CrossRef]
- Ren, P.-G.; Wang, H.; Huang, H.-D.; Yan, D.-X.; Li, Z.-M. Characterization and performance of dodecyl amine functionalized graphene oxide and dodecyl amine functionalized graphene/high-density polyethylene nanocomposites: A comparative study. J. Appl. Polym. Sci. 2013, 131, 39803. [Google Scholar] [CrossRef]
- Kuila, T.; Bose, S.; Mishra, A.K.; Khanra, P.; Kim, N.H.; Lee, J.H. Effect of functionalized graphene on the physical properties of linear low density polyethylene nanocomposites. Polym. Test. 2012, 31, 31–38. [Google Scholar] [CrossRef]
- Quiles-Díaz, S.; Enrique-Jimenez, P.; Papageorgiou, D.G.; Ania, F.; Flores, A.; Kinloch, I.; Gómez-Fatou, M.; Young, R.; Salavagione, H. Influence of the chemical functionalization of graphene on the properties of polypropylene-based nanocomposites. Compos. Part A Appl. Sci. Manuf. 2017, 100, 31–39. [Google Scholar] [CrossRef]
- Tayebi, M.; Ramazani, S.A.A.; Mosavian, M.T.H.; Tayyebi, A. LDPE/EVA/graphene nanocomposites with enhanced mechanical and gas permeability properties. Polym. Adv. Technol. 2015, 26, 1083–1090. [Google Scholar] [CrossRef]
- Honaker, K.; Vautard, F.; Drzal, L. Investigating the mechanical and barrier properties to oxygen and fuel of high density polyethylene–graphene nanoplatelet composites. Mater. Sci. Eng. B 2017, 216, 23–30. [Google Scholar] [CrossRef]
- Gaska, K.; Kádár, R.; Rybak, A.; Siwek, A.; Gubanski, S.M. Gas Barrier, Thermal, Mechanical and Rheological Properties of Highly Aligned Graphene-LDPE Nanocomposites. Polymers 2017, 9, 294. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Potts, J.R.; Dreyer, D.R.; Bielawski, C.W.; Ruoff, R.S. Graphene-based polymer nanocomposites. Polymers 2011, 52, 5–25. [Google Scholar] [CrossRef]
- Castelaín, M.; Martínez, G.; Ellis, G.J.; Salavagione, H.J. A versatile chemical tool for the preparation of conductive graphene-based polymer nanocomposites. Chem. Commun. 2013, 49, 8967. [Google Scholar] [CrossRef]
- Castelaín, M.; Martínez, G.; Marco, C.; Ellis, G.J.; Salavagione, H.J. Effect of Click-Chemistry Approaches for Graphene Modification on the Electrical, Thermal, and Mechanical Properties of Polyethylene/Graphene Nanocomposites. Macromolecules 2013, 46, 8980–8987. [Google Scholar] [CrossRef]
- Cruz-Aguilar, A.; Navarro-Rodriguez, D.; Pérez-Camacho, O.; Fernández-Tavizón, S.; Gallardo-Vega, C.A.; García-Zamora, M.; Barriga-Castro, E.D. High-density polyethylene/graphene oxide nanocomposites prepared via in situ polymerization: Morphology, thermal, and electrical properties. Mater. Today Commun. 2018, 16, 232–241. [Google Scholar] [CrossRef]
- Park, S.; He, S.; Wang, J.; Stein, A.; Macosko, C.W. Graphene-polyethylene nanocomposites: Effect of graphene functionalization. Polymers 2016, 104, 1–9. [Google Scholar] [CrossRef]
- Vassiliou, A.; Kontopoulou, M.; Docoslis, A. A Noncovalent Compatibilization Approach to Improve the Filler Dispersion and Properties of Polyethylene/Graphene Composites. ACS Appl. Mater. Interfaces 2014, 6, 1916–1925. [Google Scholar] [CrossRef]
- Lu, T.; Ye, H.; Zheng, A.; Xu, X.; Xu, C.; Wang, H.; Sun, L.; Xu, L. Hybrid modification of high-density polyethylene with hyperbranched polyethylene-functionalized multiwalled carbon nanotubes and few-layered graphene. J. Appl. Polym. Sci. 2017, 134, 44848. [Google Scholar] [CrossRef]
- Du, J.; Zhao, L.; Zeng, Y.; Zhang, L.; Li, F.; Liu, P.; Liu, C. Comparison of electrical properties between multi-walled carbon nanotube and graphene nanosheet/high density polyethylene composites with a segregated network structure. Carbon 2011, 49, 1094–1100. [Google Scholar] [CrossRef]
- Wang, B.; Li, H.; Li, L.; Chen, P.; Wang, Z.; Gu, Q. Electrostatic adsorption method for preparing electrically conducting ultrahigh molecular weight polyethylene/graphene nanosheets composites with a segregated network. Compos. Sci. Technol. 2013, 89, 180–185. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, G.; Xiao, L.; Wang, H.; Zhang, Q.; Zhao, Z. Preparation and electrical conductivity of graphene/ultrahigh molecular weight polyethylene composites with a segregated structure. Carbon 2012, 50, 4596–4599. [Google Scholar] [CrossRef]
- Silvestre, C.; Duraccio, D.; Cimmino, S. Food packaging based on polymer nanomaterials. Prog. Polym. Sci. 2011, 36, 1766–1782. [Google Scholar] [CrossRef]
- Wang, B.; Peng, D.; Lv, R.; Na, B.; Liu, H.; Yu, Z. Generic melt compounding strategy using reactive graphene towards high performance polyethylene/graphene nanocomposites. Compos. Sci. Technol. 2019, 177, 1–9. [Google Scholar] [CrossRef]
- Silva-Leyton, R.; Quijada, R.; Bastías, R.; Zamora, N.; Olate-Moya, F.; Palza, H. Polyethylene/graphene oxide composites toward multifunctional active packaging films. Compos. Sci. Technol. 2019, 184, 107888. [Google Scholar] [CrossRef]
- Hui, J.; Ren, P.-G.; Sun, Z.-F.; Ren, F.; Xu, L.; Zhang, Z.; Ji, X. Influences of interfacial adhesion on gas barrier property of functionalized graphene oxide/ultra-high-molecular-weight polyethylene composites with segregated structure. Compos. Interfaces 2017, 24, 1–13. [Google Scholar] [CrossRef]
- Checchetto, R.; Miotello, A.; Nicolais, L.; Carotenuto, G. Gas transport through nanocomposite membrane composed by polyethylene with dispersed graphite nanoplatelets. J. Membr. Sci. 2014, 463, 196–204. [Google Scholar] [CrossRef]
- Sun, P.Z.; Yang, Q.; Kuang, W.J.; Stebunov, Y.V.; Xiong, W.Q.; Yu, J.; Nair, R.R.; Katsnelson, M.I.; Yuan, S.J.; Grigorieva, I.V.; et al. Limits on gas impermeability of graphene. Nature 2020, 579, 229–232. [Google Scholar] [CrossRef]
- Berry, V. Impermeability of graphene and its applications. Carbon 2013, 62, 1–10. [Google Scholar] [CrossRef]
- Guo, F.; Silverberg, G.; Bowers, S.; Kim, S.-P.; Datta, D.; Shenoy, V.; Hurt, R.H. Graphene-Based Environmental Barriers. Environ. Sci. Technol. 2012, 46, 7717–7724. [Google Scholar] [CrossRef]
- Wunderlich, B.; Cormier, C.M. Heat of fusion of polyethylene. J. Polym. Sci. Part A-2 Polym. Phys. 1967, 5, 987–988. [Google Scholar] [CrossRef]
- Herbert, E.G.; Oliver, W.C.; Pharr, G.M. Nanoindentation and the dynamic characterization of viscoelastic solids. J. Phys. D Appl. Phys. 2008, 41, 074021. [Google Scholar] [CrossRef]
- Oliver, W.; Pharr, G. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- López-González, M.M.; Saiz, E.; Guzmán, J.; Riande, E. Experimental and Simulation Studies on the Transport of Argon in Polycarbonate Membranes. Macromolecules 2001, 34, 4999–5004. [Google Scholar] [CrossRef]
- Fischer-Cripps, A. Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 2006, 200, 4153–4165. [Google Scholar] [CrossRef]
- Hay, J.; Crawford, B. Measuring substrate-independent modulus of thin films. J. Mater. Res. 2011, 26, 727–738. [Google Scholar] [CrossRef]
- Coulson, C.A.; Crank, J. The Mathematics of Diffusion. Math. Gaz. 1958, 42, 165. [Google Scholar] [CrossRef]
- Barrer, R.M.; Rideal, E.K. Permeation, diffusion and solution of gases in organic polymers. Trans. Faraday Soc. 1939, 35, 628–643. [Google Scholar] [CrossRef]
- Moore, T.T.; Koros, W.J. Non-ideal effects in organic–inorganic materials for gas separation membranes. J. Mol. Struct. 2005, 739, 87–98. [Google Scholar] [CrossRef]
- Aroon, M.A.; Ismail, A.F.; Matsuura, T.; Montazer-Rahmati, M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010, 75, 229–242. [Google Scholar] [CrossRef]
- Pal, R. Permeation models for mixed matrix membranes. J. Colloid Interface Sci. 2008, 317, 191–198. [Google Scholar] [CrossRef] [PubMed]
- Picard, E.; Vermogen, A.; Gerard, J.; Espuche, E. Barrier properties of nylon 6-montmorillonite nanocomposite membranes prepared by melt blending: Influence of the clay content and dispersion stateConsequences on modelling. J. Membr. Sci. 2007, 292, 133–144. [Google Scholar] [CrossRef]
- Dunkerley, E.; Schmidt, D. Effects of Composition, Orientation and Temperature on the O2Permeability of Model Polymer/Clay Nanocomposites. Macromolecules 2010, 43, 10536–10544. [Google Scholar] [CrossRef]
- Choudalakis, G.; Gotsis, A.D. Permeability of polymer/clay nanocomposites: A review. Eur. Polym. J. 2009, 45, 967–984. [Google Scholar] [CrossRef]
- Cui, Y.; Kundalwal, S.; Kumar, S. Gas barrier performance of graphene/polymer nanocomposites. Carbon 2016, 98, 313–333. [Google Scholar] [CrossRef]
- Nielsen, L.E. Models for the Permeability of Filled Polymer Systems. J. Macromol. Sci. Part A Chem. 1967, 1, 929–942. [Google Scholar] [CrossRef]
- Yang, C.; Nuxoll, E.E.; Cussler, E.L. Reactive barrier films. AJChE J. 2001, 47, 295–302. [Google Scholar] [CrossRef]
- Lape, N.K.; Nuxoll, E.E.; Cussler, E.L. Polydisperse flakes in barrier films. J. Membr. Sci. 2004, 236, 29–37. [Google Scholar] [CrossRef]
- Bharadwaj, R.K. Modeling the barrier properties of polymer-layered silicate nanocomposites. Macromolecules 2001, 34, 9189–9192. [Google Scholar] [CrossRef]
- Salavagione, H.J.; Martínez, G.; Gómez, M.A. Synthesis of poly(vinyl alcohol)/reduced graphite oxide nanocomposites with improved thermal and electrical properties. J. Mater. Chem. 2009, 19, 5027–5032. [Google Scholar] [CrossRef]
- Jiang, X.; Drzal, L.T. Reduction in percolation threshold of injection molded high-density polyethylene/exfoliated graphene nanoplatelets composites by solid state ball milling and solid state shear pulverization. J. Appl. Polym. Sci. 2011, 124, 525–535. [Google Scholar] [CrossRef]
- Pang, H.; Chen, T.; Zhang, G.; Zeng, B.; Li, Z.-M. An electrically conducting polymer/graphene composite with a very low percolation threshold. Mater. Lett. 2010, 64, 2226–2229. [Google Scholar] [CrossRef]
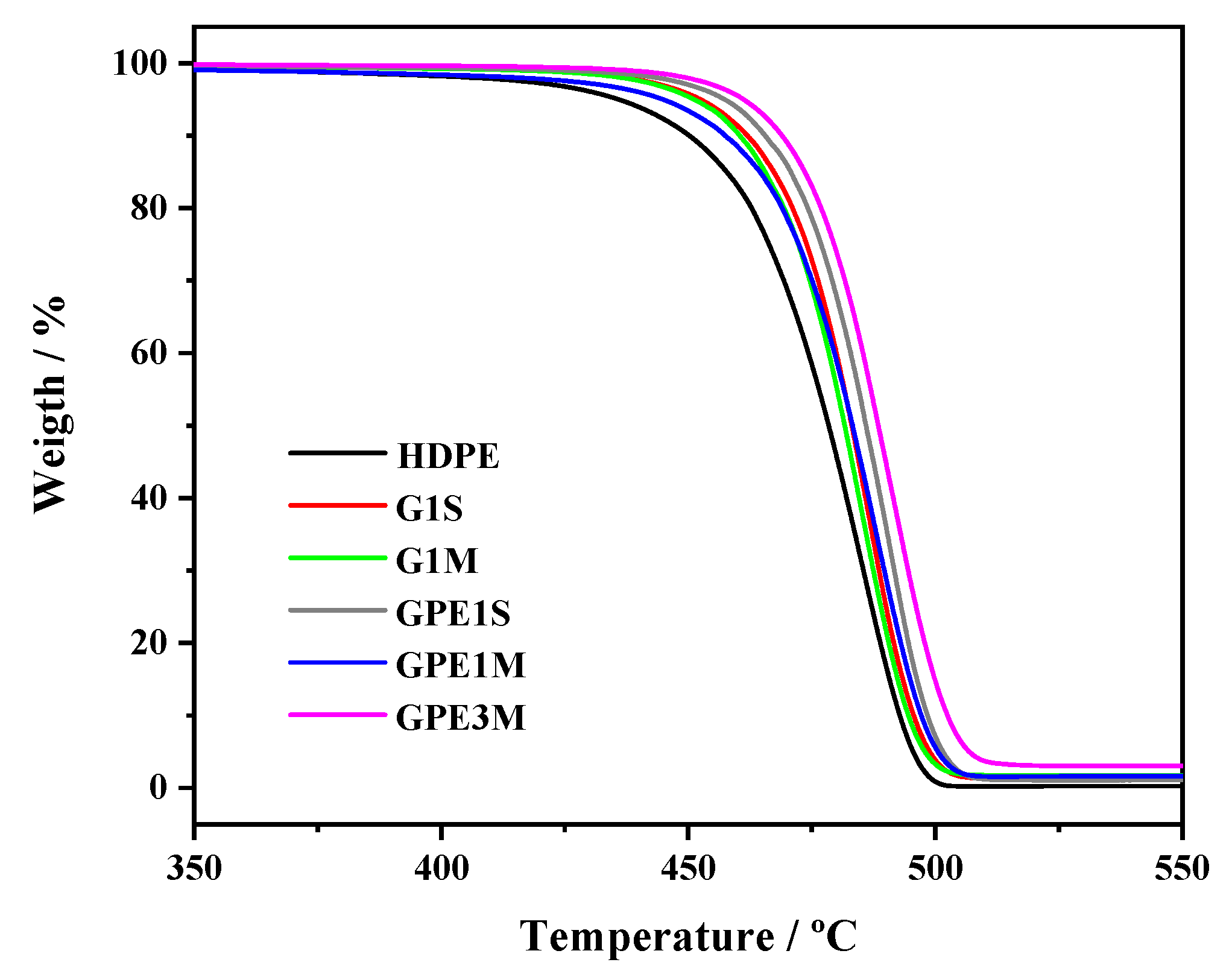

| Sample | G Content (wt %) a | Ti (°C) | T10 (°C) | Tmax (°C) | Xc (%) | Tm (°C) |
|---|---|---|---|---|---|---|
| HDPE | - | 406 ± 1 | 450 ± 1 | 485 ± 1 | 58 ± 2 | 129.3 ± 0.5 |
| G1M | 1.5 | 436 ± 1 | 460 ± 1 | 485 ± 1 | 55 ± 2 | 129. 4 ± 0.5 |
| GPE1M | 1.3 | 415 ± 1 | 457 ± 1 | 488 ± 1 | 60 ± 2 | 130.0 ± 0.5 |
| GPE3M | 2.9 | 450 ± 1 | 469 ± 1 | 491 ± 1 | 58 ± 2 | 127.3 ± 0.5 |
| G1S | 1.1 | 437 ± 1 | 462 ± 1 | 487 ± 1 | 57 ± 2 | 128.5 ± 0.5 |
| GPE1S | 0.9 | 444 ± 1 | 466 ± 1 | 490 ± 1 | 59 ± 2 | 129.6 ± 0.5 |
| Sample | E′ (GPa) | H (MPa) |
|---|---|---|
| HDPE | 1.54 ± 0.06 | 48 ± 3 |
| G1M | 1.58 ± 0.03 | 48 ± 1 |
| GPE1M | 1.62 ± 0.08 | 50 ± 3 |
| G1S | 1.66 ± 0.04 | 51 ± 2 |
| GPE1S | 1.61 ± 0.05 | 50 ± 3 |
| GPE3M | 1.85 ± 0.05 | 60 ± 1 |
| Gas | HDPE | G1S | GPE1S | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Φ | D × 107 | S × 104 | Φ | D × 107 | S × 104 | Φ | D × 107 | S × 104 | |
| O2 | 1.02 | 2.72 | 3.76 | 0.97 | 2.55 | 3.79 | 0.91 | 2.75 | 3.32 |
| N2 | 0.33 | 2.01 | 1.62 | 0.28 | 2.08 | 1.35 | 0.27 | 1.55 | 1.72 |
| CO2 | 4.21 | 1.61 | 26.08 | 3.66 | 1.50 | 24.44 | 3.53 | 1.46 | 24.24 |
| H2 | 3.44 | 25.41 | 1.35 | 3.19 | 24.59 | 1.30 | 3.15 | 24.0 | 1.31 |
| CH4 | 0.89 | 0.90 | 9.92 | 0.77 | 0.85 | 8.97 | 0.75 | 0.89 | 8.38 |
| Gas | G1M | GPE1M | GPE3M | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Φ | D × 107 | S × 104 | Φ | D × 107 | S × 104 | Φ | D × 107 | S × 104 | |
| O2 | 1.05 | 2.16 | 4.85 | 0.82 | 1.68 | 4.88 | 0.62 | 1.16 | 5.34 |
| N2 | 0.35 | 1.65 | 2.11 | 0.25 | 1.06 | 2.37 | 0.17 | 0.92 | 1.86 |
| CO2 | 4.19 | 1.43 | 29.39 | 3.28 | 1.15 | 28.37 | 2.27 | 0.92 | 24.78 |
| H2 | 3.49 | 20.57 | 1.70 | 2.71 | 11.05 | 2.45 | 1.99 | 16.16 | 1.23 |
| CH4 | 0.90 | 0.75 | 12.02 | 0.69 | 0.58 | 11.74 | 0.47 | 0.53 | 8.90 |
| Sample | Electrical Conductivity (S cm−1) |
|---|---|
| G1S | <1 × 10−8 * |
| GPE1S | ~1 × 10−7 |
| G1M | <1 × 10−8 * |
| GPE1M | <1 × 10−8 * |
| GPE3M | 4.9 × 10−6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-González, M.; Flores, A.; Marra, F.; Ellis, G.; Gómez-Fatou, M.; J. Salavagione, H. Graphene and Polyethylene: A Strong Combination Towards Multifunctional Nanocomposites. Polymers 2020, 12, 2094. https://doi.org/10.3390/polym12092094
López-González M, Flores A, Marra F, Ellis G, Gómez-Fatou M, J. Salavagione H. Graphene and Polyethylene: A Strong Combination Towards Multifunctional Nanocomposites. Polymers. 2020; 12(9):2094. https://doi.org/10.3390/polym12092094
Chicago/Turabian StyleLópez-González, Mar, Araceli Flores, Fabrizio Marra, Gary Ellis, Marián Gómez-Fatou, and Horacio J. Salavagione. 2020. "Graphene and Polyethylene: A Strong Combination Towards Multifunctional Nanocomposites" Polymers 12, no. 9: 2094. https://doi.org/10.3390/polym12092094
APA StyleLópez-González, M., Flores, A., Marra, F., Ellis, G., Gómez-Fatou, M., & J. Salavagione, H. (2020). Graphene and Polyethylene: A Strong Combination Towards Multifunctional Nanocomposites. Polymers, 12(9), 2094. https://doi.org/10.3390/polym12092094







