Shape Memory Polymer Foam with Programmable Apertures
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Sample Preparation
2.3. Characterization Methods
2.4. Demonstrators
2.5. Numerical Simulation
- Neo-Hookean model
- Ogden model
2.5.1. Neo-Hookean Model
2.5.2. Ogden Model
3. Results and Discussion
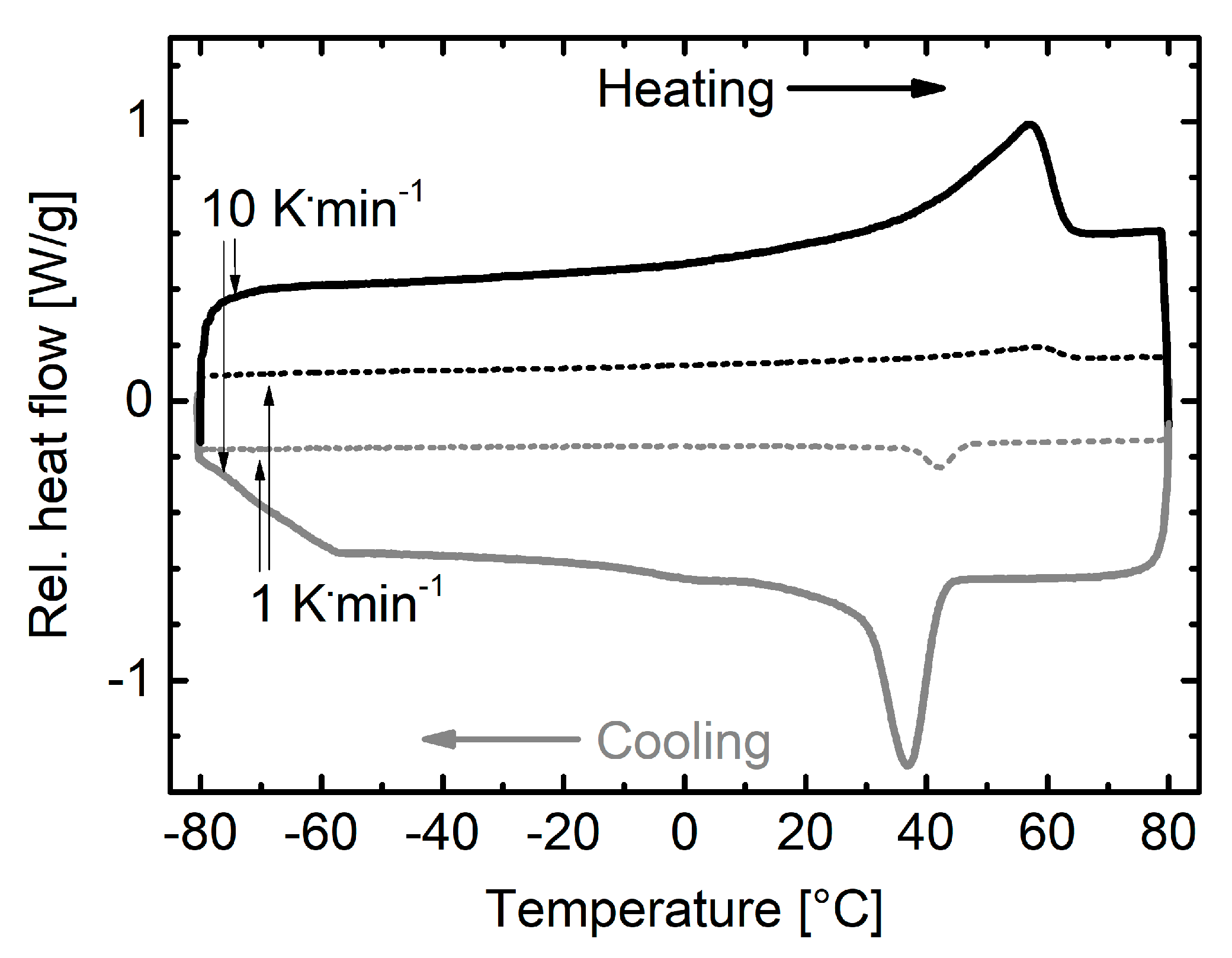
3.1. Polyester Diols
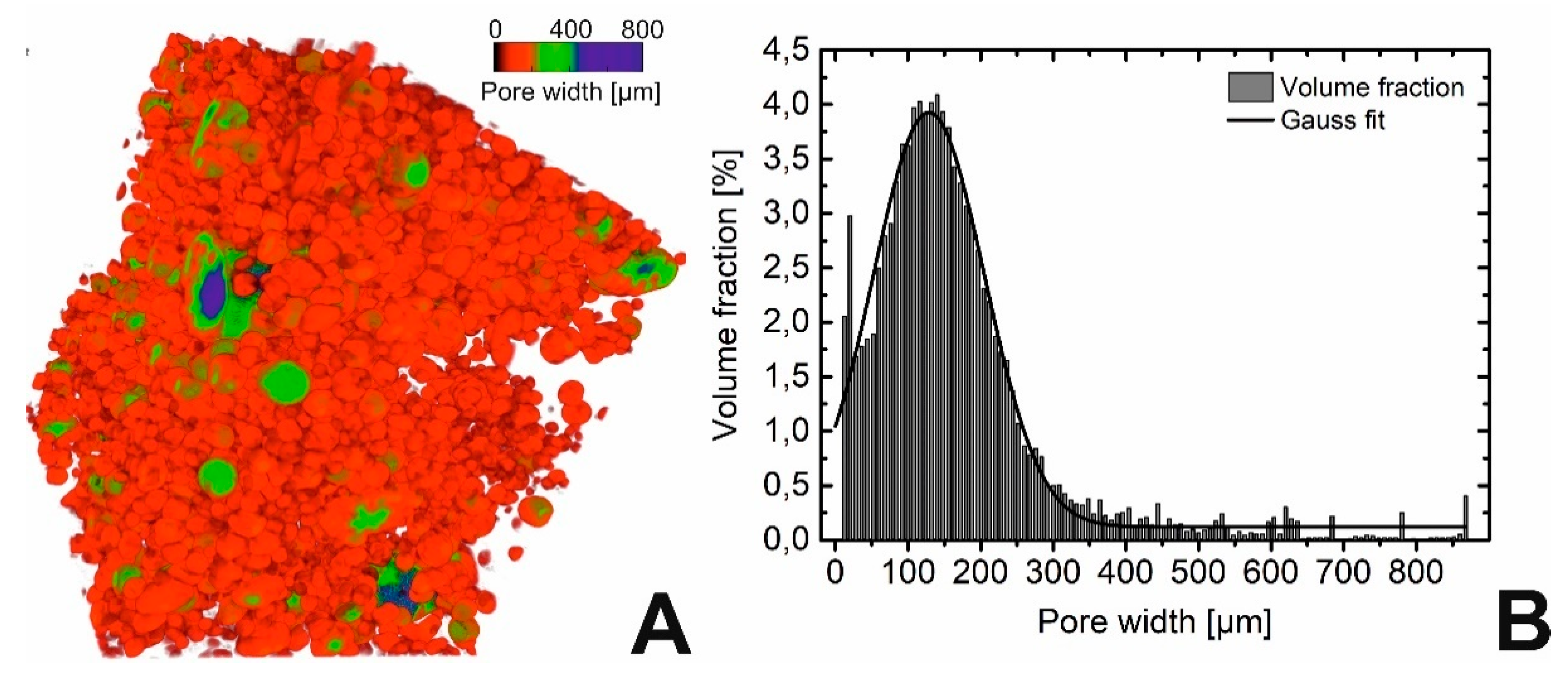
3.2. Foam Structure
3.3. Physical Properties
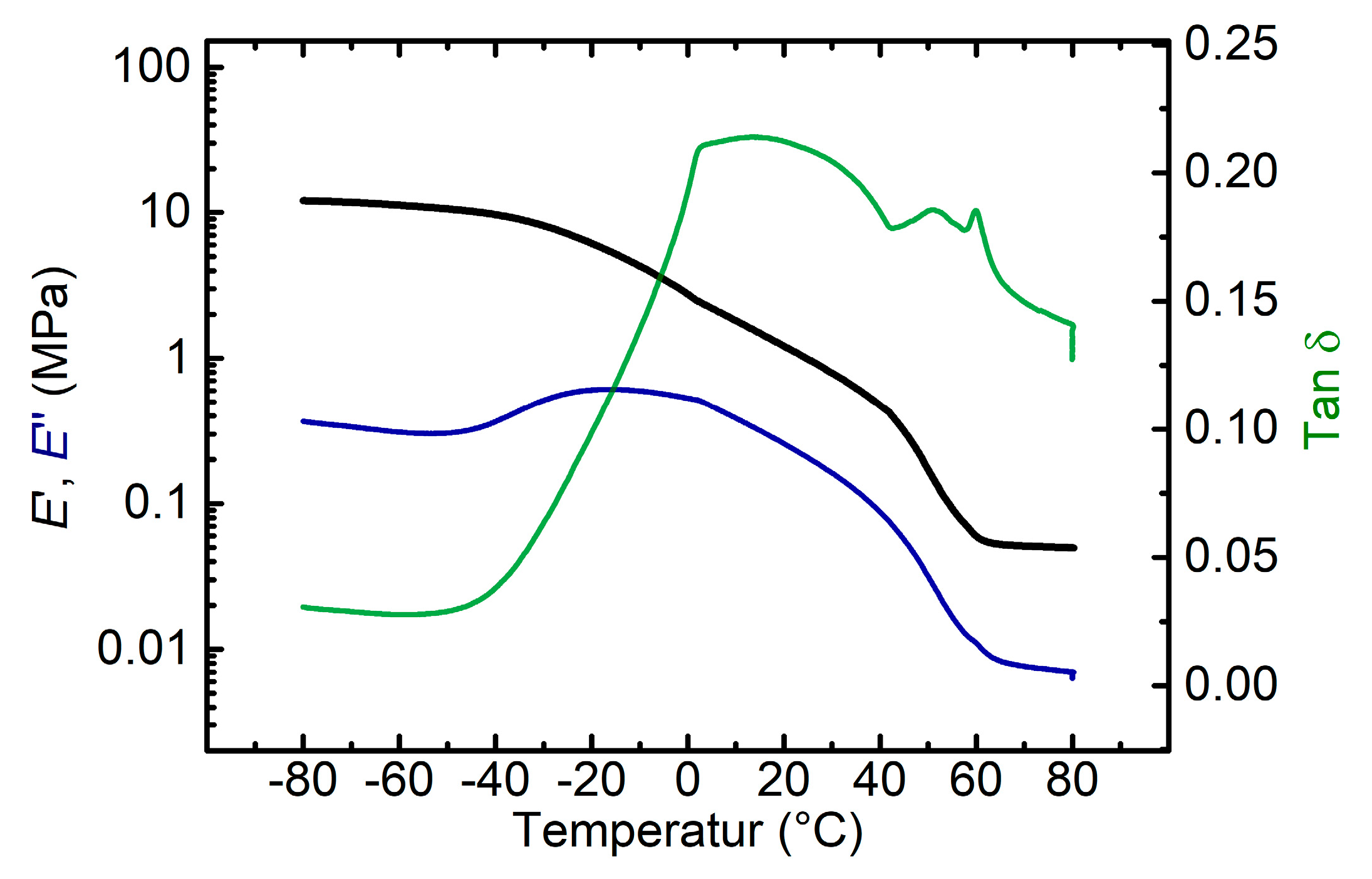
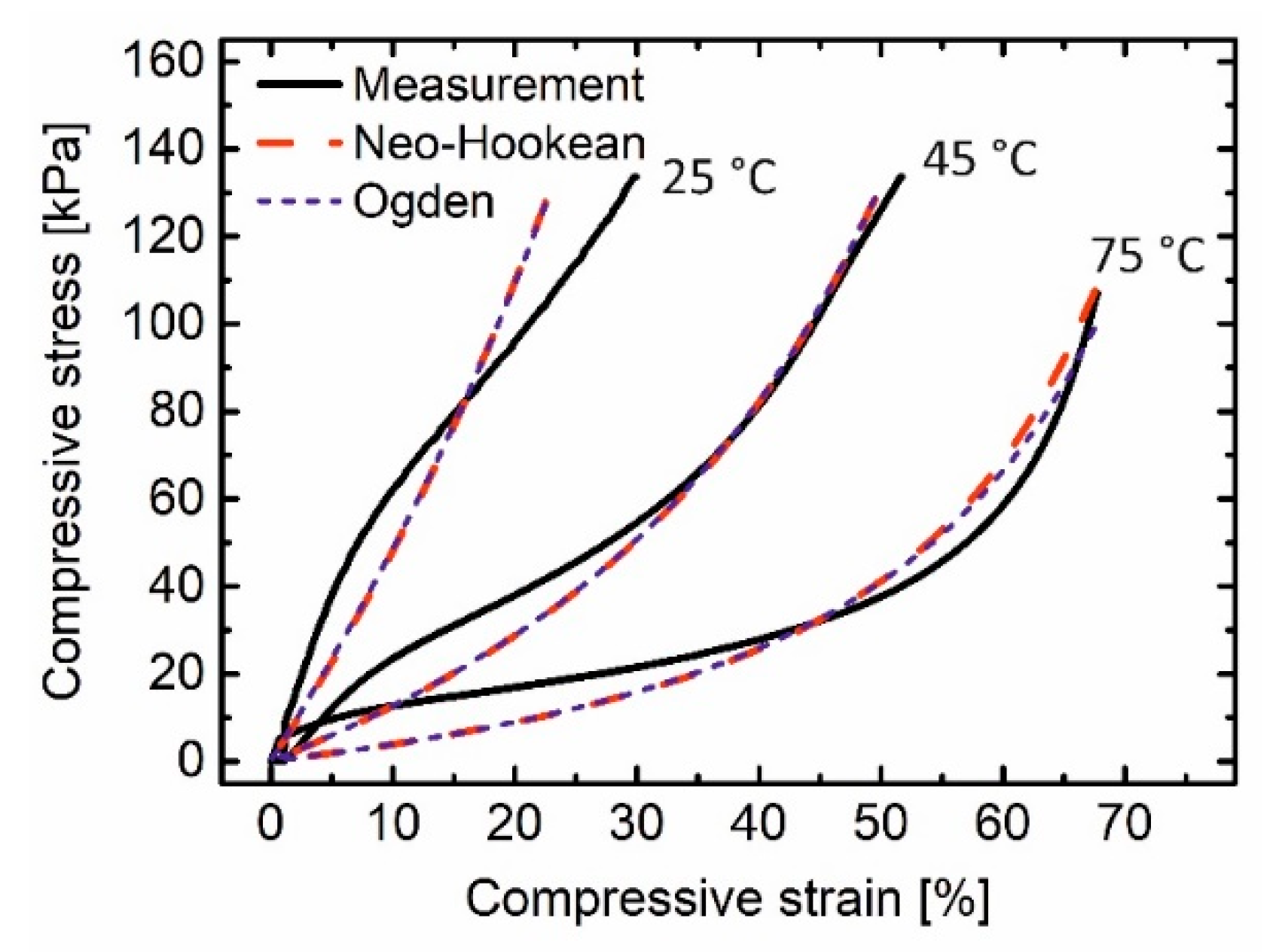
3.4. Thermomechanical Properties
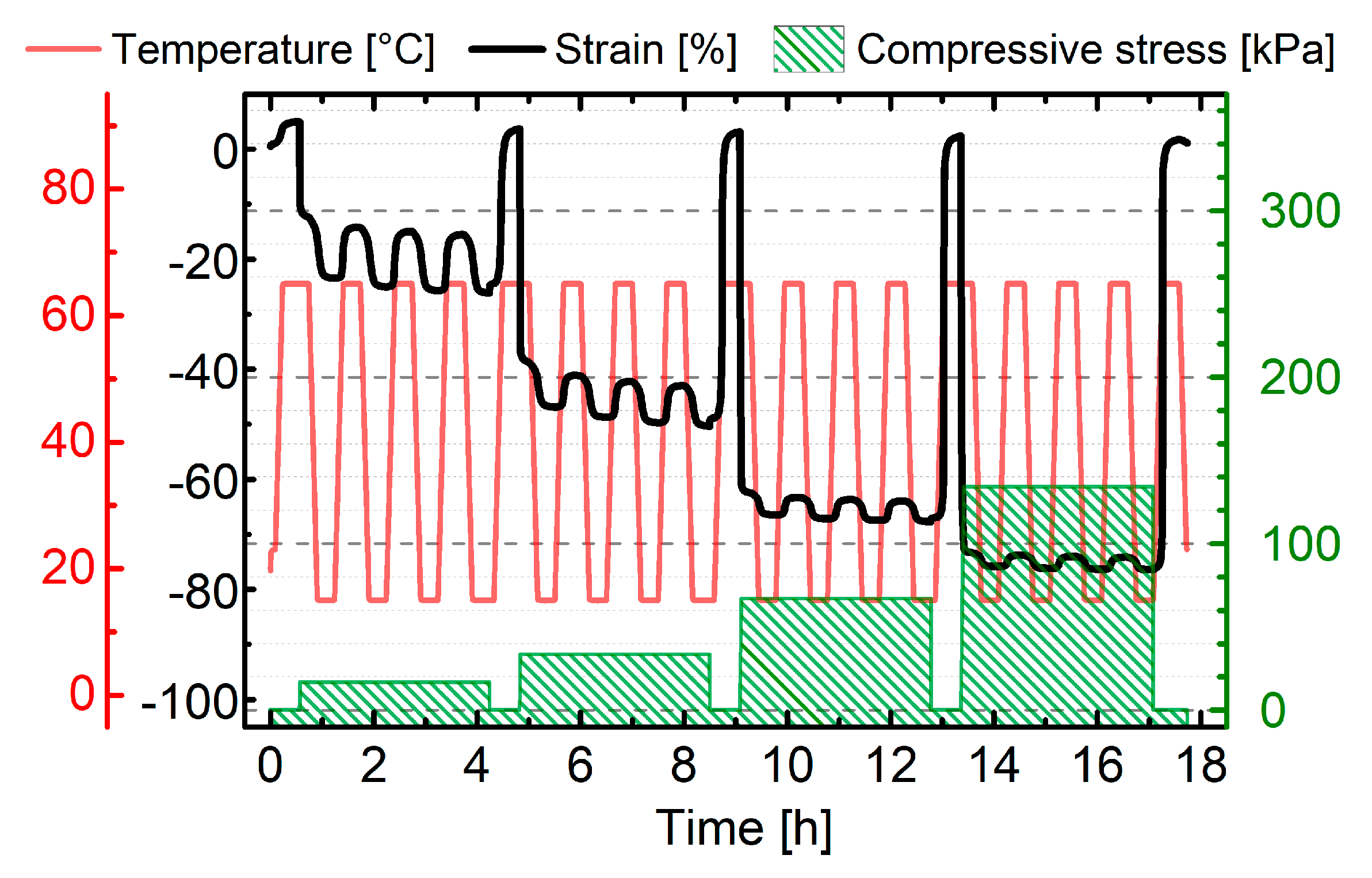
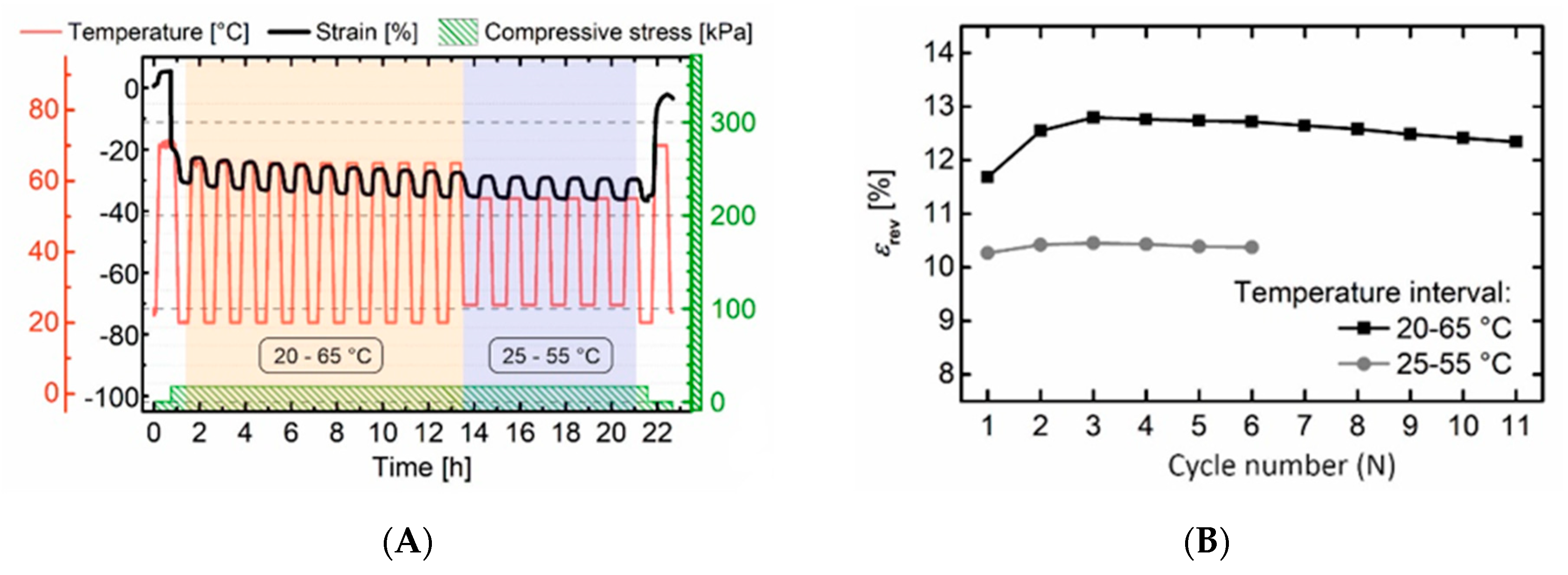
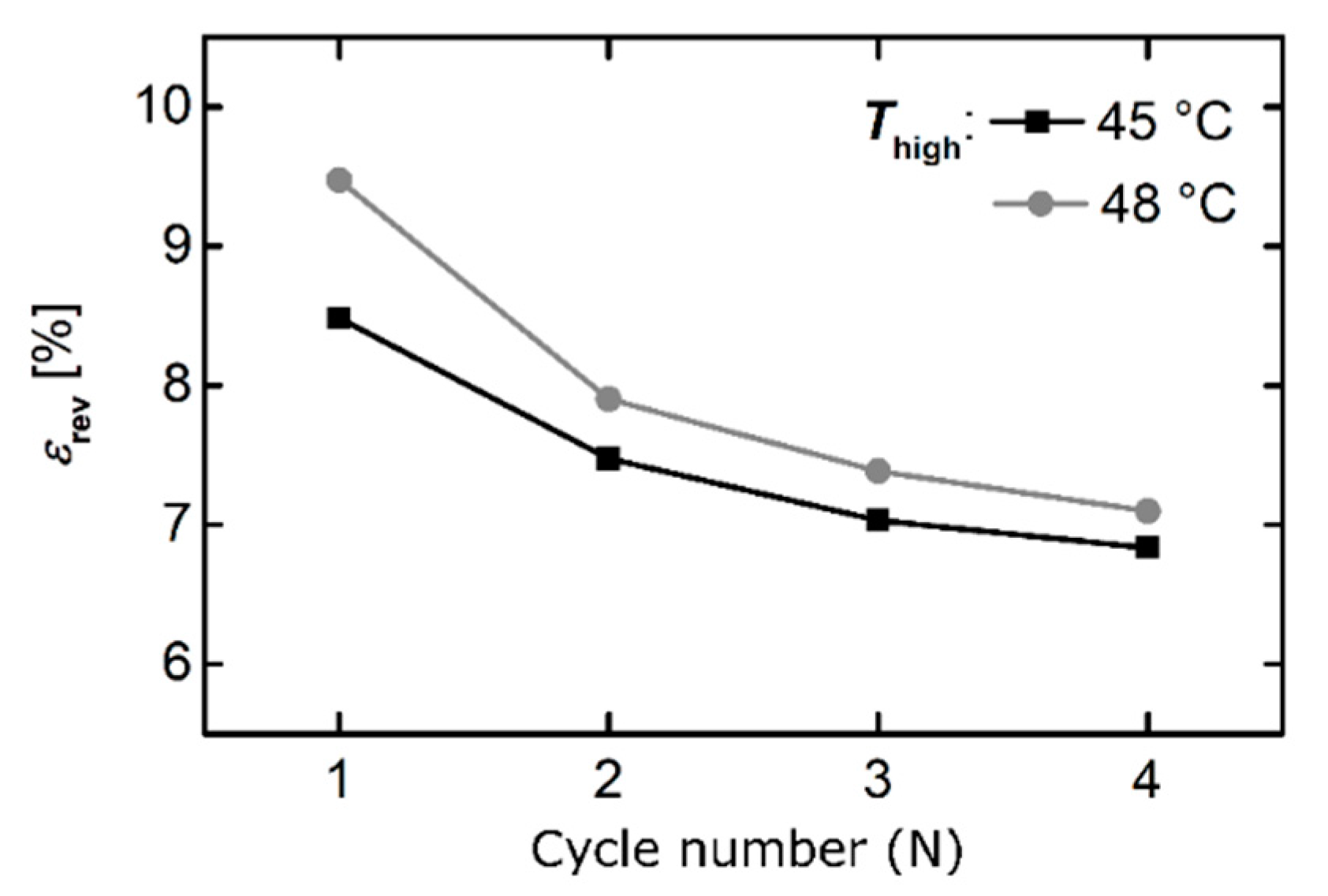
3.5. Demonstrator
3.6. Summary
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Qin, H.; Mather, P.T. Review of progress in shape-memory polymers. J. Mater. Chem. 2007, 17, 1543. [Google Scholar] [CrossRef]
- Pretsch, T. Review on the functional determinants and durability of shape memory polymers. Polymers 2010, 2, 120–158. [Google Scholar] [CrossRef]
- Pilate, F.; Toncheva, A.; Dubois, P.; Raquez, J.-M. Shape-memory polymers for multiple applications in the materials world. Eur. Polym. J. 2016, 80, 268–294. [Google Scholar] [CrossRef]
- Karger-Kocsis, J.; Kéki, S. Review of progress in shape memory epoxies and their composites. Polymers 2017, 10, 34. [Google Scholar] [CrossRef]
- Sun, L.; Wang, T.X.; Chen, H.M.; Salvekar, A.V.; Naveen, B.S.; Xu, Q.; Weng, Y.; Guo, X.; Chen, Y.; Huang, W.M. A brief review of the shape memory phenomena in polymers and their typical sensor applications. Polymers 2019, 11, 1049. [Google Scholar] [CrossRef]
- Pretsch, T.; Jakob, I.; Müller, W. Hydrolytic degradation and functional stability of a segmented shape memory poly(ester urethane). Polym. Degrad. Stab. 2009, 94, 61–73. [Google Scholar] [CrossRef]
- Ji, F.L.; Hu, J.L.; Chui, S.S.-Y. Influences of phase composition and thermomechanical conditions on shape memory properties of segmented polyurethanes with amorphous reversible phase. Polym. Eng. Sci. 2012, 52, 1015–1026. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Y.; Xiong, Z.; Liu, X.; Na, H.; Zhang, R.; Zhu, J. Highly recoverable rosin-based shape memory polyurethanes. J. Mater. Chem. A 2013, 1, 3263. [Google Scholar] [CrossRef]
- Li, F.; Zhang, X.; Hou, J.; Xu, M.; Luo, X.; Ma, D.; Kim, B.K. Studies on Thermally stimulated shape memory effect of segmented polyurethanes. J. Appl. Polym. Sci. 1997, 64, 1511–1516. [Google Scholar] [CrossRef]
- Jeong, H.M.; Lee, S.Y.; Kim, B.K. Shape memory polyurethane containing amorphous reversible phase. J. Mater. Sci. 2000, 35, 1579–1583. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Yuen, C.-W.; Chan, L.; Zhuo, H. Triple shape memory effect in multiple crystalline polyurethanes. Polym. Adv. Technol. 2010, 21, 377–380. [Google Scholar] [CrossRef]
- Chung, Y.-C.; Khiem Nguyen, D.; Won Choi, J.; Chul Chun, B. The effect of soft segment content and linker length on shape recovery and mechanical properties of laterally linked polyurethane copolymer. J. Appl. Polym. Sci. 2011, 120, 2063–2073. [Google Scholar] [CrossRef]
- Pretsch, T.; Müller, W. Shape memory poly(ester urethane) with improved hydrolytic stability. Polym. Degrad. Stab. 2010, 95, 880–888. [Google Scholar] [CrossRef]
- Wang, W.; Jin, Y.; Ping, P.; Chen, X.; Jing, X.; Su, Z. structure evolution in segmented poly(ester urethane) in shape-memory process. Macromolecules 2010, 43, 2942–2947. [Google Scholar] [CrossRef]
- Fritzsche, N.; Pretsch, T. Programming of temperature-memory onsets in a semicrystalline polyurethane elastomer. Macromolecules 2014, 47, 5952–5959. [Google Scholar] [CrossRef]
- Mirtschin, N.; Pretsch, T. Programming of one- and two-step stress recovery in a poly(ester urethane). Polymers 2017, 9, 98. [Google Scholar] [CrossRef]
- Shirole, A.; Perotto, C.U.; Balog, S.; Weder, C. Tailoring the shape memory properties of segmented poly(ester urethanes) via blending. ACS Appl. Mater. Interfaces 2018, 10, 24829–24839. [Google Scholar] [CrossRef]
- Chalissery, D.; Pretsch, T.; Staub, S.; Andrä, H. additive manufacturing of information carriers based on shape memory polyester urethane. Polymers 2019, 11, 1005. [Google Scholar] [CrossRef]
- Ji, F.L.; Hu, J.L.; Li, T.C.; Wong, Y.W. Morphology and shape memory effect of segmented polyurethanes. Part 1: With crystalline reversible phase. Polymer 2007, 48, 5133–5145. [Google Scholar] [CrossRef]
- Pretsch, T. Triple-shape properties of a thermoresponsive poly(ester urethane). Smart Mater. Struct. 2010, 19, 015006. [Google Scholar] [CrossRef]
- Ping, P.; Wang, W.; Chen, X.; Jing, X. Poly(caprolactone) polyurethane and its shape-memory property. Biomacromolecules 2005, 6, 587–592. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Hu, J.; Liu, Y.; Liem, H.; Zhu, Y.; Meng, Q. Effect of molecular weight on shape memory behavior in polyurethane films. Polym. Int. 2007, 56, 1128–1134. [Google Scholar] [CrossRef]
- Mondal, S.; Hu, J.L. Studies of shape memory property on thermoplastic segmented polyurethanes: Influence of PEG 3400. J. Elastomers Plast. 2007, 39, 81–91. [Google Scholar] [CrossRef]
- Raquez, J.-M.; Vanderstappen, S.; Meyer, F.; Verge, P.; Alexandre, M.; Thomassin, J.-M.; Jérôme, C.; Dubois, P. Design of cross-linked semicrystalline poly(ε-caprolactone)-based networks with one-way and two-way shape-memory properties through Diels-Alder reactions. Chem. Eur. J. 2011, 17, 10135–10143. [Google Scholar] [CrossRef] [PubMed]
- Behl, M.; Kratz, K.; Zotzmann, J.; Nöchel, U.; Lendlein, A. Reversible bidirectional shape-memory polymers. Adv. Mater. 2013, 25, 4466–4469. [Google Scholar] [CrossRef]
- Behl, M.; Kratz, K.; Noechel, U.; Sauter, T.; Lendlein, A. Temperature-memory polymer actuators. Proc. Natl. Acad. Sci. USA 2013, 110, 12555–12559. [Google Scholar] [CrossRef]
- Bothe, M.; Pretsch, T. Bidirectional actuation of a thermoplastic polyurethane elastomer. J. Mater. Chem. A 2013, 1, 14491. [Google Scholar] [CrossRef]
- Chung, T.; Romo-Uribe, A.; Mather, P.T. Two-way reversible shape memory in a semicrystalline network. Macromolecules 2008, 41, 184–192. [Google Scholar] [CrossRef]
- Bothe, M.; Pretsch, T. Two-way shape changes of a shape-memory poly(ester urethane). Macromol. Chem. Phys. 2012, 213, 2378–2385. [Google Scholar] [CrossRef]
- Song, H.; Fang, Z.; Jin, B.; Pan, P.; Zhao, Q.; Xie, T. Synergetic chemical and physical programming for reversible shape memory effect in a dynamic covalent network with two crystalline phases. ACS Macro Lett. 2019, 8, 682–686. [Google Scholar] [CrossRef]
- Fan, L.F.; Huang, Y.N.; Rong, M.Z.; Zhang, M.Q. A simple and universal strategy for preparing external stress-free two-way shape memory polymers by making use of the chemical crosslinkages derived from peroxide initiator. Express Polym. Lett. 2020, 14, 295–308. [Google Scholar] [CrossRef]
- Delaey, J.; Dubruel, P.; van Vlierberghe, S. Shape-memory polymers for biomedical applications. Adv. Funct. Mater. 2020, 1909047. [Google Scholar] [CrossRef]
- Scalet, G. Two-way and multiple-way shape memory polymers for soft robotics: An overview. Actuators 2020, 9, 10. [Google Scholar] [CrossRef]
- Ke, D.; Chen, Z.; Momo, Z.Y.; Jiani, W.; Xuan, C.; Xiaojie, Y.; Xueliang, X. Recent advances of two-way shape memory polymers and four-dimensional printing under stress-free conditions. Smart Mater. Struct. 2020, 29, 23001. [Google Scholar] [CrossRef]
- Sokolowski, W.M.; Chmielewski, A.B.; Hayashi, S.; Yamada, T. Cold hibernated elastic memory (CHEM) self-deployable structures. In Proceedings of the Smart Structures and Materials 1999: Electroactive Polymer Actuators and Devices, 1999 Symposium on Smart Structures and Materials, Newport Beach, CA, USA, 1 March 1999; Bar-Cohen, Y., Ed.; SPIE: Bellingham, WA, USA, 1999; pp. 179–185. [Google Scholar]
- Tobushi, H.; Okumura, K.; Endo, M.; Hayashi, S. Thermomechanical properties of polyurethane-shape memory polymer foam. J. Intell. Mater. Syst. Struct. 2001, 12, 283–287. [Google Scholar] [CrossRef]
- Tobushi, H.; Shimada, D.; Hayashi, S.; Endo, M. Shape fixity and shape recovery of polyurethane shape-memory polymer foams. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2003, 217, 135–143. [Google Scholar] [CrossRef]
- Hasan, S.M.; Nash, L.D.; Maitland, D.J. Porous shape memory polymers: Design and applications. J. Polym. Sci. Part B Polym. Phys. 2016, 54, 1300–1318. [Google Scholar] [CrossRef]
- Baker, R.M.; Henderson, J.H.; Mather, P.T. Shape memory poly(ε-caprolactone)-co-poly(ethylene glycol) foams with body temperature triggering and two-way actuation. J. Mater. Chem. B 2013, 1, 4916. [Google Scholar] [CrossRef]
- Lu, L.; Cao, J.; Li, G. A polycaprolactone-based syntactic foam with bidirectional reversible actuation. J. Appl. Polym. Sci. 2017, 134, 45225. [Google Scholar] [CrossRef]
- Zharinova, E.; Heuchel, M.; Weigel, T.; Gerber, D.; Kratz, K.; Lendlein, A. Water-blown polyurethane foams showing a reversible shape-memory effect. Polymers 2016, 8, 412. [Google Scholar] [CrossRef]
- D’Agostino, D.; Zangheri, P.; Castellazzi, L. Towards nearly zero energy buildings in europe: A focus on retrofit in non-residential buildings. Energies 2017, 10, 117. [Google Scholar] [CrossRef]
- Barrett, R.M.; Barrett, R.P. Thermally Adaptive Building Coverings: Theory and Application. In Volume 2: Modeling, Simulation and Control; Bio-Inspired Smart Materials and Systems; Energy Harvesting, Proceedings of the ASME 2016 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Stowe, VT, USA, 28–30 September 2016; Paper No. SMASIS2016-9014, V002T06A001; American Society of Mechanical Engineers: New York, NY, USA, 2016; ISBN 978-0-7918-5049-7. [Google Scholar]
- Cui, H.; Overend, M. A review of heat transfer characteristics of switchable insulation technologies for thermally adaptive building envelopes. Energy Build. 2019, 199, 427–444. [Google Scholar] [CrossRef]
- Kimber, M.; Clark, W.W.; Schaefer, L. Conceptual analysis and design of a partitioned multifunctional smart insulation. Appl. Energy 2014, 114, 310–319. [Google Scholar] [CrossRef]
- Ghosh, A.; Norton, B. Advances in switchable and highly insulating autonomous (self-powered) glazing systems for adaptive low energy buildings. Renew. Energy 2018, 126, 1003–1031. [Google Scholar] [CrossRef]
- Loonen, R.C.G.M.; Trčka, M.; Cóstola, D.; Hensen, J.L.M. Climate adaptive building shells: State-of-the-art and future challenges. Renew. Sustain. Energy Rev. 2013, 25, 483–493. [Google Scholar] [CrossRef]
- Favoino, F.; Jin, Q.; Overend, M. Design and control optimisation of adaptive insulation systems for office buildings. Part 1: Adaptive technologies and simulation framework. Energy 2017, 127, 301–309. [Google Scholar] [CrossRef]
- Clifford, D.T.; Zupan, R.J.; Brigham, J.C.; Beblow, R.V.; Whittock, M.; Davis, N. Application of the dynamic characteristics of shape-memory polymers to climate adaptive building facades. In Proceedings of the 12th Conference of Advanced Building Skins, Bern, Switzerland, 2–3 October 2017; Advanced Building Skins GmbH: Lucerne, Switzerland, 2017. [Google Scholar]
- Yoon, J. Design-to-fabrication with thermo-responsive shape memory polymer applications for building skins. Archit. Sci. Rev. 2020, 1–15. [Google Scholar] [CrossRef]
- Corigliano, A.; Rizzi, E.; Papa, E. Experimental characterization and numerical simulations of a syntactic-foam/glass-fibre composite sandwich. Compos. Sci. Technol. 2000, 60, 2169–2180. [Google Scholar] [CrossRef]
- Díaz, A.; Katsarava, R.; Puiggalí, J. Synthesis, properties and applications of biodegradable polymers derived from diols and dicarboxylic acids: From polyesters to poly(ester amide)s. Int. J. Mol. Sci. 2014, 15, 7064–7123. [Google Scholar] [CrossRef]
- Debuissy, T.; Pollet, E.; Avérous, L. Synthesis of potentially biobased copolyesters based on adipic acid and butanediols: Kinetic study between 1,4- and 2,3-butanediol and their influence on crystallization and thermal properties. Polymer 2016, 99, 204–213. [Google Scholar] [CrossRef]
- German Institute for Standardization e.V. DIN EN ISO 4629-2 Binders for Paints and Varnishes—Determination of Hydroxyl Value—Part 2: Titrimetric Method Using a Catalyst; Beuth Verlag GmbH: Berlin, Germany, 2016. [Google Scholar]
- German Institute for Standardization e.V. DIN EN ISO 2114 Plastics (Polyester Resins) and Paints Varnishes (Binders)—Determination of Partial Acid Value and Total Acid Value; Beuth Verlag GmbH: Berlin, Germany, 2002. [Google Scholar]
- Zhao, H.; Hao, T.-H.; Hu, G.-H.; Shi, D.; Huang, D.; Jiang, T.; Zhang, Q.-C. Preparation and characterization of polyurethanes with cross-linked siloxane in the side chain by sol-gel reactions. Materials 2017, 10, 247. [Google Scholar] [CrossRef] [PubMed]
- German Institute for Standardization e.V. DIN EN 12664 Thermal Performance of Building Materials and Products—Determination of Thermal Resistance by Means of Guarded Hot Plate and Heat Flow Meter Methods—Dry and Moist Products with Medium and Low Thermal Resistance; Beuth Verlag GmbH: Berlin, Germany, 2001. [Google Scholar]
- Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Philos. Trans. R. Soc. Lond. A 1951, 243, 251–288. [Google Scholar] [CrossRef]
- Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. A 1948, 241, 379–397. [Google Scholar] [CrossRef]
- Kilian, H.-G.; Enderle, H.F.; Unseld, K. The use of the van der Waals model to elucidate universal aspects of structure-property relationships in simply extended dry and swollen rubbers. Colloid Polym. Sci. 1986, 264, 866–876. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Pulla, S.S.; Souri, M.; Karaca, H.E.; Lu, Y.C. Characterization and strain-energy-function-based modeling of the thermomechanical response of shape-memory polymers. J. Appl. Polym. Sci. 2015, 132. [Google Scholar] [CrossRef]
- Esposito, M.; Sorrentino, L.; Krejčí, P.; Davino, D. Modelling of a visco-hyperelastic polymeric foam with a continuous to discrete relaxation spectrum approach. J. Mech. Phys. Solids 2020, 142, 104030. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Clarendon Press: Oxford, UK; New York, NY, USA, 2009; ISBN 0198570279. [Google Scholar]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Proc. R. Soc. Lond. A 1972, 326, 565–584. [Google Scholar] [CrossRef]
- Tobajas, R.; Ibarz, E.; Gracia, L. A comparative study of hyperelastic constitutive models to characterize the behavior of a polymer used in automotive engines. In Proceedings of the 2nd International Electronic Conference on Materials, 2–16 May 2016; Available online: http://www.sciforum.net/conference/ecm-2 (accessed on 19 August 2020).
- Gan, Z.; Abe, H.; Doi, Y. Temperature-Induced Polymorphic Crystals of Poly(butylene adipate). Macromol. Chem. Phys. 2002, 203, 2369–2374. [Google Scholar] [CrossRef]
- Endres, E.; Kleser, J. Wärmedämmstoffe aus Polyurethan-Hartschaum Herstellung-Anwendung-Eigenschaften; IVPU–Industrieverband Polyurethan-Hartschaum e.V.: Stuttgart, Germany, 2008. [Google Scholar]
- Federation of European Rigid Polyurethane Foam Associations. Thermal Insulation Materials Made of Rigid Polyurethane Foam (PUR/PIR)Properties—Manufacture. Report N°1; Federation of European Rigid Polyurethane Foam Associations: Brussels, Belgium, 2006. [Google Scholar]
- Rashmi, B.J.; Rusu, D.; Prashantha, K.; Lacrampe, M.F.; Krawczak, P. Development of water-blown bio-based thermoplastic polyurethane foams using bio-derived chain extender. J. Appl. Polym. Sci. 2013, 128, 292–303. [Google Scholar] [CrossRef]
- Lee, S.H.; Jang, M.K.; Hee Kim, S.; Kim, B.K. Shape memory effects of molded flexible polyurethane foam. Smart Mater. Struct. 2007, 16, 2486–2491. [Google Scholar] [CrossRef]
- Frisch, H.L.; Frisch, K.C.; Klempner, D. Glass transitions of topologically interpenetrating polymer networks. Polym. Eng. Sci. 1974, 14, 646–650. [Google Scholar] [CrossRef]
- Schellenberg, J.; Wallis, M. Dependence of Thermal Properties of Expandable Polystyrene Particle Foam on Cell Size and Density. J. Cell. Plast. 2010, 46, 209–222. [Google Scholar] [CrossRef]
- Thirumal, M.; Khastgir, D.; Singha, N.K.; Manjunath, B.S.; Naik, Y.P. Effect of foam density on the properties of water blown rigid polyurethane foam. J. Appl. Polym. Sci. 2008, 108, 1810–1817. [Google Scholar] [CrossRef]
- Adnan, S.; Tuan Noor, M.T.I.; ‘Ain, N.H.; Devi, K.P.P.; Mohd, N.S.; Shoot Kian, Y.; Idris, Z.B.; Campara, I.; Schiffman, C.M.; Pietrzyk, K.; et al. Impact of the hard-segment concentration on highly resilient polyurethane foams based on palm olein polyol. J. Appl. Polym. Sci. 2017, 134, 45440. [Google Scholar] [CrossRef]
- Hawkins, M.C.; O’Toole, B.; Jackovich, D. Cell Morphology and Mechanical Properties of Rigid Polyurethane Foam. J. Cell. Plast. 2005, 41, 267–285. [Google Scholar] [CrossRef]
- Obi, B. Polymeric Foams Structure-Property-Performance: A Design Guide; Elsevier Science: Amsterdam, The Netherlands, 2017; ISBN 9781455777563. [Google Scholar]
- Linul, E.; Vălean, C.; Linul, P.-A. Compressive Behavior of Aluminum Microfibers Reinforced Semi-Rigid Polyurethane Foams. Polymers 2018, 10, 1298. [Google Scholar] [CrossRef]
- BASF SE. Thermoplastische Polyurethan-Elastomere (TPU). Elastollan—Materialeigenschaften; BASF SE: Ludwigshafen am Rhein, Germany, 2017. [Google Scholar]
- Covestro Solution Center. Thermische Eigenschaften. Available online: https://solutions.covestro.com/de/highlights/artikel/thema/produkttechnologie/thermische-eigenschaften-tpu (accessed on 31 July 2020).
- Pandini, S.; Dioni, D.; Paderni, K.; Messori, M.; Toselli, M.; Bontempi, E.; Riccò, T. The two-way shape memory behaviour of crosslinked poly(ε-caprolactone) systems with largely varied network density. J. Intell. Mater. Syst. Struct. 2016, 27, 1388–1403. [Google Scholar] [CrossRef]
- Zhang, N.; Cao, B.; Wang, Z.; Zhu, Y.; Lin, B. A comparison of winter indoor thermal environment and thermal comfort between regions in Europe, North America, and Asia. Build. Environ. 2017, 117, 208–217. [Google Scholar] [CrossRef]
- Vincentz Network GmbH & Co. KG. Fassadenfarbe Verhindert Aufheizen der Fassade. Available online: https://www.farbeundlack.de/Wissenschaft-Technik/Anwendungsbereiche/Bautenfarben/Fassadenfarbe-verhindert-Aufheizen-der-Fassade (accessed on 31 July 2020).



| Polyester | Hydroxy Value (mg(KOH)·g−1) | Acid Value(mg(KOH)·g−1) | Mn1 (g·mol−1) | Tm,peak2 (°C) | ΔHm 3 (J·g−1) | Tc,peak4 (°C) | ΔHc 5 (J·g−1) |
|---|---|---|---|---|---|---|---|
| PDA | 32.0 | 0.2 | 3500 | 69 | 139 | 57 | 142 |
| PBA | 50.5 | 0.1 | 2220 | 47/52 | 87 | 32 | 75 |
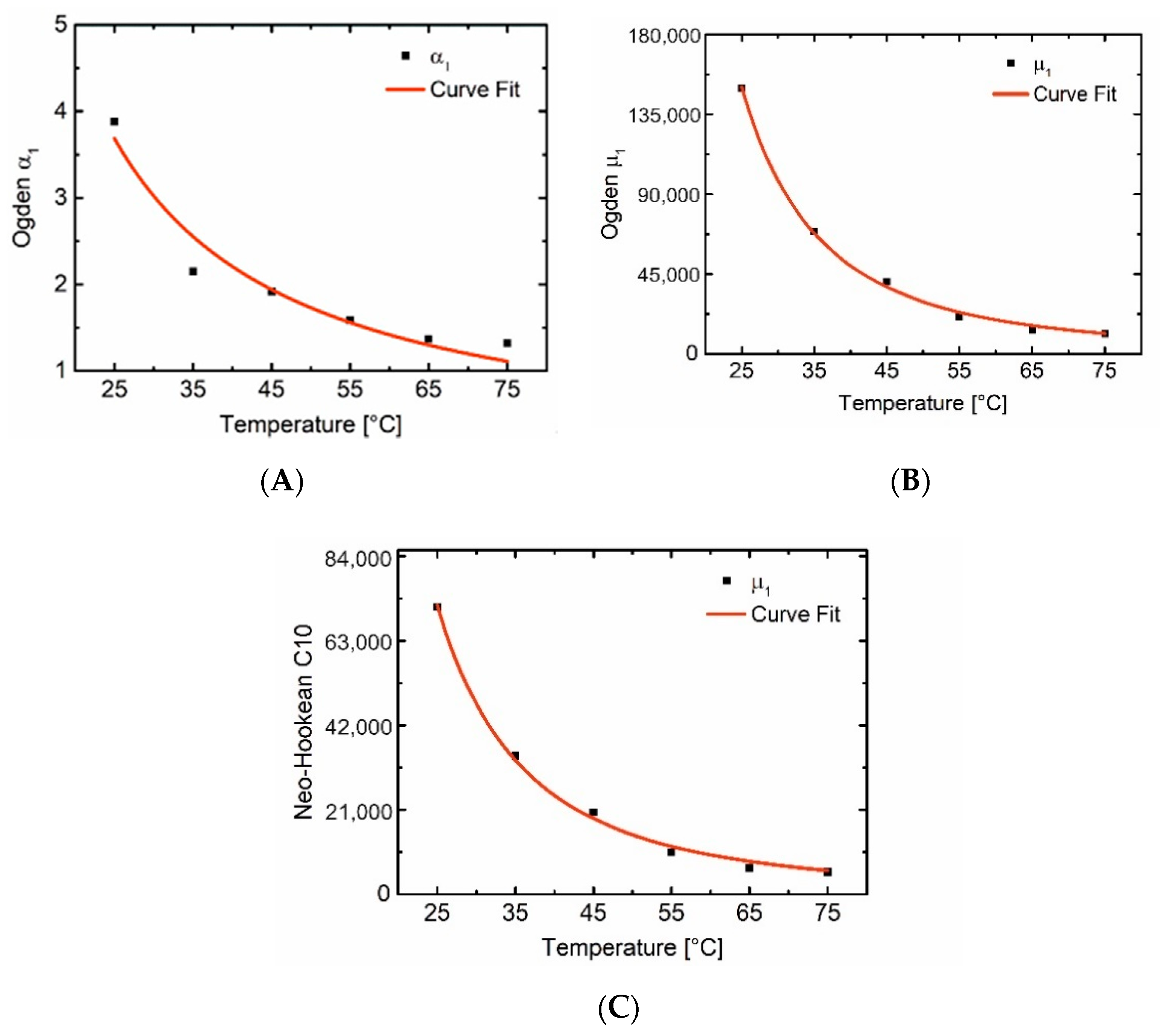
| Temperature (°C) | Ogden | R² | Neo-Hookean | R² | |
|---|---|---|---|---|---|
| µ1 | α1 | C10 | |||
| 25 | 149,753.0 | 3.9 | 0.9575 | 71,360.0 | 0.9589 |
| 35 | 69,164.4 | 2.1 | 0.9890 | 34,424.3 | 0.9889 |
| 45 | 40,593.3 | 1.9 | 0.9966 | 20,340.7 | 0.9966 |
| 55 | 20,800.7 | 1.6 | 0.9984 | 10,455.4 | 0.9976 |
| 65 | 13,008.8 | 1.4 | 0.9961 | 6480.9 | 0.9933 |
| 75 | 11,239.6 | 1.3 | 0.9929 | 5557.2 | 0.9897 |
| Model Parameter | a | b | R² |
|---|---|---|---|
| Ogden µ1 | 2.96 × 108 | −2.36 | 0.9982 |
| Ogden α1 | 124 × 06 | −1.09 | 0.9456 |
| Neo-Hookean C10 | 1.10 × 108 | −2.28 | 0.9973 |
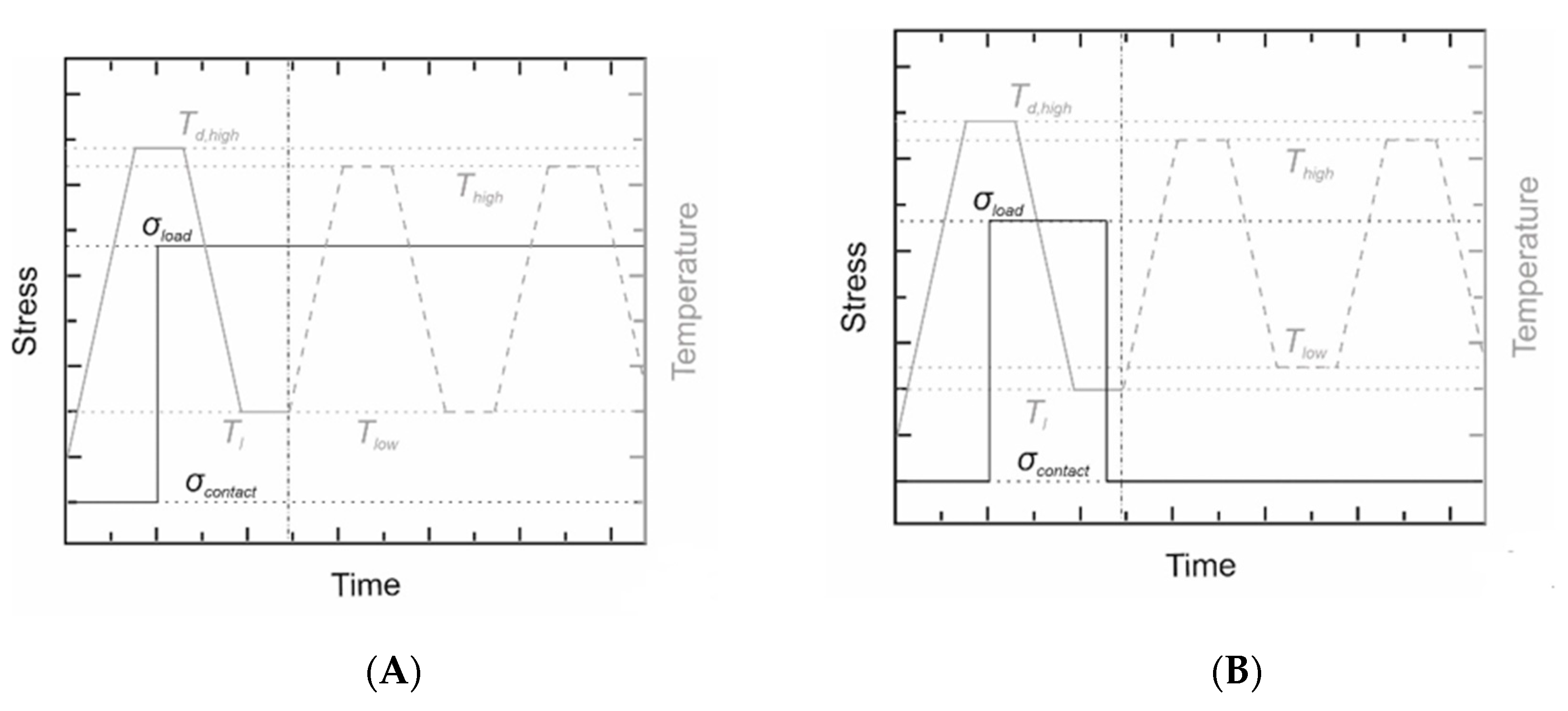
| Entry | Tlow (°C) | Thigh (°C) | tiso1 (min) | ΔT 2 (°C) | εTlow3 (%) | εrev (%) |
|---|---|---|---|---|---|---|
| 1 | 15 | 65 | 20 | 50 | 25.6 | 12.2 |
| 2 | 25 | 65 | 20 | 40 | 26.2 | 11.5 |
| 3 | 35 | 65 | 20 | 30 | 22.5 | 5.7 |
| 4 | 20 | 55 | 20 | 35 | 28.0 | 10.6 |
| 5 | 20 | 65 | 20 | 45 | 28.2 | 12.2 |
| 6 | 20 | 75 | 20 | 55 | 28.8 | 12.8 |
| Entry | Tlow (°C) | Thigh (°C) | tiso1 (min) | ΔT 2 (°C) | εTlow3 (%) | εrev (%) |
|---|---|---|---|---|---|---|
| 1 | 20 | 45 | 30 | 25 | 38.7 | 3.9 |
| 2 | 25 | 45 | 30 | 20 | 38.7 | 3.3 |
| 3 | 20 | 50 | 30 | 30 | 38.5 | 9.3 |
| 4 | 25 | 50 | 30 | 25 | 38.6 | 8.7 |
| 5 | 30 | 50 | 30 | 20 | 38.3 | 7.3 |
| 6 | 25 | 55 | 40 | 30 | 34.0 | 11.4 |
| 7 | 30 | 55 | 50 | 25 | 34.5 | 10.8 |
| 8 | 35 | 55 | 60 | 20 | 33.8 | 9.0 |
| Entry | σload (kPa) 1 | Thigh (°C) | εTlow 2 (%) | εThigh 2 (%) | εrev (%) |
|---|---|---|---|---|---|
| 1 | 16.7 | 42 | 32.4 | 28.3 | 6.1 |
| 2 | 16.7 | 45 | 21.2 | 15.4 | 7.4 |
| 3 | 16.7 | 48 | 12.7 | 7.9 | 5.5 |
| 4 | 16.7 | 51 | 8.7 | 4.8 | 4.2 |
| 5 | 16.7 | 54 | 6.7 | 3.2 | 3.7 |
| 6 | 33.3 | 42 | 55.3 | 51.7 | 8.2 |
| 7 | 33.3 | 45 | 37.6 | 31.0 | 10.6 |
| 8 | 33.3 | 48 | 16.9 | 11.4 | 6.7 |
| 9 | 33.3 | 51 | 9.8 | 5.5 | 4.7 |
| 10 | 33.3 | 54 | 7.3 | 3.6 | 4.0 |
| 11 | 50.0 | 42 | 65.6 | 64.2 | 4.1 |
| 12 | 50.0 | 45 | 61.8 | 58.7 | 7.9 |
| 13 | 50.0 | 48 | 29.3 | 22.5 | 9.7 |
| Polymer Type | Foaming Process | εrev (%) | Tlow (°C) | Thigh (°C) | Actuation Mode | Reference |
|---|---|---|---|---|---|---|
| PCL-co-PEG | porogen leaching | 15 | −20 | 80 | compression/constant load | [39] |
| Crosslinked PCL | incorporation of glass microspheres | N/A | N/A | N/A | compression/load-free | [40] |
| Crosslinked PCL | incorporation of glass microspheres | >10 | 0 | 59 | elongation */load-free | [40] |
| PCL-PU | water-blown | 12 | 10 | 50 | compression/load-free | [41] |
| PEUU | water-blown | >13 | 20 | 65 | compression/constant load | current work |
| PEUU | water-blown | >10 | 25 | 55 | compression/load-free | current work |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walter, M.; Friess, F.; Krus, M.; Zolanvari, S.M.H.; Grün, G.; Kröber, H.; Pretsch, T. Shape Memory Polymer Foam with Programmable Apertures. Polymers 2020, 12, 1914. https://doi.org/10.3390/polym12091914
Walter M, Friess F, Krus M, Zolanvari SMH, Grün G, Kröber H, Pretsch T. Shape Memory Polymer Foam with Programmable Apertures. Polymers. 2020; 12(9):1914. https://doi.org/10.3390/polym12091914
Chicago/Turabian StyleWalter, Mario, Fabian Friess, Martin Krus, Seyed Mohammad Hassan Zolanvari, Gunnar Grün, Hartmut Kröber, and Thorsten Pretsch. 2020. "Shape Memory Polymer Foam with Programmable Apertures" Polymers 12, no. 9: 1914. https://doi.org/10.3390/polym12091914
APA StyleWalter, M., Friess, F., Krus, M., Zolanvari, S. M. H., Grün, G., Kröber, H., & Pretsch, T. (2020). Shape Memory Polymer Foam with Programmable Apertures. Polymers, 12(9), 1914. https://doi.org/10.3390/polym12091914






